Калькулятор степеней онлайн | umath.ru

Калькулятор степеней поможет просто и быстро возвести число в степень онлайн. При этом показатель степени может быть как положительным, так и отрицательным!

Что такое степень числа?

Как возвести число в степень?

Чтобы понять, как возводить число в степень, рассмотрим несколько простых примеров.

Возведём в пятую степень число то есть вычислим значение выражения По определению, данному выше,

Вычислим, чему равно то есть чему равно число возведённое в третью степень.

Отрицательный показатель степени

Показатели степени могут быть не только положительными, но и отрицательными.

   

Например,

   

а

   

Как пользоваться калькулятором степеней

Калькулятор помогает возводить число в степень онлайн. Основанием степени могут быть любые целые числа и десятичные дроби. Показатель степени тоже может быть любой десятичной дробью, однако следует помнить о том, что для отрицательных чисел не определена операция возведения в нецелую степень.

При записи дробных чисел можно использовать как точку, так и запятую. В ответе большие числа записываются в так называемом «научном формате», то есть число выглядит как <число>e<количество нулей>. Например, , а

umath.ru

Онлайн калькулятор дробей с решением со степенями со скобками с буквами

Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и  десятичных дробей.
Основные возможности:

  1. Сложение, вычитание, деление и умножение дробей.
  2. Расчет дробей с подробнейшим решением.
  3. Расчет дробей со степенями, скобками и буквами.
  4. Сокращение дробей.
  5. Поддержка до трех дробей онлайн.

На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Калькулятор умеет:

  1. Вносить целую часть дроби в числитель для смешанных дробей.
  2. Расчет дробей со скобками- поддержка до двух уровней вложенности скобок.
  3. Расчет дробей со степенями — степенью может быть только число.
  4. Расчет дробей с буквами — любые анг. буквы или символы.
  5. Сокращение дробей — только для дробей без букв.

Основные символы:

  1. * символ звездочки интерпретируется как умножение.
  2. / слеш интерпретируется как деление.
  3. + и — интерпретируются как сложение и вычитание.
  4. ^ символ интерпретируется как степень.
  5. ( ) символы интерпретируются как открывающаяся и закрывающаяся скобки.

Подробности:

  1. Между двумя буквами необязательно ставить знак умножения (если они умножаются). Пример вместо x*x можно написать xx.
  2. После знака степени ^ должно стоять число степени. Если оно отрицательно необходимо заключить его в скобки. Пример x^2+1 или x^(-2) +1.
  3. При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК.
  4. При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.

calculatori.ru

Калькулятор степеней онлайн: формула, примеры с решением

Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.

Основные действия со степенями

В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:

am × an = a(m+n).

Если разделить 134 на 132, то нам потребуется вычислить дробь вида:

(13 × 13 × 13 × 13) / (13 × 13).

Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:

am / an = a(m – n).

Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:

(am)n = a(m × n).

Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь:

154 / 154.

Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150. Следовательно:

154 / 154 = 150 = 1.

Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:

a0 = 1.

При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.

(8 × 8) / (8 × 8 × 8 × 8).

Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:

a-m

 = 1 / am

При этом для значения -1 правило трансформируется в элегантную формулу:

a-1 = 1 / a.

И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:

a(m/n) есть корень n-ной степени из am.

Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.

Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.

Примеры из реальной жизни

Депозит в банке

Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:

Рост = a × e(kt),

где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.

Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.

Школьная задача

Пусть в школьной задаче требуется построить график функции y = x

2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.

Заключение

Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.

bbf.ru

Математический калькулятор с расширенными возможностями.

Математический калькулятор онлайн

Незаменимый помощник для студентов и инженеров, позволяющий производить вычисления начиная с элементарной линейной математики и заканчивая дифференциальными исчислениями и основами метафизики. Расчет тригонометрических функций, логарифмов, факториалов, решение квадратных уравнений в поле комплексных чисел, вычисления биномиальных коэффициентов, расчет матриц, конвертация величин и построение графиков.

Стильный интерфейс бесплатного математического калькулятора прост и понятен, его не нужно устанавливать на компьютер, достаточно зайти на нашу страничку и можно комфортно им пользоваться.



Удобный и простой инженерный калькулятор с богатым арсеналом возможностей для математических расчетов и между тем с приятным и понятным интерфейсом, способен выполнять практически любые арифметические действия и сложные математические вычисления.

Инженерный калькулятор позволяет использовать много разных математических функций:
• решение гиперболических, тригонометрических и обратных тригонометрических функций:

• возведение в степень и извлечение корней:
• решение матриц и уравнений:
• построение графиков и конвертертация величин:
• вычисление логарифмов и экспоненты:
• дифференцирование и интегрирование функций:
• нахождение факториала, абсолютной величины числа, значения аргумента функции, биноминального коэффициента, наибольшего общего делителя, наименьшего общего кратного:
• Использование мнимой единицы при расчётах комплексных чисел:
• Выделение целой действительной части и исключение действительной части:
• Разложение числа на простые множители.

Инженерный калькулятор позволяет конвертировать физические величины разных систем измерений (масса, расстояние, время, компьютерные информационные единицы измерения и др. С возможностями нашего калькулятора вы сможете моментально перевести фунты в килограммы, мили в километры, секунды в часы и т.д.

Для выполнения математических расчетов, просто введите последовательность математических выражений в соответствующее поле и для получения результата нажмите на кнопку со знаком равенства.

Для построения графиков достаточно в поле ввода с помощью панели инструментов записать функцию и нажать на кнопку с изображением графика. Кнопка с надписью Unit предназначена для перехода в конвертер величин, для вычисления матриц нажмите на кнопку Matrix. В таблице указаны все клавиши (со значком * вызывается через дополнительную клавишу II) калькулятора и выполняемые ими операции.

Клавиша Символ Операция
pi pi Постоянная pi
е е Число Эйлера
% % Процент
( ) ( ) Открыть/Закрыть скобки
, , Запятая
sin sin(α) Синус угла
cos cos(β) Косинус
tan tan(y) Тангенс
sinh sinh() Гиперболический синус
cosh cosh() Гиперболический косинус
tanh tanh() Гиперболический тангенс
sin-1 asin() Обратный синус
cos-1 acos() Обратный косинус
tan-1 atan() Обратный тангенс
sinh-1 asinh() Обратный гиперболический синус
cosh-1 acosh() Обратный гиперболический косинус
tanh-1 atanh() Обратный гиперболический тангенс
x2 ^2 Возведение в квадрат
х3 ^3 Возведение в куб
xy ^ Возведение в степень
10x 10^() Возведение в степень по основанию 10
ex exp() Возведение в степень числа Эйлера
√x sqrt(x) Квадратный корень
3√x sqrt3(x) Корень 3-ей степени
y√x sqrt(x,y) Извлечение корня
log2x log2(x) Двоичный логарифм
log log(x) Десятичный логарифм
ln ln(x) Натуральный логарифм
logyx log(x,y) Логарифм
I / II Сворачивание/Вызов дополнительных функций
Unit Конвертер величин
Matrix Матрицы
Solve Уравнения и системы уравнений
изображение графика Построение графиков
* mod mod Деление с остатком
* ! ! Факториал
* i / j i / j Мнимая единица
* Re Re() Выделение целой действительной части
* Im Im() Исключение действительной части
* |x| abs() Модуль числа
* Arg arg() Аргумент функции
* nCr ncr() Биноминальный коэффициент
* gcd gcd() НОД
* lcm lcm() НОК
* sum sum() Суммарное значение всех решений
* fac factorize() Разложение на простые множители
* diff diff() Дифференцирование
* Deg Градусы
* Rad Радианы

Теперь, когда вам понадобится калькулятор, приходите на сайт и используйте бесплатный научный калькулятор.


ncor.ru

Калькулятор степеней — возвести в степень онлайн

Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.

Что такое натуральная степень числа?

Число p называют n-ой степенью числа a, если p равно числу a, умноженному само на себя n раз: p = an = a·...·a
n — называется показателем степени, а число a — основанием степени.

Как возвести число в натуральную степень?

Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:

Пример 1. Возвести число три в четвёртую степень. То есть необходимо вычислить 34
Решение: как было сказано выше, 34 = 3·3·3·3 = 81.
Ответ: 34 = 81.

Пример 2. Возвести число пять в пятую степень. То есть необходимо вычислить 55
Решение: аналогично, 55 = 5·5·5·5·5 = 3125.
Ответ: 55 = 3125.

Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.

Что такое отрицательная степень числа?

Отрицательная степень -n числа a — это единица, поделённая на a в степени n: a-n = .

При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.

Как возвести число в целую отрицательную степень?

Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.

Пример 1. Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2-4

Решение: как было сказано выше, 2-4 = = = 0.0625.

Ответ: 2-4 = 0.0625.

programforyou.ru

Решение примеров со степенями

Решение Преобразуем, степени в числителе по свойству , а степени из знаменателя поднимем в числитель, при этом они изменят знак:

   

Далее воспользуемся тем фактом, что при умножении степеней с одинаковыми основаниями показатели степеней складываются

   

Используя свойства степеней: и , получим:

   

   

ru.solverbook.com

Очень продвинутый онлайн калькулятор

Как Вы, наши уважаемые читатели и читательницы, уже могли догадаться, речь пойдет об онлайн калькуляторах, если быть точнее — об одном из самых полезных и, частенько, незаменимых изобретений человека, которое не так давно перекочевало в интернет.

Мы долго выбирали роль самого классного, удобного и полезного онлайн калькулятора и выбор пал на молодой вебдванольный сервис — Web20calc.

Вы, наверное, уже успели возмутиться относительно важности этой темы? Честно говоря, это Вы зря — калькулятор Windows ему совсем не ровня, а ближайшие соперники — типа eCalc, может и превосходят его в функционале, но стоят от 45 евро за копию и при этом устанавливаются на ПК или нетбук или Iphone, что нам не так и нужно.

Данный онлайн калькулятор может:

  • Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел). Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего).
  • Кроме тангенса, косинуса, синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса, арккотангенса и прочих.
  • Доступны в арсенале логарифмы, факториалы и другие интересные функции


Но самое главное — данный онлайн калькулятор умеет строить графики!!! Если не верите, смотрим на скриншот:

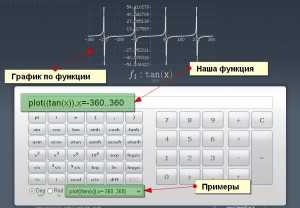
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или  буквенное представление этой функции (Plot).

Чтобы построить график в онлайн калькуляторе, достаточно записать функцию, например такую как у нас в скриншоте:

plot(tan(x)),x=-360..360

Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.

Построить можно абсолютно любую функцию, с любым количеством переменных, например такую:

plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать.

Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.

Для сравнения с калькулятором Майкрософта, приводим наглядный скриншот

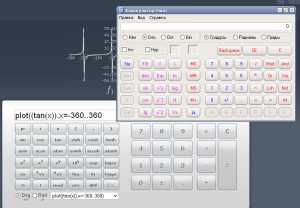
Думаем игра «Найдите N отличий» Вам знакома. Теперь пора подвести некоторые итоги:

С помощью онлайн калькулятора мы можем:

  • Серьезно облегчить себе жизнь в школе или институте.
  • Получить профессиональный онлайн калькулятор в бесплатное пользование.
  • Считать огромные числа на любом компьютере в любой точке планеты.
  • Строить графики по сложным функциям прямо онлайн.
  • Не захламлять свой ноутбук приложениями  и, тем более, не тратить на них деньги.

Вполне добротный список преимуществ.
Update 21.10.2011: Мы оформили более удобную страницу с примерами для эффективного использования калькулятором — посмотреть. Её можно открыть с любой точки нашего сайта.
Update 02.12.2010: Теперь можно опробовать этот калькулятор  в действии прямо у нас в журнале:

UPDATE 09.04.2011: Функции арктангенса, арксинуса и т.д. запускаются кнопками:
tan-1, sin-1 и т.д.
Включить продвинутые функции для решения матриц, построения графиков, дифференциалов и другого можно с помощью специальных клавиш:

Для полной функциональности нужно использовать оригинал, но этот тоже сойдет для быстрых рассчетов.

Технический калькулятор | Онлайн калькулятор (⇒)

 

Сейчас другие читают

itpride.net