« Сила Ампера и сила Лоренца»
Технологическая карта урока физики в 9 классе Решение задач на тему: « Сила Ампера и сила Лоренца»
Дидактическая цель: создать условия для совершенствования знаний, умений, навыков.
Цель урока: совершенствовать навыки решения задач на применение силы Ампера и силы Лоренца; закрепить знание силы Ампера и силы Лоренца при решении задач; проверить уровень знаний, полученных при изучении данной темы.
Задачи урока:
Образовательные:
Продолжить развитие умения использовать теоретические знания при решении задач.
Продолжить формировать обобщенное умение решать задачи.
Сформировать умение решать задачи с использованием формул для расчета силы Ампера и силы Лоренца.
Проконтролировать степень усвоения знаний, умений и навыков по данной теме.
Развивающие:
Продолжить работу по формированию умения анализировать, делать выводы.
Воспитательные:
Продолжать работу по формированию внимания, усидчивости, аккуратности, доброжелательного отношения к товарищам, воспитание умения слушать мнение других.
— Совершенствовать навыки самостоятельной работы.
воспитывать патриотизм, интернационализм, чувство гордости за достижения человеческого разума и за достижения советской науки и народа, самоотверженно кующего основу Победы.
Личностные:
Способствовать саморазвитию и самообразованию учащихся на основе мотивации к обучению и познанию.
Формировать целостную картину мира.
Формировать осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению.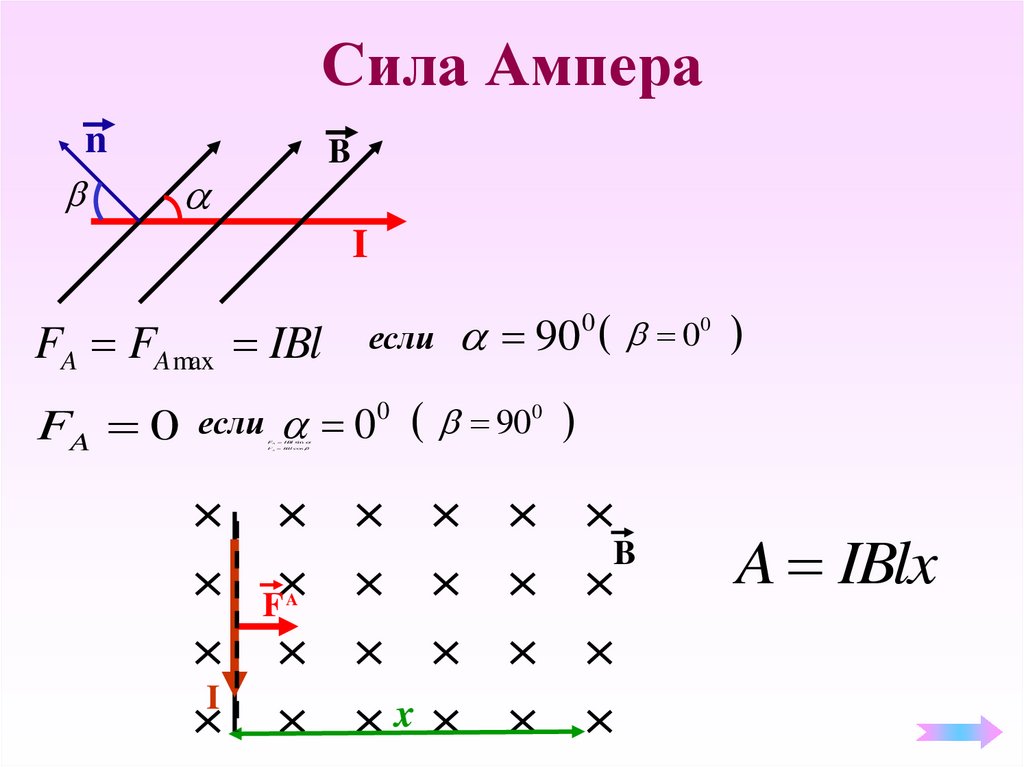
Формировать умение контролировать процесс и результат деятельности (в частности, за счет рефлексии).
Метапредметные:
Использовать основные интеллектуальные операций: постановка задачи, формулирование гипотез, анализа и синтеза, сравнения, обобщения, систематизации, выявления причинно-следственных связей, поиска аналогов, формулирования выводов для решения задач.
Организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.
Создавать, применять и преобразовывать знаково-символические средства для решения задач.
Самостоятельно планировать пути достижения целей
Предметные:
Владеть правилом левой руки, понятием Силы Ампера, Силы Лоренца.
Формировать умения решать задачи на тему «Сила Ампера.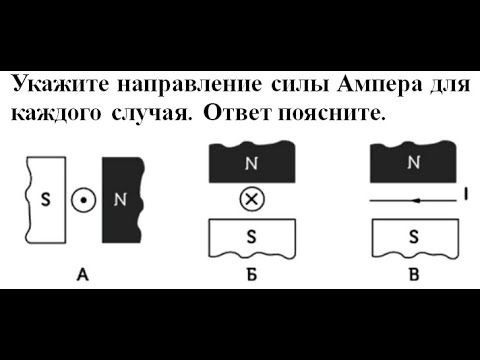 Сила Лоренца».
Сила Лоренца».
Использовать приобретенные знания в повседневной деятельности.
Тип урока: урок совершенствования знаний, умений и навыков.
Оборудование, материалы: проектор, компьютер, экран, доска,
Учебник Физика 9 класс
Методы обучения: словесный, репродуктивный, проблемный (решение задач), частично-поисковый, эвристическая беседа.
Формы обучения: фронтальная, групповая, индивидуальная.
Методы контроля: письменный, устный.
Межпредметные связи: математика.
Методическое и дидактическое сопровождение урока:
— Презентация в Microsoft Power Point;
— Компьютер, экран, мультимедиапроектор;
— Учебник Физика 9 класс;
— Раздаточный дидактический материал (конспект урока) для учащихся.
СТРУКТУРА УРОКА
№ П/П | Этапы урока | Время (мин) | Задачи этапа | Деятельность | Метод | Организационная форма | |
учителя | обучающихся | ||||||
1 | Организационный этап | 1 | Проверить готовность к уроку | Приветствие. Проверка готовности обучающихся к работе | Проверяют готовность своего рабочего места | Информационный | Индивидуальная |
2 | Этап подготовки обучающихся к активному и сознательному усвоению знаний (целепологание и мотивация) | 2 | Подготовить к закреплению материала | В ходе беседы помогает сформулировать тему и цель занятия. | Отвечают на вопросы, определяют тему и цель занятия. | Словесный | Фронтальная |
3 | Актуализация знаний и умений | 10 | Повторить основные понятия и формулы | Предлагает ответить на вопросы | Отвечают на вопросы преподавателя. Вспоминают основные понятия и формулы по данной теме | Словесный | Фронтальная |
4 | Этап решения типовых задач по теме: «Сила Ампера. Сила Лоренца». | 15 | Отработать умения решать задачи по данной теме | Организует работу обучающихся по решению задач и контролирует ход ее решения и результат | Совместное и самостоятельное решение задач по данной теме | Практический | Индивидуальная, групповая и фронтальная |
5 | Рефлексия, подведение итогов занятий | 5 | Осознать и оценить уровень сформированности навыков решения задач | Организует обсуждение, оценивает степень выполнения решения задач, анализирует итоги урока | Дают оценку результатов своей работы. | Анализ | Индивидуальная |
6 | Этап информации обучающихся о домашнем задании | 2 | Задает домашнее задание | Определяют для себя уровень домашнего задания | Информационный | Индивидуальная | |
Ход урока:
1. Организационный момент. Приветствие. Проверка готовности обучающихся к работе.
2. Этап подготовки обучающихся к активному и сознательному усвоению знаний (целепологание и мотивация) В ходе беседы помогает сформулировать тему и цель занятия. Помогает сформулировать план занятия.
3. Актуализация знаний:
1. Чем порождается магнитное поле?
2.Что понимают под силовыми линиями магнитного поля?
3. Каким образом можно определить направление силовых линий магнитного поля?
Каким образом можно определить направление силовых линий магнитного поля?
4.Какая сила называется силой Ампера? Запишите на доске формулу для расчёта Силы Ампера.
5.Как находят направление силы Ампера?
6.Запишите на доске формулу для расчёта Силы Лоренца
7. Как находят направление силы Лоренца?
4. Формирование умений.
Решение задачу доски и тетради:
1.В магнитном поле с индукцией 5 Тл движется электрон со скоростью 104 м/с, направленной перпендикулярно линиям индукции магнитного поля. Чему равен модуль силы, действующей на электрон со стороны магнитного поля?
2.Определите по правилу левой руки направление силы Ампера.
Физминутка (гимнастика для глаз)
Работа в группах:
Хочу обратить ваше внимание на то, что любое физическое явление и открытие имеют широкое применение в повседневной жизни.
Именно Амперу пришла идея о том, что комбинацией проводников и магнитных стрелок можно создать устройство, которое предаёт информацию на расстояние.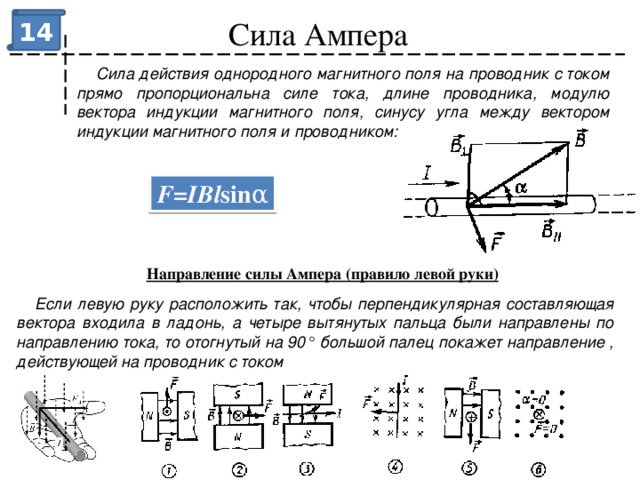 Однако широкое распространение электромагнитный телеграф приобрёл после того, как Самюэль Морзе создал более удобный аппарат и, главное, разработал двоичную азбуку, состоящую из точек и тире, которая так и называется «Азбука Морзе»
Однако широкое распространение электромагнитный телеграф приобрёл после того, как Самюэль Морзе создал более удобный аппарат и, главное, разработал двоичную азбуку, состоящую из точек и тире, которая так и называется «Азбука Морзе»
До 34-х лет Сэмюэль Морзе был крайне далек от техники. Он увлекался живописью.
Натолкнуло Морзе на мысль создать быстрый способ передачи информации печальное событие. Он не успел застать в живых больную жену. Это событие так потрясло Морзе, что он решил создать такую систему, с помощью которой можно было передавать сообщения на дальние расстояния. Однако на это ушло больше десяти лет.
Однажды на корабле он увидел фокусы. Провод под напряжением подносили к компасу, и его стрелка начинала крутиться. Художник тут же нарисовал схему будущего телеграфа.Реализовать свою идею ему помог промышленник Стив Вейл и сын Вейла Альфред . Вейл он дал на разработки и опыты деньги и помещение. Помощником у Морзе стал сын Вейла. И в результате упорного в 1844 году был послан первый сигнал длиной 1700 футов, текст которого был таким: «Дивны дела твои, Господи!».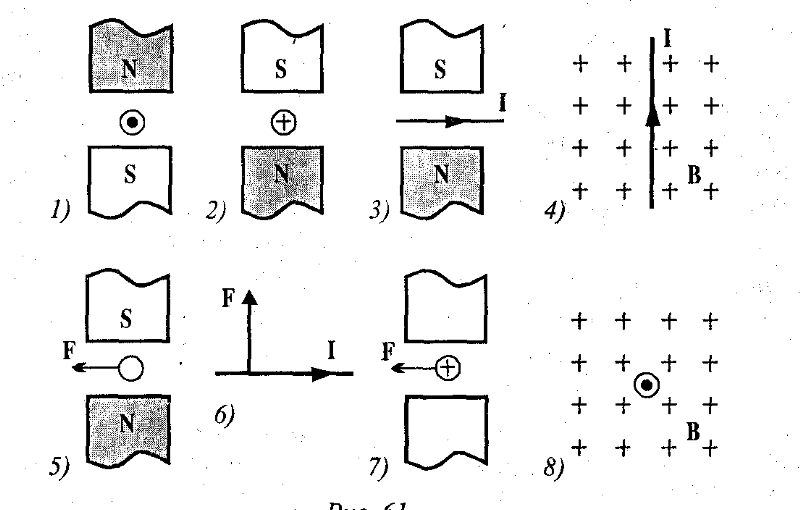
Сейчас работаем в группах. Вы радисты. У каждой группы своя азбука. С ее помощью вы должны прочитать фразу. Для этого надо решить задачи.( 5 баллов за работу)
1. Какая сила действует на протон, движущийся со скоростью 106м/с в магнитном поле с индукцией 0.2 Тл перпендикулярно линиям индукции? 2. Определите модуль силы, действующей на проводник длиной 20 см при силе тока 10 А в магнитном поле с индукцией 0.13 Тл, если угол α между вектором В и проводником равен 90°; 3. Определите, с какой силой магнитное поле, созданное током, действует на проводник, если магнитная индукция поля 1.5 Тл, рабочая длина проводника 0.4 м и по нему протекает ток 50 А. 4. Вычислите магнитную индукцию поля, если оно действует на проводник с силой 50 Н. Рабочая длина проводника, помещенного в магнитное поле, составляет пол метра, а сила тока, протекающего в нем, 0,2 А. 5. Какова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного поля действует сила 32 Н. | 1. По проводнику длиной 45 см протекает ток силой 20 А. Чему равна индукция магнитного поля, в которое помещен проводник, если на проводник действует сила 9 мН? 2. Сила тока в проводнике 4 А, длина активной части проводника 0.2 м, магнитное поле действует на проводник с силой 0.1 Н. Определите индукцию магнитного поля, если линии индукции поля и ток взаимно перпендикулярны. 3. На проводник длиной 50 см, находящийся в однородном магнитном поле с магнитной индукцией 0.1 Тл, действует сила 0.05 Н. Вычислите силу тока, если угол между направлением силы тока и вектором магнитной индукции взаимно перпендикулярны. 4. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 900 к вектору магнитной индукции. 5. Проводник с током 5 А находится в магнитном поле с индукцией 10 Тл. Определить длину проводника, если магнитное поле действует на него с силой 20Н и перпендикулярно проводнику. |
1 группа
ответы | коды |
3,2*104 | связи не пойдут, |
500 | в бой без |
30 | И танки |
0,25 | продержится пехота, |
3,2*10-12 | Без связи не |
2 группа
ответы | коды |
0,4 | армии зовут. |
0,3 | Не зря нас нервом |
1 | с тобой работа, |
0,125 | у нас |
10-3 | Такая, брат, |
Зашифрованная фраза:
Без связи не продержится пехота
И танки в бой без связи не пойдут
Такая брат у нас с тобой работа
Не зря нас нервом армии зовут
Пускай врагу коварно не иметься
Но знает даже самый злейший враг
Пока в груди связиста сердце бьется
Греметь на магистрали будет связь
Действительно, песня эта была особо популярна у бойцов и офицеров.
Азбука Морзе наибольшее применение нашла в военных структурах.
Хочу заметить, что связист в армии – профессия невероятно ответственная, и столь же опасная.
Управление войсками без надежных средств связи просто немыслимо — подразделения нельзя оперативно собрать в ударный кулак или эффективно руководить ими на поле боя. Пехота, артиллерия и гвардейские минометчики в основном использовали проводные телефоны, а танковые войска, авиация и ВМФ активно осваивали радиосвязь.
Радиосвязь и полевая телефонная связь во время Второй мировой войны привнесли много нового в тактику управления войсками. Тактика глубоких прорывов, наступления крупных механизированные соединений, выброса воздушных десантов в тыл противника — все эти мероприятия требовали обеспечения войск надежной связью с командованием.
«Спасибо за подвиг» — говорим мы ветеранам Великой Отечественной войны, труженикам тыла и всем тем, кто погиб, защищая нашу Родину.
И мы должны быть достойны наших предков. Должны хорошо учиться и делать новые открытия
Должны хорошо учиться и делать новые открытия
Самостоятельная работа :
Для того чтобы делать открытия надо иметь хорошие знания, закрепим их тестом который у вас на столе.
Ответе на вопросы теста.
Тест по теме: «Сила Ампера. Сила Лоренца».
Вариант 1 | |
1. На рис. показан проводник с током, помещённый между полюсами магнита. Укажите направление силы Ампера S N А) Г) У) | |
+ + + _ V + + + | 2. Заряженная частица движется в магнитном поле, направление которого указано точками, если линии магнитной индукции направлены к читателю, или крестиками, если они направлены за чертёж. Определить направление силы Лоренца. р ) к) л) |
3. С) Положить стержень рядом с катушкой; усилится | |
Тест по теме: «Сила Ампера. Сила Лоренца».
Вариант 2 | |
1.На рис. показан проводник с током, помещённый между полюсами магнита, и указано направление силы Ампера. Укажите полюсы магнита. , N S N К N B N S ) У) С) | |
+ + _ + V + | 3. Заряженная частица движется в магнитном поле, направление которого указано точками, если линии магнитной индукции направлены к читателю, или крестиками, если они направлены за чертёж. В) А) Р) |
8. Как взаимодействуют одноименные полюсы магнитов? А) Отталкиваются друг от друга | |
Кто получил слово «УРА» в листе самооценки ставит 3 балла, соответственно сколько букв на нужном месте столько баллов.
5. Подведение итогов урока. Анализ результатов. Рефлексия учащихся.
Просуммируйте баллы и переведите в оценку. Поставьте в дневник.
Оцените каждый вид деятельности. Кто желает озвучить, что у него получилось.
1.Лист самооценки знаний ученика .———————————————
Лист самооценки знаний ученика | Ф.И. участника |
фронтальный опрос (ответ-1 балл) | |
Решение задач у доски (ответ-1 балл) | |
Работа по группам (5 баллов) | |
Тест (3 балла) | |
Оценка за урок: Больше 10-9 б — 5 6-8 б — 4 5-3 б — 3 Меньше 3 б — 2 | |
Оцениваемые виды деятельности | Система оценивания: оценить каждый вид деятельности «2» — согласен, «1» — не совсем так, «0» -не согласен |
Активно участвую в обсуждении вопросов и задач. | |
Ясно и кратко формулирую свою позицию. | |
Решаю задачи быстро и правильно. | |
Могу объяснить решение задачи и помочь одноклассникам. | |
Знаю все формулы и единицы измерения. | |
Могу работать самостоятельно и в группе. | |
Могу правильно оценить свою работу и работу одноклассников. | |
Участвую в подведении итогов урока. |
Расшифровка:
0-4 Минимальный, или не вносил вклад;
5-8 Среднее число;
9-12 Выше среднего числа;
13-16 Выдающийся.
6. Этап информации обучающегося о домашнем задании.
Ваше домашнее задание: решить к следующему занятию
1уровень упр33 (3-5) стр.157
2 уровень задание огэ по теме (для тех кто сдает огэ)
Дополнительное задание: Написать азбукой Морзе:«Дивны дела твои, Господи!».
Решение задач по теме «Сила Ампера»
Урок решения задач
По теме :
«Магнитное поле. Применение правил буравчика, правой и левой руки»
Цели урока:
- 1. развитие интереса, умения и навыков к решению тестовых и графических задач.
- 2. совершенствование полученных знаний и умений
- 3. уметь решать задачи на описание магнитного поля тока и его действия :сила Ампера и сила Лоренца направление линий магнитной индукции.
Определить направление силы Ампера:
N
F A
S
Определить направление силы Ампера:
N
F A
S
Определить направление силы Ампера:
N
S
F A
Определить направление силы Ампера:
F A
N
S
Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током.
1
2
3
4
а) 1, б)2, в)3, г)4
Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током. Предполагаемые направления силы Ампера указаны стрелочками.
1
2
3
4
а) 1, б)2, в)3, г)4
Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током. Предполагаемые направления силы Ампера указаны стрелочками.
1
2
3
4
а) вверх, б)вниз, в) к нам, г) от нас.
Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током. Предполагаемые направления силы Ампера указаны стрелочками.
1
2
3
4
а) 1, б) 2, в) 3, г) 4
Определить положение полюсов магнита, создающего магнитное поле.
а) слева – северный полюс,
б) слева – южный полюс.
Обнаружить магнитное поле можно по…
А) по действию на любой проводник,
Б) действию на проводник, по которому течет электрический ток,
В) заряженный теннисный шарик, подвешенный на тонкой нерастяжимой нити,
Г) на движущиеся электрические заряды.
а) А и Б, б) А и В, в) Б и В, г) Б и Г.
Закончить фразу: «Если электрический заряд неподвижен, то вокруг него существует…
а) магнитное поле,
б) электрическое поле,
в) электрическое и магнитное поле.
Закончить фразу: «Если электрический заряд движется, то вокруг него существует…
а) магнитное поле,
б) электрическое поле,
в) электрическое и магнитное поле.
Закончить фразу: «Вокруг проводника с током существует…
а) магнитное поле,
б) электрическое поле,
в) электрическое и магнитное поле.
Какие силы проявляются во взаимодействии двух проводников с током?
а) силы магнитного поля,
б) силы электрического поля,
в) сила всемирного тяготения.
Какие утверждения являются верными?
А.В природе существуют электрические заряды.
Б.В природе существуют магнитные заряды.
В.В природе не существует электрических зарядов.
Г.В природе не существует магнитных зарядов.
а) А и Б, б) А и В, в) А и Г, г) Б, В и Г.
На рисунке показана картина магнитных линий прямого тока. В какой точке магнитное поле самое сильное?
а) б) в)
Два параллельных проводника, по которым текут токи противоположных направлений…
а) взаимно притягиваются,
б) взаимно отталкиваются,
в) никак не взаимодействуют.
Два параллельных проводника длиной по 1 м, расположенные на расстоянии 1 м друг от друга при протекании по ним электрического тока, притягиваются с силой 1 ∙10 -7 Н. Это значит, что по проводникам текут токи…
Это значит, что по проводникам текут токи…
а) противоположных направлений по 1 А,
б) одного направления по 1 А,
в) противоположных направлений по 0,5 А,
г) одного направления по 0,5 А.
Как будут взаимодействовать друг с другом два параллельных проводника А и Б?
а ) они будут притягиваться,
б) они будут отталкиваться,
в) они не будут взаимодействовать .
Определить направление тока по известному направлению магнитных линий
Определить направление тока в проводнике по направлению магнитных линий
Магнитная стрелка отклонится, если её разместить вблизи…
А) вблизи потока электронов,
Б) вблизи потока атомов водорода,
В) вблизи потока отрицательных ионов,
Г) вблизи потока положительных ионов,
Д) вблизи потока ядер атома кислорода.
а) все ответы верны, б) А, Б, В, и Г,
в) Б, В, Г, г) Б, В, Г, Д
9.
 5 Закон Ампера – Введение в электричество, магнетизм и электрические цепи
5 Закон Ампера – Введение в электричество, магнетизм и электрические цепиЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объясните, как закон Ампера связывает магнитное поле, создаваемое током, со значением тока
- Рассчитать магнитное поле длинного прямого провода, тонкого или толстого, по закону Ампера
Фундаментальное свойство статического магнитного поля состоит в том, что, в отличие от электростатического поля, оно не является консервативным. Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от и известен как 
На рис. 9.5.1 показана произвольная плоскость, перпендикулярная бесконечному прямому проводу, ток по которому направлен за пределы страницы. Линии магнитного поля представляют собой окружности, направленные против часовой стрелки и центрированные на проводе. Для начала рассмотрим над закрытыми путями и . Обратите внимание, что один путь () охватывает проводник, а другой () — нет. Поскольку силовые линии круглые, является произведением и проекцией на окружность, проходящую через . Если радиус этого конкретного круга , проекция , и
(рис. 9.5.1)
Рисунок 9.5.1 Ток длинного прямого провода направлен за пределы страницы. Интеграл равен и соответственно для путей и .С учетом уравнения 9.3.1,
(9.5.1)
Для пути, который циркулирует по проводу, и
(9.5.2)
Путь , с другой стороны, циркулирует как через положительные (против часовой стрелки), так и отрицательные (по часовой стрелке) (см.
(9.5.3)
Распространение этого результата на общий случай есть закон Ампера.
ЗАКОН АМПЕРА
По произвольному замкнутому пути,
(9.5.4)
где – полный ток, проходящий через любую открытую поверхность, периметр которой является путем интегрирования. Необходимо учитывать только токи внутри пути интегрирования.
Чтобы определить, является ли конкретный ток положительным или отрицательным, согните пальцы правой руки в направлении пути интегрирования, как показано на рисунке 9..5.1. Если проходит в том же направлении, что и ваш вытянутый большой палец, положительный; если проходит в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
Стратегия решения задач: закон Ампера
Чтобы рассчитать магнитное поле, создаваемое током в проводе(ах), выполните следующие шаги:
- Определите симметрию тока в проводе(ах).
 Если симметрии нет, используйте закон Био-Савара для определения магнитного поля.
Если симметрии нет, используйте закон Био-Савара для определения магнитного поля. - Определите направление магнитного поля, создаваемого проводом (проводами), по правилу правой руки 2.
- Выберите петлю пути, в которой магнитное поле либо постоянно, либо равно нулю.
- Рассчитать ток внутри контура.
- Вычислите линейный интеграл вокруг замкнутого контура.
- Приравняйте к и найдите .
ПРИМЕР 9.5.1
Использование закона Ампера для расчета магнитного поля, создаваемого проводом
Используйте закон Ампера для расчета магнитного поля, создаваемого постоянным током в бесконечно длинном тонком прямом проводе, как показано на рисунке 9..5.2.
(рис. 9.5.2)
Рисунок 9.5.2 Возможные составляющие магнитного поля из-за тока , направленного за пределы страницы. Радиальная составляющая равна нулю, потому что угол между магнитным полем и траекторией прямой.Стратегия
Рассмотрим произвольную плоскость, перпендикулярную проводу, с током, направленным за пределы страницы. Возможные компоненты магнитного поля в этой плоскости показаны в произвольных точках на окружности радиусом с центром на проводе. Поскольку поле цилиндрически симметрично, ни , ни не меняются в зависимости от положения на этой окружности. Также из симметрии радиальные линии, если они есть, должны быть направлены либо все внутрь, либо все наружу от провода. Это означает, однако, что должен существовать чистый магнитный поток через произвольный цилиндр, концентричный проводнику. Радиальная составляющая магнитного поля должна быть равна нулю, так как . Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Возможные компоненты магнитного поля в этой плоскости показаны в произвольных точках на окружности радиусом с центром на проводе. Поскольку поле цилиндрически симметрично, ни , ни не меняются в зависимости от положения на этой окружности. Также из симметрии радиальные линии, если они есть, должны быть направлены либо все внутрь, либо все наружу от провода. Это означает, однако, что должен существовать чистый магнитный поток через произвольный цилиндр, концентричный проводнику. Радиальная составляющая магнитного поля должна быть равна нулю, так как . Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Решение
На этом пути постоянна и параллельна , поэтому
Таким образом, закон Ампера сводится к
Наконец, поскольку является единственным компонентом , мы можем опустить индекс и написать
.
Это согласуется с приведенным выше расчетом Био-Савара.
Значение
Закон Ампера хорошо работает, если у вас есть путь интегрирования, по которому можно получить результаты, которые легко упростить. Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
ПРИМЕР 9.5.2
Расчет магнитного поля толстой проволоки по закону Ампера
Радиус длинного прямого провода на рисунке 9.5.3 равен , и по проводу течет ток , равномерно распределенный по его поперечному сечению. Найдите магнитное поле как внутри, так и снаружи провода.
(рис. 9.5.3)
Рисунок 9.5.3 (a) Модель провода с током радиуса a и тока . (b) Поперечное сечение того же провода, показывающее радиус a и петлю Ампера радиусом .Стратегия
Эта задача имеет ту же геометрию, что и пример 9.5.1, но замкнутый ток изменяется по мере того, как мы перемещаем путь интегрирования снаружи провода внутрь провода, где он не фиксирует весь заключенный ток (см. рис. 9.5.3). .
рис. 9.5.3). .
Решение
Для любого кругового пути радиусом с центром на проводе:
По закону Ампера это равно полному току, проходящему через любую поверхность, ограниченную путем интегрирования.
Сначала рассмотрим круговой путь внутри провода, например, показанный в части (а) на рис. 9.5.3. Нам нужен ток, проходящий через область, ограниченную путем. Она равна плотности тока, умноженной на замкнутую площадь. Поскольку ток однороден, плотность тока внутри пути равна плотности тока во всем проводе, которая равна . Следовательно, ток, проходящий через область, ограниченную путем, равен
.
Мы можем учитывать это соотношение, потому что плотность тока постоянна по площади провода. Следовательно, плотность тока на участке провода равна плотности тока на всей площади. Используя закон Ампера, получаем
, а магнитное поле внутри провода равно
.
Вне провода ситуация идентична ситуации с бесконечно тонким проводом из предыдущего примера; то есть
Вариант с показан на рис. 9.5.4.
9.5.4.
(рис. 9.5.4)
Рисунок 9.5.4 Изменение магнитного поля, создаваемого током в длинном прямом проводе радиусом .Значение
Результаты показывают, что по мере увеличения радиального расстояния внутри толстой проволоки магнитное поле увеличивается от нуля до известного значения магнитного поля тонкой проволоки. Вне провода поле падает независимо от того, толстый провод или тонкий.
Этот результат аналогичен тому, как закон Гаусса для электрических зарядов ведет себя внутри равномерного распределения зарядов, за исключением того, что закон Гаусса для электрических зарядов имеет однородное объемное распределение заряда, тогда как закон Ампера здесь имеет однородную область распределения тока. Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
распространение.
ПРИМЕР 9.5.3
Использование закона Ампера с произвольными путями
Используйте закон Ампера для оценки текущих конфигураций и путей на рис. 9.5.5.
(рис. 9.5.5)
Рисунок 9.5.5 Текущие конфигурации и пути для примера 12.8.Стратегия
Закон Ампера гласит, что где является полным током, проходящим через замкнутый контур. Самый быстрый способ оценить интеграл — это вычислить его, найдя чистый ток через петлю. Положительные токи текут по большому пальцу правой руки, если ваши пальцы скручиваются в направлении петли. Это подскажет нам знак ответа.
Решение
(a) Ток, протекающий вниз по контуру, равен току, выходящему из контура, поэтому чистый ток равен нулю. Таким образом, .
(b) Единственный ток, который следует учитывать в этой задаче, потому что это единственный ток внутри контура. Правило правой руки показывает нам, что ток, идущий вниз по контуру, имеет положительное направление. Поэтому ответ таков.
Поэтому ответ таков.
(c) Правило правой руки показывает нам, что ток, идущий вниз по контуру, имеет положительное направление. Есть тока, идущего вниз и идущего вверх. Следовательно, общий ток равен и .
Значение
Если бы все токи закручивались так, что один и тот же ток входил бы в петлю и из петли, то суммарный ток был бы равен нулю и магнитного поля не было бы. Вот почему провода в электрическом шнуре расположены очень близко друг к другу. Токи, протекающие к устройству и от устройства по проводу, равны нулевому общему току, протекающему через петлю Ампера вокруг этих проводов. Следовательно, никакие блуждающие магнитные поля не могут присутствовать в проводах с током.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 9.6
Попробуйте использовать закон Ампера для расчета магнитных полей конечного прямого провода и круглой проволочной петли. Почему это не полезно для этих расчетов?
Цитаты Кандела
Контент по лицензии CC, конкретное указание авторства
- Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Контурный закон Ампера и проблемы, связанные с ним
Андре-Мари Ампер, французский физик, предложил Контурный закон Ампера . Ампер родился в Лионе, Франция, 20 января 1775 года. Отец обучал его дома, и в молодом возрасте он проявил склонность к математике. Ампер был математиком и физиком, наиболее известным своей работой по электродинамике, Закону Ампера, а также подтверждением и расширением работы Эрстеда о связи между электричеством и магнетизмом.
Он также был изобретателем астатической иглы, которая является ключевым компонентом современного астатического гальванометра. Он был первым, кто показал, что магнитное поле образуется, когда два параллельных провода заряжены электричеством. Он широко известен как один из пионеров в области электромагнетизма. В его честь названа единица измерения силы тока «ампер».
В его честь названа единица измерения силы тока «ампер».
Закон циркуляции Ампера
«Вокруг каждой замкнутой кривой линейный интеграл магнитного поля B равен μ 0 раз больше чистого тока I, протекающего через область, содержащуюся на кривой».
i.e.
∮B’dl’ = μ 0 ∑i = μ 0 (i 1 +i 3 –i 2 )
where,
μ 0 обозначает проницаемость пустого пространства, а B обозначает магнитное поле в месте на границе поверхности, которое образует угол ” с элементом длины ‘dl’.
«Петля Ампера» также известна как 9-я петля.0012 сумма всех произведений B’dl по всему циклу .
Примечание:
- (i 1 +i 3 –i 2 ) — это полный ток, протекающий через вышеуказанный контур. Любой ток за пределами области не включается в суммарный ток, но мы должны учитывать магнитное поле, обусловленное всеми токами, при расчете B’dl’ (как внутри, так и вне контура токов)
- Правила знаков: (положительный внешний ток, отрицательный внутренний ток)
- Это правило применяется только к стабильным токам.
 Этот закон остается верным независимо от размера и формы замкнутой трассы, охватывающей ток (петля Ампера).
Этот закон остается верным независимо от размера и формы замкнутой трассы, охватывающей ток (петля Ампера). - Фраза B’dl’=0 не означает, что магнитное поле B равно нулю повсюду на пути, но означает, что по нему не проходит никакого чистого тока.
- Направление замкнутого пути — по часовой стрелке, когда поток течет от наблюдателя. Закрытый маршрут направлен против часовой стрелки, когда течение течет в направлении наблюдателя.
Альтернативная форма циркулярного закона Ampere
Мы знаем, что,
∮b’dl ‘= μ 0 ∑i = μ 0 (I 1 +I 1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111. i 2 )
Используя B’=µ 0 H’ (где H= поле намагничивания)
∮B’dl’=µ 0 ∑i=µ 0 (i 1 2 i 3 –i 2 )
∮μ 0 H’.dl’=μ 0 Σi
∮H’.
dl’=Σi
Противоречие закона Ампера о цепях
Согласно Джеймсу Клерку Максвеллу, закон Ампера применим только для постоянного тока или когда электрическое поле не меняется со временем. Рассмотрим конденсатор с плоскими пластинами, заряжаемый батареей, чтобы продемонстрировать несоответствие. Во время зарядки по подключенным проводам протекает переменный во времени ток.
Применение закона Ампера для петли l 1 и l 2
Для петли 1− ∮l 1 B’⋅dl’=μ 0 i
Для петли 2− ∮l 2 B’⋅dl’=0 (i=0 между пластинами).
Однако замечено, что на практике между пластинами существует магнитное поле, когда они заряжаются или разряжаются. В результате закон Ампера не работает.
т.е.
Модифицированный закон цепей Ампера или Ампер – закон цепей Максвелла
Максвелл предположил, что в процессе зарядки между пластинами конденсатора должен проходить некоторый ток. Он дал ему термин «ток смещения». В результате обновленный закон выглядит следующим образом:
Он дал ему термин «ток смещения». В результате обновленный закон выглядит следующим образом:
∮ B’⋅dl’=μ 0 (i c +i d )
or
∮B’⋅dl’=μ 0 (i c +ε 0 x dϕ E /dt)
где; и конденсатор.
Примечание:
- Величина тока смещения (i d ) равна величине тока проводимости (i c ).
- Сумма ic и id в цепи всегда непрерывна, даже если они не непрерывны.
Применение окружного закона Ампера
Применяется закон Ампера.
- Необходимо определить магнитное поле, создаваемое цилиндрическим проводом.
- Необходимо определить магнитное поле, создаваемое бесконечным листом, несущим электричество.
- Необходимо определить магнитное поле внутри соленоида и тороида.
- Необходимо определить магнитное поле внутри проводника.

- Для определения сил, существующих между проводниками с током.
Примеры задач
Задача 1. Длинный соленоид имеет 200 витков на см и пропускает ток 2,5 А. Чему равно магнитное поле в его центре?
Решение:
B=μ 0 ni 9.
Задача 2: Средний радиус тороида, сделанного на кольце из немагнитного материала, составляет 0,1 м, и он имеет 500 витков. Если по нему течет ток 0,5 А, какое магнитное поле создается вдоль его оси внутри тороида?
Решение:
B=μ0ni; где n=N/2πR
∴B=4π×10 –7 ×500/(2π×0,1)×0,5
=5×10 –4 T.
Задача 3: Каково магнитное поле для соленоида, показанного на рисунке, в точке P?
Решение:
B = μ 0 /4π x 2πni (SINα+SINβ)
из рисунка α = (90 O —30 O ) = (90 O —30 O ) = (90 O —30 O ) = (90 O –30 O ) = (90 O –30 O ) = (90 O –30 O ) = (90 O –30 ).
β=(90 o –60 o )=30 o
∴B=μ 0 ni/2 x (sin60 o ) 4 o +sin30 o0011 = μ 0 ni/4(√3+1).
Задача 4: На рисунке показано поперечное сечение полого цилиндрического проводника с внутренним радиусом R и внешним радиусом 2R, по цилиндру течет равномерно распределенный ток вдоль его оси. Чему будет равна магнитная индукция в точке Р на расстоянии 3R/2 от оси цилиндра?
Решение:
Используя B=μ 0 i/2πr x (r 2 –a 2 /b 2 –a 2 ), здесь r=3R/2, a=R, b=2R
B=μ 0 i/2π(3R/2)×[(3R/2)–R 2 /(2R) 2 –R 2 ]
=5⋅μ 0 i/36πr
Задача 5. Какова напряженность магнитного поля в точке на оси бесконечно длинная прямая тонкостенная трубка с током I?
Решение:
Поскольку трубка полая внутри, а по амперовой петле ток не течет, магнитное поле равно нулю.

 Помогает сформулировать план занятия.
Помогает сформулировать план занятия.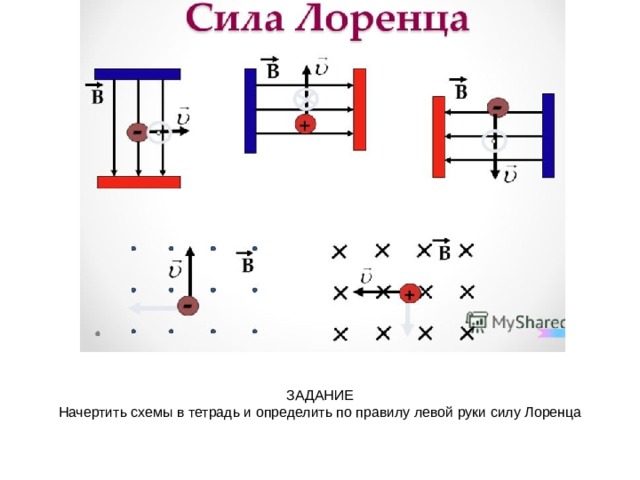 Анализируют затруднения при решении задач
Анализируют затруднения при решении задач Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.
Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.
Leave A Comment