12. Уравнения, содержащие модуль. Рациональные уравнения
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Уравнения, содержащие модуль
Если в уравнении некоторые выражения, содержащие неизвестное, стоят по знаком модуля, то решение исходного уравнения ищется отдельно на каждом из промежутков знакопостоянства этих выражений.Пример 1
Решить уравнение |3x-6|=x+2.
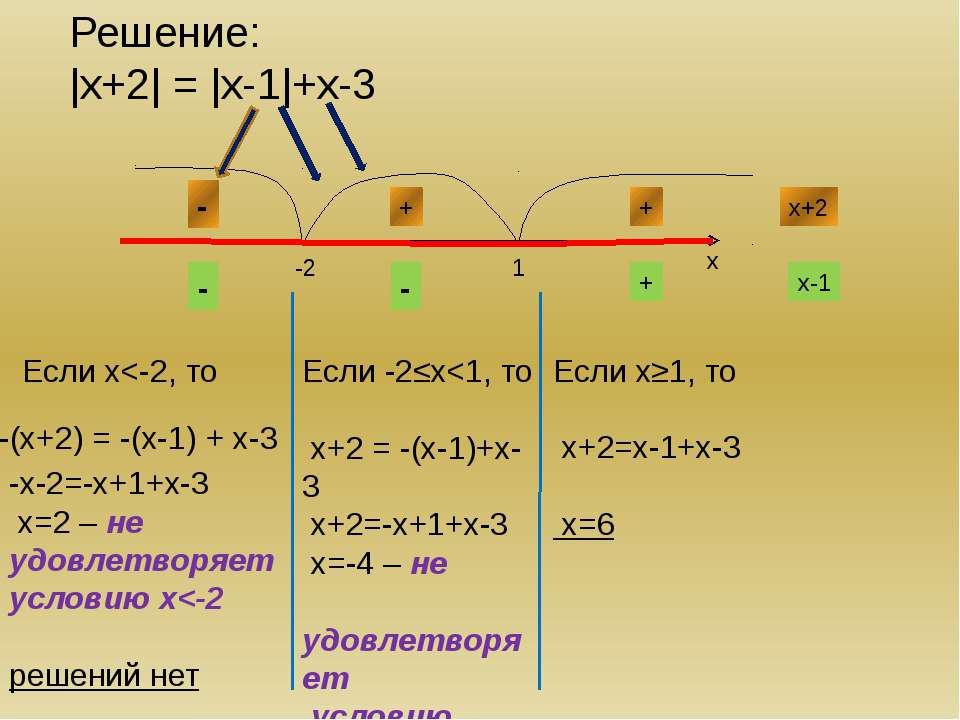
Решение:
Рассмотрим первый случай: 3х-6≥0, тогда 3х-6=х+2, 2х=8, х=4.
Рассмотрим второй случай: 3х-6<0, тогда 3х-6=-(х+2), 4х=4, х=1.
Ответ: 1; 4.
Пример 2
Решить уравнение |x-2| — 3|x-1| + 4|x-3| = 5.
Отметим на координатной прямой точки:
х-2=0 х-1=0 х-3=0х=2 х=1 х=3
Рассмотрим решения уравнения на промежутках (-∞; 1]; (1; 2]; (2; 3] и (3; +∞).
При х≤1: -(х-2) + 3(х-1) -4(х-3)=5, -х+2+3х-3-4х+12=5, -2х=-6, х=3. Ответ не принадлежит промежутку, следовательно нет решений.
При 1<х≤2: -(х-2) — 3(х-1) -4(х-3)=5, -х+2-3х+3-4х+12=5, -8х=-12, х=1,5. Ответ принадлежит промежутку.
При 2<х≤3: х-2 — 3(х-1) -4(х-3)=5, х-2-3х+3-4х+12=5, -6х=-8, х=4/3. Ответ не принадлежит промежутку, следовательно нет решений.
При х>3: х-2 — 3(х-1) +4(х-3)=5, х-2-3х+3+4х-12=5, 2х=16, х=8. Ответ принадлежит промежутку.
Ответ: 1,5; 8.
Рациональные уравнения Рациональным уравнением называется уравнение вида
где P(x), Q(x) — многочлены.
Решение уравнения сводится к решению системы:Пример
Решить уравнение
Решение:
x2-4=0, х-2≠0,x2=4, х≠ 2.
х=-2 или х=2.
Число 2 не может быть корнем.
Ответ: -2.
УПРАЖНЕНИЯ 1.
Из данных уравнений выберите те, которые не имеют корней:а) |x|+4=1; |x-5|=2; |x+3|=-6. б) |1+x|=3; |1-x|=-4; 8+|x|=2.
Решение:
а) |x|+4=1 не имеет корней, т.к. |x|=-3 и модуль не может быть отрицательным числом; |x-5|=2 имеет корни; |x+3|=-6 не имеет корней, т.к. модуль не может быть отрицательным числом.
Ответ: |x|+4=1; |x+3|=-6.
2. Решите уравнение:
а) |5x|=15; б) |2x|=16.
Решение:
а) |5x|=15;
|5||x|=15;
5|x|=15;
|x|=3;
x=3 или x=-3.
3. Решите уравнение:
а) |5x+1|=5; б) |2x-1|=10.
Решение:а) |5x+1|=5;
Ответ: -1,2; 0,8.
а) |5x2+3x-1|=-x2-36; б) |3x2-5x-4|=-4x2-23.
Решение:
а) |5x2+3x-1|=-x2-36. Рассмотрим выражение -x2-36, оно принимает отрицательные значения при любых значениях х, следовательно уравнение |5x2+3x-1|=-x2-36 не имеет корней.
Ответ: нет корней
5. Решите уравнение: Решение:
Ответ: -1/3.
6. Решите уравнение:
Решение:
14х2-5x-1=0,
7. Решите уравнение:
Решение:
8. Решите уравнение: Решение:
х ≠3.
Ответ: -4; 1.
9. Найдите, при каком значении переменной значение выражения
равно: а) -6; б) 6.
Решение:10. Решите уравнение:
Решение:
а) Разложим знаменатели на множители:
х2-36=(x-6)(x+6).
108-24x+х2=(x-6)(x-18).
2x-36=2(x-18).
11. Решите уравнение:
а) х2-6|x|=0; б) х2+4|x|=0.
Решение:а) х2-6|x|=0;
х≥0: х2-6x=0; х(х-6)=0, x1=0, x2=6.
x<0: х2+6x=0; х(х+6)=0, x1=0, x2=-6.
Ответ: -6; 0; 6.
12.Решите уравнение:
а) х2
а) х2-3|x|+2=0.
х≥0: х2-3x+2=0; D=9-8=1, x1=2, x2=1.
x<0: х2+3x+2=0; D=9-8=1, x1=-2, x2=-1.
Ответ: -2; -1; 1; 2.
13. Решите уравнение:
а) |x-2|+|x-4|=5; б) |x-1|-|x-4|=6.
Решение:а) |x-2|+|x-4|=5.
x≤2: -(x-2)-(x-4)=5, -x+2-x+4=5, x=0,5.
2<x≤4: x+2-(x-4)=5, x-2-x+4=5, 2=5 — нет решений.
x>4: x-2+x-4=5, 2x=11, x=5,5.
Ответ: 0,5; 5,5.
14.Решите уравнение:
а) |3- |4- |x|||=5; б) 8-|2 -|x|||=3.
Решение:а) |3- |4- |x|||=5;
3- |4- |x||=5 или 3- |4- |x||=-5;
|4-|x||=-2 — нет решений |4-|x||=8
4-|x|=8 или 4-|x|=-8
|x|=-4 — нет решений |x|=12
х=12 или х=-12.
Ответ: -12; 12.
15. Решите уравнение:
Решение:
а)
3x-7≥0: х2-3x+10=0; D=9-40=-31<0 — нет корней.
3x-7<0: х2-3x-10=0; D=9+40=49, x1=5, x2=-2.
3x-7≠0, x≠7/3.
Ответ: -2; 5.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Какие из чисел -4; -1; 2; 1,5; 2,5 являются корнями уравнения:
а) |3x-1|=5; б) |4-2x|=1?
а) |3x|=21; б) |2x|=-12.
3. Решите уравнение:
а) |2x-5|=1; б) |3x+6|=18.
4. Решите уравнение:
5. Решите уравнение:
6. Решите уравнение:
7. Решите уравнение:
8. Решите уравнение:
9. Решите уравнение:
а) 3(x-1) = |2x-1|; б) |5-2x|=|x+4|.
10. Решите уравнение:
а) |х2+x|=12; б) |х2-3x|=10.
Проверь себя
Решить уравнение x 1 x 3 0. Уравнения. Примеры тождественных преобразований уравнений. Основные проблемы
Цели:
- Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
- Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
- Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.
Тип урока : комбинированный.
Оборудование: графопроектор.
Наглядность: таблица «Теорема Виета».
Ход урока
1. Устный счет
а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а?
б) Сколько корней может иметь кубическое уравнение?
в) С помощью чего мы решаем уравнение третьей и четвертой степени?
г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2
2.
Самостоятельная работа (в группах)
Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»
1 группа
Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6
Составить уравнение:
B=1 -2-3+6=2; b=-2
с=-2-3+6+6-12-18= -23; с= -23
d=6-12+36-18=12; d= -12
е=1(-2)(-3)6=36
х 4 —
Решение . Целые корни ищем среди делителей числа 36.
р = ±1;±2;±3;±4;±6…
р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера
р 3 (x) = х 3 -х 2 -24x -36
р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2
р 2 (x) = х 2 -3х -18=0
х 3 =-3, х 4 =6
Ответ: 1;-2;-3;6 сумма корней 2 (П)
2 группа
Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5
Составить уравнение:
B=-1+2+2+5-8; b= -8
с=2(-1)+4+10-2-5+10=15; с=15
D=-4-10+20-10= -4; d=4
е=2(-1)2*5=-20;е=-20
8+15+4х-20=0 (это уравнение решает на доске 3 группа)
р = ±1;±2;±4;±5;±10;±20.
р 4 (1)=1-8+15+4-20=-8
р 4 (-1)=1+8+15-4-20=0
р 3 (x) = х 3 -9х 2 +24x -20
р 3 (2) = 8 -36+48 -20=0
р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5
Ответ: -1;2;2;5 сумма корней 8(Р)
3 группа
Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3
Составить уравнение:
В=-1+1-2+3=1;в=-1
с=-1+2-3-2+3-6=-7;с=-7
D=2+6-3-6=-1; d=1
е=-1*1*(-2)*3=6
х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)
Решение. Целые корни ищем среди делителей числа 6.
р = ±1;±2;±3;±6
р 4 (1)=1-1-7+1+6=0
р 3 (x) = х 3 — 7x -6
р 3 (-1) = -1+7-6=0
р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3
Ответ:-1;1;-2;3 Сумма корней 1(О)
4 группа
Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3
Составить уравнение:
B=-2-2-3+3=-4; b=4
с=4+6-6+6-6-9=-5; с=-5
D=-12+12+18+18=36; d=-36
е=-2*(-2)*(-3)*3=-36;е=-36
х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)
Решение.
Целые корни ищем среди делителей числа -36
р = ±1;±2;±3…
р(1)= 1 + 4-5-36-36 = -72
р 4 (-2) = 16 -32 -20 + 72 -36 = 0
р 3 (х) = х 3 +2х 2 -9х-18 = 0
р 3 (-2)= -8 + 8 + 18-18 = 0
р 2 (х) = х 2 -9 = 0; x=±3
Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)
5 группа
Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4
Составить уравнение
х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)
Решение . Целые корни ищем среди делителей числа 24.
р = ±1;±2;±3
р 4 (-1) = 1 -10 + 35 -50 + 24 = 0
р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0
p 3 (-2) = -8 + 36-52 + 24 = О
р 2 (х) = x 2 + 7x+ 12 = 0
Ответ:-1;-2;-3;-4 сумма-10 (И)
6 группа
Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8
Составить уравнение
B=1+1-3+8=7;b=-7
с=1 -3+8-3+8-24= -13
D=-3-24+8-24= -43; d=43
х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске)
Решение .
Целые корни ищем среди делителей числа -24.
р 4 (1)=1-7-13+43-24=0
р 3 (1)=1-6-19+24=0
р 2 (x)= х 2 -5x — 24 = 0
х 3 =-3, х 4 =8
Ответ: 1;1;-3;8 сумма 7 (Л)
3. Решение уравнений с параметром
1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1)
Ответ записать в порядке возрастания
R=Р 3 (-1)=-1+3-m-15=0
х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0
По условию х 1 = — 1; Д=1+15=16
Р 2 (х) = х 2 +2х-15 = 0
х 2 =-1-4 = -5;
х 3 =-1 + 4 = 3;
Ответ:- 1;-5; 3
В порядке возрастания: -5;-1;3. (Ь Н Ы)
2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.
Решение: R=Р 3 (1) = Р 3 (-2)
Р 3 (1) = 1-3 + а- 2а + 6 = 4-а
Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а
x 3 -Зх 2 -6х + 12 + 6 = х 3 -Зх 2 -6х + 18
x 2 (x-3)-6(x-3) = 0
(х-3)(х 2 -6) = 0
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю, а другой при этом имеет смысл.
3 группа . Корни: -1; 2; 6; 10;
4 группа . Корни: -3; 2; 2; 5;
5 группа . Корни: -5; -2; 2; 4;
6 группа . Корни: -8; -2; 6; 7.
Приложение
Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн.
Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы.
Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.
Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ.
Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий.
Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции.
Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета.
Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории.
В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность.
Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их.
Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи.
Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы.
Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители.
Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение.
В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах.
Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы.
Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная.
Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов.
Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц.
Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид
aх + b = 0 , где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.
Например, все уравнения:
2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.
Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения .
Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.
А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.
Решение любых линейных уравнений сводится к решению уравнений вида
aх + b = 0.
Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим
Если a ≠ 0, то х = ‒ b/a .
Пример 1. Решите уравнение 3х + 2 =11.
Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.
Выполним вычитание, тогда
3х = 9.
Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9: 3.
Значит, значение х = 3 является решением или корнем уравнения.
Ответ: х = 3 .
Если а = 0 и b = 0 , то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.
Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.
Приведем подобные члены:
0х = 0.
Ответ: х — любое число .
Если а = 0 и b ≠ 0 , то получим уравнение 0х = — b.
Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .
Пример 3. Решите уравнение х + 8 = х + 5.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.
Приведем подобные члены:
0х = ‒ 3.
Ответ: нет решений.
На рисунке 1 изображена схема решения линейного уравнения
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.
Пример 4. Пусть надо решить уравнение
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)
3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим
х = 7.
Как видим, корень уравнения равен семи.
Вообще такие уравнения можно решать по следующей схеме :
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;
г) привести подобные члены;
д) решить уравнение вида aх = b,которое получили после приведения подобных членов.
Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2 ), третьего (Пример. 1, 3 ) и даже с пятого этапа, как в примере 5.
Пример 5. Решите уравнение 2х = 1/4.
Находим неизвестное х = 1/4: 2,
х = 1/8 .
Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.
Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.
2х + 6 = 5 – 6х
2х + 6х = 5 – 6
Ответ: ‒ 0, 125
Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.
– 30 + 18х = 8х – 7
18х – 8х = – 7 +30
Ответ: 2,3
Пример 8. Решите уравнение
3(3х – 4) = 4 · 7х + 24
9х – 12 = 28х + 24
9х – 28х = 24 + 12
Пример 9. Найдите f(6), если f (x + 2) = 3 7-х
Решение
Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.
Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.
Если х = 4, тогда
f(6) = 3 7-4 = 3 3 = 27
Ответ: 27.
Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ . Буду рада Вам помочь!
Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0.
Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн , вначале приведите уравнение к общему виду:
ax 2 + bx + c = 0
Заполните соответственно поля формы:
Как решить квадратное уравнение
| Как решить квадратное уравнение: | Виды корней: |
| 1. Привести квадратное уравнение к общему виду: Общий вид Аx 2 +Bx+C=0 Пример: 3х — 2х 2 +1=-1 Приводим к -2х 2 +3х+2=0 2. Находим дискриминант D. 3. Находим корни уравнения. | 1. Действительные корни. Причем. x1 не равно x2 Ситуация возникает, когда D>0 и A не равно 0. 2. Действительные корни совпадают. x1 равно x2 3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1) 1/2 5. Уравнение имеет бесчисленное множество решений. 6. Уравнение решений не имеет. |
Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений .
Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x 2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число 1/2 !
x1=(-В+D 1/2)/2А = (-3+7)/2 = 2
x2=(-В-D 1/2)/2А = (-3-7)/2 = -5
Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10
Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х 2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k 2 – AC = 16 – 16 = 0
X = -k/A = 4
Подставим
(x-4)*(x-4) = (x-4)2 = X 2 – 8x + 16
Пример 3. Решение квадратного уравнения с комплексными корнями.
13х 2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b 2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.
3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
Оператор expand раскроет скобки и разложит выражение, например expand (x – 1)(x2+x+1) приведёт выражение к x3 -2x +1.
Оператор partial fractions разложит отношение многочленов в сумму простейших дробей.
minimize минимизирует функцию, а maximize максимизирует
Число «Пи» записывается, как pi
Тригонометрические функции: sin, cos, tan, ctan, arcsin, arccos, arctan, arcctan
Команда series раскладывает функцию в ряд, например: taylor series sinx at x=0 даст нам разложение функции sin(x) в ряд Тейлора в точке x=0
Производные и интегралы
Чтобы найти предел, необходимо в начале функции подставить lim, а после записать саму функцию, в конце указать к чему стремится предел: as-> далее число (бесконечность записывается infinity).
8
Оператор factor раскладывает число на множители
! выводит факториал, например 123!
Оператор gcd выводит наибольший общий делитель, например gcd 164, 88 выводит наибольший общий делитель чисел 164 и 88
Урок 12. решение алгебраических уравнений разложением на множители — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №12. Решение алгебраических уравнений разложением на множители.
Перечень вопросов, рассматриваемых в теме
1) типы алгебраических уравнений;
2) решение алгебраические уравнения методом разложения на множители;
3) методы решения алгебраических уравнений.
Глоссарий по теме
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над множеством F.
Степенью алгебраического уравнения называют степень многочлена P.
Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Биквадратными называются уравнения вида ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Симметрическим уравнением 3-ей степени называют уравнение вида: ax3 + bx2 + bx + a = 0, где a, b – заданные числа.
Уравнение вида anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что такое алгебраическое уравнение?
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над полем F.
Степенью алгебраического уравнения называют степень многочлена P.
Например, уравнение
является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.
Связанные определения. Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Примеры и разбор решения заданий тренировочного модуля
- Алгебраические уравнения, решаемые разложением на множители:
Пример 1.
x3 – 3x – 2 = 0.
Решение: I способ
D(–2) : ,
Можно догадаться, что число х1 = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.
(х + 1)( х2 –х–2) = 0;
х + 1 = 0 или х2 –х–2 = 0;
х1 = –1 х2,3 = ;
х2,3 = ;
х2 = –1, х3 = 2
Ответ: –1; 2.
II способ
x3 + х2 – х2 – х – 2x – 2 = 0;
(x3 + х2) – (х2 + х) – 2(x + 1) = 0;
х2(х + 1) – х(х + 1) – 2(х + 1) = 0;
(х + 1) (х2 –х–2) = 0;
(х + 1) (х + 1) (х –2) = 0;
(х –2) = 0;
х1 = –1, х2 = 2
Ответ: –1; 2.
- Уравнения, сводящиеся к алгебраическим
- Биквадратные уравнения
На прошлом уроке мы познакомились с данным видом уравнений
Определение. Биквадратными называются уравнения вида ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Метод решения
Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х2.
Новое квадратное уравнение относительно переменной у: ay2+by+c=0.
Решая это уравнение, мы получаем корни квадратного уравнения
y1 и y2.
Решая эти два уравнения (y1=x12 и y2=x12) относительно переменной x, мы получаем корни данного биквадратного уравнения.
Порядок действий при решении биквадратных уравнений
- Ввести новую переменную у=х2
- Подставить данную переменную в исходное уравнение
- Решить квадратное уравнение относительно новой переменной
- После нахождения корней (y1; y2) подставить их в нашу переменную у=х2 и найти исходные корни биквадратного уравнения
Пример 2.
х4 – 8х2 – 9 = 0.
Решение: Пусть у = х2, где у 0; у2 – 8у – 9 = 0;
По формулам Виета:
у1 = –1; у2 = 9;
Первое решение отбрасываем ( у 0),
а из второго находим х1 = –3; х2 = 3.
Ответ: х1 = –3; х2 = 3.
2 Симметрические уравнения
Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.
Симметрическим уравнением 3-ей степени называют уравнение вида ax3 + bx2 + bx + a = 0, где a, b – заданные числа.
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:
10. У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.
(х + 1)(ах2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах2 + (b – а)x + а = 0,
первое уравнение и доказывает интересующее нас утверждение.
20. У симметрического уравнения корней, равных нулю, нет.
30. При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.
Пример 3.
х3 + 2x2 + 2х + 1 = 0.
Решение: У исходного уравнения обязательно есть корень х = –1.
Разлагая далее левую часть на множители, получим
(х + 1)(x2 + х + 1) = 0.
Квадратное уравнение
x2 + х + 1 = 0 не имеет корней.
Ответ: –1.
2 Возвратные уравнения
Уравнение вида anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n.
Рассмотрим возвратное уравнение четвёртой степени вида
ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.
Порядок действий при решении возвратных уравнений вида ax4 + bx3 + cx2 + bx + a = 0:
- разделить левую и правую части уравнения на .
При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения; - группировкой привести полученное уравнение к виду
При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;- ввести новую переменную , тогда выполнено
, то есть ;
в новых переменных рассматриваемое уравнение является квадратным: at2 +bt+c–2a=0;
- решить его относительно t, возвратиться к исходной переменной.
Пример 4
2x4 – 3x3 – 7x2 –15x + 50 = 0.
Решение: Разделим на x2, получим:
Введем замену:
Пусть
тогда 2t2 – 3t – 27 = 0
t=-3 x2+3x+5=0 D<0 | 2×2-9x+10=0 x=2; x=2,5 |
Ответ: .
Решите уравнение:а) (х + 4)2 = 3х + 40; б) (2х
Решите уравнение:
а) (х + 4)2 = 3х + 40; б) (2х — 3)2 = 11х — 19;
в) 3(х + 4)2 = 10x + 82; г) 15х2 + 17 = 15(х + 1)2;
д) (х + 1)2 = 7918 — 2х; е) (х + 2)2 = 3131 — 2х;
ж) (x + 1)2 = (2х — 1)2; з) (х — 2)2 + 48 = (2 — 3х)2.
Решение:
а) (х + 4)2 = 3х + 40; х2 + 8х + 16 — 3х-40 = 0; х2 + 5х — 24 = 0;
D = 25 + 4 • 24 = 25 + 96 = 121; х = (-5±11)/2; x1 = -8; х2 = 3;
б) (2х — 3)2 = 11х — 19; 4х2 — 12х + 9 — 11х + 19 = 0; 4х2 — 23х + 28 = 0;
D = 232 — 4 • 4 • 28 = 529 — 448 = 81; х = (23±9)/8; x1 = 1,75; х2 = 4;
в) 3(х + 4)2 = 10x + 82; 3х2 + 24х + 48 = 10х + 32; 3х2 + 14х + 16 = 0;
D = 72 — 3 • 16 = 49 — 48 = 1; х = (-7±1)/3; x1 = — 2 2/3; х2 = — 2;
г) 15х2 + 17 = 15(х + 1)2; 15х2+ 17 = 15х2 + 30х + 15; 30x = 2; x = 1/15;
д) (х + 1)2 = 7918 — 2х; х2 + 2х + 1 — 7918 + 2х = 0; х2 + 4х — 7917 = 0;
D1 = 22 + 7917 = 7921; х = -2 ± 89; x1 = -91; х2 = 87;
е) (х + 2)2 = 3131 — 2х; х2 + 4х + 4 — 3131 + 2х = 0; х2 + 6х — 3127 = 0;
D1 = 32 + 3127 = 3136; х = -3 ± 56; x1 = -59; х2 = 53;
ж) (x + 1)2 = (2х — 1)2; (2х — 1)2 — (х + 1)2 = 0; (2х — 1 — х — 1) (2х — 1 + x + 1) = 0; (х — 2) • х = 0; х2 — 2х = 0; х(х — 2) = 0; x1 = 0; х2 = 2;
з) (х — 2)2 + 48 = (2 — 3х)2; х2 — 4х + 4 + 48 = 4 — 12х + 9х2; 8х2 — 8х — 48 = 0; х2 — х — б = 0;
D = 1 + 24 = 25; х = (1±5)/2; x1 = -2; х2 = 3.
Похожие задачи:
Внеклассный урок — Уравнения и неравенства с модулем
Уравнения и неравенства с модулемМодулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 6 является 6, модулем числа –6 тоже является 6.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |6|, |х|, |а| и т.д.
(Подробнее – в разделе «Модуль числа»).
Уравнения с модулем.
Пример 1. Решить уравнение
|10х – 5| = 15.
Решение.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
│10х – 5 = 15
│10х – 5 = –15
Решаем:
│10х = 15 + 5 = 20
│10х = –15 + 5 = –10
↕
│х = 20 : 10
│х = –10 : 10
↕
│х = 2
│х = –1
Ответ: х1 = 2, х2 = –1.
Пример 2. Решить уравнение
|2х + 1| = х + 2.
Решение.
Поскольку модуль – число неотрицательное, то х + 2 ≥ 0. Соответственно:
х ≥ –2.
Составляем два уравнения:
│2х + 1 = х + 2
│2х + 1 = –(х + 2)
Решаем:
│2х + 1 = х + 2
│2х + 1 = –х – 2
↕
│2х – х = 2 – 1
│2х + х = –2 – 1
↕
│х = 1
│х = –1
Оба числа больше –2. Значит, оба являются корнями уравнения.
Ответ: х1 = –1, х2 = 1.
Пример 3. Решить уравнение
|х + 3| – 1
————— = 4
х – 1
Решение.
Уравнение имеет смысл, если знаменатель не равен нулю – значит, если х ≠ 1. Учтем это условие. Наше первое действие простое – не просто освобождаемся от дроби, а преобразуем ее так, чтобы получить подмодульное выражение в чистом виде:
|х + 3| – 1 = 4 · (х – 1),
|х + 3| – 1 = 4х – 4,
|х + 3| = 4х – 4 + 1,
|х + 3| = 4х – 3.
Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число – то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:
4х – 3 ≥ 0
4х ≥ 3
х ≥ 3/4
Таким образом, у нас появилось второе условие: корень или корни уравнения должны быть не меньше 3/4.
В соответствии с правилом модуля составляем совокупность двух уравнений и решаем их:
│х + 3 = 4х – 3
│х + 3 = –(4х – 3)
↕
│ х + 3 = 4х – 3
│ х + 3 = –4х + 3
↕
│х – 4х = –3 – 3
│х + 4х = 3 – 3
↕
│х = 2
│х = 0
Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.
У нас было два условия: корень уравнения должен быть не меньше 3/4, но не может быть равен 1. То есть х ≠ 1, х ≥ 3/4.
Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.
Ответ: х = 2.
Неравенства с модулем.
Пример 1. Решить неравенство:
|х — 3| < 4
Решение.
Правило модуля гласит:
|а| = а, если а ≥ 0.
|а| = –а, если а < 0.
Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая:
х – 3 ≥ 0 и х – 3 < 0.
1) При х – 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х – 3 < 4.
2) При х – 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:
–(х – 3) < 4. Раскрыв скобки, получаем:
–х + 3 < 4.
Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:
│ х – 3 ≥ 0
│ х – 3 < 4
и
│ х – 3 < 0
│–х + 3 < 4
Решим их:
│х ≥ 3
│ х < 7
и
│х < 3
│х > –1
Итак, у нас в ответе объединение двух множеств:
3 ≤ х < 7 U –1 < х < 3.
Определяем наименьшее и наибольшее значения. Это –1 и 7. При этом х больше –1, но меньше 7. Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от –1 до 7, исключая эти крайние числа.
Ответ: –1 < х < 7.
Или: х ∈ (–1; 7).
Дополнения.
1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).
Выражение |х — 3| < 4 означает, что расстояние от точки х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа – к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:
–1 < х < 7.
2) Но есть еще одно решение, которое проще даже графического способа.
Для этого наше неравенство надо представить в следующем виде:
–4 < х – 3 < 4.
Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число –4 являются границами решения неравенства.
Далее мы просто переносим влево и вправо число –3 с обратным знаком, оставляя х в одиночестве:
–4 + 3 < х < 4 + 3
–1 < х < 7.
Пример 2. Решить неравенство
|х – 2| ≥ 5
Решение.
Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны –3 и больше или равны 7. А значит, мы уже получили ответ.
Ответ: –3 ≥ х ≥ 7.
Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:
–5 ≥ х – 2 ≥ 5
–5 + 2 ≥ х ≥ 5 + 2
Ответ тот же: –3 ≥ х ≥ 7.
Или: х ∈ [–3; 7]
Пример решен.
Пример 3. Решить неравенство:
6х2 – |х| – 2 ≤ 0
Решение.
Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х < 0. При х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:
6х2 – х – 2 ≤ 0.
Теперь о втором случае: если х < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:
6х2 – (–х) – 2 ≤ 0.
Раскрываем скобки:
6х2 + х – 2 ≤ 0.
Таким образом, мы получили две системы уравнений:
│6х2 – х – 2 ≤ 0
│ х ≥ 0
и
│6х2 + х – 2 ≤ 0
│ х < 0
Надо решить неравенства в системах – а это значит, надо найти корни двух квадратных уравнений.
Для этого приравняем левые части неравенств к нулю.
Начнем с первого:
6х2 – х – 2 = 0.
Как решается квадратное уравнение – см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:
х1 = –1/2, х2 = 2/3.
Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от –1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[–1/2; 2/3].
Теперь решим второе квадратное уравнение:
6х2 + х – 2 = 0.
Его корни:
х1 = –2/3, х2 = 1/2.
Вывод: при х < 0 корнями исходного неравенства являются также все числа от –2/3 до 1/2.
Объединим два ответа и получим итоговый ответ: решением является все множество чисел от –2/3 до 2/3, включая и эти крайние числа.
Ответ: –2/3 ≤ х ≤ 2/3.
Или: х ∈ [–2/3; 2/3].
Показательные уравнения и неравенства
Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ах = аb, где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:
Теорема. Если а > 0, а ≠ 1 и ах1 = ах2, то х1 = х2.
Обоснуем рассмотренное утверждение.
Предположим, что равенство х1 = х2 не выполняется, т.е. х1 < х2 или х1 = х2. Пусть, например, х1 < х2. Тогда если а > 1, то показательная функция у = ах возрастает и поэтому должно выполняться неравенство ах1 < ах2; если 0 < а < 1, то функция убывает и должно выполняться неравенство ах1 > ах2. В обоих случаях мы получили противоречие условию ах1 = ах2.
Рассмотрим несколько задач.
Задача 1.
Решить уравнение 4 ∙ 2х = 1.
Решение.
Запишем уравнение в виде 22 ∙ 2х = 20 – 2х+2 = 20, откуда получаем х + 2 = 0, т.е. х = -2.
Ответ. х = -2.
Задача 2.
Решить уравнение 23х ∙ 3х = 576.
Решение.
Так как 23х = (23)х = 8х, 576 = 242, то уравнение можно записать в виде 8х ∙ 3х = 242 или в виде 24х = 242.
Отсюда получаем х = 2.
Ответ. х = 2.
Задача 3.
Решить уравнение 3х+1 – 2∙3х — 2 = 25.
Решение.
Вынося в левой части за скобки общий множитель 3х — 2, получаем 3х — 2 ∙ (33 – 2) = 25 – 3х — 2∙ 25 = 25,
откуда 3х — 2 = 1, т.
е. х – 2 = 0, х = 2.
Ответ. х = 2.
Задача 4.
Решить уравнение 3х = 7х.
Решение.
Так как 7х ≠ 0, то уравнение можно записать в виде 3х/7х = 1, откуда (3/7)х = 1, х = 0.
Ответ. х = 0.
Задача 5.
Решить уравнение 9х – 4 ∙ 3х – 45 = 0.
Решение.
Заменой 3х = а данное уравнение сводится к квадратному уравнению а2 – 4а – 45 = 0.
Решая это уравнение, находим его корни: а1 = 9, а2 = -5, откуда 3х = 9, 3х = -5.
Уравнение 3х = 9 имеет корень 2, а уравнение 3х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ. х = 2.
Решение показательных неравенств часто сводится к решению неравенств ах > аb или ах < аb.
Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции.
Рассмотрим некоторые задачи.
Задача 1.
Решить неравенство 3х < 81.
Решение.
Запишем неравенство в виде 3х < 34. Так как 3 > 1, то функция у = 3х является возрастающей.
Следовательно, при х < 4 выполняется неравенство 3х < 34, а при х ≥ 4 выполняется неравенство 3х ≥ 34.
Таким образом, при х < 4 неравенство 3х < 34 является верным, а при х ≥ 4 – неверным, т.е. неравенство
3х < 81 выполняется тогда и только тогда, когда х < 4.
Ответ. х < 4.
Задача 2.
Решить неравенство 16х +4х – 2 > 0.
Решение.
Обозначим 4х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.
Это неравенство выполняется при t < -2 и при t > 1.
Так как t = 4х, то получим два неравенства 4х < -2, 4х > 1.
Первое неравенство не имеет решений, так как 4х > 0 при всех х € R.
Второе неравенство запишем в виде 4х > 40, откуда х > 0.
Ответ. х > 0.
Задача 3.
Графически решить уравнение (1/3)х = х – 2/3.
Решение.
1) Построим графики функций у = (1/3)х и у = х – 2/3.
2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что
х = 1 – корень данного уравнения:
(1/3)1 = 1/3 и 1 – 2/3 = 1/3.
Иными словами, мы нашли один из корней уравнения.
3) Найдем другие корни или докажем, что таковых нет. Функция (1/3)х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х < 1, наоборот, значения первой функции больше 1/3, а второй – меньше 1/3.
Геометрически это означает, что графики этих функций при х > 1 и х < 1 «расходятся» и потому не могут иметь точек пересечения при х ≠ 1.
Ответ. х = 1.
!!! Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3)х > х – 2/3 выполняется при х < 1, а неравенство (1/3)х < х – 2/3 – при х > 1.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Учебное пособие по калькулятору алгебры— MathPapa
Это руководство по использованию калькулятора алгебры , пошагового калькулятора для алгебры.
Решение уравнений
Сначала перейдите на главную страницу Калькулятора алгебры. В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить.
Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле.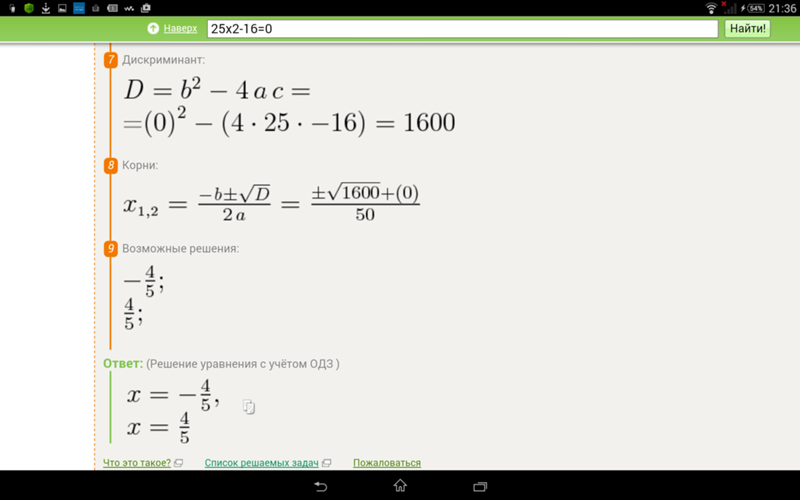
(экспонента: «в степени»)
Построение графика
Для построения графика уравнения введите уравнение, которое начинается с «y =» или «x =».2.
Вычисление выражений
Калькулятор алгебры может вычислять выражения, содержащие переменную x.
Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите подставить для x. Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6.
Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y.Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите вычислить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4).
Проверка ответов для решения уравнений
Так же, как калькулятор алгебры можно использовать для вычисления выражений,
Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x.
В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Поскольку ответ правильный, калькулятор алгебры показывает зеленый знак равенства.
Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно».
Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенных точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y.Пример: x + y = 7; х + 2у = 11 @ (3,4).
Режим планшета
Если вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру.
Статьи по теме
Вернуться к калькулятору алгебры »
Как найти набор решений
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.
Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Решение линейных уравнений с нулевым Солнцем, Без Солнца и «Все-x» Солнцем
Purplemath
Есть три типа решений, которые могут вызвать путаницу.
Мы рассмотрим по одному примеру каждого из них, и я объясню различия. Затем мы поработаем над смесью типов уравнений, чтобы вам было удобнее различать типы решений.
Чтобы решить это уравнение, мне сначала нужно упростить левую часть, взяв «минус» в скобки и объединив «похожие» термины:
MathHelp.com
5 — (3 x + 4)
5 — 1 (3 x ) — 1 (+4)
5 — 3 x — 4
5 — 4 — 3 x
1-3 x
Теперь я могу решить обычным способом:
1–3x = 1
-1 -1
————
-3x = 0
— —
-3-3
х = 0
Является ли « x = 0» допустимым решением? Да, действительно, потому что ноль — допустимое число.
Дело не в том, что решение — «ничто»; дело в том, что решение — это «что-то», а это «что-то» равно нулю. Итак, мой ответ:
Студенты, как правило, могут привыкнуть к тому, что ноль является решением уравнения, но разница между решением «ноль» (это решение является числовым значением) и «ничего» (возможно, является физической мерой чего-то вроде «без яблок» или «нет денег») может вызвать недоумение.
Убедитесь, что вы понимаете, что «ноль» сам по себе не является «ничем». Ноль — это числовое значение, которое (в «реальной жизни» или в контексте словесной проблемы) может означать , что нет «ничего» чего-то или другого, но сам ноль — реальная вещь; это существует; это что-то».
Решить 11 + 3
x -7 = 6 x + 5-3 x
Во-первых, объедините одинаковые термины; затем решите:
Гм.
.. подожди минутку …
С каких это пор четыре когда-либо равно пяти? Никогда! Существует ли какое-либо возможное значение x , которое «исправит» это уравнение, чтобы оно говорило что-то, имеющее смысл? Будет ли любое значение x когда-либо заставить это уравнение работать?
Нет; это просто невозможно. Я выполнил все свои шаги правильно, но эти шаги привели к уравнению (а) без переменных и (б) не имело смысла.Поскольку не существует значения x , которое заставило бы это уравнение работать, то и решения этого уравнения нет. Вот мой ответ на это упражнение:
. Вот логика приведенного выше примера: когда вы пытаетесь решить уравнение, вы исходите из (неустановленного) предположения, что на самом деле — это решение. Когда вы в конечном итоге получаете чушь (например, бессмысленное уравнение «4 = 5» выше), это означает, что ваше первоначальное предположение (а именно, что исходное уравнение действительно имело решение) было неверным; на самом деле решения нет.
Поскольку утверждение «4 = 5» совершенно неверно, и с момента нет значения x, которое когда-либо могло бы сделать его истинным , то это уравнение не имеет решения.
Advisory: этот ответ полностью отличается от ответа на первое упражнение вверху этой страницы, где было , значение x , что будет работать (это значение решения равно нулю). Не путайте эти две очень разные ситуации : «решение существует и имеет нулевое значение» никоим образом не то же самое, что «никакого значения решения не существует вообще».
И не путайте приведенное выше уравнение типа «без решения» со следующим типом уравнения:
Решить 6
x + 5-2 x = 4 + 4 x + 1
Сначала я объединю похожие термины; тогда решу:
Для предыдущего уравнения я получил «5 = 4», и не было значения x , которое могло бы сделать уравнение истинным.
Этот результат противоположен этому. Существует ли какое-либо возможное значение x для этого уравнения, которое может сделать приведенное выше утверждение ложным? Нет; 5 равно , всегда будет равно 5. Фактически, поскольку в последней строке вычислений нет « x », значение x явно не имеет отношения к уравнению; x может быть чем угодно, и уравнение останется верным. Итак, решение:
Это решение также может быть указано как «все действительные числа», «все действительные числа», «вся числовая строка», «(–∞, + ∞)» или « x ∈ & reals;» (последнее означает « x является членом набора действительных чисел»).Вы должны ожидать увидеть некоторые вариации в жаргоне от одного учебника к другому, поэтому не удивляйтесь различиям в форматировании.
Обратите внимание, что, если бы я решил уравнение вычитанием 5 из любой части исходного уравнения, я бы получил:
Другими словами, я бы получил еще одно тривиально верное утверждение.
Я также мог бы вычесть 4 x с любой стороны, или я мог бы разделить обе части приведенного выше уравнения на 4, или я мог бы разделить на 4, а затем вычесть x с любой стороны, или я мог бы вычесть как 4 x , так и 5 с обеих сторон исходного уравнения.Каждый из них — это еще один способ получить другой тривиально верный результат, например «0 = 0». Но независимо от конкретных предпринятых шагов результат (тривиально верное уравнение) всегда будет одним и тем же, и решение останется тем же: «все x ».
Поскольку (как я перечислил выше) существует множество способов прийти к одному и тому же выводу для этого типа уравнения, вы не должны удивляться, если для уравнений «все действительные числа» или «без решения» вы не используйте те же шаги, что и некоторые из ваших одноклассников.Существует бесконечно много всегда верных уравнений (например, «0 = 0») и бесконечно много бессмысленных уравнений (например, «3 = 4»), также будет много способов (правильно) прийти к этим ответам.
Основным выводом из приведенных выше примеров должны быть следующие правила:
x = 0: регулярное решение регулярного уравнения
чушь (например, 3 = 4): нет решения
тривиально верно (например, 0 = 0): решение — все действительные числа
К сожалению, хотя вы почти наверняка встретите хотя бы один из этих вопросов типа «нет решения» или «все реально» в следующем тесте (и, вероятно, также в финале), обычно их не так много в наборе домашних заданий, и ваш инструктор, вероятно, предоставил только по одному образцу каждого типа.Это не дает вам большой практики в интерпретации этих типов решений, поэтому давайте еще несколько примеров.
Во-первых, я умножу 3 на скобку в левой части. Потом решу.
3x + 12 = 3x + 11
-3x -3x
——————
12 = 11
Моя математика верна, но результат — ерунда.Двенадцать никогда не будет равняться одиннадцати. Итак, мой ответ:
Решите 6 — 2 (
x + 3) = –2 x
Я буду умножать и упрощать в левой части. Потом решу.
6-2 (x + 3) = -2x
6 — 2x — 6 = -2x
6-6 — 2x = -2x
0 — 2x = -2x
-2x = -2x
+ 2x + 2x
———
0 = 0
Ноль всегда будет равняться нулю, и в последней строке моей работы нет даже какой-либо переменной, поэтому переменная явно не имеет значения.Это уравнение верно независимо от значения x . Итак, мой ответ:
Решите 2 (
x + 1) + x = 3 ( x + 2) — 2
Мне нужно умножить и упростить каждую часть этого уравнения.
2 (х + 1) + х = 3 (х + 2) — 2
2х + 2 + х = 3х + 6 — 2
2х + х + 2 = 3х + 4
3х + 2 = 3х + 4
-3x -3x
———————-
2 = 4
Нет; никогда не правда.
Решить 5
x + 7 = 4 (2 x + 1) — 3 x -2
Мне нужно упростить правую часть, а затем посмотреть, к чему это приведет.
5x + 7 = 4 (2x + 1) — 3x — 2
5x + 7 = 8x + 4 — 3x — 2
5x + 7 = 8x — 3x + 4-2
5х + 7 = 5х + 2
-5x -5x
——————
7 = 2
Нет; никогда не правда.
Я разверну левую часть, а затем решу.
8 (x + 2) = 2x + 16
8х + 16 = 2х + 16
-2x -2x
——————
6x + 16 = 16
-16 -16
——————
6x + 0 = 0
—— —
6 6
х = 0
Это уравнение действительно имеет значение решения , равное нулю.
Решить 1,5
x + 4 = 4 ( x + 1) — 2,5 x
Я расширяю и упрощаю в правой части, а затем решаю.
1,5x + 4 = 4 (x + 1) — 2,5x
1,5x + 4 = 4x + 4 — 2,5x
1,5x + 4 = 4x — 2,5x + 4
1.5х + 4 = 1,5х + 4
-1,5x -1,5x
———————
4 = 4
Это всегда правда, поэтому мой ответ:
Я разверну левую часть, а затем решу.
2 (x + 5) = 2x + 5
2x + 10 = 2x + 5
-2x -2x
——————
10 = 5
Нет; никогда не правда.
URL: https://www.purplemath.com/modules/solvelin5.htm
уравнений абсолютных значений
уравнений абсолютных значений Уравнения абсолютных значенийВыполните следующие действия, чтобы найти равенство абсолютных значений который содержит одно абсолютное значение:
- Выделите абсолютное значение на одной стороне уравнения.
- Число на другой стороне уравнения отрицательное? Если вы ответили утвердительно, то уравнение не имеет решения. Если вы ответили нет, переходите к шагу 3.
- Напишите два уравнения без абсолютных значений. Первое уравнение установит количество внутри столбцов, равное количеству на другом сторона знака равенства; второе уравнение установит количество внутри столбцы равны противоположному числу на другой стороне.
- Решите два уравнения.
Выполните следующие действия, чтобы найти абсолютное значение равенства
который содержит два абсолютных значения (по одному с каждой стороны уравнения):
- Напишите два уравнения без абсолютных значений. Первый уравнение установит количество внутри столбцов с левой стороны равным количество внутри полос с правой стороны. Второе уравнение установит количество внутри столбцов с левой стороны равным противоположному количества внутри полос с правой стороны.
- Решите два уравнения.
Давайте рассмотрим несколько примеров.
Пример 1: Решить | 2x — 1 | + 3 = 6
| Шаг 1: Изолировать абсолютное значение | | 2x — 1 | + 3 = 6 | 2x — 1 | = 3 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 3, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 2x — 1 = 3 | 2х — 1 = -3 |
| Шаг 4: Решить оба уравнения | 2x — 1 = 3 2x = 4 х = 2 | 2х — 1 = -3 2x = -2 х = -1 |
Пример 2: Решить | 3x — 6 | — 9 = -3
| Шаг 1: Изолировать абсолютное значение | | 3х — 6 | — 9 = -3 | 3x — 6 | = 6 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 6, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 3x — 6 = 6 | 3х — 6 = -6 |
| Шаг 4: Решить оба уравнения | 3x — 6 = 6 3x = 12 х = 4 | 3х — 6 = -6 3x = 0 х = 0 |
Пример 3: Решить | 5x + 4 | + 10 = 2
| Шаг 1: Изолировать абсолютное значение | | 5x + 4 | + 10 = 2 | 5x + 4 | = -8 |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Да, это отрицательное число, -8.Нет решения к этой проблеме. |
Пример 4: Решить | x — 7 | = | 2x — 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 7 = 2х — 2 | х — 7 = — (2х — 2) |
| Шаг 4: Решить оба уравнения | х — 7 = 2х — 2 -x — 7 = -2 -x = 5 х = -5 | х — 7 = -2x + 2 3x — 7 = 2 3x = 9 х = 3 |
Пример 5: Решить | x — 3 | = | x + 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = х + 2 | х — 3 = — (х + 2) |
| Шаг 4: Решить оба уравнения | х — 3 = х + 2 — 3 = -2 ложное заявление Нет решения из этого уравнения | х — 3 = -x — 2 2x — 3 = -2 2x = 1 х = 1/2 |
Итак, единственное решение этой проблемы — x = 1/2
Пример 6: Решить | x — 3 | = | 3 — x |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = 3 — х | х — 3 = — (3 — х) |
| Шаг 4: Решить оба уравнения | х — 3 = 3 — х 2x — 3 = 3 2x = 6 х = 3 | х — 3 = — (3 — х) х — 3 = -3 + х -3 = -3 Все действительные числа являются решениями этого уравнения |
Поскольку 3 входит в набор действительных чисел, мы просто скажем, что решение этого уравнения — все действительные числа
Математическая сцена — Уравнения III — Урок 2
Математическая сцена — Уравнения III — Урок 2 — Квадратные уравнения| 2008 Rasmus ehf и Jhann sak Ptursson | Уравнения III |
Урок 2 Уравнения кубической и четвертой степени
Как мы можем решить уравнения, такие как кубическое уравнение показано здесь?
x 3 — x 2 4x + 4 = 0
Существует чрезвычайно сложная формула решения кубические уравнения.Некоторые калькуляторы имеют встроенную формулу и поэтому могут использоваться для решения кубических уравнений.
Мы собираемся узнать, как эти уравнения могут быть решены с помощью факторизация. Если уравнение имеет решения, которые являются целыми числами a, b и c, то мы можем разложить уравнение на множители следующим образом:
x 3 — x 2 4x + 4 = (x — а) (х — б) (х — в) = 0
Умножая скобки, видим, что константа член 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе.
abc = 4
Все решения a, b и c должны быть множителями 4, поэтому не так много целых чисел, которые нам нужно учитывать.
У нас есть только следующие возможности:
1, 2 и 4
Хорошо изучите каждое из этих чисел, чтобы найти, какие являются решениями уравнения.
f (1) = 1 3 — 1 2 4 × 1 + 4 = 0 1 — решение
f (-1) = (-1) 3 — (-1) 2 4 × (-1) + 4 = 6
f (2) = 2 3 — 2 2 4 × 2 + 4 = 0 2 — решение
f (−2) = (−2) 3 — (−2) 2 4 × (−2) + 4 = 0 −2 — решение
Мы нашли три решения, поэтому нам не нужно попробуйте 4 и −4 как кубический уравнение имеет максимум три решения.
Эти три числа дают нам значения a, b и c и мы можем факторизовать уравнение.
x 3 — x 2 4x + 4 = (x — 1) (х — 2) (х + 2) = 0
Этот метод включает поиск целых чисел, которые являются множителями
(можно разделить на) постоянный член, а затем проверить,
целые числа являются решениями уравнения.
К сожалению, мы не можем предполагать, что решения уравнения третьей степени являются
все целые числа.
Однако, если мы можем найти одно целочисленное решение, допустим, что это x = a, тогда
теорема остатка, мы знаем, что (x — a) является фактором уравнения. Мы
можно найти другой множитель, квадратичный множитель, путем деления. Затем мы можем решить квадратное уравнение, используя
формула решения квадратичных.
Пример 1
Решите уравнение x 3 — 3x 2 2x + 4 = 0
Ставим числа, кратные 4 в уравнение, чтобы проверить, верны ли какие-либо из них.
f (1) = 1 3 — 3 × 1 2 2 × 1 + 4 = 0 1 — решение
f (−1) = (−1) 3 — 3 × (−1) 2 2 × (-1) + 4 = 2
f (2) = 2 3 — 3 × 2 2 2 × 2 + 4 = −4
f (−2) = (−2) 3 — 3 × (−2) 2 2 × (−2) + 4 = −12
f (4) = 4 3 — 3 × 4 2 2 × 4 + 4 = 12
f (−4) = (−4) 3 — 3 × (−4) 2 2 × (−4) + 4 = −100
Единственное целочисленное решение — x = 1.Когда мы нашли одно решение, нам действительно не нужно проверять другие числа, потому что теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить квадратичный получаем из деления.
Теперь мы можем разложить наши выражение следующим образом:
x 3 — 3x 2 2x + 4 = (х — 1) (х 2 — 2х — 4) = 0
Теперь нам остается решить квадратичную уравнение.
x 2 — 2x — 4 = 0
Воспользуемся формулой квадратичных с a = 1, b = −2 и c = −4.
Мы нашли все три решения уравнение x 3 — 3x 2 2x + 4 = 0. Это: эфтирфаранди:
.х = 1
х = 1 + 5
x = 1- 5
Пример 2
Мы можем легко использовать тот же метод для решения уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f (x) = x 4 — x 3 — 5x 2 + 3x + 2 = 0.
Сначала мы находим целые множители постоянный член, 2. Целочисленные множители 2 равны 1 и 2.
f (1) = 1 4 — 1 3 — 5 × 1 2 + 3 × 1 + 2 = 0 1 — раствор
f (−1) = (−1) 4 — (−1) 3 — 5 × (−1) 2 + 3 × (−1) + 2 = −4
f (2) = 2 4 — 2 3 — 5 × 2 2 + 3 × 2 + 2 = −4
f (−2) = (−2) 4 — (−2) 3 — 5 × (−2) 2 + 3 × (−2) + 2 = 0 ср. нашли второй решение.
Два найденных нами решения 1 и −2 означают, что мы можем разделить на x —
1 и x + 2, и остатка не будет. Сделайте это в два этапа.
Сначала разделим на x + 2
Теперь разделите полученный кубический коэффициент по x — 1.
Теперь мы разложили на множители
f (x) = x 4 — x 3 — 5x 2 + 3x + 2 в
f (x) = (x + 2) (x — 1) (x 2 — 2x — 1) и только
Осталось решить квадратное уравнение
x 2 — 2x — 1 = 0.Мы используем формула с a = 1, b = −2 и c = −1.
Всего мы нашли четыре решения. Их:
х = 1
х = −2
х = 1 +
х = 1 —
Иногда мы можем решить уравнение третьей степени, заключив в скобки члены два на два и найдя множитель что у них общего.Давайте посмотрим на это на примере.
Пример 3.
Решите уравнение x 3 — 2x 2 — 4x + 8 = 0
x 3 — 2x 2 — 4x + 8 = 0 (x 3 — 2x 2 ) — (4x — 8) = 0 [x 2 (x — 2) — 4 (x — 2)] = 0 (x — 2) [x 2 — 4] = 0 (х — 2) (х — 2) (х + 2) = 0 | Здесь скобка (x — 2) является общим множителем и может быть вынесена за пределы общая скобка. |
Обратите внимание, что скоба (x — 2) происходит дважды, когда мы закончили факторизацию. x = 2 — это поэтому двойное решение, и у нас есть только два разных:
х = 2 и х = -2 .Лауснир: x = 2 og x = −2 .
Примеры, которые мы рассмотрели до сих пор, являются уравнения, в которых член с наибольшей степенью имеет коэффициент 1.
Как мы иметь дело с уравнениями, где этот коэффициент — какое-то другое число?
Общая форма — f (x) = ax 3 + bx 2 + cx + d, где a, b, c и d — целые числа.
Мы можем искать целочисленные решения в том же как и раньше, проверяя факторы постоянного члена d. Если мы найдем целочисленное решение, тогда мы можем разделить и найти другие решения, как и раньше.
Если ни один из факторов d не дает нам решения
затем мы ищем решения, которые являются дробями.
Предположим, что существует дробное решение, и назовем его
решение x = t / n.
Это означает, что x — t / n является фактором f (x), или, если мы умножаем на n, то xn — t является множителем.
Теперь предположим, что мы разделили f (x) на xn.
— t и нашли квадратичный множитель, мы можем назвать его
Ax 2 + Bx + C.
Теперь у нас есть результат
ax 3 + bx 2 + cx + d = (xn — t) (Ax 2 + Bx + C)
сравнивая коэффициенты x 3 на
обе стороны уравнения мы видим, что a = nA и, следовательно, n должно быть множителем
а.
Аналогичным образом, сравнивая постоянные члены, мы видим, что
d = −tC и, следовательно, t является фактором d.
Мы заключаем, что любая дробь является решением кубическое уравнение ax 3 + bx 2 + cx + d должен иметь вид t / n, где t — множитель числа d, а n — фактор числа a.
Обобщение для функции степени n:
ф (х) = a n x n + a n − 1 x n − 1 + × × × × + а 1 х + 0
с коэффициентами a 0 , а 1 , а 2 , × × × × × а n − 2 , n − 1 и n .
Если эта функция имеет рациональное решение, скажем, t / n, тогда t — коэффициент 0 , а n — коэффициент n .
Пример 4
Решите уравнение f (x) = 2x 3 — 7x 2 + 4x + 3 = 0.
Возможные целые корни f (x) — это делители 3, это 1 и 3. Дроби, которые могут быть корнями, — это эти четыре числа, разделенные на множители 2.Итак, полный список рациональных чисел, которые нам нужно рассмотреть, — это , 1, 3 / 2 и 3.Сразу видно, что нам не нужно рассмотрите любые отрицательные значения, поскольку все они будут давать отрицательные значения для f (x), а не 0.
Теперь попробуем другие возможностиf () = 2 () 3 — 7 () 2 + 4 × + 3 = 3
f (1) = 2 × 1 3 -7 × 2 + 4 × 1 + 3 = 2
ф ( 3 / 2 ) = 2 ( 3 / 2 ) 3 -7 ( 3 / 2 ) 2 + 4 × 3 / 2 + 3 = 0, поэтому мы нашли решение.
x = 3 / 2 — решение, поэтому (x — 3 / 2 ) является множителем. Разделить на (x — 3 / 2 ) может быть сложно. Поэтому мы умножаем на 2 и вместо этого делим на (2x — 3). Если (x — 3 / 2 ) является фактор
, то (2x — 3).
Теперь нам нужно решить уравнение x 2 — 2x — 1 = 0.Мы уже решили это уравнение в примере 2. Решения: 1 + 2 og 1 — 2.
Итак, мы нашли три решения. Их:
х = 3 / 2 = 1
х = 1 + 2
х = 1 — 2
Попробуйте пройти тест 2 по уравнениям III.
Не забудьте использовать контрольный список для следите за своей работой.
Решение рациональных уравнений
Решение рациональных уравнений
Рациональное уравнение Уравнение, содержащее по крайней мере одно рациональное выражение.уравнение, содержащее хотя бы одно рациональное выражение. Рациональные выражения обычно содержат переменную в знаменателе. По этой причине мы позаботимся о том, чтобы знаменатель не был равен 0, отметив ограничения и проверив наши решения.
Решите рациональные уравнения, удаляя дроби, умножая обе части уравнения на наименьший общий знаменатель (LCD).
Пример 1: Решить: 5x − 13 = 1x.
Решение: Сначала отметим, что x ≠ 0, а затем умножим обе стороны на ЖК-дисплей, 3 x :
Проверьте свой ответ, заменив 12 на x , чтобы убедиться, что вы получили истинное утверждение.
Ответ: Решение — 12.
После умножения обеих частей предыдущего примера на ЖК-дисплей нам осталось решить линейное уравнение.Это не всегда так; иногда мы останемся с квадратным уравнением.
Пример 2: Решить: 2−1x (x + 1) = 3x + 1.
Решение: В этом примере есть два ограничения: x ≠ 0 и x ≠ −1. Начните с умножения обеих сторон на ЖК-дисплей, x (x + 1).
После распределения и деления общих множителей остается квадратное уравнение. Чтобы решить эту проблему, перепишите его в стандартной форме, коэффициент, а затем установите каждый коэффициент равным 0.
Проверьте, решают ли эти значения исходное уравнение.
Ответ: Решения -1/2 и 1.
До этого момента все возможные решения решали исходное уравнение. Однако это может быть не всегда. Умножение обеих сторон уравнения на переменные множители может привести к посторонним решениям. Решение, которое не решает исходное уравнение, то есть решения, которые не решают исходное уравнение.Полный список шагов для решения рационального уравнения представлен в следующем примере.
Пример 3: Решить: xx + 2 + 2×2 + 5x + 6 = 5x + 3.
Решение:
Шаг 1: Разложите все знаменатели на множители и определите ЖК-дисплей.
ЖК-дисплей равен (x + 2) (x + 3).
Шаг 2: Определите ограничения. В данном случае это x ≠ −2 и x ≠ −3.
Шаг 3: Умножьте обе части уравнения на ЖК-дисплей. Распространяйте осторожно, а затем упрощайте.
Шаг 4: Решите полученное уравнение. Результатом является квадратное уравнение. Перепишите его в стандартной форме с коэффициентом, а затем установите каждый коэффициент равным 0.
Шаг 5: Проверьте наличие посторонних решений. Всегда подставляйте в исходное уравнение или его факторизованный эквивалент.В этом случае выберите факторный эквивалент для проверки:
Здесь −2 — постороннее решение, не входящее в набор решений. Важно отметить, что −2 — это ограничение.
Ответ: Решение — 4.
Если этот процесс приводит к решению, которое является ограничением, игнорируйте его как постороннее решение.
Попробуй! Решите: xx − 5 + 3x + 2 = 7xx2−3x − 10.
Ответ: −3
Иногда все потенциальные решения являются посторонними, и в этом случае мы говорим, что решения исходного уравнения не существует. В следующих двух примерах мы демонстрируем два способа, по которым рациональное уравнение не может иметь решений.
Пример 4: Решить: 3xx2−4−2x + 2 = 1x + 2.
Решение: Чтобы идентифицировать ЖК-дисплей, сначала разложите знаменатели на множители.
Умножьте обе стороны на наименьший общий знаменатель (LCD), (x + 2) (x − 2), аккуратно распределив.
Уравнение противоречит и поэтому не имеет решения.
Ответ: Нет решения, ∅
Пример 5: Решите: xx − 4−4x + 5 = 36×2 + x − 20.
Решение: Сначала разложите знаменатели на множители.
Обратите внимание, что ограничения x ≠ 4 и x ≠ −5. Чтобы очистить дроби, умножьте на ЖК-дисплей (x − 4) (x + 5).
Оба эти значения являются ограничениями исходного уравнения; следовательно, оба посторонние.
Ответ: Нет решения, ∅
Попробуй! Решите: 1x + 1 + xx − 3 = 4xx2−2x − 3.
Ответ:
∅Важно отметить, что этот метод очистки алгебраических дробей работает только для уравнений. Не пытайтесь очищать алгебраические дроби при упрощении выражений. Напоминаем, что у нас
Необходимо упростить выражения и решить уравнения.Если мы умножим выражение на ЖК-дисплей, x (2x + 1), мы получим другое выражение, которое не эквивалентно.
Буквенные уравнения
Буквальные уравнения или формулы часто являются рациональными уравнениями. Следовательно, методы, описанные в этом разделе, могут использоваться для решения конкретных переменных. Предположим, что все выражения переменных в знаменателе отличны от нуля.
Пример 6: Решите относительно x : z = x − 5y.
Решение: Цель — выделить x . Предполагая, что y ненулевое значение, умножьте обе стороны на y и затем прибавьте 5 к обеим сторонам.
Ответ: x = yz + 5
Пример 7: Решите относительно c : 1c = 1a + 1b.
Решение: В этом примере цель состоит в том, чтобы изолировать c . Мы начинаем с умножения обеих сторон на ЖК-дисплей, a⋅b⋅c, осторожно распределяя.
В правой части уравнения вычтем c .
Затем разделите обе части уравнения на величину (b + a).
Ответ: c = abb + a
Попробуй! Решите относительно y : x = y + 1y − 1.
Ответ: y = x + 1x − 1
Основные выводы
- Начните решать рациональные уравнения с умножения обеих частей на ЖК-дисплей.Полученное эквивалентное уравнение может быть решено с использованием методов, изученных до этого момента.
- Умножение обеих сторон рационального уравнения на выражение переменной вводит возможность посторонних решений. Следовательно, мы должны проверять решения на соответствие множеству ограничений. Если решение является ограничением, то оно не является частью домена и не имеет отношения к делу.
- При умножении обеих частей уравнения на выражение, аккуратно распределите и умножьте каждый член на это выражение.
- Если все полученные решения являются посторонними, то исходное уравнение не имеет решений.
Тематические упражнения
Часть A: Рациональные уравнения
Решить.
1. 12 + 1x = 18
2. 13−1x = 29
3. 13x − 23 = 1x
4. 25x − 1x = 310
5. 12x + 1 = 5
6.33x − 1 + 4 = 5
7. 2x − 3x + 5 = 2x + 5
8. 5x2x − 1 = x − 12x − 1
9. 5x − 7 = 6x − 9
10. 5x + 5 = 3x + 1
11. x6−6x = 0
12. 5x + x5 = −2
13. хх + 12 = 2х
14. 2xx + 5 = 16 − x
15. 1x + x2x + 1 = 0
16. 9x3x − 1−4x = 0
17. 1−2x = 48×2
18. 2−9x = 5×2
19.1 + 12x = 12x − 2
20. 1−3x − 5x (3x − 4) = — 1x
21. x2 = 14x + 3
22. 3×2 = х + 13 − х
23. 6 = −3x + 3x − 1
24. 12x − 2 = 2 + 6 (4 − x) x − 2
25. 2 + 2xx − 3 = 3 (x − 1) x − 3
26. xx − 1 + 16x − 1 = x (x − 1) (6x − 1)
27. 12×2−81 = 1x + 9−2x − 9
28. 14×2−49 = 2x − 7−3x + 7
29. 6xx + 3 + 4x − 3 = 3xx2−9
30.3xx + 2−17x − 2 = −48×2−4
31. х − 1 + 3 = 0
32. 4 − y − 1 = 0
33. y − 2−4 = 0
34. 9x − 2−1 = 0
35,3 (x − 1) −1 + 5 = 0
36,5−2 (3x + 1) −1 = 0
37. 3 + 2x − 3 = 2x − 3
38. 1x = 1x + 1
39. хх + 1 = х + 1x
40. 3x − 13x = xx + 3
41. 4x − 7x − 5 = 3x − 2x − 5
42. xx2−9 = 1x − 3
43.3x + 4x − 8−28 − x = 1
44. 1x = 6x (x + 3)
45. 3x = 1x + 1 + 13x (x + 1)
46. xx − 1−34x − 1 = 9x (4x − 1) (x − 1)
47. 1x − 4 + xx − 2 = 2×2−6x + 8
48. xx − 5 + x − 1×2−11x + 30 = 5x − 6
49. xx + 1−65×2 + 4x − 1 = −55x − 1
50. −8×2−4x − 12 + 2 (x + 2) x2 + 4x − 60 = 1x + 2
51. xx + 2−20×2 − x − 6 = −4x − 3
52. х + 7x − 1 + x − 1x + 1 = 4×2−1
53.х − 1x − 3 + x − 3x − 1 = −x + 5x − 3
54. х − 2x − 5 − x − 5x − 2 = 8 − xx − 5
55. х + 7x − 2−81×2 + 5x − 14 = 9x + 7
56. хх − 6 + 1 = 5х + 3036 − х2
57. 2xx + 1−44x − 3 = −74×2 + x − 3
58. x − 5x − 10 + 5x − 5 = −5xx2−15x + 50
59. 5×2 + 5x + 4 + x + 1×2 + 3x − 4 = 5×2−1
60. 1×2−2x − 63 + x − 9×2 + 10x + 21 = 1×2−6x − 27
61. 4×2−4 + 2 (x − 2) x2−4x − 12 = x + 2×2−8x + 12
62. x + 2×2−5x + 4 + x + 2×2 + x − 2 = x − 1×2−2x − 8
63.6xx − 1−11x + 12×2 − x − 1 = 6x2x + 1
64. 8x2x − 3 + 4x2x2−7x + 6 = 1x − 2
Часть B: Буквальные уравнения
Решите для указанной переменной.
65. Решите относительно r : t = Dr.
66. Решить относительно b : h = 2Ab.
67. Решите относительно P : t = IPr.
68. Решить относительно π: r = C2π.
69. Решите относительно c : 1a = 1b + 1c.
70. Решим относительно y : m = y − y1x − x1.
71. Решите относительно w : P = 2 (l + w).
72. Решите относительно t : A = P (1 + rt).
73. Решите относительно м : s = 1n + m.
74. Решить относительно S : h = S2πr − r.
75. Решите относительно x : y = xx + 2.
76. Решите относительно x : y = 2x + 15x.
77.Решите относительно R : 1R = 1R1 + 1R2.
78. Решите относительно S1: 1f = 1S1 + 1S2.
Часть C: Обсуждение
79. Объясните, почему умножение обеих частей уравнения на ЖК-дисплей иногда дает посторонние решения.
80. Объясните связь между методом перекрестного умножения и умножением обеих частей рационального уравнения на ЖК-дисплей.
81. Объясните, как мы можем отличить рациональное выражение от рационального уравнения.Как мы относимся к ним по-другому?
ответов
1: −8/3
3: -1
5: −2/5
7: 5/2
9: −3
11: −6, 6
13: −4, 6
15: -1
17: −6, 8
19: −4, 6
21: −7, 4
23:
25:
27: −39
29: 4/3, 3/2
31: -1/3
33: -1/2, 1/2
35: 2/5
37:
39: -1/2
41:
43: −7
45: 5
47: -1
49:
51: −4
53: 5/3
55:
57: 1/2
59: −6, 4
61: 10
63: 1/3
65: r = Dt
67: P = Itr
69: c = abb − a
71: ш = P − 2l2
73: m = 1 − sns
75: х = 2y1 − y
77: R = R1R2R1 + R2
Решение уравнения абсолютных значений
Далее мы узнаем, как решить уравнение для абсолютных значений .Чтобы решить такое уравнение, как [latex] | 2x — 6 | = 8 [/ latex], мы замечаем, что абсолютное значение будет равно 8, если количество внутри столбцов абсолютного значения равно [latex] 8 [/ latex] или [латекс] -8 [/ латекс]. Это приводит к двум различным уравнениям, которые мы можем решить независимо.
[латекс] \ begin {array} {lll} 2x — 6 = 8 \ hfill & \ text {или} \ hfill & 2x — 6 = -8 \ hfill \\ 2x = 14 \ hfill & \ hfill & 2x = — 2 \ hfill \\ x = 7 \ hfill & \ hfill & x = -1 \ hfill \ end {array} [/ latex]
Полезно знать, как решать проблемы, связанные с функциями абсолютного значения.Например, нам может потребоваться определить числа или точки на линии, которые находятся на заданном расстоянии от заданной контрольной точки.
Общее примечание: уравнения абсолютных значений
Абсолютное значение x записывается как [latex] | x | [/ latex]. Он имеет следующие свойства:
[латекс] \ begin {array} {l} \ text {If} x \ ge 0, \ text {then} | x | = x. \ Hfill \\ \ text {If} x <0, \ text {тогда } | x | = -x. \ hfill \ end {array} [/ latex]
Для действительных чисел [латекс] A [/ латекс] и [латекс] B [/ латекс], уравнение вида [латекс] | A | = B [/ латекс] с [латексом] B \ ge 0 [/ latex], будут решения, когда [latex] A = B [/ latex] или [latex] A = -B [/ latex].Если [latex] B <0 [/ latex], уравнение [latex] | A | = B [/ latex] не имеет решения.
Уравнение абсолютного значения в форме [latex] | ax + b | = c [/ latex] имеет следующие свойства:
[латекс] \ begin {array} {l} \ text {If} c <0, | ax + b | = c \ text {не имеет решения}. \ Hfill \\ \ text {If} c = 0, | ax + b | = c \ text {имеет одно решение}. \ hfill \\ \ text {If} c> 0, | ax + b | = c \ text {имеет два решения}. \ hfill \ end {array} [ / латекс]
Как: решить уравнение абсолютного значения.
- Изолировать выражение абсолютного значения по одну сторону от знака равенства.
- Если [latex] c> 0 [/ latex], запишите и решите два уравнения: [latex] ax + b = c [/ latex] и [latex] ax + b = -c [/ latex].
Пример 8: Решение уравнений абсолютных значений
Решите следующие уравнения абсолютных значений:
а. [латекс] | 6x + 4 | = 8 [/ латекс]
б. [латекс] | 3x + 4 | = -9 [/ латекс]
c. [латекс] | 3x — 5 | -4 = 6 [/ латекс]
г. [латекс] | -5x + 10 | = 0 [/ латекс]
Решение
а. [латекс] | 6x + 4 | = 8 [/ латекс]
Напишите два уравнения и решите каждое:
[латекс] \ begin {array} {ll} 6x + 4 \ hfill & = 8 \ hfill & 6x + 4 \ hfill & = — 8 \ hfill \\ 6x \ hfill & = 4 \ hfill & 6x \ hfill & = — 12 \ hfill \\ x \ hfill & = \ frac {2} {3} \ hfill & x \ hfill & = — 2 \ hfill \ end {array} [/ latex]
Два решения: [латекс] x = \ frac {2} {3} [/ latex], [latex] x = -2 [/ latex].
г. [латекс] | 3x + 4 | = -9 [/ латекс]
Нет решения, так как абсолютное значение не может быть отрицательным.
г. [латекс] | 3x — 5 | -4 = 6 [/ латекс]
Выделите выражение абсолютного значения и запишите два уравнения.
Leave A Comment