Равномерное движение
Формула скорости движения при равномерном движении: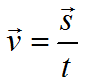
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: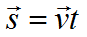
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле: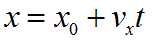
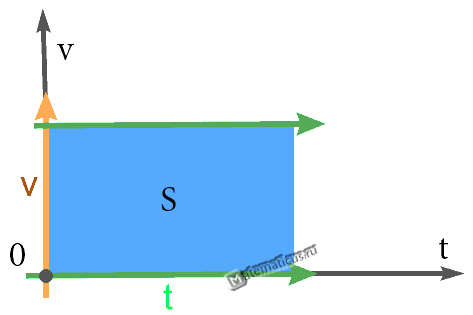
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении: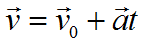
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с2
Формула для нахождения перемещения при равноускоренном движении: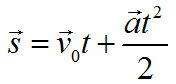
или
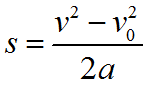
Уравнение равноускоренного движения в проекции на оси координат:
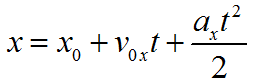
Формула для определения ускорения при равноускоренном прямолинейном движении:
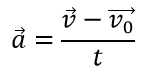
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:
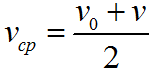
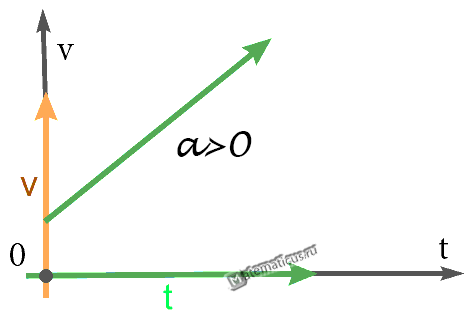
График — Равноускоренное движение при a>0
Равнозамедленное движение
Формула скорости при равнозамедленном движении:
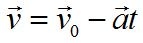
Формула перемещения при равнозамедленном движении:
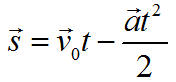
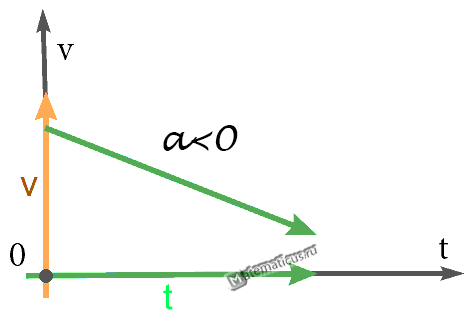
График — Равнозамедленное движение при a<0
Свободное падение
Постоянная величина скорости свободного падения тела равна g=9,8 м/с
Формула для вычисления скорости при свободном падении тела: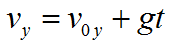
Формула для вычисления перемещения при свободном падении тела: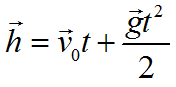
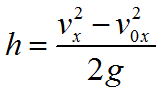
Формула координаты при свободном падении тела: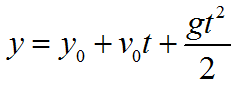
Формула высоты с которой тело свободно падает:
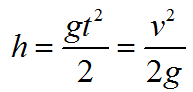
Формула для определения скорости тела в конце свободного падения:
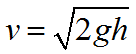
Время свободного падения тела равно:
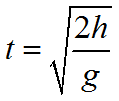
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
Репетитор-онлайн — подготовка к ЦТ
Пример 2. Материальная точка движется вдоль оси Ox. Проекция ее скорости с течением времени меняется по закону v = 9,0 − 1,5t, где скорость задана в метрах в секунду, время — в секундах. Определить путь, пройденный материальной точкой за интервал времени от 4,0 с до 7,0 с.
Решение. При равнопеременном движении зависимость проекции скорости от времени имеет вид:
vx = v0x + axt,
где v0x = 9,0 м/с — проекция начальной скорости; ax = −1,5 м/с2 — проекция ускорения на указанную координатную ось.
Запишем уравнение движения материальной точки:
x(t)=x0+v0xt+axt22=x0+9,0t−0,75t2,
где x0 — начальная координата точки.
Точка остановки, вычисленная по формуле
τост=v0a=9,01,5=6,0 c,
попадает в интервал времени, указанный в условии задачи.
В интервале времени от t1 = 4,0 c до τост = 6,0 с точка движется равнозамедленно. Следовательно, пройденный путь вычисляем по формуле
S1=|x(τост)−x(t1)|,
где
x ( τ ост ) = x 0 + 9,0 τ ост − 0,75 τ ост 2 =
=x0+9,0⋅6,0−0,75⋅(6,0)2=(x0+27) м;
x(t1)=x0+9,0t1−0,75t12=x0+9,0⋅4,0−0,75⋅(4,0)2=(x0+24) м.
Таким образом, путь S1, пройденный материальной точкой в указанном интервале времени, равен:
S1=|x(τост)−x(t1)|=|(x0+27)−(x0+24)|=3,0 м.
В интервале времени от τост = 6,0 с до t2 = 7,0 c точка движется равноускоренно. Следовательно, пройденный путь вычисляем по формуле
S1=|x(t2)−x(τост)|,
где
x ( τ ост ) = x 0 + 9,0 τ ост − 0,75 τ ост 2 =
=x0+9,0⋅6,0−0,75⋅(6,0)2=(x0+27) м;
x ( t 2 ) = x 0 + 9,0 t 2 − 0,75 t 2 2 =
=x0+9,0⋅7,0−0,75⋅(7,0)2=(x0+26,25) м.
Таким образом, путь S2, пройденный материальной точкой в указанном интервале времени, равен:
S2=|x(t2)−x(τост)|=|(x0+26,25)−(x0+27)|=0,75 м≈0,8 м.
Суммарный путь S, пройденный материальной точкой в интервале времени от 4,0 с до 7,0 с, составляет
S=S1+S2≈3,0+0,8=3,8 м.
Равнозамедленное движение Википедия
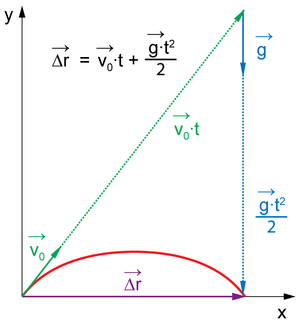 Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения
Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного паденияРавноуско́ренное движе́ние — движение тела, при котором его ускорение a → {\displaystyle {\vec {a}}} постоянно по модулю и направлению[1].
Скорость при этом определяется формулой
- v → ( t ) = v → 0 + a → t {\displaystyle {\vec {v}}(t)={\vec {v}}_{0}+{\vec {a}}t} ,
где v → 0 {\displaystyle {\vec {v}}_{0}} — начальная скорость тела, t {\displaystyle t} — время. Траектория имеет вид участка параболы или прямой.
Примером такого движения является полёт камня, брошенного под углом α {\displaystyle \alpha } к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением a → = g → {\displaystyle {\vec {a}}={\vec {g}}} , направленным вертикально вниз.
Частным случаем равноускоренного движения является равнозамедленное, когда векторы v → {\displaystyle {\vec {v}}} и a → {\displaystyle {\vec {a}}} противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для α = 90 0 {\displaystyle \alpha =90^{0}} при подъёме).
Содержание
- 1 Характер равноускоренного движения
- 2 Перемещение и скорость
- 3 Условие осуществления
- 4 Теорема о кинетической энергии точки
- 5 Криволинейное равноускоренное движение
- 6 См. также
Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / tМгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
= ‘
Проекция вектора скорости на ось ОХ:
vx = x’это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
= ' = "Учитывая, что 0 – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
Отсюда формула скорости равнопеременного движения в любой момент времени:
= 0 + tЕсли тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axtЗнак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = vВысота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна: В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
Равнозамедленное движение Википедия
Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного паденияРавноуско́ренное движе́ние — движение тела, при котором его ускорение a → {\displaystyle {\vec {a}}} постоянно по модулю и направлению[1].
Скорость при этом определяется формулой
- v → ( t ) = v → 0 + a → t {\displaystyle {\vec {v}}(t)={\vec {v}}_{0}+{\vec {a}}t} ,
где v → 0 {\displaystyle {\vec {v}}_{0}} — начальная скорость тела, t {\displaystyle t} — время. Траектория имеет вид участка параболы или прямой.
Примером такого движения является полёт камня, брошенного под углом α {\displaystyle \alpha } к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением a → = g → {\displaystyle {\vec {a}}={\vec {g}}} , направленным вертикально вниз.
Частным случаем равноускоренного движения является равнозамедленное, когда векторы v → {\displaystyle {\vec {v}}} и a → {\displaystyle {\vec {a}}} противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для α = 90 0 {\displaystyle \alpha =90^{0}} при подъёме).
Характер равноускоренного движения
Равноускоренное движение происходит в плоскости, содержащей векторы ускорения a → {\displaystyle {\vec {a}}} и начальной скорости v → 0 {\displaystyle {\vec {v}}_{0}} . С учётом того, что v → = d r → / d t {\displaystyle {\vec {v}}={\rm {d}}{\vec {r}}/{\rm {d}}t} (здесь r → {\displaystyle {\vec {r}}} — радиус-вектор), траектория описывается выражением
- r → ( t ) = r → 0 + v → 0 t + a → t 2 2 {\displaystyle {\vec {r}}(t)={\vec {r}}_{0}+{\vec {v}}_{0}t+{\frac {{\vec {a}}t^{2}}{2}}} .
На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со- или противо- направленности) векторов a → {\displaystyle {\vec {a}}} и v → 0 {\displaystyle {\vec {v}}_{0}} превращается в отрезок прямой.
Для каждой из координат, скажем y {\displaystyle y} , могут быть записаны аналогичные по структуре выражения:
- y ( t ) = y 0 + v 0 y t + a y t 2 2 {\displaystyle y(t)=y_{0}+v_{0y}t+{\frac {a_{y}t^{2}}{2}}} ,
где a y {\displaystyle a_{y}} — составляющая ускорения вдоль оси y {\displaystyle y} , а r → 0 = x 0 i → + y 0 j → + z 0 k → {\displaystyle {\vec {r}}_{0}=x_{0}{\vec {i}}+y_{0}{\vec {j}}+z_{0}{\vec {k}}} — радиус-вектор материальной точки в момент t = 0 {\displaystyle t=0} ( i → {\displaystyle {\vec {i}}} , j → {\displaystyle {\vec {j}}} , k → {\displaystyle {\vec {k}}} — орты).
В примере с камнем x 0 = y 0 = z 0 = 0 {\displaystyle x_{0}=y_{0}=z_{0}=0} , компоненты ускорения a x = a z = 0 {\displaystyle a_{x}=a_{z}=0} , a y = − g {\displaystyle a_{y}=-g} , начальной скорости v x 0 = v 0 cos α {\displaystyle v_{x0}=v_{0}\cos \alpha } , v y 0 = v 0 sin α {\displaystyle v_{y0}=v_{0}\sin \alpha } , v z 0 = 0 {\displaystyle v_{z0}=0} , при этом x ( t ) = v 0 x t {\displaystyle x(t)=v_{0x}t} , а значит, y = tg α ⋅ x − g / 2 v 0 2 cos 2 α ⋅ x 2 {\displaystyle y=\operatorname {tg} \alpha \cdot x-g/2v_{0}^{2}\cos ^{2}\alpha \cdot x^{2}} .
Перемещение и скорость
В случае равноускоренного движения любая из компонент скорости, например v x {\displaystyle v_{x}} , зависит от времени линейно:
- v x = v 0 x + a x t {\displaystyle v_{x}=v_{0x}+a_{x}t} .
При этом имеет место следующая связь между перемещением ( Δ x = x − x 0 {\displaystyle \Delta x=x-x_{0}} ) вдоль координаты x {\displaystyle x} и скоростью вдоль той же координаты:
- Δ x = v x 2 − v 0 x 2 2 a x {\displaystyle \Delta x={\frac {v_{x}^{2}-v_{0x}^{2}}{2a_{x}}}} .
Отсюда можно получить выражение для x {\displaystyle x} -составляющей конечной скорости тела при известных x {\displaystyle x} -составляющих начальной скорости и ускорения:
- v x = ± v 0 x 2 + 2 a x Δ x {\displaystyle v_{x}=\pm {\sqrt {v_{0x}^{2}+2a_{x}\Delta x}}} .
Если a x = 0 {\displaystyle a_{x}=0} , то v x = v o x {\displaystyle v_{x}=v_{ox}} , а Δ x = v 0 x t {\displaystyle \Delta x=v_{0x}t} .
Выражения для смещений Δ y {\displaystyle \Delta y} , Δ z {\displaystyle \Delta z} и компонент скорости вдоль координат y {\displaystyle y} и z {\displaystyle z} принимают точно такой же вид, как для Δ x {\displaystyle \Delta x} и v x {\displaystyle v_{x}} , но символ x {\displaystyle x} всюду заменяется на y {\displaystyle y} или z {\displaystyle z} .
Суммарно, по теореме Пифагора, перемещение составит
- | Δ r → | = ( Δ x ) 2 + ( Δ y ) 2 + ( Δ z ) 2 {\displaystyle |\Delta {\vec {r}}|={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}}}} ,
а модуль конечной скорости находится как
- | v → | = v x 2 + v y 2 + v z 2 {\displaystyle |{\vec {v}}|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}} .
Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени t {\displaystyle t} , модуль скорости тела | v → | {\displaystyle |{\vec {v}}|} превысит величину скорости света в вакууме c {\displaystyle c} , что исключается теорией относительности.
Условие осуществления
Равноускоренное движение реализуется при действии на тело (материальную точку) постоянной силы F → {\displaystyle {\vec {F}}} , обычно в однородном гравитационном или электростатическом поле, если величина скорости тела значительно меньше, чем скорость света c {\displaystyle c} . Тогда, по второму закону Ньютона, ускорение составит
- a → = F → m , {\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}
где через m {\displaystyle m} обозначена масса тела. В примере с камнем роль F → {\displaystyle {\vec {F}}} играет сила тяжести.
Если же скорость тела сопоставима со скоростью света, то закон Ньютона в выписанном виде неприменим. При этом, в случае действия постоянной силы, происходит так называемое релятивистски равноускоренное движение, при котором постоянно только собственное ускорение, а ускорение в фиксированной ИСО приближается к нулю со временем по мере приближения величины скорости к её пределу c {\displaystyle c} .
Теорема о кинетической энергии точки
Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:
- m a x Δ x = m v x 2 2 − m v 0 x 2 2 {\displaystyle ma_{x}\Delta x={\frac {mv_{x}^{2}}{2}}-{\frac {mv_{0x}^{2}}{2}}} .
Записав аналогичные соотношения для координат y {\displaystyle y} и z {\displaystyle z} и просуммировав все три равенства, получим соотношение:
- F → ⋅ Δ r → = m v 2 2 − m v 0 2 2 {\displaystyle {\vec {F}}\cdot \Delta {\vec {r}}={\frac {mv^{2}}{2}}-{\frac {mv_{0}^{2}}{2}}} .
Слева стоит работа постоянной равнодействующей силы F → {\displaystyle {\vec {F}}} , а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения[2].
Криволинейное равноускоренное движение
Криволинейным равноускоренным (равнопеременным) называется движение по любой кривой, при котором составляющая ускорения, параллельная скорости, является постоянной. Такое движение не подпадает под определение равноускоренного, но в математическом плане может быть рассмотрено аналогично.
В этом случае вводится обобщённая координата S {\displaystyle S} , часто называемая путём. Эта координата соответствует длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:
- Δ S = v 2 − v 0 2 2 a τ {\displaystyle \Delta S={\frac {v^{2}-v_{0}^{2}}{2a_{\tau }}}} ,
где a τ {\displaystyle a_{\tau }} — тангенциальное ускорение, которое «отвечает» за изменение модуля скорости тела. Для скорости получаем:
- v = ± v 0 2 + 2 a τ Δ S {\displaystyle v=\pm {\sqrt {v_{0}^{2}+2a_{\tau }\Delta S}}} .
При a τ = 0 {\displaystyle a_{\tau }=0} имеем движение с постоянной по модулю скоростью.
См. также
Равноускоренное движениеПримечания
Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.
Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:
- вектор скорости тела при равнопеременном движении
(1)
- где
- вектор перемещения тела при равнопеременном движении
(2)
- где
- — вектор перемещения тела
Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.
Рис. 1. Равноускоренное движение 1
Пример 1. Тело движется прямо с начальной скоростью и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:
- Для уравнения (1):
- Для уравнения (2):
В общем случае, мы не можем предугадать направления векторов и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.
Рис. 2. Равноускоренное движение-2
Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения () направлен против оси OX (рис. 2). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 3. Равноускоренное движение-3
Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения () направлен против движения, а значит, по оси OX (рис. 3). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 4. Равноускоренное движение-4
Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения () направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.
Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:
(3)
Подставим (3) в (2) при условии :
= = =
(4)
Таким образом, мы получили формулу, в которой нет параметра времени.
Поделиться ссылкой:
Превышение скорости в камере даст вам возможность добиться красивой замедленной работы в посте. Но если вы не будете следовать правильной формуле в комнате редактирования, ваши результаты будут не идеальными.
Правило 180-градусного затвора гласит, что ваша выдержка затвора должна быть в два раза больше, чем ваша частота кадров. Итак, если вы снимаете в режиме 24p, вам нужно, чтобы скорость затвора была установлена на 1/48. Если ваша выдержка выше или ниже, вы получите нежелательные результаты — резкий «эффект быстрого кадра» или размытость в замедленном режиме.
Если вы снимали какое-то время, то это может быть для вас второй натурой. Но в комнате редактирования все может запутаться для кинематографистов…

Давайте предположим, что вы захватили клип 48 кадров в секунду с выдержкой 1/96. В посте, если бы вы замедлили этот клип до 50%, вы бы получили идеальный эффект замедленного воспроизведения, поскольку он будет эффективно воспроизводиться со скоростью 24 кадра в секунду с выдержкой 1/48. Но если вы вообще не замедлили этот клип и просто поместили его на временную шкалу 24 кадра в секунду, вы, по сути, работали бы с кадром, эквивалентным 24p, с выдержкой 1/96 вместо 1/48.Это придаст вашим кадрам такой быстрый вид, который я описал ранее, и явно не будет соответствовать правилу выдержки 180 градусов.
Суть всего этого в том, что очень важно, чтобы знал точный процент, необходимый для замедления отснятого материала в посте , чтобы выдержать этот поворот на 180 градусов. Пример 48 кадров в секунду является простым, поскольку он в два раза больше, чем 24 кадра в секунду.

Вот некоторые из общих скоростей перевыпуска кадров с соответствующими процентами, до которых они должны быть снижены в посте (в проекте / графике 24p):
- 30 кадр / с = 80%
- 48 кадр / с = 50%
- 60fps = 40%
- 80 кадр / с = 30%
- 96 кадр / с = 25%
- 100 кадр / с = 24%
- 120fps = 20%
- 150fps = 16%
- 180fps = 13%
- 240fps = 10%
Если вы работаете с частотой кадров, которой нет в этом списке, вы можете просто использовать эту формулу для расчета целевого процента:
24 / Количество FPS = Процент замедленного движения.
И, конечно, если вы снимаете с другой частотой кадров (например, 25 кадров в секунду PAL или 30 кадров в секунду NTSC), просто используйте частоту кадров вашего проекта вместо «24» в формуле. В приведенном ниже видео от пользователя Vimeo — jL подробно объясняется скорость затвора, а также приведены отличные примеры того, как различные скорости затвора будут влиять на ваши кадры.
У вас есть какие-нибудь дополнительные советы для видеооператоров и режиссеров? Поделитесь ими в комментариях ниже!
,Procectile Motion — Определение и Формула | Снаряд
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классам
- Учебная записка по 12-му классу
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
- ML Решения Aggarwal Class 10 Maths
- ML Решения Aggarwal Class 9 Математика
- ML Решения Aggarwal Class 8 Maths
- ML Решения Aggarwal Class 7 Математические решения
- ML 6 0004
- ML 6
- Selina Solution для 8 класса
- Selina Solutions для 10 класса
- Selina Solution для 9 класса 9
- Frank Solutions для класса 10 Maths
- Frank Solutions для класса 9 Maths
- IAS 2019 Mock Test 1
- IAS 2019 Mock Test 2
- KPSC KAS экзамен
- UPPSC PCS экзамен
- MPSC экзамен
- RPSC RAS экзамен
- TNPSC группа 1
- APPSC группа 1
- BPSC экзамен
- экзамен
- экзамен
- WPSS
- экзамен
- WPSS
- экзамен
- JPS
- экзамен
- экзамен
- PMS
- экзамен
- PMS
- экзамен
- экзамен
- экзамен
- 9000
- Ключ ответа UPSC 2019
- IA S Коучинг Бангалор
- IAS Коучинг Дели
- IAS Коучинг Ченнаи
- IAS Коучинг Хайдарабад
- IAS Коучинг Мумбаи
- Бумага
- JEE JEE 9000
- JEE
- JEE-код
- JEE J0003 S0004000
- JEE Вопрос бумаги
- бином
- JEE Статьи
- Квадратное уравнение
- BYJU’S NEET Программа
- NEET 2020
- NEET КРИТЕРИИ 2020
- NEET Примеры Papers
- NEET Подготовка
- NEET Программа курса
- Поддержка
- Жалоба Разрешение
- Customer Care
- Поддержка центр
- GSEB
- GSEB Силабус
- GSEB Вопрос бумаги
- GSEB образец бумаги
- GSEB Книги
- MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- MSBSHSE Образцы документов
- MSBSHSE Вопросные записки
- AP Board
- -й год APSERT
- -й год SBSUS
- -й год
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS SUBSUS
- SUBSUS SUBSUS
- SUBSUS SUBSUS
SUBSUS
- MP Board Syllabus
- MP Board Образцы документов
- MP Board Учебники
- Assam Board Syllabus
- Assam Board Учебники Sample Board Paperss
- Бихарская доска Syllabus
- Бихарская доска Учебники
- Бихарская доска Вопросные бумаги
- Бихарская модель Бумажные макеты
- доска
- Sislabus
- Совет 9408 S0008
- Sisplus
- S0008
- Sample P000S
- Sample
- S000S PSEB Syllabus
- учебники PSEB
- учебные материалы PSEB
- учебное пособие Раджастхан Syllabus
- учебники RBSE
- учебные вопросы RBSE
- JKBOSE Программа курса
- JKBOSE Примеры Papers
- JKBOSE экзамен Pattern
- TN Совет Силабус
- TN Совет вопрос Papers
- TN Board Примеры Papers
- Samacheer Kalvi Книги
- JAC Силабус
- JAC учебники
- JAC Вопрос Papers
- Telangana Совет Силабус
- Telangana совет учебники
- Telangana Совет Вопрос Papers
- KSEEB KSEEB Силабус
- KSEEB Модель Вопрос Papers
- KBPE Силабус
- KBPE Учебники
- KBPE Вопрос Papers
- UP Совет Силабус
- UP Совет Книги
- UP Совет Вопрос Papers
- Западная Бенгалия Совет Силабус
- Западная Бенгалия Совет учебниками
- West Bengal совет Вопрос документы
- Банк экзаменов
- SBI Exams
- PIL, Exams
- RBI Exams
- PIL, РРБ экзамен
- SSC Exams
- SSC JE
- SSC GD
- SSC CPO 900 04
- SSC CHSL
- SSC CGL
- RRB экзаменов
- RRB JE
- RRB NTPC
- RRB ALP
- L0003000000 L0003000000000000 UPSC CAPF
- Список государственных экзаменов Статьи
- Класс 1
- Класс 2
- Класс 3
- Физические вопросы
- Вопросы химии
- Химические вопросы
- Химические вопросы
- Вопросы химии
- Химические науки
- Вопросы химии
- Вопросы
- Вопросы по науке
- Вопросы ГК
- Обучение на дому
- Программа CAT BYJU’S
- CAT
- CAT
- CAT
- CAT
- CAT
- CAT
- CAT
- CAT
- FreeBS 40004 CAT 2020 Exam Pattern
- Физика
- Вывод физических формул
- Diff.Между в физике
- Использование в физике
- Типы и классификация
- Соотношение между в физике
- Значение констант
- Константы в физике
- Физика Искусство
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология

Leave A Comment