8 класс. Геометрия. Окружность. Вписанный угол. Центральный угол. — Взаимное расположение прямой и окружности.
Комментарии преподавателяНапомним важное определение – определение окружности]
Определение:
Окружностью с центром в точке О и радиусом R называют множество всех точек плоскости, удаленных от точки О на расстояние R.
Обратим внимание на то, что окружностью называют именно множество всех точек, удовлетворяющих описанному условию. Рассмотрим пример:
Точки A, B, C, D квадрата равноудалены от точки Е, но они не являются окружностью (рис. 1).
Рис. 1. Иллюстрация к примеру
В данном случае фигура является окружностью, так как это все множество точек, равноудаленных от центра.
Если соединить любые две точки окружности – получаем хорду. Хорда, проходящая через центр, называется диаметром.
MB – хорда; АВ – диаметр; MnB – дуга, она стягивается хордой МВ;
Угол называется центральным.
Точка О – центр окружности.
Рис. 2. Иллюстрация к примеру
Таким образом, мы вспомнили, что такое окружность и основные ее элементы. Теперь перейдем к рассмотрению взаимного расположения окружности и прямой.
Задана окружность с центром О и радиусом r. Прямая Р, расстояние от центра до прямой, то есть перпендикуляр ОМ, равна d.
Считаем, что точка О не лежит на прямой Р.
По заданным окружности и прямой нам необходимо найти число общих точек.
В первом случае, когда расстояние d меньше радиуса окружности r, точка М лежит внутри окружности. От этой точки мы отложим два отрезка – МА и МВ, длинна которых будет . Значения r и d нам известны, d меньше r, значит, выражение существует и точки А и В существуют. Эти две точки лежат на прямой по построению. Проверим, лежат ли они на окружности. Вычислим по теореме Пифагора расстояние ОА и ОВ:
Значения r и d нам известны, d меньше r, значит, выражение существует и точки А и В существуют. Эти две точки лежат на прямой по построению. Проверим, лежат ли они на окружности. Вычислим по теореме Пифагора расстояние ОА и ОВ:
Рис. 3. Иллюстрация к случаю 1
Расстояние от центра до двух точек равно радиусу окружности, таким образом, мы доказали, что точки А и В принадлежат окружности.
Итак, точки А и В принадлежат прямой по построению, принадлежат окружности по доказанному – окружность и прямая имеют две общих точки. Докажем, что других точек нет (рис. 4).
Рис. 4. Иллюстрация к доказательству
Для этого возьмем на прямой произвольную точку С и предположим, что она лежит на окружности – расстояние ОС=r. В таком случае треугольник равнобедренный и его медиана ON, которая не совпадает с отрезком ОМ, является высотой.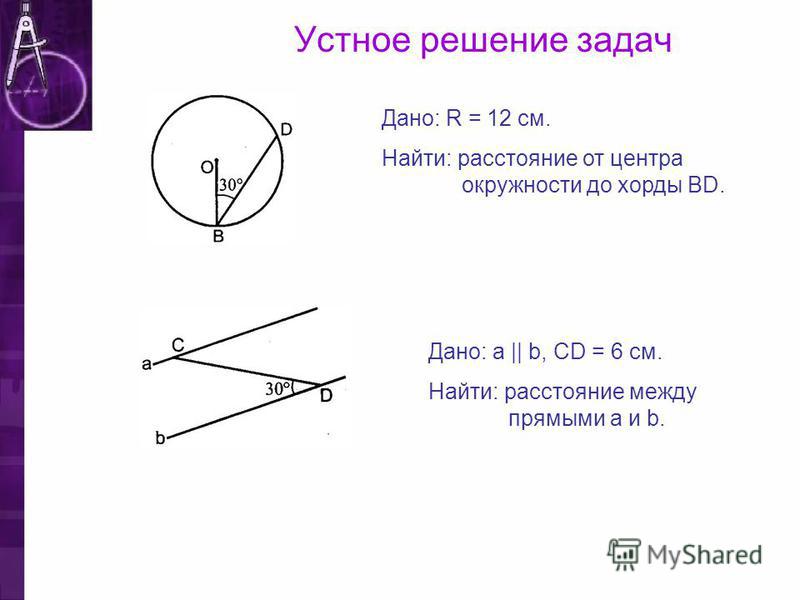
Таким образом, на прямой Р нет других общих точек с окружностью. Мы доказали, что в случае, когда расстояние d меньше радиуса окружности r, прямая и окружность имеют только две общие точки.
Случай второй – расстояние от центра окружности до прямой равно радиусу окружности (рис. 5):
Рис. 5. Иллюстрация к случаю 2
Напомним, что расстояние от точки до прямой – это длина перпендикуляра, в данном случае ОН – перпендикуляр. Так как, по условию, длина ОН равна радиусу окружности, то точка Н принадлежит окружности, таким образом, точка Н общая для прямой и окружности.
Докажем что других общих точек нет. От противного: предположим, что точка С на прямой принадлежит окружности. В таком случае, расстояние ОС равно r, и тогда ОС равно ОН. Но в прямоугольном треугольнике гипотенуза ОС больше катета ОН. Получили противоречие. Таким образом, предположение неверно и нет никакой точки кроме Н, общей для прямой и окружности. Мы доказали, что в данном случае общая точка единственная.
Получили противоречие. Таким образом, предположение неверно и нет никакой точки кроме Н, общей для прямой и окружности. Мы доказали, что в данном случае общая точка единственная.
Случай 3 – расстояние от центра окружности до прямой больше радиуса окружности:
Расстояние от точки до прямой – длина перпендикуляра. Проводим из точки О перпендикуляр к прямой Р, получаем точку Н, которая не лежит на окружности, так как ОН по условию больше радиуса окружности. Докажем, что любая другая точка прямой не лежит на окружности. Это хорошо видно из прямоугольного треугольника , гипотенуза ОМ которого больше катета ОН, а значит, больше радиуса окружности, таким образом, точка М не принадлежит окружности, как и любая другая точка на прямой. Мы доказали, что в данном случае окружность и прямая не имеют общих точек (рис. 6).
Рис. 6. Иллюстрация к случаю 3
6. Иллюстрация к случаю 3
Рассмотрим теорему. Предположим, что прямая АВ имеет две общих точки с окружностью (рис. 7).
Рис. 7. Иллюстрация к теореме
Имеем хорду АВ. Точка Н, по условию, – середина хорды АВ и лежит на диаметре СD.
Требуется доказать, что в таком случае диметр перпендикулярен хорде.
Доказательство:
Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как .
Точка Н, по условию, – середина хорды, значит середина медианы АВ равнобедренного треугольника. Мы знаем, что медиана равнобедренного треугольника перпендикулярна его основанию, значит, является высотой: , отсюда , таким образом, доказано, что диаметр, проходящий через середину хорды, перпендикулярен ей.
Справедлива и обратная теорема: если диаметр перпендикулярен хорде, то он проходит через ее середину.
Задана окружность с центром О, ее диаметр СD и хорда АВ. Известно, что диаметр перпендикулярен хорде, нужно доказать, что он проходит через ее середину (рис. 8).
Рис. 8. Иллюстрация к теореме
Доказательство:
Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как . ОН, по условию, – высота треугольника, так как диаметр перпендикулярен хорде. Высота в равнобедренном треугольнике одновременно является медианой, таким образом, АН=НВ, значит, точка Н является серединой хорды АВ, значит, доказано, что диаметр, перпендикулярный хорде, проходит через ее середину.
Прямую и обратную теорему можно обобщить следующим образом.
Теорема:
Диаметр перпендикулярен хорде тогда и только тогда, когда он проходит через ее середину.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/okruzhnost/vzaimnoe-raspolozhenie-pryamoy-i-okruzhnosti
http://www. youtube.com/watch?v=knZu5-MW6QA
youtube.com/watch?v=knZu5-MW6QA
http://ppt4web.ru/uploads/ppt/1402/c3c8c0e3fde2cce4bcb6ddc8ca3a978b.ppt
http://player.myshared.ru/1246878/data/images/img10.jpg
http://www.kmrz.ru/catimg/40/400239.jpg
| Развернуть структуру обучения | Свернуть структуру обучения |
| Определение хордыХорда — это отрезок, который соединяет две точки заданной кривой.  Хорда может быть у дуги, окружности, эллипса и т.д. Хорда может быть у дуги, окружности, эллипса и т.д. На рисунке хорда обозначена как отрезок AB красного цвета. Оба его конца находятся на окружности Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Свойства хорды к окружности
Свойства хорды и вписанного углаНа рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности — AB
Свойства хорды и центрального углаНа рисунке [2] центральный угол обозначен как AOB, хорда как AB.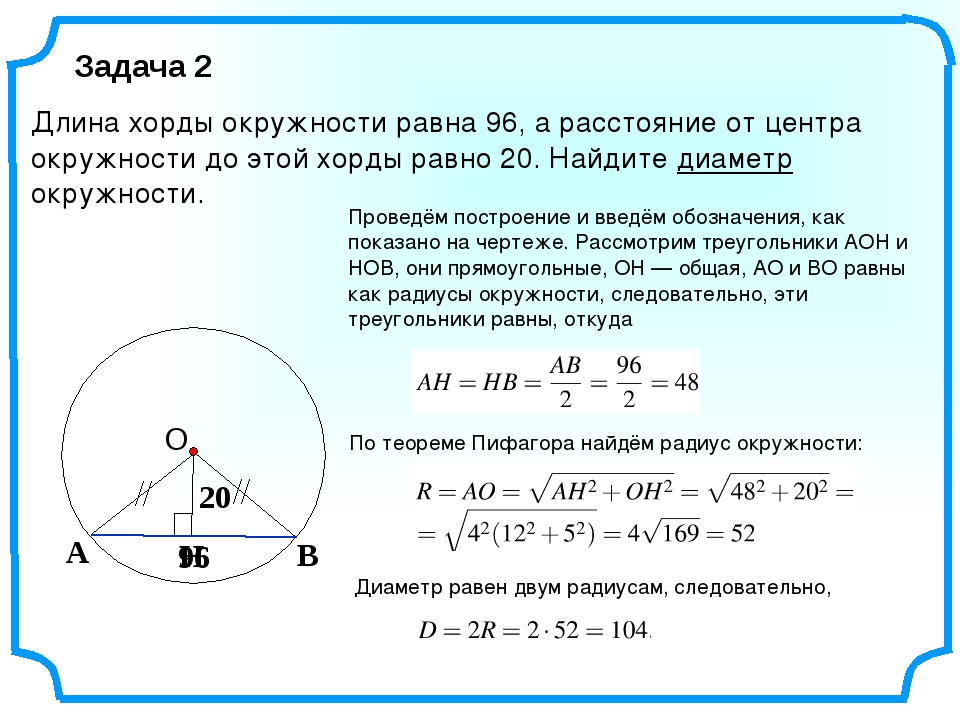
Формулы нахождения хордыОбозначения в формулах: l — длина хорды α — величина центрального угла R — радиус окружности d — длина перпендикуляра, проведенного от центра окружности к хорде Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задачПримечание.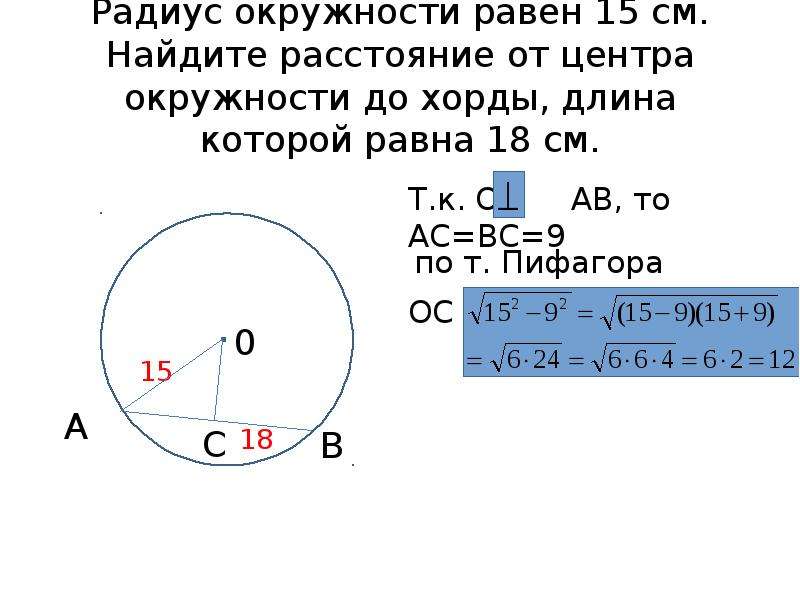 Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.Задача.
Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 Откуда Ответ: 5√10 Задача.
Решение.  Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг). Поскольку градусная мера окружности равна 360 градусам, то 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны:
90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
|
Глава VII.
 Окружность
ОкружностьГЛАВА VII.
ОКРУЖНОСТЬ.
§ 22. Взаимное положение прямой и окружности,
взаимное положение двух окружностей.
Касательная к окружности.
634. Через точку, данную на дуге окружности, не определяя её центра, провести к окружности касательную.
635. Около круга радиуса 10 см описана равнобедренная трапеция с острым углом, равным 30°. Найти её боковую сторону.
636. Около круга радиуса R описан ромб. Найти его высоту.
637. Две окружности имеют общий центр. Доказать, что хорды большей окружности, касающиеся меньшей окружности, равны между собой.
638*. Провести касательную к данной окружности, параллельную данной прямой. Рассмотреть случаи, когда:
а) центр окружности находится вне чертежа;
б) центр окружности известен.
639. 1) К данной окружности провести две касательные, составляющие между собой данный угол.
2) К данной окружности провести касательную, составляющую с данной прямой данный угол α.
640. Данным радиусом описать окружность, которая касалась бы данной прямой в данной на ней точке.
641*. На практике часто для проведения касательной к данной окружности через данную вне её точку пользуются одной линейкой. Решить следующие задачи, используя указанный приём построения касательной:
а) построить треугольник по стороне и высотам, проведённым к двум другим сторонам;
б) построить треугольник по двум сторонам и высоте, проведённой к третьей стороне; в) построить равнобедренный треугольник по основанию и высоте, проведённой к боковой стороне.
642. Диаметр АВ и хорда АС окружности с центром в точке О образуют угол, равный 30°.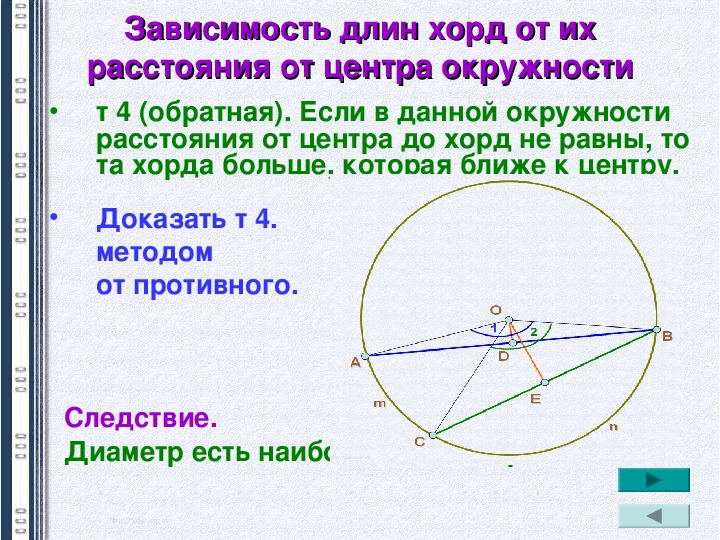 Касательная, проходящая через точку С, пересекает прямую АВ в точке D. Доказать, что ОС = 1/2ОD.
Касательная, проходящая через точку С, пересекает прямую АВ в точке D. Доказать, что ОС = 1/2ОD.
643*. Через точку В, взятую на окружности, с центром вточке О, проведены хорда АВ (дуга АВ меньше 90°) и касательная к окружности. Продолжение диаметра, перпендикулярногорадиусу ОА, пересекает касательную и продолжение хорды соответственно в точках С и D. Доказать, что отрезки ВС и CD равны.
644. В данный угол вписать окружность радиуса 4 см.
645. 1) Доказать, что две касательные, проведённые к одной окружности через одну точку, взятую вне окружности, равны.
2) Касательные к окружности образуют угол, равный 60°. Доказать, что:
а) отрезок, соединяющий их точку пересечения с центром окружности, равен диаметру окружности;
б) отрезок, соединяющий точки касания, равен длине касательной от точки пересечения касательных до точки касания.
646. Угол ВАС, образованный касательными АВ и АС к одной окружности, равен 60°; длина ломаной линии ВАС равна 1 м. Определить расстояние между точками касания В и С.
647. Из точки, лежащей вне окружности радиуса R, проведены к ней две взаимно перпендикулярные касательные. Найти длину каждой касательной.
648. Доказать, что общие внутренние касательные АВ и CD к двум окружностям равны (A,B,C,D — точки касания, черт. 198).
649. На чертеже 199 АВ и CD — общие внешние касательные к двум окружностям
(А, В, С и D — точки касания). Доказать, что АВ = CD.
650. Через точку М, взятую вне окружности, проведены к ней касательные МА и MB
(А и В — точки касания), и через произвольную точку С меньшей дуги АВ проведена касательная KL к окружности. Доказать, что периметр треугольника KML (черт. 200) не зависит от положения точки С.
200) не зависит от положения точки С.
651. На чертеже 201 АВ, CD, KL — касательные к окружности, АВ параллельна CD. Доказать, что / KOL равен 90°.
Взаимное положение двух окружностей.
652. Как расположены друг относительно друга две окружности, если:
а) расстояние между их центрами равно 15 см, а радиусы их равны 3 см и 8 см;
б) расстояние между их центрами равно 200 мм, а диаметры их равны 320 мм и 80 мм; в) расстояние между их центрами равно 8 см, а диаметры их равны 20 см и 2 см;
г) расстояние между их центрами равно 200 мм, а радиусы их равны 420 мм и 260 мм?
653. Начертить окружности, расположенные друг относительно друга так, как это указано на чертеже 202, построить центр симметрии и оси симметрии для каждого случая расположения окружностей (окружности имеют равные радиусы).
654. Найти радиусы двух окружностей, имеющих общий центр, если диаметр большей окружности делится меньшей окружностью на 3 части, равные 9 см, 12 см, 9 см.
655. 1) Радиусы двух окружностей, имеющих общий центр, относятся, как 2 : 7. Найти диаметры этих окружностей, если ширина кольца, образованного ими, равна 24 см.
2) Найти диаметры двух окружностей, имеющих общий центр, если известно, что они относятся, как 2 : 5, а одна из трёх частей, на которые диаметр большей окружности делится меньшей окружностью, равна 9 см (два решения).
656. 1) Две окружности касаются внешним образом. Радиусы окружностей относятся, как 2 : 3. Найти диаметры окружностей, если расстояние между центрами окружностей равно 10 см.
2) Две окружности касаются внутренним образом. Определить радиусы этих окружностей, если они относятся, как 5 : 2, а расстояние между центрами равно 15 см.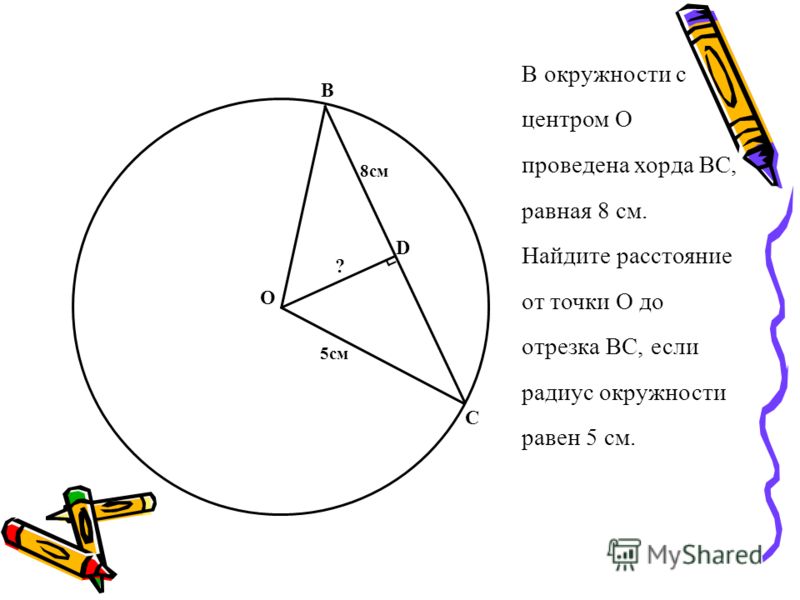
657. 1) Две окружности расположены одна внутри другой. Диаметр большей окружности, проходящий через центр меньшей окружности, делится меньшей окружностью на три части, равные 2 см, 10 см и 6 см. Найти диаметры окружностей и расстояние между центрами окружностей.
2) Две окружности, радиусы которых относятся, как 2 : 5, расположены одна внутри другой. Диаметр большей окружности, проходящий через центр меньшей окружности, делится меньшей окружностью на три части, крайние из которых равны 10 см и 5 см. Найти радиусы этих окружностей и расстояние между их центрами.
658. Общая хорда двух равных пересекающихся окружностей, радиус которых равен R, видна из их центров под углом 120°. Сделать чертёж. Найти расстояние между центрами окружностей.
ОТВЕТЫ
Как определить радиус дуги или сегмента круга и найти центр
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463. 1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:
tg(a/4) = 2Н/L (278.1.2)
тогда
а/4 = arctg(2H/L)
R = H/(1 — cos(a/2)) (278.1.3)
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад — для того, чтобы напомнить формулы — есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются.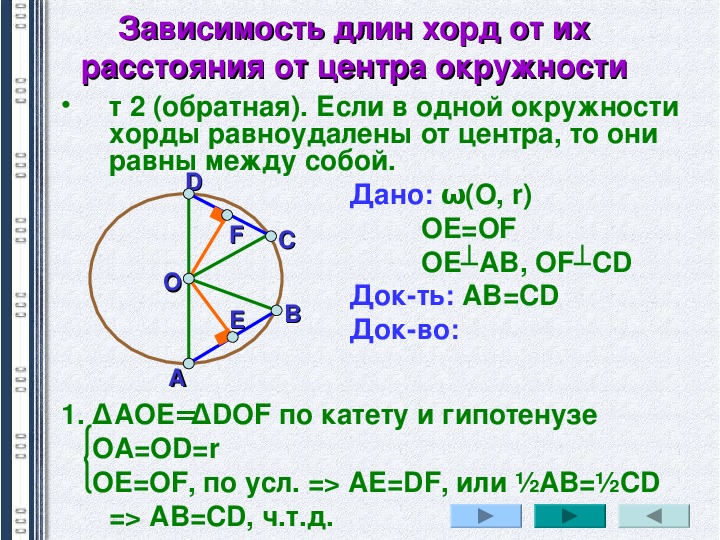 С каждой новой точкой разница измерений будет все меньше.
С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2R
O — центр круга
π ≈ 3.14
Формула для определения длины радиуса, если известна площадь круга :
Формула для определения длины радиуса, если известна длина окружности :
R — радиус окружности (круга)
h — высота сегмента
L — длина хорды
O — центр круга
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Сегмент — часть круга ABC, отсеченная хордой AC
h — высота сегмента ABC
L — хорда AC
R — радиус кружности
O — центр окружности
α — центральный угол AOC
Формула высоты через радиус и центральный угол, (h):
Формула высоты через хорду и центральный угол, (h):
Формула высоты через радиус и хорду, (h):
Дополнительные формулы для окружности:
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, (L):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Радиус | Отрезок, соединяющий центр окружности с любой точкой окружности | |
| Хорда | Отрезок, соединяющий две любые точки окружности | |
| Диаметр | Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности | |
| Касательная | Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания | |
| Секущая | Прямая, пересекающая окружность в двух точках |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Радиус |
Отрезок, соединяющий центр окружности с любой точкой окружности |
| Хорда |
Отрезок, соединяющий две любые точки окружности |
| Диаметр |
Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности |
| Касательная |
Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания |
| Секущая |
Прямая, пересекающая окружность в двух точках |
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. | |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. | |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины | Большая из двух хорд расположена ближе к центру окружности. | |
| Равные дуги | У равных дуг равны и хорды. | |
| Параллельные хорды | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды |
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. |
| Равные хорды |
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности |
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. |
| Две хорды разной длины |
Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |
У равных дуг равны и хорды. |
| Параллельные хорды |
Дуги, заключённые между параллельными хордами, равны. |
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды | Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство | |
| Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство | |
| Касательная и секущая, проведённые к окружности из одной точки | Справедливо равенство Посмотреть доказательство | |
| Секущие, проведённые из одной точки вне круга | Справедливо равенство: Посмотреть доказательство |
| Пересекающиеся хорды | |
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство | |
| Касательные, проведённые к окружности из одной точки | |
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство | |
| Касательная и секущая, проведённые к окружности из одной точки | |
Справедливо равенство Посмотреть доказательство | |
| Секущие, проведённые из одной точки вне круга | |
Справедливо равенство: Посмотреть доказательство | |
| Пересекающиеся хорды |
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство |
| Касательные, проведённые к окружности из одной точки |
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство |
| Касательная и секущая, проведённые к окружности из одной точки |
Справедливо равенство Посмотреть доказательство |
| Секущие, проведённые из одной точки вне круга |
Справедливо равенство: Посмотреть доказательство |
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Рис. 1
Тогда справедливо равенство
Доказательство. Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A, лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Рис. 2
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство. Заметим, что угол ABC образован касательной AB и хордой BC, проходящей через точку касания B. Поэтому величина угла ABC равна половине угловой величины дуги BC. Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC. Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A, лежащей вне круга, к окружности проведены секущие AD и AF (рис. 3).
3).
Рис. 3
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство. Проведём из точки A касательную AB к окружности (рис. 4).
Рис. 4
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке. Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Рис. 5
Доказательство. Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:
Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG, получим
| (1) |
Воспользовавшись теоремой синусов, применённой к треугольнику AKG, получим
| (2) |
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Поэтому
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL, получим равенство
откуда вытекает равенство
x = y ,
что и завершает доказательство теоремы о бабочке.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Определение центра окружности и центра дуги окружности
Взаимное пересечение перпендикуляров, восставленных в середине каждой хорды, определяет центр окружности (точку О). На фиг. 9,6 показано нахождение центра дуги окружности (построение аналогично предыдущему).
Выпрямление дуги окружности
Определение длины 1 дуги АВ окружности (приближенный способ, фиг. 10).
Через хорду АВ проводят перпендикуляр (фиг. 10,а), пересекающий дугу в точке К. Из точек С и D, как из центров, радиусами г, равными d— диаметру окружности, проводят две дуги до взаимного их пересечения в точке 01.
Расстояние между точками пересечения лучей 01А и O1B с касательной, проведенной к окружности в точке К, определяет приближенное значение спрямленной дуги (отрезок А1В1).
Расстояние между точками С1 и D1 определяет приближенную длину полуокружности. При отсутствии центра окружности
длина дуги АВ (фиг. 10,6) может быть определена следующим путем: хорду А В делят на четыре равные части; одну четвертую часть откладывают от точки В на дуге АВ; полученную точку С соединяют с точкой деления 1. Отрезок 1—С равен половине длины дуги АВ; CD — приближенное значение длины всей дуги АВ.
Отрезок 1—С равен половине длины дуги АВ; CD — приближенное значение длины всей дуги АВ.
Определение длины окружности. Длину окружности определяют по формуле l=П*D, где l — длина окружности, П = 3,14159, a D—диаметр окружности. На фиг. 11,а показана длина l окружности диаметра D.
Графически длина окружности приближенно может быть определена путем суммирования длины двух сторон аз равностороннего треугольника и двух сторон а\ квадрата, вписанных в окружность, как это показано на фиг. 11,6 (2аз + 2а4). Точность определения — 0,01. На фиг. 11,в длина окружности определена следующим способом: из центра О под углом 30° проводят прямую до пересечения ее в точке А с касательной к окружности; от точки А откладывают отрезок АВ, равный трем радиусам R; из точки В, как из центра, радиусом ВМ проводят дугу окружности до пересечения с касательной прямой в точках С и D. Отрезок CD будет равен длине окружности. Точность определения — 0,0001.
Определение приближенной длины очерка эллипса (фиг. 12). Для определения длины очерка эллипса ACBD соединяют точки А и С и из центра О радиусом, равным АС, засекают на осях эллипса точки М и N. Измерив длину отрезка MN, умножают ее на 3,14 и получают приближенную длину очерка эллипса (l = 3,14*MN).
12). Для определения длины очерка эллипса ACBD соединяют точки А и С и из центра О радиусом, равным АС, засекают на осях эллипса точки М и N. Измерив длину отрезка MN, умножают ее на 3,14 и получают приближенную длину очерка эллипса (l = 3,14*MN).
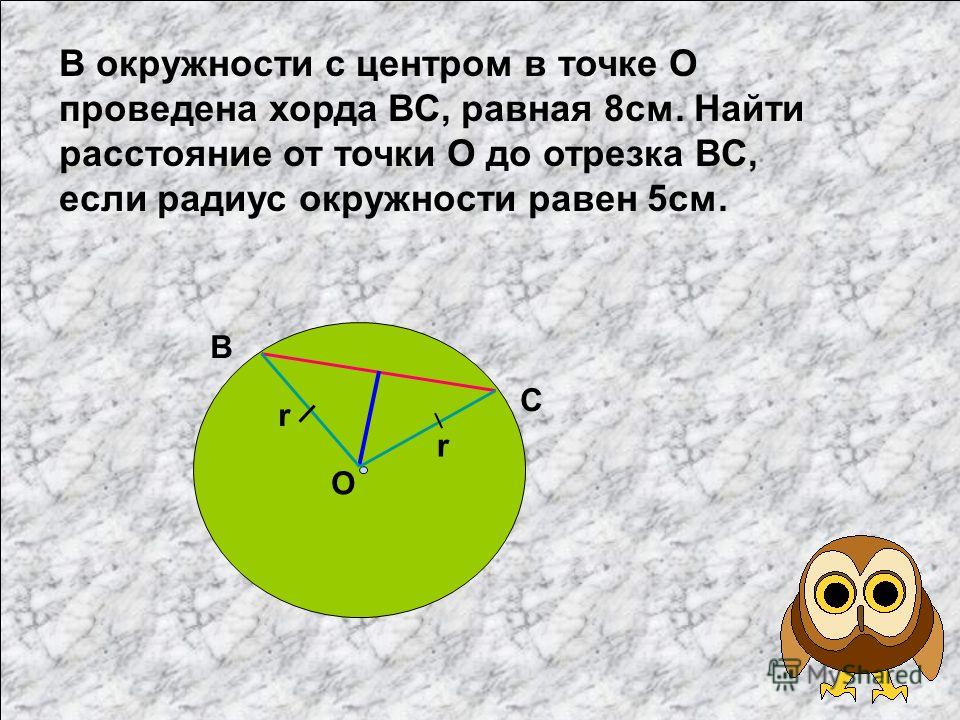
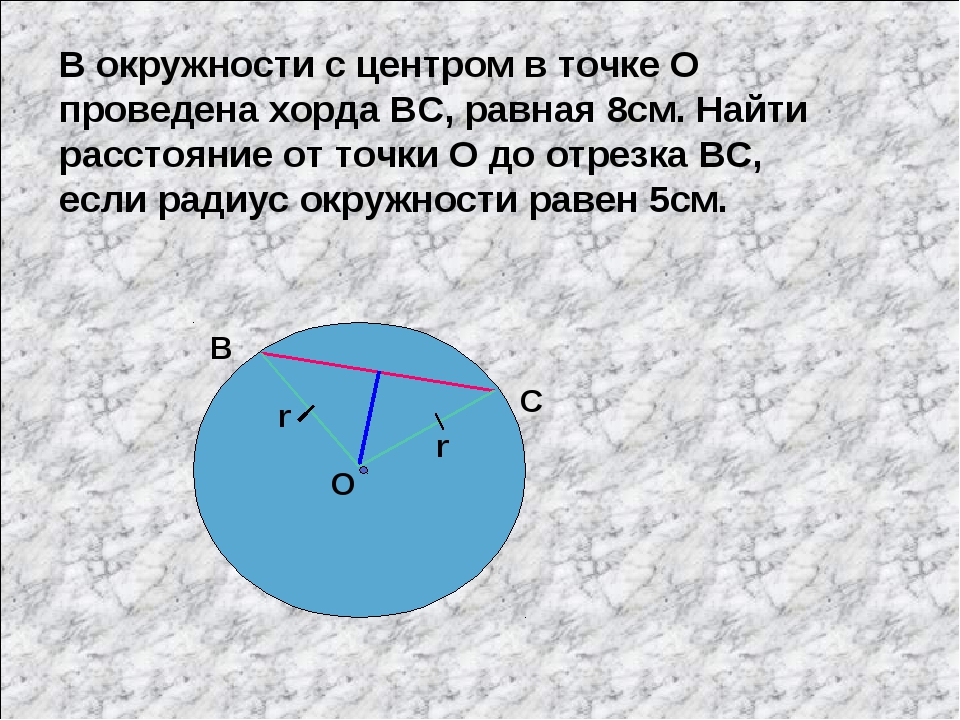
Как найти расстояние хорды от центра окружности
Пример 1:
Хорда длиной 16 см нарисована по окружности радиусом 10 см. Найдите расстояние хорды от центра круга.
Решение:
AB — хорда длиной 16 см.
C — середина AB.
OB — радиус длиной 10 см
AB = 16 см
AC = (1/2) ⋅ 16 = 8 см
OB = 10 см
В прямоугольном треугольнике OAC.
OC 2 = OA 2 — AC 2
= √ (10 2 -8 2 )
= √ (100-64)
= √36 см
OC = 6 см
Итак, расстояние хорды от центра составляет 6 см
Пример 2:
Радиус окружности составляет 15 см, а длина одной из его хорды — 18 см. Найдите расстояние хорды от центра.
Найдите расстояние хорды от центра.
Решение:
AB — хорда длиной 18 см.
C — середина AB.
OB — радиус длиной 10 см
AB = 18 см
AC = (1/2) ⋅ 18 = 9 см
OB = 15 см
В прямоугольном треугольнике OCB.
OC 2 = OB 2 — BC 2
= √ (15 2 — 9 2 )
= √ (225-81)
= √144
OC = 12 см
Итак, расстояние хорды от центра составляет 12 см.
Пример 3:
Хорда длиной 20 см проводится на расстоянии 24 см от центра окружности.Найдите радиус круга.
Решение:
Здесь прямая OC перпендикулярна AB, которая разделяет хорду равной длины.
In Δ OCB,
OB 2 = OC 2 + BC 2
OB 2 = 24 2 + 10 2
BC 2 = 576 + 100
BC 2 = 676
BC = √676
BC = √ (26 ⋅ 26)
BC = 26 см
Итак, радиус круга равен 26 см.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Задачи со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами
Задачи со словами
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи со словами с уравнениями
Проблемы со словами с линейным неравенством
ЗадачиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л. Метод CM для решения задач времени и работы
Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении в степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
хорд окружности — объяснение и примеры
Из этой статьи вы узнаете:
- Что такое хорда круга,
- Свойства хорды и
- Как найти длину аккорд по разным формулам.

Что такое аккорд круга?
По определению, хорда — это прямая линия, соединяющая 2 точки на окружности круга. Диаметр круга считается самой длинной хордой, потому что он соединяется с точками на окружности круга.
В круге ниже AB, CD и EF — хорды круга. Хорда CD — это диаметр окружности.
Свойства хорды
- Радиус окружности — это серединный перпендикуляр хорды.
- Длина хорды увеличивается по мере уменьшения перпендикулярного расстояния от центра окружности до хорды и наоборот.
- Диаметр — это самая длинная хорда окружности, при этом перпендикулярное расстояние от центра окружности до хорды равно нулю.
- Два радиуса, соединяющие концы хорды с центром круга, образуют равнобедренный треугольник.
- Две хорды равны по длине, если они равноудалены от центра окружности.Например, хорда AB равна хорде CD , если PQ = QR
Как найти хорду круга?
Есть две формулы для определения длины хорды. Каждая формула используется в зависимости от предоставленной информации.
Каждая формула используется в зависимости от предоставленной информации.
- Длина хорды с учетом радиуса и расстояния до центра окружности.
Если длина радиуса и расстояние между центром и хордой известны, то формула для определения длины хорды имеет вид,
Длина хорды = 2√ (r 2 — d 2 )
Где r = радиус окружности и d = перпендикулярное расстояние от центра окружности до хорды.
На приведенном выше рисунке длина хорды PQ = 2√ (r 2 — d 2 )
- Длина хорды с учетом радиуса и центрального угла
Если радиус и центральный угол хорды известны, то длина хорды определяется как,
Длина хорды = 2 × r × синус (C / 2)
= 2r синус (C / 2)
Где r = радиус окружности
C = угол, стянутый в центре хордой
d = перпендикулярное расстояние от центра окружности до хорды.
Давайте разберемся с несколькими примерами, связанными с хордой круга.
Пример 1
Радиус круга составляет 14 см, а расстояние по перпендикуляру от хорды до центра составляет 8 см. Найдите длину хорды.
Решение
Заданный радиус, r = 14 см и расстояние по перпендикуляру, d = 8 см,
По формуле Длина хорды = 2√ (r 2 −d 2 )
Заменить.
Длина хорды = 2√ (14 2 −8 2 )
= 2√ (196-64)
= 2√ (132)
= 2 x 11,5
= 23
Итак , длина пояса — 23 см.
Пример 2
Перпендикулярное расстояние от центра окружности до хорды составляет 8 м. Рассчитайте длину хорды, если диаметр окружности 34 м.
Решение
Дано, расстояние, d = 8 м.
Диаметр, D = 34 м. Итак, радиус, r = D / 2 = 34/2 = 17 м
Длина хорды = 2√ (r 2 −d 2 )
Путем подстановки
Длина хорды = 2√ (17 2 — 8 2 )
= 2√ (289 — 64)
= 2√ (225)
= 2 x 15
= 30
Итак, длина хорды составляет 30 м.
Пример 3
Длина хорды круга составляет 40 дюймов. Если перпендикулярное расстояние от центра до хорды составляет 15 дюймов.Какой радиус хорды?
Раствор
Учитывая, что длина хорды = 40 дюймов.
Расстояние, d = 15 дюймов
Радиус, r =?
По формуле Длина хорды = 2√ (r 2 −d 2 )
40 = 2√ (r 2 -15 2 )
40 = 2√ (r 2 — 225)
Квадрат с обеих сторон
1600 = 4 (r 2 — 225)
1600 = 4r 2 — 900
Добавьте 900 с обеих сторон.
2500 = 4r 2
Разделив обе стороны на 4, мы получим
r 2 = 625
√r 2 = √625
r = -25 или 25
Длина не может никогда — отрицательное число, поэтому мы выбираем только положительное 25.
Следовательно, радиус круга равен 25 дюймам.
Пример 4
Учитывая, что радиус окружности, показанной ниже, составляет 10 ярдов, а длина PQ — 16 ярдов. Рассчитайте расстояние OM .
Рассчитайте расстояние OM .
Раствор
PQ = длина хорды = 16 ярдов.
Радиус, r = 10 ярдов.
OM = расстояние, d =?
Длина хорды = 2√ (r 2 −d 2 )
16 = 2√ (10 2 — d 2 )
16 = 2√ (100 — d 2 )
Квадрат с двух сторон.
256 = 4 (100 — d 2 )
256 = 400 — 4d 2
Вычтем 400 с обеих сторон.
-144 = — 4d 2
Разделите обе стороны на -4.
36 = d 2
d = -6 или 6.
Таким образом, перпендикулярное расстояние составляет 6 ярдов.
Пример 5:
Рассчитайте длину пояса PQ в круге, показанном ниже.
Решение
Учитывая центральный угол, C = 80 0
Радиус окружности, r = 28 см
Длина хорды PQ =?
По формуле длина хорды = 2r синус (C / 2)
Заменить.
Длина хорды = 2r синус (C / 2)
= 2 x 28 x синус (80/2)
= 56 x синус 40
= 56 x 0,6428
= 36
Следовательно, длина пояс PQ 36 см.
Пример 6
Рассчитайте длину хорды и центральный угол хорды в круге, показанном ниже.
Решение
Дано,
Перпендикулярное расстояние, d = 40 мм
Радиус, r = 90 мм.
Длина хорды = 2√ (r 2 −d 2 )
= 2√ (90 2 -40 2 )
= 2 √ (8100 — 1600)
= 2√ 6500
= 2 x 80,6
= 161,2
Итак, длина хорды составляет 161,2 мм
Теперь вычислите угол, образуемый хордой.
Длина хорды = 2r синус (C / 2)
161,2 = 2 x 90 синус (C / 2)
161,2 = 180 синус (C / 2)
Разделим обе стороны на 180.
0.8956 = синус (C / 2)
Найдите синус, обратный 0,8956.
C / 2 = 63,6 градуса
Умножить обе стороны на 2
C = 127,2 градуса.
Итак, центральный угол, образуемый хордой, равен 127,2 градуса.
Предыдущий урок | Главная страница | Следующий урок
Хорда круга: определение и формула — видео и стенограмма урока
Примеры
Чтобы проиллюстрировать это дальше, давайте рассмотрим несколько точек отсчета на том же круглом озере, что было раньше.Если бы каждая точка отсчета (т. Е. Зона кормления уток, столы для пикника, вы, фонтан с водой и рыбацкая пристань) находилась прямо на окружности этого озера, то каждая линия, соединяющая точку с другой точкой на круге, была бы хордами.
На этом изображении мы добавили буквы для каждой контрольной точки, чтобы мы могли легко обозначить хорды.
- Леска между рыболовным пирсом и вами теперь является хордой AC
- Линия между фонтаном и местом кормления уток теперь проходит по хорде BE
- Ограда между вами и столиками для пикника — аккорд CD
И так далее…
Ассоциированный словарь
Если бы у нас была хорда, проходящая непосредственно через центр круга, ее бы назвали диаметром .Если бы у нас была линия, которая не останавливалась бы на окружности круга, а вместо этого продолжалась бы в бесконечность, она больше не была бы хордой; он будет называться секансом .
Формулы
Формулы для определения длины хорды различаются в зависимости от того, какую информацию об окружности вы уже знаете.
Формула 1 : Если вы знаете радиус и значение угла, образуемого в центре хордой, формула будет выглядеть так:
Мы можем использовать эту диаграмму, чтобы найти длину хорды, подставив в формулу радиус и угол, образованный хордой в центре. Итак, если мы подставим значения радиуса и измерения угла в научный калькулятор, мы получим значение длины хорды примерно 5,74.
Итак, если мы подставим значения радиуса и измерения угла в научный калькулятор, мы получим значение длины хорды примерно 5,74.
Формула 2 : Если вы знаете радиус и перпендикулярное расстояние от хорды до центра окружности, формула будет выглядеть так:
Помните, что d в этой формуле — это перпендикулярное расстояние от хорды до центра окружности.
Здесь мы знаем, что радиус равен 5, а расстояние по перпендикуляру от хорды до центра равно 4. Итак, если мы подставим значения радиуса и расстояние по перпендикуляру от хорды до центра круга, мы получили бы значение длины хорды как 6.
Теорема Пифагора
Если вы посмотрите на формулу 2, она, по сути, является вариацией теоремы Пифагора.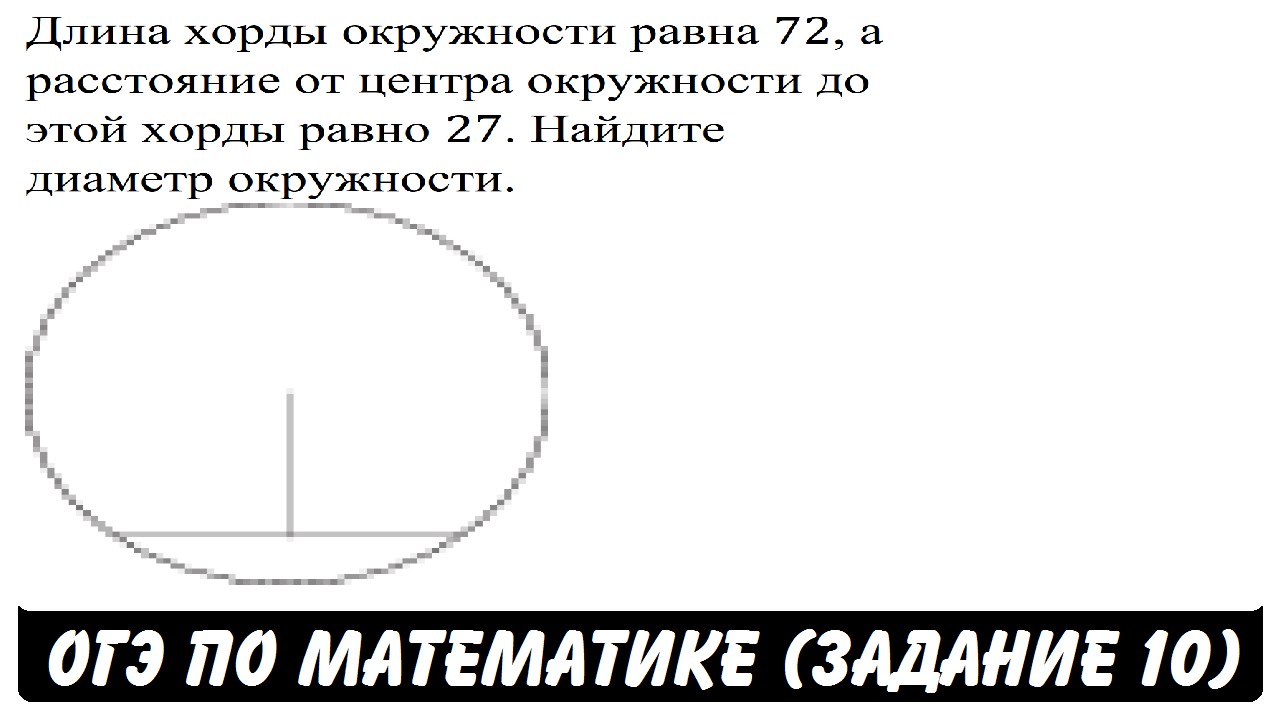 Мы можем найти хорду круга, используя формулу 2, но мы также можем использовать теорему Пифагора. Давайте посмотрим на эту цифру:
Мы можем найти хорду круга, используя формулу 2, но мы также можем использовать теорему Пифагора. Давайте посмотрим на эту цифру:
Теорема Пифагора утверждает, что квадраты двух сторон прямоугольного треугольника равны квадрату гипотенузы. На этой диаграмме мы видим, что хорда Z делится пополам перпендикулярной линией OZ и образует два прямых угла в середине хорды Z. Следовательно, она образует два прямоугольных треугольника AZO и OZB.На этой конкретной диаграмме расстояние между перпендикулярной линией между началом координат (центром круга) и хордой Z равно 3. Поскольку хорда Z делится пополам на OZ, она по существу разделена на две равные линии. Итак, если AZ равно 4, ZB также равно 4. OZ и AZ составляют стороны прямоугольного треугольника OZA. Гипотенуза OZA имеет значение 5. Гипотенуза также является радиусом круга с центром O.
Применение теоремы Пифагора к хорде формул круга очень важно для полного понимания того, где мы получаем формулы .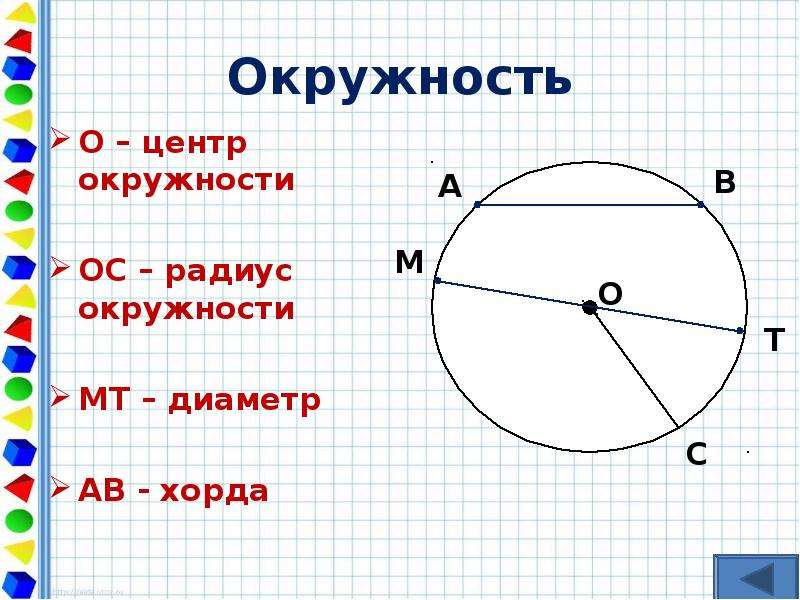
Итоги урока
Давайте рассмотрим. Хорда окружности — это линия, соединяющая две точки на окружности окружности . Если бы у нас была хорда, проходящая прямо через центр круга, ее бы назвали диаметром . Если бы у нас была линия, которая не останавливалась бы на окружности круга, а вместо этого продолжалась бы в бесконечность, она больше не была бы хордой; он будет называться секансом .
Чтобы найти длину хорды круга, мы могли бы использовать две формулы:
Если вы знаете радиус и значение угла, образуемого хордой в центре, формула будет выглядеть так:
Если известен радиус и перпендикулярное расстояние от центра окружности до хорды, формула будет выглядеть так:
Эта формула по существу является вариацией теоремы Пифагора ( a в квадрате + b в квадрате = c в квадрате), где a и b являются сторонами прямоугольного треугольника и c — гипотенуза.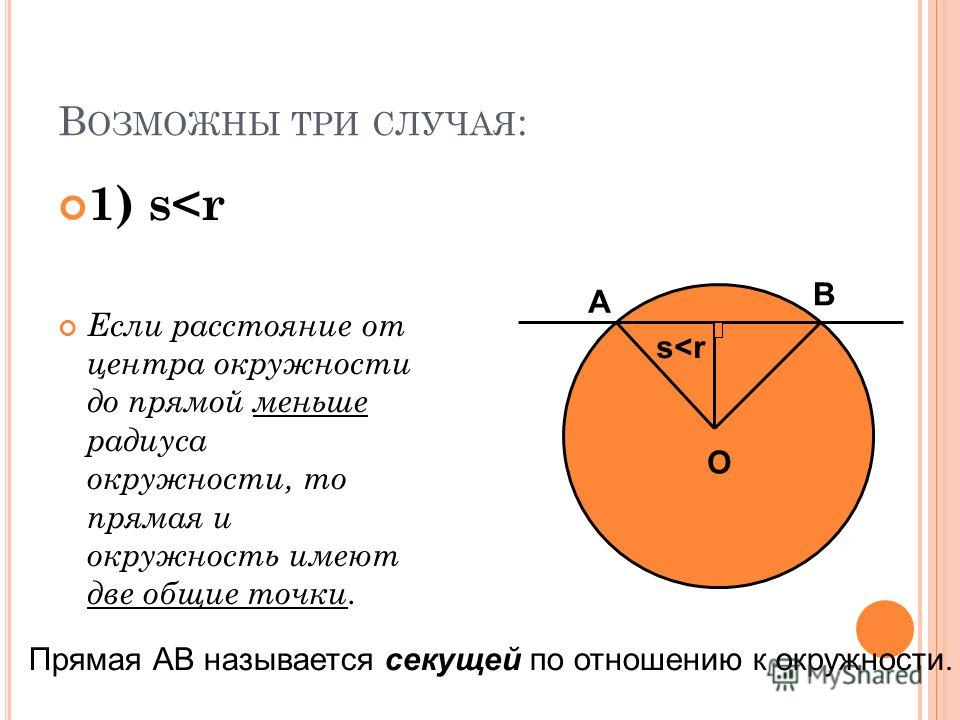 Иногда для определения длины хорды можно использовать теорему Пифагора вместо этой формулы.
Иногда для определения длины хорды можно использовать теорему Пифагора вместо этой формулы.
Примечания к аккордам
- Хорда — это длина между двумя точками на окружности
- Хорду можно рассчитать двумя способами:
Результаты обучения
Закончив, вы должны уметь:
- Определить хорду круга
- Напишите две формулы для определения длины хорды
- Вспомните разницу между хордой, диаметром и секущей
Как рассчитать длину хорды
Обновлено 3 ноября 2020 г.
Автор Chris Deziel
Хорда — это отрезок прямой, соединяющий любые две точки на окружности окружности.Диаметр круга, отрезок прямой, проходящий через центр, также является его самой длинной хордой. Вы можете рассчитать длину хорды, исходя из длины радиуса и угла, образованного линиями, соединяющими центр окружности с двумя концами хорды. Вы также можете рассчитать длину хорды, если знаете как радиус, так и длину правой биссектрисы, то есть расстояние от центра окружности до центра хорды.
Вы также можете рассчитать длину хорды, если знаете как радиус, так и длину правой биссектрисы, то есть расстояние от центра окружности до центра хорды.
TL; DR (слишком длинный; не читал)
Вы можете рассчитать длину хорды окружности, если знаете радиус и одну из двух других переменных.Одна из переменных — это длина перпендикулярной линии от хорды до центра круга. Другой — угол, образованный двумя радиусными линиями, которые касаются точек пересечения хорды и окружности окружности.
Основная стратегия расчета длины хорды
Тригонометрическая процедура для расчета длины хорды начинается с продления радиальных линий до каждой точки, в которой хорда пересекает окружность окружности. Это создает треугольник с одной вершиной в центре круга и вершиной в каждой из точек пересечения.Если вы продлите перпендикулярную линию от хорды до центра круга, это разделит угол этой вершины пополам и создаст два прямоугольных треугольника по обе стороны от хорды.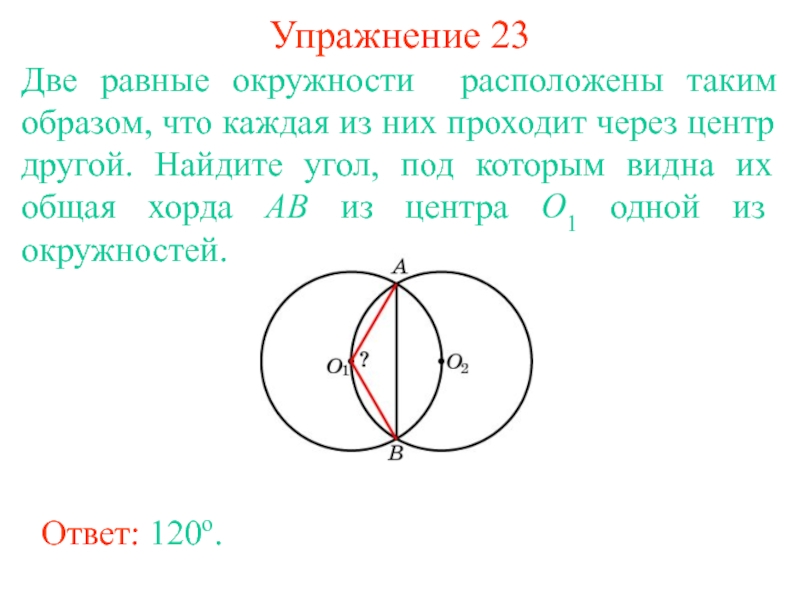 Если весь угол равен θ (тета), угол по обе стороны от линии биссектрисы составляет θ /2.
Если весь угол равен θ (тета), угол по обе стороны от линии биссектрисы составляет θ /2.
Теперь вы можете задать уравнение, которое связывает длину хорды ( c ) с радиусом ( r ) и углом между двумя радиусными линиями ( θ ). Поскольку половина линии хорды ( c /2) образует противоположную линию в прямоугольном треугольнике, а r образует гипотенузу, верно следующее:
\ sin \ bigg (\ frac { θ} {2} \ bigg) = \ frac {c / 2} {r}
c = \ text {длина хорды} = \ sin \ bigg (\ frac {θ} {2} \ bigg)
Если вы знать радиус окружности и можно измерить угол θ , у вас есть все необходимое для расчета длины хорды.
Расчет длины хорды, когда угол не измеряется
На практике может быть трудно измерить угол, образованный радиусными линиями. Например, вы можете планировать возвести забор, который простирается от одной точки на круглом участке земли до другой, и вам нужно знать, какой длины должен быть забор. Вы все равно можете использовать тригонометрию, чтобы найти ответ, если вы знаете радиус и можете измерить расстояние от хорды до центра круга. Пока линия перпендикулярна хорде, она делит ее пополам и образует прямоугольный треугольник.2}
Вы все равно можете использовать тригонометрию, чтобы найти ответ, если вы знаете радиус и можете измерить расстояние от хорды до центра круга. Пока линия перпендикулярна хорде, она делит ее пополам и образует прямоугольный треугольник.2}
Основная информация об окружностях (Геометрия, Круги) — Mathplanet
Круг — это все точки в одной плоскости, которые находятся на равном расстоянии от центральной точки. Круг состоит только из точек на границе. Вы можете представить себе круг как обруч. Кругом являются только точки на границе. Точки внутри хула-хупа не являются частью круга и называются внутренними точками.
Расстояние между средней точкой и границей круга называется радиусом.Отрезок, концы которого находятся на окружности и проходит через среднюю точку, называется диаметром. Диаметр в два раза больше радиуса. Отрезок, концы которого находятся на круговой границе, но не проходят через среднюю точку, называется хордой.
Расстояние по окружности называется окружностью C и может быть определено с помощью радиуса r или диаметра d:
$$ \ C = 2 \ pi r $$
$$ C = \ pi d $$
Круг равен 360 °. Длина дуги l определяется путем подстановки градуса дуги v и длины окружности C в следующую формулу: $$ l = C \ cdot \ frac {v} {360} $$ Когда диаметры пересекаются в центре круга, они образуют центральные углы.Например, когда вы разрезаете торт, вы начинаете свои кусочки с середины. Пример Как и в случае с тортом выше, мы делим круг на 8 частей с одинаковым углом. Окружность круга составляет 20 единиц длины. Определите длину дуги каждой детали. Сначала нам нужно найти угол для каждой части, поскольку мы знаем, что полный круг равен 360 °, мы можем легко сказать, что каждая часть имеет угол 360/8 = 45 °. Мы подставляем эти значения в нашу формулу для длины дуг: $$ l = C \ cdot \ frac {v} {360} $$ $$ l = 20 \ cdot \ frac {45} {360} = 2. Следовательно, длина наших дуг составляет 2,5 единицы длины. Мы могли бы еще проще сказать это, просто разделив окружность на количество частей одинакового размера: 20/8 = 2,5 Каков угол дуги окружности, если мы разделим круг на 12 частей одинакового размера Линия, соединяющая две точки на окружности или кривой.(произносится как «шнур») Попробуйте это Перетащите любую оранжевую точку. Синяя линия всегда будет хордой к кругу. Синяя линия на рисунке выше называется «хордой круга c». Аккорд очень похож на
секущая, но где секущая — это линия, растягивающая
до бесконечности в обоих направлениях, аккорд — это
отрезок, который покрывает только часть внутри круга. Серединный перпендикуляр хорды всегда проходит через центр окружности. На рисунке вверху страницы нажмите «Показать правую биссектрису». Если две хорды круга пересекаются, в результате пересечения образуются четыре отрезка линии, которые имеют интересную взаимосвязь. См. Теорему о пересекающихся хордах. (C) Открытый справочник по математике, 2011 г. Проблема параллельных хордов Если у нас есть круг, для которого нам известны соответствующие длины двух параллельных хорд и расстояние между двумя хордами, найдите радиус круга. Для удобства обозначений, пусть длины двух поясов будут равны 2a и 2b , а расстояние между ними будет c . Проблема, вероятно, требует рассмотрения двух случаев: Случай 1. Обе параллельные хорды находятся на одной стороне от центра окружности. Случай 2. Центр окружности находится между двумя параллельными хордами. Дано a , b и c , как определено в приведенном выше эскизе. Какое условие у a , b и c для определения того, находятся ли параллельные хорды на одной стороне от центра, или одна из них — диаметр, или они находятся на противоположных сторонах центра? Расширение. Обратная задача : Учитывая длину двух параллельных хорд и радиус окружности, найдите ДВЕ возможности для расстояния между параллельными хордами. То есть, учитывая длину хорд 2a и 2b и радиус r окружности, найдите c, расстояние между параллельными хордами. Справа — СОЗДАННЫЙ пример с a = 5 см b = 4 см r = 6 см Каждая хорда DC и D’C ‘имеет длину 8 см и параллельна хорде EF, которая составляет 10 см .Радиус r = 6 см . Согласно ИЗМЕРЕНИЮ, значение c между EF и DC составляет приблизительно 1,15 см ; значение c между EF и D’C ‘составляет приблизительно 7,74 см. Вы можете разделить круг на более мелкие части. Часть круга называется дугой, а дуга — в соответствии с ее углом. Дуги делятся на малые дуги (0 °
Вы можете разделить круг на более мелкие части. Часть круга называется дугой, а дуга — в соответствии с ее углом. Дуги делятся на малые дуги (0 ° 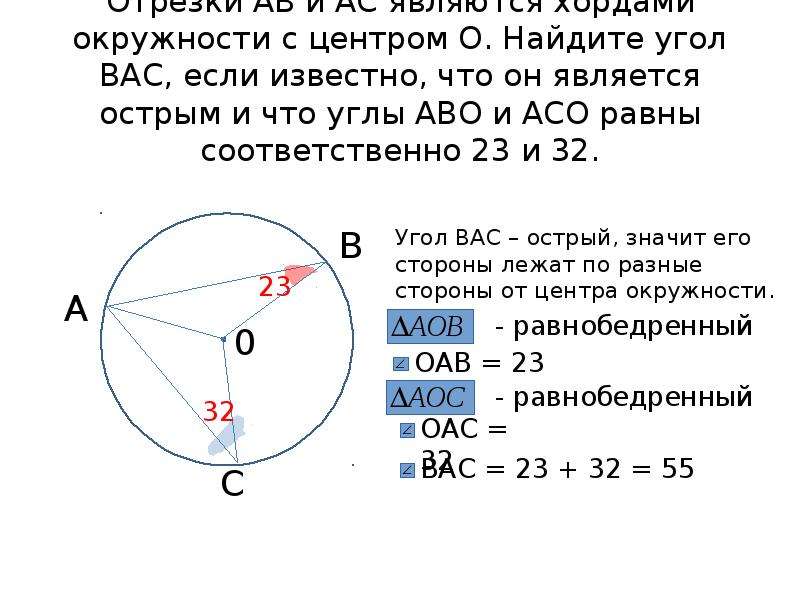 5 $$
5 $$
Видеоурок Chord — Определение математического слова
Chord — Определение математического слова — Math Open Reference Хорда, проходящая через центр круга, также является диаметром круга.
Хорда, проходящая через центр круга, также является диаметром круга. Расчет длины пояса
Ниже приведены две формулы длины хорды.Выберите один исходя из того, что вам дано для начала. 1. Учитывая радиус и центральный угол
Ниже приведена формула длины хорды, если вы знаете радиус и центральный угол. где
r — радиус окружности
c — угол, образованный хордой в центре
sin — функция синуса (см. Обзор тригонометрии) 2. Учитывая радиус и расстояние до центра
Ниже приведена формула длины хорды, если вы знаете радиус и перпендикулярное расстояние от хорды до центра окружности.Это простое приложение
Теорема Пифагора. где
r — радиус окружности
d — расстояние по перпендикуляру от хорды до центра окружности В поисках центра
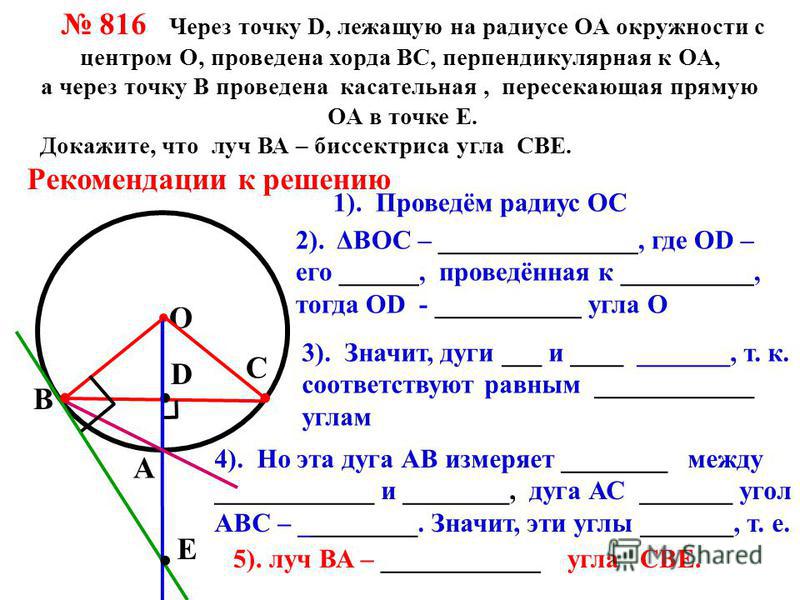 Затем двигайтесь
одну из точек P, Q вокруг и увидите, что это всегда так. Это можно использовать, чтобы найти центр круга: нарисуйте одну хорду и ее правую биссектрису.Центр должен быть где-то на этой линии.
Повторите это, и две биссектрисы встретятся в центре круга.
Пошаговые инструкции см. В разделе «Поиск центра круга» в главе «Конструкции».
Затем двигайтесь
одну из точек P, Q вокруг и увидите, что это всегда так. Это можно использовать, чтобы найти центр круга: нарисуйте одну хорду и ее правую биссектрису.Центр должен быть где-то на этой линии.
Повторите это, и две биссектрисы встретятся в центре круга.
Пошаговые инструкции см. В разделе «Поиск центра круга» в главе «Конструкции». Пересекающиеся аккорды
Другие темы в круге
Общие
Уравнения окружности
Углы по окружности
Дуги
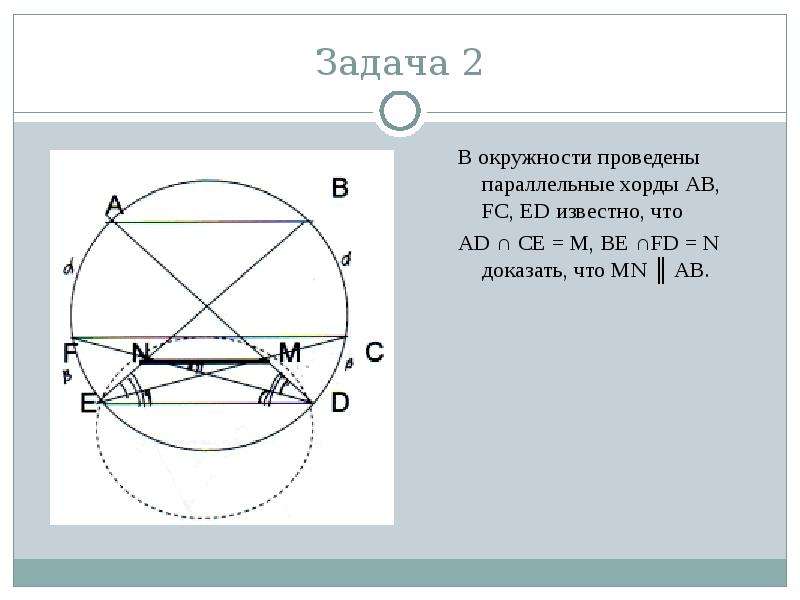
Все права защищены. Задача о параллельных аккордах
Задача о параллельных аккордах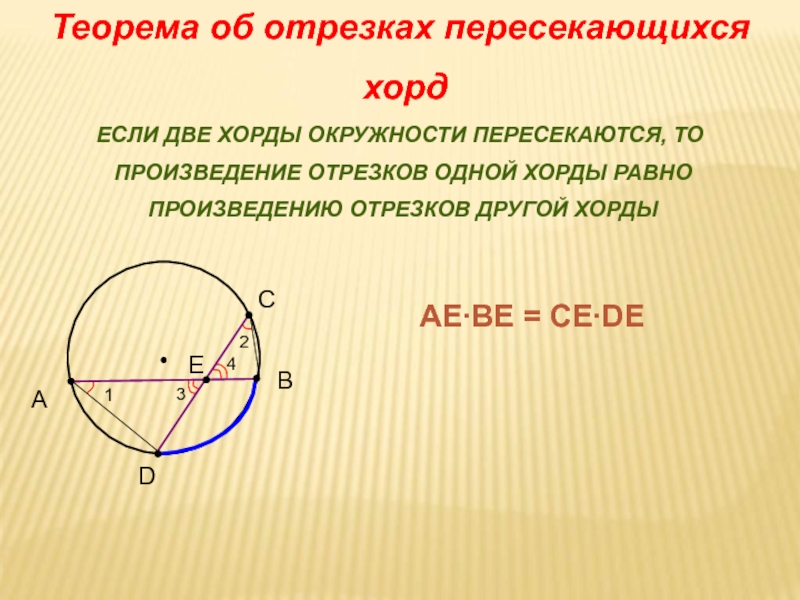



 Радiани i градуси
Радiани i градуси Верно и обратное
Верно и обратное



Leave A Comment