Радиус вписанной в квадрат окружности равен 4√2 найти радиус окружност…

Лучший ответ по мнению автора
05. 10.16
Лучший ответ по мнению автора

science
Читать ответы

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

чему равны индуктивность и энергия магнитного поля соленоида , если при силе тока, равной 4А, магнитный поток через соленоид и равен 0,4 вб

гусь тяжелее утки на 2.

..

Найдите углы,образованные при пересечении двух прямых,если разность двух из них равна 64

Помогите составить условие задачи: у Иры в коллекции есть 26марок,посвящённые историческим событиям,а так же марки,посвящённые архитектуре и спорту,марок по архитектуре у неё на 15 больше чем по

Соленоид и резистор соединены параллельно и подключены к источнику токаю Определите количество теплоты, выделяющейся в резисторе сопротивлением R0,…

Пользуйтесь нашим приложением

Квадрат и его свойства, диагонали квадрата, площадь квадрат, теорема

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:

квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

  1. Все углы квадрата — прямые, все стороны квадрата — равны.


  2. Диагонали квадрата равны и пересекаются под прямым углом.

  3. Диагонали квадрата делятся точкой пересечения пополам.
  4. Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).

  5. Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:

 

 

 

 

Периметр квадрата P в 4 раза больше его стороны и равен: 

Площадь квадрата равна квадрату его стороны: .

Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть
.

Доказательство:

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

что и требовалось доказать.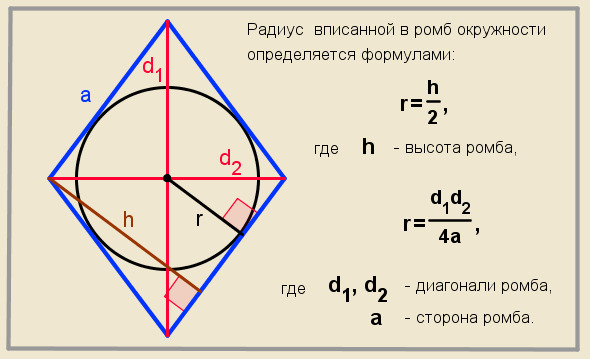

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

Доказательство:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

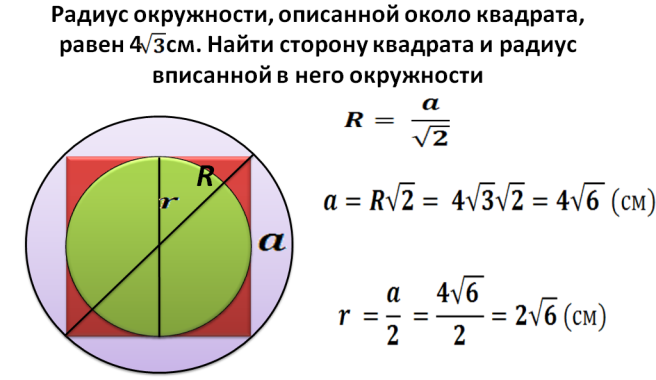
Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

Доказательство:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

По теореме

Тогда , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

  1. Все стороны равны и среди внутренних углов есть прямой угол.
  2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна .

Решение:

Мы знаем, что . Тогда .

Ответ: 2.

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

Тогда по формуле площади квадрата:

Второй способ решения:

Воспользуемся формулой для площади ромба:

Ответ: 0,5

Задача 3.

Найдите радиус окружности, описанной около квадрата со стороной, равной .

Решение:

Радиус описанной окружности равен половине диагонали квадрата, поэтому

Ответ: 2.

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Решение:

Диаметр окружности равен стороне квадрата: .

Ответ: 8.

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Ответ: 56.

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

Поэтому

Ответ: 22.

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата: 

Периметр квадрата со стороной 3 равен: 

Ответ: 12.

Задача 8. Найдите площадь квадрата, в который вписан круг площадью .

Решение:

Площадь круга  откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .

 

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Решение:

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .

Ответ: 5.

 

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 07. 02.2023

Square in a Circle Calculator

Создано Madhumathi Raman

Отзыв от Wojciech Sas, PhD и Стивена Вудинга

Последнее обновление: 31 октября 2022 г.

Содержание:
  • Как использовать калькулятор квадрата в круге?
  • Как найти максимальный квадрат в круге?
  • Как найти самый большой круг в квадрате?
  • Что означает квадратура круга?
  • Часто задаваемые вопросы

Используя этот калькулятор квадрата в круге, вы можете найти самый большой квадрат в круге . Это также поможет вам найти самый большой круг внутри квадрата. Будь то геометрия 📐, строительство 🏗️ или повседневная жизнь 🚶, мы часто сталкиваемся с составными фигурами, такими как квадрат, описанный вокруг круга 🔵, или квадрат, вписанный в круг. Этот калькулятор поможет вам найти размеры 📏 таких фигур, когда известно одно из измерений!

Задумывались ли вы когда-нибудь ‘Какая самая большая круглая пицца 🍕 я могу поместиться в этот квадрат 🔲 ?’ или ‘Какой самый большой квадратный кусок торта 🎂 я могу поместить в эту круглую тарелку 🍽️?’ или ‘Какой самый большой круглый крытый бассейн 🏊 я могу поместиться в этой квадратной комнате?’ Что ж, не удивляйтесь больше! Потому что наш калькулятор квадрата в круге поможет вам найти ответы на эти и другие вопросы!

Как использовать калькулятор квадрат в круге?

Используя калькулятор квадрата в круге, вы можете найти любое из следующего:

  • Размеры самый большой квадрат в круге :

    • Чтобы найти это, введите значение радиуса круга или площадь .
    • Калькулятор покажет длину стороны и площадь самого большого квадрата, который может поместиться внутри круга!

  • Размеры самого большого круга внутри квадрата :

    • Чтобы найти это, введите значение стороны или площади квадрата .
    • Калькулятор отобразит радиус и площадь самого большого круга, который может поместиться внутри квадрата!

  • Размеры квадрата с той же площадью, что и у круга :

    • Чтобы найти это, введите значение радиуса круга или площадь .
    • Калькулятор покажет длину стороны квадрата с той же площадью, что и у круга!

  • Размеры круга с той же площадью, что и у квадрата :

    • Чтобы найти это, введите значение стороны или площади квадрата .
    • Калькулятор отобразит радиус круга с той же площадью, что и квадрат!

Таким образом, вы можете использовать этот калькулятор квадрата в круге несколькими различными способами, в зависимости от ваших потребностей!

Как найти максимальный квадрат в круге?

Чтобы узнать, как найти самый большой квадрат в круге с помощью калькулятора квадрата внутри круга, выполните следующие действия:

  1. Введите значение радиуса или площади окружности .

  2. Калькулятор найдет какого размера квадрат вписывается в круг по формуле:
    длина стороны = √2 × радиус

  3. Будут показаны длина стороны и площадь квадрата внутри круга !

Таким образом, вы можете найти максимальный квадрат, который вы можете нарисовать в данном круге.

Как найти самый большой круг в квадрате?

Чтобы узнать, как найти самый большой круг в квадрате с помощью калькулятора квадрата внутри круга, выполните следующие действия:

  1. Введите значение стороны или площади квадрата, описанного вокруг окружности.

  2. Калькулятор найдет какого размера круг помещается в квадрат по формуле:

    радиус=длина стороны3\большой\текст{радиус} = \frac{\text{длина стороны}}{2}радиус=2длина стороны​

  3. Будут отображаться радиус и площадь круга внутри квадрата !

Таким образом, когда квадрат описывает окружность , вы можете найти радиус и площадь окружности .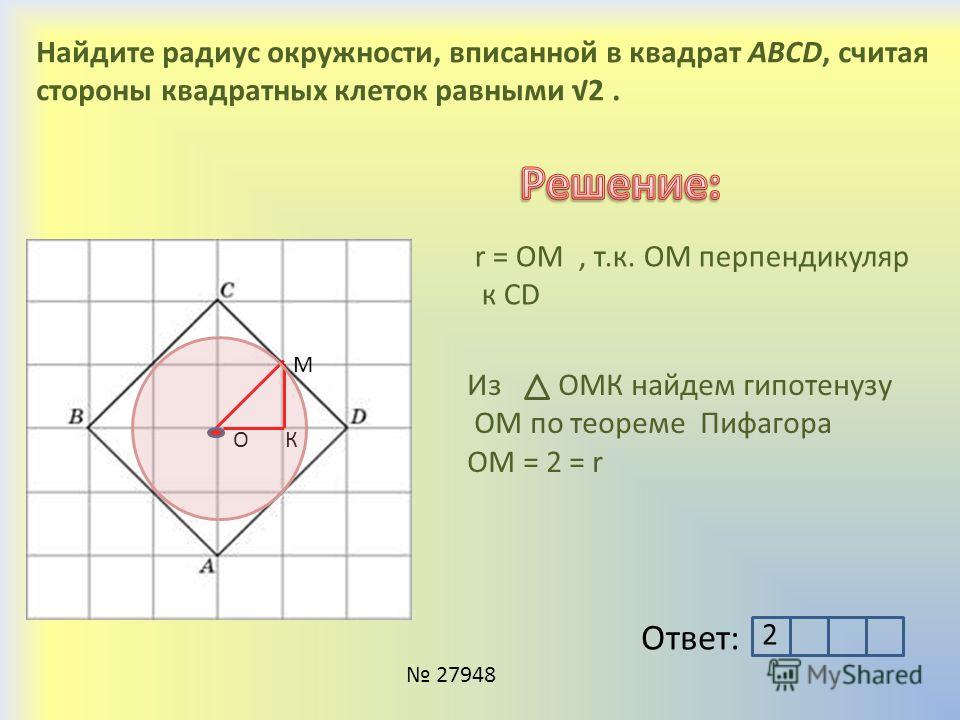

Что означает квадратура круга?

Квадрат круга относится к нахождению квадрата с той же площадью , что и у круга.

Для круга с радиус r , квадрат с той же площадью будет иметь длину стороны r√π . Так, например, если данный круг имеет радиус из 10 см , то квадрат с той же площадью, что и у круга , будет иметь длину стороны из 10√π см .

В качестве альтернативы, мы также можем преобразовать данный квадрат в круглую форму, выполнив обратную операцию.

Интересно отметить, что мы можем приблизить квадрат к кругу, постепенно увеличивая количество сторон, чтобы получить правильные многоугольники, такие как пятиугольник, шестиугольник, семиугольник, восьмиугольник и т. д., пока мы не получим круг ⭕.

🙋 Изучите различные свойства этих правильных многоугольников , воспользовавшись нашим калькулятором пятиугольников, нашим калькулятором шестиугольников и нашим калькулятором восьмиугольников.

Часто задаваемые вопросы

Как преобразовать квадрат в круг?

Преобразование квадрата в круг означает нахождение круга той же площади, что и квадрат . Таким образом, если мы хотим преобразовать квадрат в круглую фигуру, радиус полученного круга будет с/√π , где s — сторона квадрата .

Какой самый большой квадрат может быть в круге с радиусом 10 см?

Если у нас есть круг радиусом 10 см , то мы можем сделать следующее, чтобы найти самый большой квадрат, вписанный в круг:

  1. Самый большой квадрат, вписанный в круг радиусом r будет длина стороны из r√2 .
  2. Так для круга радиус 10 см , самый большой квадрат в нем будет иметь длину стороны 10√2 см .
  3. Это значение длины стороны можно округлить до 14,1421 см .
  4. Площадь квадрата будет равна 200 см² .

Какой самый большой круг может быть в квадрате со стороной 10 см?

Если у нас есть квадрат, описанный вокруг круга со стороной 10 см , то наибольшую окружность, вписанную в квадрат, можно найти следующим образом:

  1. Наибольшая окружность, вписанная в квадрат со стороной s , будет иметь радиус с/2 .
  2. Итак, для квадрата со стороной 10 см самый большой круг в нем будет иметь радиус 5 см .
  3. Площадь круга будет равна 78,54 см² .

Каков радиус круга, площадь которого равна площади квадрата со стороной 10 см?

Если у нас есть квадрат со стороной 10 см , его площадь будет 100 см² . Таким образом, круг с той же площадью будет иметь радиус из 10/√π или 5,64 см .

Мадхумати Раман

Я хочу найти

Радиус круга (r)

Площадь круга (A)

Размеры самого большого квадрата в круге

Сторона квадрата (s)

Площадь квадрата (Aₛ)

Проверить 9 подобных калькуляторов окружности ⭕

Длина дугиПлощадь окружностиРассчитать окружность: найти c, d, a, r… Еще 6

Что из следующего уравнение окружности, вписанной в квадрат?

Математическая помощь Круг Уравнения Координатная плоскость

Анна Л.

спросил 03.06.16

В стандартной координатной плоскости xy вершины квадрата имеют координаты (0,4), (4,4), (4,0) и (0,0). Какое из следующих уравнений является уравнением окружности, вписанной в квадрат?

 

А . (x+2) 2 +(y+2) 2 =2

B. (x-2) 2 +(y-2) 2 =2

C. (x-2) ) 2 +(y-2) 2 =4

D. (x+2) 2 +(y-2) 2 =4

E. (x+2) 2 +(у+2) 2 =8

Подписаться І 3

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Дэррил К. ответил 03.06.16

Репетитор

Новое в Византе

Опытный репетитор по математике

Смотрите таких репетиторов

Смотрите таких репетиторов

Нарисуйте квадрат в системе координат xy, обозначающий вершины. Окружность, вписанная внутрь квадрата, будет касаться каждого края квадрата. Нарисуйте круг внутри квадрата. Сначала найдите центр квадрата, который является серединой диагонали. Эта точка также будет центром круга.

 

Используя (0,0) и (4,4), мы имеем ((0+4)/2, (0+4)/2) = (2,2).

 

Найдите радиус круга, заметив, что радиус равен половине длины стороны. Найдите длину стороны, используя формулу расстояния, и разделите на 2. Используя (0,0) и (4,0), мы получим

 

d = sqrt( (4-0) 2 + (0-0 ) 2 ) = 4 → r = 4/2 = 2

 

Теперь используйте стандартное уравнение для окружности с центром (2,2) и радиусом = 2

 

(х — 2) 2 + (у — 2) 2 = 2 2

Голосовать за 0 Голосовать против

Подробнее

Отчет

Марк О. ответил 03.06.16

Репетитор

4,8 (181)

Не просто проходи; учиться! Незначительное химическое образование и многолетний опыт репетиторства

Об этом репетиторе ›

Об этом репетиторе ›

Формула для окружности: (x-h) 2 + (y-k) 2 = r 2 , где (h,k) — центр окружности, а r — радиус.