как найти, свойства, формула, что является центром
Содержание:
- Вписанная окружность — в какую фигуру нельзя вписать
-
Теорема о вписанной окружности
- Правило о центре вписанной окружности
-
Формула нахождения радиуса вписанной окружности
- Треугольник
- Равносторонний треугольник
- Равнобедренный треугольник
- Прямоугольный треугольник
- Равнобедренная трапеция
- Квадрат
- Ромб
- Многоугольник
- Шестиугольник
Содержание
- Вписанная окружность — в какую фигуру нельзя вписать
-
Теорема о вписанной окружности
- Правило о центре вписанной окружности
-
Формула нахождения радиуса вписанной окружности
- Треугольник
- Равносторонний треугольник
- Равнобедренный треугольник
- Прямоугольный треугольник
- Равнобедренная трапеция
- Квадрат
- Ромб
- Многоугольник
- Шестиугольник
Вписанная окружность — в какую фигуру нельзя вписать
Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.
Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.
Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны.
Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Следствие
Из этого следует, что вписанная окружность не будет таковой, если не будет касаться всех сторон фигуры.
Окружность точно можно вписать в следующие геометрические фигуры:
- треугольник;
- выпуклый правильный многоугольник;
- квадрат;
- равнобедренная трапеция;
- ромб.

При этом окружность в данные фигуры может быть вписана лишь единожды.
Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.
Окружность точно нельзя вписать в следующие геометрические фигуры:
- прямоугольник;
- параллелограмм (если он не является ромбом).
Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.
Теорема о вписанной окружности
Теорема о вписанной окружности гласит, что в любой треугольник и в любой выпуклый многоугольник и четырехугольник с равными суммами длин противоположных сторон можно вписать окружность, но только одну.
Правило о центре вписанной окружности
Центр окружности при этом будет находиться в точке пересечения биссектрис фигуры.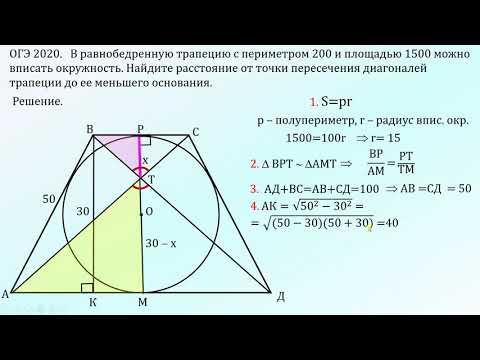 2}},\)
2}},\)
где r — радиус,
a и b — стороны треугольника,
h — высота.
Равносторонний треугольник
Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:
\(r=\frac a{2\sqrt3},\)
где r — радиус,
a — сторона треугольника.
Равнобедренный треугольник
Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:
\(r=\frac b2\sqrt{\frac{2a-b}{2a+b}},\)
где r — радиус,
a и b — стороны треугольника.
Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:
\(r=A\times\frac{\sin\left(a\right)\times\cos\left(a\right)}{1+\cos\left(a\right)}= A\times\cos\left(a\right)\times\tan\left(\frac a2\right),\)
\(r=\frac b2\times\frac{\sin\left(a\right)}{1+\cos\left(a\right)}=\frac b2\times\tan\left(\frac a2\right),\)
где r — радиус,
A и b — стороны треугольника,
a — угол при основании.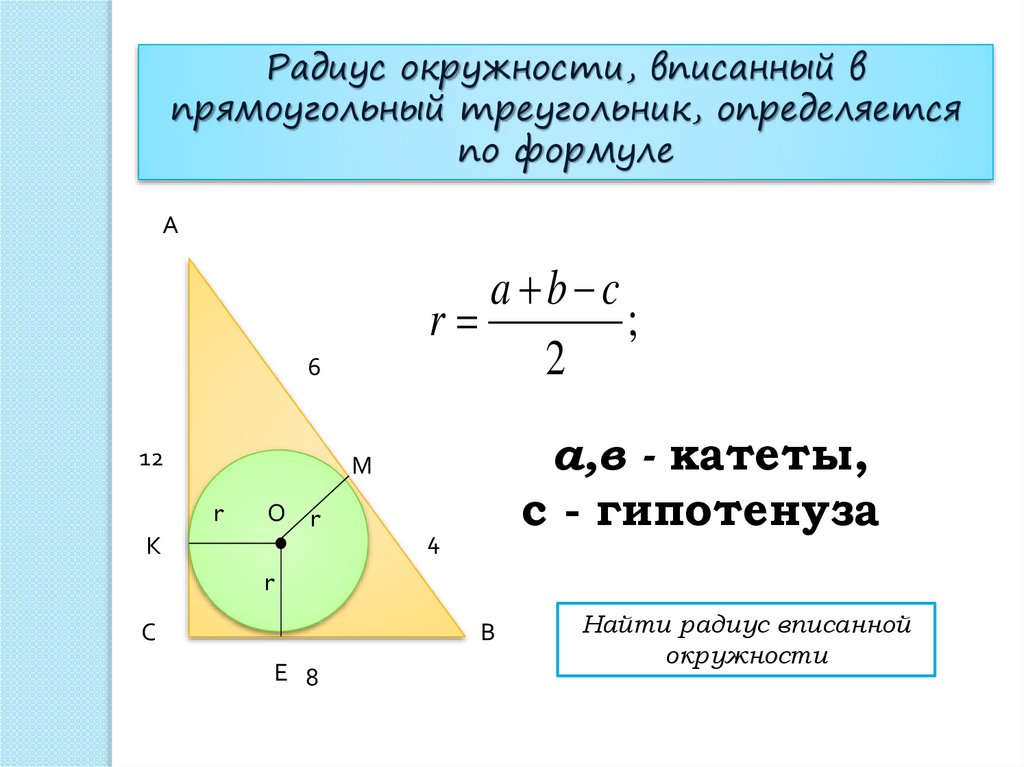 \circ}N}\right)},\)
\circ}N}\right)},\)
где r — радиус,
N — количество сторон многоугольника.
Шестиугольник
Формула нахождения радиуса окружности, вписанной в шестиугольник:
\(r=\frac{\sqrt3}2\times a,\)
где r — радиус,
a — сторона шестиугольника.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Задание №1207. Тип задания 16. ЕГЭ по математике (профильный уровень)
Решение
а) План решения.
1. Сделаем чертёж, считая для определённости, что AD>BC (для пункта а) это не имеет значения).
2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.
3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать по теореме синусов для \triangle ABD. {\circ}, равен половине гипотенузы). Отсюда \frac{O_1N}x=\frac{2O_1N}{O_1N-x} , \frac1x =\frac2{O_1N-x} , O_1N-x=2x, x= \frac13 O_1N= \frac13\cdot \frac12 MN= \frac16\cdot \frac {a\sqrt 3} 2= \frac{a\sqrt 3}{12} , x=\frac{a\sqrt 3}{12} , то есть O_2T=\frac{a\sqrt 3}{12}.
{\circ}, равен половине гипотенузы). Отсюда \frac{O_1N}x=\frac{2O_1N}{O_1N-x} , \frac1x =\frac2{O_1N-x} , O_1N-x=2x, x= \frac13 O_1N= \frac13\cdot \frac12 MN= \frac16\cdot \frac {a\sqrt 3} 2= \frac{a\sqrt 3}{12} , x=\frac{a\sqrt 3}{12} , то есть O_2T=\frac{a\sqrt 3}{12}.
3. \frac{CD}{O_2T} = \frac a{\left( \dfrac{a\sqrt 3}{12} \right)} = 4\sqrt 3.
Ответ
4\sqrt 3.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Трапеция PQRS вписана в окружность, которая касается окружности в точках M, A, N, B. Радиус окружности равен 10 см. Длина каждой непараллельной стороны равна 21 см. Чему равен периметр трапеции?
КВАНТОВАЯ КОТ-ГЕОМЕТРИЯ-ВОПРОС БАНК
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Дата обновления: 27.06.2022
Text Solution
A
82 см
B
84 см
C
85,5 см
D
Нельзя определить
Ответ
Правильный ответ B
Ответ
. оформление и отличные оценки на экзаменах.
оформление и отличные оценки на экзаменах.Видео по теме
Окружность вписана в трапецию, одна из непараллельных сторон которой перпендикулярна двум параллельным сторонам. Тогда А) диаметр вписанной окружности есть среднее геометрическое длин параллельных сторон Б) диаметр вписанной окружности есть среднее гармоническое длин параллельных сторон В) площадь трапеции есть площадь прямоугольник, длины сторон которого равны длинам параллельных сторон трапеции D) площадь трапеции равна половине площади прямоугольника, длины сторон которого равны длинам параллельных сторон трапеции
यदि समलम समलम्ब (ट्रैपीजियम) की समांतर भुजाए 8 सेमी औ औ औ औ औ सेमी औ औ व n ट्रैपीजियम के के मध मध बिंदु हो तो Mn की लम्बाई बत के के मध बिंदु हो तो Mn की लम्ब बत बत विकणों मध मध बिंदु तो तो की n ट्ब बत विकणों मध मध बिंदु तो तो लम n लम्बverैपीजियम के
23273844
Параллельные стороны трапеции 48 см, 40 см, а расстояние между ними 14 см. Найдите радиус круга, площадь которого равна площади трапеции.
43958069
Стороны трапеции равны 24 см и 20 см. Расстояние между ними 7 см. Найдите радиус окружности, площадь которой равна площади трапеции.
43958144
Трапеция PQRS вписана в окружность, которая касается окружности в точках M, A, N, B. Радиус окружности равен 10 см. Длина каждой непараллельной стороны равна 21 см. Чему равен периметр трапеции?
449930744
Равнобедренная трапеция, параллельные стороны которой относятся как 1:4. . Найдите площадь трапеции, если сумма двух параллельных сторон равна 70 см, а расстояние между ними по перпендикуляру равно 12 см.
643471939
Трапеция вписана в окружность, которая касается всех ее сторон, и линия, соединяющая середины непараллельных сторон трапеции, делит трапецию так, что площадь одной части составляет половину площади другая часть. Если длины непараллельных сторон равны 8 см и 16 см, найдите длину наименьшей стороны трапеции.
643471942
Текст Решение
Покажите, что прямоугольник с максимальным периметром, который можно вписать в круг радиусом 10 см, является квадратом со стороной 10√2 см.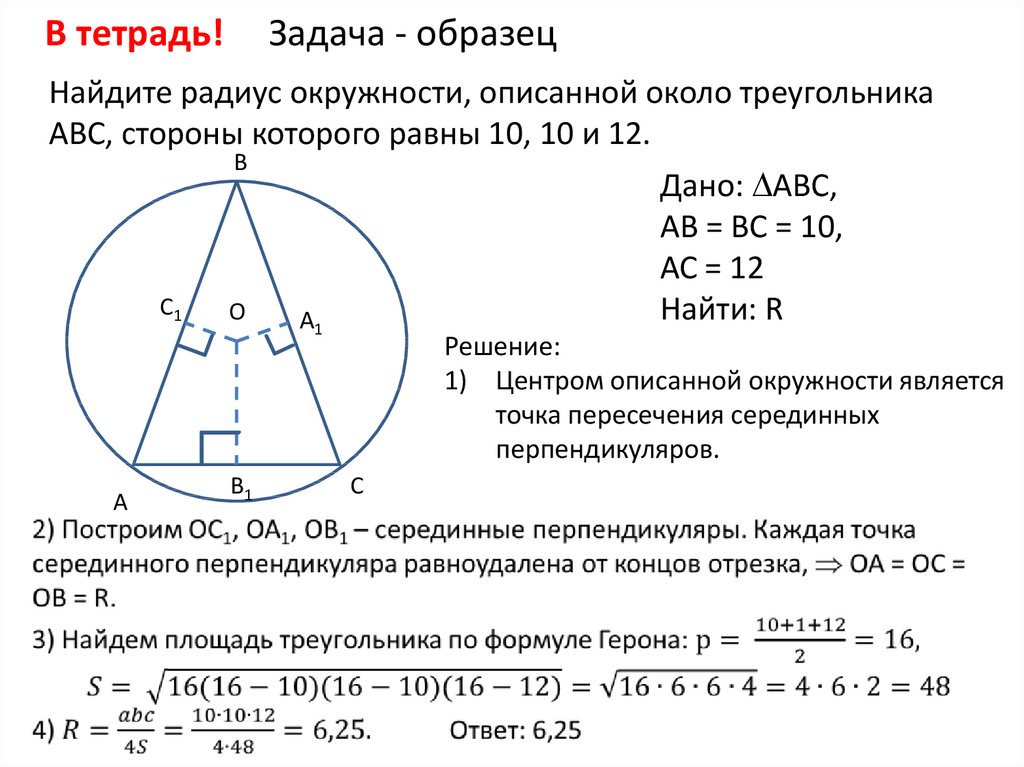
644027301
एक समलंब क|
645478470
Параллельные стороны трапеции равны 48 см, 40 см, а расстояние между ними 14 см. Найдите радиус круга, площадь которого равна площади трапеции.
645949484
Стороны трапеции равны 20 см и 10 см. Его непараллельные стороны равны по 13 см каждая. Найдите площадь трапеции?
646302998
11. Параллельные стороны трапеции равны 20 см и 10 см. Его непараллельные стороны равны. каждая по 13 см. Найдите площадь трапеции.
646311987
ABCD — трапеция. Внутренний круг касается всех его сторон. Радиус окружности равен 2 см, а АВ = 3 см. BCD прямой угол и AB||CD. Найдите площадь трапеции.
646460476
Если параллельные стороны трапеции равны 8 см и 4 см, M и N — середины диагоналей трапеции, то длина MN равна
646460806
Если параллельные стороны трапеции равны 8 см и 4 см, M и N — середины диагоналей трапеции, тогда длина MN равна
646931878
чему равен радиус вписанной окружности внутри треугольника со стороной 3,65 в?
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяУкажите эту страницу следующим образом:
«Каков радиус вписанной окружности внутри треугольника со стороной 3,65 дюйма?» 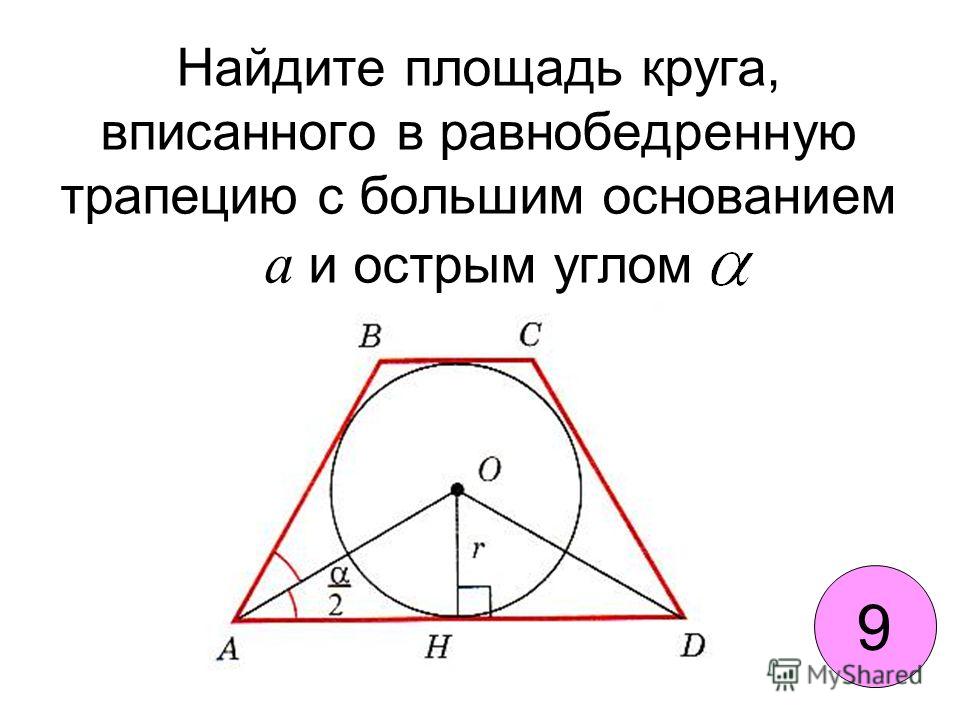 , https://www.enotes.com/homework-help/what-radius-an-inscribed-circle-inside-triangle-300861.
По состоянию на 12 марта 2023 г.
, https://www.enotes.com/homework-help/what-radius-an-inscribed-circle-inside-triangle-300861.
По состоянию на 12 марта 2023 г.
Ответы экспертов
Найдите радиус окружности, вписанной в равносторонний треугольник со стороной 3,65 дюйма.
Центр вписанной окружности является точкой пересечения биссектрис треугольника. Кроме того, треугольник касается окружности со всех трех сторон.
(1)От центра круга провести радиус до точки касания стороны треугольника. Начерченный радиус перпендикулярен стороне треугольника. Радиус также делит сторону треугольника пополам. (Треугольник равносторонний и, следовательно, равнобедренный — биссектрисы угла вершины равнобедренного треугольника также являются медианами и высотами.) 9circ ~~3.161` и поймите, что центр вписанной окружности — это не только пересечение биссектрисы угла, но в равностороннем треугольнике также пересечение медиан и высот. Тогда длина радиуса вписанной окружности составляет 2/3 высоты или 1,05 дюйма)
См.
 eNotes Ad-Free
eNotes Ad-FreeНачните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы воспитателя
Математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 09 октября 2017 г.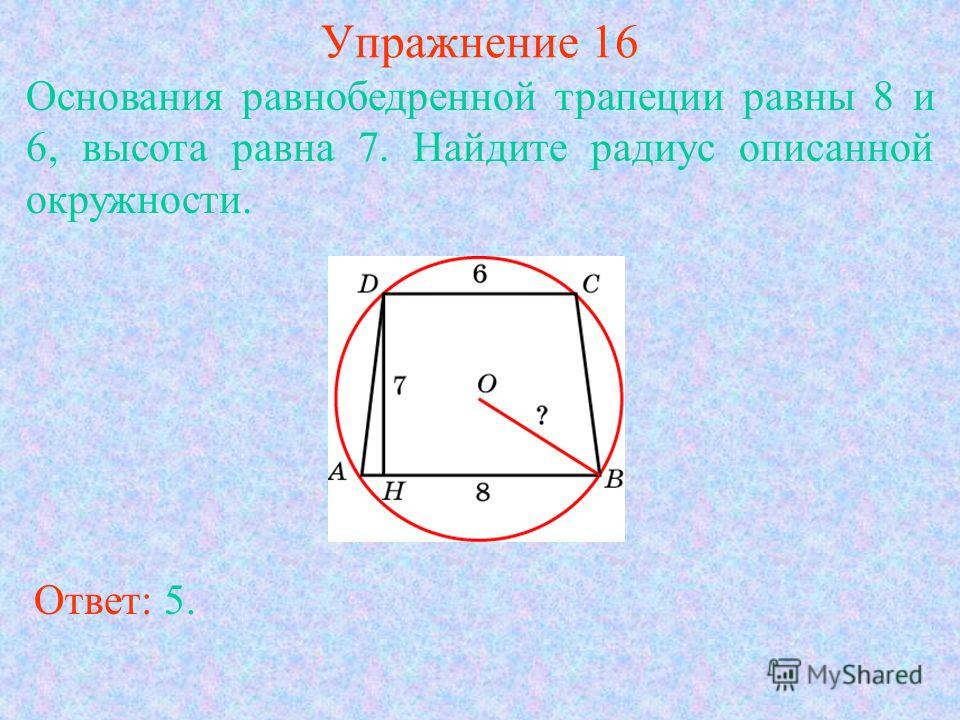

Leave A Comment