Закон Ома — формулировка простыми словами, определение
Покажем, как применять знание физики в жизни
Начать учиться
175.5K
Резистор — смелый элемент, потому что умудряется противостоять хитрому и умному электрическому току. О том, почему ток вдруг хитрый, и как все величины электрической цепи взаимосвязаны — в этой статье.
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней.
Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] ρ — удельное сопротивление [Ом · мм2/м] |
Единица измерения сопротивления — ом.
Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток.
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Таблица удельных сопротивлений различных материалов
Материал | Удельное сопротивление ρ, Ом · мм2/м |
Алюминий | 0,028 |
Бронза | 0,095–0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан (сплав NiCu + Mn) | 0,5 |
Латунь | 0,025–0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43–0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди, цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин (сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром (сплав никеля, хрома, железа и марганца) | 1,05–1,4 |
Олово | 0,12 |
Платина | 0,107 |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103–0,137 |
Титан | 0,6 |
Хромаль | 1,3–1,5 |
Цинк | 0,054 |
Чугун | 0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным.
В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает
Вот так резистор изображается на схемах:
В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит.
Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь.
Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи I — сила тока [A] ε — ЭДС [В] R — сопротивление нагрузки [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален.
В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает.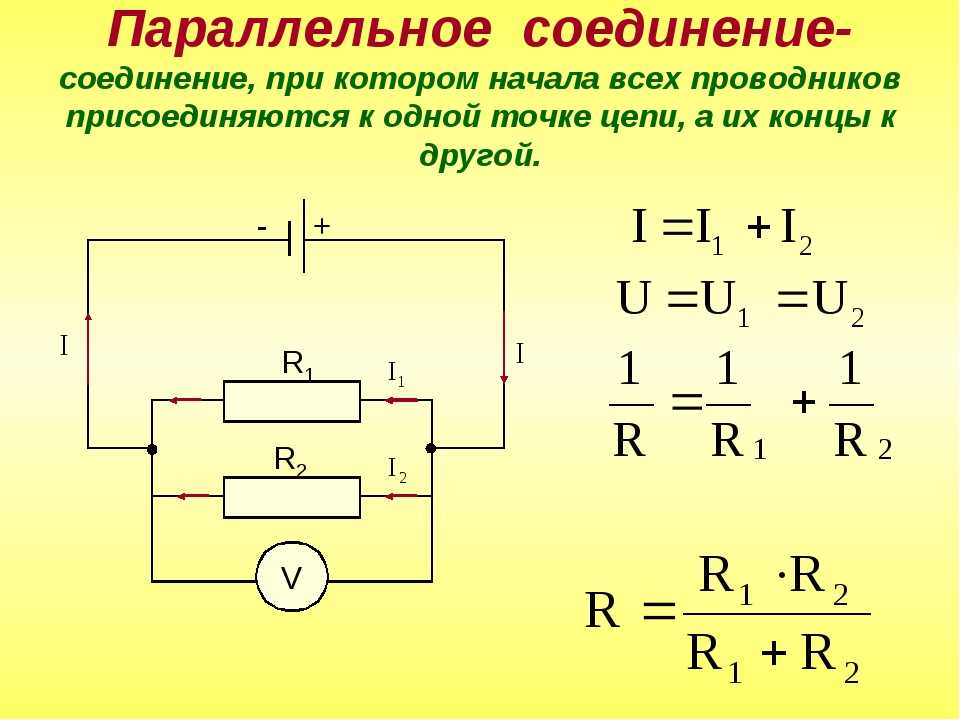
При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0.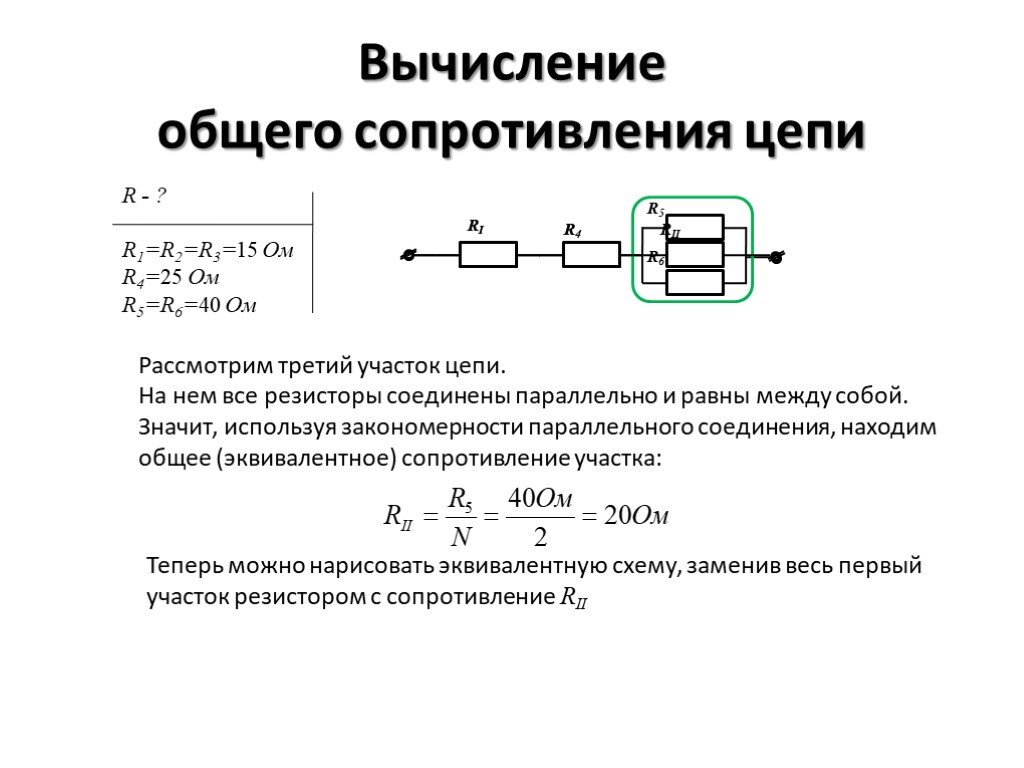
Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Последовательное соединение | Параллельное соединение | |
Схема | Резисторы следуют друг за другом | Между резисторами есть два узла Узел — это соединение трех и более проводников |
Сила тока | Сила тока одинакова на всех резисторах I = I1 = I2 | Сила тока, входящего в узел, равна сумме сил токов, выходящих из него I = I1 + I2 |
Напряжение | Общее напряжение цепи складывается из напряжений на каждом резисторе U = U1 + U2 | Напряжение одинаково на всех резисторах U = U1 = U2 |
Сопротивление | Общее сопротивление цепи складывается из сопротивлений каждого резистора R = R1 + R2 | Общее сопротивление для бесконечного количества параллельно соединенных резисторов 1/R = 1/R1 + 1/R2 + … + 1/Rn Общее сопротивление для двух параллельно соединенных резисторов Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов R = R1/n |
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?
Начнем с того, что все электронные компоненты изготавливаются по ГОСТу.
То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.
Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.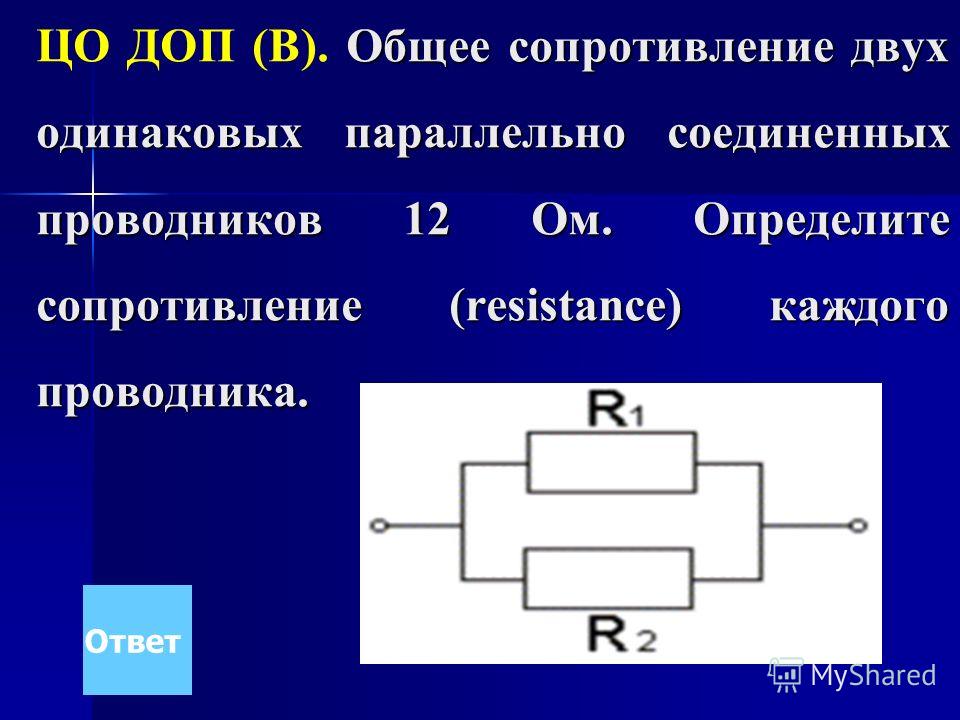
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Ответ: общее сопротивление цепи равно Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соединены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
Решение:
Найдем сначала сопротивление лампы.
Rлампы = R/2 = 10/2 = 5 Ом
Теперь найдем общее сопротивление двух параллельно соединенных резисторов.
Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
R + r = ε/I
r = ε/I − R
Подставим значения:
r = 12/0,5 − 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.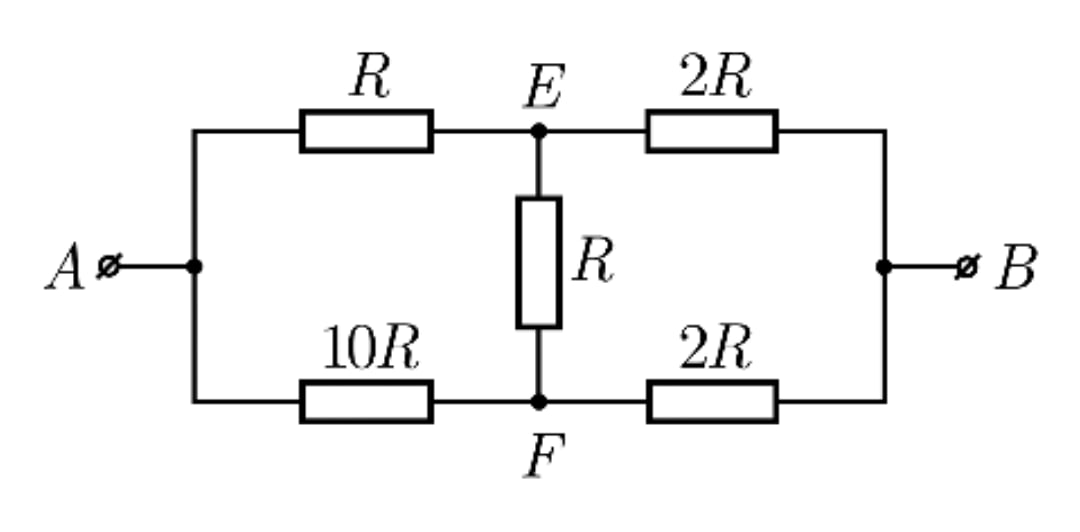
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Карина Хачатурян
К предыдущей статье
Сила тока
К следующей статье
Удельная теплоемкость вещества
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Электрический ток, сила, сопротивление. Закон Ома. Централизованное тестирование
Всего вопросов: 9
Вопрос 1. К источнику тока с ЭДС и внутренним сопротивлением r=1 Ом подключен проводник с удельным сопротивлением , площадь поперечного сечения которого S=1,1 мм2.
Если сила тока в цепи I=2 А, то длина l проводника равна:
| A. | 1,5 м |
| B. | 1,3 м |
| C. | 2 м |
| D. | 1,7 м |
| E. | 1 м |
Вопрос 2. Электрическая цепь, схема которой приведена на рисунке, состоит из шести одинаковых резисторов. Если при напряжении на зажимах источника тока U0=55В сила тока в цепи I=10 А, то сопротивление R одного резистора равно:
| A. | 6 Ом |
| B. | 3 Ом |
| C. | 2 Ом |
D. |
8,5 Ом |
| E. | 4,5 Ом |
Вопрос 3. Электрическая цепь, схема которой приведена на рисунке, подключена к источнику постоянного тока с внутренним сопротивлением r=2 Ом. Емкости конденсаторов C1=4 мкФ и C2=6 мкФ, сопротивления резисторов R1=20 Ом, R2=10 Ом, R3=10 Ом и R4=20 Ом. Если напряжение на конденсаторе C1 составляет U1=2,4 В, то ЭДС источника тока равна:
| A. | 14 В |
| B. | 21 В |
| C. | 16 В |
| D. | 10 В |
| E. | 20 В |
Вопрос 4.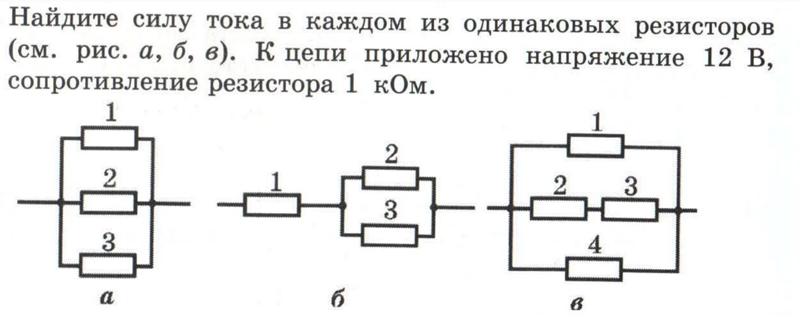
Электрическая цепь, схема которой приведена на рисунке, состоит из пяти резисторов сопротивлением R=72 Ом каждый, трех идеальных амперметров и источника постоянного тока с ЭДС . Если внутреннее сопротивление источника тока r=1 Ом, то напряжение Uз на резисторе Rз равно:
| A. | 3,6 В |
| B. | 4 В |
| C. | 2,4 В |
| D. | 1,8 В |
| E. | 5,4 В |
Вопрос 5. График зависимости сопротивления полупроводникового терморезистора, подключенного к источнику постоянного тока, напряжение на клеммах которого U=12 В, от температуры приведен на рисунке. Если температура терморезистора t=00С, то сила тока I в цепи равна:
A. |
20 мА |
| B. | 10 мА |
| C. | 25 мА |
| D. | 15 мА |
| E. | 30 мА |
Вопрос 6. В цепи, схема которой приведена на рисунке, сопротивления резисторов R1=2 Ом, R2=4 Ом, R3=6 Ом, R4=3 Ом. Если напряжение на клеммах источника постоянного тока U=24 В, то сила тока I2 в резисторе R2 равна:
| A. | 1,5 А |
| B. | 2 А |
| C. | 4,5 А |
| D. | 1 А |
| E. | 3 А |
Вопрос 7.
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока с внутренним сопротивлением r=0,27 Ом и резисторов, сопротивления которых R1=24r, R2=2r,
R3=3r,
R4=4r,
R5=5r,
R6=6r,
R7=20r,
R8=8r. Если ЭДС источника , то мощность P1, выделяемая на резисторе R1, равна:
| A. | 6 Вт |
| B. | 9,6 Вт |
| C. | 3 Вт |
| D. | 32 Вт |
| E. | 18 Вт |
Вопрос 8. В электрической цепи, схема которой приведена на рисунке, сопротивления резисторов R1=300 Ом, R2=600 Ом, R3=300 Ом и R4=400 Ом.
Если сила тока в резисторе R3 составляет I3=60 мА, то напряжение U4 на резисторе R4 равно:
| A. | 54 В |
| B. | 6 В |
| C. | 27 В |
| D. | 12 В |
| E. | 3 В |
Вопрос 9. Пять резисторов, сопротивления которых R1=120 Ом, R2=30 Ом, R3=15 Ом, R4=60 Ом и R5=24 Ом, соединены параллельно и подключены к источнику постоянного тока. Если в резисторе R4 сила тока I4=0,15 А, то сила тока I в источнике равна:
A. |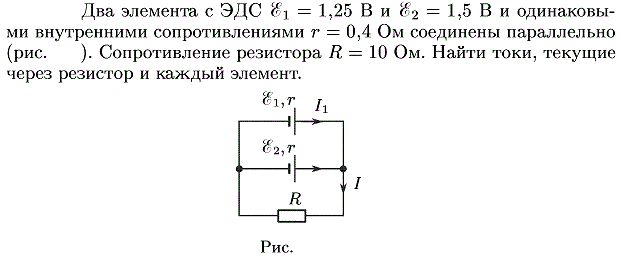
3,5 А |
| B. | 4,8 А |
| C. | 2,4 А |
| D. | 1,5 А |
| E. | 4,6 А |
Пять одинаковых резисторов сопротивлением 1 Ом каждый изначально расположены, как показано на рисунке четкими линиями. Если сложить два сопротивления, как показано пунктирными линиями, то изменение сопротивления в окончательном и первоначальном порядке будет Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Обновлено: 27-06-2022
Текстовое решение
Ответ
Правильный ответ A
Ответ
Пошаговое решение от экспертов, которое поможет вам в сомнениях и получении отличных оценок на экзаменах.
Похожие видео
Сеть, показанная на рисунке, представляет собой набор из девяти одинаковых резисторов.
Сопротивление сети между точками А и В равно 1,5 Ом. Сопротивление r равно
10966750
Каждый резистор, показанный на рисунке, представляет собой бесконечную сеть сопротивления 1 Ом. Эффективное сопротивление между точками A и B равно
10966755
Как изменится сопротивление цепи между A и F, состоящей из пяти одинаковых проводников, если два одинаковых проводника соединить, как показано на рисунке пунктирной линией?
10966813
Четыре одинаковых сопротивления, каждое из которых имеет значение R, расположены, как показано на рисунке. Найдите эквивалентное сопротивление между A и B.
11309075
Как изменится сопротивление цепи между А и В, состоящей из пяти одинаковых сопротивлений, если два одинаковых сопротивления сложить, как показано пунктирной линией в
11309095
Как изменится в сопротивлении цепи, состоящей из пяти одинаковых проводников, если добавить два одинаковых проводника, как показано на рисунке пунктирной линией.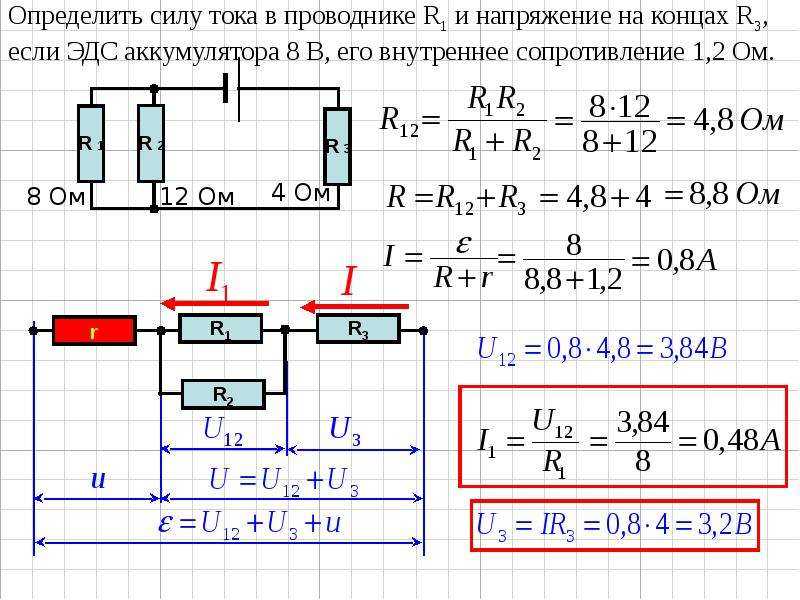
12228940
В сети, показанной на рисунке, каждое сопротивление равно 1 Омега. Эффективное сопротивление между А и В равно
15665447
В показанном расположении величина каждого сопротивления составляет 1 Ом. Эквивалентное сопротивление между O и A равно
18249294
Text Solution
На рисунке показана бесконечная сеть резисторов сопротивлением 1 Ом каждый. Эффективное сопротивление между A и B равно
278684529
Пять одинаковых резисторов сопротивлением 1 Ом изначально расположены, как показано на рисунке темными линиями. Если сложить два одинаковых сопротивления, как показано штриховыми линиями, то изменение сопротивления в окончательном и исходном расположении составит
642971829
Сеть, показанная на рисунке, представляет собой набор из девяти одинаковых резисторов. Сопротивление сети между точками А и В равно 1,5 Ом. Сопротивление r составляет
643184053
Каждый резистор, показанный на рисунке, представляет собой бесконечную сеть сопротивления 1 Ом.
Эффективное сопротивление между точками A и B равно
643184056
Как изменится сопротивление цепи между A и F, состоящей из пяти одинаковых проводников, если два одинаковых проводника соединить, как показано на рисунке пунктирной линией?
643184112
В показанном расположении величина каждого сопротивления равна 1 Ом. Эквивалентное сопротивление между O и A равно
643191340
В сети, показанной на рисунке, каждое сопротивление равно 1 Ом. Эффективное сопротивление между A и B равно
643989775
Пять одинаковых резисторов сопротивлением $R = 1500\,\Omega$ подключены к батарее $300\,V$, как показано на схеме. Показания идеального амперметра $A$ равны (A) $\dfrac{1}{5}\,A$(B) $\dfrac{3}{5}\,A$(C) $\dfrac{2 {5}\,A$(D) $\dfrac{4}{5}\,A$
Подсказка
Текущее значение, отображаемое на амперметре, определяется по формуле закона Ома. Значение сопротивления, подставляемое в закон Ома, является полным сопротивлением.
Общее сопротивление определяется по формуле резистора при параллельном включении.
Закон Ома утверждает, что
$\Rightarrow V = IR$
Где $V$ — напряжение, $I$ — ток, а $R$ — сопротивление.
Формула сопротивления в параллельном режиме определяется следующим образом:
$\Rightarrow \dfrac{1}{{{R_T}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2} }} + \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_4}}} + \dfrac{1}{{{R_5}}}$
Где ${R_T}$ — это общее сопротивление, а ${R_1}$, ${R_2}$ и т. д. — сопротивления, соединенные параллельно.
Полный пошаговый ответ
Учитывая, что все сопротивления равны, поэтому ${R_1} = {R_2} = {R_3} = {R_4} = {R_5} = R = 1500\,\Omega $
Напряжение в цепи равно, $V = 300\,V$
Теперь,сопротивление в параллельной формуле определяется как,
$\Rightarrow \dfrac{1}{{{R_T}}} = \dfrac{1}{ {{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_4}}} + \dfrac{1 }{{{R_5}}}\,………………\влево( 1 \вправо)$
Подставляя значение равного сопротивления пяти сопротивлений, соединенных параллельно в приведенном выше уравнении (1), тогда приведенное выше уравнение (1) записывается как
$\Rightarrow \dfrac{1}{{{R_T} }} = \dfrac{1}{R} + \dfrac{1}{R} + \dfrac{1}{R} + \dfrac{1}{R} + \dfrac{1}{R}$
добавив члены в приведенное выше уравнение, то приведенное выше уравнение запишется как
$\Rightarrow \dfrac{1}{{{R_T}}} = \dfrac{5}{R}$
Взяв обратное значение с обеих сторон , то приведенное выше уравнение записывается как
$\Rightarrow {R_T} = \dfrac{R}{5}$
Теперь закон Ома утверждает, что
$\Rightarrow V = IR\,.
………….. .\left( 2 \right)$
В этом уравнении $R$ представляет собой полное сопротивление, поэтому, подставив напряжение и полное сопротивление в приведенное выше уравнение (2), уравнение (2) запишется как
$ \Rightarrow 300 = I \times \dfrac{R}{5}$
Переставив члены, тогда
$\Rightarrow \dfrac{{300 \times 5}}{R} = I$
Подставив значения сопротивления в приведенное выше уравнение, то
$\Rightarrow I = \dfrac{{300 \times 5}}{{1500}}$
При умножении слагаемых, тогда
$\Rightarrow I = \dfrac{{1500}}{{1500}}$
By сократив члены, то
$\Rightarrow I = 1\,A$
Ток через одно сопротивление будет $= 1 \times \dfrac{1}{5}$
Ток через амперметр $= \dfrac{1}{5 } \times {3} = \dfrac{3}{5}$.
Итак, правильный вариант (Б).
Примечание
Пять сопротивлений имеют одинаковое сопротивление, поэтому значение не подставляется в формулу резистора при параллельном подключении. Если пять резисторов имеют разное сопротивление, значение пяти различных резисторов должно быть заменено в формуле резистора при параллельном соединении.
Leave A Comment