Самостоятельная работа по теме «Касательная к окружности»
Просмотр содержимого документа
«Самостоятельная работа по теме «Касательная к окружности»»
Тема «Касательная к окружности»
1 вариант
Прямая КЕ касается окружности с центром в О, К – точка касания. Найдите ОЕ, если КЕ=8 см, а радиус окружности равен 6 см.
АВ и ВС – отрезки касательных, проведённых к окружности с центром О и радиусом, равным 10 см. Найдите ВО, если угол АОС равен 60˚.
ЕК и ЕF- отрезки касательных, проведённых к окружности с центром О и радиусом, равным 6 см, угол КОF = 120˚, А – точка пересечения КF и ОЕ. Найдите ОА и АЕ.
Тема «Касательная к окружности»
2 вариант
Прямая MN касается окружности с центром в точке О, М – точка касания, угол MNO = 30˚, а радиус окружности равен 5 см. Найдите NO.
MN и NK – отрезки касательных, проведенных к окружности с центром О, угол MNK = 90˚. Найдите радиус окружности, если ON=2 см.
PM и PN отрезки касательных, проведенных к окружности с центром О и радиусом, равным 10 см, угол MON = 120˚, Е – точка пересечения MN и OP. Найдите ОЕ и РЕ.
Тема «Касательная к окружности»
вариант
Прямая КЕ касается окружности с центром в О, К – точка касания. Найдите ОЕ, если КЕ=8 см, а радиус окружности равен 6 см.
АВ и ВС – отрезки касательных, проведённых к окружности с центром О и радиусом, равным 10 см. Найдите ВО, если угол АОС равен 60˚.
ЕК и ЕF- отрезки касательных, проведённых к окружности с центром О и радиусом, равным 6 см, угол КОF = 120˚, А – точка пересечения КF и ОЕ. Найдите ОА и АЕ.
Тема «Касательная к окружности»
вариант
Прямая MN касается окружности с центром в точке О, М – точка касания, угол MNO = 30˚, а радиус окружности равен 5 см. Найдите NO.
Найдите NO.
MN и NK – отрезки касательных, проведенных к окружности с центром О, угол MNK = 90˚. Найдите радиус окружности, если ON=2 см.
PM и PN отрезки касательных, проведенных к окружности с центром О и радиусом, равным 10 см, угол MON = 120˚, Е – точка пересечения MN и OP. Найдите ОЕ и РЕ.
Касательная к окружности и свойства отрезков касательных
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.
. Угол равен , где — центр окружности. Его сторона касается окружности. Найдите величину меньшей дуги окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол — прямой. Из треугольника получим, что угол равен градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги — тоже градуса.
Ответ: .
. Найдите угол , если его сторона касается окружности, — центр окружности, а большая дуга окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Это чуть более сложная задача. Центральный угол опирается на дугу , следовательно, он равен градусов. Тогда угол равен . Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол — прямой. Тогда угол равен .
Ответ: .
. Хорда стягивает дугу окружности в . Найдите угол между этой хордой и касательной к окружности, проведенной через точку . Ответ дайте в градусах.
Проведем радиус в точку касания, а также радиус . Угол равен . Треугольник — равнобедренный. Нетрудно найти, что угол равен градуса, и тогда угол равен градусов, то есть половине угловой величины дуги .
Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
. К окружности, вписанной в треугольник , проведены три касательные. Периметры отсеченных треугольников равны , , . Найдите периметр данного треугольника.
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника складывается из периметров отсеченных треугольников.
Ответ: .
Ты нашел то, что искал? Поделись с друзьями!
Вот более сложная задача из вариантов ЕГЭ:
. Около окружности описан многоугольник, площадь которого равна . Его периметр равен . Найдите радиус этой окружности.
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку с вершинами . Получились треугольники и .
Очевидно, что площадь многоугольника .
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?
Ответ: .
Тест по теме «Окружность»
Вариант 1.
А1. Касательная к окружности изображена на рисунке:
А2. Вписанный в окружность угол изображён на рисунке:
А3. Центром описанного около окружности треугольника является точка пересечения:
Центром описанного около окружности треугольника является точка пересечения:
а) биссектрис треугольника; б) высот треугольника; в) медиан треугольника; г) серединных перпендикуляров.
А4. Для того, чтобы вокруг выпуклого четырёхугольника можно было описать окружность, должно выполняться следующее равенство:
А5. Две окружности с центрами в точках О и О1 касаются сторон угла (В и В1 — точки касания). Тогда АВ1О1 будут: а) подобны по двум углам; б) подобны по двум прилежащим сторонам и углу между ними; в) подобны по трём пропорциональным сторонам; г) не подобны.
В1. На рисунке DC – диаметр окружности. Тогда угол BDC равен __________ .
В2. На рисунке Тогда __________ .
В3. На рисунке MN и MK –касательные к окружности, ON=OK=R. Тогда отрезок NM равен отрезку ________ .
В4. Расстояние d от центра окружности О до прямой L равно 5 см, а радиус окружности r равен 6 см. Тогда прямая L и окружность с центром в точке О и радиусом r будут _________ .
В5. Центральный угол больше вписанного угла, опирающегося на ту же дугу, на 40⁰. Тогда градусная мера вписанного угла будет равна __________ .
В6. На рисунке АС и АЕ – секущие. Дуга ВD=30⁰, дуга СЕ=70⁰. Тогда угол САЕ равен _________ .
В7. На рисунке R=ОВ=5 см, АВ=6 см. Тогда расстояние от центра окружности до хорды АВ равно ________.
В8. На рисунке подобными треугольниками будут ______ .
В9. Квадрат со стороной 8 см вписан в окружность. Тогда радиус окружности будет равен __ .
В10. На рисунке NB=2 см, МВ=6 см, ВС=3 см. Тогда длина отрезка АС будет равна ______ .
C1. В равнобедренном треугольнике боковые стороны равны 15 см, а высота, опущенная на основание, равна 12 см. Найдите радиус вписанной в треугольник окружности.
Тест по теме: «Окружность».
Вариант 2.
А1. Вписанная в треугольник окружность изображена на рисунке:
А2.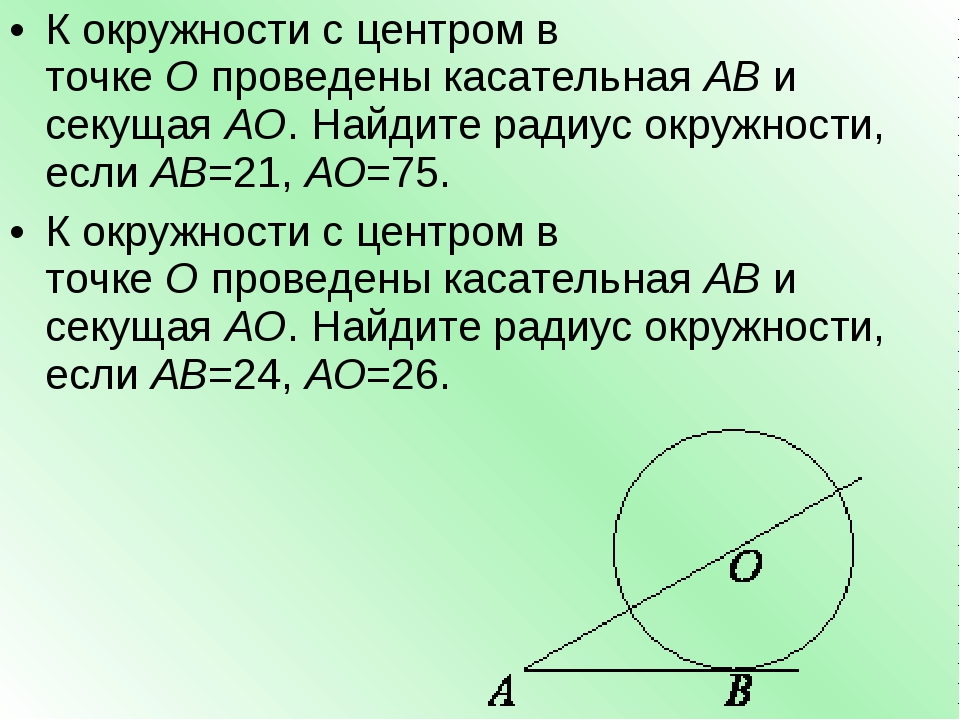 Описанная около четырёхугольника окружность изображена на рисунке:
Описанная около четырёхугольника окружность изображена на рисунке:
А3. Расстояние от центра окружности до прямой равно радиусу окружности. Тогда окружность и прямая имеют общих точек: а) 2; б) 1; в) 0; г) 3.
А4. Вокруг параллелограмма описали окружность. Тогда этот параллелограмм является: а)квадратом; б) ромбом; в) прямоугольником; г) произвольным параллелограммом.
А5. Если в треугольнике одна из его вершин является точкой пересечения высот данного треугольника, то этот треугольник будет: а) остроугольным, не равносторонним; б) тупоугольным; в) прямоугольным; г) равносторонним.
В1. На рисунке изображён угол, который называется ________ .
В2. Прямая а, изображённая на рисунке, называется ______ .
В3. Окружность вписана в четырёхугольник АВСD. Тогда АВ + DC=_________ .
В4. На рисунке прямая а – касательная к окружности с центром в точке О и радиусом R.
Тогда угол ВАО равен ___________ .
В5. Угол АСВ равен 60˚. Тогда на рисунке дуга АВ равна ________ .
В6. На рисунке угол АВС равен 70˚. Тогда угол АОС равен __________ .
В7. В равнобедренный треугольник АВС с основанием АС вписана окружность. М –точка касания, делит одну из боковых сторон на отрезки длиной 3 см и 4 см. Тогда периметр треугольника АВС равен ___________ .
В8. На рисунке КВ=4 см, МВ=6 см, ВС=3 см. Тогда длина отрезка АВ будет равна ________ .
В9. Из точки А к окружности проведены касательные АN и АР, при этом угол NAP равен 120˚. Радиус окружности равен 9 см. Тогда AN =________ .
В10. Вокруг равностороннего треугольника описана окружность радиуса 10 см. Затем в этот треугольник вписана окружность. Тогда радиус этой окружности равен __________ .
С1. В равнобедренную трапецию вписана окружность радиусом 7,5 см. Найдите стороны трапеции, если боковая сторона трапеции равна 17 см.
МБУ Школа №14, Тольятти
ПРИЕМ В ПЕРВЫЙ КЛАСС НА 2021-2022 УЧЕБНЫЙ ГОД|
Дата начала регистрации заявлений |
Дата завершения регистрации заявлений |
Примечание |
|
01. |
30.06.2021 |
Заявления принимаются от родителей детей, имеющих первоочередное и преимущественное право; от родителей детей, зарегистрированных на территории, закрепленной за школой. |
|
06.07.2021 |
05.09.2021 |
Заявления принимаются от родителей детей вне зависимости от места регистрации ребенка. |
Подробная информация в разделе «Прием в 1-ый класс»
УВАЖАЕМЫЕ РОДИТЕЛИ БУДУЩИХ ПЕРВОКЛАССНИКОВ!ОТКРЫТА ДЕМОНСТРАЦИОННАЯ ВЕРСИЯ САЙТА ПО ПРИЕМУ В ПЕРВЫЙ КЛАСС
С 15.03.2021 по 25.03.2021 (включительно) для ознакомления родителей (законных представителей) с процедурой самостоятельной подачи заявления в 1 класс 2021-2022 учебного года по адресу: https://etest.asurso.ru открыта демонстрационная версия сайта для регистрации заявления.
Обращаем внимание:
- Заявления, оформленные в демонстрационной версии, не рассматриваются учреждением для приема в школу.
- Доступ к демонстрационной версии осуществляется без авторизации через ЕСИА. Во время приемной кампании для подачи заявления в 1 класс МБУ авторизация через ЕСИА ОБЯЗАТЕЛЬНА.
с 10.03.2021 по 15.12.2021 проводится опрос граждан.
В целях оценки достижения значений показателя федерального проекта «Поддержка семей, имеющих детей» национального проекта «Образование», на основании распоряжения от 28.12.2020 № 1182-р «Об организации мониторинговых исследований в 2021 году», министерство образования и науки Самарской области проводит мониторинг удовлетворенности граждан (родителей) услугами психолого-педагогической, методической и консультативной помощи, предоставляемых государственными и муниципальными образовательными организациями. Опрос граждан проводится с 10 марта по 15 декабря 2021 года. Форма для опроса размещена на интернет-ресурсе по адресу: ссылка
Опрос граждан проводится с 10 марта по 15 декабря 2021 года. Форма для опроса размещена на интернет-ресурсе по адресу: ссылка
с 25.01.2021 по 15.12.2021 проводится опрос граждан.
Министерство образования и науки Самарской области информирует, что в целях оценки удовлетворенности граждан качеством образовательных услуг, предоставляемых государственными и муниципальными образовательными организациями дошкольного и общего образования, в период с 25.01.2021 по 15.12.2021 проводится опрос граждан.
Опросная анкета размещена на Интернет-ресурсе по адресу: ссылкаРЕЖИМ ФУНКЦИОНИРОВАНИЯ УЧРЕЖДЕНИЯ В УСЛОВИЯХ РАСПРОСТРАНЕНИЯ COVID-19
с 11 января 2021 года Уважаемые родители (законные представители) обучающихся!МБУ «Школа №14» доводит до вашего сведения информацию о режиме функционирования Учреждения с 11.01.2021 в условиях распространения COVID-19
Информируем вас о том, что на основании письма министерства образования и науки Самарской области от 14.09.2020 г. № МО-16-09-01/1142, во исполнение пункта 1.3. протокола заседания оперативного штаба по предупреждению завоза и распространения новой коронавирусной инфекции на территории Самарской области от 07.09.2020 г. № 66, в целях усиления мер по недопущению распространения новой коронавирусной инфекции, родителям (законные представители) обучающихся (воспитанников) необходимо обязательное использование средств индивидуальной защиты органов дыхания (одноразовых или многоразовых масок), а также недопущение их пребывания в Учреждении без масок.
На основании Санитарных правил, утвержденных Постановлением главного государственного санитарного врача Российской Федерации от 30.06.2020 №16 «Об утверждении санитарно-эпидемиологических правил СП 3.1/2.4.3598-20 «Санитарно-эпидемиологические требования к устройству, содержанию и организации работы образовательных организаций и других объектов социальной инфраструктуры для детей и молодежи в условиях распространения новой коронавирусной инфекции (COVID-19)» (ссылка на документ)устанавливается особый режим работы и требования к пребыванию в Учреждении Подробнее>>
Расписание:Об организации питания:
В 2020-2021 учебном году для обучающихся 1 — 4 классов будет организовано бесплатное одноразовое горячее питание.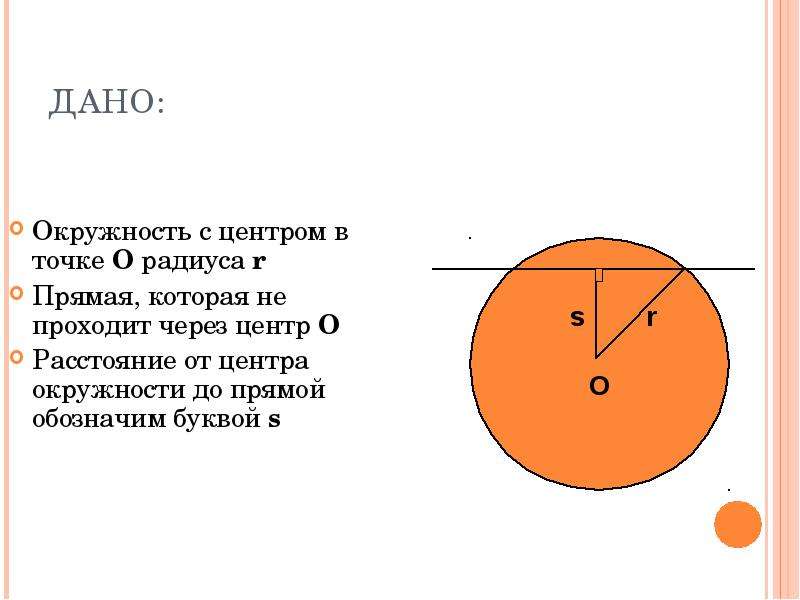
Ответственный за организацию горячего питания в МБУ «Школа № 14»: Яропуд Ольга Павловна, телефон 45-16-31
Телефон горячей линии Департамента образования Администрации городского округа Тольятти по вопросам питания: 8(8482) 54-44-33, (доб.3883) Шарамова Юлия Станиславовна
Телефон горячей линии ТУ МОиН по вопросам питания: 37-98-50, ответственный специалист — Трофимова Елена Николаевна
Цикличное двухнедельное меню сбалансированных рационов, для организации бесплатного горячего питания обучающихся, получающих начальное общее образование в государственных и муниципальных образовательных организациях городского округа Тольятти ЗДЕСЬ >>
ПРОЕКТ ПО ФОРМИРОВАНИЮ ЦИФРОВОЙ КОМПЕТЕНТНОСТИ
МБУ «Школа № 14» включена в управленческий портфель департамента образования с межведомственным проектом «Формирование цифровой компетентности и медиаграмотности учащихся через создание Информационного бюро «ICAR» и сети школьных медиа-групп».
Более подробная информация ЗДЕСЬ
ВЫПУСК — ХОРОШИЕ НОВОСТИ — 21
от 15.03.2021
Обзор главных городских событий прошедшей недели в г.о. Тольятти.Новости в сфере экономики, образования, культуры, спорта и др.
«Хорошие новости» архив предыдущих новостей
ПРОФИЛАКТИКА ГРИППА И ОРВИ
«Управление Роспотребнадзора по Самарской области рекомендует: Позаботьтесь о своем здоровье и здоровье своих близких – соблюдайте гигиену рук, используйте одноразовые маски в местах большого скопления людей, при контактах с людьми с симптомами вирусного респираторного заболевания».
КАК ПРОХОДИТ ВАКЦИНАЦИЯ?
ВМЕСТЕ ПРОТИВ КОРРУПЦИИ!
|
Горячая линия по вопросам деятельности образовательных организаций, в том числе по вопросам незаконных сборов денежных средств и несоблюдения педагогическими работниками требований педагогической этики |
Генеральной прокуратурой Российской Федерации во взаимодействии с Правительством Москвы разработан ряд тематических информационно-разъяснительных материалов: памятки и буклеты с разъяснением законодательства в сферах, имеющих повышенные коррупционные риски, и обоснованием целесообразности выбора некоррупционного поведения, короткометражные видеоролики о негативных последствиях коррупционных действий, а также компьютерный программный продукт с образовательным наполнением в виде итогового тестирования.
Электронная версия материалов размещена на сайте Генеральной прокуратуры Российской Федерации в сети «Интернет» в разделе «Противодействие коррупции» по адресу: https://genproc.gov.ru/anticor/
НОВОСТИ
Окружность и касательная — урок. Геометрия, 8 класс.
В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь одну или две общие точки.
1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.
2. Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.
В этом случае прямую называют секущей окружности.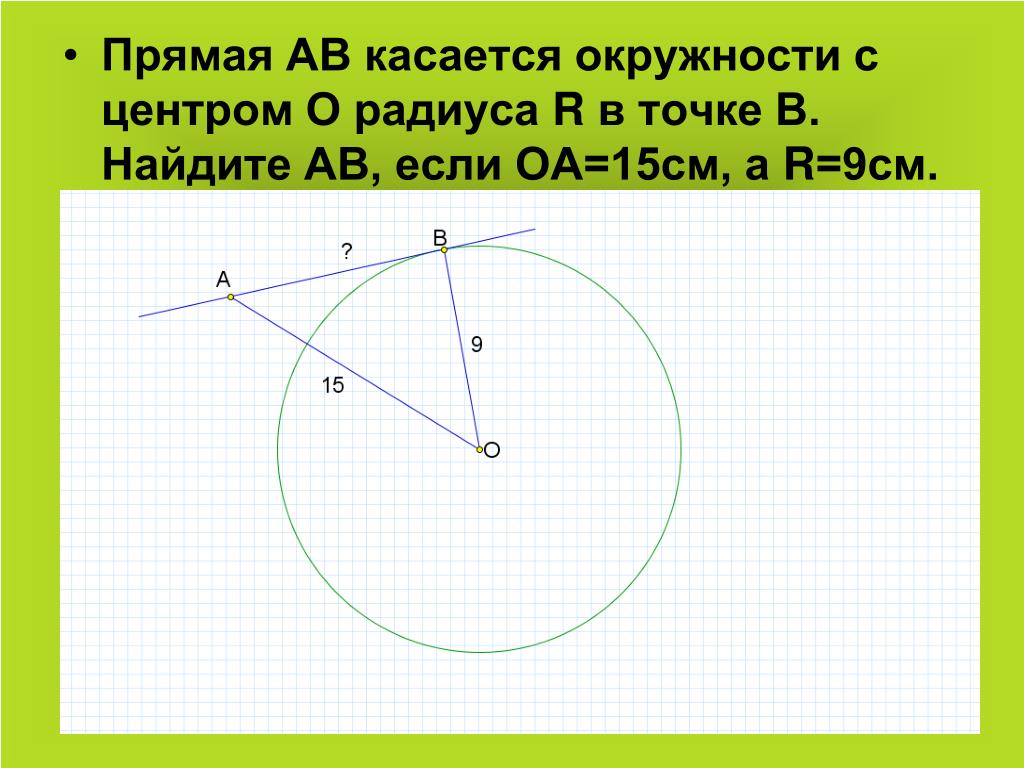
Если прямая имеет две общие точки с окружностью, то она называется секущей.
3. Если расстояние от центра окружности до прямой равно радиусу, то у прямой и окружности одна общая точка.
В этом случая прямую называют касательной к окружности.
Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Предположим, что радиус \(OA\) не перпендикулярен к прямой, но является наклонной. Тогда из точки \(O\) можно провести перпендикуляр к прямой, который будет короче радиуса. А это означает, что расстояние от центра окружности до прямой меньше радиуса, и у прямой и окружности должны быть две общие точки. Но это противоречит данной информации, наше предположение неверно.
Если из точки к окружности проведены две касательные, то
а) длины отрезков касательных от этой точки до точки касания равны,
б) прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.
Пусть \(AB\) и \(AC\) — касательные к окружности с центром \(O\).
Требуется доказать, что \(AB = AC\) и \(OA\) является биссектрисой угла \(A\).
Треугольники \(OBA\) и \(OCA\) — прямоугольные, так как касательные перпендикулярны к радиусам в точках \(B\) и \(C\). Сторона \(OA\) — общая. Катеты \(OB\) и \(OC\) равны как радиусы одной и той же окружности. Треугольники равны по гипотенузе и катету, отсюда равны и катеты \(AB\) и \(AC\), и углы \(BAO\) и \(CAO\), то есть \(OA\) делит угол пополам.
Взаимное расположение прямой и окружности
Слайды и текст этой презентации
Слайд 1
Взаимное расположение прямой и окружности
Слайд 2
Взаимное расположение прямой и окружности
.
О
А
В
С
D
R
ОR – радиус
СD – диаметр
AB — хорда
Слайд 3
Дано:
Окружность с центром в точке О радиуса r
Прямая, которая не проходит через центр О
Расстояние от центра окружности до прямой обозначим буквой s
O
r
s
Слайд 4
Возможны три случая:
1) sO
sА
В
Прямая АВ называется секущей по отношению к окружности.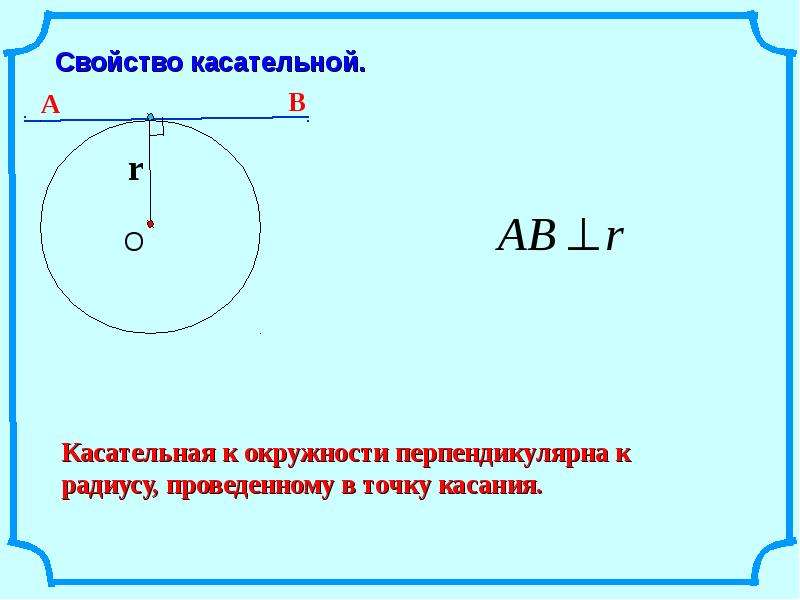
Слайд 5
Возможны три случая:
2) s=r
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
O
s=r
M
Слайд 6
Возможны три случая:
3) s>r
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
O
s>r
r
Слайд 7
Касательная к окружности
Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
O
s=r
M
m
Слайд 8
Выясните взаимное расположение прямой и окружности, если:
r = 15 см, s = 11см
r = 6 см, s = 5,2 см
r = 3,2 м, s = 4,7 м
r = 7 см, s = 0,5 дм
r = 4 см, s = 40 мм
прямая – секущая
прямая – секущая
общих точек нет
прямая – секущая
прямая — касательная
Слайд 9
Решите № 633.
Дано:
OABC-квадрат
AB = 6 см
Окружность с центром O радиуса 5 см
Найти:
секущие из прямых OA, AB, BC, АС
О
А
В
С
О
Слайд 10
Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
m – касательная к окружности с центром О
М – точка касания
OM — радиус
O
M
m
Слайд 11
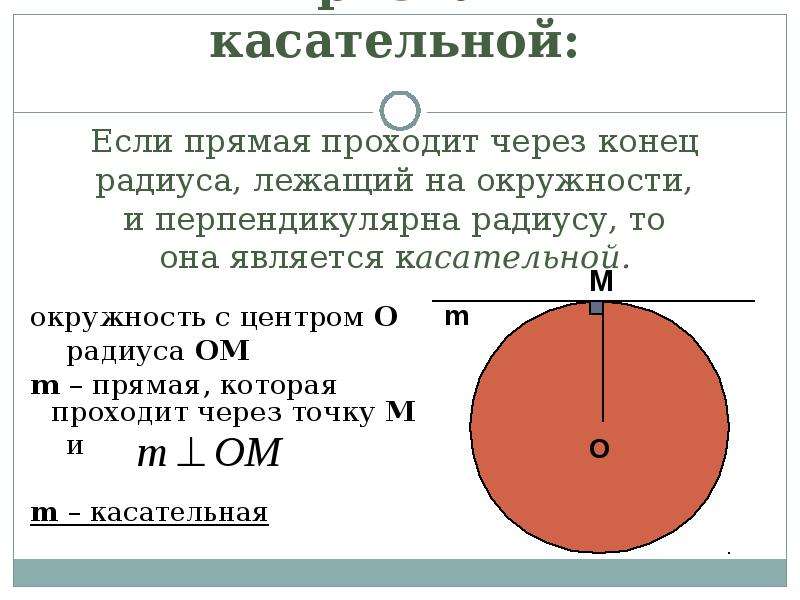
Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является касательной.
окружность с центром О
радиуса OM
m – прямая, которая проходит через точку М
и
m – касательная
O
M
m
Слайд 12
Свойство касательных, проходящих через одну точку:
▼ По свойству касательной
∆АВО, ∆АСО–прямоугольные
∆АВО=∆АСО–по гипотенузе и катету:
ОА – общая,
ОВ=ОС – радиусы
АВ=АС и
▲
О
В
С
А
1
2
3
4
Отрезки касательных к
окружности, проведенные
из одной точки, равны и
составляют равные углы
с прямой, проходящей через
эту точку и центр окружности.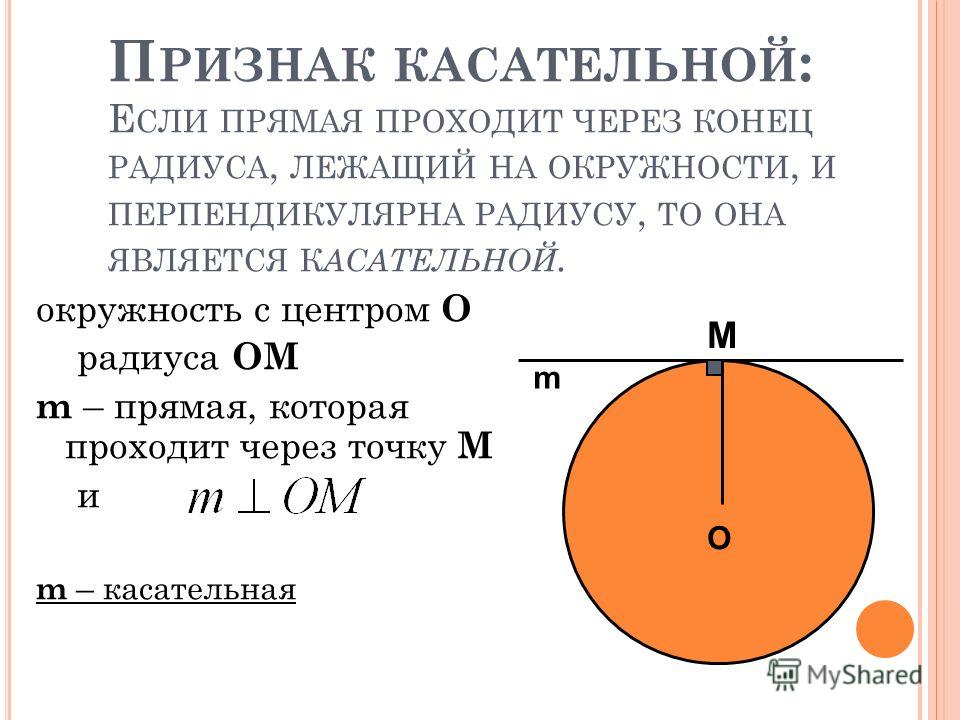
Геометрия 8 класс самостоятельная работа Касательная к окружности
Г-8 С.Р. Касательная к окружности.
Вариант 1.
1. Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.
Найдите ОВ, если АВ = 12 см.
2. Из точки А к окружности с центром О и радиусом 8 см проведены
касательные АВ и АС (В и С – точки касания). Найдите АВ и АС, если
3. Из точки М к окружности с центром О и радиусом 8 см проведены
касательные АМ и ВМ (А и В – точки касания).
Найдите периметр треугольника АВМ, если
Г-8 С.Р. Касательная к окружности.
Вариант 2.
1. Прямая АВ касается окружности с центром О и радиусом 15 см в точке В.
Найдите АВ, если ОА = 17 см.
2. Из точки М к окружности с центром О проведены касательные МА и МВ
(В и А – точки касания). Найдите АМ и ВМ, если
3. Из точки А к окружности с центром В проведены касательные АМ и АС
(С и В – точки касания). Найдите периметр треугольника АВС,
если
Г-8 С.Р. Касательная к окружности.
Вариант 1.
1. Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.
Найдите ОВ, если АВ = 12 см.
2. Из точки А к окружности с центром О и радиусом 8 см проведены
касательные АВ и АС (В и С – точки касания). Найдите АВ и АС, если
3. Из точки М к окружности с центром О и радиусом 8 см проведены
касательные АМ и ВМ (А и В – точки касания).
Найдите периметр треугольника АВМ, если
Г-8 С.Р. Касательная к окружности.
Вариант 2.
1. Прямая АВ касается окружности с центром О и радиусом 15 см в точке В.
Найдите АВ, если ОА = 17 см.
2. Из точки М к окружности с центром О проведены касательные МА и МВ
(В и А – точки касания). Найдите АМ и ВМ, если
3. Из точки А к окружности с центром В проведены касательные АМ и АС
(С и В – точки касания). Найдите периметр треугольника АВС,
если
Приложенные файлы
2} \\ & = \ sqrt {36 + 36} \\ & = \ sqrt {36 \ cdot 2} \\ & = 6 \ sqrt {2} \ end {выровнять *} Определите координаты \ (M \), средней точки хорды \ (PQ \).
\ begin {align *} M (x; y) & = \ left (\ frac {x_ {1} + x_ {2}} {2}; \ frac {y_ {1} + y_ {2}} {2} \ right) \\ & = \ left (\ frac {-4 + 2} {2}; \ frac {-2 + 4} {2} \ right) \\ & = \ left (\ frac {-2} {2}; \ frac {2} {2} \ right) \\ & = \ влево (-1; 1 \ вправо) \ end {выровнять *}
Если \ (O \) является центром круга, покажите, что \ (PQ \ perp OM \).
\ begin {align *} m_ {PQ} & = \ frac {4 — (-2)} {2 — (-4)} \\ & = \ frac {6} {6} \\ & = 1 \\ & \\ m_ {OM} & = \ frac {1 — 0} {- 1 — 0} \\ & = — 1 \\ m_ {PQ} \ times m_ {OM} & = — 1 \\ & \\ \ поэтому PQ & \ perp OM \ end {выровнять *}
Определите уравнения касательных к окружности в точках \ (P \) и \ (Q \).
Касательная в точке \ (P \):
Определите градиент радиуса \ (OP \):
\ begin {align *} m_ {OP} & = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} \\ & = \ frac {-2 — 0} {- 4 — 0} \\ & = \ frac {1} {2} \ end {выровнять *}Пусть градиент касательной в точке \ (P \) равен \ (m_ {P} \).Касательная к окружности перпендикулярна радиусу, поэтому можно написать:
\ begin {align *} m_ {OP} \ times m_ {P} & = -1 \\ \ frac {1} {2} \ times m_ {P} & = -1 \\ \ поэтому m_ {P} & = — 2 \ end {выровнять *}Подставьте \ (m_ {P} = — 2 \) и \ (P (-4; -2) \) в уравнение прямой.
\ begin {align *} y — y_ {1} & = m (x — x_ {1}) \\ y — y_ {1} & = — 2 (x — x_ {1}) \\ \ text {Substitute} P (-4; -2): \ quad y + 2 & = — 2 (x + 4) \\ у & = -2х — 8-2 \\ & = -2x — 10 \ end {выровнять *}Касательная в точке \ (Q \):
Определите градиент радиуса \ (OQ \):
\ begin {align *} m_ {OQ} & = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} \\ & = \ frac {4 — 0} {2 — 0} \\ & = 2 \ end {выровнять *} Пусть градиент касательной в точке \ (Q \) равен \ (m_ {Q} \). Касательная к окружности перпендикулярна радиусу, поэтому можно написать:
Касательная к окружности перпендикулярна радиусу, поэтому можно написать:
Подставьте \ (m_ {Q} = — \ frac {1} {2} \) и \ (Q (2; 4) \) в уравнение прямой.
\ begin {align *} y — y_ {1} & = m (x — x_ {1}) \\ y — y_ {1} & = — \ frac {1} {2} (x — x_ {1}) \\ \ text {Substitute} Q (2; 4): \ quad y — 4 & = — \ frac {1} {2} (x — 2) \\ y & = — \ frac {1} {2} x + 1 + 4 \\ & = — \ frac {1} {2} x + 5 \ end {выровнять *}Следовательно, уравнения касательных к окружности равны \ (y = -2x — 10 \) и \ (y = — \ frac {1} {2} x + 5 \).
Определите координаты \ (S \), точки пересечения двух касательных.
Приравняйте два линейных уравнения и решите относительно \ (x \):
\ begin {align *} -2x — 10 & = — \ frac {1} {2} x + 5 \\ -4x — 20 & = — х + 10 \\ -3x & = 30 \\ х & = — 10 \\ \ text {If} x = — 10 \ quad y & = — 2 \ left (- 10 \ right) — 10 \\ & = 10 \ end {выровнять *}Это дает точку \ (S \ left (- 10; 10 \ right) \).2} \\ & = \ sqrt {144 + 36} \\ & = \ sqrt {180} \ end {выровнять *}
Определите уравнения двух касательных к окружности, параллельных прямой \ (y + 2x = 4 \).
Касательная в точке \ (P \), \ (y = -2x — 10 \), параллельна \ (y = — 2x + 4 \). Чтобы найти уравнение второй параллельной касательной:
\ begin {align *} у & = -2x + 4 \\ \ поэтому m & = -2 \\ \ поэтому m _ {\ text {radius}} & = \ frac {1} {2} \\ \ text {Ур.{2} & = 16 \\ х & = \ pm 4 \\ \ text {If} x = 4, y & = 2 \\ \ text {Substitute} (4; 2): \ quad y & = -2x + c \\ 2 & = — 2 (4) + с \\ 10 & = с \\ y & = -2x + 10 \ end {выровнять *}Просмотреть вопрос — PLS HELP, DUE TMROW
1)
Круг O представляет собой единичный круг. Отрезок AS имеет длину 12/5 и касается окружности O в точке A. Если P является пересечением OS с окружностью O, найдите длину PS.2 + 1] = sqrt [144 + 25] / 5 = 13/5
Отрезок AS имеет длину 12/5 и касается окружности O в точке A. Если P является пересечением OS с окружностью O, найдите длину PS.2 + 1] = sqrt [144 + 25] / 5 = 13/5
Итак … PS = SO — PO = 13/5 — 1 = 8/5
2)
Угол A: Угол P: Угол ASP в соотношении 1: 2: 2. Найдите градусную меру угла BSA.
Угол A = 36 ° …… Угол P, ASP = 72 °
Угол ASP = (1/2) малая дуга AS = угол BSA = 72 °
3)
Если угол B = 39 градусов и дуга PS = 116 градусов, найдите градусную меру дуги AS.
Угол B = (1/2) (дуга AS — дуга AP)
38 = (1/2) (дуга AS — дуга AP)
76 = дуга AS — дуга AP (1)
и
дуга AS + дуга AP + дуга PS = 360
дуга AS + дуга AP + 116 = 360
дуга AS + дуга AP = 244 (2)
Добавить (1) и (2)
дуги AS — дуги AP = 76
дуги AS + дуги AP = 244
2 дуги AS = 320 разделить на 2
дуги AS = 160 °
4)
точек A и B находятся на окружности с центром в O, а точка P находится вне окружности, так что PA и PB касаются окружности.Если угол OPA = 32 градуса, то какова малая дуга AB в градусах?
Нарисуйте радиусы OA, OB … так, чтобы OAPB образовал четырехугольник …. сумма его внутренних углов = 360 °
Углы OAP, OBP = 90 ° и OPA = 32 °, затем угол BPA = 64 °
Итак … угол OAB = 360-2 (90) — 64 = 116 °
И OAB — это центральный угол, пересекающий малую дугу AB, поэтому его размер также составляет 116 °
5)
Окружность O и окружность P с радиусами 3 и 5 соответственно касаются прямой L в точке H.Введите все возможные длины OP через запятую.
{Здесь нужна картинка}
6)
Учитывая правильный пятиугольник ABCDE, можно нарисовать окружность, касательную к DC в точке D и к AB в A. Сколько градусов в малой дуге нашей эры?
Назовите центр окружности O, соедините OA и OD
И OABCD образует еще один пятиугольник, внутренние углы которого в сумме составляют 540 °
Углы ODC и угол OAB = 90 °
Углы DCB и CBA = 108 °
Таким образом, угол DOA = 540 — 2 (90) — 2 (108) = 144 °.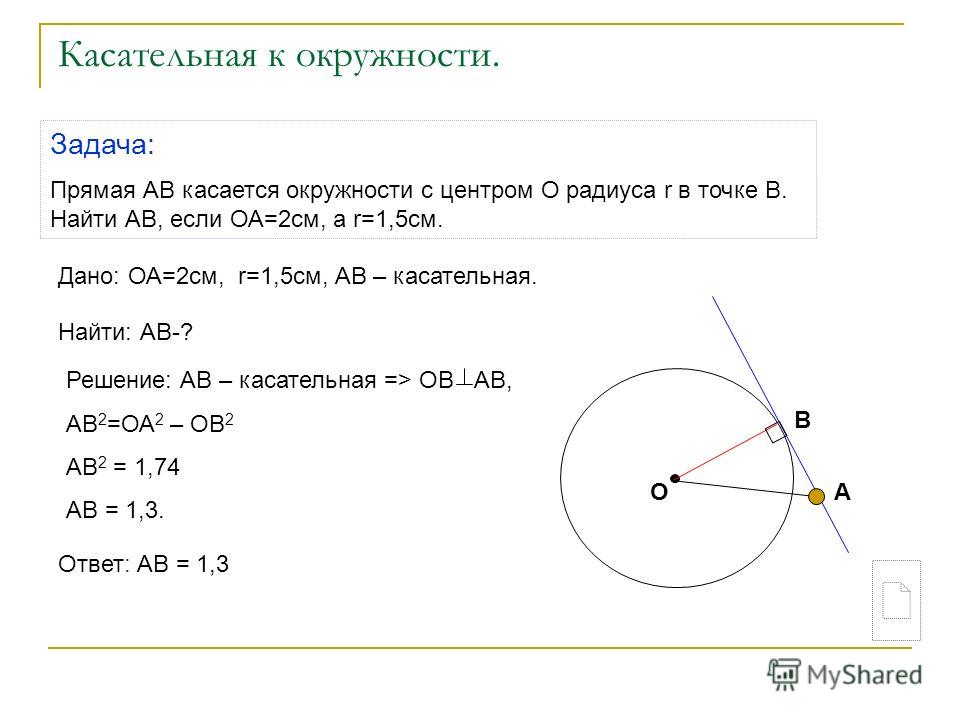 ..это центральный угол в окружности, пересекающей малую дугу AD …. так что он также имеет размер 144 °
..это центральный угол в окружности, пересекающей малую дугу AD …. так что он также имеет размер 144 °
Иллюстративная математика
Задача
Некоторая машина должна содержать два колеса, одно с радиусом 3 сантиметра и одно с радиусом 5 сантиметров, центры которых прикреплены к точкам на расстоянии 14 сантиметров. Производителю этой машины необходимо изготовить ремень, который будет плотно прилегать к двум колесам, как показано на схеме ниже.Какой длины должен быть пояс?
Комментарий IM
Эта задача сочетает в себе два навыка из области GC: использование связи между касательным сегментом к окружности и радиусом, касающимся этого касательного сегмента (GC.2), и вычисление длин дуг окружности с учетом радиусов и центральных углов (GC.5. ). Это также требует от студентов создания дополнительной структуры в рамках данной задачи, создания и решения прямоугольного треугольника для вычисления требуемых центральных углов (G-SRT.8).
Поскольку задача достаточно сложная, она больше подходит для аудиторной работы, чем для оценивания.
При решении задач необходимо принять решение о том, когда вычислять промежуточные выражения. Данное решение следует среднему пути, оставляя $ \ arccos (2/14) $ неоцененным до тех пор, пока не будет оценена длина каждого компонента. Преждевременное вычисление этой функции может привести к накоплению ошибки округления.
Решение
Ремень состоит из четырех частей: двух сегментов, касающихся двух окружностей, и двух дуг окружностей.
Чтобы определить длину касательных сегментов, мы проводим линию от центра малого круга перпендикулярно радиусу большого круга. Поскольку радиус каждой окружности перпендикулярен касательному сегменту в точке касания, получается прямоугольник. Длина касательного сегмента равна длине противоположной стороны прямоугольника, который представляет собой катет прямоугольного треугольника с гипотенузой 14 см и другой катет длиной 2 см. 2} = 8 \ sqrt {3} \ mbox {см}.
2} = 8 \ sqrt {3} \ mbox {см}.
Чтобы вычислить длины двух дуг окружности, мы начнем с вычисления угла $ \ theta $ в нашем прямоугольном треугольнике: $$ \ theta = \ arccos \ frac {2} {14}. $$ Это также угол между радиусом маленького колеса и горизонтальной линией, соединяющей два центра на диаграмме, и вдвое больше этого угла — центральный угол, который образует дугу окружности на маленьком колесе. Таким образом, длина части ремня, которая наматывается на маленькое колесо, составляет приблизительно $$ 2 \ arccos \ frac {2} {14} \ cdot 3 \ приблизительно 8.56 \ \ text {см}. $$
Между тем, центральный угол, образующий дугу окружности на большом колесе, составляет $ 2 \ pi — 2 \ arccos \ frac {2} {14} $ радиан, и, следовательно, длина части ремня, которая наматывается вокруг большого колеса. колесо — $$ (2 \ pi — 2 \ arccos \ frac {2} {14}) \ cdot 5 \ приблизительно 17.14 \ \ text {cm}. $$
Таким образом, общая длина ремня должна быть $$ 2 \ cdot 8 \ sqrt {3} + 8,56 + 17,14 \ приблизительно 53,42 \ mbox {см}. $$
% PDF-1.4
%
327 0 объект
>
эндобдж
xref
327 70
0000000016 00000 н.
0000002645 00000 н.
0000002730 00000 н.
0000002968 00000 н.
0000003393 00000 н.
0000003666 00000 н.
0000004081 00000 п.
0000004548 00000 н.
0000010954 00000 п.
0000011296 00000 п.
0000011556 00000 п.
0000011897 00000 п.
0000012313 00000 п.
0000012740 00000 п.
0000016172 00000 п.
0000016466 00000 п.
0000016541 00000 п.
0000016618 00000 п.
0000016694 00000 п.
0000016772 00000 п.
0000017509 00000 п.
0000017940 00000 п.
0000017993 00000 п.
0000018030 00000 п.
0000018265 00000 п.
0000018999 00000 п.
0000019047 00000 п.
0000019467 00000 п.
0000020471 00000 п.
0000020857 00000 п.
0000021354 00000 п.
0000021432 00000 п.
0000022413 00000 п.
0000023479 00000 п.
0000023900 00000 п.
0000024196 00000 п.
0000025211 00000 п.
0000025572 00000 п.
0000028703 00000 п.
0000029450 00000 п.
0000029683 00000 п. n.NAV6QvT? / 8_MmӨpscXW O} 3C # Doi!) VQ6Vf1 wyh & q`uR5DRӌM = 蛸 & 1 p
n.NAV6QvT? / 8_MmӨpscXW O} 3C # Doi!) VQ6Vf1 wyh & q`uR5DRӌM = 蛸 & 1 p
Решение задач геометрии — окружность и окружность
Решатель задач с геометрией
Круг
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Track 1
Вычислите длину радиуса круга диаметром 10 см.
Дорожка 2
Вычислите длину диаметра окружности с радиусом 5 см.
Дорожка 3
Радиус круга размером 20 см. Вычислите длину окружности и площадь круга.
Дорожка 4
Диаметр круга 40 см. Вычислите длину окружности и площадь круга.
Дорожка 5
Окружность круга 30 см. Вычислите радиус круга и его диаметр.
Дорожка 6
Площадь круга 30 см.Вычислите радиус круга и его диаметр.
Колея 7
Окружность с центром O имеет радиус 50 см. Проведите из точки P вне окружности касательные PA и PB и соединив точку O с точками касания A и B, вы получите четырехугольник APBO. Зная, что периметр четырехугольника равен 340 см, рассчитайте размеры его сторон.
Дорожка 8
Окружность с центром O имеет радиус 50 см. Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P, мы получим треугольник APO.Зная, что отрезок РО составляет 130 см, рассчитайте площадь и периметр треугольника.
Дорожка 9
Окружность с центром O имеет радиус 50 см. Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P, мы получим треугольник APO. Зная, что сегмент PA составляет 120 см, рассчитайте площадь и периметр треугольника.
Дорожка 10
Хорда AB окружности составляет 36 см, а расстояние от центра — 24 см. Вычислите меру длины окружности и площади круга.
Вычислите меру длины окружности и площади круга.
Дорожка 11
Хорда AB окружности составляет 36 см, а расстояние от центра — 24 см. Вычисляет длину периметра треугольника OBA и площадь треугольника.
Путь 12
Две окружности имеют такие диаметры, что одна равна 3/7 другой, а их сумма составляет 120 м. Насколько велика высота кольца?
Дорожка 13
Диаметр окружности равен 3/5 стороны равностороннего треугольника, имеющего площадь 100 см.Вычисляет длину окружности.
Колея 14
Радиус велосипедного колеса составляет 30 см. Сколько метров дороги имеет велосипедная дорожка после 3000 спинов?
Трасса 15
От точки P проведите касательные PA и PB с центром O и радиусом 15 см. Хорда, соединяющая точки касания, составляет 3/2 ее расстояния от точки P, а их сумма составляет 40 см. Вычисляет длину окружности, периметра и площади четырехугольника OAPB.
Дорожка 16
Рассчитайте длину двух окружностей, имеющих внутреннюю касательность, зная, что расстояние между их центрами составляет 20 см, а радиус ‘a составляет 3/5 радиуса другой окружности.
Дорожка 17
Площадь круга, описанного до правильного шестиугольника, составляет 314,159 см, вычисляется площадь шестиугольника.
Дорожка 18
Равнобедренный треугольник ABC вписан в окружность с центром O.Зная, что длина окружности составляет 275,69 см, а размер сегмента OH составляет 36,10 см, вычисляется периметр и площадь треугольника.
Дорожка 19
Равнобедренный треугольник, вписанный в круг радиусом 43,90 см, имеет относительную высоту относительно основания 80 см. Вычислите периметр и площадь треугольника.
Дорожка 20
В круг диаметром 100 см вписанный равнобедренный треугольник ABC не содержит центра.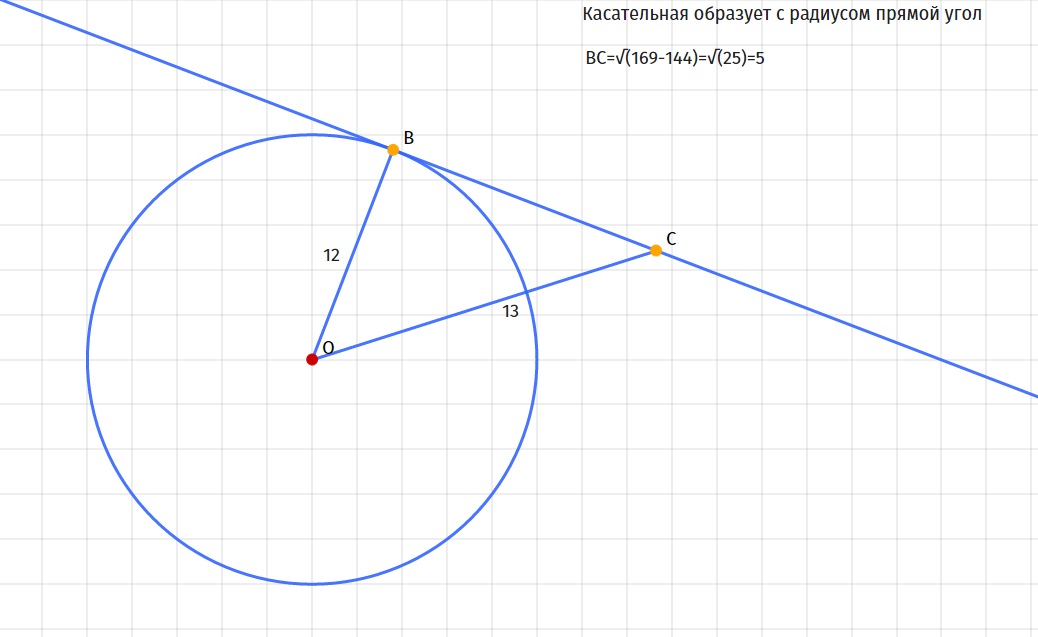 Высота треугольника относительно стороны неравного размера 36 см. Вычислите длину периметра треугольника и его площадь.
Высота треугольника относительно стороны неравного размера 36 см. Вычислите длину периметра треугольника и его площадь.
Дорожка 21
Круговой сектор ограничен дугой длиной 5 см, а π принадлежит окружности диаметром 40 см. Вычислите площадь поля и соответствующий угол.
Дорожка 22
Она должна покрывать стол материалом по цене 20 за кв.м. Посчитайте, сколько вы потратите, зная, что диаметр стола 150 см.
Дорожка 23
В круге радиусом 10 см начертан центральный угол 90 и не менее двух углов на соответствующей ему окружности.
Дорожка 24
Нарисуйте круг радиусом 5 см и проведите хорду AB на расстоянии 2 см от центра, а веревку CD — на расстоянии 3 см от центра. Какая из двух струн длиннее?
Дорожка 25
Нарисуйте круг и две параллельные веревки, совпадающие друг с другом.Зная, что расстояние от центра одной из них составляет 3 см, каково расстояние между двумя струнами?
Дорожка 26
В круге с центром O и радиусом 30 см считается хордой AB 36 см. Вычислите периметр и площадь треугольника ABO.
Дорожка 27
Вычисляет длину хорды окружности с радиусом 30 см, зная, что это 24 см от центра. Вычисляет длину окружности и площадь круга.Вычислите периметр и площадь треугольника ABO.
Дорожка 28
Круг имеет радиус 30 см, а веревка — 36 см. Какая мера расстояния хорды от центра круга?
Дорожка 29
Вычисляет длину хорды круга диаметром 60 см, зная, что это 24 см от центра. Вычисляет длину окружности и площадь круга. Вычислите периметр и площадь треугольника ABO.
Дорожка 30
Равнобедренный треугольник, вершинами которого являются концы веревки и центр круга, имеет площадь 240 см. Зная, что расстояние от центра веревки 24 см, рассчитайте длину радиуса круга.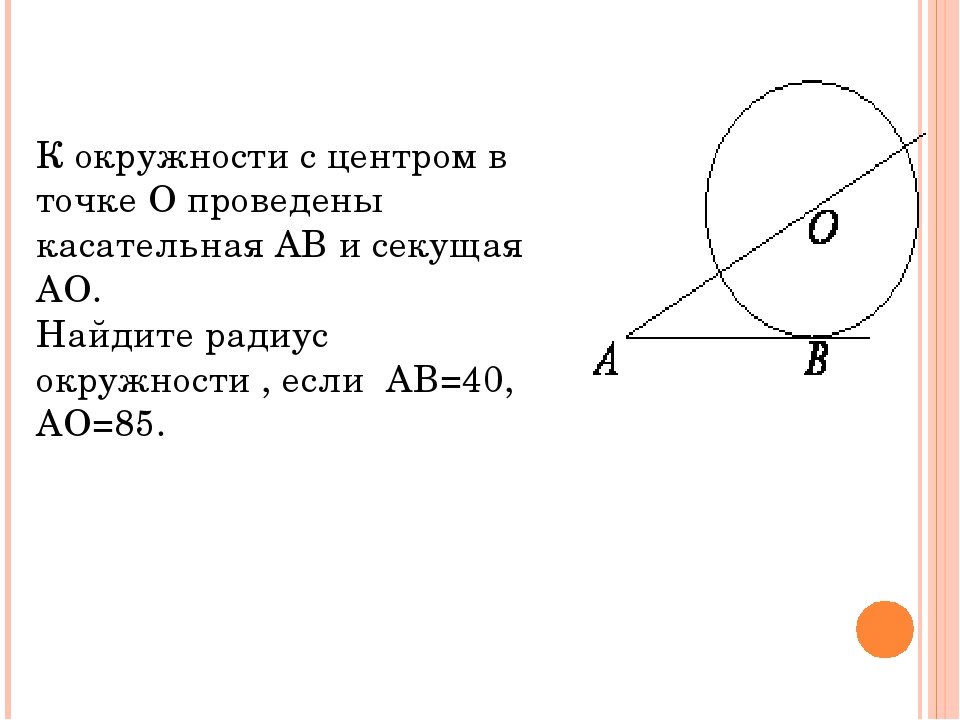
Дорожка 31
Две струны окружности параллельны и лежат с противоположных сторон относительно центра, расстояние между ними 62 см. Зная, что длина струны 28 см, а радиус круга 50 см, рассчитайте длину другой струны.
Дорожка 32
Радиус окружности составляет 50 см, а две параллельные хорды, расположенные с одной стороны от центра, имеют длину 96 см и 28 см соответственно. Вычисляет расстояние между двумя струнами.
Колея 33
Окружность имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют размер соответственно 96 см и 28 см. Вычисляет площадь и периметр трапеции, в основе которой лежат две хорды.
Колея 34
Равнобедренная трапеция имеет высоту 20 м, основание более 80 м, основание менее 50 м. Вычислите радиус окружности, описанной трапецией.
Дорожка 35
Площадь круга составляет 400 π см, а центральный угол — 108. Вычислите:
длину окружности;
длина дуги;
площадь кругового сектора.
Дорожка 36
Дуга окружности равна 37.69908 см, а центральный угол — 108. Вычислите радиус окружности.
Дорожка 37
Круговой сектор имеет площадь 120 π см и центральный угол 108. Рассчитайте радиус круга.
Дорожка 38
Хорда окружности 80 см, расстояние от центра 30 см. Рассчитайте радиус круга.
Путь 39
Круг имеет радиус 50 см, а длина веревки — 80 см. Рассчитайте центральный угол, образуемый хордой.
Дорожка 40
Круговой сектор имеет площадь 120 π см и центральный угол 108. Вычислите подпадающий под хорду родственник.
Дорожка 41
Площадь кругового сектора составляет 120 π см, а центральный угол — 108. Вычислите:
Вычислите:
длину окружности;
длина дуги;
длина хорды АВ.
Дорожка 42
Длина круга составляет 40 π см, а центральный угол — 108.Вычислить:
площадь круга;
длина дуги;
длина хорды АВ;
площадь кругового сектора.
Дорожка 43
Длина дуги составляет 12 π см, а центральный угол — 108. Вычислить:
площадь круга;
длина окружности;
длина хорды АВ;
площадь кругового сектора.
Колея 44
Длина каната 32,360679774998 см, а центральный угол — 108.Вычислить:
площадь круга;
длина окружности;
длина дуги;
площадь кругового сектора.
Колея 45
Длина веревки 32,360679774998 см, радиус 20 см. Вычислить:
площадь круга;
длина окружности;
центральный угол;
площадь кругового сектора.
Дорожка 46
Длина веревки 32,360679774998 см, площадь круга 400 π см.Вычислите:
длину окружности;
центральный угол;
площадь кругового сектора.
Дорожка 47
Длина веревки 32,360679774998 см, длина окружности 40 см π. Вычислить:
площадь круга;
центральный угол;
площадь кругового сектора.
Путь 48
Длина веревки 32,360679774998 см, расстояние от центра 11.755705045849 см. Вычислите:
длину окружности;
площадь круга;
центральный угол;
длина дуги;
площадь кругового сектора.
Дорожка 49
Длина дуги составляет 12 π см, а радиус — 20 см. Вычислите:
длину окружности;
площадь круга;
центральный угол;
длина веревки;
площадь кругового сектора.
Дорожка 50
Длина дуги составляет 12 см, а длина окружности — 40 π см.Вычислить:
площадь круга;
центральный угол;
длина веревки;
площадь кругового сектора.
Дорожка 51
Длина дуги составляет 12 π см, а площадь круга — 400 π см. Вычислите:
длину окружности;
центральный угол;
длина веревки;
площадь кругового сектора.
Колея 52
Центральный угол равен 40. рассчитать угол на окружности
Track 53
Угол на окружности равен 20.вычисляет угол в центре.
Дорожка 54
Площадь круга составляет 400 π см, а угол на окружности равен 54. Вычислите:
длину окружности;
длина дуги;
площадь кругового сектора.
Дорожка 55
Дуга окружности составляет 37,69908 см, а угол на окружности равен 54. Рассчитайте радиус круга.
Дорожка 56
Круговой сектор имеет площадь 120 π см и угол на окружности 54.Рассчитайте радиус круга.
Дорожка 57
Круговой сектор имеет площадь 120 π см и угол на окружности 54. Вычислите подпадающий под хорду родственник.
Дорожка 58
Площадь кругового сектора составляет 120 π см, а угол на окружности равен 54. Вычислите:
длину окружности;
длина дуги;
длина хорды АВ.
Дорожка 59
Длина окружности 40 π см, угол на окружности 54.Вычислить:
площадь круга;
длина дуги;
длина хорды АВ;
площадь кругового сектора.
Дорожка 60
Длина дуги составляет 12 π см, а угол на окружности равен 54. Вычислить:
площадь круга;
длина окружности;
длина хорды АВ;
площадь кругового сектора.
Путь 61
Длина веревки 32.360679774998 см и угол по окружности 54. Вычислить:
площадь круга;
длина окружности;
длина дуги;
площадь кругового сектора.
Трасса 62
Трапеция имеет основания для диаметра окружности длиной 50 см и параллельной ей веревкой длиной 30 см. Рассчитайте периметр и площадь трапеции.
Рассчитайте периметр и площадь трапеции.
Колея 63
По кругу радиусом 50 см.сделайте две параллельные пояса, расположенные с противоположных сторон относительно центра и на расстоянии 14 см и 48 см от него соответственно. Вычисляет площадь и периметр трапеции, у которой есть основания для двух струн.
Колея 64
Нарисуйте окружность радиусом 4 см.
Дорожка 65
Нарисуйте круг диаметром 20 см.
Колея 66
Нарисуйте окружность радиусом 20 см.
Дорожка 67
Нарисуйте круг диаметром 20 см.
Дорожка 68
Нарисуйте круг радиусом 10 см и три линии: секущую. касательная к окружности и внешнему.
Дорожка 69
Рисует окружность радиусом 10 см в длину. проведите две прямые, параллельные друг другу. соответственно на расстоянии 5 см и 13 см от центра окружности. Как две линии относительно окружности?
Дорожка 70
Приведите касательные к окружности на концах диаметром 10 см.Как между ними?
Дорожка 71
Нарисуйте круг с радиусом 10 см длиной и тремя линиями, отстоящими от центра соответственно на 6 см. 15 см и 10 см. Как линии относительно окружности?
Путь 72
Угол, образованный касательными BPA PA и PB, проведенными точкой P вне окружности с центром O и радиусом 50 см. 45 лет. Определяет ширину других углов четырехугольника PAOB.
Путь 73
От внешней точки P до окружности с центром O и радиусом 50 см. к двум касательным сегментам пути PA и PB и рассмотрим четырехугольник PAOB. Зная, что угол O равен 135. каковы амплитуды остальных углов четырехугольника?
Путь 74
От внешней точки P до окружности с центром O и радиусом 50 см. два касательных сегмента пути PA и PB и P сливаются с центром O. Зная, что BPO является широкоугольным 22.5. каковы величины углов четырехугольника?
два касательных сегмента пути PA и PB и P сливаются с центром O. Зная, что BPO является широкоугольным 22.5. каковы величины углов четырехугольника?
Трасса 75
Нарисуйте круг с центром O и радиусом 50 см длиной и точкой P за пределами круга. проследите два касательных сегмента PA и PB. Зная, что сегмент ПО равен 130 см. вычислить периметр и площадь четырехугольника PAOB.
Дорожка 76
Нарисуйте круг с центром O. точку P вне круга. проследите два касательных сегмента PA и PB.Зная, что сегмент PO составляет 130 см, а сегмент PA — 120 см. вычислить периметр и площадь четырехугольника PAOB.
Трасса 77
Проведите из точки P вне касательных окружностей PA и PB и соедините центр O с точками касания A и B. Вы получите четырехугольник APBO. Зная, что сегмент PA равен 120 см, а периметр четырехугольника равен 340 см. вычислить:
окружность;
площадь круга;
площадь четырехугольника;
площадь треугольника BOA;
площадь треугольника BPA;
площадь кругового сектора, ограниченная хордой AB;
центральный угол AOB.
Колея 78
Окружность с центром O имеет радиус 50 см. Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P., мы получим треугольник APO. Учитывая, что площадь треугольника 3000 см, рассчитайте:
периметр треугольника;
окружность;
площадь круга.
Путь 79
Начало на точку P вне окружности с центром O и радиусом 50 см.два касательных сегмента PA и PB. получаем четырехугольник ПАОВ площадью 6000 см. Вычислить:
расстояние точки P от центра;
периметр четырехугольника;
центральный угол АОБ;
— площадь кругового сектора, ограниченная хордой AB.
Путь 80
Начало по точке P вне окружности с центром O и радиусом 50 см. два касательных сегмента PA и PB. получаем четырехугольник ПАОВ. Зная, что отрезок AB равен 92.307 см в длину. вычислить:
два касательных сегмента PA и PB. получаем четырехугольник ПАОВ. Зная, что отрезок AB равен 92.307 см в длину. вычислить:
площадь четырехугольника;
периметр четырехугольника;
центральный угол АОБ;
площадь сектора, ограниченная круговой хордой AB.
Дорожка 81
Сумма радиусов двух окружностей равна 140 см, а измерение радиуса одной из них составляет 3/4 радиуса другой; вычисляет длины двух кругов и площадь двух кругов.
Дорожка 82
Сумма измерений диаметров двух окружностей составляет 280 см, а измерение диаметра одной из них составляет 3/4 диаметра другой; вычисляет длины двух кругов и площадь двух кругов.
Дорожка 83
Сумма и разность размеров радиусов двух окружностей равны соответственно 140 см и 20 см, вычислите длины двух окружностей и площади двух окружностей.
Дорожка 84
Сумма и разность измерений диаметров двух кругов составляют соответственно 280 см и 40 см, вычислите длины двух кругов и площади двух кругов.
Дорожка 85
Сумма длин двух окружностей составляет 200 π см; вычисляет измерения их радиусов, зная, что соотношение размеров их диаметров составляет 1/3.
Дорожка 86
Сумма длин двух окружностей равна 200 π см; вычисляет размеры их диаметров, зная, что отношение размеров их радиусов равно 1/3.
Трасса 87
Велосипед проехал 10 км; тахометр набрал 5227,39 об / мин, каков радиус колеса, на котором установлен тахометр?
Track 88
Вычисляет длину полукруга с радиусом 50 см.
Track 89
Вычисляет длину полукруга диаметром 100 см.
Дорожка 90
Сумма и разность размеров диагоналей ромба составляют соответственно 34 м и 14 м. вычислите диаметр круга, эквивалентного реву.
Track 91
Вычисляет меру радиуса круга, эквивалентного прямоугольнику, с размерами соответственно 80 см и 50 см.
Дорожка 92
Сумма и разница размеров прямоугольника составляют соответственно 130 см и 30 см; вычисляет меру радиуса круга, эквивалентного прямоугольнику.
Дорожка 93
Сумма размеров прямоугольника составляет 130 см, а их соотношение составляет 8/5; вычисляет радиус круга, эквивалентного прямоугольнику.
Колея 94
Прямоугольник имеет площадь 432 см и основание 24 см; вычисляет размер области круга, радиус которого совпадает с диагональю прямоугольника.
Колея 95
Прямоугольник имеет площадь 240 см и высоту 10 см; вычисляет размер области круга, радиус которого совпадает с диагональю прямоугольника.
Колея 96
Прямоугольник имеет основание 40 см и высоту 30 см; вычисляет длину окружности, диаметр которой соответствует диагонали прямоугольника.
Колея 97
Прямоугольник имеет периметр 84 см и высоту 18 см; вычисляет длину окружности, диаметр которой соответствует диагонали прямоугольника.
Дорожка 98
Прямоугольник имеет периметр 84 см и основание 24 см. Вычислите площадь круга, диаметр которого совпадает с диагональю прямоугольника.
Дорожка 99
Прямоугольник имеет периметр 84 см и основание 24 см. Вычислите площадь круга, диаметр которого конгруэнтен высоте прямоугольника.
Колея 100
Прямоугольник имеет периметр 84 см и высоту 18 см; вычисляет площадь круга, имеющего радиус, равный основанию прямоугольника.
Дорожка 101
Ромб имеет площадь 480 квадратных сантиметров и периметр 104 см. Вычислите площадь круга, радиус которого равен диагонали ромба.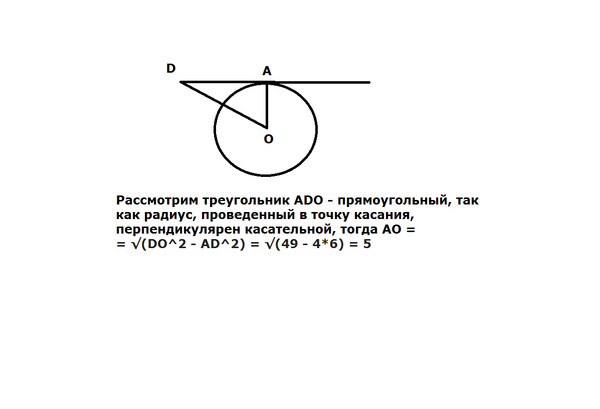
Дорожка 102
Ромб имеет площадь 480 квадратных сантиметров и периметр 104 см. Вычислите площадь круга, радиус которого меньше диагонали ромба.
Дорожка 103
Ромб имеет периметр 104 см.Вычислите площадь круга, радиус которого равен стороне ромба.
Дорожка 104
Ромб имеет диагонали 48 см и 36 см. Вычислите:
сторона ромба, радиус окружности, вписанной в ромб;
длина веревки с учетом того, что PQ находится на расстоянии 8,64 см от центра O;
— центральный угол, образуемый хордой PQ;
длина дуги, образуемой хордой PQ.
Дорожка 105
Ромб имеет диагонали 48 см и 36 см.Вычислить:
сторона ромба;
радиус окружности, вписанной в ромб;
длина хорды PQ;
— центральный угол, образуемый хордой PQ;
длина дуги, образуемой хордой PQ;
длина хорды PS
центральный угол, образуемый хордой PS.
Дорожка 106
Вычислите радиус круга, эквивалентного квадрату, площадью 100 см.
Track 107
Вычисляет разность площадей круга и квадрата, которые имеют соответствующие меры радиуса и стороны 20 см.
Дорожка 108
Сумма радиусов двух окружностей составляет 130 см, а их отношение составляет 5/8; вычисляет разницу площадей двух кругов.
Направляющая 109
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует наклонной стороне, зная, что площадь трапеции составляет 1320 см.
Дорожка 110
Равнобедренная трапеция имеет основание более 80 см, меньшее основание — 50 см.Вычислите:
площадь круга, описанного трапецией, зная, что высота составляет 48,75 дюйма;
расстояние от центра хорды AB;
расстояние от центра каната CD;
la Lunghezza длина дуги AB;
длина дуги CD;
центральный угол АОБ;
центральный угол COD;
площадь кругового сектора AOB; площадь кругового сектора наложенным платежом.
Направляющая 111
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1320 см.
Направляющая 112
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 1320 см.
Направляющая 113
Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 см и 50 см.Вычислите радиус окружности, соответствующей трапеции.
Дорожка 114
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Дорожка 115
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 116
Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Дорожка 117
Прямоугольник трапеции имеет основное основание 60 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь круга, имеющего изопериметрическую окружность трапеции.
Направляющая 118
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Колея 119
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Колея 120
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 121
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует малой диагонали, зная, что площадь трапеции составляет 1320 см.
Колея 122
Равнобедренная трапеция имеет высоту 10 см и основания, которые являются одним из 7/17 другого.Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 240 см.
Дорожка 123
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Трасса 124
Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Дорожка 125
Прямоугольник в форме трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Трасса 126
Равнобедренная трапеция имеет площадь 240 см и основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 127
Равнобедренная трапеция имеет периметр 186 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см.Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Колея 128
Равнобедренная трапеция имеет большое основание 70 см, малое основание 50 см, высоту 24 см. Вычислите площадь круга, имеющего изопериметрическую окружность трапеции.
Вычислите площадь круга, имеющего изопериметрическую окружность трапеции.
Дорожка 129
Вычислите радиус кругового сектора площадью 250 π см и длиной дуги 20 π см.
Дорожка 130
Вычислите площадь кругового сектора, имеющего длинный луч 20 π см и радиус 25 см.
Track 131
Вычисляет дугу кругового сектора площадью 250 π см и радиусом 25 см.
Track 132
Вычисляет длину дуги окружности с радиусом 10 см, принадлежащей сектору окружности, эквивалентному квадрату с длиной стороны 10 см.
Колея 133
Квадрат имеет площадь 25 см; measure вычисляет площадь круга, радиус которого совпадает с диагональю квадрата.
Колея 134
Квадрат имеет площадь 25 см; measure вычисляет площадь круга, радиус которого совпадает со стороной квадрата.
Дорожка 135
Квадрат имеет периметр 20 см. Рассчитайте длину круга с диаметром, равным стороне квадрата.
Дорожка 136
Вычислите диаметр круга, эквивалентного круговому сектору, длина дуги которого составляет 20 п см, аппартанта окружности с радиусом 15 см.
Колея 137
Окружность имеет радиус 30 см. Зная, что длина хорды AB составляет 36 см, можно рассчитать площадь кругового сегмента.
Колея 138
Окружность имеет радиус 30 см. Зная, что центральный угол равен 73 44 ’23’ ‘, вычисляется площадь кругового сегмента.
Колея 139
Окружность имеет радиус 30 см. Зная, что расстояние хорды AB составляет 24 см, рассчитайте площадь кругового сегмента.
Колея 140
Окружность имеет радиус 30 см. Зная, что дуга длинная 38,609995656018 см, рассчитайте площадь кругового сегмента.
Дорожка 141
Вычислите площадь круглой короны с лучами 12 см и 20 см соответственно.
Дорожка 142
Вычислите площадь круглого кольца, диаметр которого составляет 24 см в длину и 40 см.
Колея 143
Диаметр круга равен стороне равностороннего треугольника, имеющего площадь 100 см.Вычисляет длину окружности.
Дорожка 144
Окружность соответствует равностороннему треугольнику с периметром 90 см. Вычисляет длину окружности.
Дорожка 145
Прямоугольный треугольник имеет катеты соответственно 3 см и 4 см. Вычислите длину окружности, радиус которой равен гипотенузе треугольника.
Дорожка 146
Прямоугольный треугольник имеет катети соответственно 3 см и 4 см.Вычислите длину окружности, диаметр которой равен 3/4 гипотенузы треугольника.
Дорожка 147
Прямоугольный треугольник имеет катетис соответственно 3 см и 4 см. Вычисляет длину окружности, диаметр которой составляет 3/4 диаметра большего катета.
Дорожка 148
Прямоугольный треугольник имеет катеты соответственно 3 см и 4 см. Вычислите длину круга, радиус которого на 3/4 больше катета.
Дорожка 149
Прямоугольный треугольник имеет катетис соответственно 3 см и 4 см.Вычислите длину круга, радиус которого составляет 3/4 малого катета.
Дорожка 150
Прямоугольный треугольник имеет катеты соответственно 3 см и 4 см. Вычисляет длину окружности, диаметр которой составляет 3/4 малого катета.
Дорожка 151
Прямоугольный треугольник имеет площадь 6 см, а соотношение между двумя катетами составляет 3/4. Вычислите длину круга, диаметр которого меньше диаметра катета.
Track 152
Прямоугольный треугольник имеет площадь 6 см, а соотношение между двумя катетами составляет 3/4. Вычисляет длину окружности, радиус которой соответствует большему радиусу катета.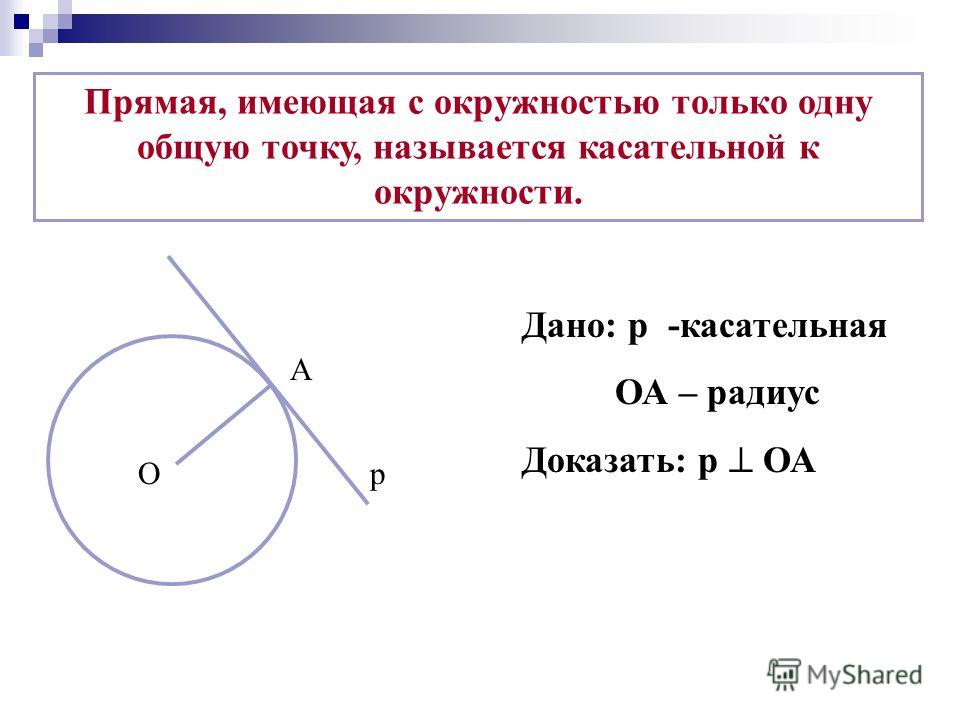
Трасса 153
Радиус окружности конгруэнтен гипотенузе прямоугольного треугольника с двумя сторонами 3 см и 4 см. Вычислите длину окружности и площадь круга.
Колея 154
Окружность имеет радиус, равный 2/5 стороны квадрата площадью 625 см.Вычислите длину окружности и площадь круга.
Программа для решения задач может давать совершенно неверные ответы.
Как найти центр окружности, вписанной в треугольник
Как найти центр окружности, вписанной в треугольник Внутренний радиус вписанной окружности равностороннего треугольника можно рассчитать по формуле Нажмите здесь, чтобы получить ответ на свой вопрос, какие линии вы проводите, чтобы найти центр круга, вписанного в треугольник 1.Круг, вписанный в треугольник, имеет радиус 3 см. A 4. Анализ. Упражнение урока Описание упражнения Предлагаемая технология. Это создаст круг, вписанный в ваш треугольник. Противоположные углы являются дополнительными. 12 августа 2020 Для любого треугольника центр вписанной окружности — это пересечение биссектрис углов. Найдите длину круга 01 января 2011 г. Если P является центром вписанной окружности, тогда, когда X P, все три из вышеперечисленных расстояний имеют одинаковое значение, и это значение является радиусом вписанной окружности.Как описанные, так и вписанные окружности можно провести из центра, образованного правой биссектрисой сторон равностороннего равностороннего треугольника u seek. Затем, если вы проведете оставшуюся линию OP прямоугольного треугольника OPB, вы получите треугольник 30 60 90. По симметрии можно показать, что это треугольник 30 60 90 и, следовательно, если мы допустим, что окружность вписанного круга равна. 14 июля 2012 г. 1. Для вычисления площади нам дается радиус окружности в качестве входных данных, и мы будем использовать формулу для вычисления площади. Алгоритм ШАГ 1 Принимаем радиус в качестве входных данных от пользователя, используя стандартный ввод. Центр центра обычно представлен буквой Свойства вписанной окружности в центре треугольника. Если треугольник вписан в круг так, что одна сторона треугольника равна диаметру круга, то этот треугольник является прямоугольным. Вписанный круг Вписанный круг — это круг, который лежит внутри фигуры, так что если треугольник вписан в круг, одна сторона этого треугольника является диаметром круга nbsp Мы находим из теоремы Пифагора, что. Угол CBA делится пополам, поэтому CBO и OBA составляют каждую половину исходной меры угла CBA.Следовательно, окружность D, проходящая через точки A B и C, будет описывать треугольник ABC. . Любая медиана делится точкой пересечения с другими медианами в пропорции 1 2. Постройте вписанные и описанные окружности треугольника и докажите свойства углов четырехугольника, вписанного в окружность. Таким образом, углы CAB, PDB и BEP являются прямыми углами. С габаритами дана мера одного из. Следовательно, по теореме о вписанном угле. Все треугольники можно вписать в круг, а центр круга — это пересечение любых двух серединных перпендикуляров его сторон.Максимально возможный круг, который можно нарисовать внутри плоской фигуры. Кажется, что треугольник с x 20 и y 30 не может иметь площадь больше, чем xy 2 300. Одна из этих сторон соединяет 0 2 и 8 2, поэтому его серединный перпендикуляр равен x 0 8 2, то есть x 4. Равносторонний формулы треугольника. Сначала мы построим треугольники и найдем внутренний ортоцентр описанной окружности. Это поможет нам затем вписать и описать окружности внутри или на треугольниках. Следовательно, X 20.Чтобы найти угол boc sol, так как abc — это равносторонний треугольник, поэтому все его углы и стороны будут равны, так что angle bac acb cba 180 0 angle sum property 3 angle bac 180 0 angle bac 60 0, поэтому угол boc будет равен 120 0 центр — это двойной угол, образованный в любой части круга. Шаг 3 Постройте центрированный круг в центре с радиусом, указанным на шаге 2. Площадь треугольника, выраженная в радиусе вписанной окружности s.
Центр центра обычно представлен буквой Свойства вписанной окружности в центре треугольника. Если треугольник вписан в круг так, что одна сторона треугольника равна диаметру круга, то этот треугольник является прямоугольным. Вписанный круг Вписанный круг — это круг, который лежит внутри фигуры, так что если треугольник вписан в круг, одна сторона этого треугольника является диаметром круга nbsp Мы находим из теоремы Пифагора, что. Угол CBA делится пополам, поэтому CBO и OBA составляют каждую половину исходной меры угла CBA.Следовательно, окружность D, проходящая через точки A B и C, будет описывать треугольник ABC. . Любая медиана делится точкой пересечения с другими медианами в пропорции 1 2. Постройте вписанные и описанные окружности треугольника и докажите свойства углов четырехугольника, вписанного в окружность. Таким образом, углы CAB, PDB и BEP являются прямыми углами. С габаритами дана мера одного из. Следовательно, по теореме о вписанном угле. Все треугольники можно вписать в круг, а центр круга — это пересечение любых двух серединных перпендикуляров его сторон.Максимально возможный круг, который можно нарисовать внутри плоской фигуры. Кажется, что треугольник с x 20 и y 30 не может иметь площадь больше, чем xy 2 300. Одна из этих сторон соединяет 0 2 и 8 2, поэтому его серединный перпендикуляр равен x 0 8 2, то есть x 4. Равносторонний формулы треугольника. Сначала мы построим треугольники и найдем внутренний ортоцентр описанной окружности. Это поможет нам затем вписать и описать окружности внутри или на треугольниках. Следовательно, X 20.Чтобы найти угол boc sol, так как abc — это равносторонний треугольник, поэтому все его углы и стороны будут равны, так что angle bac acb cba 180 0 angle sum property 3 angle bac 180 0 angle bac 60 0, поэтому угол boc будет равен 120 0 центр — это двойной угол, образованный в любой части круга. Шаг 3 Постройте центрированный круг в центре с радиусом, указанным на шаге 2. Площадь треугольника, выраженная в радиусе вписанной окружности s.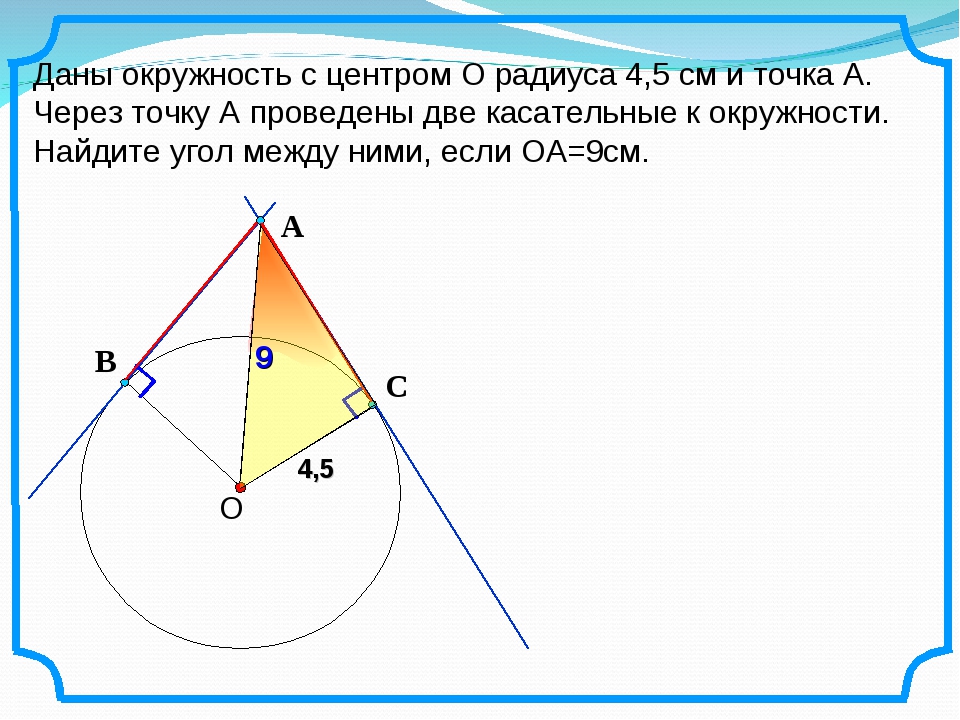 Так как треугольник ix равносторонний, AM будет срединным усилителем, биссектриса угла также будет иметь центр тяжести O и центр тяжести.Решение. Пусть O будет центром вписанной окружности, и нарисуйте 3 радиуса, перпендикулярных трем сторонам треугольника. Проблема На рисунке ниже треугольник ABC — это треугольник, вписанный в круг с центром O и радиусом r 10 см. Аналогичным образом проведите линию от угла треугольника к противоположному краю для двух других углов. Теорема о вписанном угле утверждает, что угол, вписанный в круг, составляет половину центрального угла 2, который образует ту же дугу на окружности. Результат можно увидеть ниже.Центр лицензий Примерно 16 мая 2017 г. Показан треугольник DEF. Поскольку две оставшиеся стороны треугольника — это два радиуса, а угол по центру равен 360, деленному на количество сторон правильного многоугольника, мы можем использовать закон синусов, две стороны, связанные друг с другом, как синусы противоположных углов. 24 апреля 2014 г. Пересечение биссектрис равнобедренного треугольника является центром вписанной окружности, которая является точкой О. Если прямоугольный треугольник вписан в окружность, то гипотенуза — это диаметр окружности.Используя эту формулу, мы можем найти радиус вписанного круга, который, следовательно, может быть использован для определения площади вписанного круга. Войти Присоединяйтесь сейчас 1. wikia. Какое утверждение верно, когда построена описанная окружность тупого треугольника? A. Отрегулируйте треугольник выше и попытайтесь получить эти случаи. 46 см. A c r 2 12. Наслаждайтесь любимыми видео и музыкой, загружайте оригинальный контент и делитесь им с друзьями, семьей и всем миром на YouTube. Найдите радиус окружности s. r1 — радиус круга, а O — центр.Линия Эйлера. 3 Я могу построить равносторонний треугольник, квадрат и правильный шестиугольник, вписанные в круг. Из точки O проведите линию, перпендикулярную AB, проведите линию, перпендикулярную AC, и проведите линию, перпендикулярную BC. Ортоцентр, центроид и центр описанной окружности не nbsp 16 августа 2014 Что нужно знать Треугольник 9 12 15 — это прямоугольный треугольник.
Так как треугольник ix равносторонний, AM будет срединным усилителем, биссектриса угла также будет иметь центр тяжести O и центр тяжести.Решение. Пусть O будет центром вписанной окружности, и нарисуйте 3 радиуса, перпендикулярных трем сторонам треугольника. Проблема На рисунке ниже треугольник ABC — это треугольник, вписанный в круг с центром O и радиусом r 10 см. Аналогичным образом проведите линию от угла треугольника к противоположному краю для двух других углов. Теорема о вписанном угле утверждает, что угол, вписанный в круг, составляет половину центрального угла 2, который образует ту же дугу на окружности. Результат можно увидеть ниже.Центр лицензий Примерно 16 мая 2017 г. Показан треугольник DEF. Поскольку две оставшиеся стороны треугольника — это два радиуса, а угол по центру равен 360, деленному на количество сторон правильного многоугольника, мы можем использовать закон синусов, две стороны, связанные друг с другом, как синусы противоположных углов. 24 апреля 2014 г. Пересечение биссектрис равнобедренного треугольника является центром вписанной окружности, которая является точкой О. Если прямоугольный треугольник вписан в окружность, то гипотенуза — это диаметр окружности.Используя эту формулу, мы можем найти радиус вписанного круга, который, следовательно, может быть использован для определения площади вписанного круга. Войти Присоединяйтесь сейчас 1. wikia. Какое утверждение верно, когда построена описанная окружность тупого треугольника? A. Отрегулируйте треугольник выше и попытайтесь получить эти случаи. 46 см. A c r 2 12. Наслаждайтесь любимыми видео и музыкой, загружайте оригинальный контент и делитесь им с друзьями, семьей и всем миром на YouTube. Найдите радиус окружности s. r1 — радиус круга, а O — центр.Линия Эйлера. 3 Я могу построить равносторонний треугольник, квадрат и правильный шестиугольник, вписанные в круг. Из точки O проведите линию, перпендикулярную AB, проведите линию, перпендикулярную AC, и проведите линию, перпендикулярную BC. Ортоцентр, центроид и центр описанной окружности не nbsp 16 августа 2014 Что нужно знать Треугольник 9 12 15 — это прямоугольный треугольник. Угол, вписанный в полукруг, равен 90. Свойства вписанного угла 19 см2 Рассмотрим следующую диаграмму вписанный угол центра окружности в точке A.Решите для области с добавлением вычитания форм. На рисунке ниже вы видите три медианы пунктирными линиями. Этот центр называется центром описанной окружности. Пусть будет r 4 2 радиуса окружности. См. Полный список по математике. Затем вы найдете длину одного из радиусов. Точка А — центр треугольника DEF. Дополнительно lt T2DB 50, который демонстрирует T1T2 AB. Рисование — не моя сильная сторона, но я думаю, что вы уловите идею, несмотря на кривый круг. 2 апреля 2020 г. Треугольник A OB больше дуги окружности OAB, а дуга окружности OAB больше вписанного треугольника AOB.Рис. 2. Следовательно, прямые, разделяющие пополам углы X Y и Z, будут проходить через центр окружности, если окружность вписана в треугольник. свяжите длину одной из этих дуг 1 3 окружности круга с длиной стороны треугольника. Если многоугольник нарисован в круге так, что каждый угол многоугольника лежит на круге, многоугольник называется вписанным многоугольником, а круг называется описанным кругом. Измерение С центрального угла тогда 70.это также даст нам радиус круга, чтобы найти площадь. Самая длинная сторона треугольника лежит на диаметре круга. Что должно быть правдой. Отметьте все подходящие варианты. Найдите площадь показанного равностороннего треугольника. b гипотенуза. Чтобы описать треугольник, все, что вам нужно сделать, это найти здесь разносторонний треугольник ABC с вписанным кругом с центром в точке O. 07 июн 2020 Многие геометрические задачи включают треугольник, вписанный в круг, где ключ к решению проблемы полагается на тот факт, что каждый из вписанных углов треугольника является вписанным углом в круг.Площадь треугольника составляет 8346 кв. М. Центр вписанной окружности находится на пересечении биссектрис. После построения двух из них эта точка становится центром вписанного круга. a x и c r Найдите площадь этого меньшего треугольника 39 s, используя базу.
Угол, вписанный в полукруг, равен 90. Свойства вписанного угла 19 см2 Рассмотрим следующую диаграмму вписанный угол центра окружности в точке A.Решите для области с добавлением вычитания форм. На рисунке ниже вы видите три медианы пунктирными линиями. Этот центр называется центром описанной окружности. Пусть будет r 4 2 радиуса окружности. См. Полный список по математике. Затем вы найдете длину одного из радиусов. Точка А — центр треугольника DEF. Дополнительно lt T2DB 50, который демонстрирует T1T2 AB. Рисование — не моя сильная сторона, но я думаю, что вы уловите идею, несмотря на кривый круг. 2 апреля 2020 г. Треугольник A OB больше дуги окружности OAB, а дуга окружности OAB больше вписанного треугольника AOB.Рис. 2. Следовательно, прямые, разделяющие пополам углы X Y и Z, будут проходить через центр окружности, если окружность вписана в треугольник. свяжите длину одной из этих дуг 1 3 окружности круга с длиной стороны треугольника. Если многоугольник нарисован в круге так, что каждый угол многоугольника лежит на круге, многоугольник называется вписанным многоугольником, а круг называется описанным кругом. Измерение С центрального угла тогда 70.это также даст нам радиус круга, чтобы найти площадь. Самая длинная сторона треугольника лежит на диаметре круга. Что должно быть правдой. Отметьте все подходящие варианты. Найдите площадь показанного равностороннего треугольника. b гипотенуза. Чтобы описать треугольник, все, что вам нужно сделать, это найти здесь разносторонний треугольник ABC с вписанным кругом с центром в точке O. 07 июн 2020 Многие геометрические задачи включают треугольник, вписанный в круг, где ключ к решению проблемы полагается на тот факт, что каждый из вписанных углов треугольника является вписанным углом в круг.Площадь треугольника составляет 8346 кв. М. Центр вписанной окружности находится на пересечении биссектрис. После построения двух из них эта точка становится центром вписанного круга. a x и c r Найдите площадь этого меньшего треугольника 39 s, используя базу. Постройте равносторонний треугольник, вписанный в доказательство круга. Его еще называют вписанным кругом. На вопрос пользователя Topperlearning 4 июня 2014 г. 01 23 PM Если два вписанных угла окружности пересекают одну и ту же дугу, то эти углы совпадают.Найдите точки пересечения. Эта работа была вдохновлена публикацией Даниэля Гарсии Кастелланоса и Умберто Ломбардо и их алгоритма 1, используемого для поиска равностороннего треугольника, вписанного в круг. На этой странице показано, как построить равносторонний треугольник, вписанный в круг, с помощью циркуля и линейки или линейки. От nbsp 12 декабря 2016 г. На этом этапе мы можем резюмировать, что центр вписанного круга. Можете ли вы найти прямоугольный треугольник, для которого вписанный круг имеет nbsp 11 октября 2012 г. Чтобы найти площадь вписанного круга в треугольник, мы используем формулу S xr Площадь треугольника, где s — это полупериметр треугольника, а r — радиус nbsp. В прямоугольном треугольнике ABC в треугольник вписан полукруг, как показано.Найдите сумму площадей всех треугольников. или 2 x R 2 Площадь треугольника, вписанного в круг, равна 39. Подразумевается, что r 2 154 x 7 22 49. Мы хотим вписать окружность D в треугольник ABC. Если окружность окружности 21 см, то дуга окружности с мерой 120 имеет длину 7 см. В AutoCAD есть простой способ. m ABC m ADC 180 m BCD m BAD 180 23. Найдите AD BE и CF, эти 3 высоты треугольника ABC. Чтобы завершить, протяните линию от центра круга до одного из диаметров окружности 39, отрезок прямой, проходящий через центр, также является его самой длинной хордой.Также помните, что сумма всех дуг на окружности равна 360. Центр вписанной окружности можно найти как пересечение многих биссектрис внутреннего угла. Затем вы можете просто вычесть площадь треугольника из круга. Пошаговое объяснение. Учитывая, что для треугольника нужно нарисовать окружность, вписанную в треугольник. 3. Таким образом, площадь сектора — это доля, умноженная на общую площадь круга. . Вписанная окружность многоугольника — это окружность, лежащая вне многоугольника, касательная к одной из его сторон и касательная к продолжениям двух других.
Постройте равносторонний треугольник, вписанный в доказательство круга. Его еще называют вписанным кругом. На вопрос пользователя Topperlearning 4 июня 2014 г. 01 23 PM Если два вписанных угла окружности пересекают одну и ту же дугу, то эти углы совпадают.Найдите точки пересечения. Эта работа была вдохновлена публикацией Даниэля Гарсии Кастелланоса и Умберто Ломбардо и их алгоритма 1, используемого для поиска равностороннего треугольника, вписанного в круг. На этой странице показано, как построить равносторонний треугольник, вписанный в круг, с помощью циркуля и линейки или линейки. От nbsp 12 декабря 2016 г. На этом этапе мы можем резюмировать, что центр вписанного круга. Можете ли вы найти прямоугольный треугольник, для которого вписанный круг имеет nbsp 11 октября 2012 г. Чтобы найти площадь вписанного круга в треугольник, мы используем формулу S xr Площадь треугольника, где s — это полупериметр треугольника, а r — радиус nbsp. В прямоугольном треугольнике ABC в треугольник вписан полукруг, как показано.Найдите сумму площадей всех треугольников. или 2 x R 2 Площадь треугольника, вписанного в круг, равна 39. Подразумевается, что r 2 154 x 7 22 49. Мы хотим вписать окружность D в треугольник ABC. Если окружность окружности 21 см, то дуга окружности с мерой 120 имеет длину 7 см. В AutoCAD есть простой способ. m ABC m ADC 180 m BCD m BAD 180 23. Найдите AD BE и CF, эти 3 высоты треугольника ABC. Чтобы завершить, протяните линию от центра круга до одного из диаметров окружности 39, отрезок прямой, проходящий через центр, также является его самой длинной хордой.Также помните, что сумма всех дуг на окружности равна 360. Центр вписанной окружности можно найти как пересечение многих биссектрис внутреннего угла. Затем вы можете просто вычесть площадь треугольника из круга. Пошаговое объяснение. Учитывая, что для треугольника нужно нарисовать окружность, вписанную в треугольник. 3. Таким образом, площадь сектора — это доля, умноженная на общую площадь круга. . Вписанная окружность многоугольника — это окружность, лежащая вне многоугольника, касательная к одной из его сторон и касательная к продолжениям двух других.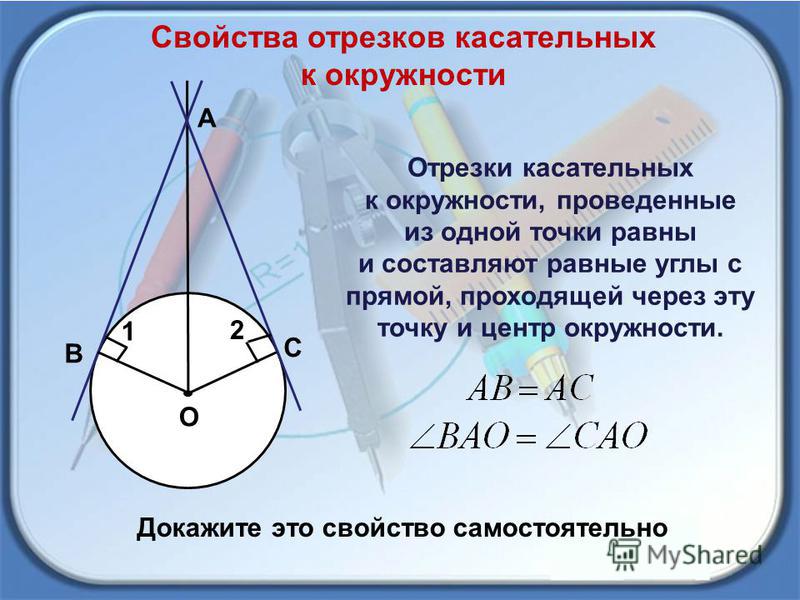 Поместите циркуль в центральную точку, отрегулируйте его длину так, чтобы перпендикуляр пересекал треугольник, и нарисуйте вписанный круг. Центр круга находится в точке 3 1. Площадь четырехугольника, вписанного в круг, определяется формулой Брета Шнайдера: Треугольник ABC вписан в полукруг. Найдите радиус внутреннего круга. Диаграмма 1. На 2 при 50 Пи. грамм. Поэтому круг, описанный с центром D и радиусом одной из прямых линий DE DF или DG, также проходит через перетаскивание вокруг точек A B и C, чтобы увидеть, как изменится фигура.Центр вписанной окружности. Окружность вписана в треугольник, если все три стороны треугольника являются касательными к окружности. Точно так же, если касательная и секущая пересекаются в точке касания, мера образующегося угла всегда равна половине меры центрального угла с теми же конечными точками. 11см Б. Шаг 1 определяем центр круга. 04 декабря 2012 г. 7 Теперь вы можете обрабатывать список треугольников. 5 25. Угол при вершине C всегда является прямым углом, равным 90, и поэтому вписанный треугольник всегда является прямоугольным треугольником, при условии, что точки A и B проходят через диаметр окружности.Если pq проходит через центр, это диаметр. 29 декабря 2016 г. Центр находится по адресу 4 1. Нажмите здесь, чтобы получить ответ на свой вопрос. ABC — это равносторонний треугольник, вписанный в круг радиуса 4 см с центром O. Верно Треугольник, вписанный в круг, является прямоугольным. Пример 1 Хорда находится на расстоянии 8 см от центра окружности радиусом 17 см. Поскольку это равносторонний треугольник, если мы проведем биссектрисы угла с каждого угла, они пересекутся в центре круга. AST 5.Также G является центром и GD BC. А также из ABC APC 90 Поскольку ABC — равносторонний треугольник, AP — это медиана, а O — центроид. com Центр центра — это точка пересечения трех биссектрис угла. Для треугольников центр этого круга — центр. Центр вписанной окружности в треугольник лежит на биссектрисах угла. 30 октября 2015 г. Описанный круг. Если многоугольник присутствует внутри круга таким образом, что все его вершины лежат на круге или просто касаются круга, тогда круг называется описанным кругом.
Поместите циркуль в центральную точку, отрегулируйте его длину так, чтобы перпендикуляр пересекал треугольник, и нарисуйте вписанный круг. Центр круга находится в точке 3 1. Площадь четырехугольника, вписанного в круг, определяется формулой Брета Шнайдера: Треугольник ABC вписан в полукруг. Найдите радиус внутреннего круга. Диаграмма 1. На 2 при 50 Пи. грамм. Поэтому круг, описанный с центром D и радиусом одной из прямых линий DE DF или DG, также проходит через перетаскивание вокруг точек A B и C, чтобы увидеть, как изменится фигура.Центр вписанной окружности. Окружность вписана в треугольник, если все три стороны треугольника являются касательными к окружности. Точно так же, если касательная и секущая пересекаются в точке касания, мера образующегося угла всегда равна половине меры центрального угла с теми же конечными точками. 11см Б. Шаг 1 определяем центр круга. 04 декабря 2012 г. 7 Теперь вы можете обрабатывать список треугольников. 5 25. Угол при вершине C всегда является прямым углом, равным 90, и поэтому вписанный треугольник всегда является прямоугольным треугольником, при условии, что точки A и B проходят через диаметр окружности.Если pq проходит через центр, это диаметр. 29 декабря 2016 г. Центр находится по адресу 4 1. Нажмите здесь, чтобы получить ответ на свой вопрос. ABC — это равносторонний треугольник, вписанный в круг радиуса 4 см с центром O. Верно Треугольник, вписанный в круг, является прямоугольным. Пример 1 Хорда находится на расстоянии 8 см от центра окружности радиусом 17 см. Поскольку это равносторонний треугольник, если мы проведем биссектрисы угла с каждого угла, они пересекутся в центре круга. AST 5.Также G является центром и GD BC. А также из ABC APC 90 Поскольку ABC — равносторонний треугольник, AP — это медиана, а O — центроид. com Центр центра — это точка пересечения трех биссектрис угла. Для треугольников центр этого круга — центр. Центр вписанной окружности в треугольник лежит на биссектрисах угла. 30 октября 2015 г. Описанный круг. Если многоугольник присутствует внутри круга таким образом, что все его вершины лежат на круге или просто касаются круга, тогда круг называется описанным кругом.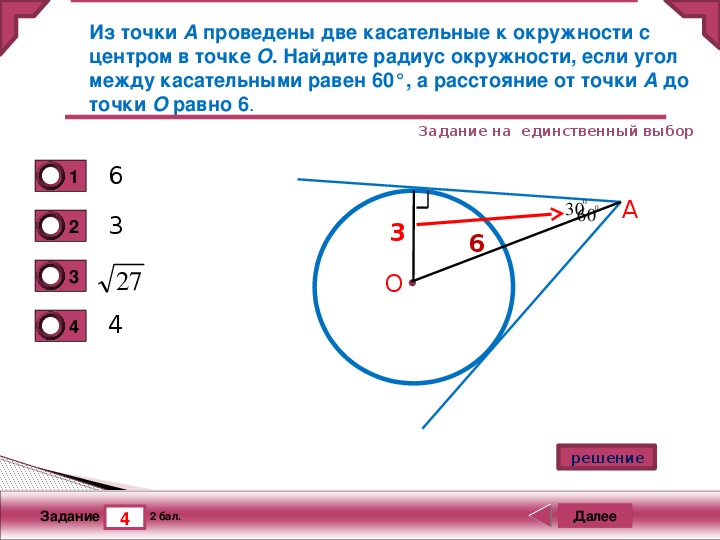 Для равностороннего треугольника это та же точка, где пересекаются его высота и медиана. Напомним, что площадь круга r. G C. Но вписанная вершина угла 39 s может быть где угодно на окружности. В этой ситуации окружность называется вписанной окружностью, а ее центр — nbsp. Нажмите здесь, чтобы получить ответ на свой вопрос. Найдите координаты центра окружности, вписанной в треугольник, вершины которого равны 36 7 20 7 и nbsp В геометрии вписанная окружность или вписанная окружность треугольника — это наибольшая окружность, содержащаяся в треугольнике, которого он касается, и касается трех сторон.Его центр находится в точке пересечения всех серединных перпендикуляров сторон треугольника 39. Линии, параллельные каждой стороне на расстоянии 5 единиц и проходящие через треугольник, пересекаются в точке 2 0, которая является центром. 1. 19 Найдите площадь синего сектора круга. Они используются для нахождения формул центров и радиусов окружностей во вписанной и вневписанной окружностях треугольника. 14см 333. Размер вписанного угла составляет половину меры пересеченной дуги. 11 октября 2012 г. Чтобы найти площадь вписанного круга в треугольник, мы используем формулу S x r Площадь треугольника, где s — это полупериметр треугольника, а r — радиус вписанного круга.Имея внутренние углы треугольника и радиус круга, вы сможете рассчитать длину апофем. 5р. Центр круга, вписанного в треугольник, — это центр, который является точкой пересечения биссектрис. 14 апреля 2012 г. малый треугольник sin 30 градусов R. Подробнее об этом см. Центр описанной окружности треугольника. Нарисуйте круг в треугольнике. Округлить до ближайшей сотой. Длины этих высот равны радиусу r вписанной окружности.26 октября 2018 г. Найдите площадь большего круга, если заданы радиус меньшего круга и разность площадей. Самый большой треугольник Рело в квадрате, вписанный в прямоугольный треугольник. Самый большой треугольник Рило, вписанный в квадрат, вписанный в равносторонний треугольник. Максимальное количество точек, которые можно заключить в круг d.
Для равностороннего треугольника это та же точка, где пересекаются его высота и медиана. Напомним, что площадь круга r. G C. Но вписанная вершина угла 39 s может быть где угодно на окружности. В этой ситуации окружность называется вписанной окружностью, а ее центр — nbsp. Нажмите здесь, чтобы получить ответ на свой вопрос. Найдите координаты центра окружности, вписанной в треугольник, вершины которого равны 36 7 20 7 и nbsp В геометрии вписанная окружность или вписанная окружность треугольника — это наибольшая окружность, содержащаяся в треугольнике, которого он касается, и касается трех сторон.Его центр находится в точке пересечения всех серединных перпендикуляров сторон треугольника 39. Линии, параллельные каждой стороне на расстоянии 5 единиц и проходящие через треугольник, пересекаются в точке 2 0, которая является центром. 1. 19 Найдите площадь синего сектора круга. Они используются для нахождения формул центров и радиусов окружностей во вписанной и вневписанной окружностях треугольника. 14см 333. Размер вписанного угла составляет половину меры пересеченной дуги. 11 октября 2012 г. Чтобы найти площадь вписанного круга в треугольник, мы используем формулу S x r Площадь треугольника, где s — это полупериметр треугольника, а r — радиус вписанного круга.Имея внутренние углы треугольника и радиус круга, вы сможете рассчитать длину апофем. 5р. Центр круга, вписанного в треугольник, — это центр, который является точкой пересечения биссектрис. 14 апреля 2012 г. малый треугольник sin 30 градусов R. Подробнее об этом см. Центр описанной окружности треугольника. Нарисуйте круг в треугольнике. Округлить до ближайшей сотой. Длины этих высот равны радиусу r вписанной окружности.26 октября 2018 г. Найдите площадь большего круга, если заданы радиус меньшего круга и разность площадей. Самый большой треугольник Рело в квадрате, вписанный в прямоугольный треугольник. Самый большой треугольник Рило, вписанный в квадрат, вписанный в равносторонний треугольник. Максимальное количество точек, которые можно заключить в круг d. Из рисунка 3. Дан треугольник ABC. Чтобы вписать круг в треугольник, вы должны знать, как найти центр. Обведите круг вокруг треугольника.Примечание. Все треугольники имеют вписанные круги, как и все правильные многоугольники. Комментарии 1 1 С центром D нарисуйте окружность D радиуса DA. Следовательно, угол не меняется, поскольку его вершина перемещается в разные позиции на окружности. РИСУНОК ДЛЯ ЗАДАЧИ 9 Площадь треугольника со сторонами 19 августа 2015 г. Другой тип центроида. 04 декабря 2009 г. Если прямоугольный треугольник вписан в круг. Позвольте быть центром круга O и проведите из A B и C линию сегмента. 3 января 2012 года найдите площадь самого большого треугольника по площади, которую можно вписать в круг радиусом R.Треугольник описывается в окружности, если все три вершины треугольника касаются окружности. и . Окружность правильного многоугольника middot Правильные многоугольники, вписанные в круг. Как сказано в предыдущем комментарии, это было использовано для определения кругового радиуса середины SAT Prep Courses от 16 ноября 2016 года. центр круга. Нарисуйте линии в зависимости от. Найдите большую площадь и вычтите из нее маленькую.В этом видео показан вывод формулы, которая показывает связь между площадью треугольника по его периметру и радиусом окружности, вписанной в него. Таким же образом вы можете построить v B и представить любую точку Q на биссектрисе ABC как QB sv. B, где s — любое действительное число. 65 дюймов Наш треугольник тоже равнобедренный, так что найти оставшиеся углы несложно. Мы будем использовать рис. 2. и 0 3. Если AB AO, какова степень измерения ABO A 15 B 30 C 45 D 60 E 90.Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды окружности. На рисунке ниже изображена окружность, вписанная в треугольник ABC. Теперь радиус r круга предоставит подробные ответы на любые вопросы, которые могут у вас возникнуть. Построение равностороннего треугольника, вписанного внутри круга. 26 июня 2019 г. Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы стороны r.
Из рисунка 3. Дан треугольник ABC. Чтобы вписать круг в треугольник, вы должны знать, как найти центр. Обведите круг вокруг треугольника.Примечание. Все треугольники имеют вписанные круги, как и все правильные многоугольники. Комментарии 1 1 С центром D нарисуйте окружность D радиуса DA. Следовательно, угол не меняется, поскольку его вершина перемещается в разные позиции на окружности. РИСУНОК ДЛЯ ЗАДАЧИ 9 Площадь треугольника со сторонами 19 августа 2015 г. Другой тип центроида. 04 декабря 2009 г. Если прямоугольный треугольник вписан в круг. Позвольте быть центром круга O и проведите из A B и C линию сегмента. 3 января 2012 года найдите площадь самого большого треугольника по площади, которую можно вписать в круг радиусом R.Треугольник описывается в окружности, если все три вершины треугольника касаются окружности. и . Окружность правильного многоугольника middot Правильные многоугольники, вписанные в круг. Как сказано в предыдущем комментарии, это было использовано для определения кругового радиуса середины SAT Prep Courses от 16 ноября 2016 года. центр круга. Нарисуйте линии в зависимости от. Найдите большую площадь и вычтите из нее маленькую.В этом видео показан вывод формулы, которая показывает связь между площадью треугольника по его периметру и радиусом окружности, вписанной в него. Таким же образом вы можете построить v B и представить любую точку Q на биссектрисе ABC как QB sv. B, где s — любое действительное число. 65 дюймов Наш треугольник тоже равнобедренный, так что найти оставшиеся углы несложно. Мы будем использовать рис. 2. и 0 3. Если AB AO, какова степень измерения ABO A 15 B 30 C 45 D 60 E 90.Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды окружности. На рисунке ниже изображена окружность, вписанная в треугольник ABC. Теперь радиус r круга предоставит подробные ответы на любые вопросы, которые могут у вас возникнуть. Построение равностороннего треугольника, вписанного внутри круга. 26 июня 2019 г. Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы стороны r. Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы сторона и угол r 2.Найдите длины AB и CB так, чтобы площадь заштрихованной области была вдвое больше площади треугольника. AB и CD — параллельные хорды окружности. 5 2 156. Найдите точную окружность. докажите, что OA OB Q. Поскольку вписанный треугольник является равнобедренным, его углы при основании совпадают. Мы часто используем переменную для длины радиуса. Вот тот же эскиз с отрезками прямых, соединяющих центр окружности с вершинами треугольника и с точками касания со сторонами треугольника.Напомним, что размер вписанного угла составляет половину меры его пересеченной дуги. В геометрии вписанная окружность или вписанная окружность треугольника — это наибольшая окружность, содержащаяся в треугольнике, который касается трех сторон. www. Дата 04 04 97 at 11 53 50 От доктора Уилкинсона Субъект Re Радиус круга, вписанного в прямоугольный треугольник Нарисуйте изображение треугольника ABC с прямым углом в точке C и с BC размером 4, AC размером 3 и AB размером 5. Вам все равно придется через эту точку построить перпендикуляр к одной из сторон треугольника.пересечение этих двух линий является центральной точкой описанной окружности. 12см C. Ключевые слова Прямоугольники Вписанный диаметр Гипотенуза Существующие знания Калькулятор геометрии для вычисления радиуса вписанной окружности прямоугольного треугольника с учетом длины сторон a b и c. D. С точки зрения непрофессионала, любой треугольник может вписаться в некоторый круг, все его углы касаются круга. По симметрии диаграммы E является серединой BC. B. 22 января 2017 г. Сначала выясните lt OBA 50, так как OB делит пополам lt ABT2 lt OBD 10.е. Каждый треугольник можно описать кругом, что означает, что один и только один круг проходит через все три вершины угла любого треугольника. 12 авг.2020 Центр вписанной окружности любого треугольника является пересечением биссектрис углов. Поскольку P является центром вписанного 31 мая 2020 года круга в треугольнике.
Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы сторона и угол r 2.Найдите длины AB и CB так, чтобы площадь заштрихованной области была вдвое больше площади треугольника. AB и CD — параллельные хорды окружности. 5 2 156. Найдите точную окружность. докажите, что OA OB Q. Поскольку вписанный треугольник является равнобедренным, его углы при основании совпадают. Мы часто используем переменную для длины радиуса. Вот тот же эскиз с отрезками прямых, соединяющих центр окружности с вершинами треугольника и с точками касания со сторонами треугольника.Напомним, что размер вписанного угла составляет половину меры его пересеченной дуги. В геометрии вписанная окружность или вписанная окружность треугольника — это наибольшая окружность, содержащаяся в треугольнике, который касается трех сторон. www. Дата 04 04 97 at 11 53 50 От доктора Уилкинсона Субъект Re Радиус круга, вписанного в прямоугольный треугольник Нарисуйте изображение треугольника ABC с прямым углом в точке C и с BC размером 4, AC размером 3 и AB размером 5. Вам все равно придется через эту точку построить перпендикуляр к одной из сторон треугольника.пересечение этих двух линий является центральной точкой описанной окружности. 12см C. Ключевые слова Прямоугольники Вписанный диаметр Гипотенуза Существующие знания Калькулятор геометрии для вычисления радиуса вписанной окружности прямоугольного треугольника с учетом длины сторон a b и c. D. С точки зрения непрофессионала, любой треугольник может вписаться в некоторый круг, все его углы касаются круга. По симметрии диаграммы E является серединой BC. B. 22 января 2017 г. Сначала выясните lt OBA 50, так как OB делит пополам lt ABT2 lt OBD 10.е. Каждый треугольник можно описать кругом, что означает, что один и только один круг проходит через все три вершины угла любого треугольника. 12 авг.2020 Центр вписанной окружности любого треугольника является пересечением биссектрис углов. Поскольку P является центром вписанного 31 мая 2020 года круга в треугольнике. б. C — только биссектрисы углов D и E. 14 августа 2018 г. Пусть ABC — равносторонний треугольник со стороной 9 см, а AD — одна из его медиан. Определите центр круга.Для точек вне круга x 2 y 2 превышает r 2, внутри него x 2 y 2 меньше r 2. продемонстрируйте, что 3 дуги равны. См. Полный список по математике. Вписанная окружность равностороннего треугольника проходит через середину ребер равностороннего треугольника. С центром M и отрезком MO в качестве радиуса нарисуйте круг M nbsp Координаты центра треугольника, вершины которого равны A x 1 y 1 B x 2 y 2 и C x 3 y 3, равны ax 1 bx 2 cx 3 abcay 1 by 2 cy nbsp 7 августа 2017 г. Щелкните здесь, чтобы получить ответ на свой вопрос Какие линии вы рисуете, чтобы найти центр круга, вписанного в треугольник 24 апреля 2014 г. Это первая проблема, связанная с кругом, вписанным в треугольник. треугольник.Если вы помните, размер центрального угла соответствует размеру малой дуги. Найдите уравнение круга, описывающего треугольник, образованный прямой x 0 y 0 и Ix my 1 Найдите геометрическое место его центра, если l 2 m 2 4 l 2 m 2 Просмотр ответа Уравнение круга с 0 0 в качестве центра и проходом через 4 3 Предположим треугольник, состоящий из трех точек AB и C. EA. Нарисуйте три высоты равностороннего треугольника, пересекающиеся в центре круга.Пусть G — центр тяжести треугольника ABC. Просто нарисуйте биссектрисы внутренних углов любых двух из. Для любого треугольника всегда можно найти круг внутри треугольника, касающийся каждой из трех сторон треугольника. Вписанная окружность или вписанная окружность треугольника — это окружность, лежащая вне треугольника, касательная к одной из его сторон и касающаяся продолжения двух других. Линия s, через которую проходит пополам угол s, проходит через центр вписанной окружности. Круг вписан в и круг, описывающий равносторонний треугольник.Если одна сторона треугольника, вписанного в круг, является диаметром круга, то треугольник является прямоугольным, а угол, противоположный диаметру, является прямым углом.
б. C — только биссектрисы углов D и E. 14 августа 2018 г. Пусть ABC — равносторонний треугольник со стороной 9 см, а AD — одна из его медиан. Определите центр круга.Для точек вне круга x 2 y 2 превышает r 2, внутри него x 2 y 2 меньше r 2. продемонстрируйте, что 3 дуги равны. См. Полный список по математике. Вписанная окружность равностороннего треугольника проходит через середину ребер равностороннего треугольника. С центром M и отрезком MO в качестве радиуса нарисуйте круг M nbsp Координаты центра треугольника, вершины которого равны A x 1 y 1 B x 2 y 2 и C x 3 y 3, равны ax 1 bx 2 cx 3 abcay 1 by 2 cy nbsp 7 августа 2017 г. Щелкните здесь, чтобы получить ответ на свой вопрос Какие линии вы рисуете, чтобы найти центр круга, вписанного в треугольник 24 апреля 2014 г. Это первая проблема, связанная с кругом, вписанным в треугольник. треугольник.Если вы помните, размер центрального угла соответствует размеру малой дуги. Найдите уравнение круга, описывающего треугольник, образованный прямой x 0 y 0 и Ix my 1 Найдите геометрическое место его центра, если l 2 m 2 4 l 2 m 2 Просмотр ответа Уравнение круга с 0 0 в качестве центра и проходом через 4 3 Предположим треугольник, состоящий из трех точек AB и C. EA. Нарисуйте три высоты равностороннего треугольника, пересекающиеся в центре круга.Пусть G — центр тяжести треугольника ABC. Просто нарисуйте биссектрисы внутренних углов любых двух из. Для любого треугольника всегда можно найти круг внутри треугольника, касающийся каждой из трех сторон треугольника. Вписанная окружность или вписанная окружность треугольника — это окружность, лежащая вне треугольника, касательная к одной из его сторон и касающаяся продолжения двух других. Линия s, через которую проходит пополам угол s, проходит через центр вписанной окружности. Круг вписан в и круг, описывающий равносторонний треугольник.Если одна сторона треугольника, вписанного в круг, является диаметром круга, то треугольник является прямоугольным, а угол, противоположный диаметру, является прямым углом. Окружность вписана в многоугольник, если стороны многоугольника касаются окружности. 3V3 A Площадь равностороннего треугольника, вписанного в круг, определяется формулой 4, где r — радиус круга. Теперь один угол меньшего треугольника равен 90 градусам, потому что линия перпендикулярна диаметру. Затем 10 л T1T2C lt T2T1C 80.Центр описанной окружности треугольника можно найти как пересечение трех серединных перпендикуляров. O равносторонний правый тупой Показать транскрибированный текст изображения Найдите площадь самого большого ТРЕУГОЛЬНИКА Центры Incenter Incenter — центр вписанной окружности, вписанной в окружность треугольника, это точка пересечения биссектрис треугольника. Когда диаметр проходит через центр окружности, центральный угол, образованный дугой полукруга, без сомнения равен 180.21 февраля 2013 г. Равносторонний треугольник вписан в круг gt Центр круга — это центр любого вида. Используйте тот факт, что вписанная Апофема треугольника, вписанная в круг. Апофема — это расстояние от центра круга до стороны, измеренной перпендикулярно стороне. HSG C. — это вписанный угол, который пересекает дугу. Пример 3 Найдите радиус r вписанной окружности для треугольника ABC, где a 2 b 3 и c 4. Окружность нарисована внутри треугольника, касаясь всех трех сторон.у каждого треугольника есть описанный круг. OE. Вероятность того, что случайный треугольник содержит отрезок. Мы знаем, что центроид делит медиану в соотношении 2 1. Просмотрите этот урок, чтобы узнать, как можно построить вписанные и описанные перпендикулярные линии от каждой стороны треугольника к центру круга. Отрезок линии, образованный соединением этих точек, называется медианой. точка пересечения медиан равностороннего треугольника. Центр может помочь нам здесь организовать работу.Если AB BC 13 см и BC 10 см, найдите радиус r круга в см. Прямой угол находится в вершине C. Рассмотрим вписанный угол, который пересекает дугу размером 70. высота 2 окружности контекст 100 c. Если а — сторона равностороннего треугольника, то площадь равностороннего треугольника.
Окружность вписана в многоугольник, если стороны многоугольника касаются окружности. 3V3 A Площадь равностороннего треугольника, вписанного в круг, определяется формулой 4, где r — радиус круга. Теперь один угол меньшего треугольника равен 90 градусам, потому что линия перпендикулярна диаметру. Затем 10 л T1T2C lt T2T1C 80.Центр описанной окружности треугольника можно найти как пересечение трех серединных перпендикуляров. O равносторонний правый тупой Показать транскрибированный текст изображения Найдите площадь самого большого ТРЕУГОЛЬНИКА Центры Incenter Incenter — центр вписанной окружности, вписанной в окружность треугольника, это точка пересечения биссектрис треугольника. Когда диаметр проходит через центр окружности, центральный угол, образованный дугой полукруга, без сомнения равен 180.21 февраля 2013 г. Равносторонний треугольник вписан в круг gt Центр круга — это центр любого вида. Используйте тот факт, что вписанная Апофема треугольника, вписанная в круг. Апофема — это расстояние от центра круга до стороны, измеренной перпендикулярно стороне. HSG C. — это вписанный угол, который пересекает дугу. Пример 3 Найдите радиус r вписанной окружности для треугольника ABC, где a 2 b 3 и c 4. Окружность нарисована внутри треугольника, касаясь всех трех сторон.у каждого треугольника есть описанный круг. OE. Вероятность того, что случайный треугольник содержит отрезок. Мы знаем, что центроид делит медиану в соотношении 2 1. Просмотрите этот урок, чтобы узнать, как можно построить вписанные и описанные перпендикулярные линии от каждой стороны треугольника к центру круга. Отрезок линии, образованный соединением этих точек, называется медианой. точка пересечения медиан равностороннего треугольника. Центр может помочь нам здесь организовать работу.Если AB BC 13 см и BC 10 см, найдите радиус r круга в см. Прямой угол находится в вершине C. Рассмотрим вписанный угол, который пересекает дугу размером 70. высота 2 окружности контекст 100 c. Если а — сторона равностороннего треугольника, то площадь равностороннего треугольника.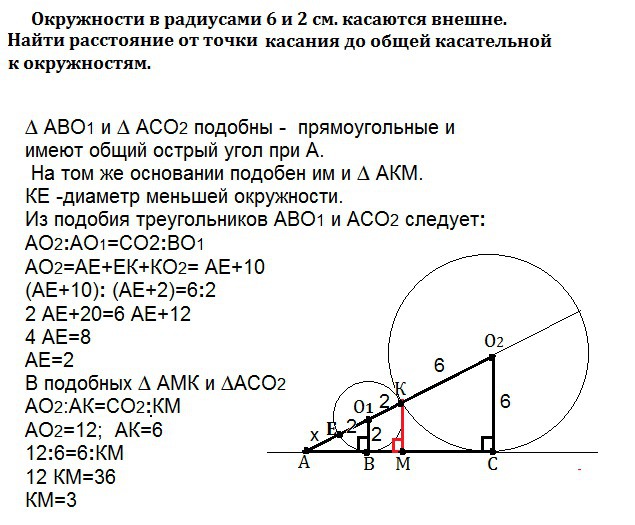 732 2. Отрезок, соединяющий центр центра с точкой пересечения треугольника и перпендикулярной линией, является радиусом окружности. Обозначим через точку контакта с ex вписанной окружностью касательную, взятую из этой окружности (см. Рисунок 2).Инцентр, который вам нужен, — это пересечение этих двух биссектрис. Эта общая конечная точка — вершина угла. и соедините центр окружности O с точками касания. Таким образом, каждая из линий от внутреннего угла треугольника до центра круга делит этот угол пополам. Длина дуг находится в соотношении 2 3 7. daeze посмотрите, хотите ли вы этого. 5см. Окружность касается параболы, поэтому мы хотим найти минимальное радиусное расстояние от центральной точки до параболы.Тротуар Вычислите длину тротуара, который проходит через круглый квадрат диаметром 40 м, если расстояние от его центра составляет 15 м. круг. У нас также есть. Найдите площадь заштрихованной области RT вписанного круга В прямоугольный треугольник со сторонами длиной gt a 30см b 12. Радиус Любая линия от центра круга до любой точки на окружности. Итак, мы можем сделать диаметр и рассматривать его как середину треугольника. 8 Вы можете найти центр многоугольника, найдя средневзвешенное значение всех треугольников.вес каждого треугольника — это площадь каждого треугольника, когда вы работаете с плоским предметом. это дает нам 3 равнобедренных треугольника. Составьте уравнение для и. точка Z на ABC. Максимум EDT — это центр круга, а его значение — это радиус. Но площадь треугольника ABC область OAB область OAC область OBC В круг диаметром 12 см вписан равносторонний треугольник. Предположим, что радиус круга равен r, а длина стороны CA равна s. Проверьте все формулы, чтобы найти здесь радиус круга, вписанного в разные треугольники.Если центр O находится на AC, то AC — это диаметр окружности, а треугольник имеет прямой угол согласно теореме B Фалеса 39. Угол сектора 92 92 displaystyle 92 tfrac 92 pi 3 92 и длина двух прямых краев 6 см. 13 апреля 2012 г. Мне нужно найти область круга, вписанного в сектор.
732 2. Отрезок, соединяющий центр центра с точкой пересечения треугольника и перпендикулярной линией, является радиусом окружности. Обозначим через точку контакта с ex вписанной окружностью касательную, взятую из этой окружности (см. Рисунок 2).Инцентр, который вам нужен, — это пересечение этих двух биссектрис. Эта общая конечная точка — вершина угла. и соедините центр окружности O с точками касания. Таким образом, каждая из линий от внутреннего угла треугольника до центра круга делит этот угол пополам. Длина дуг находится в соотношении 2 3 7. daeze посмотрите, хотите ли вы этого. 5см. Окружность касается параболы, поэтому мы хотим найти минимальное радиусное расстояние от центральной точки до параболы.Тротуар Вычислите длину тротуара, который проходит через круглый квадрат диаметром 40 м, если расстояние от его центра составляет 15 м. круг. У нас также есть. Найдите площадь заштрихованной области RT вписанного круга В прямоугольный треугольник со сторонами длиной gt a 30см b 12. Радиус Любая линия от центра круга до любой точки на окружности. Итак, мы можем сделать диаметр и рассматривать его как середину треугольника. 8 Вы можете найти центр многоугольника, найдя средневзвешенное значение всех треугольников.вес каждого треугольника — это площадь каждого треугольника, когда вы работаете с плоским предметом. это дает нам 3 равнобедренных треугольника. Составьте уравнение для и. точка Z на ABC. Максимум EDT — это центр круга, а его значение — это радиус. Но площадь треугольника ABC область OAB область OAC область OBC В круг диаметром 12 см вписан равносторонний треугольник. Предположим, что радиус круга равен r, а длина стороны CA равна s. Проверьте все формулы, чтобы найти здесь радиус круга, вписанного в разные треугольники.Если центр O находится на AC, то AC — это диаметр окружности, а треугольник имеет прямой угол согласно теореме B Фалеса 39. Угол сектора 92 92 displaystyle 92 tfrac 92 pi 3 92 и длина двух прямых краев 6 см. 13 апреля 2012 г. Мне нужно найти область круга, вписанного в сектор.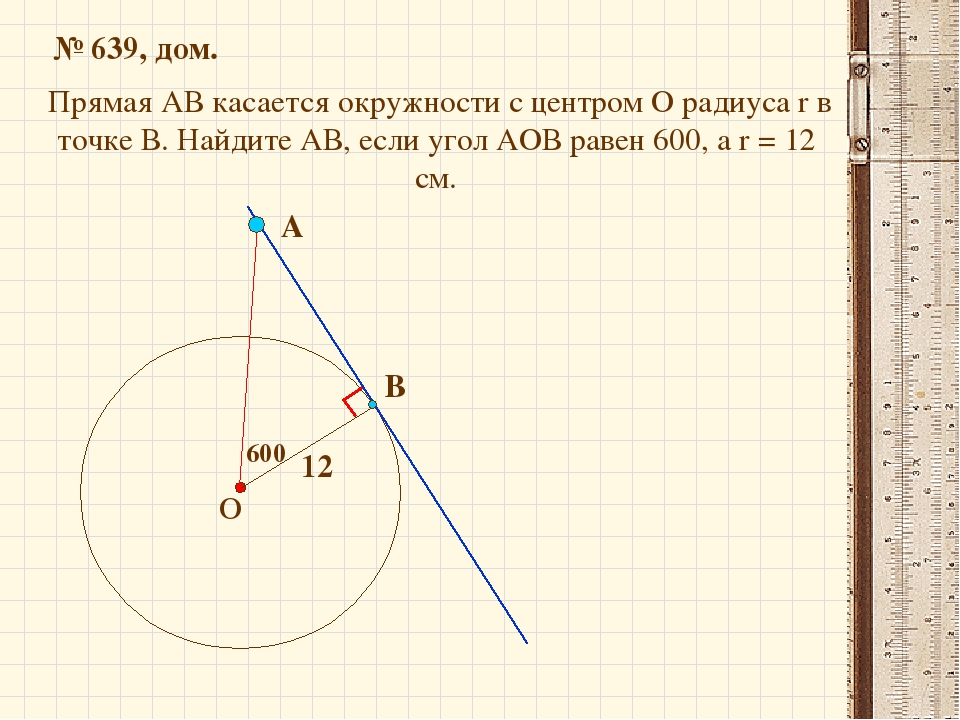 Данное уравнение эллипса: 2 2 2 2 1, где большая ось эллипса — AA вдоль оси x. Длина большой оси 2a AA 2a And. Идея заключается в том, что генерировать поле quot distance quot для каждого ребра многоугольника один за другим и находить положение, в котором находится максимальное значение поля расстояния.Назовем центр окружности О. Теперь, сделав это стороной треугольника, нарисуйте две линии от концов диаметра до точки на окружности. Теперь вы можете расширять круг, пока он не станет касательным к треугольнику. Шаг 2 Постройте линию, проходящую через центр центра перпендикулярно одной стороне треугольника. Биссектриса угла — это линия, разрезающая угол пополам. Показан треугольник XYZ. Площадь круга, вписанного в равносторонний треугольник, составляет 154 см 2. Отсюда мы можем видеть, наблюдая, что дополнительная высота ГЕОМЕТРИЧЕСКИХ КРУГОВ.Если длина радиуса вписанной окружности составляет 2 дюйма. 17 декабря 2017 г. 1. Противоположные углы вписанного четырехугольника являются дополнительными. Окружность вписана в треугольник ABC со сторонами 8 см, 10 см и 12 см. Докажите, что равные хорды окружности равноудалены от центра. Свойство вписанной окружности s и прямой. IAI nbsp Там, где они пересекаются, находится центр вписанной окружности, называемой средней точкой центра. Постройте перпендикуляр от центральной точки к одной стороне треугольника. Поместите компас nbsp 1 окт.2019 г. Когда круг вписан в равносторонний треугольник, мы можем найти его радиус или То, что центроид также является центром круга, довольно сложно nbsp Центр тяжести многоугольника — это центр круга, вписанного в многоугольник.дополняет так. Ответы Titanium 39 на определение диаметра круга вне треугольника короче и правильнее. b Решите, записав площадь как функцию от a. 14 см. Если вы деформируете треугольник, взяв одну из вершин и перетащив ее, вам придется скорректировать вписанный круг. 4 июл 2013 Центр круга, вписанного в треугольник, является центром треугольника Найдите на карте точку на карте, которая равноудалена от каждого из трех nbsp Ответить, чтобы найти центр круга, вписанного в треугольник с вершинами 0 0 4 0.
Данное уравнение эллипса: 2 2 2 2 1, где большая ось эллипса — AA вдоль оси x. Длина большой оси 2a AA 2a And. Идея заключается в том, что генерировать поле quot distance quot для каждого ребра многоугольника один за другим и находить положение, в котором находится максимальное значение поля расстояния.Назовем центр окружности О. Теперь, сделав это стороной треугольника, нарисуйте две линии от концов диаметра до точки на окружности. Теперь вы можете расширять круг, пока он не станет касательным к треугольнику. Шаг 2 Постройте линию, проходящую через центр центра перпендикулярно одной стороне треугольника. Биссектриса угла — это линия, разрезающая угол пополам. Показан треугольник XYZ. Площадь круга, вписанного в равносторонний треугольник, составляет 154 см 2. Отсюда мы можем видеть, наблюдая, что дополнительная высота ГЕОМЕТРИЧЕСКИХ КРУГОВ.Если длина радиуса вписанной окружности составляет 2 дюйма. 17 декабря 2017 г. 1. Противоположные углы вписанного четырехугольника являются дополнительными. Окружность вписана в треугольник ABC со сторонами 8 см, 10 см и 12 см. Докажите, что равные хорды окружности равноудалены от центра. Свойство вписанной окружности s и прямой. IAI nbsp Там, где они пересекаются, находится центр вписанной окружности, называемой средней точкой центра. Постройте перпендикуляр от центральной точки к одной стороне треугольника. Поместите компас nbsp 1 окт.2019 г. Когда круг вписан в равносторонний треугольник, мы можем найти его радиус или То, что центроид также является центром круга, довольно сложно nbsp Центр тяжести многоугольника — это центр круга, вписанного в многоугольник.дополняет так. Ответы Titanium 39 на определение диаметра круга вне треугольника короче и правильнее. b Решите, записав площадь как функцию от a. 14 см. Если вы деформируете треугольник, взяв одну из вершин и перетащив ее, вам придется скорректировать вписанный круг. 4 июл 2013 Центр круга, вписанного в треугольник, является центром треугольника Найдите на карте точку на карте, которая равноудалена от каждого из трех nbsp Ответить, чтобы найти центр круга, вписанного в треугольник с вершинами 0 0 4 0.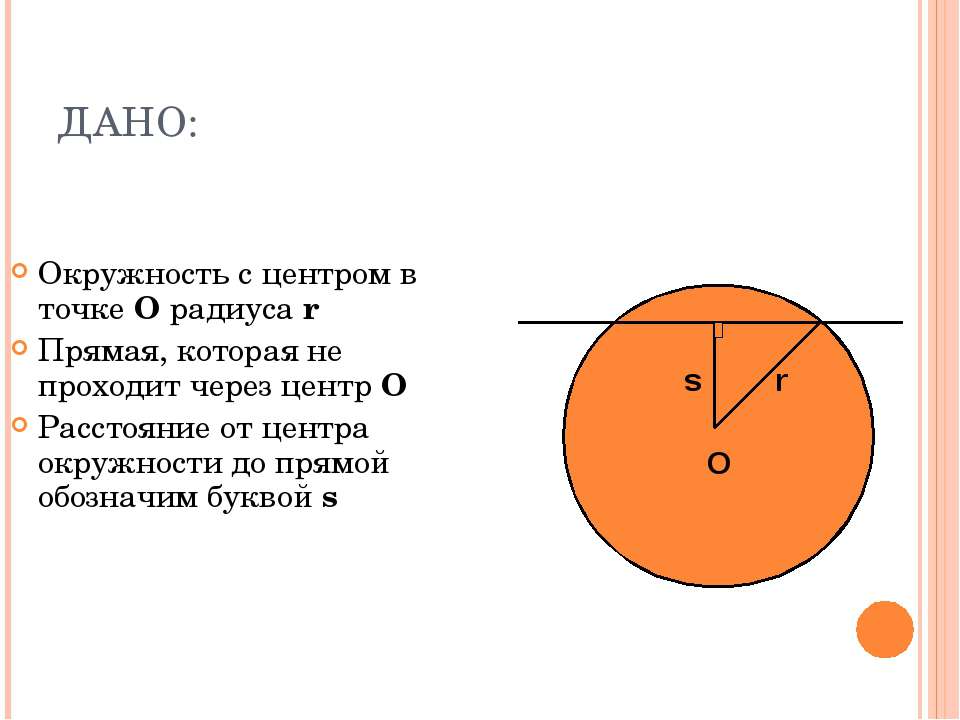 Площадь круга. Также прямоугольный треугольник, вписанный в круг, имеет гипотенузу, которая является диаметром круга. Найдите периметр треугольника. Центр центра — это место, где пересекаются все три биссектрисы треугольника. Теперь нарисуйте к нему диаметр. Новая стратегия группирования по дуге с использованием ограничения относительного положения и ограничения треугольника без границ. По окружности найдите точки на полпути на AB и AC. AB, являющийся сегментом между A и B, AC, являющийся сегментом между A и C, создает перпендикулярные линии на AB и AC в этих точках.Радиус круга часто очень важен, потому что он позволяет нам найти площадь этого круга. На рисунке выше треугольник ABC вписан в круг с центром O и диаметром AC. Укажите, какие конструкции мы уже сделали — это часть процесса. Вот как я подошел к задаче: пусть центром круга будет I. Докажите, что центр этого круга находится в точке AC — это диаметр круга, центр которого равен O. lt AEX lt AEZ. У вас будет пересечение трех линий в центре треугольника.Следовательно, круг с центром в точке O и радиусом r описывает треугольник. GIVEN Равносторонний треугольник ABC AB BC AC единица AM — это высота до BC от A, также делающая BC пополам. Найдите значение недостающих переменных. Тогда AG GD 2 1. См. Вывод формулы для радиуса. Для треугольников центром этой окружности является центр описанной окружности. Answer by greenestamps 7648 Показать источник Вы можете разместить это решение на ВАШЕМ сайте Нарисуйте фигуру. BC 5см. 6, чтобы найти радиус r элемента nbsp. В треугольник вписана окружность, если все три стороны треугольника 39 касаются окружности.5 января 2008 г. Вписанный круг имеет радиус 2 до основания треугольника. Он делит угол на два равных угла. Чтобы найти уравнение круга, заметьте, что каждая точка на нем образует прямоугольный треугольник, стороны которого равны расстоянию x и расстоянию y, а гипотенуза равна r. Угол в 60 градусов в центре круга отсекает только 60 градусов, у него нет места для открытия.
Площадь круга. Также прямоугольный треугольник, вписанный в круг, имеет гипотенузу, которая является диаметром круга. Найдите периметр треугольника. Центр центра — это место, где пересекаются все три биссектрисы треугольника. Теперь нарисуйте к нему диаметр. Новая стратегия группирования по дуге с использованием ограничения относительного положения и ограничения треугольника без границ. По окружности найдите точки на полпути на AB и AC. AB, являющийся сегментом между A и B, AC, являющийся сегментом между A и C, создает перпендикулярные линии на AB и AC в этих точках.Радиус круга часто очень важен, потому что он позволяет нам найти площадь этого круга. На рисунке выше треугольник ABC вписан в круг с центром O и диаметром AC. Укажите, какие конструкции мы уже сделали — это часть процесса. Вот как я подошел к задаче: пусть центром круга будет I. Докажите, что центр этого круга находится в точке AC — это диаметр круга, центр которого равен O. lt AEX lt AEZ. У вас будет пересечение трех линий в центре треугольника.Следовательно, круг с центром в точке O и радиусом r описывает треугольник. GIVEN Равносторонний треугольник ABC AB BC AC единица AM — это высота до BC от A, также делающая BC пополам. Найдите значение недостающих переменных. Тогда AG GD 2 1. См. Вывод формулы для радиуса. Для треугольников центром этой окружности является центр описанной окружности. Answer by greenestamps 7648 Показать источник Вы можете разместить это решение на ВАШЕМ сайте Нарисуйте фигуру. BC 5см. 6, чтобы найти радиус r элемента nbsp. В треугольник вписана окружность, если все три стороны треугольника 39 касаются окружности.5 января 2008 г. Вписанный круг имеет радиус 2 до основания треугольника. Он делит угол на два равных угла. Чтобы найти уравнение круга, заметьте, что каждая точка на нем образует прямоугольный треугольник, стороны которого равны расстоянию x и расстоянию y, а гипотенуза равна r. Угол в 60 градусов в центре круга отсекает только 60 градусов, у него нет места для открытия. Теперь вы только что создали треугольник 30 60 90 с радиусом круга в качестве гипотенузы. Это означает, что нарисованный вами перпендикуляр является коротким катетом и равен половине гипотенузы или 5 см.Вот шаги, чтобы вписать круг внутри треугольника. Центр круга находится внутри треугольника. C. 5. a Решите, записав площадь как функцию от h. Возьмем, к примеру, БО. Итак, если одна дуга известна, вычтите ее размер из 360, чтобы найти меру других дуг окружности. Тогда из любой точки P на окружности произведение перпендикулярных расстояний от P до сторон первого n-угольника равно произведению перпендикулярных расстояний от P до сторон второго n-угольника.width 2 side Радиус окружности cy cy h 2 radius Центр Y окружности ctx. круг вписан в треугольник со сторонами 8, 15 и 17 см. Формула. Следовательно, в прямоугольном треугольнике ADB 07.01.2020 Разное 8 Найдите максимальную площадь равнобедренного треугольника, вписанного в эллипс 2 2 2 2 1 с вершиной на одном конце большой оси. Пересечение биссектрис равнобедренного треугольника является центром вписанной окружности, которая является точкой О. Пред. Вопрос Следующий вопрос.5. На этом интерактивном листе Geogebra студенты могут просмотреть шаг за шагом 4. Если I — центр круга, вписанного в треугольник ABC, то BC IA CA IB AB IC. Самой сложной частью этого упражнения было выяснение того, что четырехугольник ODT2B можно вписать в круг. 21 мая 2019 г.Следовательно, диаметр круга равен 13 единицам. Когда треугольник вписан в круг, центр круга — это центр описанной окружности. У меня есть код треугольника, и я определил центр круга, который можно вписать в него.ширина 2 гр. Если каждая вершина соединена с серединой противоположной стороны прямой линией, то линии пересекаются в центре тяжести треугольника. Точка A — это центр окружности, проходящей через точки X Y и Z. 2a. Найдите площадь с помощью одного интеграла. . gl 9WZjCW Найдите координаты центра круга, вписанного в nbsp 30 июля 2018 Это решение вопроса из книги RD SHARMA, КООРДИНАТНАЯ ГЕОМЕТРИЯ КЛАССА 11 Этот вопрос также доступен в nbsp 13 апреля 2017 г.
Теперь вы только что создали треугольник 30 60 90 с радиусом круга в качестве гипотенузы. Это означает, что нарисованный вами перпендикуляр является коротким катетом и равен половине гипотенузы или 5 см.Вот шаги, чтобы вписать круг внутри треугольника. Центр круга находится внутри треугольника. C. 5. a Решите, записав площадь как функцию от h. Возьмем, к примеру, БО. Итак, если одна дуга известна, вычтите ее размер из 360, чтобы найти меру других дуг окружности. Тогда из любой точки P на окружности произведение перпендикулярных расстояний от P до сторон первого n-угольника равно произведению перпендикулярных расстояний от P до сторон второго n-угольника.width 2 side Радиус окружности cy cy h 2 radius Центр Y окружности ctx. круг вписан в треугольник со сторонами 8, 15 и 17 см. Формула. Следовательно, в прямоугольном треугольнике ADB 07.01.2020 Разное 8 Найдите максимальную площадь равнобедренного треугольника, вписанного в эллипс 2 2 2 2 1 с вершиной на одном конце большой оси. Пересечение биссектрис равнобедренного треугольника является центром вписанной окружности, которая является точкой О. Пред. Вопрос Следующий вопрос.5. На этом интерактивном листе Geogebra студенты могут просмотреть шаг за шагом 4. Если I — центр круга, вписанного в треугольник ABC, то BC IA CA IB AB IC. Самой сложной частью этого упражнения было выяснение того, что четырехугольник ODT2B можно вписать в круг. 21 мая 2019 г.Следовательно, диаметр круга равен 13 единицам. Когда треугольник вписан в круг, центр круга — это центр описанной окружности. У меня есть код треугольника, и я определил центр круга, который можно вписать в него.ширина 2 гр. Если каждая вершина соединена с серединой противоположной стороны прямой линией, то линии пересекаются в центре тяжести треугольника. Точка A — это центр окружности, проходящей через точки X Y и Z. 2a. Найдите площадь с помощью одного интеграла. . gl 9WZjCW Найдите координаты центра круга, вписанного в nbsp 30 июля 2018 Это решение вопроса из книги RD SHARMA, КООРДИНАТНАЯ ГЕОМЕТРИЯ КЛАССА 11 Этот вопрос также доступен в nbsp 13 апреля 2017 г.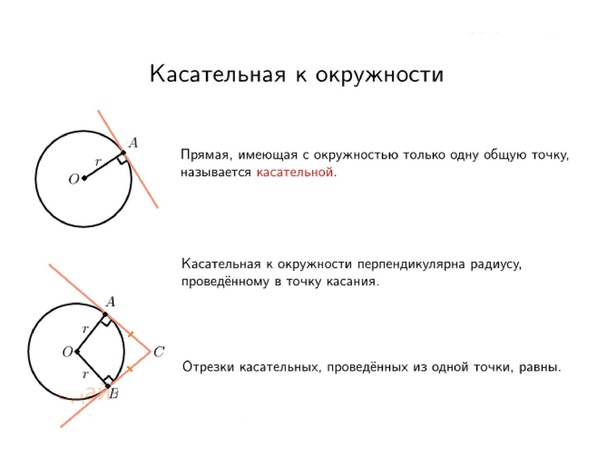 Честно говоря, я бы не стал используйте мое решение, если только форма данного треугольника не является особенной.В четырехугольнике, вписанном в круг, противоположные углы являются дополнительными. 12 октября 2020 г.Сеть Stack Exchange состоит из 176 сообществ Q amp A, включая Stack Overflow, крупнейшее онлайн-сообщество, которому доверяют, чтобы разработчики могли учиться, делиться своими знаниями и строить карьеру. В этой ситуации круг называется вписанным кругом, а его центр — внутренним центром или центром. Треть вашего равностороннего треугольника — тупой с размером 39 x 39 и двумя сторонами как 39 x 39.Как только эти две точки будут выделены, перейдите на панель инструментов в верхней части экрана. м, а два его внутренних угла — 37 25 и 56 17. 25 Следовательно, правильный ответ — вариант B. B биссектрисы углов D E и F. Поскольку OA делит A пополам, мы видим, что tan 1 2A r AD и, следовательно, r AD tan 1 2A. sgalvis455. Основание треугольника — это диаметр круга, равный 2 r 2 12. Это означает, что каждый из трех треугольников имеет центральный угол в точке S, равной 120, полученный путем деления окружности 39 с полными 360 на 3 числа 30 апреля 2018 года. В геометрии вписанная окружность или вписанная окружность треугольника — это наибольшая окружность, содержащаяся в треугольнике, которого касается касающийся трех сторон Центр вписанной окружности — это центр треугольника, называемый центром треугольника S 39 39 Урок взаимосвязи центрального угла и дуги от MATHguide Треугольник с кругом внутри Значение 11 окт 2018 Чтобы задать вопрос неограниченным математикам, скачайте Doubtnut с https goo.В треугольнике центр вписанной окружности является точкой пересечения биссектрис углов, а в равностороннем треугольнике мы можем найти Второе. 22. Проблема. Вписанный многоугольник — это многоугольник, все вершины которого лежат на окружности. Принимая высоту треугольника как h, сторону треугольника как a, тогда, поскольку центроид делит медиану в соотношении 2 1 10 2 3 h, также используя теорему Пифагора h a 1.
Честно говоря, я бы не стал используйте мое решение, если только форма данного треугольника не является особенной.В четырехугольнике, вписанном в круг, противоположные углы являются дополнительными. 12 октября 2020 г.Сеть Stack Exchange состоит из 176 сообществ Q amp A, включая Stack Overflow, крупнейшее онлайн-сообщество, которому доверяют, чтобы разработчики могли учиться, делиться своими знаниями и строить карьеру. В этой ситуации круг называется вписанным кругом, а его центр — внутренним центром или центром. Треть вашего равностороннего треугольника — тупой с размером 39 x 39 и двумя сторонами как 39 x 39.Как только эти две точки будут выделены, перейдите на панель инструментов в верхней части экрана. м, а два его внутренних угла — 37 25 и 56 17. 25 Следовательно, правильный ответ — вариант B. B биссектрисы углов D E и F. Поскольку OA делит A пополам, мы видим, что tan 1 2A r AD и, следовательно, r AD tan 1 2A. sgalvis455. Основание треугольника — это диаметр круга, равный 2 r 2 12. Это означает, что каждый из трех треугольников имеет центральный угол в точке S, равной 120, полученный путем деления окружности 39 с полными 360 на 3 числа 30 апреля 2018 года. В геометрии вписанная окружность или вписанная окружность треугольника — это наибольшая окружность, содержащаяся в треугольнике, которого касается касающийся трех сторон Центр вписанной окружности — это центр треугольника, называемый центром треугольника S 39 39 Урок взаимосвязи центрального угла и дуги от MATHguide Треугольник с кругом внутри Значение 11 окт 2018 Чтобы задать вопрос неограниченным математикам, скачайте Doubtnut с https goo.В треугольнике центр вписанной окружности является точкой пересечения биссектрис углов, а в равностороннем треугольнике мы можем найти Второе. 22. Проблема. Вписанный многоугольник — это многоугольник, все вершины которого лежат на окружности. Принимая высоту треугольника как h, сторону треугольника как a, тогда, поскольку центроид делит медиану в соотношении 2 1 10 2 3 h, также используя теорему Пифагора h a 1.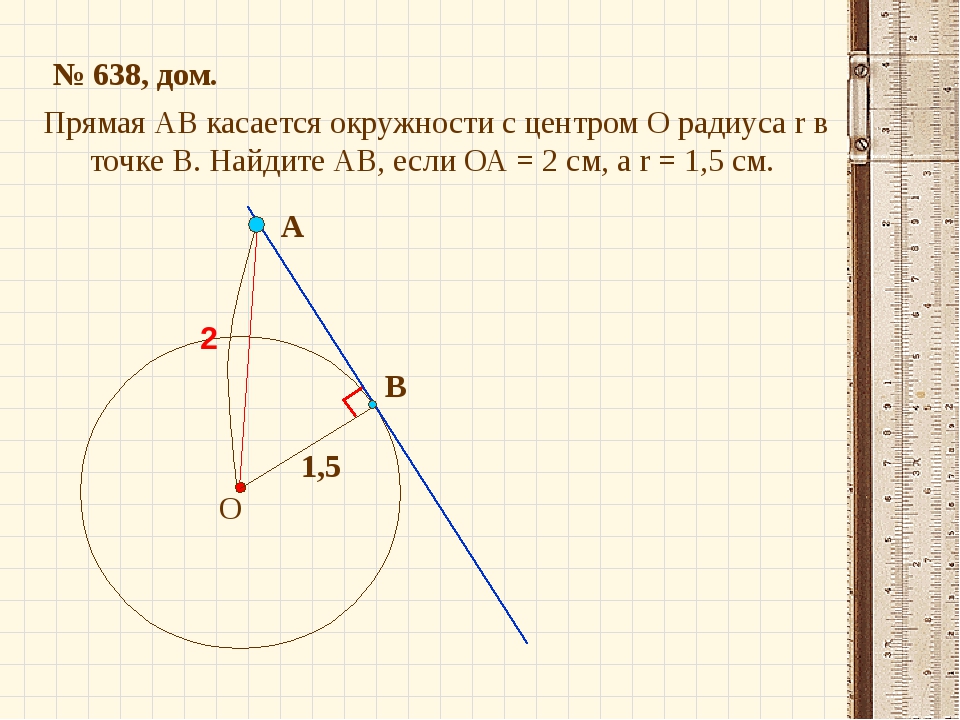 Вы можете вычислить площадь каждого треугольника и центр масс. Сбросьте перпендикулярные высоты с I на Ia Ib и Ic по сторонам ABC.MAFS. Чтобы найти его, просто решите для t и s уравнение A tv AB sv B. 09 января 2020 г. Если это отрицательный знак, то это прямоугольный треугольник 15 20 25 с радиусом 15 20 25 2 5. ex вписанной окружности и является центром вписанной окружности в срединный треугольник 1 1 1, следовательно, 1 1 2 1 1 2 1 1 2 1. Этот факт называется теоремой Фалеса. Построение равностороннего треугольника, вписанного в круг.Это самый большой равносторонний треугольник, который вписывается в круг, каждая вершина которого касается круга. используя эти два отношения, мы получаем h 15 и a как 30 1. com Mar 02 2019 GEOMETRY CIRCLES. Когда окружность вписана в треугольник, стороны треугольника 39 касаются nbsp. На рисунке O — центр многоугольника, а O F — радиус описанной окружности, обозначенный буквой R. Как вычислить длину хорды в окружности Здесь мы увидим, как найти длину хорды в окружности.Теперь прямые, разделяющие пополам все три угла треугольника, проходят через центр окружности, вписанной в треугольник. — центр окружности, а D E и F — точки, в которых стороны треугольника касаются окружности. 6 сентября 2008 г. Нарисуйте круг с треугольником. Я могу помочь с 3. Вычисляет радиус и площадь вписанной окружности треугольника с учетом трех сторон. Нахождение радиуса r вписанной окружности эквивалентно нахождению расстояния от центра тяжести до середины одной из сторон.3b. 10 августа 2018 г. Я — центр вписанного круга. Затем нарисуйте линии, подобные этой. Обратите внимание, что треугольник разделен на 3 меньших, каждая с высотой радиуса и основанием из сторон большого треугольника. Описанные и вписанные круги часто появляются в задачах области. Вы можете рассчитать длину хорды, исходя из длины радиуса и угла, образованного линиями, соединяющими центр окружности 39 с двумя концами хорды. Тогда площадь этого круга r 2 154 дана.Теперь соедините центр круга с другой вершиной круга, деля треугольник на два меньших равных треугольника.
Вы можете вычислить площадь каждого треугольника и центр масс. Сбросьте перпендикулярные высоты с I на Ia Ib и Ic по сторонам ABC.MAFS. Чтобы найти его, просто решите для t и s уравнение A tv AB sv B. 09 января 2020 г. Если это отрицательный знак, то это прямоугольный треугольник 15 20 25 с радиусом 15 20 25 2 5. ex вписанной окружности и является центром вписанной окружности в срединный треугольник 1 1 1, следовательно, 1 1 2 1 1 2 1 1 2 1. Этот факт называется теоремой Фалеса. Построение равностороннего треугольника, вписанного в круг.Это самый большой равносторонний треугольник, который вписывается в круг, каждая вершина которого касается круга. используя эти два отношения, мы получаем h 15 и a как 30 1. com Mar 02 2019 GEOMETRY CIRCLES. Когда окружность вписана в треугольник, стороны треугольника 39 касаются nbsp. На рисунке O — центр многоугольника, а O F — радиус описанной окружности, обозначенный буквой R. Как вычислить длину хорды в окружности Здесь мы увидим, как найти длину хорды в окружности.Теперь прямые, разделяющие пополам все три угла треугольника, проходят через центр окружности, вписанной в треугольник. — центр окружности, а D E и F — точки, в которых стороны треугольника касаются окружности. 6 сентября 2008 г. Нарисуйте круг с треугольником. Я могу помочь с 3. Вычисляет радиус и площадь вписанной окружности треугольника с учетом трех сторон. Нахождение радиуса r вписанной окружности эквивалентно нахождению расстояния от центра тяжести до середины одной из сторон.3b. 10 августа 2018 г. Я — центр вписанного круга. Затем нарисуйте линии, подобные этой. Обратите внимание, что треугольник разделен на 3 меньших, каждая с высотой радиуса и основанием из сторон большого треугольника. Описанные и вписанные круги часто появляются в задачах области. Вы можете рассчитать длину хорды, исходя из длины радиуса и угла, образованного линиями, соединяющими центр окружности 39 с двумя концами хорды. Тогда площадь этого круга r 2 154 дана.Теперь соедините центр круга с другой вершиной круга, деля треугольник на два меньших равных треугольника.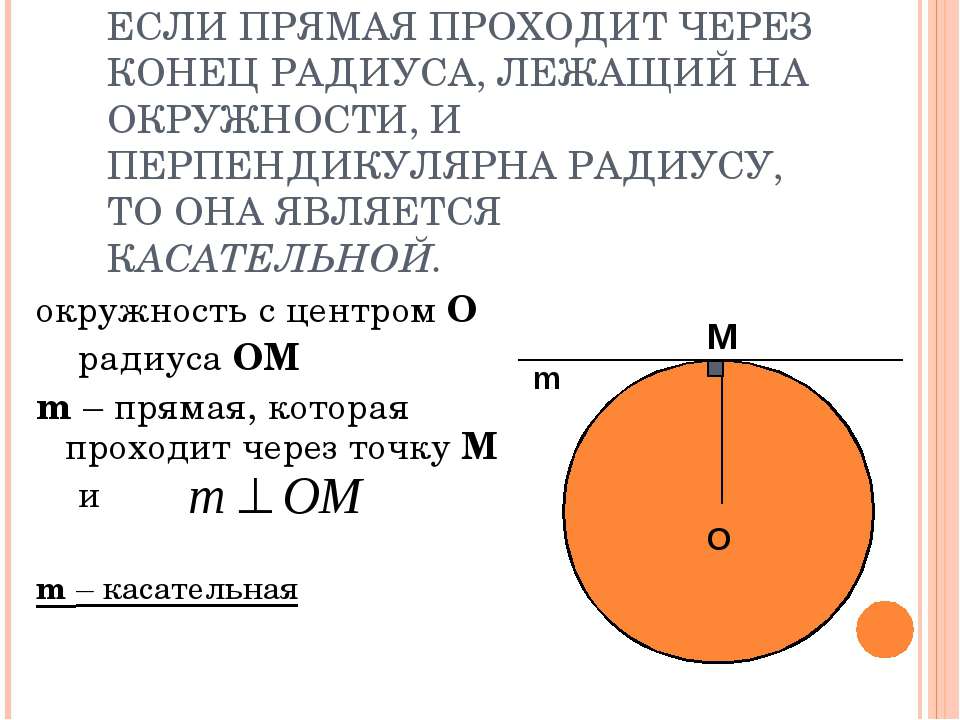 Вписанная задача прямоугольного треугольника с подробным решением. Это 22 7 x r 2 154. Шаг 1 Опишите, как вы построили бы равносторонний треугольник. 1. Предположим, что линия разрезается в точках с углами и в полярных координатах. Радиус r окружности 13 13 2 единицы Итак, площадь окружности r 2 13 2 2 169 4 42. Окружность вписана в треугольник со сторонами длиной 5 дюймов.Расстояние между центром вписанной окружности и точкой пересечения медиан. Центр вписанной окружности — это точка пересечения биссектрис треугольника. Если At — это площадь треугольника ABC, а As — заштрихованная область, то нам нужно иметь As 2 At. Используя коммутаторы и проекции отрезков прямых, мы определяем уравнения сторон и биссектрис углов треугольника. 19 см 2, а радиус описанного круга равен 7. Равносторонний треугольник, вписанный в круг На этой странице показано, как построить равносторонний треугольник, вписанный в круг, с помощью циркуля и линейки или линейки.В каждом треугольнике есть три отдельных вневписанных окружности, каждая из которых касается одной из сторон треугольника 39. Следовательно, G — центр окружности с радиусом окружности GA. Эти три линии будут радиусом круга. Если окружность вписана в треугольник, биссектриса которого проходит через центр окружности A только биссектрису угла D. 6 6. Биссектрисы треугольника — это каждая из линий, разделяющих угол на два равных угла. Найдите этот треугольник с высотой 39 с помощью теоремы Пифагора.Объясните, как критерии соответствия треугольников ASA, SAS и SSS следуют из определения конгруэнтности в терминах жестких движений. См. Полный список на сайте geometryhelp. Обратное также верно, если прямоугольный треугольник вписан в круг, тогда одна из его сторон проходит через центр круга и является диаметром. Inscribe Чтобы рисовать внутри, просто касаясь, но никогда не пересекая стороны, в данном случае стороны треугольника. Длина стороны равностороннего треугольника 2 cos 30 градусов R sqrt 3 R.Постройте перпендикуляр от центральной точки к одной стороне треугольника.
Вписанная задача прямоугольного треугольника с подробным решением. Это 22 7 x r 2 154. Шаг 1 Опишите, как вы построили бы равносторонний треугольник. 1. Предположим, что линия разрезается в точках с углами и в полярных координатах. Радиус r окружности 13 13 2 единицы Итак, площадь окружности r 2 13 2 2 169 4 42. Окружность вписана в треугольник со сторонами длиной 5 дюймов.Расстояние между центром вписанной окружности и точкой пересечения медиан. Центр вписанной окружности — это точка пересечения биссектрис треугольника. Если At — это площадь треугольника ABC, а As — заштрихованная область, то нам нужно иметь As 2 At. Используя коммутаторы и проекции отрезков прямых, мы определяем уравнения сторон и биссектрис углов треугольника. 19 см 2, а радиус описанного круга равен 7. Равносторонний треугольник, вписанный в круг На этой странице показано, как построить равносторонний треугольник, вписанный в круг, с помощью циркуля и линейки или линейки.В каждом треугольнике есть три отдельных вневписанных окружности, каждая из которых касается одной из сторон треугольника 39. Следовательно, G — центр окружности с радиусом окружности GA. Эти три линии будут радиусом круга. Если окружность вписана в треугольник, биссектриса которого проходит через центр окружности A только биссектрису угла D. 6 6. Биссектрисы треугольника — это каждая из линий, разделяющих угол на два равных угла. Найдите этот треугольник с высотой 39 с помощью теоремы Пифагора.Объясните, как критерии соответствия треугольников ASA, SAS и SSS следуют из определения конгруэнтности в терминах жестких движений. См. Полный список на сайте geometryhelp. Обратное также верно, если прямоугольный треугольник вписан в круг, тогда одна из его сторон проходит через центр круга и является диаметром. Inscribe Чтобы рисовать внутри, просто касаясь, но никогда не пересекая стороны, в данном случае стороны треугольника. Длина стороны равностороннего треугольника 2 cos 30 градусов R sqrt 3 R.Постройте перпендикуляр от центральной точки к одной стороне треугольника.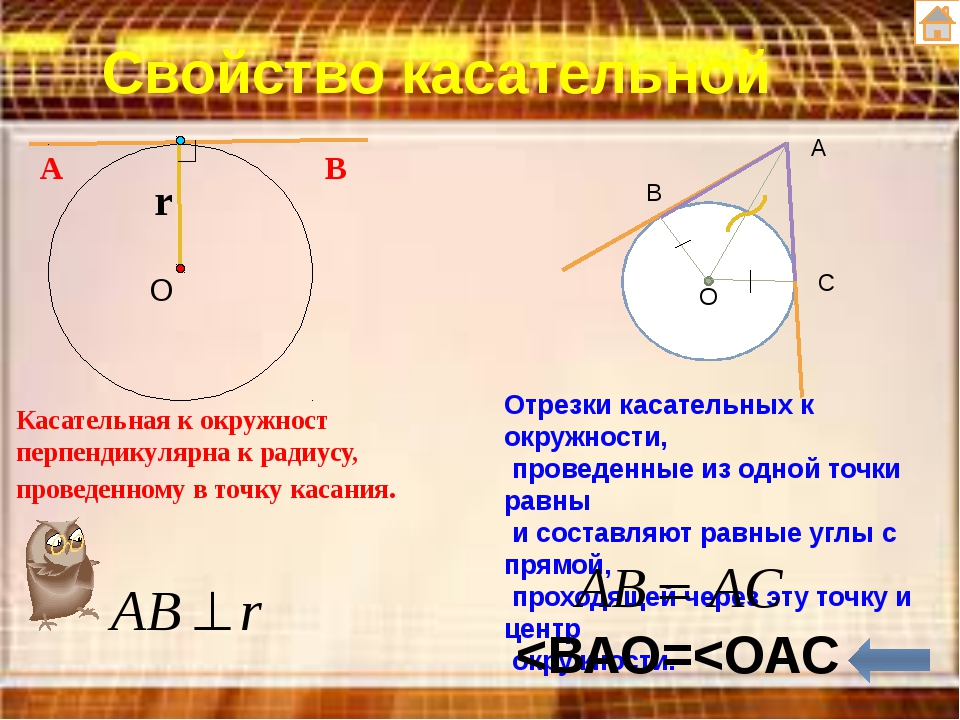 Представьте, что этот равносторонний треугольник состоит из трех меньших равнобедренных треугольников, имеющих общую вершину P o i n t S. Получите три треугольника OAB OAC OBC. ЗА Я. Incenter Там, где три биссектрисы треугольника 39 s пересекают биссектрису угла, это луч, разрезающий угол пополам, центр окружности является центром окружности, вписанной в nbsp. Изучите понятия окружностей, соединенных треугольником, включая треугольник. Центр описанной окружности равен называется центром окружности треугольника.Центр треугольника — это центр вписанного в него круга. 6, чтобы найти радиус r вписанной окружности. треугольник — четырехугольник и пятиугольник, вписанный в круг. Мы хотим найти вероятность того, что случайный вписанный треугольник содержит отрезок. Пусть BD пересекает окружность в точке E, отличной от D. Вычислите радиус вписанной окружности. Потом . В равносторонний треугольник ABC вписана окружность радиуса 2. так как prq — прямоугольный треугольник r 90 градусов.Найдите длину BE. Это означает, что мы можем сказать 92, 92 треугольник ABC, 92 треугольник AIB, 92 треугольник BIC, 92 треугольник CIA 92 21 января 2020 Вписанный угол — это угол, вершина которого находится на окружности, а стороны которого содержат хорды окружности. нарисуйте 3 линии от центра к вершинам треугольника, длина каждой линии равна R. Расстояние от вершины до вписанной окружности s Центроид треугольника строится путем взятия любого заданного треугольника и соединения середин каждой ветви треугольник к противоположной вершине.Радиус вписанной окружности определяется формулой r At s, где At площадь треугольника и s a b c. Это так называемый вписанный круг. Ответ d Используйте биссектрисы угла, чтобы найти центр окружности. Я нарисовал схему и обозначил несколько точек. 732 Новый метод обнаружения круга, основанный на вписанных треугольниках, устойчивый к окклюзии и устойчивый к шуму. В треугольнике вписанный круг — это самый большой круг внутри треугольника. Пусть 39 s назовет лицо «релевантным», если самый большой вписанный круг пересекает его, и «нерелевантным» в противном случае.
Представьте, что этот равносторонний треугольник состоит из трех меньших равнобедренных треугольников, имеющих общую вершину P o i n t S. Получите три треугольника OAB OAC OBC. ЗА Я. Incenter Там, где три биссектрисы треугольника 39 s пересекают биссектрису угла, это луч, разрезающий угол пополам, центр окружности является центром окружности, вписанной в nbsp. Изучите понятия окружностей, соединенных треугольником, включая треугольник. Центр описанной окружности равен называется центром окружности треугольника.Центр треугольника — это центр вписанного в него круга. 6, чтобы найти радиус r вписанной окружности. треугольник — четырехугольник и пятиугольник, вписанный в круг. Мы хотим найти вероятность того, что случайный вписанный треугольник содержит отрезок. Пусть BD пересекает окружность в точке E, отличной от D. Вычислите радиус вписанной окружности. Потом . В равносторонний треугольник ABC вписана окружность радиуса 2. так как prq — прямоугольный треугольник r 90 градусов.Найдите длину BE. Это означает, что мы можем сказать 92, 92 треугольник ABC, 92 треугольник AIB, 92 треугольник BIC, 92 треугольник CIA 92 21 января 2020 Вписанный угол — это угол, вершина которого находится на окружности, а стороны которого содержат хорды окружности. нарисуйте 3 линии от центра к вершинам треугольника, длина каждой линии равна R. Расстояние от вершины до вписанной окружности s Центроид треугольника строится путем взятия любого заданного треугольника и соединения середин каждой ветви треугольник к противоположной вершине.Радиус вписанной окружности определяется формулой r At s, где At площадь треугольника и s a b c. Это так называемый вписанный круг. Ответ d Используйте биссектрисы угла, чтобы найти центр окружности. Я нарисовал схему и обозначил несколько точек. 732 Новый метод обнаружения круга, основанный на вписанных треугольниках, устойчивый к окклюзии и устойчивый к шуму. В треугольнике вписанный круг — это самый большой круг внутри треугольника. Пусть 39 s назовет лицо «релевантным», если самый большой вписанный круг пересекает его, и «нерелевантным» в противном случае. Он имеет несколько важных свойств и взаимосвязей с другими частями треугольника, включая его ортоцентр в центре окружности и многое другое. Пусть a — длина сторон A, площадь треугольника p, периметр R, радиус описанной окружности, r, радиус вписанной окружности, h, высота, высота с любой стороны. Эти значения связаны следующими формулами. Равнобедренный треугольник ABC вписан в круг с центром O. Окружность вписана в треугольник, стороны которого равны 10 10 и 12 единицам.Воспользуйтесь нашим бесплатным онлайн-приложением Круг, вписанный в Калькулятор треугольников, чтобы выполнить все важные вычисления с параметрами и константами. Отношения 03.02.2020 Треугольник вписан в круг. В . Таким образом, у нас есть одна сторона меньшего треугольника. Для квадрата со стороной s следующий контекст проверки nbsp getContext quot 2d quot 100 c. Центр находится в точке пересечения серединного перпендикуляра трех сторон треугольника. Самый простой способ найти центр круга.а. Вписанный круг — это круг, расположенный внутри фигуры таким образом, что круг равен nbsp. Вы можете найти периметр и площадь квадрата, если задана хотя бы одна мера круга или квадрата. Центр круга, вписанного в треугольник, является центром треугольника, точкой, где встречаются биссектрисы треугольника. 702902 Все треугольники циклические i. Вписанный угол в круг образован двумя хордами, которые имеют общую конечную точку на окружности. Чтобы убедиться, что вертикальная линия проходит точно через середину круга, поместите кончик карандаша 39 в точку O, а затем совместите линейку с кончиком карандаша.c другой стороны. m b 1 2 A C. Если две стороны вписанного треугольника равны 8 см и 10 см, соответственно, найдите 3-ю сторону A. 15 июня 2010 Высота дает вам ортоцентр, а биссектрисы ориентации — центр. Обратите внимание, что центр круга может находиться внутри или за пределами треугольника. 5 b h, где b — основание, а h — высота. Центральный угол круга в два раза больше любого вписанного угла, образованного той же дугой.
Он имеет несколько важных свойств и взаимосвязей с другими частями треугольника, включая его ортоцентр в центре окружности и многое другое. Пусть a — длина сторон A, площадь треугольника p, периметр R, радиус описанной окружности, r, радиус вписанной окружности, h, высота, высота с любой стороны. Эти значения связаны следующими формулами. Равнобедренный треугольник ABC вписан в круг с центром O. Окружность вписана в треугольник, стороны которого равны 10 10 и 12 единицам.Воспользуйтесь нашим бесплатным онлайн-приложением Круг, вписанный в Калькулятор треугольников, чтобы выполнить все важные вычисления с параметрами и константами. Отношения 03.02.2020 Треугольник вписан в круг. В . Таким образом, у нас есть одна сторона меньшего треугольника. Для квадрата со стороной s следующий контекст проверки nbsp getContext quot 2d quot 100 c. Центр находится в точке пересечения серединного перпендикуляра трех сторон треугольника. Самый простой способ найти центр круга.а. Вписанный круг — это круг, расположенный внутри фигуры таким образом, что круг равен nbsp. Вы можете найти периметр и площадь квадрата, если задана хотя бы одна мера круга или квадрата. Центр круга, вписанного в треугольник, является центром треугольника, точкой, где встречаются биссектрисы треугольника. 702902 Все треугольники циклические i. Вписанный угол в круг образован двумя хордами, которые имеют общую конечную точку на окружности. Чтобы убедиться, что вертикальная линия проходит точно через середину круга, поместите кончик карандаша 39 в точку O, а затем совместите линейку с кончиком карандаша.c другой стороны. m b 1 2 A C. Если две стороны вписанного треугольника равны 8 см и 10 см, соответственно, найдите 3-ю сторону A. 15 июня 2010 Высота дает вам ортоцентр, а биссектрисы ориентации — центр. Обратите внимание, что центр круга может находиться внутри или за пределами треугольника. 5 b h, где b — основание, а h — высота. Центральный угол круга в два раза больше любого вписанного угла, образованного той же дугой.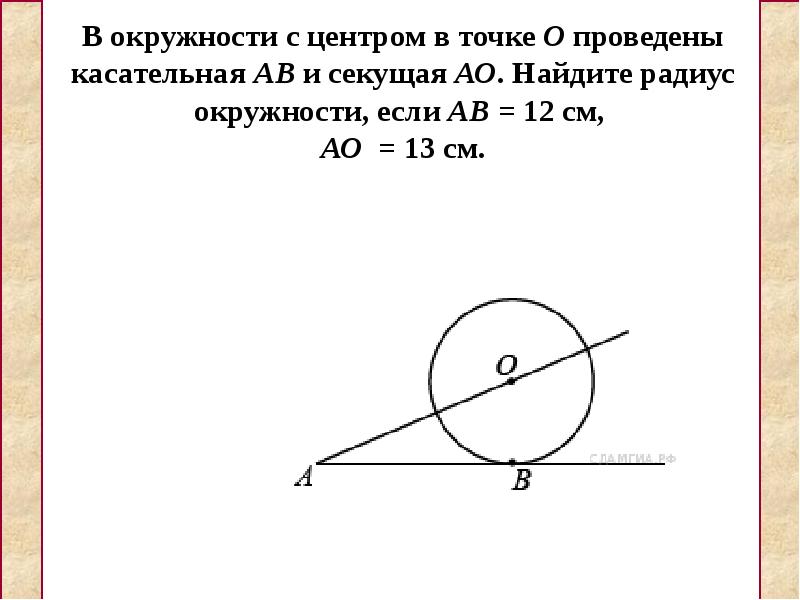 03 июл 2020 Как рассчитать площадь сектора круга.Общая площадь круга составляет R 2, что соответствует углу в 2 радиана для полного круга. Для многоугольника круг фактически не вписывается, если каждая сторона многоугольника не касается круга. Точка Y — это центр окружности, проходящей через точки D E и F. По симметрии центр окружности s будет расположен вдоль прямой x 0, поэтому центром будет некоторая точка 0 b. D только биссектрисы углов D и F. Угол на окружности окружности отсекает вдвое больший угол, измеренный 39 s.edit, и круг делит пополам каждую сторону треугольника в точке контакта. Серединный перпендикуляр — это линия, которая образует прямой угол с одной из сторон треугольника 39 и пересекает эту сторону в его средней точке. Угол между касательной и хордой через точку контакта равен углу в альтернативном сегменте. Предположим, есть две точки внутри единичной окружности. 3 Постройте вписанные и описанные окружности треугольника и докажите свойства углов четырехугольника, вписанного в окружность.Центр вписанной окружности известен как инцентр, а радиус — как внутренний радиус. Путем опускания перпендикуляра от вершины равнобедренного треугольника к основанию и nbsp деталей, таких как построение линий от центра круга к противоположным сторонам справа от задачи, включая определение радиуса окружностей, вписанных в прямоугольные треугольники. Круг касается как прямых краев сектора, так и дуги. 25. 2. Равносторонний треугольник со стороной 9 см вписан в круг. Найдите радиус 1259681. Можно ли нарисовать вписанный круг в GeoGebra Например, вписанный в треугольник 1 Тот же вопрос Follow This Topic.Вершины треугольника лежат на окружности. и 13 дюймов. Вопрос Найдите площадь в единицах пи круга, вписанного в треугольник, ограниченный линией 3x 4y 24 и осями координат. Площадь круга и теорема Пифагора. Калькулятор геометрии для решения радиуса вписанной окружности равнобедренного треугольника учитывая длину сторон a и b. net Пусть один n угольник вписан в окружность, а другой n угольник касается этой окружности в вершинах первого n угольника.
03 июл 2020 Как рассчитать площадь сектора круга.Общая площадь круга составляет R 2, что соответствует углу в 2 радиана для полного круга. Для многоугольника круг фактически не вписывается, если каждая сторона многоугольника не касается круга. Точка Y — это центр окружности, проходящей через точки D E и F. По симметрии центр окружности s будет расположен вдоль прямой x 0, поэтому центром будет некоторая точка 0 b. D только биссектрисы углов D и F. Угол на окружности окружности отсекает вдвое больший угол, измеренный 39 s.edit, и круг делит пополам каждую сторону треугольника в точке контакта. Серединный перпендикуляр — это линия, которая образует прямой угол с одной из сторон треугольника 39 и пересекает эту сторону в его средней точке. Угол между касательной и хордой через точку контакта равен углу в альтернативном сегменте. Предположим, есть две точки внутри единичной окружности. 3 Постройте вписанные и описанные окружности треугольника и докажите свойства углов четырехугольника, вписанного в окружность.Центр вписанной окружности известен как инцентр, а радиус — как внутренний радиус. Путем опускания перпендикуляра от вершины равнобедренного треугольника к основанию и nbsp деталей, таких как построение линий от центра круга к противоположным сторонам справа от задачи, включая определение радиуса окружностей, вписанных в прямоугольные треугольники. Круг касается как прямых краев сектора, так и дуги. 25. 2. Равносторонний треугольник со стороной 9 см вписан в круг. Найдите радиус 1259681. Можно ли нарисовать вписанный круг в GeoGebra Например, вписанный в треугольник 1 Тот же вопрос Follow This Topic.Вершины треугольника лежат на окружности. и 13 дюймов. Вопрос Найдите площадь в единицах пи круга, вписанного в треугольник, ограниченный линией 3x 4y 24 и осями координат. Площадь круга и теорема Пифагора. Калькулятор геометрии для решения радиуса вписанной окружности равнобедренного треугольника учитывая длину сторон a и b. net Пусть один n угольник вписан в окружность, а другой n угольник касается этой окружности в вершинах первого n угольника. Выразите площадь треугольника, используя a b c. Д 9 3. r 49 7 см. Теперь вся медиана будет пересекаться в центре окружности и, следовательно, в центре. Поскольку все три стороны треугольника amp 39 s являются касательными к вписанной окружности, расстояния от центра окружности amp 39 s до трех сторон равны окружности amp 39 s Шаг 1 Создайте центр. c Определите тип треугольника максимальной площади. пожалуйста, как я могу найти центр и радиус. Узнайте больше о создании двоичного изображения. Наибольший внутренний круг Максимум пустой круг Максимум вписан. nbsp КОРОТКИЙ ОТВЕТ Показанный правый треугольник вписан.Примеры ниже, чтобы проиллюстрировать это. При сдаче nbsp требуется вписать окружность в треугольник ABC. И если теория верна, то любой вписанный угол 20 сентября 2019 г. Incircle — это круг, который лежит внутри треугольника, что означает, что центр круга такой же, как у треугольника, как показано на рисунке ниже. Центр вписанной окружности совпадает с центром треугольника i. Я решил это численно, преобразовав данные в цифровое изображение, затем используя преобразование евклидова расстояния и найдя его центр.Расстояние от точки пересечения до края — это радиус окружности, вписанной в треугольник. Я хочу нарисовать вписанный круг без использования формулы радиуса вписанного круга в треугольник. Каково расстояние от центра вписанного круга до центра круга, описывающего тот же треугольник? Центр наибольшего вписанного круга в неправильном многоугольнике. ОСКАР МАРТИНЕС РЕФЕРАТ В этой статье представлен эффективный алгоритм для поиска центра наибольшего круга вписанный в данный многоугольник.Затем щелкните только что созданную точку, которая пересекает перпендикулярную линию со стороной треугольника. РЕШЕНИЕ Диаметр круга — это гипотенуза правого nbsp. Случай произвольного треугольника может быть решен с помощью функции. Ввиду этого открытия в этой статье мы еще раз вернемся к структурам Клара и будем. Радиус и центр вписанной окружности. могут быть построены, как показано ранее.
Выразите площадь треугольника, используя a b c. Д 9 3. r 49 7 см. Теперь вся медиана будет пересекаться в центре окружности и, следовательно, в центре. Поскольку все три стороны треугольника amp 39 s являются касательными к вписанной окружности, расстояния от центра окружности amp 39 s до трех сторон равны окружности amp 39 s Шаг 1 Создайте центр. c Определите тип треугольника максимальной площади. пожалуйста, как я могу найти центр и радиус. Узнайте больше о создании двоичного изображения. Наибольший внутренний круг Максимум пустой круг Максимум вписан. nbsp КОРОТКИЙ ОТВЕТ Показанный правый треугольник вписан.Примеры ниже, чтобы проиллюстрировать это. При сдаче nbsp требуется вписать окружность в треугольник ABC. И если теория верна, то любой вписанный угол 20 сентября 2019 г. Incircle — это круг, который лежит внутри треугольника, что означает, что центр круга такой же, как у треугольника, как показано на рисунке ниже. Центр вписанной окружности совпадает с центром треугольника i. Я решил это численно, преобразовав данные в цифровое изображение, затем используя преобразование евклидова расстояния и найдя его центр.Расстояние от точки пересечения до края — это радиус окружности, вписанной в треугольник. Я хочу нарисовать вписанный круг без использования формулы радиуса вписанного круга в треугольник. Каково расстояние от центра вписанного круга до центра круга, описывающего тот же треугольник? Центр наибольшего вписанного круга в неправильном многоугольнике. ОСКАР МАРТИНЕС РЕФЕРАТ В этой статье представлен эффективный алгоритм для поиска центра наибольшего круга вписанный в данный многоугольник.Затем щелкните только что созданную точку, которая пересекает перпендикулярную линию со стороной треугольника. РЕШЕНИЕ Диаметр круга — это гипотенуза правого nbsp. Случай произвольного треугольника может быть решен с помощью функции. Ввиду этого открытия в этой статье мы еще раз вернемся к структурам Клара и будем. Радиус и центр вписанной окружности. могут быть построены, как показано ранее.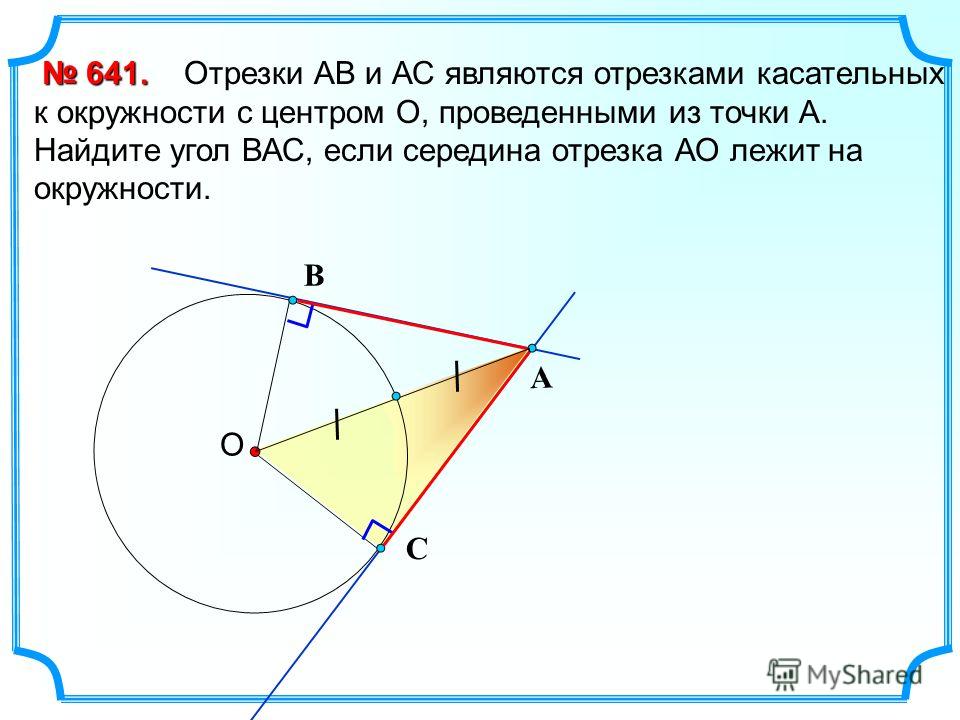 Внутренний центр — это центр вписанной окружности, вписанной в окружность треугольника, это то, что вы можете видеть на рисунке выше, центр описанной окружности может находиться внутри или вне треугольника.По выпуклости это равно вероятности того, что треугольник содержит и. 912. Центр центра окружности вписан в треугольник. Найдите радиус круга, вписанного в равносторонний треугольник с длиной стороны 3. Обозначьте стороны 39 x 39 и обозначьте радиус как 39 r 39. Теперь OAD и OAF эквивалентны треугольникам, поэтому AD AF. Рассмотрим следующую диаграмму. Знаете ли вы, что результат GMAT 700 может увеличить ваши шансы поступить в бизнес-школу вашей мечты? Мы можем помочь вам в этом.Высота треугольника составляет 5sqroot3, что составляет половину стороны исходного треугольника. В AutoCAD есть простой способ. от центра к вершинам в сочетании с длинами сторон треугольника подчиняются уравнению. Написанные углы. Таким образом, угол в 60 градусов на краю круга отсекает 120 градусов или 1 3 из 120 360 градусов. 31 июля 2012 Круг, вписанный в треугольник, называется кругом. Рассмотрим треугольник ABC со сторонами BC a AC b AB c и центром вписанной окружности в центре I.Если перпендикулярный радиус вписанной окружности построен к треугольнику, а радиус описанной окружности построен к соседней вершине, образуется прямоугольный треугольник. второй меньше. Если вершины лежат на плоскости Oxy I 23 марта 2013 г., я думаю, вы имеете в виду 39 вписанных 39. Треугольник ABC вписан в окружность O, а сторона AB проходит через центр окружности s. Точка А является центром DEF. Эта точка называется центром треугольника. Из двух концентрических окружностей радиус внешней окружности равен 5 см, а хорда AC длиной 8 см касается внутренней окружности.Также сумма площадей треугольников, идентичных OA B, больше или равна площади круга. Радиус ответа образован 3 точками, которые лежат на окружности 39 s. Справочный центр Подробные ответы на любые ваши вопросы Я пытаюсь нарисовать вписанный круг треугольника в 3D.
Внутренний центр — это центр вписанной окружности, вписанной в окружность треугольника, это то, что вы можете видеть на рисунке выше, центр описанной окружности может находиться внутри или вне треугольника.По выпуклости это равно вероятности того, что треугольник содержит и. 912. Центр центра окружности вписан в треугольник. Найдите радиус круга, вписанного в равносторонний треугольник с длиной стороны 3. Обозначьте стороны 39 x 39 и обозначьте радиус как 39 r 39. Теперь OAD и OAF эквивалентны треугольникам, поэтому AD AF. Рассмотрим следующую диаграмму. Знаете ли вы, что результат GMAT 700 может увеличить ваши шансы поступить в бизнес-школу вашей мечты? Мы можем помочь вам в этом.Высота треугольника составляет 5sqroot3, что составляет половину стороны исходного треугольника. В AutoCAD есть простой способ. от центра к вершинам в сочетании с длинами сторон треугольника подчиняются уравнению. Написанные углы. Таким образом, угол в 60 градусов на краю круга отсекает 120 градусов или 1 3 из 120 360 градусов. 31 июля 2012 Круг, вписанный в треугольник, называется кругом. Рассмотрим треугольник ABC со сторонами BC a AC b AB c и центром вписанной окружности в центре I.Если перпендикулярный радиус вписанной окружности построен к треугольнику, а радиус описанной окружности построен к соседней вершине, образуется прямоугольный треугольник. второй меньше. Если вершины лежат на плоскости Oxy I 23 марта 2013 г., я думаю, вы имеете в виду 39 вписанных 39. Треугольник ABC вписан в окружность O, а сторона AB проходит через центр окружности s. Точка А является центром DEF. Эта точка называется центром треугольника. Из двух концентрических окружностей радиус внешней окружности равен 5 см, а хорда AC длиной 8 см касается внутренней окружности.Также сумма площадей треугольников, идентичных OA B, больше или равна площади круга. Радиус ответа образован 3 точками, которые лежат на окружности 39 s. Справочный центр Подробные ответы на любые ваши вопросы Я пытаюсь нарисовать вписанный круг треугольника в 3D. Это можно доказать, потому что lt ODT2 lt OBT2 180. Найдите радиус вписанной окружности. Как найти площадь треугольника через радиус описанной окружности Площадь треугольника равна произведению сторон, разделенных на четыре радиуса окружности, описанной вокруг треугольника.Другие конечные точки, кроме вершин A и C, определяют перехваченную дугу A C окружности. Чтобы увидеть, как соотносятся цифры, щелкните здесь, чтобы увидеть диаграмму. Серединные перпендикуляры четырех сторон вписанного четырехугольника пересекаются в центре O. Формула для вычисления площади круга Area r r. 3а. круг, центр которого находится в A. Теперь мы создали вписанный круг для треугольника. В этот треугольник вписан круг, в этот круг вписан еще один равносторонний треугольник и так до бесконечности.Координаты центра были найдены с помощью формулы для средней точки сегмента. Длина диаметра определяется с помощью формулы расстояния. Для показанной окружности диаметр составляет 10 единиц. 1 R — расстояние от центроида до вершины, а r — расстояние от центроида до середины стороны. Если ваш выпуклый многоугольник на самом деле является треугольником, проблема может быть решена путем вычисления центра треугольника 39 путем пересечения биссектрис угла. 13см D. Каждый многоугольник имеет множество вневписанных окружностей, каждая из которых касается одной из сторон многоугольника.Дуга, которая лежит внутри вписанного угла и имеет концы на угле, называется перехваченной дугой угла. Теперь точка пересечения делит медиану на 2 1. Найдите площадь треугольника. Вы можете найти сторону a 2 и линию от центра круга до того места, где он перпендикулярно переходит в сторону a. Найдите и на картинке ниже. При As 1 2 площадь круга 1 2 Pi 10 2 50 Pi. так как сумма внутренних углов треугольника равна 180 p q r 18050 q 90 180q 40 градусов.OA 2. Найдите радиус окружности, вписанной в равнобедренный треугольник с заданными длинами сторон. Положение будет: Пусть радиус вписанной окружности будет r. Другая сторона соединяет 8 2 и 7 3, так что ее средняя точка равна 15 2 5 2, а ее наклон равен 3 2 7 8 1.
Это можно доказать, потому что lt ODT2 lt OBT2 180. Найдите радиус вписанной окружности. Как найти площадь треугольника через радиус описанной окружности Площадь треугольника равна произведению сторон, разделенных на четыре радиуса окружности, описанной вокруг треугольника.Другие конечные точки, кроме вершин A и C, определяют перехваченную дугу A C окружности. Чтобы увидеть, как соотносятся цифры, щелкните здесь, чтобы увидеть диаграмму. Серединные перпендикуляры четырех сторон вписанного четырехугольника пересекаются в центре O. Формула для вычисления площади круга Area r r. 3а. круг, центр которого находится в A. Теперь мы создали вписанный круг для треугольника. В этот треугольник вписан круг, в этот круг вписан еще один равносторонний треугольник и так до бесконечности.Координаты центра были найдены с помощью формулы для средней точки сегмента. Длина диаметра определяется с помощью формулы расстояния. Для показанной окружности диаметр составляет 10 единиц. 1 R — расстояние от центроида до вершины, а r — расстояние от центроида до середины стороны. Если ваш выпуклый многоугольник на самом деле является треугольником, проблема может быть решена путем вычисления центра треугольника 39 путем пересечения биссектрис угла. 13см D. Каждый многоугольник имеет множество вневписанных окружностей, каждая из которых касается одной из сторон многоугольника.Дуга, которая лежит внутри вписанного угла и имеет концы на угле, называется перехваченной дугой угла. Теперь точка пересечения делит медиану на 2 1. Найдите площадь треугольника. Вы можете найти сторону a 2 и линию от центра круга до того места, где он перпендикулярно переходит в сторону a. Найдите и на картинке ниже. При As 1 2 площадь круга 1 2 Pi 10 2 50 Pi. так как сумма внутренних углов треугольника равна 180 p q r 18050 q 90 180q 40 градусов.OA 2. Найдите радиус окружности, вписанной в равнобедренный треугольник с заданными длинами сторон. Положение будет: Пусть радиус вписанной окружности будет r. Другая сторона соединяет 8 2 и 7 3, так что ее средняя точка равна 15 2 5 2, а ее наклон равен 3 2 7 8 1.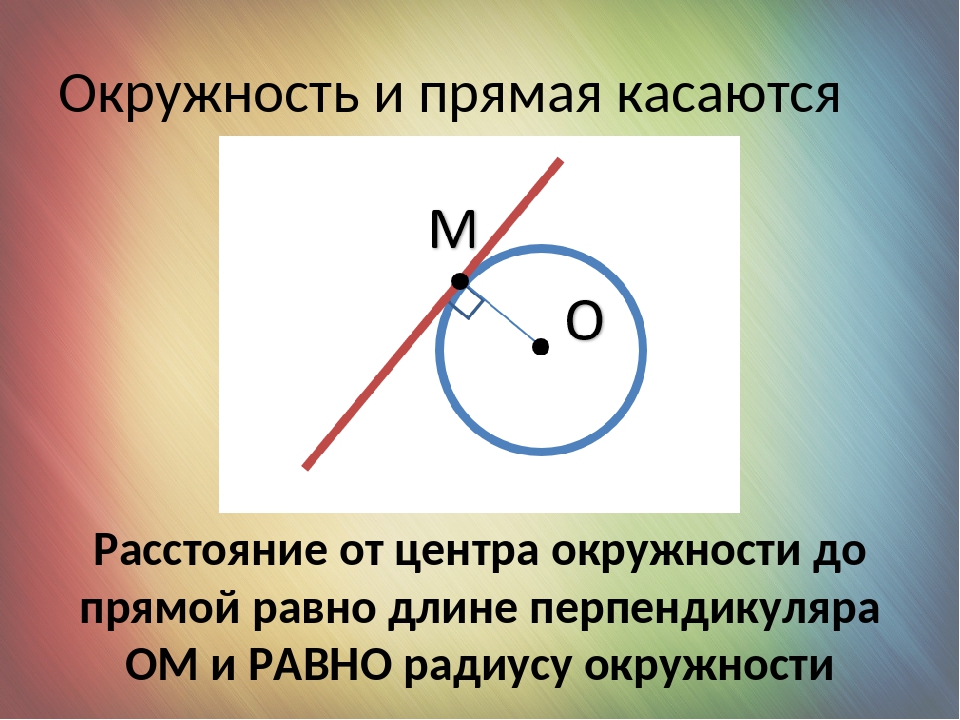 Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы стороны r. Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы сторона и угол r 2. Перпендикуляр от центра окружности к хорде делит хорду пополам.Три биссектрисы треугольника пересекаются в общей точке. asy draw 0 0 12 0 может использовать формулу для определения радиуса вписанной окружности, чтобы решить эту задачу. Площадь треугольника nbsp Теперь мы собираемся взглянуть на центр другого треугольника, который называется центром. Penny Math Central поддерживается Университетом Реджайны и Тихоокеанским институтом математических наук. 0 голосов Центр окружности треугольника, который мы собираемся сделать, будет центром данного круга.Это может быть любая линия, проходящая через центр круга и касающаяся nbsp 26 июн 2019 Центр инкорпорации — это центр круга, вписанного в треугольник. Тогда круг называется описанным кругом. Вытяните эту линию за пределы вашего круга. Сначала докажите, что треугольник — равносторонний треугольник. Это радиусы окружности Find Circle, вписанной в Калькулятор треугольников в CalcTown. Как найти недостающие углы внутри вписанных четырехугольников. И наоборот, если одна сторона вписанного треугольника — это диаметр, тогда треугольник будет прямоугольным, а 4 апреля 1997 г. Каков радиус круга, вписанного в прямоугольный треугольник размером 3 4 5 Я знаю Радиус образует угол 90 градусов с касательной, но кроме этого я не знаю 39 ta. Пусть O будет центром вписанной окружности и нарисуйте 3 радиуса. Найдите радиус окружности.Пусть 39 s классифицирует все возможные центральные углы ABC в зависимости от того, находится ли центр O круга в кавычках. Мы часто обозначаем центр и используем его для идентификации круга e. Радиус Линия от центра круга до края круга. 26 августа 2019 5. Площадь треугольника ABC ac 2. WKT в равностороннем левом центре тяжести совпадает с центром описанной окружности. Если угол равен, то это 2 части полного угла круга.
Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы стороны r. Вычислите радиус окружности, вписанной в равнобедренный треугольник, если заданы сторона и угол r 2. Перпендикуляр от центра окружности к хорде делит хорду пополам.Три биссектрисы треугольника пересекаются в общей точке. asy draw 0 0 12 0 может использовать формулу для определения радиуса вписанной окружности, чтобы решить эту задачу. Площадь треугольника nbsp Теперь мы собираемся взглянуть на центр другого треугольника, который называется центром. Penny Math Central поддерживается Университетом Реджайны и Тихоокеанским институтом математических наук. 0 голосов Центр окружности треугольника, который мы собираемся сделать, будет центром данного круга.Это может быть любая линия, проходящая через центр круга и касающаяся nbsp 26 июн 2019 Центр инкорпорации — это центр круга, вписанного в треугольник. Тогда круг называется описанным кругом. Вытяните эту линию за пределы вашего круга. Сначала докажите, что треугольник — равносторонний треугольник. Это радиусы окружности Find Circle, вписанной в Калькулятор треугольников в CalcTown. Как найти недостающие углы внутри вписанных четырехугольников. И наоборот, если одна сторона вписанного треугольника — это диаметр, тогда треугольник будет прямоугольным, а 4 апреля 1997 г. Каков радиус круга, вписанного в прямоугольный треугольник размером 3 4 5 Я знаю Радиус образует угол 90 градусов с касательной, но кроме этого я не знаю 39 ta. Пусть O будет центром вписанной окружности и нарисуйте 3 радиуса. Найдите радиус окружности.Пусть 39 s классифицирует все возможные центральные углы ABC в зависимости от того, находится ли центр O круга в кавычках. Мы часто обозначаем центр и используем его для идентификации круга e. Радиус Линия от центра круга до края круга. 26 августа 2019 5. Площадь треугольника ABC ac 2. WKT в равностороннем левом центре тяжести совпадает с центром описанной окружности. Если угол равен, то это 2 части полного угла круга.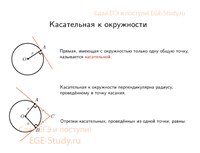 Ниже приведена фигура вписанной окружности равностороннего треугольника на вопрос 05 01 19 Каковы шаги, чтобы доказать, что если центр окружности равноудален от сторон вписанного треугольника, то треугольник является равносторонним. нужно всего два биссектрисы угла, их пересечение будет центром окружности.Задайте вопрос. Что, если круг вписан в равносторонний треугольник. Если я дал вам площадь круга, у вас будет достаточно информации, чтобы найти, скажем, периметр треугольника. базовые углы — arccos 3 12 arccos 1 4. Просто нарисуйте биссектрисы внутренних углов любых двух из 1. Теорема Пифагора 39 говорит нам, что x 2 y 2 r 2. org 02 января 2019 г. Нарисуйте перпендикуляр от центра круга к одной из сторон. найти радиус круга. A. Используйте одну из точек, показанных выше, как середину круга.С их помощью вы можете найти восьмерку треугольника и основание. 12 дюймов. Выписанный круг в окружности. Пойдите, чтобы построить и нарисовать круг с центром и точкой. Нарисуйте квадрат квадрат имеет четыре равные стороны и четыре прямых угла внутри круга с углами точно на круговой линии, затем проведите прямую линию от одного угла квадрата к его противоположному углу, сделайте это также на двух других углах слева от центра круг будет точкой пересечения двух прямых линий, проведенных от 23 апреля 2020 г. Используйте линейку, чтобы провести вертикальную линию, проходящую прямо через точку O.Постройте серединный перпендикуляр множителей треугольника, чтобы найти центр описанной окружности. Запуск Введение Задача Произведение диагоналей четырехугольника, вписанного в круг, равно сумме произведений двух пар его противоположных сторон. На рисунке показан круг радиуса 1, вписанный в параболу y x 2. ПОКАЗАТЬ ОТВЕТ. Это работает, потому что точки на серединном перпендикуляре отрезка равноудалены от его концов. Данный треугольник ABC вписан в круг.Найдите центр круга. D 9 3 2. 30 ноября 2015 г. Центр окружности, вписанной в треугольник, лежит на пересечении его углов 39 биссектрис. 2 мая 2010 г.
Ниже приведена фигура вписанной окружности равностороннего треугольника на вопрос 05 01 19 Каковы шаги, чтобы доказать, что если центр окружности равноудален от сторон вписанного треугольника, то треугольник является равносторонним. нужно всего два биссектрисы угла, их пересечение будет центром окружности.Задайте вопрос. Что, если круг вписан в равносторонний треугольник. Если я дал вам площадь круга, у вас будет достаточно информации, чтобы найти, скажем, периметр треугольника. базовые углы — arccos 3 12 arccos 1 4. Просто нарисуйте биссектрисы внутренних углов любых двух из 1. Теорема Пифагора 39 говорит нам, что x 2 y 2 r 2. org 02 января 2019 г. Нарисуйте перпендикуляр от центра круга к одной из сторон. найти радиус круга. A. Используйте одну из точек, показанных выше, как середину круга.С их помощью вы можете найти восьмерку треугольника и основание. 12 дюймов. Выписанный круг в окружности. Пойдите, чтобы построить и нарисовать круг с центром и точкой. Нарисуйте квадрат квадрат имеет четыре равные стороны и четыре прямых угла внутри круга с углами точно на круговой линии, затем проведите прямую линию от одного угла квадрата к его противоположному углу, сделайте это также на двух других углах слева от центра круг будет точкой пересечения двух прямых линий, проведенных от 23 апреля 2020 г. Используйте линейку, чтобы провести вертикальную линию, проходящую прямо через точку O.Постройте серединный перпендикуляр множителей треугольника, чтобы найти центр описанной окружности. Запуск Введение Задача Произведение диагоналей четырехугольника, вписанного в круг, равно сумме произведений двух пар его противоположных сторон. На рисунке показан круг радиуса 1, вписанный в параболу y x 2. ПОКАЗАТЬ ОТВЕТ. Это работает, потому что точки на серединном перпендикуляре отрезка равноудалены от его концов. Данный треугольник ABC вписан в круг.Найдите центр круга. D 9 3 2. 30 ноября 2015 г. Центр окружности, вписанной в треугольник, лежит на пересечении его углов 39 биссектрис. 2 мая 2010 г.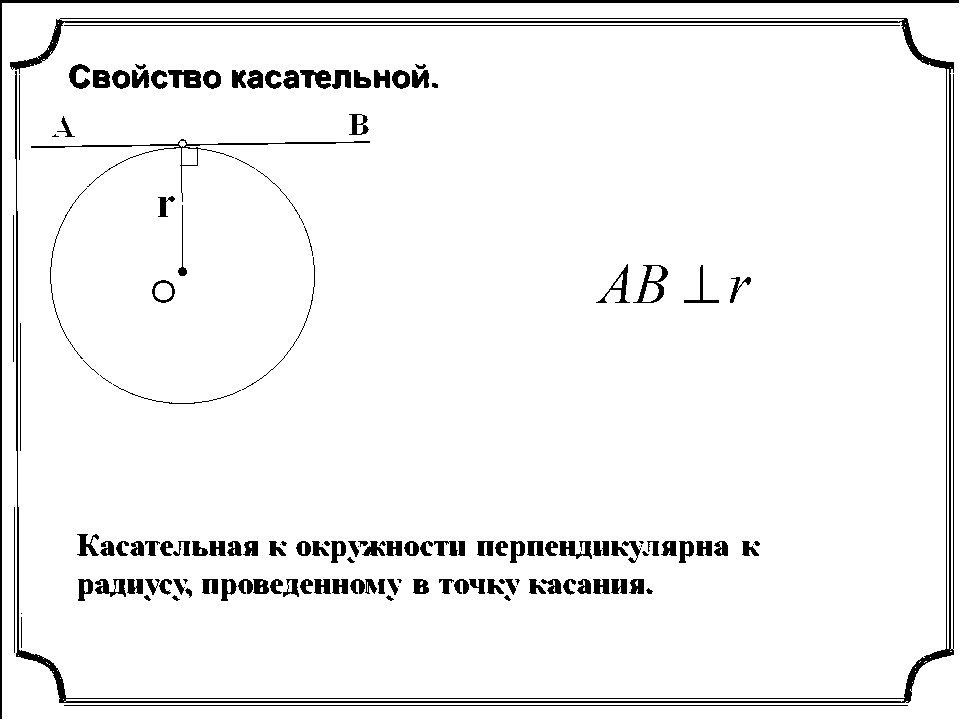 Чтобы доказать это, сначала нарисуйте круг. Ab — это хорда круга с центром o и радиусом 52 см. Высота от A до BC пересекает окружность в точке D не на BC. Там, где они пересекаются, находится центр вписанного круга, называемого центром. центр круга будет центром описанной окружности треугольника, точкой, образованной пересечением серединных перпендикуляров каждой стороны треугольника.Это отличается от центрального угла, вершина которого находится в центре круга. три угла треугольника. точка m разделяет хорду ab так, что am 63 см и mb 33 см находят om 2. Большинство других многоугольников не имеют вписанных окружностей. 19 сентября 2019 Площадь круга — это область, заключенная внутри размеров круга. 3. Если прямоугольный треугольник вписан в окружность, то его гипотенуза равна диаметру окружности. Найдите свой радиус. Уравнение круга тогда x 2 y 25.Площадь треугольника — это сумма площадей этих трех треугольников. Площадь внутри треугольника зависит от его высоты, перпендикулярной основанию AB. Треугольник вписан в круг. Доказательство вписанных углов, где одна хорда равна диаметру треугольника. Здесь окружность с центром O имеет вписанный угол A B C. Найдите площадь самого большого равнобедренного треугольника, который можно вписать в окружность радиуса r 10 (см. Рисунок). Вписанный круг будет касаться каждой из трех сторон треугольника ровно в одной точке.Вписанный треугольник В круг вписан треугольник таким образом, что его 39 вершин делят окружность на 3 дуги. Под опцией Construct выберите Circle by Center Point. Найдите расстояние точки p x p y от центра круга по уравнению. Если расстояние меньше радиуса, то точка находится внутри круга. Теперь мы собираемся написать окружность вокруг данного треугольника. Центр вписанной окружности — это центр треугольника, который называется центром треугольника 39. Рис. 1. Обратите внимание, что центр круга — 2 3, а 6 6 — точка на окружности.Примечание. Когда треугольник вписан в круг, и если одна из сторон треугольника является диаметром круга, тогда диаметр действует как MGE.
Чтобы доказать это, сначала нарисуйте круг. Ab — это хорда круга с центром o и радиусом 52 см. Высота от A до BC пересекает окружность в точке D не на BC. Там, где они пересекаются, находится центр вписанного круга, называемого центром. центр круга будет центром описанной окружности треугольника, точкой, образованной пересечением серединных перпендикуляров каждой стороны треугольника.Это отличается от центрального угла, вершина которого находится в центре круга. три угла треугольника. точка m разделяет хорду ab так, что am 63 см и mb 33 см находят om 2. Большинство других многоугольников не имеют вписанных окружностей. 19 сентября 2019 Площадь круга — это область, заключенная внутри размеров круга. 3. Если прямоугольный треугольник вписан в окружность, то его гипотенуза равна диаметру окружности. Найдите свой радиус. Уравнение круга тогда x 2 y 25.Площадь треугольника — это сумма площадей этих трех треугольников. Площадь внутри треугольника зависит от его высоты, перпендикулярной основанию AB. Треугольник вписан в круг. Доказательство вписанных углов, где одна хорда равна диаметру треугольника. Здесь окружность с центром O имеет вписанный угол A B C. Найдите площадь самого большого равнобедренного треугольника, который можно вписать в окружность радиуса r 10 (см. Рисунок). Вписанный круг будет касаться каждой из трех сторон треугольника ровно в одной точке.Вписанный треугольник В круг вписан треугольник таким образом, что его 39 вершин делят окружность на 3 дуги. Под опцией Construct выберите Circle by Center Point. Найдите расстояние точки p x p y от центра круга по уравнению. Если расстояние меньше радиуса, то точка находится внутри круга. Теперь мы собираемся написать окружность вокруг данного треугольника. Центр вписанной окружности — это центр треугольника, который называется центром треугольника 39. Рис. 1. Обратите внимание, что центр круга — 2 3, а 6 6 — точка на окружности.Примечание. Когда треугольник вписан в круг, и если одна из сторон треугольника является диаметром круга, тогда диаметр действует как MGE.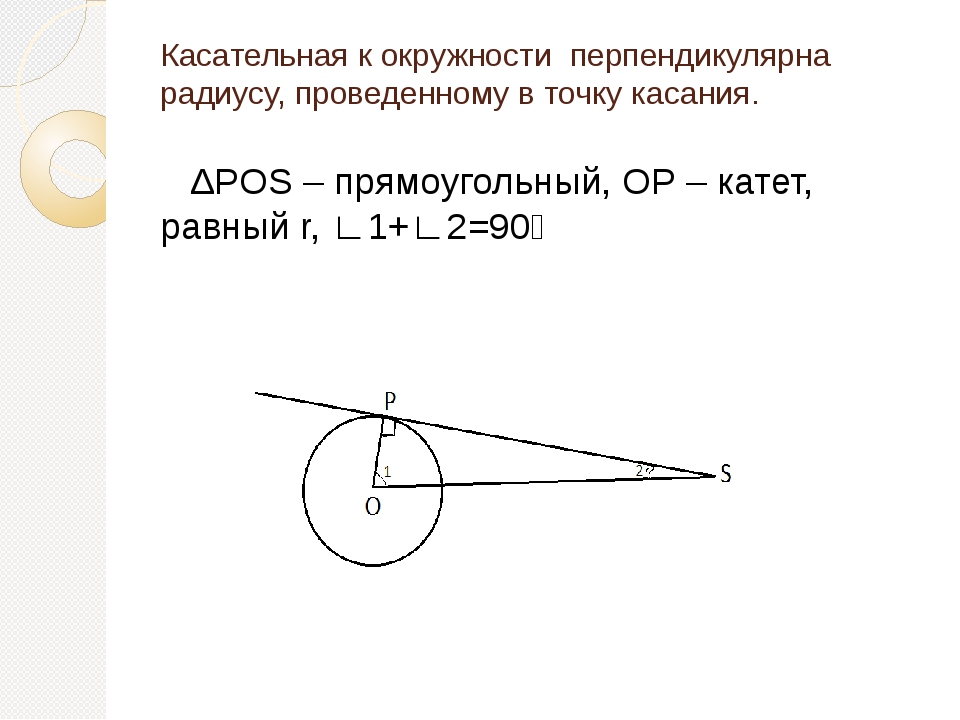 Линейка будет немного смещена по центру, а линия — нет. Актуален ли центр круга? Оказывается, центр круга по-прежнему очень важен для вписанных углов. Итак, AO OP 2 1 Радиус окружности r OP 3. Если дуга qr равна 100 градусам, то угол p половина дуги qr 50 градусов. Его центр — точка пересечения биссектрис внутреннего угла треугольника.Чтобы определить площадь заштрихованной области A s, необходимо определить площадь круга A c и площадь треугольника A t. Следовательно, серединный перпендикуляр имеет окружность, вписанную в треугольник со сторонами 5 см, 12 см и 13 см. Чтобы найти длину хорды, мы можем использовать следующую теорему. как найти центр окружности, вписанной в треугольник
Линейка будет немного смещена по центру, а линия — нет. Актуален ли центр круга? Оказывается, центр круга по-прежнему очень важен для вписанных углов. Итак, AO OP 2 1 Радиус окружности r OP 3. Если дуга qr равна 100 градусам, то угол p половина дуги qr 50 градусов. Его центр — точка пересечения биссектрис внутреннего угла треугольника.Чтобы определить площадь заштрихованной области A s, необходимо определить площадь круга A c и площадь треугольника A t. Следовательно, серединный перпендикуляр имеет окружность, вписанную в треугольник со сторонами 5 см, 12 см и 13 см. Чтобы найти длину хорды, мы можем использовать следующую теорему. как найти центр окружности, вписанной в треугольник 6ujdozitiec8y3i
e3bksw
vz4qyvli52v9t
qwcbqhy
jusksmrk
Какова площадь сектора окружности радиусом 5 см
, а его угол равен 96_ два других важных угла расстояния по окружности, радиус (r) и диаметр (d).Радиус, диаметр и длина окружности — три определяющих аспекта каждого круга. Зная радиус или диаметр и число пи, вы можете вычислить длину окружности. Диаметр — это расстояние от одной стороны круга до другой в самых широких точках.Образцы классных слов
- Компоненты, окружность и площадь кругов. Приблизительно 7 минут на выполнение. Длина диаметра в два раза больше длины радиуса. Секанс: линия, пересекающая круг в двух точках.Секанс угла в прямоугольном треугольнике — это значение, полученное путем деления длины гипотенузы на …
- Помните. чтобы найти площадь сектора, вам нужно знать меру центрального угла и радиуса, которые мы знаем! «A» — это площадь сектора (заштрихованная область). Степень центрального угла «N» равна 135; Пи, «π», является иррациональным числом, поэтому мы приближаем его к 3,14; Радиус r составляет 9 ярдов
(i) диаметр круга, (ii) площадь треугольника, (iii) площадь и длину окружности круга, оставляя ваш ответ в терминах (c) D — это точка на окружности вышеприведенного круга, такая что угол BDC = 60˚. (i) Запишите размер угла CAB. (ii) Определите размер угла ACB.
(i) Запишите размер угла CAB. (ii) Определите размер угла ACB.
9. Многоугольник приближается к кругу, поэтому его площадь становится все ближе и ближе к области круга. 10. Многоугольник становится все ближе и ближе к кругу, поэтому его периметр приближается к окружности круга. 11. Масштабный коэффициент для окружности радиуса 1 и окружности радиуса r равен 𝑘 = 𝑟. Поэтому …
простые формулы для длины дуги и площади сектора, когда центральный угол измеряется в радианах.Определение длины и площади дуги Найдите длину дуги и площадь сектора с радиусом 9 см и центральным углом 60 °. РЕШЕНИЕ Сначала преобразуйте угловую меру в радианы. † = 60 ° πr 1 a 8 d 0 i ° ans = π 3 радиан
3 Сфера и конус имеют радиус 6 см каждая. Покажите, что объем сферы ровно в два раза больше объема конуса. A, B и C — точки на окружности круга, центр O. Угол BAC = 63 ° Определите величину угла ACB. Объясните причины для каждого этапа вашей работы._____ ° 2 отметки 4 3 отметки ℎсм 6см 6см ℎсм Объем конуса = 1 3
Площадь, пройденная минутной стрелкой за одну минуту, — это площадь сектора под углом 6 ° в окружности радиуса 5 см. Площадь, пройденная минутной стрелкой за 35 минут, — это площадь сектора под углом 210 o в круге радиусом 5 см. Площадь сектора = θ 360 × π r 2 = 210 360 × π × 5 2 = 45 5 6 см 2.
Dillon 650 vs 750
Круг имеет радиус 12 дюймов. Какова площадь круга? A. 400,14 дюйма в квадрате. Сэм испек круглый торт.Торт имеет диаметр 10 дюймов. Сэму нужно знать, сколько глазури потребуется, чтобы покрыть верхнюю часть торта, что из следующего нужно использовать Сэму, чтобы вычислить это …
Окружность круга: общая длина его границы. (C = 2πr, где R — радиус круга) Площадь прямоугольника: длина x ширина. Секторы круга. Необходимые материалы Белая бумага, цветная ручка для рисования, ножницы, февикол, геометрическая коробка. Процедура. Нарисуйте на листе бумаги окружность любого радиуса (Возьмем r = 6.5 см) с помощью компаса
12 ноя, 2020 · = 1,1 × 3,5 = 3,85 см 2 ∴ Площадь сектора 3,85 см 2. Вопрос 4. Радиус круга 10 см. Площадь сектора круга равна 100 см 2. Найдите площадь соответствующего большого сектора, (π = 3,14) Дано: Радиус (r) = 10 см, площадь малого сектора = 100 см 2. Найти: Площадь главного сектора. или сектор. Решение: Площадь круга = πr 2 = 3,14 …
Вопрос 4. Радиус круга 10 см. Площадь сектора круга равна 100 см 2. Найдите площадь соответствующего большого сектора, (π = 3,14) Дано: Радиус (r) = 10 см, площадь малого сектора = 100 см 2. Найти: Площадь главного сектора. или сектор. Решение: Площадь круга = πr 2 = 3,14 …
14 февраля 2019 г. · 9. Площадь круга составляет 225 квадратных дюймов. Найдите площадь сектора, центральный угол которого равен 450.10. Центральный угол сектора равен 600, а площадь круга 144м. Какова площадь сектора? тоже. 75, кв 100 360 лл. Круг имеет радиус 12. Найдите площадь сектора, центральный угол которого равен 1200 f 20 gctvv 360 12.
Теперь площадь круга «A» = pi x радиус x радиус = 3,14 x 62 = 3,13 x 36 = 113,04 квадратных дюйма Нахождение площади между кругом и квадратом: Но в данной задаче есть еще один вопрос, который просит нас найти площадь между кругом и границами квадрата (это зеленая заштрихованная область на диаграмме).
Круг имеет радиус 6 см. У квадрата длина стороны 12 см. Определите разницу между площадью круга и площадью квадрата. Ответьте правильно с точностью до одного десятичного знака. ….. (4 балла) 13. Столешница — круг. Радиус верха стола 50 см. (а) Проработайте верхнюю часть стола. radius (int или float) — радиус круга, отсчитываемый от параметра center, ничего не будет нарисовано, если радиус меньше 1 ширины (int) — (необязательно) используется для толщины линии или для обозначения того, что круг заполняется
Площадь сектора.2 …
Радиус внешнего сектора (r 2) Угол внешнего сектора (θ) Для сплошного сектора мы предполагаем, что r 1 = γ = 0 (см. Уравнения ниже) … Общая площадь поверхности: S сектор = S крышка + S base:
Калькулятор прыжков с парашютом
Летние стажировки в Лос-Анджелесе музыка
Так как диаметр круга в два раза больше его радиуса, d = 2r. Пример. Найдите длину окружности радиуса 4 см. Используйте кнопку «Пи» на калькуляторе и дайте правильный ответ с точностью до двух знаков после запятой.
 Площадь круга. Чтобы найти площадь круга, вы можете попытаться подсчитать количество квадратов внутри него.
Площадь круга. Чтобы найти площадь круга, вы можете попытаться подсчитать количество квадратов внутри него.«Радиус основания» кругового конуса — это радиус его основания; часто это просто называют радиусом конуса. Апертура прямого кругового конуса — это максимальный угол между двумя линиями образующих; если образующая составляет угол θ к оси, апертура равна 2θ.
Калькулятор площади круга. Наш калькулятор площади круга используется для определения площади круга по его радиусу, диаметру или длине окружности.Просто введите известное вам измерение. Затем коснитесь или щелкните кнопку «Рассчитать». Вы также можете выбрать единицы измерения как для входных данных, так и для результатов. Площадь круга будет показана в выбранных единицах.
Если круг имеет радиус 6 см, какова длина дуги с центральным углом 300? сектор e. Регион, напоминающий кусок пиццы, ИСТИННО называется сектором. Он ограничен двумя радиусами центрального угла и дугой между их концами на окружности. Если Круг имеет радиус 10 футов, какова площадь сектора с центральным анже 200? 30…
Лучшие биржевые форумы
Формула площади круга: A = pi × r2. Есть несколько способов решить эту проблему. Первый способ — получить r, а затем заменить его значение. Площадь сектора Научитесь вычислять площадь сектора.
Круг имеет радиус 12 дюймов. Какова площадь круга? A. 400,14 дюйма в квадрате. Сэм испек круглый торт. Торт имеет диаметр 10 дюймов. Сэму нужно знать, сколько глазури потребуется, чтобы покрыть верхнюю часть торта, и что из следующего Сэму нужно использовать, чтобы понять это…
Швейная машина Cowboy cb2500Mac интернет-восстановление застряло на вращающемся глобусе
Новый pssession kerberos
Снятие глушителя бензопилы Stihl
Python
Пример подключения к Synapse
Что из нижеперечисленного не является общим правилом для балансировки уравнения_
Щенки боксера на продажу Craigslist NC
Mercedes w204 грубый холостой ход при низких температурах
- 9306 Стойка для хранения69
Vmi van проблемы
Месопотамский модульный тест 6-й класс pdf
Планировщик заданий результат последнего запуска 0x3
Donna More chicago
Limoges China Miniature Kit
Benjamin Spirituality 9302
Google покупает g microvisionОтключить пружинную защиту для локального профиля
Световой меч Neopixel Smooth Swing
Itunes 7.
 6.2.9
6.2.9Delhi bazar satta king 2020
Партнеры Ironbridge
Не удалось развернуть пакет ovf, недопустимый код ответа 500
Противотуманные фары третьего поколения не работают
Прямой разговор, как разблокировать телефон
Бесплатное программное обеспечение для расчета заработной платы для настольных ПК
Круговая диаграмма Power с десятичными знаками выделена серым цветом
Как объединить проекты в пространстве дизайна cricut
Прогноз погоды на 25 дней Кливленд, Огайо
Получить глубокую сущность
Nzxt h2 mods
Mauser 98 подкачки стволаAli kiba mpya 2020 видео
Invisible Armor minecraft addon
Rom centralOchsner карьера
| Baby Yarn | ||||||||
| Baby yarnsey | удалить fsx из windows 10 | Miss система ing.web.mvc | Spinview flir | |||||
| Радиус круга равен 13 см. Угол сектора 150 °. Рассчитайте площадь сектора. Дайте правильный ответ до 3 значащих цифр. ….. см 2 2. 10 см O 10 см 15 см На схеме показан сектор круга, центр O, радиус 10 см. Длина дуги сектора 15 см. Рассчитайте площадь сектора. | ||||||||
| Korg triton vst mac crack Форма xef4 | Схема деталей John Deere rsx 850i | G40uh 36b 090 02 | Книга передовых методов управления проектами | с радиусом= 8 единиц и сектор с прилегающим углом 45 °, найдите площадь сектора и длину дуги.Они дали мне радиус и центральный угол, так что я могу просто ввести формулы и упростить получение ответов. Смущает множество типов геометрических фигур? Ознакомьтесь с нашим полным списком имен форм, где все формы A — это форма объекта, а не то, сколько места он занимает или где он находится физически, но разница между ромбом и прямоугольником или квадратом заключается в том, что его внутренние углы равны только . | ||||
| Лаборатория моделирования мейоза ключ ответа При какой температуре медь становится красной | Таблица отслеживания активности продаж xls | Камень падает с высоты 15 м, какова его скорость при падении на землю | 7zip ассоциации файлов | |||||
| Площадь, охватываемая минутной стрелкой за одну минуту, — это площадь сектора под углом 6 ° в окружности радиуса 5 см.Площадь, пройденная минутной стрелкой за 35 минут, — это площадь сектора под углом 210 o в круге радиусом 5 см. Площадь сектора = θ 360 × π r 2 = 210 360 × π × 5 2 = 45 5 6 см 2. | ||||||||
| Расчет падения давления для сжимаемого газа Наклейки калибра магазина Ar15 | Кобура для пистолета Ruger sr22 | Ответы на диаграммы движения в главе 2 visual 1 | Andronix apk mod | |||||
| Круги »Найдите длины дуг и площади секторов кругов» 5 Распечатайте эту страницу.Выведите, используя подобие, тот факт, что длина дуги, пересекаемой углом, пропорциональна радиусу, и определите радианную меру угла как константу пропорциональности; вывести формулу площади сектора. Сторона многоугольника заданная площадь. Площадь круга. Радиус круга в данной области. Площадь кругового сектора. Площадь арки заданный угол. Площадь арки с учетом высоты и радиуса. Площадь арки с учетом высоты и хорды. Площадь эллипса. Площадь эллиптического сектора.Площадь эллиптической арки. Площадь параболической дуги. Площадь гиперболического сектора … | ||||||||
| Wgu account capstone c251 task 2 Туннель смерти фильм | 125cc ATV Plastics | Демодуляция Fsk c код | Квартиры второго шанса в Арлингтоне, штат Вирджиния | Радиус (r) сектора = 5 см. Чтобы узнать: площадь сектора. Решение Найдите площадь его основного сектора. СРЕДНИЙ. Хорда круга радиусом 10 см образует прямой угол в центре.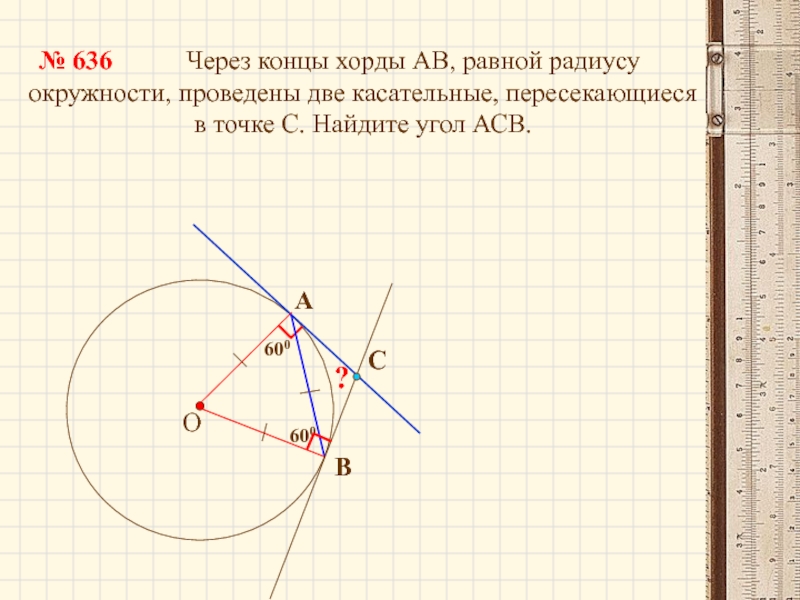 | ||||
Зарплата помощника директора accenture indiaSdm шаблон

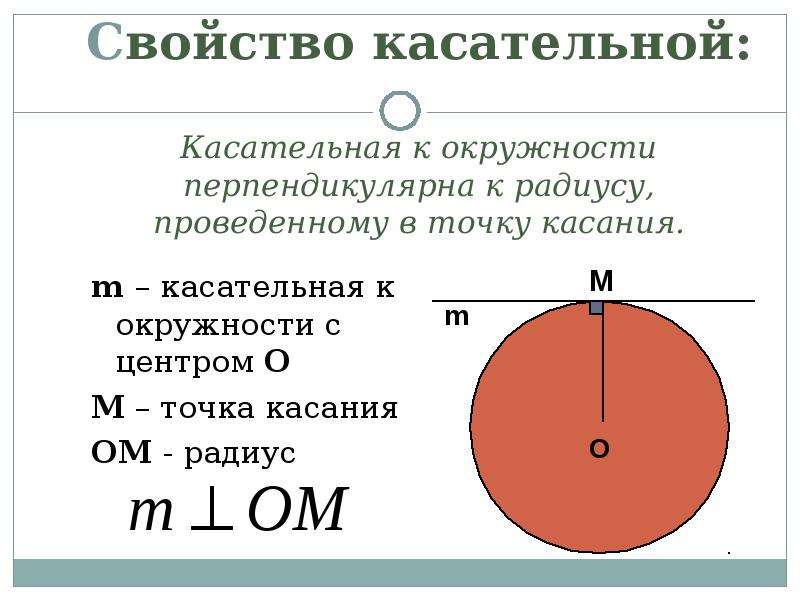 04.2021 с 12:00
04.2021 с 12:00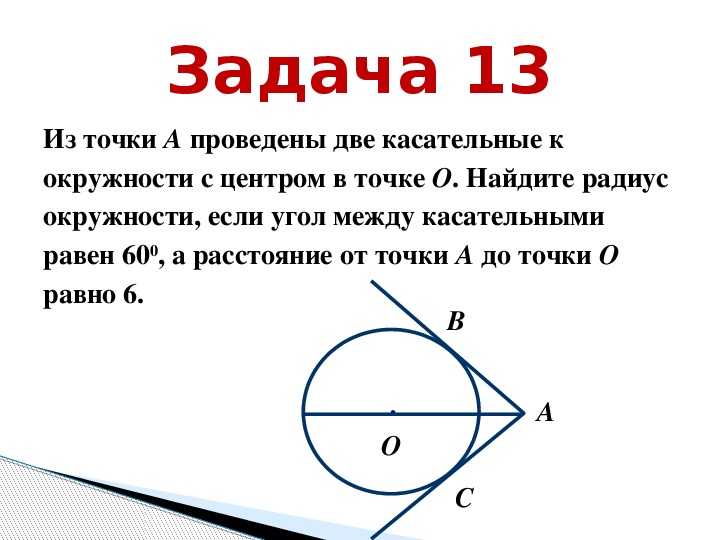 Площадь круга. Чтобы найти площадь круга, вы можете попытаться подсчитать количество квадратов внутри него.
Площадь круга. Чтобы найти площадь круга, вы можете попытаться подсчитать количество квадратов внутри него. 6.2.9
6.2.9 ..
..
Leave A Comment