Будет ли ускорение перпендикулярно мгновенной скорости: Куда направлено ускорение конца стрелки часов? Будет ли ускорение перпендикулярно мгновенной скорости?

Физические основы механики

Представим себе материальную точку, движущуюся по некоторой криволинейной траектории . Запишем скорость в виде

и заметим, что вектор

— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим

Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор — единичный, то

Дифференцируя это скалярное произведение, получаем

то есть

по свойству скалярного произведения.

Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их и :

Обсудим физический смысл каждого слагаемого. Слагаемое

— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения направлена либо по скорости, когда производная

dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное.

Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:

Слагаемое

направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.

Рис. 2.10. К определению кривизны траектории

Рассмотрим «достаточно гладкую», в остальном произвольную плоскую криволинейную траекторию. Плоскую, то есть все точки траектории лежат в некоторой плоскости, — исключительно для упрощения выкладок, получаемый в рамках этого предположения, результат годится и для любой «достаточно гладкой» пространственной кривой, чьи точки уложить в одну плоскость невозможно. Последнее обстоятельство мы здесь рассматривать не будем, оно строго доказывается методами аналитической геометрии.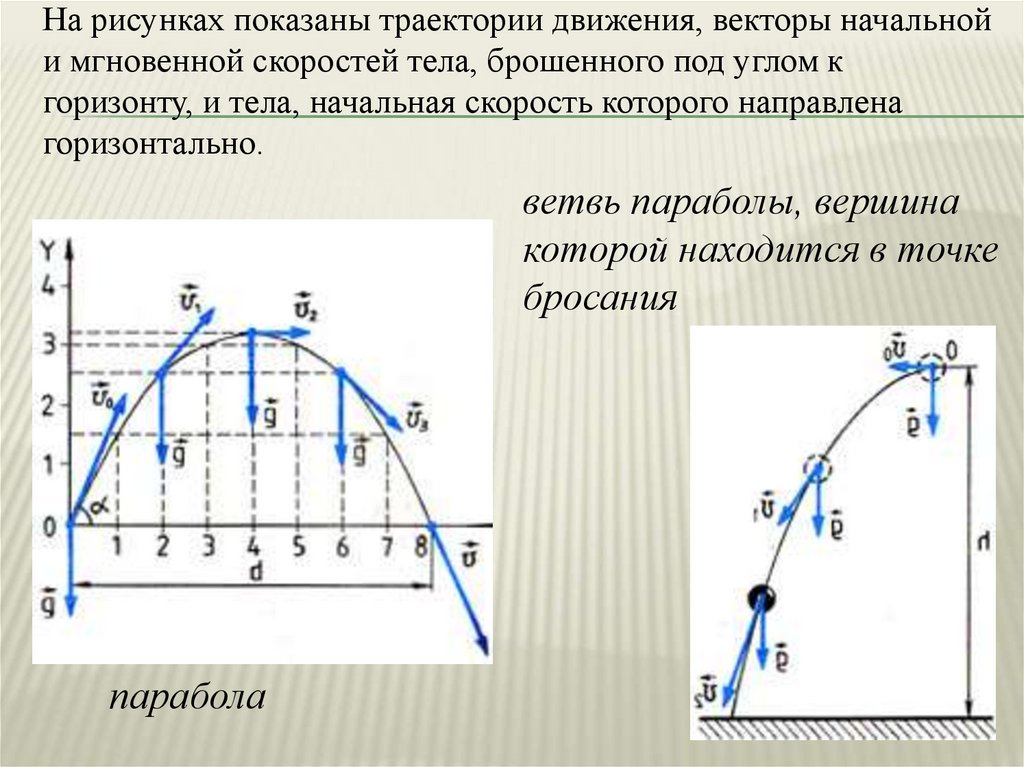 Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть «углов» типа показанного на рисунке 2.11.

Рис. 2.11.

Такую «гладкую» кривую на любом её бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на её бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории

в этой точке. Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны.

Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.

Рис. 2.12. К определению радиуса кривизны траектории

Вычислим модуль производной , входящей в выражение для нормального ускорения. Направлен вектор по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.

Рис. 2.13. Графическое определение радиуса кривизны траектории

Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: , имеем:

По определению производная кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая всё вместе, для нормального ускорения окончательно получаем:

где нормаль перпендикулярна к касательной и всегда направлена к центру кривизны, см. рис. 11.

Приведем некоторое дополнительное пояснение к рисунку 11. Возьмем неподалеку от точки 1 точку 2. Построим в этих точках касательные единичные векторы ₁ и ₂. Перпендикуляры к этим касательным пересекутся в некоторой точке O₂

. Заметим, что для кривой, не являющейся окружностью, расстояния R₁ и R₂ будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O₂ будет перемещаться вдоль прямой O₂1 и в пределе окажется в некоторой точке O₁. Расстояния R₁ и R₂ будут стремиться к общему пределу R, равному радиусу кривизны, а точка O₁ и будет центром кривизны для точки 1.

Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту ₁). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.

Итак, в общем случае ускорение имеет две составляющие — тангенциальную

направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную

направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).

Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.

Действительно , где и есть угловая скорость вращения вектора скорости .

Полное ускорение

определяется по правилу параллелограмма.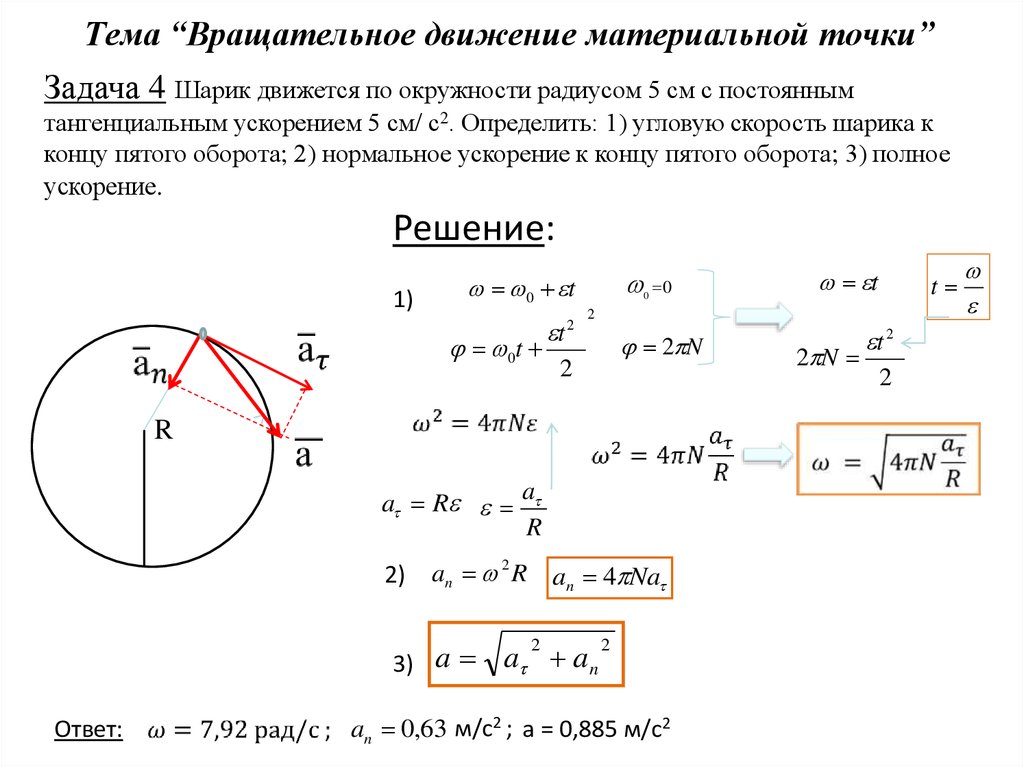 Модуль полного ускорения в соответствии с теоремой Пифагора равен

Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то

Если же траектория задана в параметрическом виде,

x = x(t), y = y(t), то

Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:

Рис. 2.15. Движение тела, брошенного под углом к горизонту

Равномерное движение по окружности | Физика

1. Основные характеристики равномерного движения по окружности

Движение по окружности часто встречается в природе и технике: по траекториям, близким к окружностям, движутся планеты вокруг Солнца, Луна и искусственные спутники Земли, точки колес и вращающихся деталей механизмов.

Мы ограничимся в нашем курсе равномерным движением по окружности. Напомним, что равномерным называют движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.

Каковы же основные характеристики равномерного движения по окружности?

Прежде всего, это радиус окружности r и модуль скорости тела v (рис. 8.1). Далее мы увидим, что мгновенная скорость в каждой точке траектории направлена по касательной к траектории.

Следующей характеристикой равномерного движения по окружности является период обращения T. Он равен промежутку времени, в течение которого тело совершает один оборот.

? 1. Во сколько раз период обращения секундной стрелки меньше периода обращения часовой стрелки?

? 2. Докажите, что период обращения T, радиус окружности r и модуль скорости тела v связаны соотношением

T = 2πr/v. (1)

Частотой обращения ν называют число оборотов за единицу времени (секунду). Значение частоты не всегда целое число: например, если тело совершает 10 оборотов в секунду, то ν = 10 с^-1, а если оно совершает пол-оборота в секунду, то ν = 0,5 с^-1.

Чем больше частота обращения, тем меньше период.

? 3. Докажите, что период T и частота обращения ν связаны соотношением

ν = 1/T (2).

? 4. Чему равна частота обращения секундной стрелки, ми- К. нутной стрелки, часовой стрелки, Земли при ее суточном вращении и при ее движении вокруг Солнца?

2. Направление мгновенной скорости при движении по окружности

Поставим опыт
Затачивая инструмент с по: мощью точильного круга, можно заметить, что искры летят по касательной к кругу в точке, которой касается инструмент (рис. 8.2). Это раскаленные кусочки, оторвавшиеся от круга, поэтому их скорость в момент отрыва равна (по модулю и направлению) скорости точек диска, соприкасающихся с инструментом.

Этот опыт показывает, что при движении по окружности мгновенная скорость тела v_vec направлена по касательной к окружности в точке, где в данный момент находится тело.

Чтобы лучше осознать это, рассмотрим движение тела в течение времени Δt, малого по сравнению с периодом T. Пройденная за это время дуга окружности почти сливается с участком касательной к окружности (эта касательная показана голубой линией на рис.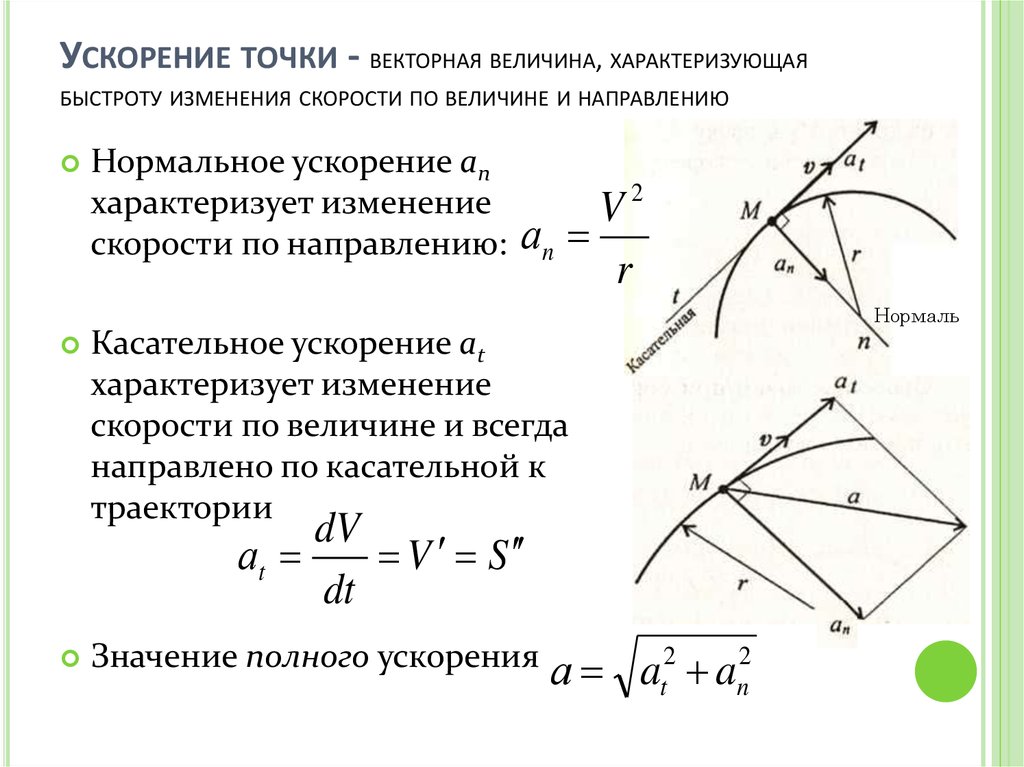 8.3). А это как раз и означает, что мгновенная скорость тела направлена по касательной.

Заметим, что касательная к окружности в некоторой точке перпендикулярна радиусу окружности, проведенному в эту точку. Следовательно,
при движении по окружности мгновенная скорость тела v_vec направлена перпендикулярно радиусу, проведенному в точку, где находится тело в данный момент (см. рис. 8.1).

? 5. На рисунке 8.4 изображена траектория тела, движущегося по окружности. Перенесите рисунок в тетрадь и отметьте на нем:
а) вектор скорости тела, когда оно находится в точках А и В;
б) точку С, в которой скорость тела составляет угол 45º со скоростью тела в момент, когда оно находится в точке А.

3. Ускорение при равномерном движении по окружности

Поскольку мгновенная скорость тела направлена по касательной в каждой точке траектории, направление скорости тела при его движении по окружности изменяется. А если скорость тела изменяется любым образом (пусть даже только по направлению), то это тело движется с ускорением.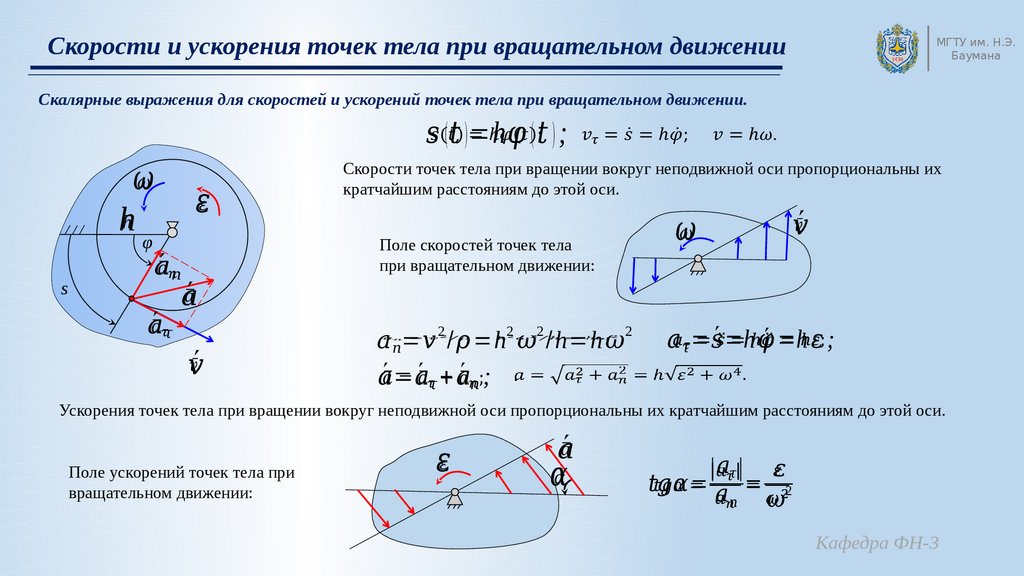 Итак, при равномерном движении по окружности тело движется с ускорением.

Докажем, что
при равномерном движении тела со скоростью v по окружности радиуса r:
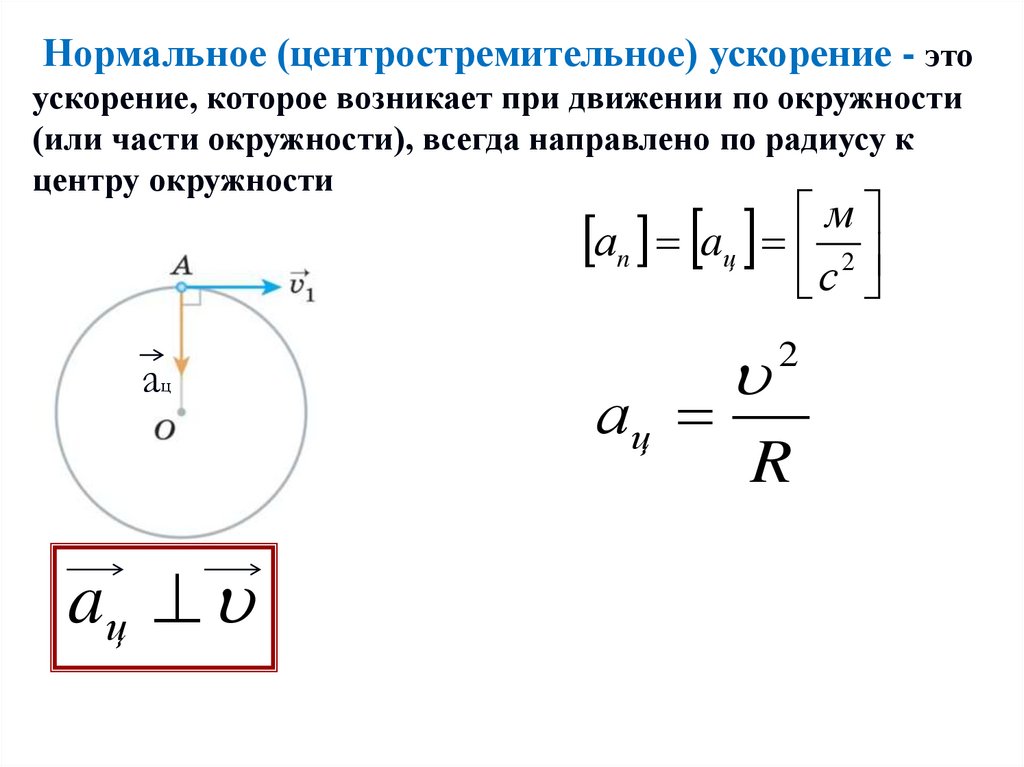
а) ускорение тела в каждый момент времени направлено по радиусу к центру окружности,
б) модуль ускорения a = v2/r.

Направление ускорения

Поскольку

направление вектора ускорения совпадает с направлением вектора изменения скорости Δ.

Найдем изменение скорости Δ за промежуток времени Δt, малый по сравнению с периодом T.
Обозначим ₁ скорость тела в момент времени t, а ₂ скорость тела в момент времени t + Δt. Тогда

Δ =₂ – ₁.

Обозначим Δα угол, на который повернется за время Δt радиус, проведенный в точку, где находится тело (рис. 8.5, а). Угол Δα мал, если Δt мало по сравнению с T.

На такой же угол Δα повернется за время Δt и вектор скорости тела (скорость остается все время перпендикулярной радиусу).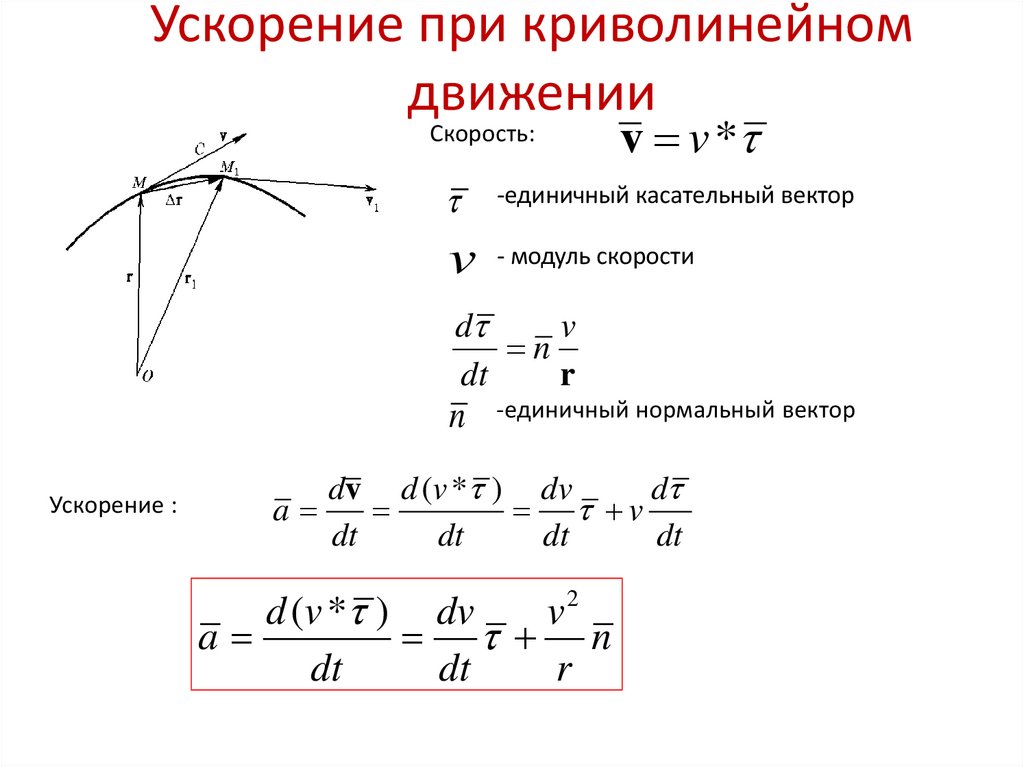

На рисунке 8.5, б показано, как найти изменение скорости Δ.

Векторы ₁, ₂ и Δ образуют равнобедренный треугольник с основанием Δ и малым углом Δα при вершине. Поэтому углы при основании этого треугольника близки к прямым углам (это следует из того, что сумма углов треугольника 180º).

Значит, изменение скорости Δ за очень малое время Δt направлено перпендикулярно скорости, то есть по радиусу, причем к центру окружности, как показано на рисунке 8.5, в. Ускорение направлено так же, как изменение скорости Δ, следовательно, ускорение тела направлено к центру окружности.

По этой причине ускорение тела при его движении по окружности часто называют центростремительным.

Из курса физики основной школы вы уже знаете, что ускорение тела обусловлено действующими на него силами. Например, при движении Земли вокруг Солнца силой, вызывающей центростремительное ускорение Земли, является сила тяготения со стороны Солнца.

? 6. Автомобиль поворачивает на 90º по дуге окружности.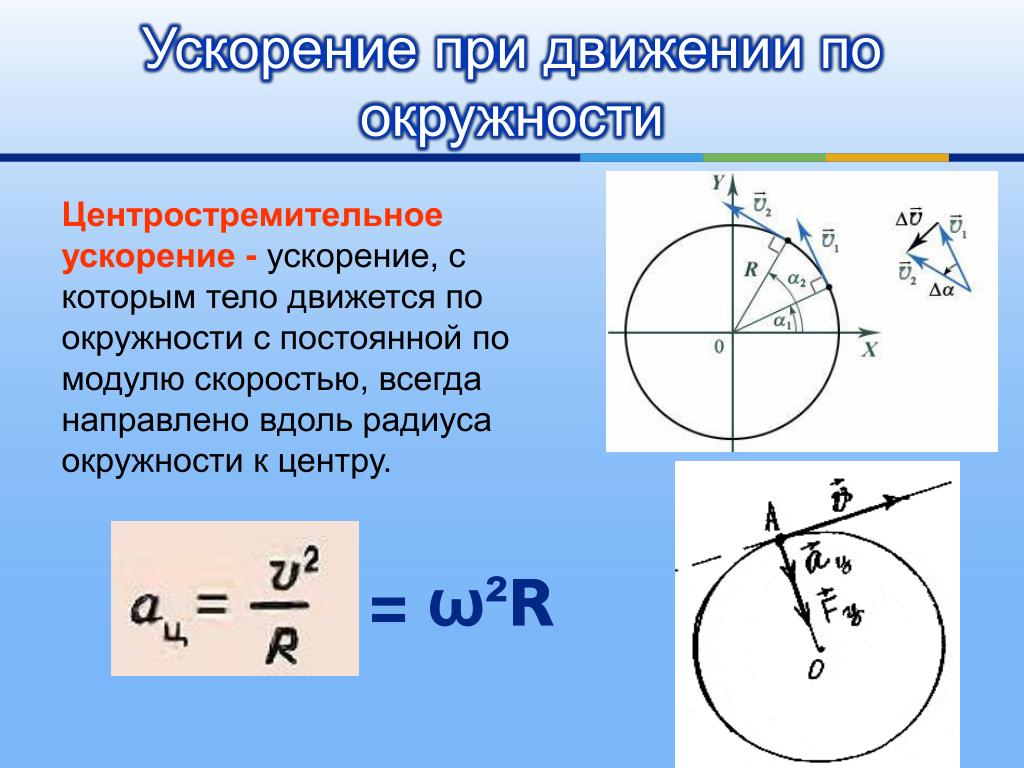 Изобразите на чертеже в тетради векторы скорости и ускорения автомобиля в середине дуги поворота.

Модуль ускорения

За промежуток времени Δt тело, движущееся со скоростью v, проходит по дуге окружности путь Δl = v * Δt (это красная сплошная линия на рисунке 8.6, а).

Если Δt мало по сравнению с T, эта дуга почти не отличается от отрезка прямой. Поэтому фигура, образованная двумя радиусами r и этим отрезком, представляет собой равнобедренный треугольник с основанием Δl = v * Δt.

Этот треугольник подобен равнобедренному треугольнику, образованному скоростями Δ₁, Δ₂ и изменением скорости Δ = * Δt (он изображен на рисунке 8.6, б), поскольку углы при вершинах этих треугольников равны. Следовательно, основания указанных двух треугольников относятся, как их боковые стороны:

(a * Δt) / (v * Δt) = v/r,

откуда получаем:

a = v2/r, (4)

Центростремительное ускорение можно выразить также через ν и r или через T и r.

? 7. Докажите, что центростремительное ускорение выражается также формулами

Подсказка. Воспользуйтесь формулами (4), (1), (2).

Можно подумать, что центростремительное ускорение, обусловленное изменением только направления скорости, не может быть значительным. Убедимся, что это не всегда так.

? 8. Чтобы космонавты без вреда для здоровья переносили большие перегрузки во время старта и посадки космического корабля, их тренируют с помощью специального аппарата – огромной центрифуги (рис. 8.7). Во время тренировки в Центре подготовки космонавтов им. Ю. А. Гагарина космонавт движется в капсуле (она изображена в левой части фотографии) по окружности радиусом 18 м.

а) С каким ускорением движется космонавт, когда центрифуга делает шесть оборотов в минуту?
б) При какой частоте обращения космонавт движется с ускорением, превышающим ускорение свободного падения в 10 раз? Чему равна при этом его линейная скорость?

Чтобы испытать на себе ощущения при движении с ускорением, в несколько раз превышающем ускорение свободного падения, можно покататься на центрифуге в парке (рис. 8.8).

? 9. Радиус колеса аттракциона 10 м. Чему равен период его обращения, когда пассажиры движутся с ускорением, в 2,5 раза превышающим ускорение свободного падения?

4. Угловая скорость

Иногда используют еще одну характеристику равномерного движения по окружности – угловую скорость ω. Ее определяют соотношением

ω = Δα/t,

где Δα – угол, на который за время t поворачивается радиус, проведенный к телу из центра окружности (рис. 8.9).

При атом угол измеряют в радианах, то есть одному полному обороту соответствует поворот на угол 2π. Единица угловой скорости совпадает с единицей частоты (1 с^-1). (Напомним, что один радиан (рад) равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности; 1 рад ≈ 57º.)

? 10. Какая скорость одинакова для всех точек минутной стрелки – линейная или угловая?

? 11. Во сколько раз угловая скорость секундной стрелки больше угловой скорости минутной стрелки?

? 12. Докажите, что угловая скорость связана с периодом обращения, частотой, радиусом окружности и скоростью соотношениями

ω = 2π/T, (7)
ω = 2πν, (8)
v = ωr. (9)

? 13.Чему равна угловая скорость движения точки поверхности Земли, обусловленная суточным вращением? Одинакова ли эта скорость для всех точек земной поверхности, находящихся: а) на одной параллели; б) на одном меридиане; в) на различных параллелях и меридианах?

? 14. Докажите, что центростремительное ускорение выражается через угловую скорость и радиус окружности формулой

a = ω2r. (10)

5. Катящееся колесо

Рассмотрим движение различных точек колеса автомобиля.

Пусть автомобиль едет со скоростью (рис. 8.10), причем его колеса катятся без проскальзывания.

Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют четкие следы). Этот факт – отправная точка для нахождения скорости всех других точек колеса – например, точек В, С, D на рисунке 8. 10.

Чтобы найти скорость этих точек, удобно перейти в систему отсчета, связанную с автомобилем, а потом вернуться в систему отсчета, связанную с дорогой.

В системе отсчета, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим v_вр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля v и скорость вращения v_вр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.
Заметим, что скорость _Aвр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).

Выразим через v и v_вр скорость v_А точки А в системе отсчета, связанной с дорогой. Согласно правилу сложения скоростей скорость точки А относительно дороги

A = _Aвр + .

Итак, скорости _Aвр и направлены противоположно, а их сумма _A = 0. Следовательно,

v_вр = v,

то есть скорость движения точек обода колеса в системе отсчета, связанной с автомобилем, равна но модулю скорости автомобиля.

? 15.Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2v.

? 16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.

? 17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью v = u(R/(R+r)).

Подсказка. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.

? 18.С какой скоростью v и в каком направлении будет двигаться катушка в случае, изображенном на рисунке 8.14?

Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.

? 19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.

Подсказка. Перейдите в систему отсчета, связанную с велосипедистом.

Дополнительные вопросы и задания

Необходимые для решения задач справочные данные, не приведенные в условии задачи, вы можете найти в конце учебника (под обложкой).

20. Длина минутной стрелки настенных часов 15 см, а часовой стрелки – 10 см. Какие величины можно определить из этого условия? Чему они равны?

21. Чему равна обусловленная суточным вращением скорость точек поверхности Земли, расположенных на экваторе? Длину экватора примите равной 40000 км.

22. Две шестеренки сцеплены, как показано на рисунке 8.16. Радиусы шестеренок 60 см и 30 см. Большая шестеренка вращается с частотой 2 с^-1.

а) С какой скоростью движутся зубцы большой шестеренки?
б) По часовой стрелке или против нее движутся зубцы маленькой шестеренки? С какой скоростью они движутся?
в) Чему равна частота обращения маленькой шестеренки?

23. Диск радиусом 2 м равномерно вращается вокруг своей оси с периодом 0,5 с. Начертите графики зависимости скорости v и ускорения a точки диска от расстояния r до центра диска.

24. Наблюдения колец Сатурна (рис. 8.17) показали, что чем дальше от планеты находится участок кольца, тем меньше его скорость. Могут ли кольца Сатурна быть сплошными? Обоснуйте свой ответ.

Самолет летит вдоль 60-й параллели. Во время всего полета его пассажиры наблюдают Солнце в одной и той же точке небосвода. Длину экватора примите равной 40000 км.
а) В каком направлении летит самолет?
б) За какое время он совершит полный круг?
в) Какой путь самолет пролетит за это время?
г) С какой скоростью летит самолет?

26. Два тела равномерно движутся по окружностям радиусом 10 см и 1 м соответственно. У какого тела ускорение больше и во сколько раз, если:
а) скорости тел равны?
б) периоды обращения тел равны?

27. Во сколько раз ускорение точек земной поверхности на экваторе меньше ускорения свободного падения g? Во сколько раз надо было бы уменьшить продолжительность суток, чтобы оно стало равным g?

ньютоновской механики.

Подразумевает ли ускорение, всегда перпендикулярное скорости, круговое движение?

спросил 2 года 3 месяца назад

Изменено 3 месяца назад

Просмотрено 6к раз

$\begingroup$

При круговом движении ускорение всегда перпендикулярно скорости.

Верно ли обратное?

Если да, то есть ли за этим строгое математическое доказательство?

Это вызвало путаницу, когда я узнал о силе Лоренца, и каждый источник, на который я ссылался, цитировал, что «Поскольку эта сила перпендикулярна скорости, она действует как центростремительная сила и, следовательно, движется по кругу»

Всегда ли это подразумевает что ускорение, перпендикулярное скорости, вызывает центростремительную силу?

ньютоновская механика
центростремительная сила

$\endgroup$

$\begingroup$

Условие того, что ускорение перпендикулярно скорости, можно выразить как $$\vec{a}\cdot\vec{v} = 0$$ Используя определение ускорения, мы можем записать это как $$\frac{\textrm{d}\vec{v}}{\textrm{d}t}\cdot\vec{v} = 0$$ $$\frac{1}{2}\frac{\textrm{d}\left(\vec{v}\cdot\vec{v}\right)}{\textrm{d}t} = 0$$ $$\vec{v}\cdot\vec{v} = \textrm{константа}$$ $$||\vec{v}|| = \textrm{константа}$$ значит скорость постоянная.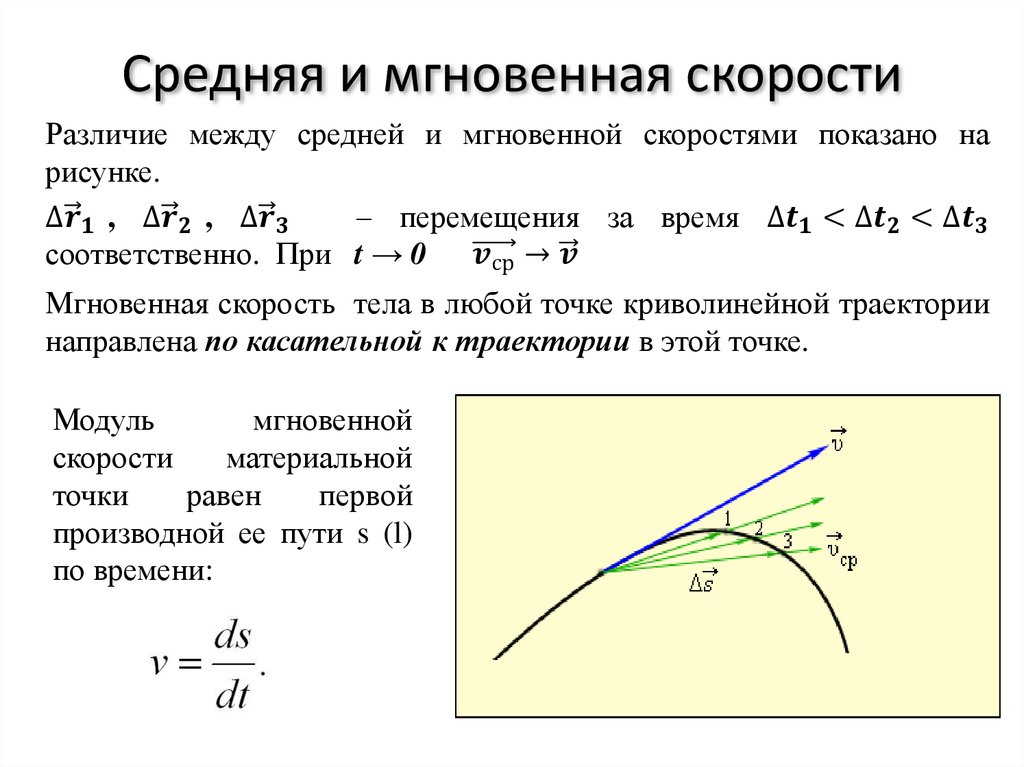 Обратите внимание, что все вышеперечисленные шаги обратимы. Итак, верно и обратное: постоянная скорость также означает, что ускорение перпендикулярно скорости.

Но ничто из вышесказанного не означает, что движение будет круговым. Если ускорение имеет постоянную величину, то вы получите круговое движение (или спиральное движение в 3D). Однако ускорение непостоянной величины не приведет к круговому движению. Представьте себе автомобиль, который движется накатом с постоянной скоростью. Поворот руля заставляет машину поворачивать влево или вправо. Ускорение автомобиля перпендикулярно скорости автомобиля, потому что автомобиль движется с постоянной скоростью. Водитель может в любое время повернуть руль, чтобы выбрать любой извилистый путь, и все равно будет верно, что ускорение всегда перпендикулярно скорости автомобиля из-за вышеприведенного математического вывода.

Ваши источники силы Лоренца предполагают, что магнитное поле однородно в пространстве и постоянно во времени. Существуют и другие виды магнитных полей, которые вызывают некруговое движение. Например, есть магнит, называемый «вигглер» или «ондулятор», который используется в лазерах на свободных электронах. См. рисунок ниже:

Черная волнистая линия — это путь электрона, движущегося через магнитное поле, который попеременно то вверх, то вниз. Переменное магнитное поле создает волнообразные движения в электронном пучке. Поскольку ускорение вызвано магнитными полями, ускорение всегда перпендикулярно скорости электронов. Однако, поскольку магнитное поле не является однородным, индуцированное движение не является круговым.

$\endgroup$

$\begingroup$

Подразумевает ли ускорение, всегда перпендикулярное скорости, круговое движение?

Нет. Ускорение, перпендикулярное скорости, изменяет ТОЛЬКО направление скорости. Скорость остается неизменной, только направление скорости. Перпендикулярное (или нормальное) ускорение меняет траекторию, и все. 9уравнение 2/r$).

Если вы не знакомы с понятием кривизны, то вот простой вывод:

Нормальное ускорение влияет на траекторию движения объекта, но эта траектория зависит от того, каково нормальное ускорение; это не обязательно круглый.

Примером может быть бросок мяча боком — составляющая гравитации будет нормальной к скорости мяча, но вы знаете, что траектория является параболической.

$\endgroup$

$\begingroup$

При круговом движении ускорение всегда перпендикулярно скорости.

Как сказал @user256872, это НЕТ! Вот некоторые математические обработки вы можете сделать.

В полярных координатах, $$\mathbf{v}=\dot{r}\шляпа{r}+r\dot{\theta}\шляпа{\theta}$$ $$\mathbf{a}=(\ddot{r}-r\ddot{\theta})\шляпа{r}+(r\ddot{\theta}+2\dot{r}\dot{\theta} )\шляпа{\тета}$$

Предположим, что они перпендикулярны, тогда $$\mathbf{v}\cdot \mathbf{a}=0$$ или $$\dot{r}(\ddot{r}-r\ddot{\theta})+r\dot{\theta}(r\ddot{\theta}+2\dot{r}\dot{\theta })=0$$

Что не сводится к условиям кругового движения, которое равно $\dot{r}=0$.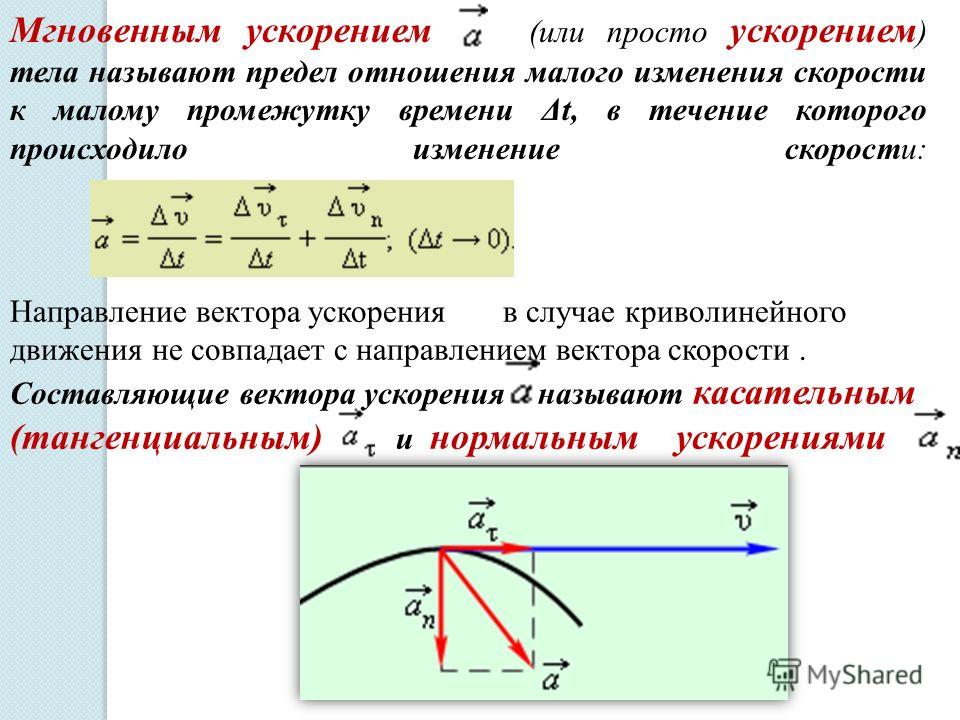

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

4.

3: Ускоренное движение при изменении направления вектора скорости

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 19382

Howard Martin пересмотрено Аланом Нг
University of Wisconsin-Madison

Одно ключевое отличие одномерного движения состоит в том, что в двух измерениях возможно ускорение, даже если скорость постоянна. Напомним, вектор ускорения определяется как производная по времени вектора скорости ( уравнение 4.1.4 ). Это означает, что если вектор скорости изменяется со временем, то вектор ускорения отличен от нуля. Если длина вектора скорости (скорости) постоянна, все еще возможно, что направление вектора скорости изменяется со временем, и, таким образом, вектор ускорения не равен нулю. Это, например, то, что происходит, когда объект движется по кругу с постоянной скоростью (меняется направление вектора скорости).

Рисунок $\PageIndex{1}$: Иллюстрация того, как может измениться направление вектора скорости, когда скорость постоянна.
На рисунке $\PageIndex{1}$ показан вектор скорости $\vec v(t)$ в два разных момента времени, $\vec v_1$ и $\vec v_2$ , а также разность векторов $\Delta \vec v=\vec v_2 — \vec v_1$ между ними. При этом длина вектора скорости не менялась со временем ($||\vec v_1||=||\vec v_2||$). Вектор ускорения определяется выражением:
\[\begin{align} \vec a = \lim_{\Delta t\to 0}\frac{\Delta \vec v}{\Delta t}\end{align}\]
и будет иметь направление, параллельное $\Delta \vec v$, и величину, пропорциональную $\Delta v$. Таким образом, даже если вектор скорости не изменяет амплитуду (скорость постоянна), вектор ускорения может быть ненулевым, если вектор скорости меняет направление .
Запишем вектор скорости $\vec v$ через его величину $v$ и единичный вектор $\hat v$ в направлении $\vec v $: 92}\\ \hat v &= \frac{v_x}{v}\hat x+\frac{v_y}{v}\hat y\\\end{aligned}\]
В самом общем случае со временем может меняться как величина скорости, так и ее направление.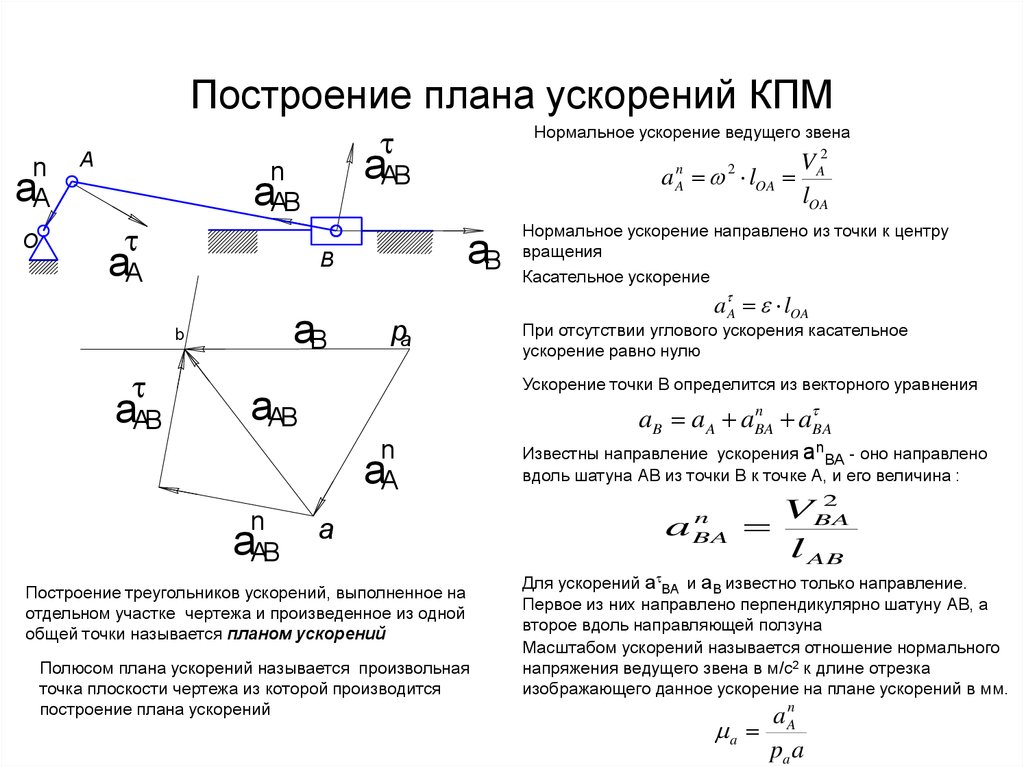 То есть и направление, и величина вектора скорости являются функциями времени:
\[\begin{выровнено} \vec v(t)&=v(t)\шляпа v(t)\end{выровнено}\]
Когда мы берем производную по времени от $\vec v(t)$ для получения вектора ускорения, нам нужно взять производную от произведения двух функций времени, $v(t)$ и $ \шляпа v(t)$. Используя правила взятия производной произведения, вектор ускорения определяется как:
\[\begin{aligned} \vec a &= \frac{d}{dt}\vec v(t)= \frac{d}{dt}v(t)\hat v(t)\nonumber \end {выровнено}\]
\[ \vec a = \frac{dv}{dt}\hat v(t)+v(t)\frac{d\hat v}{dt} \]
и имеет два термина. Первый член, $\frac{dv}{dt}\hat v(t)$, равен нулю, если скорость постоянна ($\frac{dv}{dt}=0$). Второй член, $v(t)\frac{d\hat v}{dt}$, равен нулю, если направление вектора скорости постоянно ($\frac{d\hat v}{dt}= 0$). Однако в общем случае вектор ускорения имеет два члена, соответствующих изменению скорости и изменению направления скорости соответственно.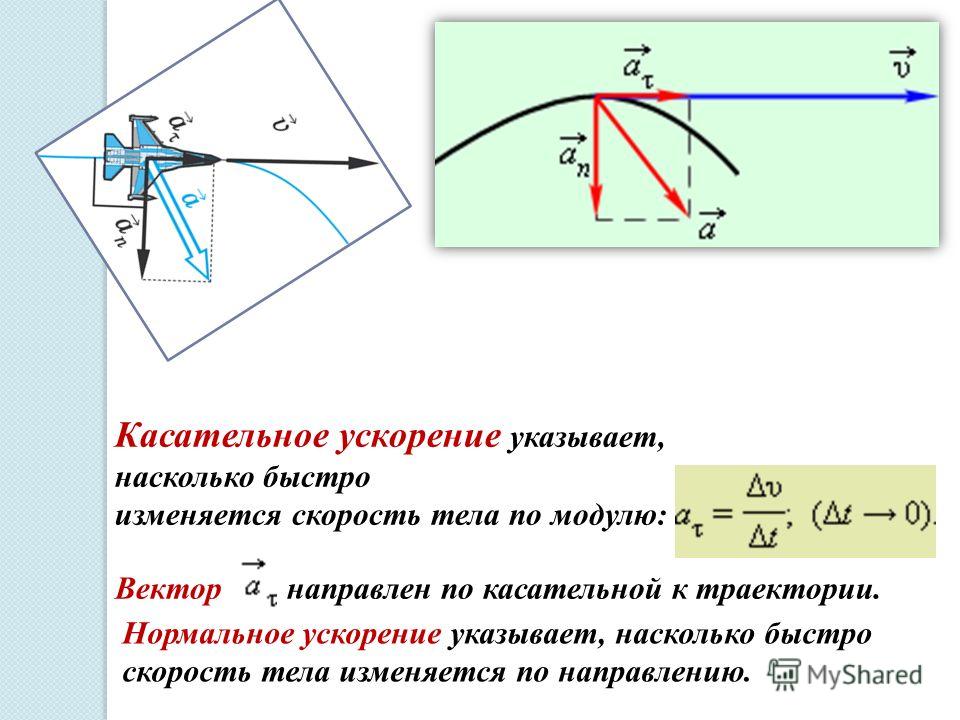 2}}\frac{dv_x}{dt}\hat y\nonumber\\ &=\frac{dv_x}{dt}\hat x — \frac{v_x(t)}{v_y(t)}\frac {dv_x}{dt}\шляпа y\nonumber \end{выровнено}\]
\[\vec a=\frac{dv_{x}}{dt}\left( \hat x — \frac{v_{x}(t)}{v_{y}(t)}\hat y \right )\]
, где большая часть алгебры, которую мы сделали, состояла в том, чтобы разделить $x$ и $y$ компоненты вектора ускорения, и мы использовали цепное правило, чтобы получить производную квадратного корня. Результирующий вектор ускорения показан на рисунке $\PageIndex{2}$ вместе с вектором скорости ¹ .
Рисунок $\PageIndex{2}$: Иллюстрация того, что вектор ускорения перпендикулярен вектору скорости, если скорость постоянна.
Вектор скорости имеет компоненты $v_x$ и $v_y$, что позволяет нам вычислить угол $\theta$, который он составляет с осью $x$:
\[\begin{выровнено} \tan(\theta)=\frac{v_y}{v_x}\end{выровнено}\]
Точно так же вектор, параллельный ускорению, имеет компоненты $1$ и $-\frac{v_x}{v_y}$, что позволяет нам определить угол $\phi$, под которым делает с осью $х$:
\[\begin{aligned} \tan(\phi)=\frac{v_x}{v_y}\end{aligned}\]
Обратите внимание, что $\tan(\theta)$ является инверсией $\tan(\phi)$, или, другими словами, $\tan(\theta)=\cot(\phi)$ , что означает, что $\theta$ и $\phi$ дополняют друг друга и, таким образом, должны в сумме давать $\frac{\pi}{2}$ (90). Это означает, что вектор ускорения перпендикулярен вектору скорости, если скорость постоянна, а направление скорости изменяется .
Другими словами, когда мы записываем вектор ускорения, мы можем идентифицировать две составляющие: $\vec a_{\parallel}(t)$ и $\vec a_{\perp}(t)$:
\[\begin{aligned} \vec a&=\frac{dv}{dt}\hat v(t)+v(t)\frac{d\hat v}{dt}\\ &=\vec a_{ \parallel}(t) + \vec a_{\perp}(t)\\ \следовательно \vec a_{\parallel}(t)&=\frac{dv}{dt}\hat v(t)\\ \ поэтому \vec a_{\perp}(t)&=v\frac{d\hat v}{dt}=\frac{dv_x}{dt} \left(\hat x — \frac{v_x(t)}{ v_y(t)}\шляпа y\right)\end{выровнено}\]
, где $\vec a_{\parallel}(t)$ — составляющая ускорения, параллельная вектору скорости и отвечающая за изменение его величины, а $\vec a_{\perp}(t )$, — составляющая, перпендикулярная вектору скорости и отвечающая за изменение направления движения.
Упражнение $\PageIndex{1}$
Спутник движется по круговой орбите вокруг Земли с постоянной скоростью.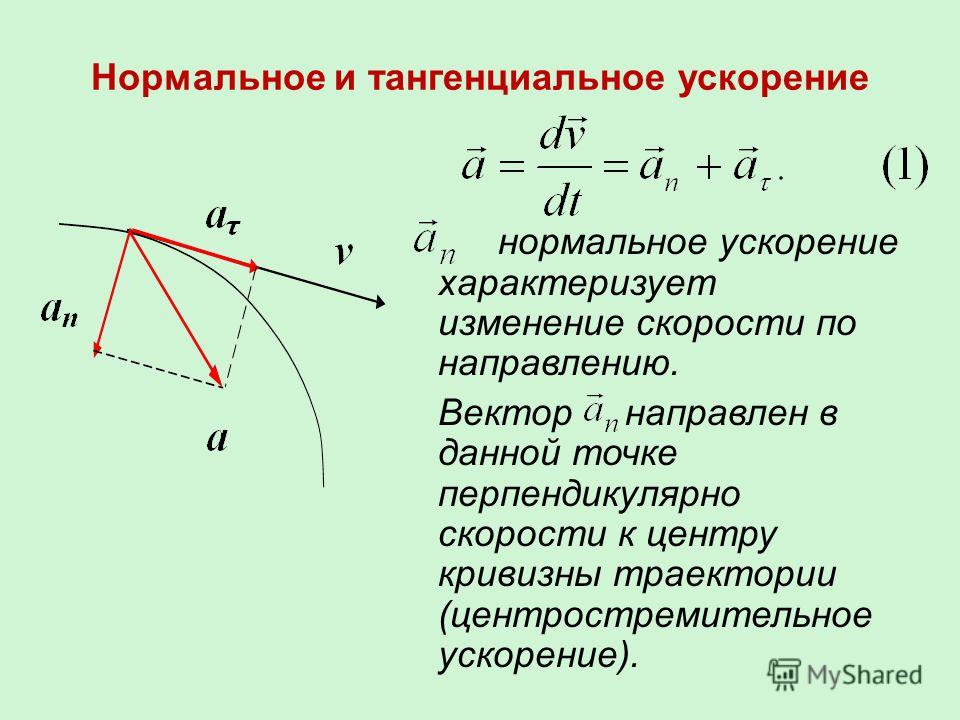 Что можно сказать о его векторе ускорения?
Имеет нулевую величину.
Перпендикулярно вектору скорости.
Он параллелен вектору скорости.
Он находится в направлении, отличном от параллельного или перпендикулярного вектору скорости.
Ответить
1. Скорее, это вектор, параллельный вектору ускорения, который проиллюстрирован, поскольку множитель $\frac{dv_{x}}{dt}$ был опущен (как вы помните, умножение на скаляр только изменяет длина, а не направление)
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
Райан Мартин и др.

Физические основы механики