Теорема о соотношениях между сторонами и углами треугольника
Урок 21. Геометрия 7 класс
Повторив, какие виды треугольников выделяют в зависимости от величины угла, а также теорему о сумме углов треугольника, приводим формулировку теоремы о соотношениях между сторонами и углами треугольника и доказываем её. Также на уроке рассматриваем признак равнобедренного треугольника.
Конспект урока «Теорема о соотношениях между сторонами и углами треугольника»
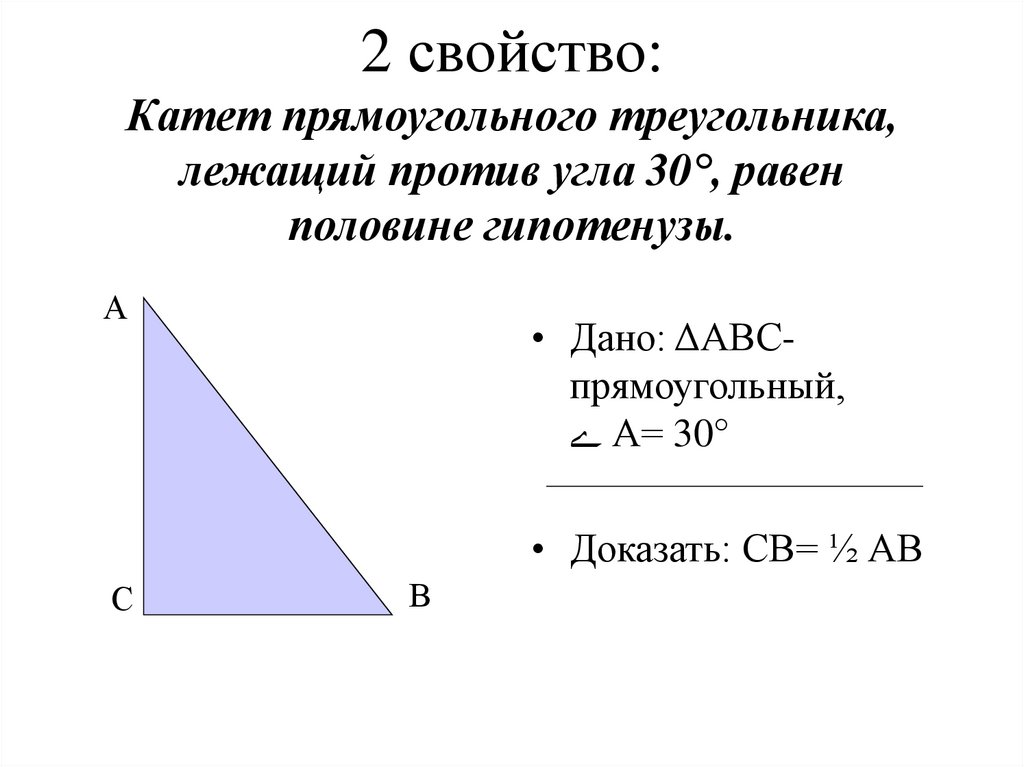
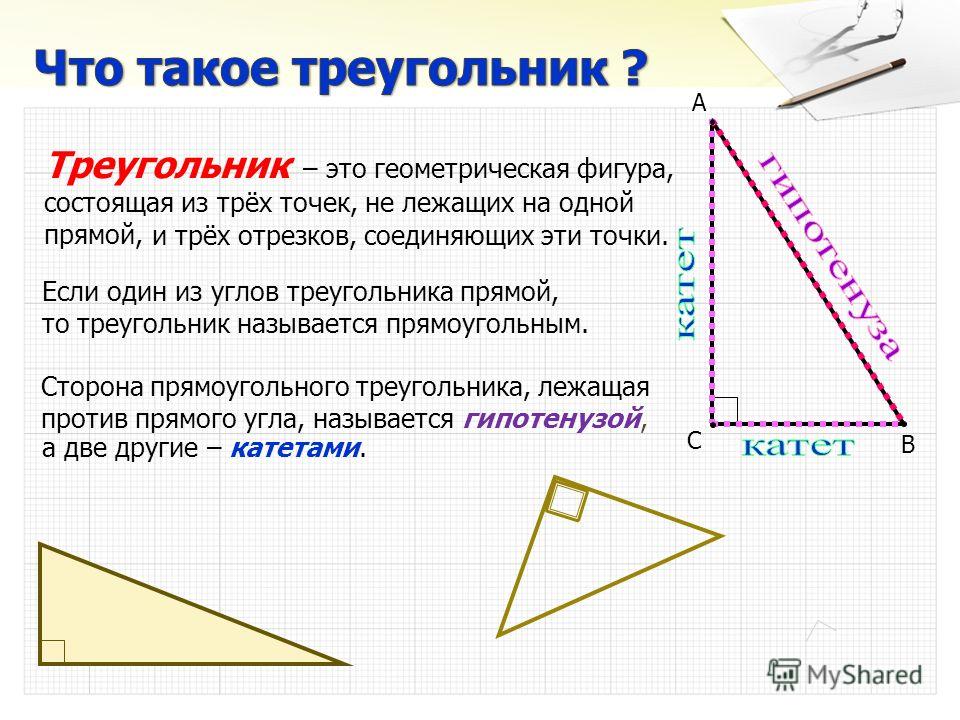
Давайте вспомним, что по величине углов выделяют остроугольные, прямоугольные и тупоугольные треугольники. А также отметим, что сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами.
Сумма углов любого треугольника равна 180 градусов.
Теорема:
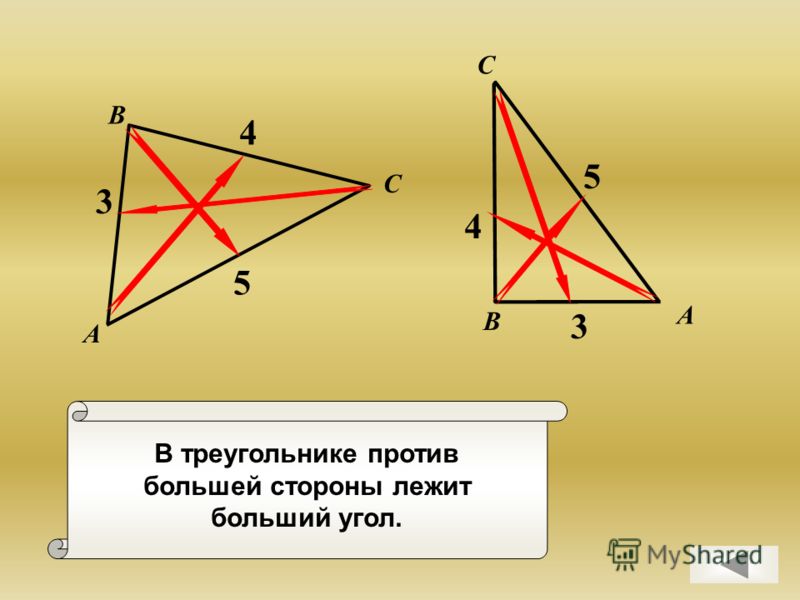
В
треугольнике против большей стороны лежит больший угол, а против большего угла
лежит большая сторона.
Доказательство:
1. Докажем, что против большей стороны лежит больший угол.
Возьмём некоторый треугольник АВС. Пусть АВ>ВС. Отложим сторону ВС на стороне АВ, то есть отрезок ВЕ=ВС.
Так как получается, что треугольник ЕВС — равнобедренный, то углы при основании равны.
В треугольнике АЕС ∠А<∠1, так как внешний угол больше любого внутреннего, не смежного с ним. В треугольнике АВС ∠С>∠2.
Получаем:
То есть, против большей стороны АВ лежит больший ∠С. Что и требовалось доказать.
2. Докажем, что против большего угла лежит большая сторона.
Пусть ∠С>∠А треугольника АВС.
Предположим, что АВ<ВС, то по доказанной первой части данной теоремы ∠С<∠А. Получили противоречие.
Если АВ=ВС, то получается, что треугольник АВС равнобедренный, а тогда ∠С=∠А. Снова противоречие.
Так
как в каждом из предыдущих случаев наше предположение неверно, тогда получаем,
что АВ>ВС.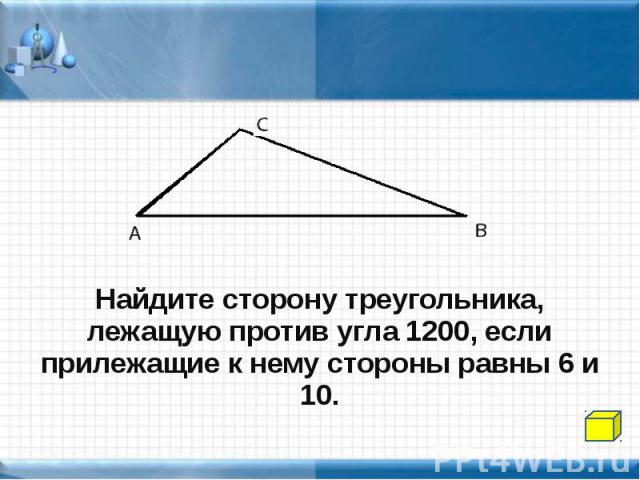
Теорема доказана.
Следствие:
В прямоугольном треугольнике АВС гипотенуза АВ больше катетов АС и ВС. Действительно, верно, так как гипотенуза лежит против прямого угла, а катеты — против острых, градусная мера которых меньше 90 градусов.
Признак равнобедренного треугольника:
Если два угла треугольника равны, то треугольник равнобедренный.
Доказательство:
Пусть АВС треугольник, у которого углы А и С равны. Докажем, что равны стороны АВ и ВС, лежащие против этих углов.
Предположим, что АВ>ВС. Тогда по предыдущей теореме ∠С, лежащий против большей стороны АВ, будет больше ∠А, лежащего против меньшей стороны ВС. Получили противоречие условию равенства углов А и С.
Предположение неверно и стороны АВ и ВС равны, то есть треугольник АВС является равнобедренным. Что и требовалось доказать.
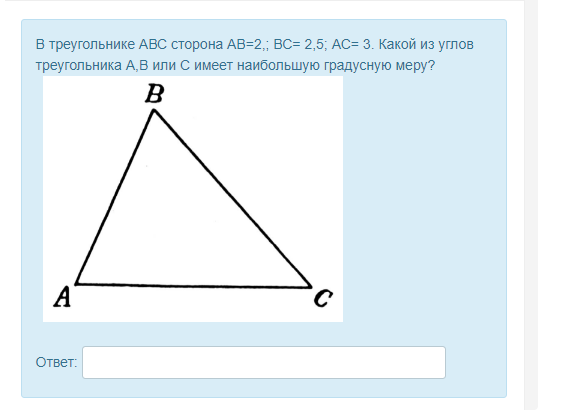
Пример.
В
треугольнике АВС сторона АВ=9 см, а сторона ВС=14 см.
По теореме о соотношениях между сторонами и углами треугольника против большей стороны лежит больший угол. Следовательно, получаем:
Так как ∠A лежит против большей стороны ВС.
Пример.
В треугольнике АВС ∠А=45 градусов, а ∠В=65 градусов. Верно ли, что сторона АС больше каждой из сторон АВ и ВС?
По теореме о сумме углов треугольника, получаем:
Воспользовавшись теоремой о соотношениях между сторонами и углами треугольника, выяснили, так как против большего угла лежит большая сторона, а в нашем случае большую градусную меру имеет ∠С, то большей стороной треугольника является сторона АВ.
Ответ: неверно, что сторона АС больше каждой из сторон АВ и ВС
Предыдущий урок 20 Остроугольный, прямоугольный и тупоугольный треугольники
Следующий урок 22 Неравенство треугольника
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 7 класс
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
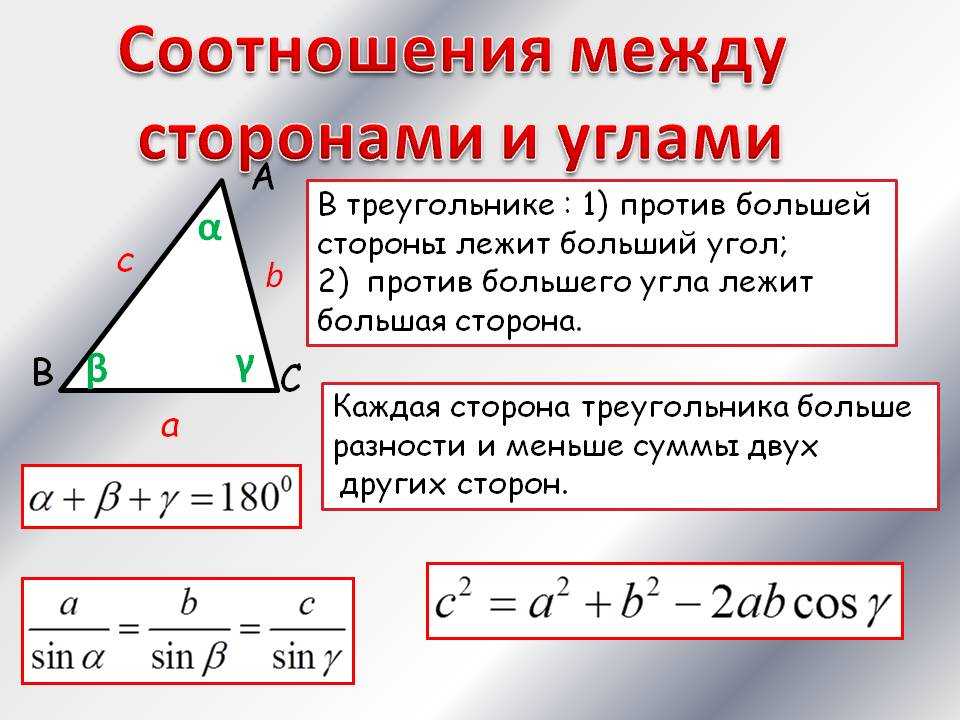
| Фигура | Рисунок | Формулировка |
| Треугольник | Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. | |
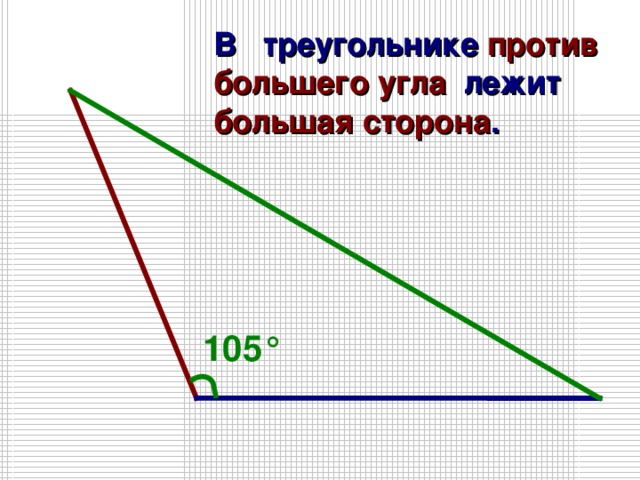
| Большая сторона треугольника | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| | ||
| Углы треугольника | Сумма углов треугольника равна 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство | |
| Больший угол треугольника | Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. | |
| Меньший угол треугольника | Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. | |
| Теорема косинусов | a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство | |
| Теорема синусов | , где R – радиус описанной окружности. Посмотреть доказательство |
| Треугольник | |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. | |
| Большая сторона треугольника | |
| Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | |
| Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | |
| Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | |
| Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| | |
| Углы треугольника | |
Сумма углов треугольника равна 180° Посмотреть доказательство | |
| Внешний угол треугольника | |
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство | |
| Больший угол треугольника | |
Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. | |
| Меньший угол треугольника | |
Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. | |
| Теорема косинусов | |
a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство | |
| Теорема синусов | |
, где R – радиус описанной окружности. Посмотреть доказательство | |
| Треугольник |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. |
| Большая сторона треугольника |
Свойство большей стороны треугольника: Против большей стороны треугольника лежит больший угол |
| Больший угол треугольника |
Свойство большего угла треугольника: Против большего угла треугольника лежит большая сторона |
| Меньшая сторона треугольника |
Свойство меньшей стороны треугольника: Против меньшей стороны треугольника лежит меньший угол |
| Меньший угол треугольника |
Свойство меньшего угла треугольника: Против меньшего угла треугольника лежит меньшая сторона |
| Длины сторон треугольника |
Неравенства трегольника: Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| |
| Углы треугольника |
Свойство углов треугольника: Сумма углов треугольника равна 180° Посмотреть доказательство |
| Внешний угол треугольника |
Свойство внешнего угла треугольника: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство |
| Больший угол треугольника |
Свойство большего угла треугольника: Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. |
| Меньший угол треугольника |
Свойство меньшего угла треугольника: Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. |
| Теорема косинусов |
Теорема косинусов: a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство |
| Теорема синусов |
Свойство меньшего угла треугольника: , где R – радиус описанной окружности. Посмотреть доказательство |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Самаров
4.25: Сравнение углов и сторон в треугольниках
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4822
Теоремы о неравенстве и порядок углов и сторон треугольников.
Теоремы SAS и SSS о неравенстве
Посмотрите на треугольник ниже. Даны стороны треугольника. Сможете ли вы определить, какой из углов больше? Наибольший угол будет напротив 18, потому что это самая длинная сторона. Точно так же наименьший угол будет лежать напротив 7, самой короткой стороны.
Рисунок \(\PageIndex{1}\) Эта идея на самом деле является теоремой: если одна сторона треугольника длиннее другой стороны, то угол, противоположный более длинной стороне, будет больше, чем угол, противолежащий более короткой стороне.
Верно и обратное: если один угол в треугольнике больше другого угла в этом треугольнике, то сторона, противоположная большему углу, будет длиннее стороны, противоположной меньшему углу.
Мы можем расширить эту идею до двух теорем, которые помогут нам сравнить стороны и углы в двух треугольниках. Если у нас есть два конгруэнтных треугольника \(\Delta ABC\) и \(\Delta DEF\), отмеченные ниже:
Рисунок \ (\PageIndex{2}\)Следовательно, если \(AB=DE\), \(BC=EF\) и \(m\угол B=m\угол E\), то \(AC=DF\ ).
Теперь составим \(m\угол B>m\угол E\). Получится ли это \(AC>DF\)? Да. Эта идея называется теоремой SAS о неравенстве .
Рисунок \(\PageIndex{3}\) Теорема SAS о неравенстве: Если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но угол между ними имеет большую меру, чем угол между ними другого треугольника, то третья сторона первого треугольника длиннее третьей стороны второго треугольника.
Если \(\overline{AB}\cong \overline{DE}\), \(\overline{BC}\cong \overline{EF}\) и \(m \угол B>m\угол E\), затем \(\overline{AC}>\overline{DF}\).
Если мы знаем третьи стороны в отличие от углов, противоположная идея также верна и называется Теорема о неравенстве SSS .
SSS Теорема о неравенстве: Если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но третья сторона первого треугольника длиннее третьей стороны второго треугольника, то внутренний угол первого треугольника две конгруэнтные стороны больше, чем угол между двумя конгруэнтными сторонами второго треугольника.
Рисунок \(\PageIndex{5}\)Если \(\overline{AB}\cong \overline{DE}\), \(\overline{BC}\cong \overline{EF}\) и \(\ overline{AC}>\overline{DF}\), затем\( m\угол B>m\угол E\).
Что, если бы вам сказали, что стороны треугольника равны 3, 4 и 5? Как определить, какой из углов треугольника больше? Самый маленький?
youtube.com/embed/P9RmhYBwcDk?vq=hd1080″ frameborder=»0″ allowfullscreen=»true»> Пример \(\PageIndex{1}\)
Если \(\overline{XM}\) является медианой \(\Delta XYZ\) и \(XY>XZ\), что мы можем сказать о \(m\угол 1\) и \(m\угол 2\)?
Рисунок \(\PageIndex{6}\)Решение
M является серединой \(\overline{YZ}\), поэтому \(YM=MZ\). \(MX=MX\) по рефлексивному свойству, и мы знаем \(XY>XZ\).
Мы можем использовать обратную теорему о неравенстве SSS, чтобы сказать \(m\угол 1>m\угол 2\).
Пример \(\PageIndex{2}\)
Ниже показан равнобедренный треугольник \(\Delta ABC\). Перечислите все, что вы можете о сторонах и углах треугольника и почему.
Рисунок \(\PageIndex{7}\)Решение
M является серединой \(\overline{YZ}\), поэтому \(YM=MZ\). \(MX=MX\) по рефлексивному свойству, и мы знаем \(XY>XZ\).
\(AB=BC\), потому что он дан.
\(m\угол A=m\угол C\), потому что если стороны равны, то их противоположные углы должны быть равны.
.
\(AD Пример \(\PageIndex{3}\) Перечислите стороны по порядку, от самой короткой до самой длинной. 9{\circ}\) — наименьший угол, поэтому \(AB\) — самая короткая сторона. По порядку ответ: \(AB\), \(BC\), \(AC\). Пример \(\PageIndex{4}\) Перечислите углы по порядку, от большего к меньшему. Решение Как и в случае со сторонами, наибольший угол находится напротив самой длинной стороны. Самая длинная сторона равна \(BC\), поэтому наибольший угол равен \(\угол A\). Далее будет \(\угол B\), а затем \(\угол C\). Пример \(\PageIndex{5}\) 9{\circ}\). Опять же, по теореме, представленной в этом разделе, порядок сторон от наименьшей к наибольшей таков: \(BD\), \(CD\) и \(BC\). По теореме о неравенстве SAS мы знаем, что \(BC>DE\), поэтому порядок всех сторон будет следующим: \(BD\), \(CE\), \(CD\), \(DE \), \(ДО Н. В вопросах 1-3 перечислите стороны в порядке от самой короткой до самой длинной. Чтобы просмотреть ответы на вопросы, откройте этот PDF-файл и найдите раздел 5.6.
Э\). Обзор
Обзор (Ответы)
Ресурсы
Словарь
Срок Определение Теорема SAS о неравенстве 
Теорема SSS о неравенстве Теорема о неравенстве SSS утверждает, что если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но третья сторона первого треугольника длиннее третьей стороны второго треугольника, то угол между двумя сторонами первого треугольника конгруэнтных сторон больше, чем угол между двумя конгруэнтными сторонами второго треугольника. Теорема о сумме треугольников Теорема о сумме треугольников утверждает, что три внутренних угла любого треугольника в сумме составляют 180 градусов.
Дополнительные ресурсы
Интерактивный элемент
ВИДЕО: Сравнение углов и сторон в Треугольниках Принципы — Основные
Действия: Сравнение углов и сторон в Треугольнике. Вопросы
Исследование.
0023 Практика: сравнение углов и сторон треугольников
Реальный мир: теорема о сумме треугольников
Эта страница под названием 4.25: Сравнение углов и сторон в треугольниках распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
ck12.org/c/geometry
- источник@https://www.
ck12.org/c/geometryОбъяснение урока: Неравенство в одном треугольнике: сравнение сторон
В этом объяснении мы научимся составлять неравенства, касающиеся длин сторон треугольника, учитывая меры углов треугольника.
В равнобедренном треугольнике, как мы можем вспомнить, углы, противоположные сторонам равной длины, имеют одинаковую меру. Верно и обратное этому утверждению: если в треугольнике два угла равны, то и стороны, противолежащие этим углам, имеют одинаковую длину. Мы можем использовать эту идею, чтобы рассмотреть, что произойдет, если у нас есть два угла в треугольнике с различными мерами.
Мы можем начать с рассмотрения равнобедренного треугольника. Мы знаем, что углы, противолежащие сторонам равной длины, имеют одинаковую меру. Мы можем сравнить длины
и измеряет углы, изменяя основание треугольника. Если мы уменьшим один из углов при основании (оставив третий угол без изменений),
тогда другой угол при основании должен увеличиться, так как сумма внутренних углов постоянна и равна 180°.
Мы также можем видеть, что это уменьшает длину стороны, противоположной меньшему углу. Другими словами, против меньшей стороны лежит меньший угол. Мы можем проследить тот же процесс, если увеличим размеры одного из углов у основания.
Поскольку мы увеличили размер одного угла, другой угол должен уменьшиться. Мы также можем видеть, что мы увеличили длину противоположной стороны. угол большей меры.
Этот результат верен в общем случае и называется теоремой сравнения сторон в треугольниках.
Теорема: Теорема сравнения сторон в треугольниках
Если у нас есть треугольник, в котором два угла имеют неравные меры, то сторона, лежащая напротив большего угла, длиннее стороны, противоположной меньшему углу. В частности, рассмотрим △𝐴𝐵𝐶.
Если мы знаем, что 𝑚∠𝐵>𝑚∠𝐴, то 𝑏>𝑎.
Также стоит отметить, что мы можем применить этот результат с обратным неравенством. В частности, если у нас есть треугольник, две стороны которого имеют неравные длины,
тогда сторона, лежащая против меньшего угла, короче, чем сторона, лежащая против угла с большей мерой.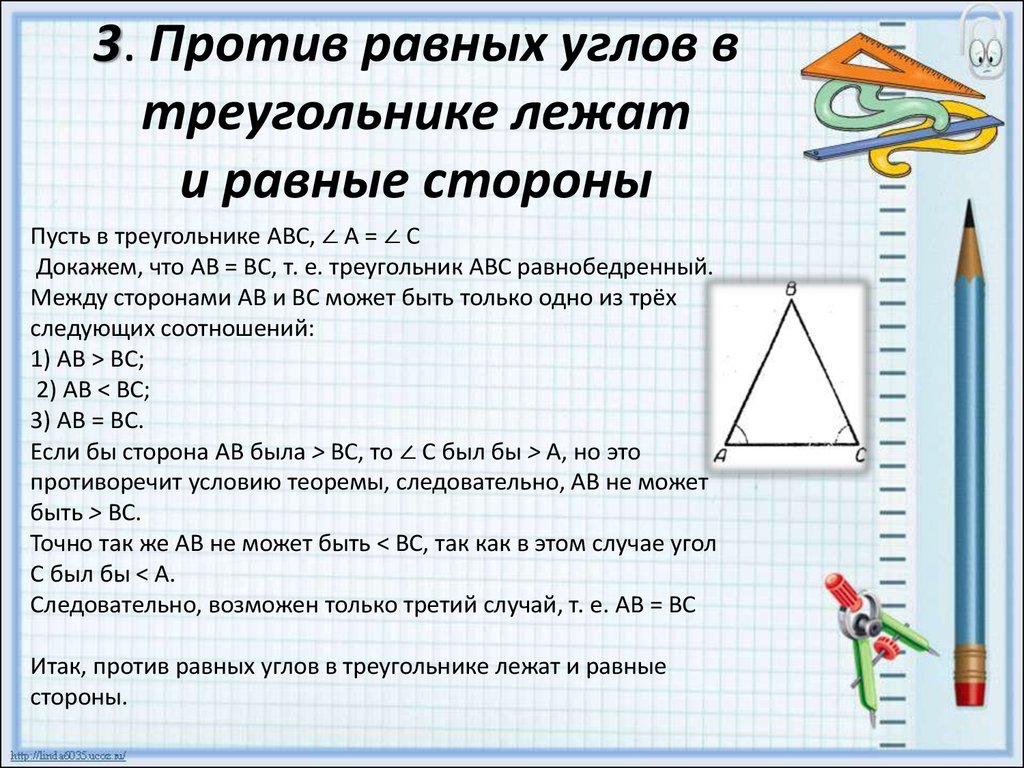
Давайте посмотрим на пример применения этого результата для построения неравенства длин сторон треугольника с использованием мер его углов.
Пример 1. Соотношение между сторонами и соответствующими углами в треугольнике
Расположите длины сторон △𝐴𝐵𝐶 от наименьшей к наибольшей.
Ответ
Нам даны две меры внутренних углов треугольника, и мы должны использовать их, чтобы расположить длины сторон в порядке возрастания. Мы можем сделать это, вспомнив, что теорема сравнения сторон для треугольников говорит нам, что если у нас есть треугольник, в котором два угла имеют неравные меры, тогда сторона, противоположная большему углу, длиннее стороны, противоположной меньшему углу.
Мы знаем, что 94>59∘∘, поэтому мы можем заключить, что сторона, противоположная ∠𝐵, длиннее, чем сторона, противоположная ∠𝐶. Таким образом, 𝐴𝐶>𝐴𝐵.
Мы можем найти меру ∠𝐴, вспомнив, что сумма мер внутренних углов треугольника равна
180∘.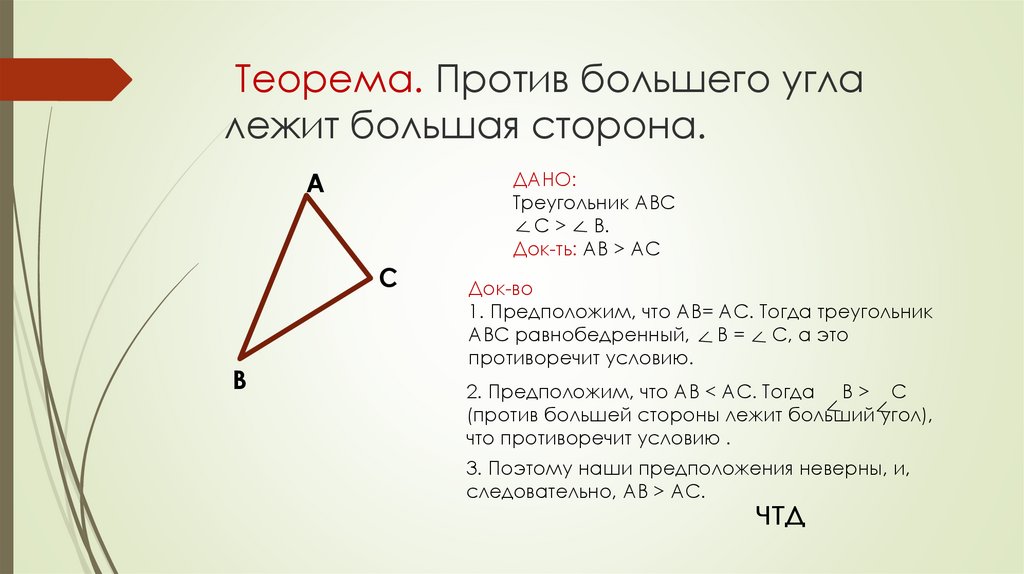
Поэтому,
𝑚∠𝐴+𝑚∠𝐵+𝑚∠𝐶=180,∘
Мы можем заменить меры ∠𝐵 и ∠𝐶, чтобы получить 𝑚∠𝐴+59+94=180.∘∘∘
Затем находим 𝑚∠𝐴: 𝑚∠𝐴=180−94−59𝑚∠𝐴=27,∘∘∘∘
Теперь мы видим, что 𝑚∠𝐶>𝑚∠𝐴, значит, сторона напротив ∠𝐶 должна быть длиннее чем сторона, противоположная ∠𝐴. Таким образом, 𝐴𝐵>𝐵𝐶.
Мы можем объединить эти два неравенства в составное неравенство: 𝐴𝐶>𝐴𝐵>𝐵𝐶.
Наконец, нам предлагается написать длины сторон от наименьшей к наибольшей. Это означает, что мы начинаем с самой короткой стороны и заканчиваем самой длинной стороной.
Мы можем обратить составное неравенство, чтобы получить стороны, перечисленные от наименьшей к наибольшей длине: 𝐵𝐶,𝐴𝐵,𝐴𝐶.
В нашем следующем примере мы будем использовать теорему сравнения сторон в треугольниках, чтобы определить, какая из двух сторон в треугольнике длиннее, используя меры двух внешних углов треугольника.
Пример 2. Заполнение неравенств для длин сторон треугольника
Как на рисунке сравнить 𝐴𝐵 и 𝐵𝐶?
Ответ
Мы хотим сравнить длины двух сторон треугольника △𝐴𝐵𝐶.
Мы можем сделать это, вспомнив, что теорема бокового сравнения
в треугольниках говорит нам, что если у нас есть треугольник, в котором два угла имеют неравные меры, то сторона, противоположная большему углу, длиннее, чем сторона
напротив меньшего угла.
Это означает, что мы можем сравнивать длины сторон треугольника, сравнивая величины углов, противоположных сторонам. Мы можем отметить углы напротив каждой стороны на схеме.
Мы видим, что ∠𝐴𝐶𝐵 и ∠𝐴𝐶𝐷 образуют прямой угол, поэтому сумма их мер дать 180∘. Таким образом, 𝑚∠𝐴𝐶𝐵+𝑚∠𝐴𝐶𝐷=180,∘
На диаграмме видно, что 𝑚∠𝐴𝐶𝐷=108∘, поэтому мы можем заменить это значение в уравнение, чтобы получить 𝑚∠𝐴𝐶𝐵+108=180.∘∘
Затем мы можем найти 𝑚∠𝐴𝐶𝐵𝑚∠𝐴𝐶𝐵=180−108=72.∘∘∘
Теперь мы можем напрямую найти 𝑚∠𝐵𝐴𝐶, заметив, что противоположный внешний угол равен ∠𝐶𝐶 △𝐴𝐵𝐶 в ∠𝐵𝐴𝐶 и ∠𝐴𝐶𝐵.
Напомним, что мера внешнего угла в треугольнике равна сумме мер противоположных внутренних углов.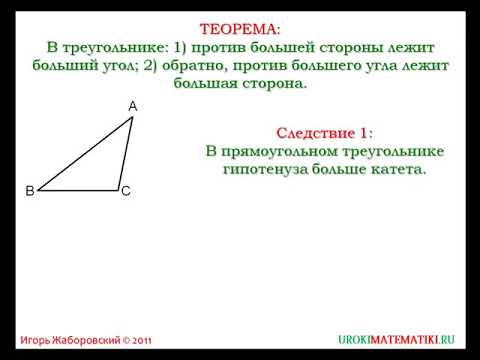
Таким образом,
𝑚∠𝐶𝐵𝐸=𝑚∠𝐵𝐴𝐶+𝑚∠𝐴𝐶𝐵.
Мы знаем, что 𝑚∠𝐶𝐵𝐸=128∘ и 𝑚∠𝐴𝐶𝐵=72∘, поэтому мы можем подставить эти значения в уравнение, чтобы получить 128=𝑚∠𝐵𝐴𝐶+72.∘∘
Мы можем вычесть 72∘ из обеих частей уравнения, чтобы получить 𝑚∠𝐵𝐴𝐶=128−72=56.∘∘∘
Мы можем добавить это на диаграмму.
Мы видим, что угол напротив 𝐴𝐵 имеет большую меру, чем угол напротив 𝐵𝐶; следовательно, это должна быть более длинная сторона.
Следовательно, 𝐴𝐵>𝐵𝐶.
В нашем следующем примере мы сравним четыре пары длин сторон в треугольниках, используя теорему сравнения сторон в треугольниках.
Пример 3. Заполнение неравенств для длин сторон треугольника
Рассмотрим данную схему.
Заполните пробелы в следующих утверждениях, используя >, или =.
- 𝐴𝐶𝐴𝐵
- 𝐴𝐵𝐵𝐶
- 𝐷𝐶𝐴𝐷
- 𝐴𝐷
- 04 310
Сначала мы вспомним теорему сравнения сторон в треугольниках, которая говорит нам, что если у нас есть треугольник, в котором два угла имеют неравные меры, тогда сторона, противоположная большему углу, длиннее стороны, противоположной меньшему углу.
Это означает, что мы можем сравнивать длины сторон треугольника, сравнивая величины углов, противоположных сторонам.
Часть 1
Мы хотим сравнить длины 𝐴𝐶 и 𝐴𝐵. Мы можем начать с выделения эти отрезки и противоположные им углы на диаграмме.
Заметим, что 90>45∘∘, поэтому сторона, противоположная прямому углу, должна быть длиннее стороны, противоположной углу измерения 45∘.
Следовательно, 𝐴𝐶>𝐴𝐵.
Часть 2
Мы можем следовать тому же процессу, чтобы сравнить длины 𝐴𝐵 и 𝐵𝐶. Выделим на диаграмме оба отрезка прямой, а также углы, противоположные каждой стороне.
Мы можем определить меру угла, противоположного 𝐵𝐶, сложив меры двух углов, которые в сумме дают форма ∠𝐵𝐴𝐶. У нас есть 𝑚∠𝐵𝐴𝐶=𝑚∠𝐵𝐴𝐷+𝑚∠𝐷𝐴𝐶=20+25=45.∘∘∘
Поскольку оба угла имеют одинаковые меры, мы можем заключить, что △𝐴𝐵𝐶 равнобедренный с 𝐵𝐶 .
Часть 3
Чтобы сравнить длины 𝐷𝐶 и 𝐴𝐷, мы можем сначала выделить оба сегмента линии на схеме, а также углы, противоположные каждой стороне.
Поскольку мера угла, противоположного 𝐷𝐶, меньше, чем мера угла, противоположного 𝐴𝐷, мы можем заключить, что 𝐷𝐶 короче 𝐴𝐷.
Следовательно, 𝐷𝐶𝐴𝐷.
Часть 4
Наконец, чтобы сравнить длины 𝐴𝐷 и 𝐴𝐶, мы выделяем оба отрезка линии на схеме, а также углы, противоположные каждой стороне.
Похоже, что мера ∠𝐴𝐷𝐶 больше, чем мера ∠𝐴𝐶𝐷. Однако для должной осмотрительности мы должны это проверить. Мы можем найти меру этого угла, используя тот факт, что сумма мер внутренних углов треугольника равна 180∘. Применяя это к △𝐴𝐶𝐷, мы имеем 𝑚∠𝐴𝐶𝐷+𝑚∠𝐶𝐴𝐷+𝑚∠𝐴𝐷𝐶=180.∘
Подстановка известных величин угла в уравнение дает 45+25+𝑚∠𝐴𝐷𝐶=180.∘∘∘
Тогда мы можем найти 𝑚∠𝐴𝐷𝐶: 𝑚∠𝐴𝐷𝐶=180−45−25=110.∘∘∘∘
Теперь мы можем видеть, что 𝑚∠𝐴𝐷𝐶>𝑚∠𝐴𝐶𝐷, поэтому сторона, противоположная ∠𝐴𝐷𝐶 длиннее стороны, противоположной ∠𝐴𝐶𝐷.
Следовательно, 𝐴𝐷𝐴𝐶.
В предыдущем примере мы видели, что сторона, противоположная прямому углу прямоугольного треугольника, длиннее другой стороны.
Можно показать, что этот результат верен в общем случае.Мы знаем, что сумма внутренних углов треугольника равна 180∘. Итак, в этом треугольнике имеем 𝑚∠𝐴+𝑚∠𝐵+𝑚∠𝐶=180,∘
Подстановка 𝑚∠𝐵=90∘ в уравнение и преобразование дает нам 𝑚∠𝐴+90+𝑚∠𝐶=180𝑚∠𝐴+𝑚∠𝐶=90.∘∘∘
Поскольку меры углов должны быть положительными, мы можем заметить, что оба этих угла имеют меры меньше 90∘. В частности, это говорит нам о том, что ∠𝐵 имеет наибольшую меру в треугольнике. Следовательно, сторона, противоположная прямому углу в прямом треугольник — самая длинная сторона. Мы называем это гипотенузой прямоугольного треугольника.
Это согласуется с нашим знанием теоремы Пифагора. Напомним, что это говорит нам о том, что в прямоугольном треугольнике квадрат длины гипотенузы равен к сумме квадратов длин двух других сторон. В нашем прямоугольном треугольнике выше это 𝑏=𝑎+𝑐.
Поскольку 𝑎,𝑏 и 𝑐 — длины, все они положительны, поэтому мы можем отметить, что 𝑏>𝑎 и 𝑏>𝑐.
Таким образом, гипотенуза должна быть наибольшей стороной.В следующем примере мы докажем неравенство, касающееся длин прямых в геометрической конструкции.
Пример 4. Доказательство неравенства, касающегося длин сторон треугольника
На рисунке заполните пробел знаком >, или =: 𝐴𝐶𝐵𝐶.
Ответ
Мы хотим сравнить длины двух сторон треугольника. Мы можем сделать это, вспомнив, что более длинная сторона будет противоположна углу с большей мерой. Начнем с выделения сторон в данном неравенстве и углов, противолежащих каждой стороне. Мы будем называть угловые меры 𝑥 и 𝑦 как показано.
Мы видим, что углы при 𝐴 составляют прямой угол, поэтому сумма их величин дает 180∘. Таким образом, 𝑥+50+70=180.∘∘∘
Решение для 𝑥 дает 𝑥=180−50−70=60.∘∘∘∘
Мы можем найти 𝑦, заметив, что это внутренний угол, альтернативный другому углу в пересечении параллельных прямых.
Затем мы можем найти 𝑦, используя тот факт, что сумма мер прямого угла равна 180∘ или отметив, что 𝑦 — это соответствующий угол измерения 70 ∘ на диаграмме.
Поскольку угол напротив 𝐴𝐶 имеет большую меру, чем угол напротив 𝐵𝐶, мы можем заключить, что 𝐴𝐶 длиннее, чем 𝐵𝐶. Следовательно, 𝐴𝐶>𝐵𝐶.
Мы можем доказать теорему сравнения сторон, рассмотрев треугольник, в котором 𝑚∠𝐴>𝑚∠𝐵.
Сначала мы можем показать, что 𝐵𝐶 и 𝐴𝐶 не имеют одинаковой длины; если они это сделали, то △𝐴𝐵𝐶 будет равнобедренным треугольником, так как у него две стороны одинаковой длины. Напомним, что углы, лежащие против сторон равной длины должны иметь равные размеры. Это означало бы, что 𝑚∠𝐴=𝑚∠𝐵, но нам говорят, что 𝑚∠𝐴>𝑚∠𝐵, так что это не может быть правдой. Следовательно, 𝐵𝐶 и 𝐴𝐶 должны иметь неравную длину.
Мы также можем показать, что 𝐴𝐶 не может быть длиннее, чем 𝐵𝐶. Напомним, что сравнение углов Теорема о треугольниках говорит нам, что если у нас есть треугольник, у которого две стороны имеют неравные длины, то угол, противолежащий большей стороне, имеет большую меру, чем угол, противоположный меньшей стороне.
Если предположить, что 𝐴𝐶 длиннее, чем 𝐵𝐶, то эта теорема говорит нам, что угол, противоположный 𝐴𝐶 должен иметь большую меру, чем угол, противолежащий 𝐵𝐶. Другими словами, у нас было бы 𝑚∠𝐵>𝑚∠𝐴. Однако нам говорят, что 𝑚∠𝐴>𝑚∠𝐵, так что такого быть не может. Следовательно, 𝐴𝐶 не может быть длиннее 𝐵𝐶.
Так как 𝐵𝐶 и 𝐴𝐶 не могут иметь одинаковую длину и 𝐴𝐶 не может быть длиннее 𝐵𝐶, есть только одна последняя возможность; 𝐵𝐶 длиннее, чем 𝐴𝐶.
В нашем следующем примере мы будем использовать теорему сравнения сторон для сравнения длин в заданной конструкции.
Пример 5. Сравнение длин сторон треугольника с использованием теоремы о сравнении сторон
Рассмотрим показанный рисунок.
Заполните пробел >, или =: 𝐴𝐵𝐵𝐶.
Ответ
Из диаграммы видно, что 𝐴𝐷=𝐷𝐶, поэтому треугольник 𝐴𝐷𝐶 равнобедренный. Углы, противоположные сторонам равных длин должны быть конгруэнтны. Мы можем добавить эти конгруэнтные углы на диаграмму.
Теперь мы можем вспомнить, что теорема сравнения сторон в треугольниках говорит нам, что если у нас есть треугольник, в котором два угла имеют неравные меры, то сторона, противоположная большему углу, длиннее стороны, противоположной меньшему углу.
Мы видим, что ∠𝐵𝐴𝐶 противоположно 𝐵𝐶 и ∠𝐴𝐶𝐵 противоположно 𝐴𝐵. Мы также можем видеть из диаграммы, что ∠𝐵𝐴𝐶 имеет большую меру, чем ∠𝐴𝐶𝐵, так как это комбинация двух углов, один из которых имеет равную меру ∠𝐴𝐶𝐵: 𝑚∠𝐵𝐴𝐶=𝑚∠𝐵𝐴𝐷+𝑚∠𝐷𝐴𝐶=𝑚∠𝐵𝐴𝐷+𝑚∠𝐴𝐶𝐵.
Можно сделать вывод, что сторона, лежащая против угла с меньшей мерой, короче. Следовательно, 𝐴𝐵𝐵𝐶.
Мы можем использовать теорему сравнения углов в треугольниках, чтобы доказать много полезных геометрических результатов. Например, рассмотрим △𝐴𝐵𝐶 и отрезок 𝐴𝐷 такой, что 𝐴𝐷⟂⃖⃗𝐵𝐶.
Мы можем показать, что 𝐴𝐷 — кратчайший отрезок от 𝐴 до ⃖⃗𝐵𝐶. Рассмотрим любую другую точку 𝐸∈⃖⃗𝐵𝐶.
Мы видим, что △𝐴𝐷𝐸 — прямоугольный треугольник, поэтому его гипотенуза — самая длинная сторона.
Таким образом,
𝐴𝐸>𝐴𝐷.Это верно для любой точки 𝐸 на ⃖⃗𝐵𝐶, поэтому 𝐴𝐷 — кратчайший отрезок прямой от 𝐴 до ⃖⃗𝐵𝐶.
Это верно для любой перпендикулярной линии из точки к прямой линии.
Свойство: Перпендикуляр от точки к линии
Отрезок перпендикулярной линии, соединяющий прямую и точку, является кратчайшей линией отрезок, соединяющий эту прямую и эту точку.
Давайте закончим повторением некоторых важных моментов из этого объяснения.
Ключевые моменты
- Если у нас есть треугольник, два угла которого неравны, то сторона, лежащая напротив большего угла, длиннее, чем сторона, лежащая напротив меньшего угла.
- В прямоугольном треугольнике гипотенуза является самой длинной стороной, поскольку она лежит против прямого угла, который является углом с наибольшей мерой.
- Отрезок перпендикулярной линии, проведенный от одной стороны треугольника к противоположной вершине, короче любого другого отрезка, проведенного от той же стороны
в ту же вершину.
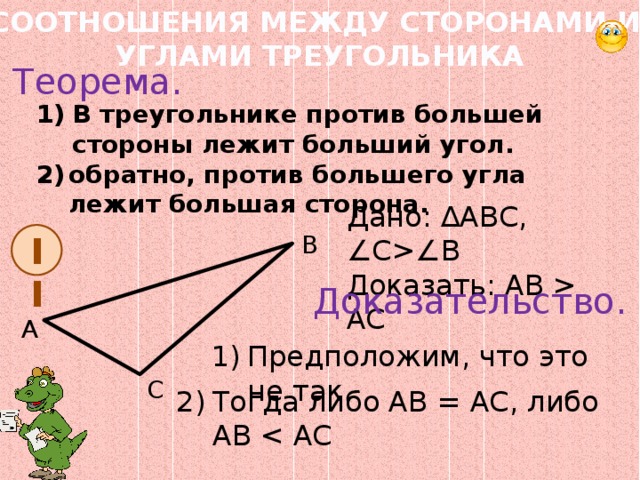
Можно показать, что этот результат верен в общем случае.
Таким образом, гипотенуза должна быть наибольшей стороной.
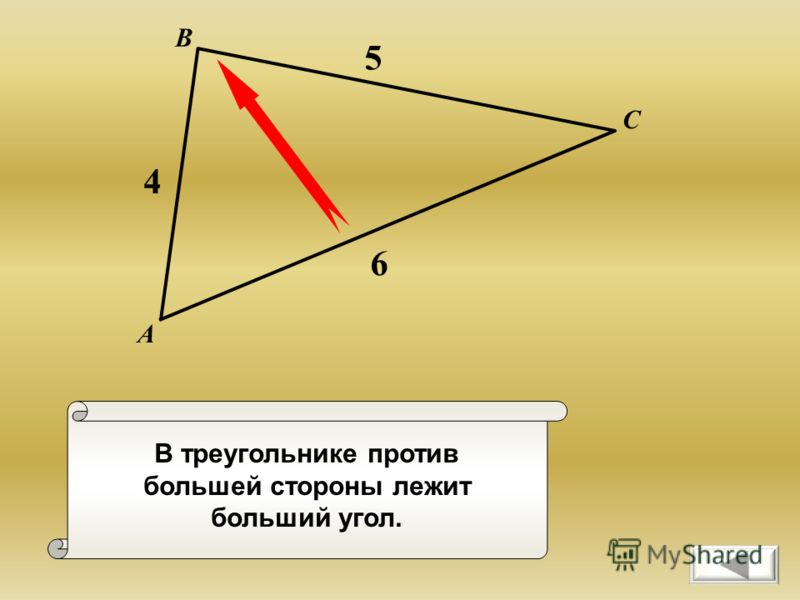
Таким образом,
𝐴𝐸>𝐴𝐷.
Leave A Comment