Теорема о соотношениях между сторонами и углами треугольника / Соотношения между сторонами и углами треугольника / Справочник по геометрии 7-9 класс

  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Соотношения между сторонами и углами треугольника
  5. Теорема о соотношениях между сторонами и углами треугольника

Теорема:

В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.

Доказательство:

1) Дано: АВС, АВАС.

   Доказать: СВ.

   Доказательство:

Отложим на стороне АВ отрезок АD, равный стороне АС.

 

АDАВ, т.к. по построению АD = АС, а по условию АСАВ, значит, точка D лежит между точками А и В. Следовательно, 1 является частью С, т.е. С1. Угол 2 внешний угол DBC, поэтому 2В. АDС — равнобедренный с основанием DC
, т.к. по построению АD = АС, следовательно, 1 =2 (углы при основании).

Итак, С1, 1 =2, значит, С2, при этом 2В, следовательно, СВ.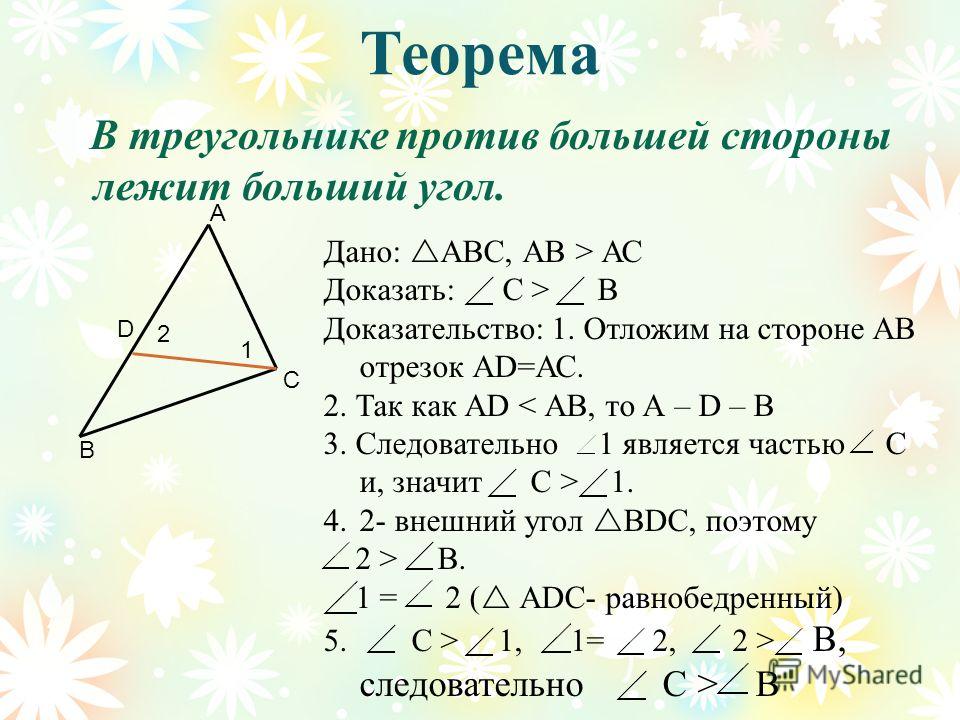

2) Дано: АВС, СВ

.

   Доказать: АВАС.

   Доказательство:

Предположим, что это не так. Тогда возможны два варианта:

  1. либо АВ = АС, тогда АВС — равнобедренный с основанием ВС, значит, С =В (как углы при основании), что противоречит условию: СВ.
  2. либо АВАС, тогда С
    В    ,     т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию: СВ.  

Значит, наше предположение неверно, следовательно, АВАС. Что и требовалось доказать.

Следствие 1

В прямоугольном треугольнике гипотенуза больше катета.

Доказательство:

Дано: АВС, ВС — гипотенуза,

А — прямой.

Доказать: ВСАС, ВС АВ.

Доказательство:

АВС — прямоугольный, А — прямой, следовательно, углы В и С острые, тогда АВ и АС, значит, ВСАС, ВСАВ (в треугольнике против большего угла лежит большая сторона).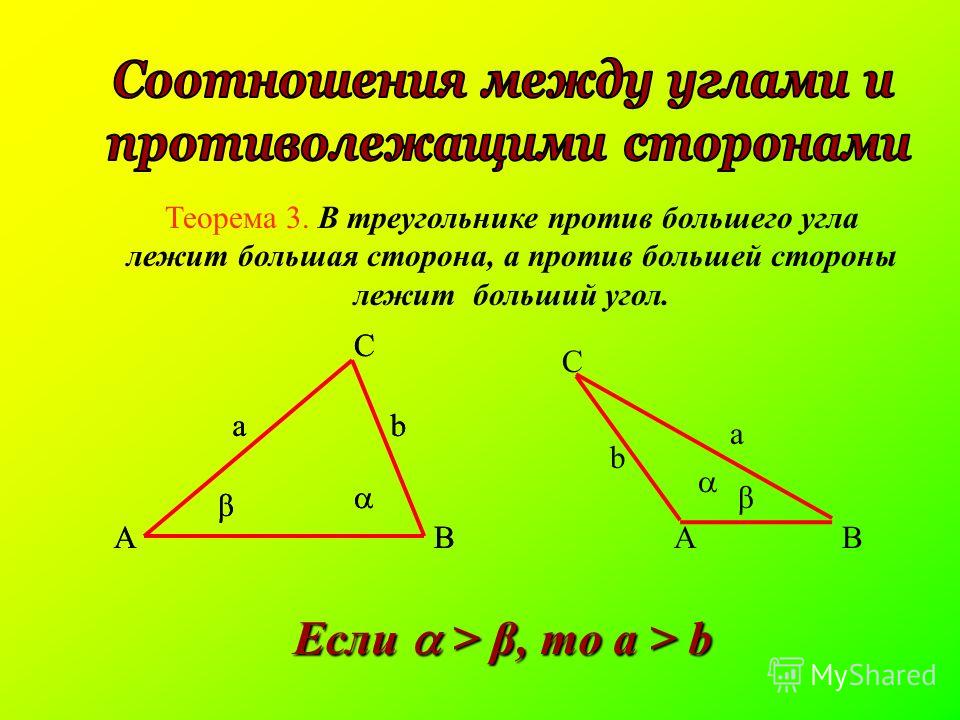

Что и требовалось доказать.

Следствие 2

Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

Доказательство:

Дано: АВС, В =С.

Доказать: АС = АВ.

Доказательство:

Предположим, что одна из сторон будет больше, т.е. АСАВ, тогда и угол лежащий против этой стороны будет больше, т.е.

ВС (в треугольнике против большей стороны лежит больший угол), а это противоречит условию: В =С, следовательно, наше предположение неверно, значит АС = АВ.

Итак, в АВС равны две стороны (АС = АВ), следовательно, данный треугольник — равнобедренный. Что и требовалось доказать.

Советуем посмотреть:

Теорема о сумме углов треугольника

Остроугольный, прямоугольный и тупоугольный треугольники

Неравенство треугольника

Некоторые свойства прямоугольных треугольников

Признаки равенства прямоугольных треугольников

Уголковый отражатель

Расстояние от точки до прямой

Расстояние между параллельными прямыми

Построение треугольника по двум сторонам и углу между ними

Построение треугольника по стороне и двум прилежащим к ней углам

Построение треугольника по трем его сторонам

Соотношения между сторонами и углами треугольника

Правило встречается в следующих упражнениях:

7 класс

Задание 239, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 240, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 241, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 245, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 312, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 340, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 816, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1025, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1036, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Теорема о соотношениях между сторонами и углами треугольника

Содержание

    Теорема о соотношениях между сторонами и углами треугольника — полезный геометрический «инструмент», позволяющий оценивать составляющие треугольника.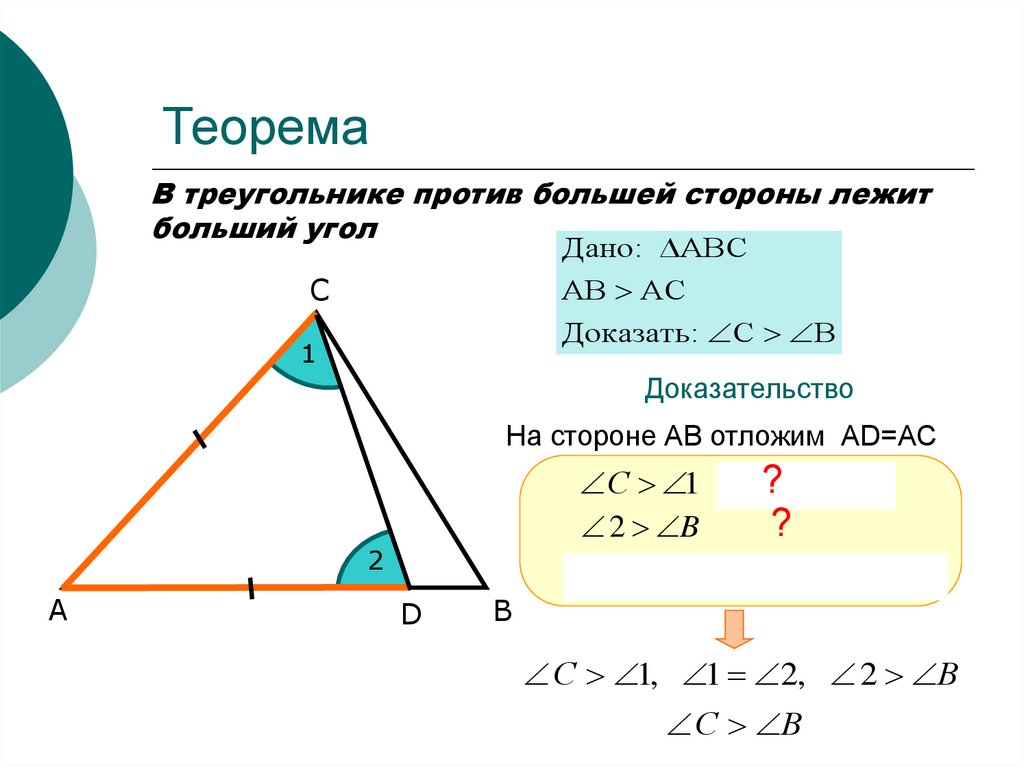 Скажем, к примеру, что вам известно следующее соотношение между углами треугольника $\bigtriangleup{ABC}$: $$\angle{C}>\angle{A}>\angle{B}$$ Хватит ли этого соотношения между углами, чтобы что-то заключить о сторонах $\bigtriangleup{ABC}$? Странно… но да. Теорема о соотношениях между сторонами и углами позволяет делать «прыжок» от углов к сторонам, и наоборот. Сегодня мы обсудим, какие соотношения между углами и сторонами существуют и как этим можно пользоваться.

    Соотношение «против большей стороны лежит больший угол»

    Здесь и далее вы столкнетесь с математическим символами неравенства — «больше» $(>)$ и «меньше» $(<)$. Вспомнить, как используются знаки неравенства, можно здесь.

    Рассмотрим $\bigtriangleup{ABC}$, в котором известно, что сторона $AB$ больше стороны $AC$. Теперь присмотримся к противолежащим сторонам углам — углам $\angle{C}$ и $\angle{B}$ соответственно.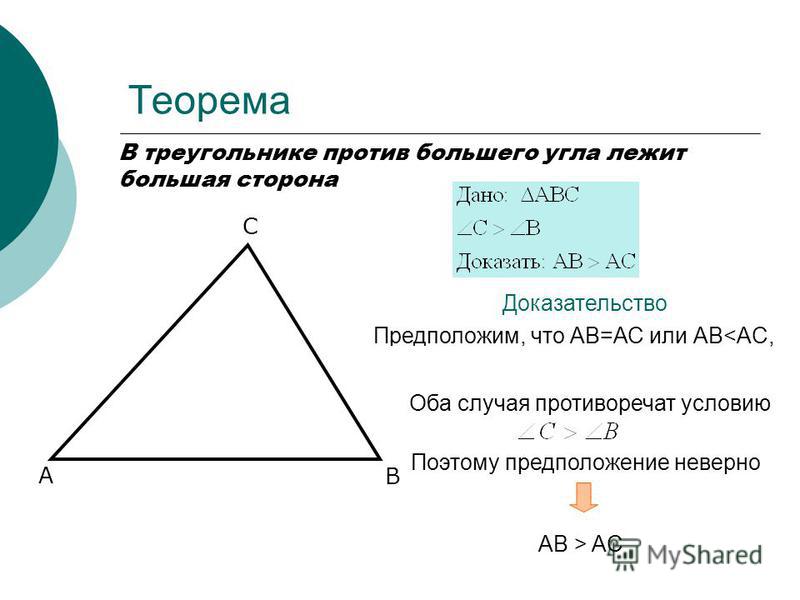 Какой из углов визуально кажется бóльшим? Даже без применения транспортира очевидно, что: $$\angle{C}>\angle{B}$$

    Докажем, что подобное соотношение между сторонами и углами треугольника работает универсально для любого треугольника:

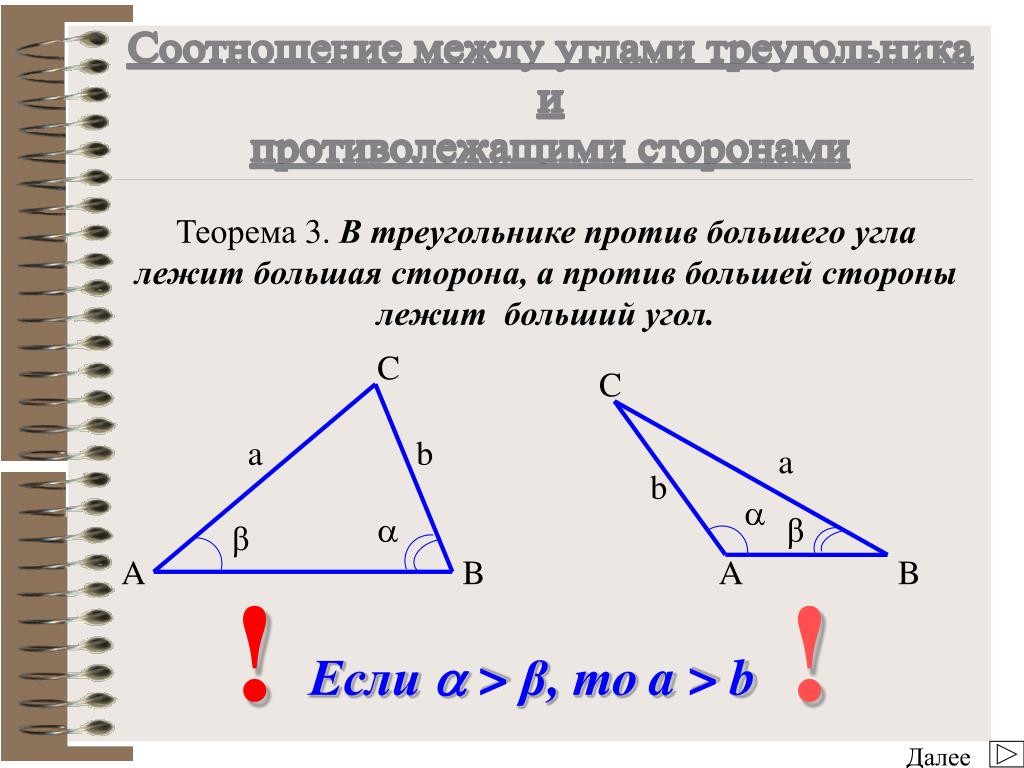
    Теорема о соотношениях между сторонами и углами треугольника. Против большей стороны треугольника лежит больший угол.

    Доказательство

    Пусть в треугольнике $\bigtriangleup{ABC}$ известно неравенство сторон $AB>AC$. Отложим на большей стороне $AB$ отрезок $AC_1$ так, что $AC_1=AC$. В полученном треугольнике $\bigtriangleup{AC_{1}C}$ отметим углы $\angle{\alpha}$ и $\angle{\beta}$. Поскольку в $\bigtriangleup{AC_{1}C}$ стороны $AC_1$ и $AC$ равны, заключаем, что $\bigtriangleup{AC_{1}C}$ — равнобедренный треугольник, где $\angle{\alpha}=\angle{\beta}$.

    Рассмотрим $\angle{\alpha}$. Он является внешним углом треугольника $\bigtriangleup{C_{1}BC}$.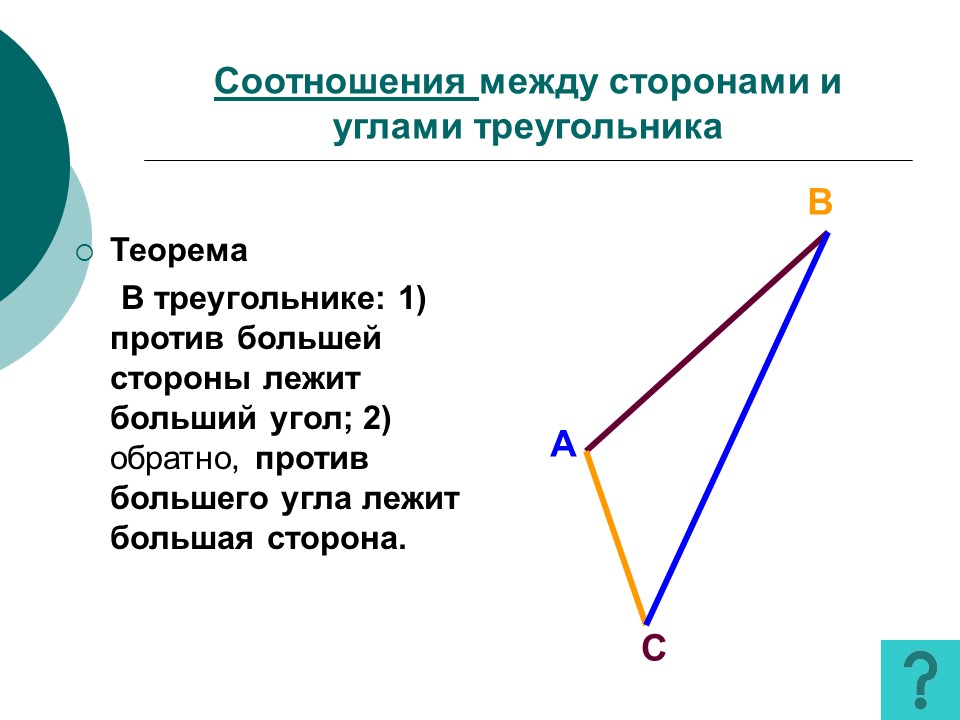 По теореме о внешнем угле треугольника известно, что внешний угол равен сумме двух других углов, не смежных с ним. Следовательно, внешний угол всегда по величине больше любого не смежного с ним внутреннего угла. Тогда $\angle{\alpha}>\angle{B}$.

    Рассмотрим $\angle{\beta}$. Он является частью угла $C$, ведь через любые две точки можно провести прямую. В данном случае — прямую, на которой расположен отрезок $CC_1$. Раз $\angle{\beta}$ — часть $\angle{C}$, можно заключить, что $\angle{C}>\angle{\beta}$. Если $\angle{C}>\angle{\beta}$ и $\angle{\alpha}>\angle{B}$, при условии, что $\angle{\alpha}=\angle{\beta}$, то очевидно, что $\angle{C}>\angle{B}$. Против большей стороны $AB$ лежит больший угол $\angle{C}$. Что и требовалось доказать.

    {"questions":[{"content":"Теорема о соотношениях между сторонами и углами треугольника заключается в том, что против большей стороны лежит  [[input-1]] угол. 
    [[speech-15]]","widgets":{"input-1":{"type":"input","inline":1,"answer":"больший"},"speech-15":{"type":"speech","text":"Впишите недостающее слово. "}}}]}

    Теорема о соотношениях между сторонами и углами: последний пункт доказательства

    Небольшой комментарий для тех, кто недопонял.

    Как мы из двух неравенств и одного равенства пришли к выводу, что угол $\angle{C}$ больше угла $\angle{B}$? Давайте еще раз представим в едином виде все имеющиеся у нас данные:

    $$\begin{cases}\angle{\alpha}=\angle{\beta} \\ \angle{B}<\angle{\alpha} \\ \angle{C}>\angle{\beta}\end{cases}$$

    И $\angle{B}$, и $\angle{C}$ сравниваются с одной и той же величиной, ведь величина углов $\angle{\alpha}$ и $\angle{\beta}$ равная. Угол $\angle{B}$ меньше некоторой величины, а угол $\angle{C}$ больше относительной той же самой величины. Конечно $\angle{C}$ будет больше $\angle{B}$. Даже еще проще: попробуйте подставить вместо $\angle{\alpha}$ любое значение. Тогда финальный штрих доказательства мгновенно станет понятен.

    Соотношение «против большего угла лежит бóльшая сторона»

    Выше мы доказали соотношения между сторонами и углами треугольника с позиции «от сторон к углам». Имеет смысл проверить, работают ли соотношения в обратную сторону. Иными словами, если задано некоторое неравенство углов, какой вывод можно сделать о соответствующих сторонах? Будет ли выше доказанная теорема справедлива как для сторон, так и для углов?

    Сформулируем обратную теорему и докажем ее:

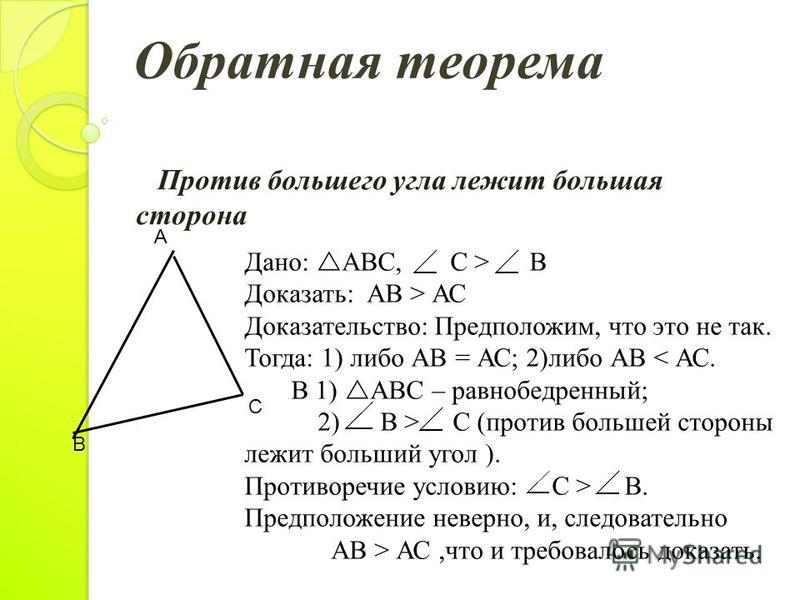
    Обратная теорема о соотношениях между сторонами и углами треугольника. Против большего угла треугольника лежит бóльшая сторона.

    Доказательство

    Пусть в треугольнике $\bigtriangleup{ABC}$ известно неравенство углов $\angle{C}>\angle{B}$ (также на чертеже: $\angle{\beta}>\angle{\alpha}$). Воспользуемся методом от противного и предположим, что неравенство $AB>AC$ неверно. Раз сторона $AB$ не больше стороны $AC$, возможно следующее:

    • либо $AB=AC$;
    • либо $AB<AC$, то есть сторона $AB$ меньше.

    Если $AB=AC$, то $\bigtriangleup{ABC}$ равнобедренный, следовательно $\angle{C}=\angle{B}$, что противоречит заданным условиям. Если $AB<AC$, тогда согласно теореме о соотношениях между сторонами и углами треугольника против большей стороны лежит больший угол и $\angle{B}>\angle{C}$, что тоже противоречит заданным условиям. Из этого следует, что неравенство $AB>AC$ верно. Против большего угла лежит бóльшая сторона. Что и требовалось доказать.  

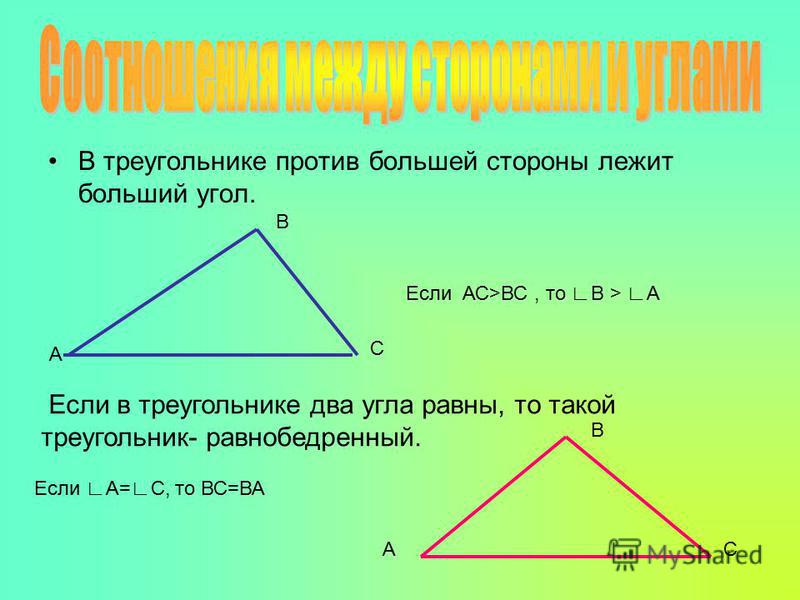
    {"questions":[{"content":"В треугольнике $\\bigtriangleup{ABC}$ угол $\\angle{A}$ больше $\\angle{B}$. Какая из сторон треугольника будет меньшей — $BC$ или $AC$?  [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$BC$","$AC$"],"answer":[1]}},"step":1,"hints":["Если $\\angle{B}

    Пример использования теоремы

    Итого, теорема о соотношениях между сторонами и углами треугольника сообщает: если есть пара сторон, в которой по значению одна сторона больше, то против большей стороны будет лежать больший по величине угол. Против меньшей — меньший. Ровно то же самое работает с парами углов. Если один из углов в паре больше, то сторона против большего угла больше. Против меньшего — меньше.    

    А теперь, вооружившись новыми знаниями, вернемся к задачке из введения в урок, с треугольником $\bigtriangleup{ABC}$, про который известно, что $\angle{C}>\angle{A}>\angle{B}$. Как будет выглядеть неравенство сторон для треугольника $\bigtriangleup{ABC}$?

    😉 Перед тем, как дать ответ, загляните сюда!

    Скрыть текст

    Навыки на миллион. Как без рисунка определять буквенные обозначения противолежащих сторон и противолежащих сторонам углов? Что же, как обычно выручает геометрическая смекалка. Точка угла расположена не на прямой, где расположена противолежащая сторона. Поскольку у нас всего три точки и три отрезка, остаются две прочие точки, на которых построен отрезок, он же противолежащая сторона.

    Смотрите, как это работает:

    Например, как обозначается сторона, противолежащая углу $\angle{A}$? Точка $A$ «занята» углом, а точки $B$ и $C$ «свободны» (расположены в другой полуплоскости), следовательно противолежащая углу $\angle{A}$ сторона обозначается как $BC$.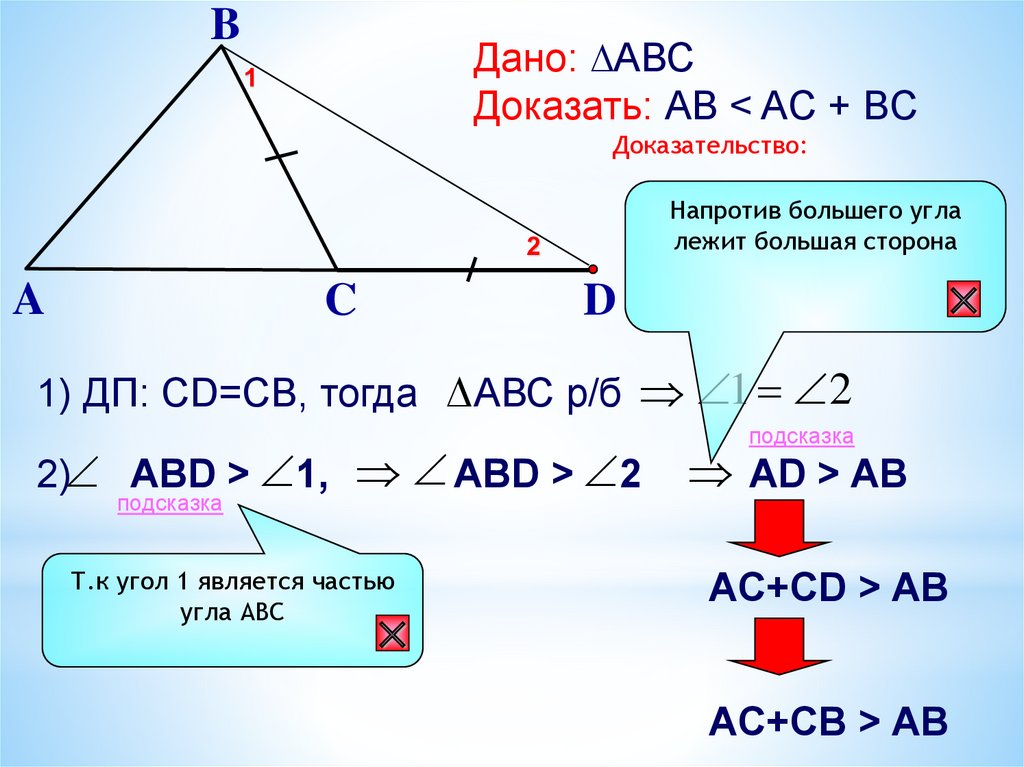

    Если «занята» точка $B$, то остаются точки $A$ и $C$ — сторона $AC$ противолежит углу $\angle{B}$. Если «занята» точка $C$, то остаются точки $A$ и $B$ — сторона $AB$ противолежит углу $\angle{C}$. Главное, держите порядок следствия точек при отрезках сторон строго так, как он задан. У нас порядок $ABC$, поэтому мы и записывали, скажем, противолежащую сторону для угла $C$ как $AB$, а не как $BA$. Не то чтобы что-то кардинально изменится, однако наука любит точность.

    {"questions":[{"content":"Только для интереса переименуем треугольник из $\\bigtriangleup{ABC}$ в $\\bigtriangleup{RGH}$. Как будет выглядеть неравенство сторон для треугольника $\\bigtriangleup{RGH}$, если известно, что $\\angle{R}>\\angle{G}>\\angle{H}$? [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$GH>RH>RG$","$HG>RG>RH$","$RG>GH>RH$"],"answer":[0]}}}]}

    Теорема о неравенстве треугольника: Примеры | Turito

    Ключевые понятия

    • Соотношение длины стороны и меры угла.
    • Неравенство треугольника.
    • Возможные длины сторон.

    Введение 

    На предыдущем занятии мы узнали о медианах, центроидах, высотах, ортоцентрах и особых случаях равнобедренного треугольника.

    На этом занятии вы узнаете о неравенствах в треугольнике, связи длин сторон и мер углов, неравенстве треугольника и возможных длинах сторон в треугольнике.

    Теоремы 

    Теорема 1

    Если одна сторона треугольника длиннее другой, то угол, противолежащий более длинной стороне, больше угла, противолежащего более короткой стороне.

    Теорема 2 

    Если угол треугольника больше другого угла, то сторона, лежащая против большего угла, длиннее стороны, противоположной меньшему углу.

    Пример 1:  

    Начертите остроугольный треугольник и соедините длины сторон и величины углов.

    Решение:  

    Предположим, что a < b < c,

    Угол, противоположный стороне a, является меньшим углом, 

    Угол, противоположный стороне c, является большим углом.

    ∠C > ∠B > ∠A

    Пример 2:

    В тупоугольном треугольнике ABC найдите больший угол и большую сторону.

    Решение:  

    Очевидно, что в тупоугольном треугольнике ABC

    ∠B — тупой угол,

    Тупоугольный угол является наибольшим в тупоугольном треугольнике.

    Итак, ∠B — больший угол.

    Из теоремы 2,  

    Если угол треугольника больше другого угла, то сторона, лежащая напротив большего угла, длиннее стороны, противоположной меньшему углу.

    Сторона, противоположная ∠B, является более длинной стороной.

    Теорема 3

    Если сторона треугольника длиннее другой стороны, то угол, лежащий против большей стороны, больше угла, лежащего против меньшей стороны.

    Доказательство:  

    Учитывая, что PQ > PR 

    Теперь докажем, что ∠PRQ > ∠PQR 

    Нарисуйте точку S на PQ так, чтобы PS = PR … (1) ∠R =

    ∠R в равнобедренном треугольнике сбн … (2)

    ∠ПРК = ∠ПРС + ∠КСС … (3)

    ∠ПРС > ∠ПРС

    ∠ПРС > ∠ПСР … (4) (начиная с (2))

    С внешнего угла теорема, ∠PSR = ∠PQR + ∠SRQ 

    Следовательно, ∠PSR > ∠PQR …(5) 

    Из (4) и (5)

    Наконец, мы заключаем, что ∠PRQ > ∠PQR 

    Значит доказано.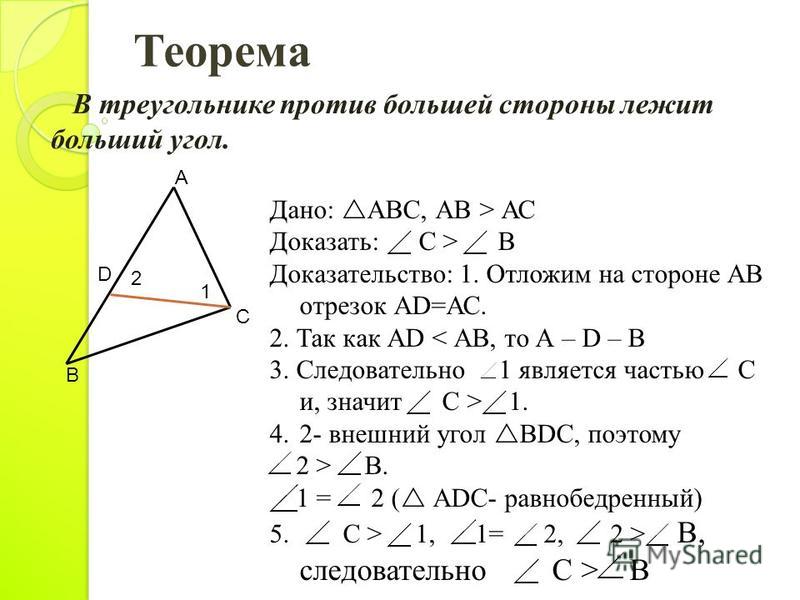

    Теорема о неравенстве треугольника 

    Неравенство треугольника 

    Каждая группа из трех сегментов не может образовывать треугольник.

    Он должен соответствовать определенным отношениям.

    Пример:  

    Если взять самую длинную сторону в качестве основания и соединить две другие стороны на первом и втором рисунках, треугольник не образуется. Это приводит к теореме о неравенстве треугольника.

    Теорема о неравенстве треугольника

    Теорема:  

    Сумма длин любых двух сторон треугольника больше третьей стороны.

    AB + BC > AC, 

    AC + AB > BC, 

    AC + BC > AB.

    Возможные длины сторон 

    Пример:    

    В треугольнике одна сторона имеет длину 12 см, другая сторона имеет длину 5. Найдите возможные длины сторон.

    Решение:  

    Пусть третья сторона треугольника равна x

    Теперь х может быть наименьшей стороной или х может быть самой длинной стороной.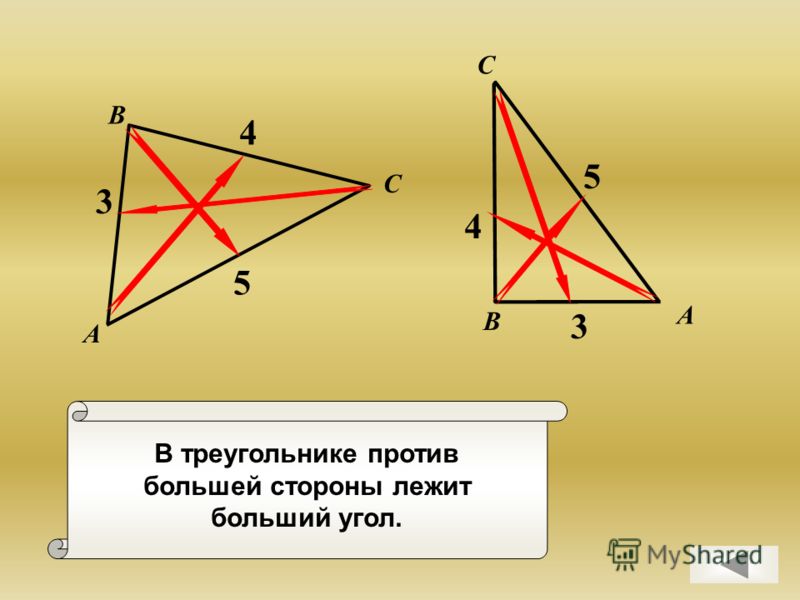

    Воспользуемся свойствами неравенства треугольника.

    12 + 5 > х

    17 > х

    х + 5 > 12

    х > 12 – 5

    х > 7

    х > 7 и х < 14. больше 7 и меньше 17.   

    Пример из реальной жизни  

    В реальной жизни неравенства треугольника используются в основном инженерами-строителями, так как в их работе требуется так много времени, чтобы найти неизвестные длины различных измерений.

    Пример:  

    В строительном поле необходимо построить треугольную форму ABC (как показано на рисунке), левая сторона треугольника равна 12 футам, а правая сторона треугольника равна 13 футам, основание 26 футов, один угол равен

    45°, а другой угол равен 54° какой будет другой угол в этом треугольнике?

    Решение:  

    Учитывая, что левая сторона треугольника равна 12 футам, а правая сторона треугольника равна 13 футам, основание равно 26 футам, один угол равен

    45°, а другой угол равен 54°.

    Так как сумма углов в треугольнике = 180°

    Значит,

    180°−(45°+54°)

    = 180° – 99° 

    = 81°

    °

    Другой угол равен 81°

    Теперь по данной теореме мы имеем ∠BAC = 81°

    Это будет вершина, которая находится в точке A, так как основание является самой длинной стороной.

    Упражнение

    • Нарисуйте треугольник со сторонами 6, 8 и 10 единиц и укажите углы 30°, 60° и 90°. Нарисуйте треугольник и отметьте углы.
    • Отметьте меньшую сторону большей стороны данной фигуры.
    • Если одна сторона треугольника 11 см, а другая 6 см. Найдите возможную длину третьей стороны.
    • Как узнать, какой угол в треугольнике больше?
    • Укажите меньший угол к большему углу из данной фигуры.
    • Какая группа длин используется для формирования треугольника?

    3, 4, 5

    4, 2, 2

    3, 2, 1

    2, 2, 2

    Q (7-10)

    • Каковы возможные значения x из приведенного выше рисунка?
    • Каковы возможные значения PQ на приведенном выше рисунке?
    • Каковы возможные значения QR на приведенном выше рисунке?
    • Каковы возможные значения RP на приведенном выше рисунке?

    Концептуальная карта

    Что мы узнали

    • Соотношение длин сторон и углов.
    • Неравенство треугольника.
    • Возможные длины сторон.

    Неравенства в треугольниках — Центр академической поддержки

    Неравенства в треугольниках

     

    Как определить, какие углы и стороны треугольника больше других?

    Мы можем использовать свойство сравнения неравенства , чтобы сделать некоторые утверждения об отношениях размеров между углами и сторонами треугольника. Свойство сравнения состояний неравенства

    Если a = b + c и c > 0, то a > b .

    Мы можем объединить эту идею с нашей теоремой о внешнем угле треугольника, чтобы получить новое утверждение. Теорема о внешнем угле треугольника утверждает, что мера внешнего угла треугольника равна сумме мер его отдаленных внутренних углов.

    Следствие теоремы о внешнем угле треугольника

    Мера внешнего угла треугольника больше меры каждого из его удаленных внутренних углов.

    Другими словами, если a = b + c , то a больше, чем b , а также больше, чем c . Эта идея приводит нас к другой теореме, которая утверждает, что больший угол в треугольнике означает большую противоположную сторону, и наоборот.

    Теорема 5-10

    Если две стороны треугольника не равны, то против большей стороны лежит больший угол.

    Теорема 5-11

    Если два угла треугольника не равны, то против большего угла лежит более длинная сторона.

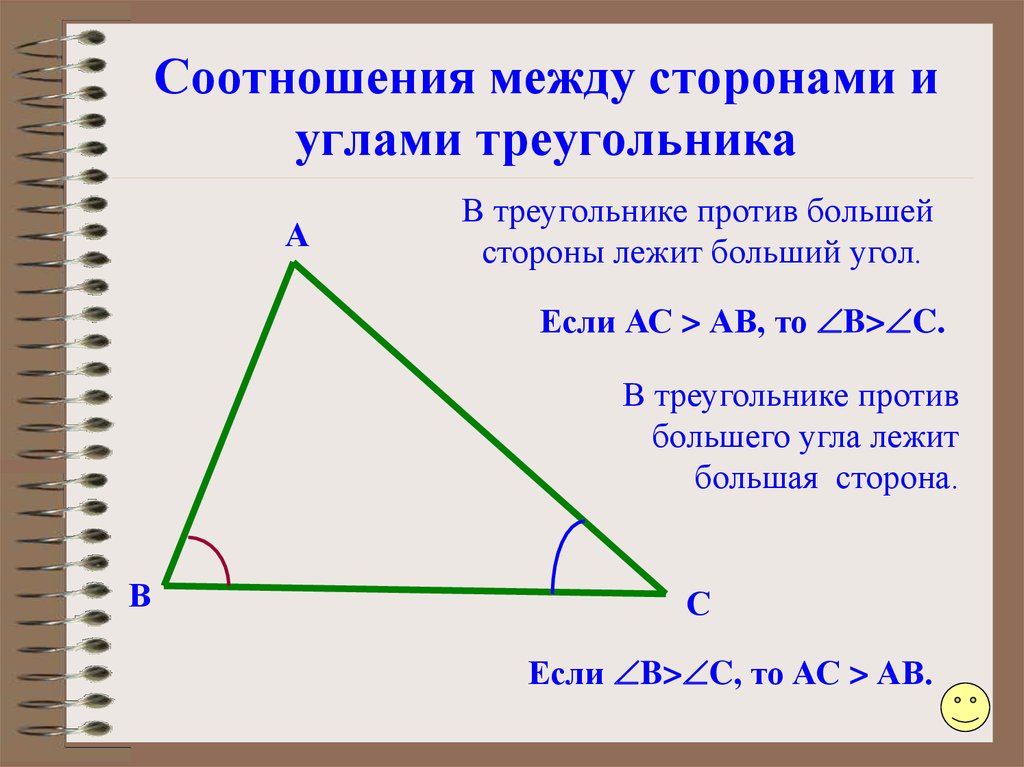    У нас также есть ограничения на то, насколько короткой может быть сторона треугольника по отношению к другим сторонам. Теорема Пифагора говорит нам, что сумма квадратов коротких сторон будет равна квадрату самой длинной стороны. Это может быть математически верным только в том случае, если сумма длин коротких сторон (не в квадрате) больше, чем длина наибольшей стороны. Путем некоторых геометрических и логических манипуляций мы можем сделать еще одно утверждение о длинах сторон в треугольниках.

    Теорема 5-12

    Сумма длин любых двух сторон треугольника больше длины третьей стороны.

    Если это не так, то фигура не является треугольником.

    Как я могу использовать эти правила для сравнения двух разных треугольников?

    Теорема 5-11 может оставаться верной при сравнении двух разных треугольников, но только при особых обстоятельствах. Эта ситуация описана в теореме о шарнире, которую иногда называют теоремой о неравенстве стороны-угла-стороны.

    Теорема о шарнире (теорема SAS о неравенстве)

    Если две стороны одного треугольника конгруэнтны двум сторонам другого треугольника, а прилежащие углы не равны, то более длинная третья сторона находится напротив большего прилежащего угла.

    Другими словами, если вы докажете, что две стороны одного треугольника равны двум сторонам другого, то большая третья сторона будет в треугольнике с большим соответствующим углом между этими сторонами.

    Related Posts

    Leave A Comment