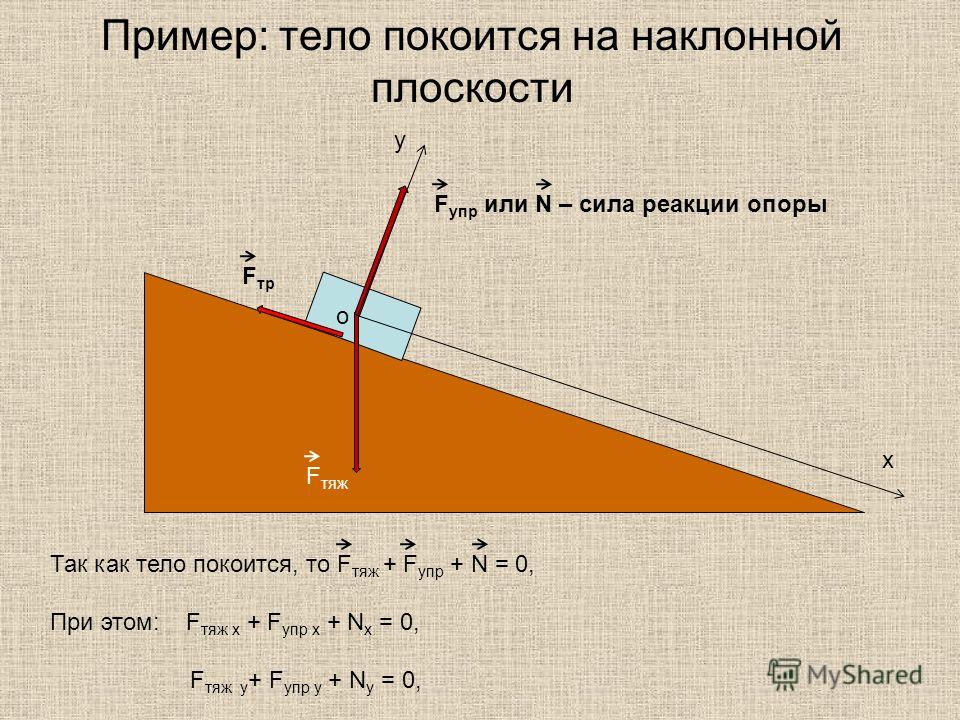
Проецирование сил. Движение по наклонной плоскости


Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Неколлинеарные силы.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением 

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y:  N = mg, тогда в данной задаче Fтр = μmg.

Получаем, что: 

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Ответ: 0,25

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Ответ: 65 Н

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей. 

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

Ответ: 4,22 кг

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска? 

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM: 

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Ответ: 6,36 м/с²

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время. 

Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с²  и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:


Запишем второй закон Ньютона на X и Y:

Ответ: 6000 кг

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Ответ: 7,5 см

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.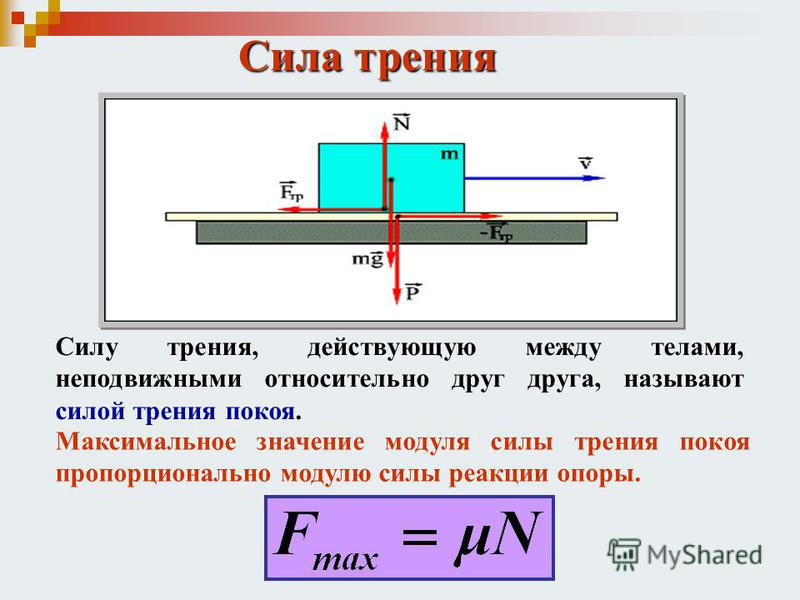

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами. 

Будь в курсе новых статеек, видео и легкого технического юмора.

Задачи на наклонную плоскость

Репетитор по физике

8 916 478 10 32

Пройти тест на эту тему

Тело на наклонной плоскости с углом наклона \( \alpha \)

Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.

Жирная зеленая точка это и есть наше тело.

Проведем из нее вектор силы тяжести \(mg\).

При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \) перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)

\(F_{тx} \; \) это проекция силы тяжести на ось x


Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой \(mg \) и фиолетовым катетом \(F_{тx} \; \)

\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)

\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)

Задача 1. 0 \)

\(F-?\)

Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.

Жирная зеленая точка это и есть наше тело.

Проведем из нее вектор силы тяжести \(mg\).

При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \) перпендикулярно ей


Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) — Внешняя сила, которую нужно найти.


Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой \(mg \) и фиолетовым катетом \(F_{тx} \; \)
\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)

\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)

По первому закону Ньютона:

\(F- F_{Тx}=0 \)

\(F- mg \cdot sin \; \alpha =0 \)

\(F= mg \cdot sin \; \alpha =1 кг \cdot 10 м/с^2 \cdot sin \;30^0=5Н \)

Ответ: \( F=5Н \)

Задача 2. 0 \)

\(F-?\)

Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.

Жирная зеленая точка это и есть наше тело.

Проведем из нее вектор силы тяжести \(mg\).

При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \) перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) — Внешняя сила, которую нужно найти.


Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой \(mg \) и фиолетовым катетом \(F_{тx} \; \)
\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)

\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)

По первому закону Ньютона:

\(F- F_{Тx}=0 \)

\(F- mg \cdot sin \; \alpha =0 \)

\(F= mg \cdot sin \; \alpha =2 кг \cdot 10 м/с^2 \cdot sin \;30^0=10Н \)

Ответ: \( F=10Н \)

Задача 3.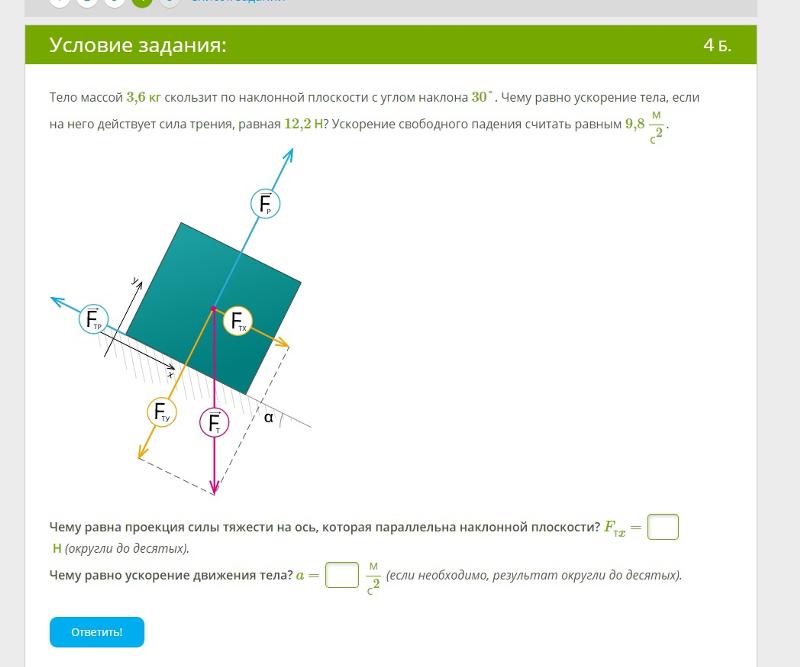 0 \)

\(F-?\)

Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.

Жирная зеленая точка это и есть наше тело.

Проведем из нее вектор силы тяжести \(mg\).

При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \) перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) — Внешняя сила, которую нужно найти.


Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой \(mg \) и фиолетовым катетом \(F_{тx} \; \)
\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)

\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)

По первому закону Ньютона:

\(F- F_{Тx}=0 \)

\(F- mg \cdot sin \; \alpha =0 \)

\(F= mg \cdot sin \; \alpha =\sqrt{2} \cdot 10 \cdot sin \;45^0= \sqrt{2} \cdot 10 \cdot \dfrac{\sqrt{2}}{2}= 10 Н \)

Ответ: \( F=10Н \)

Задача 4.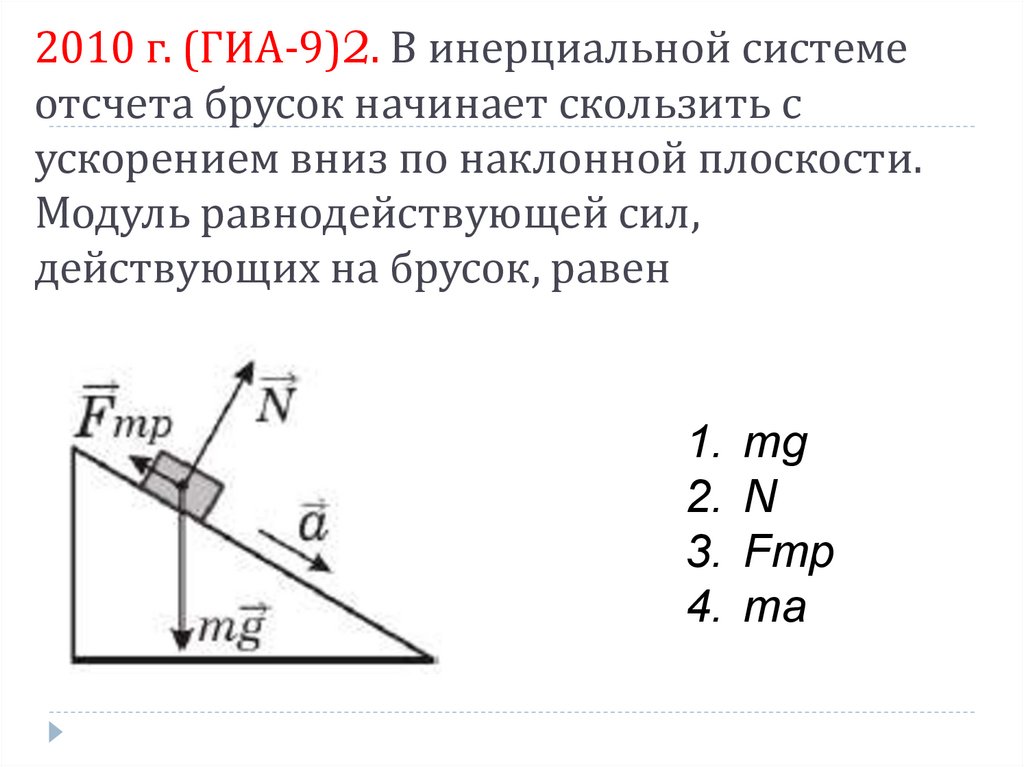 0 \)

\(F-?\)

Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.

Жирная зеленая точка это и есть наше тело.

Проведем из нее вектор силы тяжести \(mg\).

При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \) перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) — Внешняя сила, которую нужно найти.


Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой \(mg \) и фиолетовым катетом \(F_{тx} \; \)
\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)

\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)

По первому закону Ньютона:

\(F- F_{Тx}=0 \)

\(F- mg \cdot sin \; \alpha =0 \)

\(F= mg \cdot sin \; \alpha =\sqrt{27} \cdot 10 \cdot sin \;60^0= \sqrt{27} \cdot 10 \cdot \dfrac{\sqrt{3}}{2}= 5 \sqrt{81} =45 Н \)

Ответ: \( F=45Н \)

Пройти тест на эту тему

Задача 6.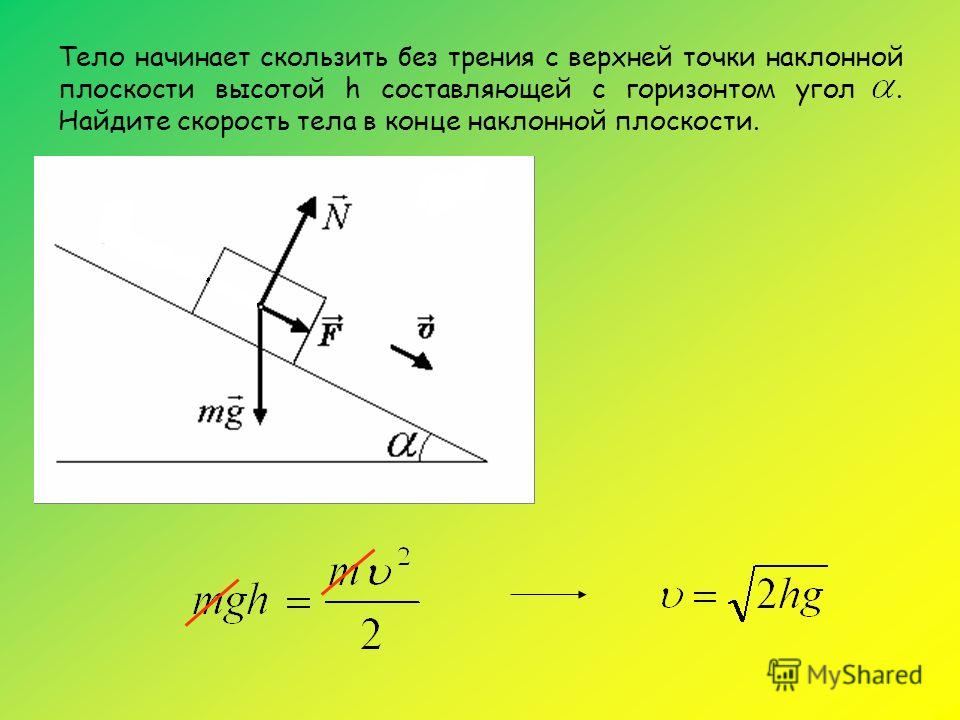 0 \)

\(a-?\)

Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.

Жирная зеленая точка это и есть наше тело.

Проведем из нее вектор силы тяжести \(mg\).

При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \) перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x

Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой \(mg \) и фиолетовым катетом \(F_{тx} \; \)
\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)

\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)

По второму закону Ньютона:

\( F_{Тx}=ma \)

\( mg \cdot sin \; \alpha = ma \)

\( g \cdot sin \; \alpha = a \)

\(a= g \cdot sin \; \alpha =10\cdot sin 45^0=10\cdot \dfrac{\sqrt{2}}{2}=7,07106781187 \approx 7,07 м/с^2 \)

Ответ: \(a=7,07 м/с^2 \)

Пройти тест на эту тему

Определение силы тяжести на наклонной плоскости

Вы можете использовать физику для определения силы тяжести на объекте, который движется по наклонной плоскости. Вы можете разбить вес объекта на составляющие, параллельные и перпендикулярные плоскости. Составляющая, перпендикулярная плоскости, вдавливает объект в поверхность плоскости. Составляющая веса, действующая вдоль плоскости, ускоряет тело вниз по плоскости. Здесь вы найдете составляющую силы тяжести, действующую вдоль плоскости, когда вертикальная сила тяжести равна F г .

Гонка тележки по пандусу.

Для расчета составляющих веса, параллельных и перпендикулярных наклонной плоскости (на рис. пандусе), необходимо знать зависимость между направлением общего веса и направлением пандуса. Самый простой способ определить это — вычислить угол между грузом и линией, перпендикулярной пандусу. Этот угол отмечен на рисунке символом тета 9.0003 , , равный углу рампы.

Существуют различные способы использования геометрии, чтобы показать, что тета равна углу наклона. Например, вы можете заметить, что угол между грузом и линией, перпендикулярной пандусу, должен дополнять угол в верхней части пандуса, который равен

.

Два угла являются дополнительными , если их сумма составляет 90 градусов.

Угол направления, перпендикулярного поверхности рампы, от угла рампы.

На этом рисунке угол рампы задается углом ABC. Угол в верхней части пандуса является дополнением к этому углу, потому что сумма углов треугольника составляет 180 градусов, поэтому угол

Угол BCA должен быть равен углу BDE , так как треугольники EBD и ABC подобны, поэтому можно сказать, что угол

Наконец, угол BCA должен быть дополнительным к углу ACF , потому что в сумме они явно составляют 90 градусов (вместе с прямым углом FCD, они образуют прямую линию), поэтому у вас наконец есть ответ:

Если вы используете тригонометрию для проецирования вектора веса на линии, перпендикулярные и параллельные пандусу (обратитесь к первому рисунку и поверните его на 30 градусов, если это поможет вам увидеть, что происходит), вы получите выражение для компонента груза перпендикулярно пандусу следующим образом:

И составляющая веса вдоль рампы такова:

Поскольку вы знаете силу, вы можете использовать второй закон Ньютона, чтобы вычислить ускорение вдоль рампы:

К этому моменту вы знаете, что ускорение тележки вдоль рампы определяется выражением

.

Это уравнение верно для любого объекта, который гравитация ускоряет вниз по склону, если не применяется трение.

Эта статья из книги:

  • Физика I для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе Physics For Dummies и Physics Essentials For Dummies. Доктор Хольцнер получил докторскую степень в Корнелле.

Эту статью можно найти в категории:

  • Физика,

Движение снаряда по наклонной плоскости Важные понятия и советы для JEE Main

В сущности, метательное движение тела относится к движению, когда объект подбрасывается в воздух в присутствии гравитационного поля Земли. Мы могли бы просто сказать, что движение любого объекта под действием силы гравитации известно как движение снаряда. Есть много примеров, которые мы видим в нашей повседневной жизни, например, подбрасывание мяча в воздух, которое показывает движение снаряда. Есть некоторые предположения, которые были сделаны в отношении движения снаряда, а именно, что эффекты, связанные с вращением земли и сопротивлением воздуха, в этом движении игнорируются. Объект, движущийся в форме параболы, имеет как вертикальное, так и горизонтальное движение в форме снаряда.

Если движение снаряда происходит по наклонной плоскости, составляющей некоторый угол с землей, то мы называем это движением снаряда по наклонной плоскости. Давайте подробно рассмотрим движение снарядов по наклонным плоскостям, обсудив, как летят снаряды по наклонной плоскости и какова дальность полета снарядов по наклонным плоскостям.

Дальность полета снаряда по наклонной плоскости

Предположим, что мяч брошен вверх по наклонной плоскости, которая составляет угол θ0 с горизонтальной поверхностью земли. Мяч брошен со скоростью u и образует с наклонной плоскостью угол ⍺. Мяч, который находится в движении снаряда, будет иметь начальную скорость, ускорение и конечную скорость. Каждую величину можно разделить на две составляющие в плоскости XY, как показано на рисунке.

Снаряд на наклонной плоскости 

На приведенном выше рисунке видно, что путь мяча или снаряда лежит из A в B. Наклонная поверхность составляет угол θ0 с горизонтом, и мяч брошен с начальным скорость u под углом ⍺ к наклонной поверхности.

Ось X параллельна наклонной плоскости, а ось Y перпендикулярна наклонной плоскости, как показано на рисунке. Горизонтальная и вертикальная составляющие начальной скорости в направлениях X и Y равны ux и uy соответственно.

Здесь ux  = ucos⍺ и uy = usin⍺

Ускорение снаряда – это ускорение свободного падения, действующее вниз в отрицательном направлении оси XY. Значит, он имеет отрицательный знак. {2}$  9{\prime}-\theta_{0}\right)+\sin \theta_{0}\right]\end{align}$ 

Это расстояние снарядов вниз по формуле наклонной плоскости. Рассмотрим уравнение траектории снаряда.

Уравнение траектории снаряда 

Предположим, что обычный снаряд в горизонтальной плоскости брошен со скоростью u под углом $\alpha$ к горизонтальной поверхности, а ускорение есть ускорение силы тяжести, которая действует только по оси Y. 9{2} \sin 2 \alpha}{g}=R\\ &y=x \tan \alpha\left(1-\dfrac{x}{R}\right) \end{align}$

Это уравнение траектории снаряда.

Решим задачу на понятие движения снаряда по формуле наклонной плоскости.

Пример: Мяч брошен с основания наклонной плоскости вверх со скоростью 10$\dfrac{m}{s}$ под углом 30 градусов к наклонной поверхности. Если наклонная поверхность составляет угол 30 градусов с горизонтом, найдите дальность полета мяча на наклонной плоскости. 9{2} 30}[\sin (2(30)+30)-\sin 30] \\ &R=\dfrac{10 \times 4}{3}\left[1-\dfrac{1}{2}\ right] \\&R=\dfrac{40}{3} \cdot \dfrac{1}{2} \\ &R=\dfrac{20}{3}=6,67 \mathrm{~m} \end{align}$

Следовательно, расстояние, пройденное мячом по наклонной плоскости, равно 6,67 метра.