Формула площадь грани параллелепипеда: Площадь поверхности параллелепипеда — формула и калькулятор

Площадь поверхности параллелепипеда — формула и калькулятор

{S_{полн} = 2(ab+bc+ac)}

Найти площадь

полной поверхностибоковой поверхности

Длина a

ммсмдммкмдюймы (in)футы (ft)

Ширина b

ммсмдммкмдюймы (in)футы (ft)

Высота c

ммсмдммкмдюймы (in)футы (ft)

Результат в

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2.

По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.

В дополнение на сайте можно найти объем параллелепипеда.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.

Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.

Содержание:

1. калькулятор площади поверхности прямоугольного параллелепипеда
2. формула площади поверхности прямоугольного параллелепипеда
3. формула площади боковой поверхности прямоугольного параллелепипеда
4. примеры задач

Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}

a — длина прямоугольного параллелепипеда

b — ширина прямоугольного параллелепипеда

c — высота прямоугольного параллелепипеда

Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}

a — длина прямоугольного параллелепипеда

b — ширина прямоугольного параллелепипеда

c — высота прямоугольного параллелепипеда

Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда

Задача 1

Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.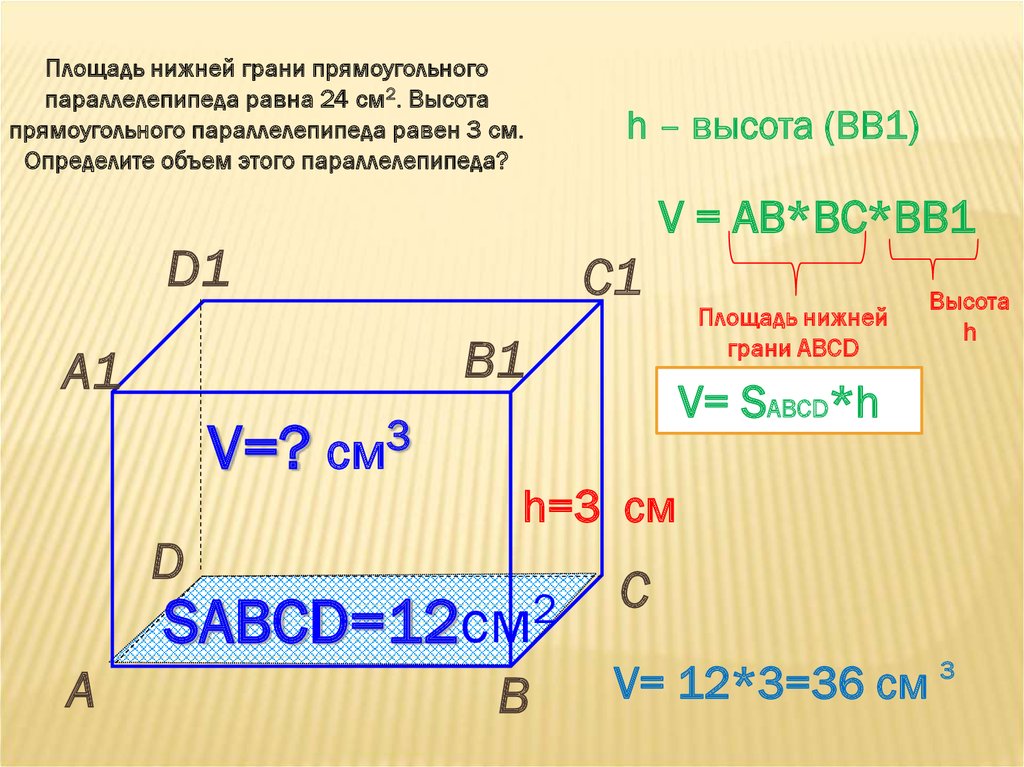 2

Ответ: 126 см²

Как всегда ответ можно проверить с помощью калькулятора .

Как найти площадь поверхности прямоугольного параллелепипеда: формула

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади прямоугольного параллелепипеда: формула и пример

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.

• Формула вычисления площади
• Пример задачи

Формула вычисления площади

Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:

S = 2 (ab + bc + ac)

Формула получена следующим образом:

1. Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
   • два основания: со сторонами a и b;
   • четыре боковые грани: со стороной a/b и высотой c.
2. Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).

Пример задачи

Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.

Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Параллелепипед – формулы, свойства, определение, примеры

Параллелепипед – это трехмерная фигура, образованная шестью параллелограммами. Слово «параллелепипед» происходит от греческого слова parallelepdon , что означает «тело, имеющее параллельные тела». Можно сказать, что параллелепипед относится к параллелограмму так же, как куб относится к квадрату. Параллелепипед имеет 6 граней в форме параллелограмма, 8 вершин и 12 ребер. Давайте разберемся со свойствами и различными формулами, связанными с площадью поверхности и объемом параллелепипеда, в следующих разделах.

1.	Что такое параллелепипед?
2.	Свойства параллелепипеда
3.	Площадь поверхности параллелепипеда
4.	Объем параллелепипеда
5.	Решенные примеры
6.	Практические вопросы
7.	Часто задаваемые вопросы о параллелепипеде

Что такое параллелепипед?

Параллелепипед представляет собой трехмерную фигуру с шестью гранями, каждая из которых имеет форму параллелограмма. У него 6 граней, 8 вершин и 12 ребер. Куб, прямоугольный параллелепипед и ромбовидный — все это частные случаи параллелепипеда. Куб – это параллелепипед, все стороны которого имеют форму квадрата. Точно так же кубоид и ромбоид являются параллелепипедами с прямоугольной и ромбовидной гранями соответственно. На приведенном ниже рисунке мы можем наблюдать параллелепипед с длинами сторон «a», «b» и «c», а «h» — высотой параллелепипеда.

Свойства параллелепипеда

Существуют определенные свойства параллелепипеда, которые помогают нам отличить его от других трехмерных фигур. Эти свойства перечислены ниже:

• Параллелепипед представляет собой трехмерную твердую форму.
• Имеет 6 граней, 12 ребер и 8 вершин.
• Все грани параллелепипеда имеют форму параллелограмма.
• Параллелепипед имеет 2 диагонали на каждой грани, называемые диагоналями граней. Всего у него 12 диагоналей граней.
• Диагонали, соединяющие вершины, не лежащие на одной грани, называются телом или пространственной диагональю параллелепипеда.
• Параллелепипедом называется призма с основанием в форме параллелограмма.
• Каждая грань параллелепипеда является зеркальным отражением противоположной грани.

Площадь поверхности параллелепипеда

Площадь поверхности параллелепипеда определяется как общая площадь, занимаемая всеми поверхностями параллелепипеда. Площадь поверхности параллелепипеда выражается в квадратных единицах, например 9.0087 2 , см ² , м ² , фут ² , ярд ² и т. д. Площадь поверхности параллелепипеда может быть двух типов:

• Боковая Площадь поверхности
• Общая площадь поверхности

Площадь боковой поверхности параллелепипеда

Площадь боковой поверхности параллелепипеда определяется как площадь боковых или боковых граней параллелепипеда. Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.

Общая площадь поверхности параллелепипеда

Общая площадь поверхности параллелепипеда определяется как площадь всех граней параллелепипеда. Чтобы вычислить TSA параллелепипеда, нам нужно найти сумму площадей, покрытых 6 гранями.

Площадь поверхности параллелепипеда Формула

Формула для расчета площади боковой поверхности и общей площади поверхности параллелепипеда:
LSA параллелепипеда = P × H

TSA параллелепипеда = LSA + 2 × B = (P × H) + (2 × B)

где,

• B = Базовая площадь
• H = Высота параллелепипеда
• P = Периметр основания

Объем параллелепипеда

Объем параллелепипеда определяется как пространство, занимаемое фигурой в трехмерной плоскости. Объем параллелепипеда выражается в кубических единицах, например, ³ , см ³ , м ³ , фут ³ , ярд ³ и т. д.

Объем параллелепипеда Формула

Объем параллелепипеда можно рассчитать, используя площадь основания и высоту. Формула для расчета объема параллелепипеда дается как,
В = В × Н
где

• B = Базовая площадь
• H = Высота параллелепипеда

 

Решенные примеры на параллелепипеде

1. Пример 1: Если базовая грань параллелепипеда имеет противоположные стороны размером 6 дюймов и 10 дюймов, а его высота равна 7 дюймам, найдите площадь боковой поверхности параллелепипеда.

   Решение:

   Используя формулу площади боковой поверхности параллелепипеда,
   LSA = периметр основания × высота 90 115 ⇒ ЛСА = 2(6 + 10) × 7
   = 224 в ³

   Ответ: Площадь боковой стороны данного параллелепипеда = 224 в ^3.

2. Пример 2: Подарок упакован в прямоугольную коробку размером 10, 7 и 8 дюймов и должен быть обернут подарочной бумагой. Сколько подарочной бумаги требуется для упаковки подарочной коробки?

   Решение:

   Размеры данной подарочной коробки,
   длина, l = 10 в
   ширина, w = 7 в
   высота, h = 8 in

   Чтобы найти необходимое количество подарочной бумаги, нам нужно найти общую площадь поверхности коробки. Поскольку форму коробки можно сравнить с прямоугольным параллелепипедом,

   ВПС = 2 (дв + вх + вл)

   = 2 (10 × 7 + 7 × 8 + 8 × 10)

   = 2 (70 + 56 + 80)

   = 412 в ² .

   Ответ: Площадь необходимой подарочной бумаги = 412 в ² .

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Забронировать бесплатный пробный урок

Практические вопросы по параллелепипеду

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о параллелепипеде

Что такое параллелепипед?

Параллелепипед представляет собой трехмерную фигуру с 6 гранями в форме параллелограмма, 12 ребрами и 8 вершинами. Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.

Каков объем параллелепипеда?

Объем параллелепипеда – это емкость, форма или общее пространство, занимаемое в трехмерной плоскости. Объем параллелепипеда в кубических единицах, например, ³ , см ³ , фут ³ , ³ и т. д.

Какова общая площадь поверхности параллелепипеда?

Полная площадь поверхности параллелепипеда – это площадь, покрытая всеми гранями параллелепипеда. Выражается в квадратных единицах, например, в ² , м ² , см ² , фут ² и т. д.

Что такое площадь боковой поверхности параллелепипеда?

Площадь боковой поверхности параллелепипеда – это площадь или область, покрываемая всеми боковыми или боковыми гранями параллелепипеда. Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.

Что такое формулы параллелепипеда?

Формулы, связанные с параллелепипедом, даны как,

• LSA параллелепипеда = P × H
• TSA параллелепипеда = (P × H) + (2 × B)
• Объем параллелепипеда = B × H

где B — площадь основания, H — высота параллелепипеда, P — периметр основания.

Что такое прямоугольный параллелепипед?

Прямоугольный параллелепипед — тип параллелепипеда, все шесть граней которого имеют прямоугольную форму, а длины параллельных ребер равны.

Какой формы параллелепипед?

Параллелепипед — это трехмерная фигура, все стороны которой имеют форму параллелограмма. Противоположные грани параллелепипеда являются зеркальным отображением друг друга.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы фигур

Параллелепипед

Параллелепипед — это трехмерная (трехмерная) фигура с шестью гранями, связанными тремя парами параллельных плоскостей, поэтому все ее грани являются параллелограммами.

В основном, он образован шестью сторонами параллелограмма, образуя трехмерную фигуру или призму, имеющую основание в виде параллелограмма.

Свойства параллелепипеда

1) Параллелепипед — это трехмерная фигура.

2) Имеет 6 граней.

3) Имеет 12 ребер и 8 вершин.

4) Грани параллелепипеда — параллелограмм.

5) Это призма с параллелограммом в основании.

6) Каждое лицо кажется зеркальным отражением противоположного лица.

7) Диагональ каждой грани называется диагональю грани.

8) Диагональ трехмерного тела параллелепипеда называется диагональю тела.

Объем параллелепипеда

Для заданного параллелепипеда пусть «A» — площадь нижней грани, а «h» — высота, тогда формула объема определяется следующим образом:

                                         Объем параллелепипеда = A × h

Поскольку нижняя грань является параллелограммом, ее площадь «A» можно рассчитать по формуле:

                                 A = площадь параллелограмма = основание × высота.

В векторной форме:

Объем параллелепипеда, натянутого на элементы a, b и c, определяется по формуле:

                                                                                      = | а × б | |с| cos ø

                                                     = | (а × б).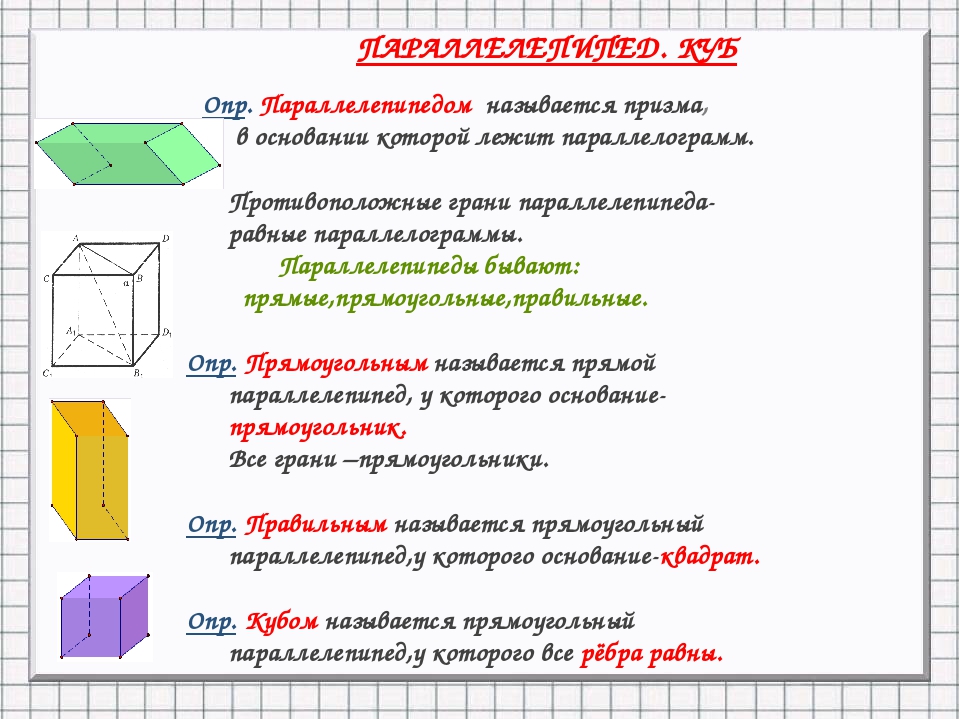 с |

Площадь поверхности параллелепипеда

1) Площадь боковой поверхности (L.S.A.)

Это произведение периметра основания и высоты параллелепипеда.

                         L.S.A. = Периметр основания × высота

2) Общая площадь поверхности (TSA)

Это сумма LSA и площади двух оснований.

                         T.S.A. = L.S.A. + 2 (площадь основания)

Существует два основных типа параллелепипедов:

1. Куб

2. Прямоугольник

Куб

Куб представляет собой параллелепипед, все шесть граней которого имеют квадратную форму.

Пример: игральные кости, кубик льда, кубик Рубика и т. д.                               

Пусть каждая сторона куба равна a единиц. Затем

1. Объем прямоугольного параллелепипеда = площадь нижней грани (квадрат) × высота

                                           = (a × a) × (a)

                                           = a3 единицы

2. L.S.A. = периметр основания (квадрат) × высота 

               = (4a) × (a)

                     = 4a2 единицы

3. T.S.A. = L.S.A. + 2(базовая площадь)

               =  (4a2)+ 2(a2) 92}}  = \sqrt 3  \times \left( a \right)\] единиц

Прямоугольный параллелепипед

Прямоугольный параллелепипед, все шесть граней которого имеют прямоугольную форму.

 Это трехмерная коробчатая структура.

Пример: коробка для спичек, тряпка, кирпичи, коробка для инструментов и т. д.                          

Обозначим длину, ширину и высоту параллелепипеда l, b и h соответственно. Тогда

1) Объем прямоугольного параллелепипеда = площадь нижней грани (прямоугольной) × высота

                             = (l × b) × (h)

                                              = l × b × h

2) L.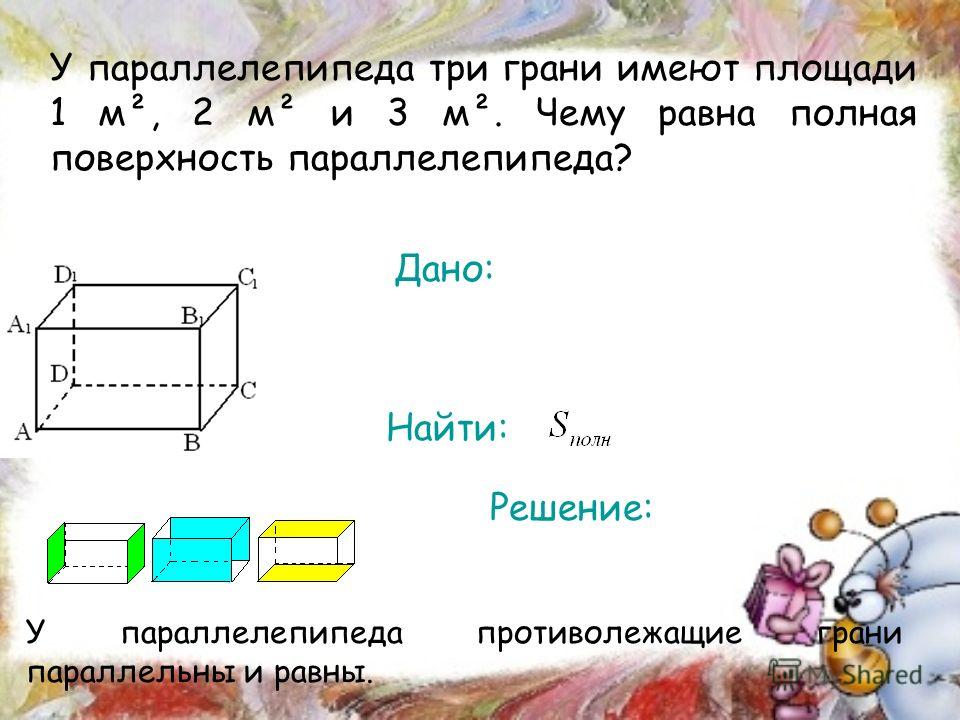 S .А. = периметр основания (прямоугольник) × высота 

               = 2(l + b) × (h)

               = 2(l + b) h

L.S.A. кубоида также можно принять как площадь четырех стен прямоугольного помещения.

3) Т.С.А. = L.S.A. + 2(площадь основания)

               = 2(l + b) h + 2(lb) 

                             = 2(lb + bh + lh) 92}}\]

Решено Примеры:

Q.1. Найдите сторону куба, площадь поверхности которого равна 600 см2.

Ответ. Площадь поверхности куба = 6 (сторона)2

            Дано, площадь поверхности куба = 600 см2

              ⇒   6 (сторона)2 =  600 см2

               ⇒     (сторона)2 = 100 см2

                       ⇒      сторона куба = 10 см.

            

Q.2. Найдите объем, L.S.A., T.S.A. Диагональ тела прямоугольного параллелепипеда, длина которого 3 см, ширина 4 см, высота 5 см.

Ответ. a.) Объем прямоугольного параллелепипеда  = l × b × h

                                               = 3 см × 4 см × 5 см

                                                = 60 см3

          b.) L.S.A. = 2(l + b) h

                    = 2 × (3 см + 4 см) × 5 см

                             = 70 см2

           c. ) Т.С.А. = 2(lb + bh + hl)

                       = 2 × {(3 см × 4 см) + (4 см × 5 см) + (5 см × 3 см)}

92}}\]

= \[\sqrt{9 + 16 + 25}\] см

= \[\sqrt{50}\] см

= 5\[\sqrt{2}\] см

Вопрос 3. Внутренние размеры прямоугольной комнаты составляют 12 м × 8 м × 4 м. Найдите общую стоимость побелки всех четырех стен комнаты, если стоимость побелки составляет 500 руб. 5 за кв. метр.

Ответ. Пусть длина комнаты = l = 12 м

                      ширина комнаты = b = 8 м

                        высота комнаты = h = 4 м

Площадь четырех стены комнаты = L.