При каких значениях a число 29 a является простым: при каких значениях а число 29*а является простым — Спрашивалка

Простые и Составные Числа

Поможем понять и полюбить математику

Начать учиться

110.4K

Числа бывают натуральные целые, простые и составные — и это то, что очень нам пригодится при решении разных задач. Этим и займемся: просто и без воды.

Основные определения

Натуральные числа больше единицы бывают простые и составные.

Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.

Например:

• 11, 13, 17, 19 — список простых чисел.
• 11 — делится только на 1 и 11.
• 13 — делится на 1 и 13.
• 17 — делится на 1 и 17.

Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.

Например:

• 9, 10, 12, 14 — примеры из списка составных чисел.
• 9  — делится на  1,  на 3 и на 9.
• 10 — делится на  1,  на  2,  на 5 и на 10.
• 12 — делится на 1, на 2, 3, 4, 6 и на 12.

Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел. Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные. Число 4 — первое наименьшее составное число.

В математике есть первые простые и составные числа, но последних таких чисел не существует.

А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Таблица простых чисел до 1000

2	3	5	7	11	13	17	19	23
29	31	37	41	43	47	53	59	61
67	71	73	79	83	89	97	101	103
107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197
199	211	223	227	229	233	239	241	251
257	263	269	271	277	281	283	293	307
311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419
421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523
541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643
647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761
769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883
887	907	911	919	929	937	941	947	953
967	971	977	983	991	997

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

К предыдущей статье

132.4K

Признаки делимости чисел

К следующей статье

Развертка прямоугольного параллелепипеда

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

определение, наименьшее и наибольшее составное число, список составных чисел

Счет в жизни человека присутствовал всегда. Для него первобытные люди использовали сначала пальцы рук. Затем – дополнительные приспособления, например узелки или веревочки. Позднее стали применять свойства чисел.

Еще в III веке до н. э. в своем известном труде «Начала» древнегреческий математик Евклид вводит понятие простых и составных чисел. Последним он дает такую характеристику: множество, составленное из единиц. К слову, в XIX веке такие числа называли еще сложными.

В шестом классе, когда ученики изучают признаки делимости числа, они знакомятся с основными свойствами простых и составных чисел. Ведь принципы их образования, главные закономерности ложатся в основу всех арифметических действий и геометрических доказательств. Считается, если ребенок поймет классификацию простых и составных чисел, то дальше все примеры и задачи по математике будут ему понятны.

Определение составных чисел

Составным называется любое натуральное число, которое имеет еще хотя бы один делитель, кроме себя и единицы.

Обратите внимание на примеры, чтобы понять разницу между простыми и составными числами

2 – это простое число. Оно делится на 1 и 2.

6 – это составное число. Оно делится на 1, 2, 3 и 6.

1 – число, которое не является ни простым, ни составным.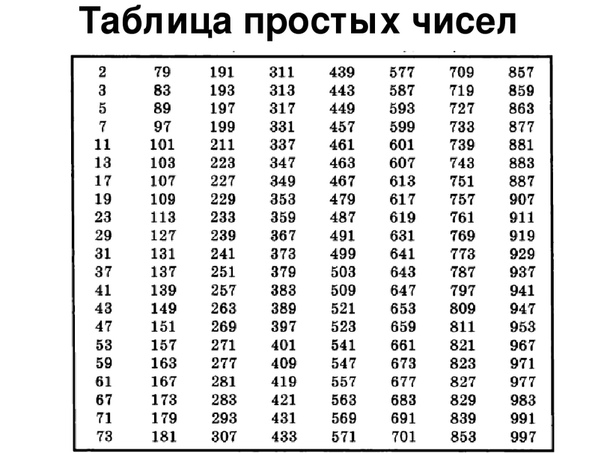 У него только один делитель – 1.

это интересно

Натуральные числа

Их разряды, классы и свойства

подробнее

Натуральные составные числа

Его пока нет, и вряд ли оно будет. Числа представляют собой бесконечность различных вариантов, которые можно расчленить на мелкие делители. Математики только выделяют самое большое простое число – здесь есть, за что бороться. Составные числа, будь то число Грэма (обозначают G64) или другие огромные числа, такого интереса не вызывают.

Натуральными составными числами являются все целые положительные числа, которые имеют два множителя больше единицы. При этом каждое составное число раскладывается на простые множители.

Рассмотрим примеры.

12 – составное число. Его можно представить как произведение двух натуральных чисел 3х4 или 6х2. В обеих парах есть простые и составные числа. Если разложить их на простые множители, получится так: 12 = 3х2х2.

77 – составное число. Его можно представить как произведение двух натуральных чисел 7х11. Оба они – простые. Значит, дальше их разложить не получится.

это интересно

Таблица составных чисел

Скачайте таблицу составных чисел и используйте ее при подготовке к урокам

подробнее

Наименьшее составное число

Наименьшее составное число – 4. Оно имеет три делителя: 1, 2 и 4.

Список составных чисел до 100

Для систематизации использования натуральных чисел разработаны специальные таблицы простых и составных чисел. В частности, в таблицу составных чисел первой сотни входят 74 числа. Открывает ее наименьшее составное число 4. Замыкает число 100 с девятью делителями: 1, 2, 4, 5, 10, 20, 25, 50, 100.

4	6	8	9	10	12	14	15	16	18	20	21
22	24	25	26	27	28	30	32	33	34	35	36
38	39	40	42	44	45	46	48	49	50	51	52
54	55	56	57	58	60	62	63	64	65	66	68
69	70	72	74	75	76	77	78	80	81	82	84
85	86	87	88	90	91	92	93	94	95	96	98
99	100

Популярные вопросы и ответы

Отвечает Павел Бучко, академический директор по математике онлайн-школы Skysmart.

Как определить, составное число или нет?

Все натуральные числа, которыми мы пользуемся при счете, делятся на три типа: простые, составные и единица. Простые числа – это те, что делятся без остатка только на 1 и на само себя. Например, числа 2, 3, 5, 53 будут простыми. Составные числа – это числа, которые имеют еще делители, помимо 1 и самого себя. Например, число 4 можно разделить без остатка на 2.

Определить, является ли число составным или простым, довольно легко, если оно небольшое. Можно использовать простой перебор: будем делить наше число на все числа меньше искомого и, если мы найдем хотя бы одно, на которое можно разделить без остатка, – значит, наше число является составным, иначе оно простое. Однако этот алгоритм очень громоздкий даже для небольших чисел, поэтому можно использовать перебор простых делителей: когда мы последовательно делим проверяемое число на простые числа от 2 до квадратного корня из проверяемого числа.

Например, мы хотим проверить является ли число 83 простым или составным, тогда мы последовательно делим его на 2, 3, 5, 7 и выясняем, что оно не делится ни на одно из этих чисел, а значит, является простым. При этом число 11 уже можно не брать, потому что 11х11 = 121, что больше 83.

Этот алгоритм не используется в практических задачах из-за большой вычислительной сложности. А для определения простоты очень больших чисел (больше, чем 10 в 100 степени) задача становится крайне сложной и требует больших вычислительных мощностей и времени работы.

Для чего математики используют составные числа?

Составные числа используются в криптографии: при шифровании информации в алгоритмах электронной цифровой подписи. Например, благодаря таким числам, мы можем безопасно делать покупки в интернете.

Можно ли запомнить все составные числа?

Составных чисел, как и простых, бесконечное множество, поэтому запомнить их все невозможно. Однако можно помнить несколько простых чисел (2, 3, 5, 7, 11, 13, 17, 19, 23, 29 и 31), чтобы проверить любое число до 1000 на простоту, пользуясь алгоритмом выше.

Является ли 29 простым числом

Является ли 29 простым числом? «Да, 29 — простое число». Число может быть классифицировано как простое или составное в зависимости от множителей, которые оно содержит; он может иметь либо только 2 фактора, либо более 2 факторов. Числа вроде 577, имеющие всего 2 делителя, то есть 1 и 577, называются простыми числами. Однако такие числа, как 106 с более чем двумя делителями, называются составными числами. Давайте выясним, как и почему 29 является простым числом?

• Ис 29простое число? — Да
• Является ли 29 составным числом? — №
• Является ли число 29 правильным квадратом? — №
• Коэффициенты 29 —
  1, 29
• Простые множители 29 — 29

Является ли 29 простым числом?

Да, 29 — простое число. Число 29 делится только на 1 и само число. Чтобы число считалось простым, оно должно иметь ровно два делителя. С 29имеет ровно два делителя, то есть 1 и 29, это простое число.

Как 29 является простым числом?

Чтобы понять, является ли число 29 простым или составным, важно найти его делители.

Делители 29: 1, 29

Следовательно, мы можем сказать, что 29 — простое число, поскольку оно имеет только 2 делителя.

☛ Калькулятор простых чисел

Является ли 29 составным числом?

Нет, так как 29 имеет только два делителя, то есть 1 и 29. Другими словами, 29не является составным числом, потому что 29 не имеет более двух делителей.

Условия задачи:

Является ли 29 простым числом?	Да
Является ли 29 составным числом?	№
Является ли 29 идеальным квадратом?	№
Кратность 29	29, 58, 87, 116, 145, 174, 203, 232, 261, 290
29 — нечетное число?	Да
Является ли 29 четным числом?	№
Является ли число 29 идеальным кубом?	№
Кубический корень из 29	3. 072313
Квадратный корень из 29	5.385165

Интересные факты:

• 1 не является ни простым, ни составным.
• Полупростое число — это составное число, являющееся произведением ровно двух простых чисел. Пример — 485 — полупростое число, так как 485 можно записать как 5 × 97.
• Числа X и Y называются взаимно простыми, если они имеют только один общий делитель, равный 1.

☛ Также проверьте:

• Является ли 54 простым числом? — №
• Является ли 121 простым числом? — №
• Является ли 26 простым числом? — №
• Является ли 123 простым числом? — №
• Является ли 1001 простым числом? — №
• Является ли 307 простым числом? — Да
• Является ли 299 простым числом? — №
• Является ли 567 простым числом? — №

 

Рабочие листы по математике и
наглядный учебный план

Простые числа — Элементарная математика

Значение

Неформальный смысл или более меньшие счетные числа.

Но только некоторые счетных чисел могут быть составлены путем умножения двух или более меньших счетных чисел.

Простые и составные числа: Мы можем построить 36 из 9 и 4 путем умножения; или мы можем построить его из 6 и 6; или с 18 и 2; или даже путем умножения 2 × 2 × 3 × 3. Числа, такие как 10, 36 и 49, из которых могут быть составлены как произведения меньших счетных чисел, называются составными числами.

Некоторые числа нельзя составить таким образом из более мелких частей. Например, он единственный способ построить 7 путем умножения и использования только при подсчете чисел равно 7 × 1. Чтобы «построить» 7, мы должны использовать 7! Так что на самом деле мы не собираем его из более мелких строительных блоков; нам это нужно для начала. Такие числа называются простыми числами.

Неофициально простые числа — это числа, которые нельзя получить путем умножения других чисел. Это хорошо передает идею, но не является достаточно хорошим определением, потому что в нем слишком много лазеек. Число 7 может быть составлено как произведение других чисел: например, это 2 × 3. Чтобы уловить идею о том, что «7 не делится на 2», мы должны четко указать, что мы ограничиваем числа, включающие только счетные числа: 1, 2, 3….

Формальное определение

Простое число — это натуральное число, имеющее ровно два различных целочисленных множителя (или делителя), а именно 1 и само число.

Разъяснение двух распространенных заблуждений

Два распространенных заблуждения:

• Число 1 — это , а не простое число.

• Число 2 является простым . (Это единственное четное простое число.)

Число 1 не простое. Почему бы и нет?

Что ж, определение исключает это. В нем говорится «два различных целочисленных множителей», и единственный способ записать 1 как произведение целых чисел — это 1 × 1, в котором таких же множителей, как друг друга, то есть не различных. Даже неформальная идея исключает это: его нельзя построить путем умножения других (целых) чисел.

Но зачем исключать?! Студенты иногда утверждают, что 1 «ведет себя» так же, как и все остальные простые числа: его нельзя «разорвать на части». И часть неформального понятия прайма — мы не можем составить 1 кроме как с помощью его, так что он должен быть строительным блоком — кажется, делает его первичным. Почему , а не включают его?

Математика не произвольна. Чтобы понять, почему из полезно исключить 1 из , рассмотрим вопрос «Сколькими способами можно записать 12 в виде произведения, используя только простые числа?» Вот несколько способов записать 12 как произведение, но они не ограничиваются простыми числами.

3 × 4

4 × 3

1 × 12

1 х 1 х 12

2 × 6

1 × 1 × 1 × 2 × 6

Использование 4, 6 и 12 явно нарушает ограничение «использование только простых чисел». Но как насчет этих?

3 × 2 × 2

2 × 3 × 2

1 × 2 × 3 × 2

2 × 2 × 3 × 1 × 1 × 1 × 1

Ну, если мы включим 1, есть бесконечно много способов записать 12 как произведение простых чисел. На самом деле, если мы назовем 1 простым числом, то существует бесконечно много способов записать 9.0182 любое число как произведение простых чисел. Включение 1 упрощает вопрос. При его исключении остаются только эти случаи:

3 × 2 × 2

2 × 3 × 2

2 × 2 × 3

Это гораздо более полезный результат, чем представление каждого числа в виде произведения простых чисел бесконечным числом способов, поэтому мы определяем простое таким образом, что оно исключает 1.

Число 2 это простое число . Почему?

Студенты иногда считают, что все простые числа нечетные. Если кто-то работает только по «шаблонам», это легко сделать, поскольку 2 — это единственное исключение, единственное четное простое число. Одно доказательство: поскольку 2 является делителем каждого четного числа, каждое четное число, большее 2, имеет не менее 90 182 трех 90 183 различных положительных делителей.

Еще один распространенный вопрос: «Все четные числа делятся на 2, значит, они не простые; 2 четно, так как же оно может быть простым?» Каждое целое число делится само на себя и на 1; все они делятся на что-то . Но если число делится на только на само по себе и на 1, то оно простое. Итак, поскольку все 90 182 других 90 183 четных чисел делятся сами на себя, на 1, и на 2 , все они составные (точно так же, как все положительные числа, кратные 3, кроме самого 3, составные).

Математическая основа

Уникальная факторизация простых чисел и деревья факторов

Вопрос «Сколькими способами можно записать число в виде произведения, используя только простые числа?» (посмотрите, почему 1 не простое число) становится даже еще интересно, если мы спросим себя, достаточно ли различны 3 × 2 × 2 и 2 × 2 × 3, чтобы считать их « различными способами». Если мы рассмотрим только набор используемых чисел — другими словами, если мы проигнорируем то, как эти числа устроены, — мы придем к замечательному и очень полезному факту (доказуемому).

Каждое целое число больше 1 можно разложить на уникальный набор простых чисел. Для любого целого числа существует только одного набора простых множителей из .

Простые числа и прямоугольники

12 квадратных плиток можно разложить на три отдельных прямоугольника.

Семь квадратных плиток можно сложить разными способами, но только одна из них образует прямоугольник.

Сколько существует простых чисел?

От 1 до 10 4 простых числа: 2, 3, 5 и 7.
От 11 до 20 снова 4 простых числа: 11, 13, 17 и 19.
От 21 до 30 только 2 простых числа: 23 и 29.
От 31 до 40 снова только 2 простых числа: 31 и 37.
От 91 до 100 только одно простое число: 97.

Похоже, они редеют. Кажется, это даже имеет смысл; по мере того, как числа становятся больше, появляется больше маленьких строительных блоков, из которых они могут быть сделаны.

Останавливаются ли когда-нибудь простые числа? Предположим на мгновение, что они в конце концов остановятся. Другими словами, предположим, что — это «наибольшего простого числа» — назовем его p 9.0183 . Итак, если бы мы перемножили вместе все известные нам простые числа (все от 2 до p ), а затем добавили 1 к этому произведению, мы бы получили новое число — назовем его q — которое не делится ни на одно из известных нам простых чисел. (Деление на любое из этих простых чисел даст в остатке 1.) Таким образом, либо q само является простым числом (и, безусловно, больше, чем p ), либо оно делится на какое-то простое число, которое мы еще не перечислили (что, следовательно, , также должно быть больше стр. ). В любом случае, предположение о существовании наибольшего простого числа — p якобы было нашим наибольшим простым числом — приводит к противоречию! Так что это предположение должно быть неверным: — это , а не «наибольшее простое число»; простые числа никогда не останавливаются.