Призма. Виды призмы | Подготовка к ЕГЭ по математике
Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.
Мы же поведем подробный разговор.
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .
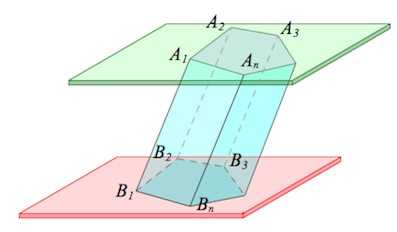
Указанные в определении равные многоугольники – основания призмы.
Боковые грани – все грани, кроме оснований (являются параллелограммами).
Боковые ребра – общие стороны боковых граней (параллельны между собой и равны).
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
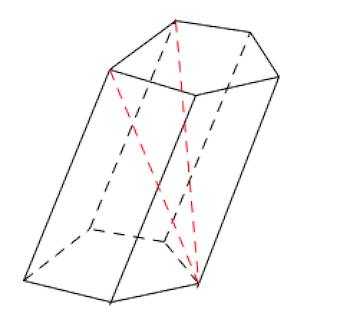
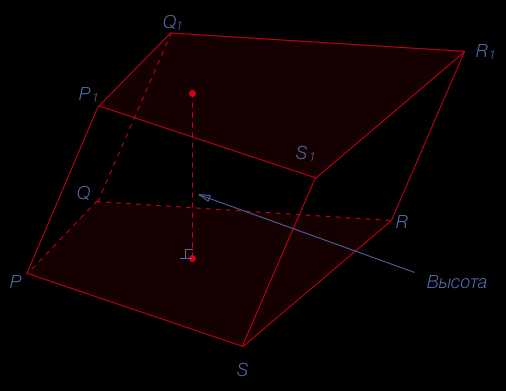
Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
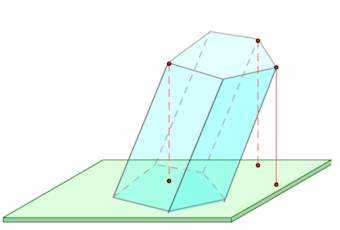
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.
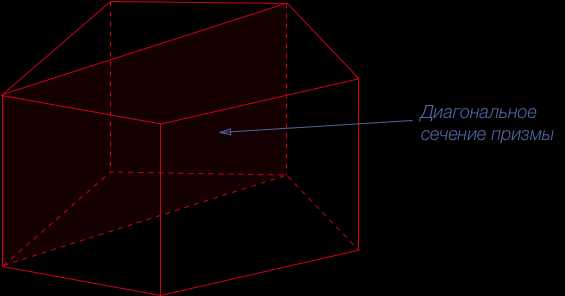
Диагональное сечение –пересечение призмы и диагональной плоскости.
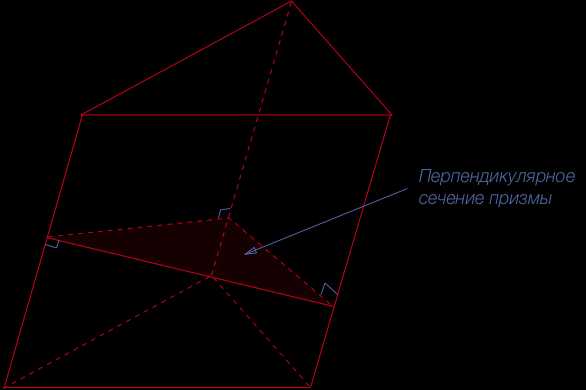
Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).
Среди прямых призм выделяют правильные.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).
Частным случаем призмы является параллелепипед.
Параллелепипед – это призма, основаниями которой являются параллелограммы.
Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.
Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Частный случай прямоугольного параллелепипеда – куб.
Куб – прямоугольный параллелепипед, все грани которого – квадраты.
Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.
Нажмите сюда чтобы увеличить
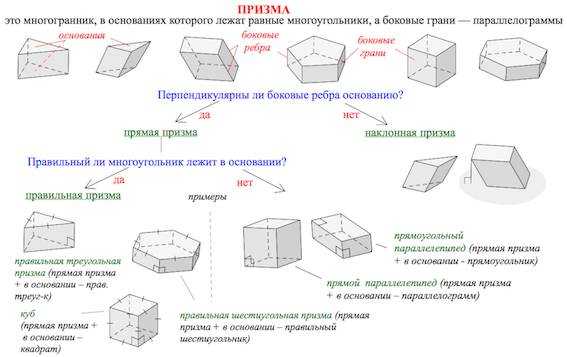
Смотрите также «Объем призмы. Площадь поверхности призмы».
egemaximum.ru
Призма | Формулы с примерами
ОпределениеПризма (n-угольная) — это многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях (
Боковые ребра — это отрезки, соединяющие соответствующие вершины оснований.
Поверхность призмы — это фигура, образованная всеми гранями призмы.Боковая поверхность призмы — это фигура, образованная боковыми гранями.
Высота призмы — это перпендикуляр, опущенный из любой точки одного основания на плоскость другого основания.
Прямая призма — это призма, боковые грани (ребра) которой перпендикулярны основаниям.

Правильная четырехугольная призма
Определение.
Правильная четырехугольная призма — это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники
Боковое ребро — это общая сторона двух смежных боковых граней
Высота призмы — это отрезок, перпендикулярный основаниям призмы
Диагональ призмы — отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани
Диагональная плоскость — плоскость, которая проходит через диагональ призмы и ее боковые ребра
Диагональное сечение — границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное сечение (ортогональное сечение) — это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам
Элементы правильной четырехугольной призмы
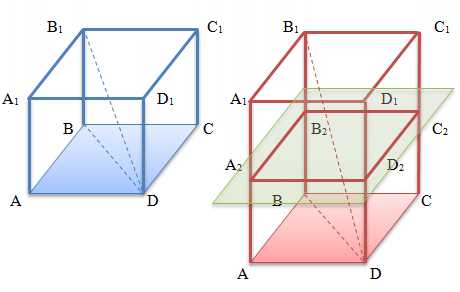
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:
- Основания ABCD и A1B1C1
- Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
- Боковая поверхность — сумма площадей всех боковых граней призмы
- Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA1, BB1, CC1 и DD1.
- Диагональ B1D
- Диагональ основания BD
- Диагональное сечение BB1D1
- Перпендикулярное сечение A2B2C2D2 .
Свойства правильной четырехугольной призмы
- Основаниями являются два равных квадрата
- Основания параллельны друг другу
- Боковыми гранями являются прямоугольники
- Боковые грани равны между собой
- Боковые грани перпендикулярны основаниям
- Боковые ребра параллельны между собой и равны
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
- Углы перпендикулярного сечения — прямые
- Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
- Перпендикулярное (ортогональное сечение) параллельно основаниям
Формулы для правильной четырехугольной призмы
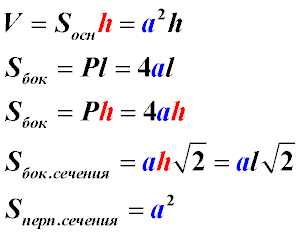
Указания к решению задач
При решении задач на тему «правильная четырехугольная призма» подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия — призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форумеЗадача.
В правильной четырёхугольной призме площадь основания 144 см2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 122 + 122 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
Ответ: 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Ответ: 25 + 10√7 ≈ 51,46 см2 .
Прямая призма | Описание курса | Диагональное сечение правильной призмы
profmeter.com.ua
Прямая и правильная призма
Прямая и правильная призма. Площади боковой и полной поверхности призмы. Параллелепипед. Прямоугольный параллелепипед
Прямая призма — это призма, имеющая перпендикулярны основ боковые ребра.
Если это условие не выполняется, то призма называется наклонной.
В прямой призмы все боковые грани — прямоугольники.
На изображении прямой призмы на плоскости боковые ребра размещают вертикально.
Прямая призма, в основе которой лежит правильный многоугольник, называется правильной призмой.
Площадь боковой поверхности прямой призмы является произведением периметра основания на высоту призмы.
Площадь боковой поверхности наклонной призмы равна произведению периметра сечения призмы плоскостью, перпендикулярной боковому ребру, на длину бокового ребра призмы.
Сумма площадей основ призмы и боковой поверхности призмы равна площади полной поверхности призмы.
Параллелепипед — это призма, основанием которой является параллелограмм.
Противоположные грани параллелепипеда параллельны и равны.
Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
Прямоугольный параллелепипед — параллелепипед, основой которого является прямоугольник, а боковые ребра перпендикулярны основам.
Боковые грани прямоугольного параллелепипеда перпендикулярны его основам.
Линейными размерами прямоугольного параллелепипеда являются длины его непараллельных ребер.
Диагонали прямоугольного параллелепипеда уровне.
Все двугранные углы прямоугольного параллелепипеда — прямые.
Квадрат любой диагонали прямоугольного параллелепипеда является суммой квадратов трех его измерений.
Точка пересечения диагоналей параллелепипеда является его центром симметрии.
Через центр симметрии прямоугольного параллелепипеда проходят три плоскости, параллельные граням, которые являются плоскостями симметрии прямоугольного параллелепипеда.
Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии.
Если у прямоугольного параллелепипеда два линейных размеры равны, то он имеет еще две плоскости симметрии, Это плоскости диагональных сечений.
Прямоугольный параллелепипед, все линейные размеры которого равны, называется кубом. Куб имеет девять плоскостей симметрии.
Все грани куба являются квадратами.
Площадь боковой поверхности куба равна квадрату его ребра, умноженному на четыре.
Площадь полной поверхности куба равна квадрату его ребра, умноженному на шесть.
xn—-7sbfhivhrke5c.xn--p1ai
Призма (математика) — это… Что такое Призма (математика)?
- Призма (математика)
Призма (математика)
Призма — многогранник, две грани которого являются конгруэнтными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Элементы призмы
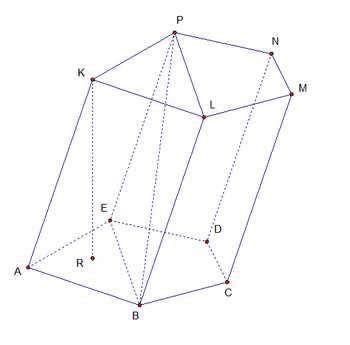
Название Определение Обозначения на чертеже Чертеж Основания Две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных плоскостях. ABCDE, KLMNP 
Боковые грани Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. ABLK, BCML, CDNM, DEPN, EAKP Боковая поверхность Объединение боковых граней. Полная поверхность Объединение оснований и боковой поверхности. Боковые ребра Общие стороны боковых граней. AK, BL, CM, DN, EP Высота Отрезок, соединяющий основания призмы и перпендикулярный им. KR Диагональ Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. BP Диагональная плоскость Плоскость, проходящая через боковое ребро призмы и диагональ основания. Диагональное сечение Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат. EBLP Перпендикулярное сечение Пересечение призмы и плоскости, перпендикулярной ее боковому ребру. Свойства призмы
- 1. Основания призмы являются равными многоугольниками.
- 2. Боковые грани призмы являются параллелограммами.
- 3. Боковые ребра призмы параллельны и равны.
- 4. Объём призмы равен произведению её высоты на площадь основания:
- 5. Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Виды призм
Призмы бывают прямые и наклонные.
Прямая призма — призма, у которой все боковые ребра перпендикулярны основанию.
- Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.
Наклонная призма — призма, у которой хотя бы одно боковое ребро не перпендикулярно основанию.
- Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
Правильная призма — прямая призма, основание которой является правильным многоугольником.
Свойства правильной призмы
- 1. Основания правильной призмы являются правильными многоугольниками.
- 2. Боковые грани правильной призмы являются равными прямоугольниками.
- 3. Боковые ребра правильной призмы равны.
См. также
Ссылки
Многогранники Правильные
(Платоновы тела)Правильные невыпуклые Звёздчатый многогранник (Звёздчатый октаэдр, Звёздчатый додекаэдр, Звёздчатый икосаэдр, Звёздчатый икосододекаэдр) Выпуклые Полуправильные многогранники или Архимедовы тела/двойственные многогранники или Каталановы тела
(Кубооктаэдр/Ромбододекаэдр, Икосододекаэдр/Ромботриаконтаэдр, Усечённый тетраэдр/Triakis tetrahedron,
Усечённый куб/Triakis octahedron, Усечённый октаэдр/Tetrakis hexahedron, Усечённый додекаэдр/Triakis icosahedron,
Усечённый икосаэдр/Pentakis dodecahedron, Ромбокубоктаэдр/Дельтоидальный икоситетраэдр,
Ромбоусечённый кубоктаэдр/Disdyakis dodecahedron, Ромбоикосододекаэдр/Дельтоидальный гексеконтаэдр,
Ромбоусечённый икосододекаэдр/Disdyakis triacontahedron,
Курносый куб/Пентагональный икоситетраэдр, Курносый додекаэдр/Пентагональный гексеконтаэдр,
Звёздчатый кубооктаэдр, правильные призма и антипризма)Формулы, теоремы, теории Прочее Wikimedia Foundation. 2010.
- Эхнатон
- Fiat (компания)
Смотреть что такое «Призма (математика)» в других словарях:
Математика в девяти книгах — (начало) «Математика в девяти книгах» (кит. трад. 九章算術 … Википедия
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия
Земляков, Александр Николаевич — Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик, выдающийся советский и российский педагог, автор учебно педагогической литературы. Биография Закончил в 1967 году с золотой… … Википедия
Правильный многогранник — Додекаэдр Правильный многогранник или платоново тело это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией … Википедия
Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия
Бипирамида — или дипирамида является трёхмерным многогранником, сформированным из двух пирамид, одна из которых является зеркальным отражением другой. Место соединения пирамид образует общую фигуру в виде многоугольника. Простая бипирамида формируется при… … Википедия
Изгибаемый многогранник — Многогранник (точнее многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело) … Википедия
Норма (философия) — «Мыслитель», Огюст Роден Философия (др. греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω люблю и σοφία мудрость) наиболее общая теория … Википедия
Определение философии — «Мыслитель», Огюст Роден Философия (др. греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω люблю и σοφία мудрость) наиболее общая теория … Википедия
dic.academic.ru
Призма
Призмой называется многогранник, у которого две грани — равные многоугольники с соответственно параллельными сторонами, а все остальные грани — параллелограммы (фиг.282,а).
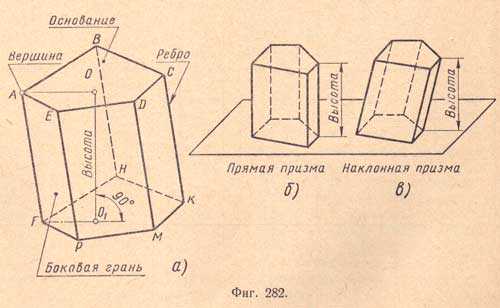
Многоугольники ABCDE и FHKMP, лежащие в параллельных плоскостях, называются основаниями призмы, перпендикуляр OO1, опущенный из любой точки основания на плоскость другого, называется высотой призмы. Параллелограммы ABHF, BCKH и т.д. называются боковыми гранями призмы, а их стороны СК, DM и т.д., соединяющие соответственные вершины оснований, — боковыми ребрами. У призмы все боковые ребра равны между собой как отрезки параллельных прямых, заключенных между параллельными плоскостями.
Призма называется прямой (фиг.282,б) или наклонной (фиг.282,в) в зависимости от того, будут ли ее боковые ребра перпендикулярны или наклонны к основаниям. У прямой призмы боковые грани — прямоугольники. За высоту такой призмы можно принять боковое ребро.
Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые грани — равные прямоугольники.
Для изображения на комплексном чертеже призмы надо знать и уметь изображать элементы, из которых она состоит (точку, прямую, плоскую фигуру).
Анализ элементов правильной призмы и их изображение на комплексном чертеже (фиг.283, а — и)
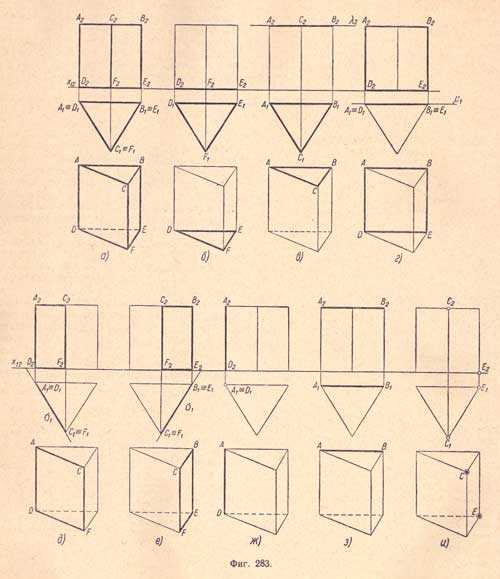
а) Комплексный чертеж призмы. Основание призмы расположено на плоскости проекций П1; одна из боковых граней призмы параллельна плоскости проекций П2.
б) Ниокнее основание призмы DEF — плоская фигура — правильный треугольник, расположенный в плоскости П1; сторона треугольника DE параллельна оси х12 — Горизонтальная проекция сливается с данным основанием и, следовательно, равна его натуральной величине; фронтальная проекция сливается с осью х12 и равна стороне основания призмы.
в) Верхнее основание призмы АВС — плоская фигура — треугольник, расположенный в горизонтальной плоскости. Горизонтальная проекция сливается с проекцией нижнего основания и закрывает собой ее, так как призма прямая; фронтальная проекция — прямая, параллельная оси х12, на расстоянии высоты призмы.
г) Боковая грань призмы ABED — плоская фигура — прямоугольник, лежащий во фронтальной плоскости. Фронтальная проекция — прямоугольник, равный натуральной величине грани; горизонтальная проекция — прямая, равная стороне основания призмы.
д) и е) Боковые грани призмы ACFD и CBEF — плоские фигуры — прямоугольники, лежащие в горизонтально — проектирующих плоскостях, расположенных под углом 60° к плоскости проекций П2. Горизонтальные проекции — прямые, расположенные к оси х12 под углом 60°, и равны натуральной величине сторон основания призмы; фронтальные проекции — прямоугольники, изображение которых меньше натуральной величины: две стороны каждого прямоугольника равны высоте призмы.
ж) Ребро AD призмы — прямая, перпендикулярная к плоскости проекций П1. Горизонтальная проекция — точка; фронтальная — прямая, перпендикулярная оси х12, равная боковому ребру призмы (высоте призмы).
з) Сторона АВ верхнего основания — прямая, параллельная плоскостям П1 и П2. Горизонтальная и фронтальная проекции — прямые, параллельные оси х12 и равные стороне данного основания призмы. Фронтальная проекция отстоит от оси х12 на расстоянии, равном высоте призмы.
и) Вершины призмы. Точка Е — вершина нижнего основания расположена на плоскости П1. Горизонтальная проекция совпадает с самой точкой; фронтальная — лежит на оси x12.Точка С — вершина верхнего основания — расположена в пространстве. Горизонтальная проекция имеет глубину; фронтальная — высоту, равную высоте данной призмы.
Отсюда следует: проектируя всякий многогранник, надо мысленно расчленить его на составные элементы и определить порядок их изображения, состоящий из последовательных графических операций. На (фиг.284 и фиг.285) приведены примеры последовательных графических операций при выполнении комплексного чертежа и наглядного изображения (аксонометрии) призм.
Изображение неправильной прямой пятиугольной призмы (фиг.284).
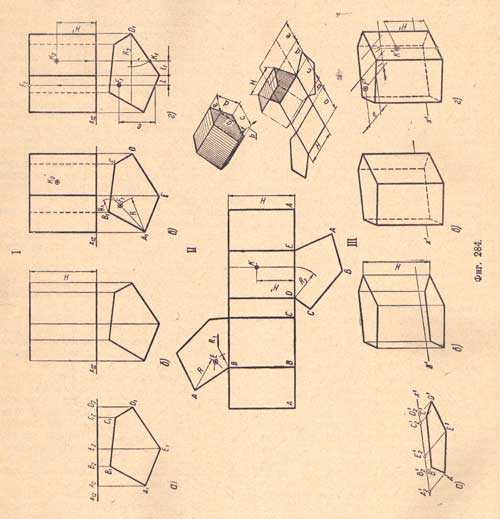
Дано:
1. Основание расположено на плоскости проекций П1.
2. Ни одна из сторон основания не параллельна оси х12.
I. Комплексный чертеж.
I, а. Проектируем нижнее основание — многоугольник, по условию лежащий в плоскости П1.
I, б. Проектируем верхнее основание — многоугольник, равный нижнему основанию с соответственно параллельными нижнему основанию сторонами, отстоящий от нижнего основания на высоту H данной призмы.
I, в. Проектируем боковые ребра призмы — отрезки, расположенные параллельно; их горизонтальные проекции — точки, сливающиеся с проекциями вершин оснований; фронтальные — отрезки (параллельные), полученные от соединения прямыми одноименных проекций вершин оснований. Фронтальные проекции ребер, проведенные из проекций вершин В и С нижнего основания, изображаем штриховыми линиями, как невидимые.
I, г. Даны: горизонтальная проекция F1 точки F на верхнем основании и фронтальная проекция К2 точки К на боковой грани. Требуется определить места их вторых проекций.
Для точки F. Вторая (фронтальная) проекция F2 точки F будет совпадать с проекцией верхнего основания, как точка, лежащая в плоскости этого основания; ее место определяется вертикальной линией связи.
Для точки К — Вторая (горизонтальная) проекция K1 точки К будет совпадать с горизонтальной проекцией боковой грани, как точка, лежащая в плоскости грани; ее место определяется вертикальной линией связи.
II. Развертка поверхности призмы — плоская фигура, составленная из боковых граней — прямоугольников, у которых по две стороны равны высоте призмы, а другие две равны соответствующим сторонам основания, и из двух равных между собой оснований — неправильных многоугольников.
Натуральные размеры оснований и сторон граней, необходимые для построения развертки, выявлены на проекциях; по ним и производим построение; на прямой последовательно откладываем стороны АВ, ВС, CD, DE и ЕA многоугольника — основания призмы, взятые из горизонтальной проекции. На перпендикулярах, проведенных из точек А, В, С, D, Е и А, откладываем взятую из фронтальной проекции высоту Н данной призмы и через отметки проводим прямую. В результате получаем развертку боковых граней призмы.
Если к этой развертке пристроить основания призмы, получим развертку полной поверхности призмы. Основания призмы следует пристраивать к соответствующей боковой грани, пользуясь методом триангуляции.
На верхнем основании призмы при помощи радиусов R и R1 определяем место точки F, а на боковой грани при помощи радиуса R3 и Н1 — точку K.
III. Наглядное изображение призмы в диметрии.
III, а. Изображаем нижнее основание призмы по координатам точек А, В, С, D и Е (фиг.284 I, a).
III, б. Изображаем верхнее основание параллельно нижнему, отстоящее от него на высоту Н призмы.
III, в. Изображаем боковые ребра, для чего соединяем прямыми соответствующие вершины оснований. Определяем видимые и невидимые элементы призмы и обводим их соответствующими линиями,
III, г. Определяем на поверхности призмы точки F и К — Точку F — на верхнем основании определяем при помощи размеров i и е; точку К — на боковой грани при помощи i1 и H’.
Для изометрического изображения призмы и определения мест точек F и К следует придерживаться той же последовательности.
Изображение неправильной наклонной четырехугольной призмы (фиг.285).
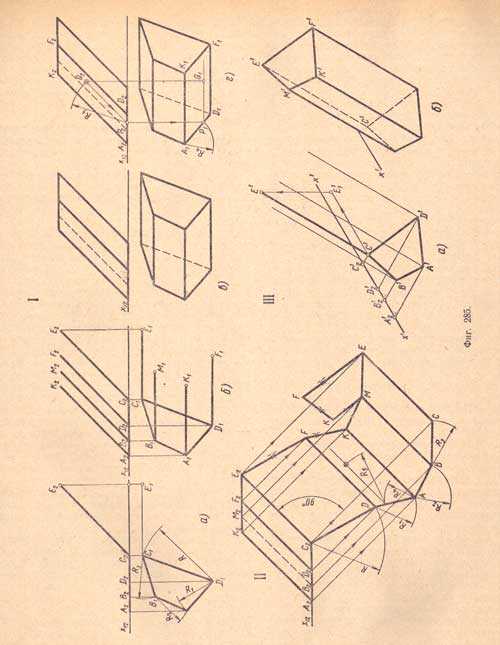
Дано:
1. Основание расположено на плоскости П1.
2. Боковые ребра параллельны плоскости П2.
3. Ни одна из сторон основания не параллельна оси x12
I. Комплексный чертеж.
I, а. Проектируем по данному условию: нижнее основание — многоугольник, лежащий в плоскости П1, и боковое ребро — отрезок, параллельный плоскости П2 и наклонный к к плоскости П1.
I, б. Проектируем остальные боковые ребра — отрезки, равные и параллельные первому ребру СЕ.
I, в. Проектируем верхнее основание призмы как многоугольник, равный и параллельный нижнему основанию, получаем комплексный чертеж призмы.
Выявляем на проекциях невидимые элементы. Фронтальную проекцию ребра ВМ и горизонтальную проекцию стороны основания CD изображаем штриховыми линиями как невидимые.
I, г. Дана фронтальная проекция Q2 точки Q на проекции A2K2F2D2 боковой грани; требуется найти ее горизонтальную проекцию. Для этого проводим через точку Q2 в проекции A2K2F2D2грани призмы вспомогательную прямую, параллельную боковым ребрам этой грани. Находим горизонтальную проекцию вспомогательной прямой и на ней при помощи вертикальной линии связи определяем место искомой горизонтальной проекции Q1 точки Q.
II. Развертка поверхности призмы.
Имея на горизонтальной проекции натуральные размеры сторон основания, а на фронтальной — размеры ребер, можно построить полную развертку поверхности данной призмы.
Будем катить призму, повертывая ее каждый раз вокруг бокового ребра, тогда каждая боковая грань призмы на плоскости будет оставлять след (параллелограмм), равный ее натуральной величине. Построение боковой развертки будем производить в следующем порядке:
а) из точек А2, В2, D2 . . . Е2 (фронтальных проекций вершин оснований) проводим вспомогательные прямые, перпендикулярные к проекциям ребер;
б) радиусом R (равным стороне основания CD) делаем на вспомогательной прямой, проведенной из точки D2, засечку в точке D; соединив прямой точки С2 и D и проведя прямые, параллельные E2С2 и C2D, получим боковую грань CEFD;
в) затем, аналогично пристроив следующие боковые грани, получим развертку боковых граней призмы. Для получения полной развертки поверхности данной призмы пристраиваем к соответствующим граням основания.
III. Наглядное изображение призмы в изометрии.
III, а. Изображаем нижнее основание призмы и ребро СЕ, пользуясь координатами согласно (фиг.284 I, a).
III, б. Изображаем боковые ребра и верхнее основание. Определив невидимые ребра и стороны основания, обводим их штриховыми линиями.
Пирамида…..
www.viktoriastar.ru
Правильная призма — Большая Энциклопедия Нефти и Газа, статья, страница 1
Правильная призма
Cтраница 1
Правильная призма — прямая и в ее основании лежит правильный многоугольник. [1]
Правильную призму заменяют призмой с углом 30 ( с той же диспергирующей способностью) и зеркальной задней гранью. Теперь одна и та же линза может служить коллиматором для входящего излучения и фокусирующим элементом для разложенного потока. [3]
Две правильные призмы или пирамиды с одним и тем же числом граней подобны, если отношения радиусов их оснований равно отношению высот. Два круглых цилиндра или конуса подобны, если у них одинаковы отношения радиусов к высотам. [4]
Основаниями правильной призмы служат квадраты. Одно из оснований призмы принадлежит большому кругу шара радиуса R, а вершины другого лежат на поверхности этого шара. Определите, какой должна быть длина высоты призмы, чтобы сумма длин всех ее ребер была наибольшей. [5]
Основанием правильной призмы служит треугольник со стороной а. Высота призмы равна Ь, Провести плоскость через одну из сторон нижнего основания и через противоположную вершину верхнего основания. [6]
Основанием правильной призмы служит шестиугольник со стороной в 3 дм высота призмы равна 13 дм. [7]
В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна диаметру окружности, вписанной в основание. [8]
В правильную призму можно вписать сферу / г. огдз и только тогда, когда ез высота равна диаметру окружности, вписанной в основание. [9]
В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна диаметру окружности, вписанной в основание. [10]
В правильной призме АВСА1В1С1 длина каждого ребра равна а. Вершины А и AI лежат на боковой поверхности цилиндра, плоскость BBfjC касается этой поверхности. Ось цилиндра параллельна прямой BjC. [11]
В правильной призме АВСА В С боковое ребро равно стороне основания. [12]
В правильной призме ABCA BtCi все ребра равны а. На ребрах АА и СС взяты соответственно точки Р и Q — середины этих ребер. [13]
В правильной призме ЛВСЛ С ] боковое ребро равно стороне основания. На ребрах ВС и СС взяты соответственно точки D и Е — середины этих ребер. [14]
В правильной призме ABCAiBiCi длина каждого ребра равна а. Вершины А и AI лежит на боковой поверхности цилиндра, плоскость BBjCiC касается этой поверхности. [15]
Страницы: 1 2 3 4
www.ngpedia.ru

Leave A Comment