11.3.1. Показательная функция, ее свойства и график.

Главная » 11 класс. Алгебра. » 11.3.1. Показательная функция, ее свойства и график

Показательная функция — одна из основных функций, изучаемая в школе и в ВУЗе. Познакомимся с основными понятиями и свойствами показательной функции, построим ее график.

  • Функцию вида y=ax, где а > 0, a≠1, х – любое число, называют показательной функцией.
  • Область определения показательной функции: D (y)=R – множество всех действительных чисел.
  • Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
  • Показательная функция  y=ax возрастает при a > 1.
  • Показательная функция y=ax убывает при 0 .

Справедливы все свойства степенной функции:

  • а0=1  Любое число (кроме нуля) в нулевой степени равно единице.
  •  а1=а  Любое число в первой степени равно самому себе.
  •  ax∙ay=ax+y   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
  •  ax:ay=ax- y  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
  • (ax)y=axy   При возведении степени в степень основание оставляют прежним, а показатели перемножают
  •  (a∙b)x=ax∙by   При возведении произведения в степень возводят в эту степень каждый из множителей.
  • (a/b)x=ax/by  При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
  •   а-х=1/ax
  •  (a/b)-x=(b/a)x.

Рассмотрим несколько примеров.

Содержание

Пример 1

1) Построить график функции y=2x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=20=1;                   Точка А.

x=1, y=21=2;                   Точка В.

x=2, y=22=4;                   Точка С.

x=3, y=23=8;                   Точка D.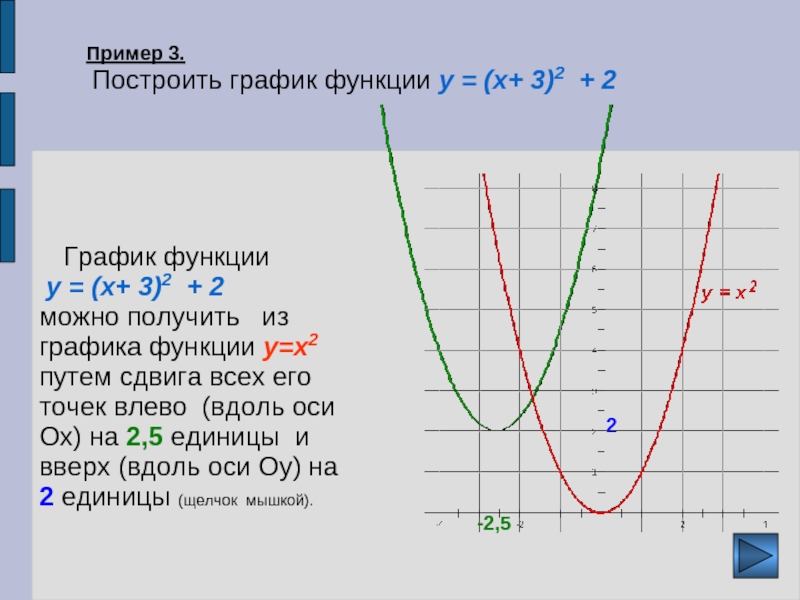              

x=-1, y=2-1=1/2=0,5;       Точка K.

x=-2, y=2-2=1/4=0,25;     Точка M.

x=-3, y=2-3=1/8=0,125;   Точка N.

Большему  значению аргумента х соответствует и большее значение функции у. Функция y=2x возрастает на всей области определения D (y)=R, так как основание функции 2 > 1.

Пример 2

2) Построить график функции y=(1/2)x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=(½)0=1;                  Точка A.

x=1, y=(½)1=½=0,5;          Точка B.

x=2, y=(½)2=¼=0,25;        Точка C.

x=3, y=(½)3=1/8=0,125;    Точка D.

x=-1, y=(½)-1=21=2;          Точка K.

x=-2, y=(½)-2=22=4;          Точка M.

x=-3, y=(½)-3=23=8;          Точка N.

 

Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D (y)=R, так как основание функции  0 1/2) .

Пример 3

3) В одной координатной плоскости построить графики функций: 

y=2x, y=3x, y=5x, y=10x. Сделать выводы.

График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.

Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля  (E (y)=R+).

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a > 1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.

Все  данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.

 

Пример 4

4) В одной координатной плоскости построить графики функций:

y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы.

Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.

Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.

Чем меньше основание а (при 0 х, тем ближе расположена кривая к оси Оу.

Все  эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.

Решить графически уравнения:

1) 3x=4-x.

В одной координатной плоскости построим графики функций: у=3х и у=4-х.

 

Графики пересеклись в точке А(1; 3).

 

Ответ: 1.

 

2) 0,5х=х+3.

 

В одной координатной плоскости строим графики функций: у=0,5х

(y=(1/2)x )

 и у=х+3.

Графики пересеклись в точке В(-1; 2).

Ответ: -1.

 

Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.

Решение.

 1) y=-2x 

Область значений показательной функции y=2x – все положительные числа, т.е.

0 x

— ∞ x

Ответ: Е(у)=(-∞; 0).

 2) y=(1/3)x+1;

0 1/3)x1, получаем:

0+1 1/3)x+1 1;

1 1/3)x+1

Ответ: Е(у)=(1; +∞).

 3) y=3x+1-5.

Запишем функцию в виде: у=3х∙3-5.

0 x 3:

0∙3 x∙3 3;

0 x∙3 5:

0-5 x∙3-5 -5;

— 5 x∙3-5

Ответ: Е(у)=(-5; +∞).

Смотрите Карту сайта, и Вы найдете нужные Вам темы!

Гипербола. График функции и свойства.

Определение

Графиком функции у=kx.., где k≠0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

  1. Область определения – любое число, кроме нуля.
  2. Область значения – любое число, кроме нуля.
  3. Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у=10x…

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х124510
у
х–1–2–4–5–10
у

Теперь делим на эти числа 10, получим значения у:

х124510
у1052,521
х–1–2–4–5–10
у–10–5–2,5–2–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.

Теперь для построения гиперболы соединим точки плавной линией.

Построить график функции у=−5x…

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х12510
у–5–2,5–1–0,5
х–1–2–5–10
у52,510,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

Задание OM1104o

Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

2) y = x/2

3) y = 2/x

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0,  а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

Ответ:

А 1

Б 3

В 2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1102o

Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x

Б) y = 3/x

В) y = 1/(3x)

Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой.

Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

  • если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
  • если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

  • чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

и наоборот:

  • чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор | оценить

Даниил Романович | Просмотров: 10.3k

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить
квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Графические уравнения и системы уравнений с помощью Пошагового решения математических задач

ВВЕДЕНИЕ В КВАДРАТИКА

Цели

В этом разделе вы будете складывать, вычитать, умножать и строить графики квадратичных уравнений.

Словарь : Стандартный формат квадратного уравнения : y = ax 2 + bx + c ; а, b, с — константы; x — независимая переменная, y — зависимая переменная. Квадраты также называются полиномов второй степени , потому что старший показатель равен 2. Уравнение пересечения наклона из второй главы, y = mx + b, называется полиномом первой степени , потому что старший показатель равен единице.

Зачем изучать квадратику? Графики квадратных уравнений представляют собой параболы (графики U-образной формы, открывающиеся вверх или вниз). Эта особенность квадратичных уравнений делает их хорошими моделями для описания пути объекта в воздухе или описания прибыли компании (примеры которых вы можете увидеть в конечной математике или в микроэкономике).0911

Пример 1. Лежащий на спине мальчик выстреливает из пращи камень прямо в воздух с начальной скоростью (сила, с которой мальчик стреляет камнем) 64 фута в секунду. Квадратное уравнение, которое моделирует высоту скалы:

h = -16t 2 +64t.

а. Найдите высоту скалы при t = 0,

В формуле h = -16t 2 + 64t замените t на 0,

h = -16(0) 2 +64(0)
h = 0

Камень находится в воздухе на ноль футов в ноль секунд. (Это момент прямо перед тем, как он выстрелит камнем в воздух.)

б. Найдите высоту скалы при t = 1,

. В формуле h = -16t 2 + 64t замените t на 1,

В одну секунду камень находится в воздухе на высоте 48 футов.

Объяснение : Возводится в квадрат только «1». -16 умножается на 1 2

c. Найдите высоту камня, когда t = 2,

В формуле h = -16t 2 + 64t замените t на 2,

Камень находится в воздухе на высоте 64 фута за 2 секунды.

Объяснение : Порядок операций требует применения показателей степени перед умножением.

д. Найдите высоту камня, когда t = 3,

. В формуле h = -16t 2 + 64t замените t на 3,

Камень находится в воздухе на высоте 48 футов за 3 секунды.

эл. Найдите высоту скалы, когда t = 4.

В формуле h = -16t 2 +64t замените t на 4.

Камень находится в воздухе на ноль футов через 4 секунды; то есть камень ударился о землю.

ф. Нанесите на график точки, полученные в частях от a до e.

Высота скалы зависит от времени, поэтому h — зависимая переменная, а t — независимая переменная. Точки имеют вид (t, h).

Согласно графику, камень достигает наибольшей высоты за 2 секунды. Максимальная высота составляет 64 фута. Максимальная или минимальная точка квадратного называется вершиной. Вы узнаете, как найти вершину, в Разделе 4.3, Квадратичные приложения и графы.

Согласно графику, камень находится на земле через ноль секунд (прямо перед тем, как мальчик выстрелит в него) и через 4 секунды (когда камень приземлится). Эти точки являются временными перехватами. Вы узнаете, как их найти, в следующем Разделе 4.2, «Применения квадратичной формулы».

Сложение и вычитание квадратичных чисел:

Словарь : Чтобы сложить или вычесть квадратичные числа, объедините одинаковые термины. Подобные термины , первоначально представленные в разделе 1.3 «Упрощение алгебраических выражений», имеют ту же переменную и тот же показатель степени. Например 2х 2 и 5x 2 похожи, а 3x 2 и 7x — нет.

Коэффициент , первоначально представленный в Разделе 1.3 «Упрощение алгебраических выражений», представляет собой число, умножающее переменную. Например, коэффициент 2x равен 2, а коэффициент -x 2 равен -1.

Правило: Чтобы объединить одинаковые термины, добавьте их коэффициенты

Вспомним распределительное свойство : Определение a(b + c) = ab + ac.


Не удалось объединить непохожие термины в скобках, поэтому мы использовали распределительное свойство. После этого мы умножили 6x на 3, а затем -5 на 3.

Использовали свойство дистрибутивности и комбинировали подобные термины.

Пример 5. Уравнение для прибыли: Прибыль = Доход — Затраты

Если уравнение доходов для компании:

, а уравнение затрат:

, найдите уравнение прибыли для компании.


Подставил уравнения выручки и затрат в формулу прибыли. Необходимо использовать скобки.

Использовал свойство распределения и умножил уравнение доходов на 1, а уравнение затрат на -1.

Комбинированные термины.

Подставил уравнения выручки и затрат в формулу прибыли. Необходимо использовать скобки. Используется распределительное свойство. Умножил уравнение дохода на 1 и уравнение затрат на -1. Комбинированные подобные термины.

Умножение двух двучленов.

Словарь : Бином состоит из двух членов (так же, как велосипед имеет два колеса).

Правило: Чтобы умножить два двучлена, умножьте каждый член первого на каждый член второго.

Пример 7. Умножить (х + 2)(5х + 3).


Умножить x на 5x и 3 и умножить 2 на 5x и 3.

Объединить подобные термины.

ФОЛЬГА — простая мнемоника, помогающая запомнить, как умножать два двучлена.

Пример 8. Умножить (8x + 6)(x + 7).

Учебный совет: Напишите карточку с объяснением мнемоники ФОЛЬГА. Чаще просматривайте карту.

Резюме

Квадратичные уравнения являются важными уравнениями в физике и микроэкономике. Техника сложения и вычитания квадратичных чисел та же самая, которую мы практиковали весь семестр; то есть добавить или вычесть подобные термины. Чтобы умножить, используйте распределительное свойство или FOIL. Вершина квадратичного уравнения будет объяснена более подробно в разделе «Квадратичные графики и приложения». Вершина — это максимальная или минимальная точка на графике квадратичного уравнения.

ПРИМЕНЕНИЕ КВАДРАТИЧНОЙ ФОРМУЛЫ

Цель

Этот раздел покажет вам, как решать квадратные уравнения.

Словарь : Квадратное уравнение равно ax 2 + bx + c = 0 . a, b и c — константы, а x — переменная.

Квадратная формула , , используется для решения квадратного уравнения.

Анализ

  • a, b и c — числа, которые будут подставлены в формулу.
    a — коэффициент при квадрате переменной,
    b — коэффициент при переменной в первой степени,
    c — константа.
  • Символ ± дает два решения уравнения.
    Одно решение со знаком +, а другое решение со знаком -, .
  • — это символ квадратного корня.
    1. Потому что 4 2 = 16.
    2. Потому что 5,916 2 = 35,
    3. Ваш калькулятор необходим для этого раздела. Убедитесь, что вы можете найти кнопку на вашем калькуляторе.
    4. Вы можете вычислять квадратный корень только из неотрицательных чисел.
    5. Если вы попытаетесь вычислить, ваш калькулятор выдаст сообщение об ошибке.
      Если вы изучите алгебру среднего уровня, вы узнаете о квадратных корнях из отрицательных чисел.

Учебный совет: Напишите квадратное уравнение и формулу квадратного уравнения на карточках, чтобы вы могли обращаться к ним, когда будете делать домашнюю работу.

Пример 1. Предположим, вы стоите на вершине утеса на высоте 375 футов над дном каньона и подбрасываете в воздух камень с начальной скоростью 82 фута в секунду. Уравнение, которое моделирует высоту скалы над дном каньона:

h = -16t 2 + 82t + 375.

Найдите время, за которое камень упадет на дно каньона.

Найдите t при h = 0.
Решите 0 = -16t 2 +82t + 375.
Определите константы a, b и c.

Объяснение : Одна сторона квадратного уравнения должна быть равна нулю.

a = -16, b = 82, c = 375

Объяснение :
a — коэффициент при переменной, возведенный в квадрат
b — коэффициент при переменной в первой степени.
с — константа.

Используйте квадратичную формулу

с a = -16, b = 82 и c = 375. этаж, а время не может быть отрицательным.

T = 8,041 секунды — это время, за которое камень достигает дна каньона.

Камень упадет на дно каньона через 8,041 секунды.

Пример 2. Владелец ранчо имеет 500 ярдов забора, чтобы оградить два смежных загона для свиней, примыкающих к сараю. Если площадь двух загонов должна составлять 20 700 квадратных ярдов, то каковы должны быть размеры загонов?

L представляет собой длину обеих ручек.

а. Используя таблицу, найдите уравнение площади ручек.

б. Упростите уравнение площади.

в. Найдите W, если A = 20 700.

Ширина 76,67 или 90 ярдов.

д. Найдите длину ручек.

Из таблицы в Части а, L = 500 — 3W . Подставьте W = 76,67 и W = 90 в уравнение для длины, L = 500 — 3w.

Размеры загонов для свиней, площадь которых составляет 20 700 квадратных ярдов, составляют 76,67 на 270 ярдов и 90 на 230 ярдов.

Пример 3. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, можно смоделировать температуру кислорода следующим квадратичным выражением:

T = 0,26 м 2 -4,1 м + 7,9

, где T измеряется в градусах Цельсия, а m представляет минуты, в течение которых проводился эксперимент. бегать. Определите, когда температура кислорода равна 0 градусов Цельсия.

Задача требует найти m при T = 0.

Температура кислорода будет равна 0 градусов Цельсия через 2,246 минуты и 13,52 минуты.

Совет по изучению: Ключевая идея, продемонстрированная в примере 3, заключается в том, как обращаться с отрицательным значением b в квадратном уравнении.

Резюме

В этом разделе показано, как решать новый тип уравнения, квадратное. Они имеют важные приложения во многих областях, таких как бизнес, физика и инженерия. Учиться разница между квадратным уравнением и квадратной формулой.

Квадратное уравнение: ax 2 + bx + c = 0.

  • Одна часть уравнения должна быть равна нулю.
  • а — коэффициент x .
  • b — коэффициент при x.
  • c — постоянный член.

Квадратная формула решает квадратное уравнение.

  • Формула дает два решения.
  • Калькулятор используется для поиска ответов.
  • Первым шагом в вычислении формулы является упрощение квадратного корня.

КВАДРАТИЧЕСКИЕ ПРИМЕНЕНИЯ И ГРАФЫ

Цели

В этом разделе исследуются дополнительные ключевые точки графа квадратичного уравнения, вершины и точки пересечения. Эти точки будут интерпретироваться в приложениях.

Пример 1. Лежащий на спине мальчик стреляет из пращи камнем прямо в воздух с начальной скоростью (сила, которую мальчик использует, чтобы выстрелить в камень) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно

9.0910 ч = -16т 2 + 64т.

(Этот пример взят из Раздела 4.1 «Введение в квадратику», стр. 317). Вершина и пересечения также помечены на графике.

Объяснение : Точка (0, 0) является точкой пересечения и времени, и высоты.

Вершина , (2,64) представляет максимальную высоту скалы. Скала достигает максимальной высоты 64 фута за 2 секунды.

Пересечения времени , (0, 0) и (4, 0) представляют, когда камень находится на земле. Камень находится на земле за ноль секунд до выстрела (это Перехват высоты ) и через 4 секунды, когда он возвращается на землю.

Чтобы построить квадратное уравнение, указанное уравнением y = ax 2 + bx + c, освойте следующие термины:

Словарь : Вершина: Вершина — это максимальная или минимальная точка на графике. Чтобы найти вершину:

а. Найдите координату x:
b. Найдите координату y: подставьте значение x, полученное в части a, в формулу y = ax 2 + bx + c.

Пересечение по оси X : Установите y = 0 и решите 0 = ax 2 + bx + c, используя квадратичную формулу,

Пересечение по оси Y : Установите x = 0 и найдите y. y всегда будет c, константой.

Учебный совет: Запишите процедуру и определения на трех карточках для удобства.

Пример 2. Компания D++ делает компьютерные игры. Стоимость создания g игр в месяц составляет C = 0,4g 2 — 32g + 625 . Доход от продажи g игр в месяц равен R = -0,6g 2 +52g. Единицы измерения g — сотни, а C и R — тысячи долларов.

а. Найдите уравнение прибыли.

б. Найдите вершину и объясните, что эта вершина означает с точки зрения создания компьютерных игр.

Формула для координаты g:

Из уравнения для прибыли a = -1, b = 84.

Вершина (42,1139). Если D+++ продаст 4 200 игр, то они получат максимальную прибыль в размере 1 139 000 долларов.

в. Найдите g и и объясните, что они означают с точки зрения создания компьютерных игр.

Чтобы найти точку пересечения g, установите P = 0.

Решите 0 = -g 2 + 84g — 625 .

Используйте квадратичную формулу, a = -1, b = 84, c = -625.

Пересечения g: (8.251, 0) и (75.75, 0).

Если они продадут 825 или 7575 игр, они окупятся.

д. Найдите P и и объясните, что они означают с точки зрения создания компьютерных игр.

Чтобы найти точку пересечения P, установите g = 0.
P = -0 2 +84*0-625
P = -625
Значение точки P равно (0, -625).
Начальные затраты компании составляют 625 000 долларов.

эл. График функции.

Нанесите точки:
Вершина. (42, 1139).
Г перехватывает. (8,251, 0) и (75,75, 0).
Перехват P. (0, -625).

Объяснение : Одним из объяснений наличия двух точек безубыточности является то, насколько эффективно компания производит продукт. Изготовление очень небольшого количества предметов обычно неэффективно. В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много изделий, компания становится неэффективной в производстве своей продукции.

Помните, что единицы g измеряются сотнями, а единицы P — тысячами.

Предположим, D+++ должен получать прибыль в размере 500 000 долларов (P = 500) в месяц. Нарисуйте эту линию на графике, полученном в части б, и найдите, где линия пересекает график квадратичного уравнения. Напишите предложение, объясняющее, что означают ответы.

Эскиз P = 500 на предыдущем графике.

P = 500 — горизонтальная линия.

Если D+++ хочет получить прибыль в размере 500 000 долларов, им нужно сделать и продать 1 672 или 6 728 игр.

Пояснение : На графике показано, где пересекаются горизонтальная линия P = 500 и уравнение прибыли P = -g 2 +84g-625. Алгебра дает точную точку, где они пересекаются.

г. Используя график и ответы к части c, определите, сколько компьютерных игр необходимо создать и продать, чтобы гарантировать прибыль более 500 000 долларов.

Компания получит прибыль более 500 000 долларов, если график прибыли окажется выше горизонтальной линии P = 500. Эта задача аналогична примеру 2d на странице 203 в разделе 2.9.«Применения графиков».

Это происходит между точками g = 16,72 и g = 67,28 или

16,72

Компания заработает более 500 000 долларов, когда создаст и продаст от 1 672 до 6 728 компьютерных игр.

Пример 3. Владелец питомника хочет пристроить к стене три соседних загона для собак одинакового размера. У него 96 метров забора.

а. Найдите формулу площади.

Объяснение : Самая трудная часть таблицы — найти значение длины. Если фермер использует 10 метров для ширины загонов, а их ширина 4, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений у него осталось по длине, из 9 вычтите 40.6, общее количество ограждений, доступных фермеру.

Формула площади загонов для собак:

b. Найдите вершину и объясните, что она означает в терминах собачьих загонов.

Формула для координаты W:

Из уравнения для прибыли, a = -4, b = 96.

Вершина (12, 576).

Вершина , (12, 576) представляет собой максимальную площадь трех собачьих загонов. Когда W = 12, максимальная площадь будет 576. (Длина всех трех загонов будет 48 или длина одного загона для собак будет 16.) Будет три загона для собак размером 12 на 16 метров.

г. Найдите W и и объясните, что они означают в терминах собачьих загонов.

Чтобы найти точку пересечения W, установите A = 0.

Решите 0 = -4W 2 + 96W.

Используйте квадратичную формулу, a = -4, b = 96, c = 0.

Пересечения W равны (0, 0) и (24, 0).

Отрезки W, (0, 0) и (24, 0) представляют собой ширину собачьих загонов, которые дадут нулевую площадь.

д. Найдите перехват A и объясните, что это означает применительно к загонам для собак.

Чтобы найти точку пересечения A, установите W = 0.

Объяснение : Если ширина прямоугольника равна нулю, то площадь должна быть равна нулю.

Пересечение А равно (0, 0).

Точка пересечения A (0, 0) — это площадь, когда W = 0.

e. Нарисуйте уравнение

Постройте точки:
Вершина. (12, 576).
W перехватывает. (0, 0) и (24, 0).
Перехват А. (0, 0).

ф. Предположим, что общая площадь должна быть 400 квадратных метров. Постройте график A = 400 и найдите размеры загонов для собак.

Эскиз A = 400 на предыдущем графике.

A = 400 — горизонтальная линия.

Поскольку ширина W известна, длину L можно найти по формуле A = LW.

Найдите L, разделив обе стороны на W.

Размеры загонов для собак, которые дают площадь 400 квадратных метров, составляют 5,367 на 74,53 и 18,63 на 21,47.

Пример 4. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, можно смоделировать температуру кислорода следующим квадратичным выражением:

T = 0,26 м 2 -4,1 м + 7,9

, где T измеряется в градусах Цельсия, а m представляет минуты, в течение которых проводился эксперимент. бегать. Постройте уравнение, найдя вершину и точки пересечения. Отметьте эти точки на графике и объясните, что означают вершины и точки пересечения с точки зрения модели.

Назад: Это та же самая модель, которая использовалась в примере 3 на стр. 332. Этот пример работал при нулевой температуре.

Найдите вершину T = 0,26 м 2 — 4,1 м + 7,9 .

Формула для m-координаты вершины: .

Вершина (7,885, -8,263).

Найдите м точек пересечения для T = 0,26 м 2 -4,1 м+ 7,9

Чтобы найти m точек пересечения, установите T = 0,

Решить 0 = 0,26 м 2 -4,1 м+ 7,9 .

Используйте квадратичную формулу, a = 0,26, b = -4,1, c = 7,9.

М точек пересечения (13,52, 0) и (2,246, 0).

Найдите точек пересечения T точки T = 0,26 м 2 — 4,1 м + 7,9

Вершина: Минимальная температура будет на 7.885 мин. Минимальная температура составит -8,263 градуса по Цельсию.

м пересечения: Температура будет равна нулю градусов Цельсия в 2.246 и 13.52 минуты.

Пересечение T: В начале эксперимента температура составляла 7,9 градусов Цельсия.

Советы по изучению: Квадратичные графики представляют собой U-образные графики. В некоторых случаях они имеют U-образную форму, как в приведенном выше примере, или форму, как в примерах с 1 по 3. Если a в уравнении y = ax 2 + bx + c положительно, то график имеет U-образную форму, т. е. есть, открытие. Если a отрицательно, то график имеет форму, т. е. раскрывается вниз. Этот факт должен быть записан на карточке для заметок.

Резюме

Графики квадратичных уравнений появляются в таких разнообразных предметах, как микроэкономика и физика. В этом разделе кратко излагаются основные идеи модуля.

Чтобы нарисовать квадратное уравнение y = ax 2 + bx + c , вы должны найти:

  • Вершина .
    Формула для координаты x:

    Чтобы найти координату y, подставьте свой ответ вместо координаты x в уравнение y = ax 2 + bx + c .
  • x перехватывает . Установите y = 0 и решите уравнение 0 = ax 2 + bx + c , используя квадратичную формулу
  • y перехват .
    Положим в уравнении x = 0, y = ax 2 + bx + c и найдем y. Обратите внимание, когда x = 0, y = c.
  • Если a отрицательное , то обычно график выглядит так:
  • Если а положительное , то обычно график выглядит так:

ФАКТОРИНГ

Цели

Факторинг — это алгебраический метод, используемый для разделения выражения на составные части. Когда составные части перемножаются вместе, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг является важным навыком в MAT 100, Intermediate Algebra.

Словарь : Алгебраическое выражение факторизуется, если последней операцией при вычислении выражения является умножение.

Пример 1. Какое выражение равно факторизовано , х 2 — 5х — 24 или (х — 8)(х + 3)?

Выберите значение x и подставьте его в выражение.

Пусть x = 3.

Поскольку последней операцией для (x — 8)(x + 3) было умножение, то (x — 8)(x + 3) факторизуется.

Объяснение : Менее формально алгебраическое выражение факторизуется, если оно имеет круглые скобки.

Словарь : Распределительное свойство есть a(b + c) = ab + ac. Левая часть факторизуется, а является общим множителем.

Вы должны иметь возможность проверить, используя свойство дистрибутива.

Объяснение : Хотя 8x 3 + 4x равно как 2x(4x 2 + 2), так и 4(2x 3 + x), ни одно из них не считается полностью факторизованным, поскольку в обоих случаях общее кратное , 2, in 2x(4x 2 +2) и x in 4(2x 3 +x) все еще могут быть факторизованы из членов в скобках.

Разложение трехчленов на множители: (Трехчлен состоит из трех членов.) Чтобы разложить трехчлен на множители, вспомните аббревиатуру FOIL.

Совет по изучению: Проверьте свои карточки для заметок на наличие определения ФОЛЬГА.

Пример 4. Умножить (x+3)(x+5).

(x+3)(x+5) учитывается, а x 2 + 8x +15 не учитывается. Чтобы разложить трехчлены, вам нужно знать, как были вычислены 8x и 15. 8x получилось из сложения 5x и 3x, а 15 получилось из умножения 5 и 3.

Пример 5. Коэффициент x 2 + 8x +15. (Это из примера 4.)

Нам нужны два числа, которые при сложении равны 8, а при умножении равны 15. 3 и 5 в сумме дают 8, а при умножении 15.

So x 2 + 8x +15 = (x + 3)(x + 5)

Пример 6. Фактор x 2 -4x- 12.

Нам нужны два числа, которые при сложении равны -4 и при умножении равно -12. -6 и 2 в сумме дают -4, а при умножении дают -12.

Так х 2 -4х -12 = (х-6)(х + 2).

Пример 7. Коэффициент x 2 — 64 .

Это не трехчлен, но он может стать им, если добавить 0x.

x 2 -64 = x 2 +0x -64

Нам нужны два числа, которые при сложении равны 0, а при умножении равны -64.

-8 и 8 прибавляются к 0 и при умножении дают -64.

Так х 2 -64 = (х-8)(х + 8).

Этот пример называется разложением на множители разности совершенных квадратов, и вы снова увидите его, если возьмете MAT 100, Средняя алгебра.

Словарь : a 2 — b 2 — это разность совершенных квадратов .
Разность совершенных квадратов имеет специальную формулу разложения на множители: a 2 — b 2 = (a — b)(a + b)

Решение квадратных уравнений на множители:

Если вы умножаете две величины и результат равен нулю, то вы знаете, что одна из величин должен быть равен нулю. В математической записи

, если a.b = 0, то a = 0 или b = 0.

Прежде чем вы подумаете, что разложение на множители для решения квадратичных уравнений намного проще, чем использование квадратной формулы, вы должны знать, что разложение на множители не всегда работает. Рассмотрите возможность изменения примера 8 всего на единицу до x 9.0918 2 — 11x + 31 = 0. Вы не можете найти два целых числа, которые при сложении равны -11, а при умножении равны 31. Чтобы разложить x 2 — 11x + 31, вы должны использовать квадратичную формулу. Вы узнаете, как факторизовать любое квадратное уравнение в Precalculus I, MAT 161.

Резюме

В этом разделе представлены два метода факторизации. Первый — это общие факторы, в которых используется распределительное свойство ab + ac = a (b + c). Другой факторизирует трехчлены. Чтобы разложить трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, средний уровень алгебры, вы увидите больше факторов.

ГЛАВА 4 ОБЗОР

В этой главе вы познакомились с квадратиками. Двумя основными темами являются квадратичные формулы и графики квадратичных уравнений. Эти темы имеют множество приложений в бизнесе, физике и геометрии. Факторинг является важной темой в MAT 100, Intermediate Algebra.

Раздел 4.1: Введение в квадратные уравнения

Раздел 4.2: Применение квадратичных формул

Определение: ax 2 + bx + c = 0 — это квадратное уравнение.

Определение: квадратичная формула.

Пример 4. Фермер хочет обнести два соседних курятника против сарая. У него 125 футов забора. Какими должны быть размеры, если он хочет, чтобы общая площадь была 700 квадратных футов.

а. Заполните таблицу, чтобы найти уравнение площади.

б. Найдите W, если A = 700.

Размеры курятника, площадь которого составляет 700 квадратных футов, составляют 35 на 20 футов и 6,667 на 105 футов.
(Чтобы получить длину, разделите 700 на 6,667 и 35.)

Раздел 4.3: Квадратичные приложения и графики

Чтобы построить квадратное уравнение, y = ax 2 + bx + c, вы должны найти:

  1. Вершина:
    Координата x вычисляется по формуле
    Координата y вычисляется путем подстановки координаты x в y = ax 2 + bx + c.
  2. Пересечение x:
    Установите y = 0 и решите 0 = ax 2 + bx + c, используя квадратичную формулу.
  3. Пересечение y:
    Подставьте x = 0 в y = ax 2 + bx + c . Обратите внимание, что когда x = 0, y = c.

Пример 5. Уравнение затрат на изготовление коробок для сока: C = 0,6B 2 — 24B + 36, а уравнение дохода: R = -0,4B 2 + 18B . B в миллионах, а C и R в тысячах долларов.

а. Найдите уравнение прибыли.

б. Нарисуйте график уравнения прибыли и объясните, что означают точки пересечения вершины, B и P с точки зрения задачи.

Вершина (21, 405).

Найдите точку пересечения B. Установите P = 0,

Пересечения B равны (0,875, 0) и (41,13, 0).

Найдите точку пересечения P. Установите B = 0.

Пересечение P равно (0, -36).

в. Предположим, что компании необходимо получить 200 000 долларов прибыли (P = 200). Нарисуйте линию P = 200 и найдите, сколько коробок сока нужно произвести компании, чтобы заработать 200 000 долларов.

Компании необходимо произвести 6,682 или 35,32 миллиона коробок сока, чтобы заработать 200 000 долларов прибыли.

Вершина (21 405) представляет максимальную прибыль.