ОГЭ. Числовая последовательность. 13 заданий. | Материал по алгебре (9 класс):
Числовые последовательности
1. Последовательность задана формулой . Какое из указанных чисел является членом этой последовательности?
1) 1 | 2) 2 | 3) 3 | 4) 4 |
2. Последовательность задана формулой . Какое из следующих чисел не является членом этой последовательности?
1) | 2) | 3) | 4) |
3. Какое из указанных чисел не является членом последовательности
1) | 2) | 3) | 4) |
4. Последовательность задана формулой . Сколько членов в этой последовательности больше 1?
Последовательность задана формулой . Сколько членов в этой последовательности больше 1?
1) 8 | 2) 9 | 3) 10 | 4) 11 |
5. Последовательности заданы несколькими первыми членами. Одна из них — арифметическая прогрессия. Укажите ее.
1) | 2) | 3) | 4) ; ; ; ; … |
6. Одна из данных последовательностей является геометрической прогрессией. Укажите эту последовательность.
1) | 2) | 3) | 4) ; ; ; ; … |
7. Какая из следующих последовательностей является арифметической прогрессией?
1) Последовательность натуральных степеней числа 2. |
2) Последовательность натуральных чисел, кратных 5. |
3) Последовательность кубов натуральных чисел. |
4) Последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя. |
8. Последовательность задана условиями , . Найдите .
9. Последовательность задана условиями , . Найдите .
10. Последовательность задана формулой . Какое из следующих чисел не является членом этой последовательности?
1) −2 | 2) | 3) | 4) 2 |
11. Последовательность задана формулой Сколько членов в этой последовательности больше 6?
12. Сколько натуральных чисел n удовлетворяет неравенству ?
13. Последовательность задана формулой Сколько членов в этой последовательности больше 3?
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает. Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция | ⇐ ПредыдущаяСтр 4 из 5Следующая ⇒ Числовые последовательности Арифметические прогрессии Геометрические прогрессии Числовые последовательности 1.
Решение. Рассмотрим несколько первых членов последовательности, начиная с
Тем самым, число 3 является членом этой последовательности.
Ответ: 3. Ответ: 3 Задание 11 № 137295 2.Последовательность задана формулой . Какое из следующих чисел не является членом этой последовательности?
Решение. Рассмотрим несколько первых членов последовательности, начиная с
Тем самым, число не является членом этой последовательности.
Ответ: 3. Ответ: 3 Задание 11 № 137296 3.Какое из указанных чисел не является членом последовательности
Решение. Рассмотрим несколько первых членов последовательности, начиная с
Тем самым, не является членом этой последовательности.
Ответ: 4. Ответ: 4 Задание 11 № 137297 4.Последовательность задана формулой . Сколько членов в этой последовательности больше 1?
Решение. Дробь, числитель и знаменатель которой положительны, больше единицы, если числитель больше знаменателя.
Ответ: 2. Ответ: 2 Задание 11 № 137298 5.Последовательности заданы несколькими первыми членами. Одна из них — арифметическая прогрессия. Укажите ее.
Решение. Арифметической прогрессией называется такая последовательность в которой разность между последующим и предыдущим членами прогрессии остается неизменной. Поэтому арифметическая прогрессия является последовательность: 1; 3; 5; … Таким образом, правильный ответ указан под номером 3.
Ответ: 3. Ответ: 3 Задание 11 № 137299 6.Одна из данных последовательностей является геометрической прогрессией. Укажите эту последовательность.
Решение. Геометрической прогрессией называют числовую последовательность, первый член которой отличен от нуля, а каждый последующий, равен предшествующему, умноженному на одно и тоже отличное от нуля число. Поэтому геометрической прогрессией является последовательность: Таким образом, правильный ответ указан под номером 2.
Ответ: 2. Ответ: 2 Задание 11 № 137300 7.Какая из следующих последовательностей является арифметической прогрессией?
Решение. Арифметической прогрессией называется такая последовательность в которой разность между последующим и предыдущим членами прогрессии остается неизменной. Поэтому арифметическая прогрессия является последовательность: 5; 10; 15; … Таким образом, правильный ответ указан под номером 2.
Ответ: 2. Ответ: 2 Задание 11 № 137306 8.Последовательность задана условиями , . Найдите . Решение. Будем вычислять последовательно: Данная последовательность образует арифметическую прогрессию. Найдем разность арифметической прогрессии: тогда
Примечание. Зная разность и первый член арифметической прогрессии, можно найти посредственно:
Ответ: −9. Ответ: -9 -9 Задание 11 № 137307 9. Решение. Найдём несколько первых членов последовательности:
Отсюда ясно, что все члены последовательности с нечётными номерами равны 4.
Ответ: 4.
Примечание. Из рекуррентной формулы, задающей n-й член последовательности, можно непосредственно получить, что
Отсюда ясно, что все члены последовательности с нечётными номерами равны первому члену последовательности, а все члены последовательности с чётными равны второму члену последовательности. Ответ: 4 Задание 11 № 341203 10. Решение. Необходимо решить неравенство:
Поскольку n — целые числа, неравенство выполняется при n равном 1, 2, 3 и 4.
Ответ: 4. Ответ: 4 Источник: Банк заданий ФИПИ Задание 11 № 341669 11.Сколько натуральных чисел n удовлетворяет неравенству ? Решение. Дробь, числитель и знаменатель которой положительны, больше двух, если числитель больше знаменателя более чем в два раза. Поэтому, имеем: Таким образом, восемнадцать натуральных чисел удовлетворяют данному неравенству.
Ответ: 18. Ответ: 18 Источник: СтатГрад: Тренировочная работа по математике 29.09.2015 вариант МА90103. Задание 11 № 351753 12.Последовательность задана формулой . Сколько членов в этой последовательности больше 3? Арифметические прогрессии 1.Дана арифметическая прогрессия: Найдите сумму первых десяти её членов. Решение. Определим разность арифметической прогрессии:
Сумма первых k-ых членов может быть найдена по формуле
Необходимо найти , имеем:
Ответ: 50. Ответ: 50 Источник: Демонстрационная версия ГИА—2013 по математике. Задание 11 № 113 2.Дана арифметическая прогрессия Найдите . Решение. Определим разность арифметической прогрессии:
Член арифметической прогрессии с номером может быть найден по формуле
Необходимо найти , имеем:
Ответ: 23. Ответ: 23 Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309. Задание 11 № 165 3.Дана арифметическая прогрессия Найдите сумму первых десяти её членов. Решение. Определим разность арифметической прогрессии :
Сумма первых k-ых членов может быть найден по формуле
Нам необходимо найти , поэтому в формулу для нахождения ставим 10 вместо :
Ответ: 75. Ответ: 75 Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1317. Задание 11 № 137301 4.Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?
Решение. Найдем разность арифметической прогрессии: Зная разность и член арифметической прогрессии, решим уравнение относительно n , подставив данные в формулу для нахождения n-го члена:
Членом прогрессии является число 102.
Ответ: 4.
Примечание. Заданная арифметическая прогрессия состоит из чисел, кратных трём. Числа 83, 95 и 100 не кратны 3, они не являются членами прогрессии; а число 102 кратно 3, оно является её членом. Ответ: 4 Задание 11 № 137302 5.Арифметические прогрессии , и заданы формулами n-го члена: , , Укажите те из них, у которых разность равна 4.
Решение. Найдем
Для каждой из прогрессий , и найдем разность:
Разность прогрессии равна 4 для прогрессии и . Таким образом, верный ответ указан под номером 2.
Ответ: 2. Ответ: 2 Задание 11 № 137303 6.
Решение. Количество мест в рядах кинозала образуют арифметическую прогрессию. По формуле для нахождения n-го члена арифметической прогрессии имеем:
Таким образом, правильный ответ указан под номером 1.
Ответ: 1. Ответ: 1 Задание 11 № 137304 7.Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
Решение. Для члена имеем: По формуле нахождения n-го члена арифметической прогрессии имеем:
Первое число, которое удовлетворяет этому условию, число 6. Таким образом, правильный ответ указан под номером 1.
Ответ: 1. Ответ: 1 Задание 11 № 137305 8.Арифметическая прогрессия задана условиями: , . Какое из данных чисел является членом этой прогрессии?
Решение. Найдем разность арифметической прогрессии:
Зная разность и первый член арифметической прогрессии, решим уравнение относительно , подставив данные в формулу для нахождения n-го члена:
Таким образом, число 48 является членом прогрессии. Правильный ответ указан под номером 3.
Ответ: 3. Ответ: 3 Задание 11 № 311254 9.Найдите сумму всех отрицательных членов арифметической прогрессии: −8,6; −8,4; . Решение. 1. Найдём разность прогрессии: . 2. Найдём число отрицательных членов прогрессии. Составим формулу -го члена: . Решим неравенство получим < 44. Значит, = 43. 3. Ответ: −189,2. Ответ: -189,2 -189,2 Задание 11 № 311330 10.Арифметическая прогрессия задана формулой n-го члена и известно, что . Найдите пятый член этой прогрессии. Решение. Найдём разность прогрессии: Тогда для пятого члена прогрессии
Ответ: 11. Ответ: 11 Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2) Задание 11 № 311363 11.В арифметической прогрессии известно, что . Найдите четвёртый член этой прогрессии. Решение. Имеем:
Ответ: 7. Ответ: 7 Источник: 9 класс. Задание 11 № 311909 12.Арифметическая прогрессия задана условиями: . Найдите сумму первых 19 её членов. Решение. Сумма n первых членов арифметической прогрессии даётся формулой
По условию, откуда получаем
Ответ: 95. Ответ: 95 Источник: МИОО: Тренировочная работа по математике 19.11.2013 вариант МА90201. Задание 11 № 314399 13.Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528? Решение. Для ответа на вопрос задачи требуется найти такое наибольшее что Рассмотрим арифметическую прогрессию с первым членом и разностью Cумма первых членов арифметической прогрессии вычисляется по формуле: в нашем случае
Найдем наибольшее натуральное решение неравенства .
Вычислим дискриминант: откуда получаем:
Таким образом, при сумма 32 слагаемых равна 528. Следовательно, наибольшее натуральное число, для которого сумма будет меньше 528, равно 31.
Ответ: 31.
Примечание. Можно заметить, что откуда сразу же получаем: или Ответ: 31 Источник: Банк заданий ФИПИ Задание 11 № 314408 14.Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; … Решение. Определим разность прогрессии:
Найдём выражение для n-го члена прогрессии:
. Найдем номер последнего положительного члена прогрессии:
Следовательно, чтобы найти сумму всех положительных членов данной арифметической прогрессии необходимо сложить её первые 28 членов. Сумма n первых членов арифметической прогрессии даётся формулой
откуда имеем:
Ответ: 162,4. Ответ: 162,4 162,4 Источник: Банк заданий ФИПИ Задание 11 № 314423 15.Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 465? Решение. Для ответа на вопрос задачи требуется найти такое наименьшее что Рассмотрим арифметическую прогрессию с первым членом и разностью Cумма первых членов арифметической прогрессии вычисляется по формуле: в нашем случае
Найдем наименьшее натуральное решение неравенства . Для этого найдём корни уравнения
Вычислим дискриминант: откуда получаем:
Таким образом, при сумма 30 слагаемых равна 465.
Ответ: 31.
Примечание. Можно заметить, что откуда сразу же получаем: или Ответ: 31 Источник: Банк заданий ФИПИ Задание 11 № 314425 16.Найдите сумму всех отрицательных членов арифметической прогрессии –7,2; –6,9; … Решение. Определим разность прогрессии:
Найдём выражение для n-го члена прогрессии:
. Найдем номер последнего отрицательного члена прогрессии:
Следовательно, чтобы найти сумму всех отрицательных членов данной арифметической прогрессии необходимо сложить её первые 24 члена. Сумма n первых членов арифметической прогрессии даётся формулой
откуда имеем:
Ответ: −90. Ответ: -90 -90 Источник: Банк заданий ФИПИ Задание 11 № 314619 17.Арифметическая прогрессия (an) задана условиями: a1 = 3, an + 1 = an + 4. Найдите a10. Решение. Определим разность арифметической прогрессии:
Член арифметической прогрессии с номером может быть найден по формуле
Необходимо найти , имеем:
Ответ: 39. Ответ: 39 Источник: Банк заданий ФИПИ Задание 11 № 314628 18.Записаны первые три члена арифметической прогрессии: 20; 17; 14. Какое число стоит в этой арифметической прогрессии на 91-м месте? Решение. Определим разность арифметической прогрессии:
Член арифметической прогрессии с номером может быть найден по формуле
Необходимо найти , имеем:
Ответ: −250. Ответ: -250 -250 Источник: Банк заданий ФИПИ Задание 11 № 314653 19.Дана арифметическая прогрессия (аn): −6; −2; 2; … . Найдите a16. Решение. Определим разность арифметической прогрессии:
Член арифметической прогрессии с номером может быть найден по формуле
Необходимо найти , имеем:
Ответ: 54. Ответ: 54 Источник: Банк заданий ФИПИ Задание 11 № 316343 20.Выписаны первые несколько членов арифметической прогрессии: −87 ; −76; −65; … Найдите первый положительный член этой прогрессии. Решение. Определим разность арифметической прогрессии:
Член арифметической прогрессии с номером может быть найден по формуле
Нам же нужно найти первый положительный член этой прогрессии, т.
Значит — первый положительный член этой прогрессии.
Ответ: 1. Ответ: 1 Источник: МИОО: Тренировочная работа по математике 19.02.2014 вариант МА90501. Задание 11 № 321384 21.В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду? Решение. Число мест в ряду представляет собой арифметическую прогрессию с первым членом и разностью Член арифметической прогрессии с номером может быть найден по формуле
Необходимо найти , имеем:
Ответ: 38. Ответ: 38 Задание 11 № 321394 22. Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Решение. Число квадратов в строке представляет собой арифметическую прогрессию с первым членом и разностью Член арифметической прогрессии с номером может быть найден по формуле
Необходимо найти , имеем:
Ответ: 122. Ответ: 122 Задание 11 № 321663 23.Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x . Решение. Найдем разность арифметической прогрессии: Поэтому
Ответ: −11. Ответ: -11 -11 Задание 11 № 339063 24.Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = 8,7. Найдите a9. Решение. Член арифметической прогрессии с номером можно найти по формуле Требуется найти
Ответ: 28,7. Ответ: 28,7 28,7 Задание 11 № 340584 25.Даны пятнадцать чисел, первое из которых равно 6, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел. Решение. Последовательность, описанная в условии, образует арифметическую прогрессию с первым членом, равным шести, и разностью 4. Пятнадцатый член данной прогрессии равен:
Ответ: 62. Ответ: 62 Источник: Демонстрационная версия ОГЭ—2018 по математике., Демонстрационная версия ГИА—2015. Задание 11 № 341190 26.Дана арифметическая прогрессия (an), разность которой равна −8,5, a1 = −6,8. Найдите a11. Решение. Член арифметической прогрессии с номером можно найти по формуле Требуется найти
Ответ: −91,8. Ответ: -91,8 -91,8 Источник: Банк заданий ФИПИ Задание 11 № 341201 27.Арифметическая прогрессия задана условиями: Найдите Решение. Воспользовавшись формулой, получаем:
Ответ: −30,4. Ответ: -30,4 -30,4 Источник: Банк заданий ФИПИ Задание 11 № 341202 28.Дана арифметическая прогрессия (an), для которой a10 = 19, a15 = 44. Найдите разность прогрессии. Решение. Член арифметической прогрессии с номером n вычисляется по формуле Зная, что a10 = 19, b15 = 44, получаем систему уравнений. Вычтем первое уравнение из второго и решим систему:
Ответ: 5. Ответ: 5 Источник: Банк заданий ФИПИ Задание 11 № 341214 29.Арифметическая прогрессия задана условием an = −0,6 + 8,6n. Найдите сумму первых 10 её членов. Решение. Сумма n первых членов арифметической прогрессии даётся формулой
Найдем разность и первый член прогрессии :
Подставим найденные значения в формулу:
Ответ: 467. Ответ: 467 Источник: Банк заданий ФИПИ Задание 11 № 341221 30.Дана арифметическая прогрессия (an), разность которой равна −2,5, a1 = −9,1. Найдите сумму первых 15 её членов. Решение. Сумма n первых членов арифметической прогрессии даётся формулой
По условию, откуда получаем
Ответ: −399. Ответ: -399 -399 Источник: Банк заданий ФИПИ Задание 11 № 341492 31.Арифметическая прогрессия задана условием an = −11,9 + 7,8n . Найдите a11. Решение. Подставим 11 вместо индекса n:
Ответ: 73,9. Ответ: 73,9 73,9 Источник: СтатГрад: Тренировочная работа по математике 07.05.2015 вариант МА90901. Задание 11 № 341518 32.Первый член арифметической прогрессии равен −11,9, а разность прогрессии равна 7,8. Найдите двенадцатый чле
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Последовательности и серии – рабочие примеры
Последовательность $\{ a_{n} \}$ — это бесконечный список чисел $$a_{1}, a_{2}, a_{3}, \ldots,$$ где у нас есть одно число $a_{n}$ для каждого положительного целого числа $n$.
Определение последовательностей.
Мы можем задать последовательность различными способами.
Выкройка. Мы можем указать его, перечислив некоторые элементы и подразумевая, что
Показанная схема продолжается.
Пример.
Например $$2, 4, 6, 8, \ldots$$ будет последовательность, состоящая из четных положительных целых чисел.
Формула. Мы также можем указать последовательность, дав формулу для термина, который соответствует целому числу $n$.
Пример.
Например, последовательность $$2, 4, 6, 8, \ldots$$ можно также задать явной формулой $$a_{n} = 2n.$$ Рекурсивно. Наконец, мы также можем предоставить правило для получения следующего члена последовательности из предыдущих. Это называется рекурсивно определенной последовательностью.
Пример.
Например, последовательность
$$2, 4, 6, 8, \ldots$$
можно указать по правилу
$$a_{1} = 2 \quad \text{ и } \quad a_{n} = a_{n-1} +2 \text{ для } n\geq 2.$$
Это правило гласит, что мы получаем следующий член, беря предыдущий член и добавляя $2$. Поскольку мы начинаем с числа 2, мы получаем все четные положительные целые числа.
Давайте обсудим эти способы определения последовательностей более подробно и рассмотрим несколько примеров.
Часть 1. Арифметические последовательностиПоследовательность, которую мы видели в предыдущем абзаце, является примером того, что называется арифметической последовательностью : каждый член получается добавление фиксированного числа к предыдущему термину.
Альтернативно, разница между последовательными сроками всегда равна такой же.
Общая формула.
Если последовательность $a_{n}$ арифметическая, то существует фиксированное число $d$, такое что $a_{n+1} -a_{n} =d$ для любого $n.$ Число $d$ обычно называют 9.0009 шаг или разница . Попробуем найти формулу члена $a_{n}$ арифметической прогрессии через $d$ и $a_{1}$.
Начнем с $a_{n} = a_{n-1} + d$. Применяя это снова, мы видим, что поскольку $a_{n-1} = a_{n-2} + d$, мы получаем, что $a_{n} = a_{n-2} + d +d = a_{n- 2} + 2d$. Мы можем продолжить этот путь и получить:
\начать{выравнивать*}
а_{п} &= а_{п} = а_{п-1} + д \\
&= a_{n-2} + d +d = a_{n-2} + 2d \\
&= a_{n-3} + d + d = a_{n-3} + 3d \\
&\vточки\\
&= а_{2} + (n-2)d \\
&= а_{1} + (n-1)d \\
\конец{выравнивание*}
Таким образом, мы получаем, что в арифметической последовательности $a_{n}$ с шагом размером $d$ формула для $a_{n}$ задается следующим образом:
$$a_{n} = a_{1} + (n-1)d$$
Мы можем продолжить этот путь и получить:
\начать{выравнивать*}
а_{п} &= а_{п} = а_{п-1} + д \\
&= a_{n-2} + d +d = a_{n-2} + 2d \\
&= a_{n-3} + d + d = a_{n-3} + 3d \\
&\vточки\\
&= а_{2} + (n-2)d \\
&= а_{1} + (n-1)d \\
\конец{выравнивание*}
Таким образом, мы получаем, что в арифметической последовательности $a_{n}$ с шагом размером $d$ формула для $a_{n}$ задается следующим образом:
$$a_{n} = a_{1} + (n-1)d$$
Пример. Рассмотрим последовательность $3, 8, 13, 18, 23, 28, \ldots$. Это арифметика? Если это так, найдите формулу для $a_{n}$ и используйте ее, чтобы найти $a_{101}$, 101-й член последовательности.
Раствор. Эта последовательность является арифметической, так как разница между каждым членом составляет 5$
(8-3 = 13-8 = 18-13 = \cdots = 5$).
с шагом $d=5$ и первым членом $a_{1} = 3$.
Наша формула выше дает $a_{n} = a_{1} + (n-1)d = 3 + (n-1)5$.
Для $a_{101}$ мы подставляем $n=101$ в эту формулу, чтобы получить $a_{101} = 3 + (100)5 = 503$.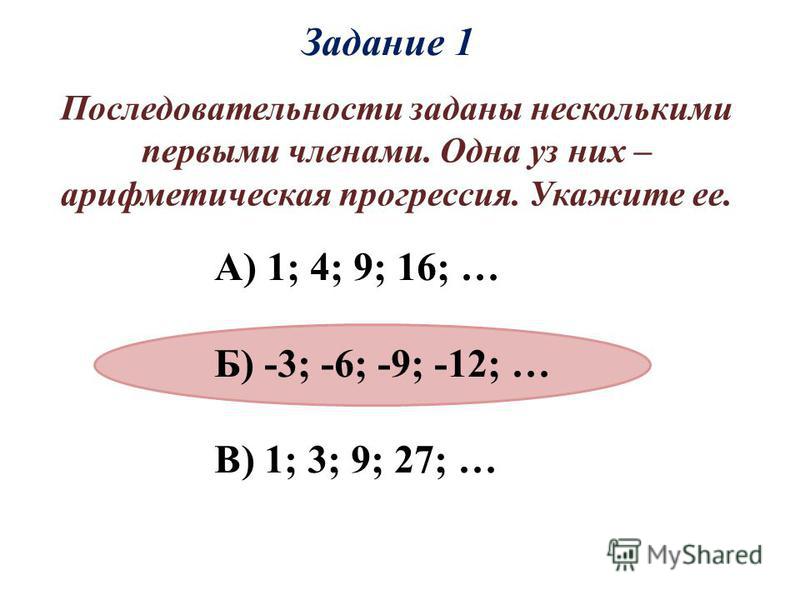
Рассмотрим последовательность $2, 4, 8, 16, 32, 64, \ldots$. Эта последовательность не является арифметической, так как разница между терминами не всегда одинакова. Если мы посмотрим внимательно, то увидим, что мы получаем следующий член последовательности как , умножая предыдущий член на то же число . Соответственно, соотношение последовательных терминов всегда одинаково (а именно $2$).
Последовательность $a_{n}$, где существует фиксированное $r$, так что $\frac{a_{n}}{a_{n-1}} = r$ для всех $n$ называется геометрическим последовательность. Число $r$ обычно называют отношением .
Общая формула.
Попробуем найти формулу члена $a_{n}$ геометрической прогрессии через $r$ и первый член.
Начнем с соотношения $\frac{a_{n}}{a_{n-1}} = r$. Это дает $a_{n} = r a_{n-1}$. Используя это снова, мы получаем $a_{n} = r (ra_{n-2}) = r^{2} a_{n-2}$. {n-1} a_{1}$$
9{n-1} a$ или
правило, что $a_{n} = r a_{n-1}$.
{n-1} a_{1}$$
9{n-1} a$ или
правило, что $a_{n} = r a_{n-1}$.
Последнее правило является примером рекурсивного правила . Рекурсивно определенная последовательность представляет собой последовательность, в которой правило для создания следующего члена в последовательности записано явно в терминах предыдущих членов.
Рассмотрим следующий (довольно известный) пример.
Пример.
Определим последовательность $a_{n}$ следующим образом: Пусть
$$a_{1} = 1 \quad , \quad a_{2} = 1 \quad \text{ и} \quad a_{n} =
a_{n-1} + a_{n-2} \text{ для } n\geq 2.$$
Это правило гласит, что для получения следующего члена последовательности необходимо сложить два предыдущих члена. Поскольку это правило требует двух предыдущих членов, нам нужно указать первые два члена последовательности $a_{1}, a_{2}$, чтобы начать работу.
Используя это, мы можем начать перечислять термины в последовательности и получить $1, 1, 2, 3, 5, 8, 13, 21, 34,\ldots$. (Это хорошо известное последовательность Фибоначчи .)
(Это хорошо известное последовательность Фибоначчи .)
Пример.
Рассмотрим рекурсивно определенную последовательность $$a_{1} = 1 \quad , \quad a_{2} = 1 \quad , \quad a_{3} = 1 \quad \text{, и} \quad a_{n} = \frac{a_{n-3}}{a_{n-1} + a_{n-2}} \text{ for } n\geq 3.$$ Назовите первые 7 членов этой последовательности.
Раствор. \начать{выравнивать*} а_{1} &= 1 \\ а_{2} &= 1 \\ а_{3} &= 1 \\ a_{4} &= \frac{1}{1+1} = \frac{1}{2} \\ a_{5} &=\frac{1}{1+\frac{1}{2}} = \frac{1}{\frac{3}{2}} = \frac{2}{3} \\ a_{6} &= \frac{1}{\frac{1}{2} + \frac{2}{3}} = \frac{1}{\frac{7}{6}} = \frac{ 6}{7} \\ a_{7} &= \frac{ \frac{1}{2}}{\frac{2}{3} + \frac{6}{7}} = \frac{ \frac{1}{2}} {\ гидроразрыва {32} {21}} = \ гидроразрыва {21} {64} \конец{выравнивание*}
Часть 4: Последовательности через списки Метод использования списка для указания последовательности, пожалуй, самый
сложно, так как это требует от нас просмотра короткого фрагмента последовательности,
и угадать шаблон или правило, которое используется для создания
термины в последовательности.
Теперь, когда мы рассмотрели еще несколько примеров последовательностей, мы можем обсудить, как искать закономерности и вычислять по заданному списку, как найти рассматриваемую последовательность.
Пример.
Когда дается список, например, $1, 3, 9, 27, 81, \ldots$ мы можем попробовать
ищите закономерность несколькими способами.
Теперь, когда мы увидели арифметические, геометрические и рекурсивные последовательности, одна вещь, которую мы можем сделать, это попытаться проверить, является ли данная последовательность
является одним из этих типов.
Арифметика? Чтобы проверить, является ли последовательность арифметической, мы проверяем, является ли
разница последовательных терминов всегда одинакова. В этом случае
изменения разницы:
$$a_2- a_1 = 3-1 =2 \neq 6 = 9-3 = a_3-a_2.$$ Геометрический? Чтобы проверить, является ли последовательность геометрической, мы проверяем, всегда ли соотношение последовательных членов одинаково. В случае, если это так, мы заключаем, что последовательность является геометрической:
$$\frac{3}{1}= \frac{9{\text{th}}$ термин в
последовательность.
В случае, если это так, мы заключаем, что последовательность является геометрической:
$$\frac{3}{1}= \frac{9{\text{th}}$ термин в
последовательность.
Раствор. Мы быстро видим, что этот ряд не является геометрическим, поскольку $\frac{1}{-3} \neq \frac{-3}{-7}$.
Теперь мы можем проверить, является ли последовательность арифметической. Если мы посмотрим на различия последовательных членов, мы получим: $-3 — 1 = -4 = -7 — (-3) = -11 — (-7)$, поэтому мы видим, что это арифметическая последовательность с разностью $d=-4$.
Итак, общий термин
$$a_{n} = a_{1} + (n-1) d = 1 + (n-1) (-4) = — 4n + 5.$$
(Мы также можем попытаться найти рекурсивное определение этой последовательности.)
Формула арифметической последовательности. Что такое формула арифметической последовательности? Примеры
Формула арифметической последовательности используется для вычисления члена n th и суммы арифметической прогрессии. Арифметическая последовательность — это последовательность, в которой общая разность между любыми двумя последовательными членами остается постоянной. Если мы хотим найти какой-либо термин/сумму терминов в арифметической последовательности, мы можем использовать формулу арифметической последовательности. Давайте разберемся с формулой арифметической прогрессии на решенных примерах.
Если мы хотим найти какой-либо термин/сумму терминов в арифметической последовательности, мы можем использовать формулу арифметической последовательности. Давайте разберемся с формулой арифметической прогрессии на решенных примерах.
Что такое формула арифметической последовательности?
Арифметическая последовательность имеет вид: а, а + d, а + 2d, а + 3d, …… до n членов. Первый член — это а, общая разница — d, n = количество терминов. Для расчета с использованием формул арифметической последовательности сначала определите первый член, количество членов и общую разность последовательности. Существуют различные формулы, связанные с арифметическим рядом, используемым для вычисления члена n th , суммы или общей разности данной арифметической последовательности.
- n й срок есть, а n = а 1 + (n — 1) d
- Сумма n членов равна S n = (n/2) [2a 1 + (n — 1) d] (или) (n/2) [a 1 + a n ]
- Общая разность, d = a n — a n — 1
В этих формулах a 1 = первый член, d = общая разность и n = количество членов.
Арифметическая последовательность Формула
Формулы арифметической последовательности имеют вид 1) d
где,
- a n = n th срок,
- a 1 = первый член и
- d общая разница
Формула 2: Сумма первых n членов арифметической последовательности вычисляется по одной из следующих формул:
- S n = (n/2) [2a 1 + (n — 1) d] (когда мы знаем первый член и общую разность)
- S n =(n/2) [a 1 + a n ] (когда первый и последний члены)
где,
- S n = сумма n слагаемых,
- a 1 = первый срок,
- a n = n th срок и
- d — общая разность между последовательными терминами
Формула 3: Формула для вычисления общей разности арифметической прогрессии имеет вид -й триместр,
Применение формулы 9 арифметической последовательности0158
Мы используем формулу арифметической прогрессии каждый день или даже каждую минуту, даже не осознавая этого. Ниже приведены несколько примеров практического применения формулы арифметической прогрессии
Ниже приведены несколько примеров практического применения формулы арифметической прогрессии
- Складывание чашек, стульев, мисок или карточного домика.
- Места на стадионе или в зрительном зале располагаются в арифметической последовательности.
- Секундная стрелка на часах движется в арифметической последовательности, так же как и минутная и часовая стрелки.
- Недели в месяце следуют арифметической последовательности, как и годы. Каждый високосный год можно определить, прибавив 4 к предыдущему високосному году.
- Количество свечей, задуваемых в день рождения, с каждым годом увеличивается как арифметическая прогрессия.
Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Заказать бесплатный пробный урок
Примеры с использованием формулы арифметической последовательности
Пример 1: Используя формулу арифметической последовательности, найти 13 th член в последовательности 1, 3, 9, 00 103
Решение:
Найти: 13 й член данной последовательности.
Поскольку разница между последовательными терминами одинакова, данная последовательность образует арифметическую последовательность.
A = 1, D = 4
с использованием формулы арифметической последовательности,
A N = A 1 + (N — 1) D
для 13 Т. n = 1 + (13 — 1)4
a n = 1 + (12)4
a n = 1 + 48
A N = 49
☛ Также Проверка: Калькулятор арифметической последовательности
Ответ: 13 TH Термин в последовательности — 49.
Пример 2: Найти первое термин в ARTITITENTIENT. где 35 член равен 687, а общая разность 14 14
Используя формулу арифметической последовательности,
a n = a 1 + (n − 1)d
687 = a 1 + (35 — 1)14
86 0 34) 14
687 = A 1 + 476
A 1 = 211
Ответ: Первый термин в последовательности составляет 211.
Пример 3: Найдите сумма следующего. ряд: 3 + 7 + 11 + ……. (до 25 слагаемых).
Решение:
Найти сумму первых 25 членов арифметической прогрессии 3, 7, 11, …….
Дано: a 1 = 3, d = 4, n = 25
данная арифметическая последовательность равна 3, 7, 11,….
Используя формулу арифметического ряда:
S n = (n/2) [2a + (n — 1) d]
Сумма первых 25 членов
S 25 =(25/2 ) [2 x 3 + (25 — 1) 4]
= (25/2) [6 + 24 x 4]
= 25/2 × 102
= 1275
Ответ: Сумма данного арифметического ряда равна 1275.
Часто задаваемые вопросы о формуле арифметической последовательности
Что такое формула арифметической последовательности в алгебре?
Формула арифметической последовательности относится к формуле для вычисления общего члена арифметической последовательности и суммы n членов арифметической последовательности.
- Общий член арифметической последовательности: a n = a 1 + (n — 1) d
- Сумма первых n членов арифметической прогрессии равна n = (n/2) [2a 1 + (n — 1) d]
где a 1 = первый член и d = общая разность последовательности.
Что такое n в формуле арифметической последовательности?
В формуле арифметической последовательности для нахождения общего термина a n = a 1 + (n — 1) d, ‘n’ относится к номеру термина в данной арифметической последовательности. Например, 2 представляет собой 2 -й -й член последовательности.
Что такое формула арифметической последовательности для суммы n членов?
Сумма первых n членов арифметической последовательности определяется как S n = (n/2) [2a 1 + (n — 1) d], где S n = сумма n членов , a 1 = первый член, а d — общая разность.
Что такое формула арифметического ряда?
Арифметический ряд есть не что иное, как сумма нескольких или всех членов арифметической прогрессии. Таким образом, формула арифметического ряда:
- S n = (n/2) [2a 1 + (n — 1) d] [ИЛИ]
- S n = (n/2) [a 1 + a n ]
Здесь a 1 — первый член арифметического ряда, а d — его общая разность.
Как использовать формулу арифметической последовательности?
Чтобы использовать формулу арифметической последовательности, сначала определите первый член (a 1 ) и общую разность (d) последовательности.


 ..
.. Последовательность задана формулой . Какое из указанных чисел является членом этой последовательности?
Последовательность задана формулой . Какое из указанных чисел является членом этой последовательности?


 Последовательность задана условиями , . Найдите .
Последовательность задана условиями , . Найдите . Таким образом, четыре члена данной последовательности больше 6.
Таким образом, четыре члена данной последовательности больше 6.

 Таким образом, правильный ответ указан под номером 4.
Таким образом, правильный ответ указан под номером 4. В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?
В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?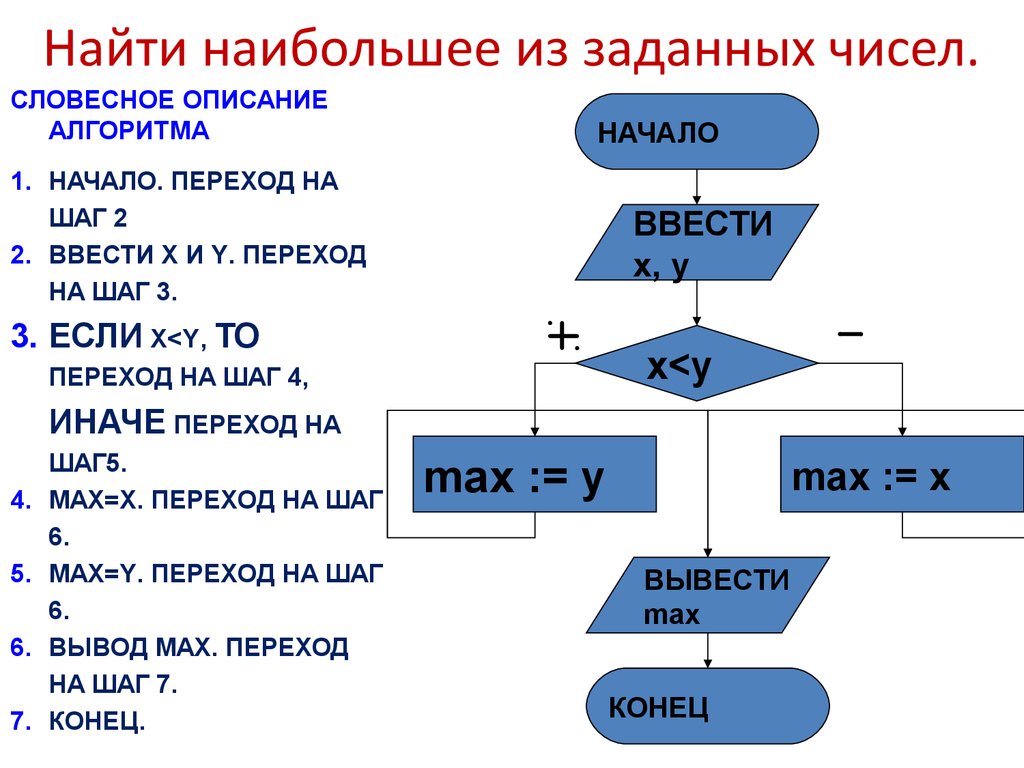 Следовательно, первым отрицательным членом прогрессии является
Следовательно, первым отрицательным членом прогрессии является ..
.. Математика. Краевая диагностическая работа. Краснодар (вар.5)
Математика. Краевая диагностическая работа. Краснодар (вар.5) Для этого найдём корни уравнения
Для этого найдём корни уравнения
 Следовательно, наименьшее натуральное число, для которого сумма будет больше 465, равно 31.
Следовательно, наименьшее натуральное число, для которого сумма будет больше 465, равно 31.

 е. нужно, чтобы выполнялось условие Решим неравенство :
е. нужно, чтобы выполнялось условие Решим неравенство : Сколько квадратов в 16-й строке?
Сколько квадратов в 16-й строке?


 ..
..
Leave A Comment