Школьная физика от Шептикина А.С.
Вариант №01
I. На рисунке изображен график зависимости модуля скорости вагона от времени в инерциальной системе отсчета. В течение каких промежутков времени суммарная сила, действующая на вагон со стороны других тел, равнялась нулю, если вагон двигался прямолинейно? | |
1. 0 — t1, t3 — t4 | |
2. 0 – t4 | |
3. t1 — t2, t2-t3 | |
4. таких промежутков времени нет |
II. Систему отсчета, связанную с Землей, будем считать инерциальной. Система отсчета, связанная с автомобилем, тоже будет инерциальной, если автомобиль. | |
1. движется равномерно по прямолинейному участку шоссе | |
2. разгоняется по прямолинейному участку шоссе | |
3. движется равномерно по извилистой дороге | |
4. по инерции вкатывается на гору |
III. Для каких физических явлений был сформулирован принцип относительности Галилея? | |
1. только для механических явлений | |
2. для механических и тепловых явлений | |
3. для механических, тепловых и электромагнитных явлений | |
4. для любых физических явлений |
IV. Молоток массой 0,8 кг ударяет по небольшому гвоздю и забивает его в доску. | |
1. 400 Н | |
2. 200 Н | |
3. 800 Н | |
4. 80 Н |
V. На левом рисунке представлены вектор скорости и вектор равнодействующей всех сил, действующих на тело. Какой из четырех векторов на правом рисунке указывает направление вектора ускорения этого тела в инерциальных системах отсчета? | |
1. 1 | |
2. 2 | |
3. 3 | |
4. 4 |
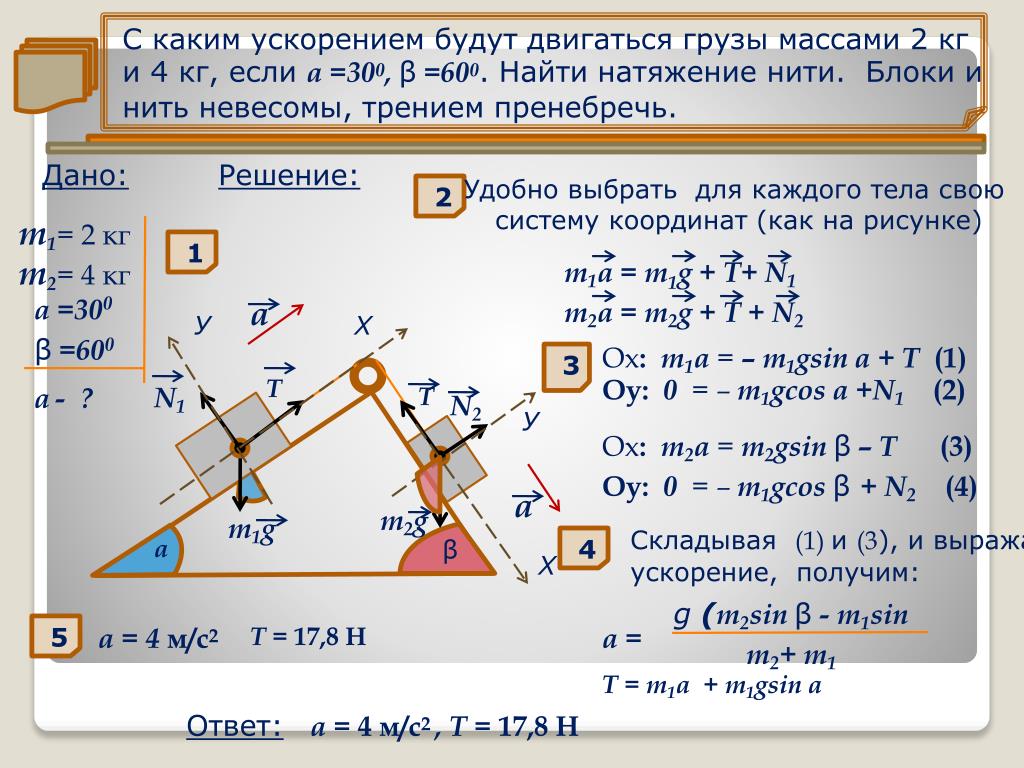
VI. Брусок массой М = 300 г соединен с грузом массой m = 200 г невесомой и нерастяжимой нитью, перекинутой через невесомый блок (см. | |
1. 1 м/с2 | |
2. 2,5 м/с2 | |
3. 7 м/с2 | |
4. 17 м/с2 |
VII. После толчка брусок скользит вверх по наклонной плоскости. В системе отсчета, связанной с плоскостью, направление оси Ох показано на левом рисунке. Направления векторов скорости v бруска, его ускорения а и равнодействующей силы F правильно показаны на рисунке | |
1. 1 | |
2. 2 | |
3. 3 | |
4. |
VIII. Космическая ракета удаляется от Земли. На каком расстоянии от земной поверхности сила гравитационного притяжения ракеты Землей уменьшится в 4 раза по сравнению с силой притяжения на земной поверхности? (Расстояние выражается в радиусах Земли R) | |
1. R | |
2. √2R | |
3. 2R | |
4. 3R |
IX. Искусственный спутник обращается по круговой орбите на высоте 600 км от поверхности планеты со скоростью 3,4 км/с. Радиус планеты равен 3400 км. Чему равно ускорение свободного падения на поверхности планеты? | |
1. 3,0 км/с2 | |
2. | |
3. 9,8 м/с2 | |
4. 9,8 км/с2 |
X. На рисунке приведены условные изображения Земли, летающей тарелки и вектора FT силы притяжения тарелки Землей. Масса летающей тарелки примерно в 10 | |
1. вдоль 1, равна Fт | |
2. вдоль 2, равна Fт | |
3. вдоль 1, в 1018 раз меньше Fт | |
4. вдоль 2, в 1018 раз больше Fт |
XI. | |
1. 10 Н/м | |
2. 20 Н/м | |
3. 100 Н/м | |
4. 0,01 Н/м |
XII. Ученик собрал установку, используя нить, пружину и штатив (см. рисунок). Деформация пружины 0,05 м, ее жесткость 40 Н/м. Сила натяжения нити равна… | |
1. 800 Н | |
2. 0,05 Н | |
3. 2 Н | |
4. 0 Н |
XIII. После удара клюшкой шайба массой 0,15 кг скользит по ледяной площадке. | |
1. 0,15 | |
2. 0,2 | |
3. 3 | |
4. 0,3 |
XIV. На горизонтальной дороге автомобиль делает разворот радиусом 9 м. Коэффициент трения шин об асфальт 0,4. Чтобы автомобиль не занесло, его скорость при развороте не должна превышать… | |
1. 36 м/с | |
2. 3,6 м/с | |
3. 6 м/с | |
4. 22,5 м/с |
XV. Книга лежит на столе. Масса книги 0,6 кг. | |
1. 75 Па | |
2. 7,5 Па | |
3. 0,13 Па | |
4. 0,048 Па |
XVI. Тело равномерно движется по плоскости. Сила давления тела на плоскость равна 20 Н, сила трения 5 Н. Коэффициент трения скольжения равен… | |
1. | |
2. 0,25 | |
3. 0,75 | |
4. 0,2 |
| Вы ответили верно на | |
| Ваша оценка: | |
| Количество баллов: |
Тестирование
ТестированиеСистему отсчёта, связанную с Землёй, будем считать инерциальной.
 Система отсчёта, связанная с автомобилем,
тоже будет инерциальной, если автомобиль
Система отсчёта, связанная с автомобилем,
тоже будет инерциальной, если автомобильдвижется равномерно по прямолинейному участку шоссе
разгоняется по прямолинейному участку шоссе
движется равномерно по извилистой дороге
по инерции вкатывается на горуПарашютист спускается вертикально с постоянной скоростью 2 м/с. Систему отсчёта, связанную с Землёй, считать инерциальной. В этом случае
вес парашютиста равен нулю
сила тяжести, действующая на парашютиста, равна нулю
сумма всех сил, приложенных к парашютисту, равна нулю
сумма всех сил, действующих на парашютиста, постоянна и не равна нулюПод действием равнодействующей силы, равной 5 Н, тело массой 10 кг движется
равномерно со скоростью 2 м/с
равномерно со скоростью 0,5 м/с
равноускоренно с ускорением 2 м/с2
равноускоренно с ускорением 0,5 м/с2Какие из перечисленных ниже пар физических величин всегда совпадают по направлению?
сила и ускорение
сила и скорость
сила и перемещение
ускорение и перемещениеНа рисунке приведены условные изображения Земли и Луны, а также вектор силы притяжения Луны Землёй.
 Известно, что масса Земли примерно в 81 раз больше массы Луны.
Вдоль какой стрелки (1 или 2) направлена и чему равна по модулю сила,
действующая на Землю со стороны Луны?
Известно, что масса Земли примерно в 81 раз больше массы Луны.
Вдоль какой стрелки (1 или 2) направлена и чему равна по модулю сила,
действующая на Землю со стороны Луны?вдоль 1, равна FЛ
вдоль 2, равна FЛ
вдоль 1, равна 81FЛ
вдоль 2, равна FЛ/81После толчка брусок скользит вверх по наклонной плоскости. В системе отсчёта, связанной с плоскостью, направление оси 0x показано на правом рисунке. На каком из рисунков правильно показаны направления векторов скорости бруска, его ускорения
и равнодействующей силы ?На какой стадии полета в космическом корабле, который становится на орбите спутником Земли, будет наблюдаться невесомость?
на стартовой позиции с включенным двигателем
при выходе на орбиту с включенным двигателем
при орбитальном полете с выключенным двигателем
при посадке с парашютом с выключенным двигателемКомета находилась на расстоянии 100 млн км от Солнца.
 При удалении кометы
от Солнца на расстояние 200 млн км сила притяжения, действующая на комету
При удалении кометы
от Солнца на расстояние 200 млн км сила притяжения, действующая на кометууменьшилась в 2 раза
уменьшилась в 4 раза
уменьшилась в 8 раз
не измениласьРакета массой 10
5 кг стартует вертикально вверх с поверхности Земли с ускорением 15 м/с2. Если силами сопротивления воздуха при старте пренебречь, то сила тяги двигателей ракеты равна5.105 Н
1,5.106 Н
2,5.106 Н
1,5.107 НК подвижной вертикальной стенке приложили груз массой 10 кг.
 Коэффициент
трения между грузом и стенкой равен 0,4. С каким минимальным ускорением
надо передвигать стенку влево, чтобы груз не соскользнул вниз?
Коэффициент
трения между грузом и стенкой равен 0,4. С каким минимальным ускорением
надо передвигать стенку влево, чтобы груз не соскользнул вниз?4.10-2 м/с2
4 м/с2
25 м/с2
250 м/с2
Ньютоновская механика — Блок на наклонной плоскости
спросил
Изменено 4 года, 6 месяцев назад
Просмотрено 6к раз
$\begingroup$
На наклонной плоскости (пандусе) лежит брусок массой $m$. Если к пандусу приложить постоянную силу $f$, так что он будет ускоряться в горизонтальном направлении с соответствующей скоростью, блок останется на той же высоте. Но что же тогда представляет собой сила, которая отменяет составляющую веса блока, параллельную плоскости, (т. е. $mgsinθ$) и препятствует скольжению блока по наклонной плоскости?
Если к пандусу приложить постоянную силу $f$, так что он будет ускоряться в горизонтальном направлении с соответствующей скоростью, блок останется на той же высоте. Но что же тогда представляет собой сила, которая отменяет составляющую веса блока, параллельную плоскости, (т. е. $mgsinθ$) и препятствует скольжению блока по наклонной плоскости?
Примечание: все поверхности не имеют трения.
- ньютоновская механика
- силы
- системы отсчета
- векторы
- диаграмма свободного тела
$\endgroup$
0
$\begingroup$
Обратите внимание: чтобы брусок (массой $m$) и наклонная плоскость (клин массой $M$) двигались вместе, они должны иметь общее горизонтальное ускорение, определяемое: $$a=\frac{ F}{М+м}$$
И, таким образом, для блока массы $m$ его горизонтальное ускорение должно быть равно этому, поэтому на маленький блок действует горизонтально результирующая сила (которую я назову $F_m$, которая определяется как $F_m=ma$ где а — общее горизонтальное ускорение бруска и клина).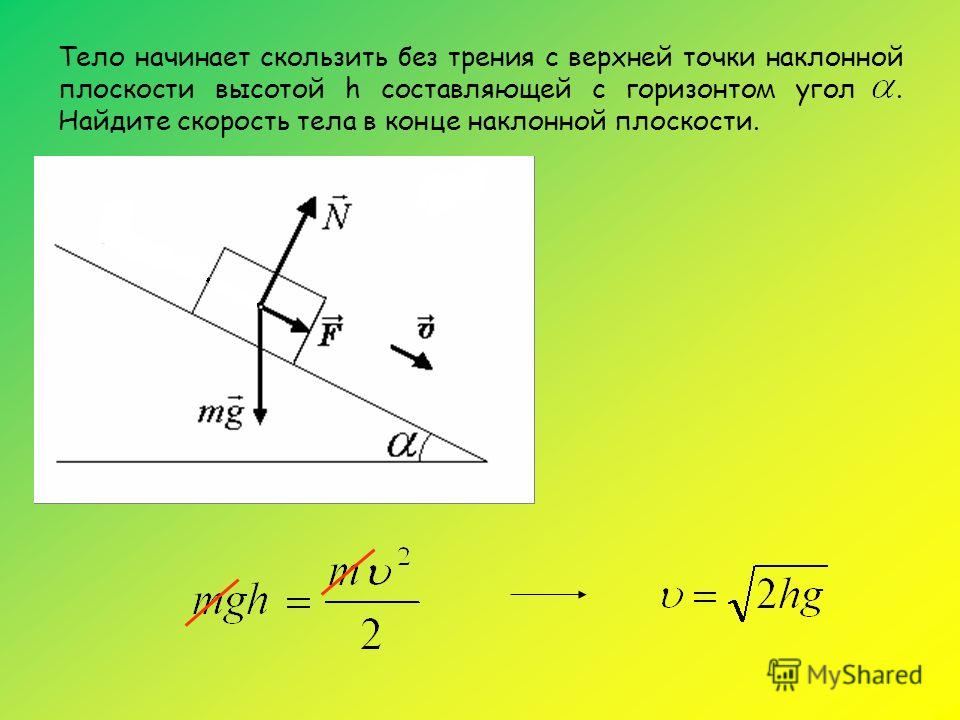
Действительно, нет никакой силы, противодействующей компоненте $mgsin(\theta)$, и вы можете видеть ниже, что ее не требуется отменять, так как она сама становится компонентом равнодействующей силы $F_m$, которая имеет компоненты $N -mgcos(\theta)$ и, как и ожидалось, $mgsin(\theta)$:
Примечание: на диаграмме показаны силы, действующие на только на блок массой $m$.
Другая диаграмма запрошена для просмотра силовой диаграммы другим способом, который даст тот же конечный результат:
$\endgroup$
8
$\begingroup$
Здесь дан правильный ответ на этот вопрос, но он заслуживает дополнительного концептуального исследования, поскольку эта проблема ясно указывает на необходимость явного рассмотрения и включения силы инерции в эту диаграмму вектора силы.
Третий закон Ньютона: Все силы во Вселенной действуют равными, но противоположно направленными парами. Сила, приложенная к любой массе, вызовет в ответ такую же силу. Обратите внимание, что Сила Инерции имеет другой характер, чем силы Поля (например, гравитационная, электрическая, магнитная). Сила инерции не оказывает устойчивой силы потенциального поля. Скорее, Сила Инерции оказывает реактивную противодействующую силу только в данный момент, ускоряя и передавая кинетическую энергию.
Сила, приложенная к любой массе, вызовет в ответ такую же силу. Обратите внимание, что Сила Инерции имеет другой характер, чем силы Поля (например, гравитационная, электрическая, магнитная). Сила инерции не оказывает устойчивой силы потенциального поля. Скорее, Сила Инерции оказывает реактивную противодействующую силу только в данный момент, ускоряя и передавая кинетическую энергию.
Задача:
- Какая $F_{внешняя}$ на бруске необходима для ускорения массы и клина со скоростью, при которой брусок подвешивается в точке на клине?
Решение:
- Гравитационная сила $F_{гравитация-спуск} = mg sin\theta$ ускоряет брусок вниз по поверхности клина без трения.
- Сохранение статического положения на блоке требует уравновешивания направленного вниз ускорения силы тяжести с направленным вверх ускорением внешней силы.
- Горизонтальное ускорение клина и блока обеспечивает векторную составляющую направленной вверх Силы: $F_{inertial-uphill}$.

- Для решения необходимо определить величину $F_{external}$, которая вносит компонент вектора силы, равный по величине и противоположный по направлению нисходящей гравитационной силе.
$\endgroup$
$\begingroup$
Блок делает ускорение вниз по наклонной плоскости. Это ускорение — это , вызванное $mgsin(\theta)$. Блок также ускоряется по нормали. Это ускорение вызвано нормальным и $mgcos(\theta)$.
Других соответствующих сил нет.
Этот кажущийся странным вид является результатом выбора системы координат вдоль плоскости и нормали к плоскости, в то время как мы уже знаем что общее ускорение направлено вдоль горизонтальной оси.
Если вы выберете горизонтальную и вертикальную оси в качестве системы координат, то только вдоль горизонтальной оси вы получите ускорение, тогда как вдоль вертикальной оси ускорение равно нулю.
$\endgroup$
7
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ньютоновская механика — Схема свободного тела блока на ускоряющем клине
Задавать вопрос
спросил
Изменено 3 года, 3 месяца назад
Просмотрено 29 тысяч раз
$\begingroup$
Рассмотрим следующую систему:
Я совершенно запутался в некоторых аспектах ситуации, описанной на этой диаграмме, в которой брусок помещается на клин, наклоненный под углом θ. (Предположим, что везде нет трения )
Рассмотрим несколько различных случаев:
кадр), что я увижу? Увижу ли я, что брусок останется на клине и будет ускоряться вместе с ним влево, или я увижу, как он движется вниз по наклонной плоскости, которая сама движется влево?
Во-вторых, в некоторых задачах упоминается , что блок движется с ускорением «по наклонной плоскости с ускорением $a$ относительно клина «. В таких задачах я выбираю клин в качестве системы отсчета, ввожу псевдосилу и разбираюсь с ситуацией. Однако, если бы я наблюдал за блоком с земли, как бы выглядело для меня его движение?
В таких задачах я выбираю клин в качестве системы отсчета, ввожу псевдосилу и разбираюсь с ситуацией. Однако, если бы я наблюдал за блоком с земли, как бы выглядело для меня его движение?
В-третьих, при построении схемы свободного тела блока, который задан как «движущийся вниз по наклонной плоскости», в каком направлении следует принять его ускорение? Прямо вниз или по плоскости?
В-четвертых, если известно, что блок не «скользит по клину», какое условие следует использовать?
Как вы можете видеть из всего этого, я совершенно запутался во всех этих меняющихся системах отсчета и ускорениях. Если бы кто-нибудь мог кратко изложить это, это было бы так полезно для меня. Надеюсь, я ясно выразил свои сомнения. Если требуется больше ясности, пожалуйста, дайте мне знать, и я соответствующим образом отредактирую свой вопрос. Заранее БОЛЬШОЕ спасибо 🙂 С уважением.
- ньютоновская механика
- силы
- динамика с ограничениями
$\endgroup$
5
$\begingroup$
Вместо того, чтобы отвечать на ваши отдельные вопросы, я дам вам общий обзор, а затем обсужу некоторые поднятые вами вопросы.
Есть много способов решения таких проблем, но для начала всегда полезно нарисовать несколько FBD вместе с некоторыми осями координат.
Я буду использовать лабораторную систему отсчета, так как, возможно, тогда будет легче описать то, что человек видит в этой системе отсчета, и я далее буду предполагать, что трения нет и что все начинается с покоя.
Другое важное допущение для первой части анализа состоит в том, что блок и клин остаются в контакте друг с другом.
Затем можно применить второй закон Ньютона, который даст уравнения с вертикальным и горизонтальным ускорениями бруска, $z$ и $x$, горизонтальным ускорением клина $X$ и нормальной реакцией между бруском и клином $N. $ как четыре неизвестных.
Проблема в том, что применение второго закона Ньютона дает только три уравнения.
Как и во многих задачах механики, четвертое уравнение исходит из геометрии системы.
Брусок контактирует с клином и относительно клина скользит вниз по клину под углом $\theta$.
То есть, если вы сядете на клин, вы увидите, как блок движется вниз по клину с ускорением, но остается в контакте.
Ускорение клина вниз относительно бруска равно $z$ (клин не движется вниз, так как стол считается неподвижным), а горизонтальное ускорение бруска относительно клина равно $x-X$.
Диаграммы векторов ускорения выглядят так:
Это дает четвертое уравнение $\tan \theta = \dfrac{z}{x-X}$
Надеюсь, этого достаточно, чтобы ответить на все ваши вопросы?
Клин должен идти влево, а блок вправо.
Это должно быть так, что результирующая горизонтальная сила, действующая на систему блоков и клиньев, равна нулю, и поэтому центр масс системы не перемещается.
Используя эту идею, можно получить уравнение, напрямую связывающее горизонтальное ускорение бруска $x$ и клина $X$; $(m_1\;x + m_2 \; X = 0 +0 \Rightarrow X = — \dfrac {m_1\; x}{m_2} $.
Если по какой-то причине ускорение клина влево больше, чем $X$ в приведенном выше примере, например, из-за внешней горизонтальной силы, действующей на клин влево, то ситуация усложняется.
Предположим, что сила такова, что горизонтальное ускорение клина слева остается постоянным с величиной $Y$.
Нормальная сила между клином и блоком уменьшится, поэтому ускорение блока $z$ вниз увеличится, тогда как его горизонтальное ускорение блока $x$ уменьшится, но он по-прежнему будет контактировать с клином.
На диаграмме ускорения следует помнить, что, поскольку ускорение клина направлено влево, величина $x-Y$ будет увеличиваться, как и величина $z$, чтобы блок оставался в контакте с клином.
Итак, если вы сядете на клин, вы увидите, что блок остается в контакте с клином, но с большим ускорением вниз, чем раньше.
Сидя в лабораторной раме, вы снова увидите клин, ускоряющийся вниз по клину, но по траектории, угол которой с горизонтом больше угла клина $\theta$.
Предельный случай достигается, когда нисходящее ускорение блока равно $g (= z) $, а его горизонтальное ускорение $x$ равно нулю.
Итак, в этом предельном случае $\tan \theta = \dfrac{g}{(-)Y}$
Любое дальнейшее увеличение горизонтального ускорения клина влево приведет к тому, что блок потеряет контакт с клином и подвергается свободному падению.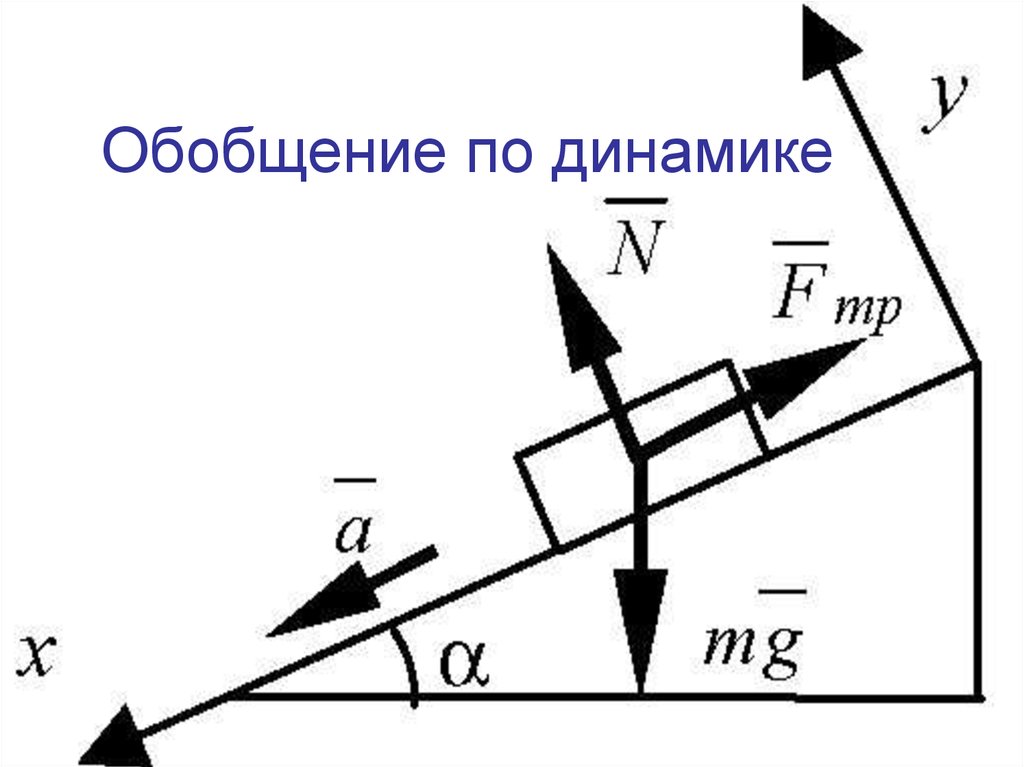
Я не совсем уверен в последней части анализа, но формула предельного ускорения $Y$, кажется, предсказывает то, что можно было бы ожидать. 9\circ$ ускорение клина $Y$ должно становиться все меньше и меньше.
$\endgroup$
7
$\begingroup$
Я заметил, что вы спрашиваете о блоке на клине. Эта проблема сложнее, чем кажется, даже без трения.
Движение легко предсказать. Клин движется влево, блок движется вниз и вправо. По горизонтали происходит сохранение импульса, поэтому горизонтальное положение центра масс не меняется. Если вы хотите решить эту проблему, вероятно, проще всего будет использовать закон сохранения энергии и импульса, а не силу и ускорение. См. Блок скользит по гладкому треугольному клину, удерживаемому на гладком полу. Найдите скорость клина, когда брусок достигнет дна. 9{\ circ} $; если $m_1<
Это может помочь разделить ускорение блока на компоненты x и y. Тогда $m_2a_2=m_1a_x$. Обратите внимание, что уравнения, составленные xylong97, неверны.
Проблема решена на многих веб-страницах и в нескольких видеороликах. Например: Задача об относительном вынужденном движении.
$\endgroup$
2
$\begingroup$
Увижу ли я, что блок останется на клине и будет ускоряться вместе с ним […]
Абсолютно не , так как нечем (силой) тянуть блок вместе с наклоном.
Нарисуйте диаграмму свободного тела блока, и вы увидите только нормальную силу $\vec n$ и вес $\vec w$. Их сумма может составлять , и никогда не останется очков.
[…] или я увижу, как он движется вниз по наклонной плоскости, которая сама движется влево?
Да . Если наклон не сдвинется на быстрее, чем на , то блок может упасть (в этом случае он, естественно, не следует поверхности наклона).
Если наклон не сдвинется на быстрее, чем на , то блок может упасть (в этом случае он, естественно, не следует поверхности наклона).
[…] клин ускоряется «вниз по наклонной плоскости с ускорением $a$ относительно клина». […] если бы я наблюдал за блоком с земли, как бы выглядело для меня его движение?
- Крайний случай : Если наклон стоит на месте, на блок будет действовать максимальная нормальная сила $\vec n$. Он скользит вниз под углом $\theta$. 9\circ$), так как наклон уходит под него одновременно.
[…] при построении диаграммы свободного тела блока, который задан как «движущийся вниз по наклонной плоскости», в каком направлении я должен принять его ускорение? Прямо вниз или по плоскости?
Согласно второму закону Ньютона $\sum \vec F=m\vec a$, ускорение $\vec a$ направлено в том же направлении, что и результирующая сила $\sum \vec F$. Поэтому при рисовании диаграммы свободного тела (по-прежнему содержащей только $\vec w$ и $\vec n$) их сумма будет указывать на ускорение.


 Скорость молотка перед ударом, равная 5 м/с, после удара равна 0, продолжительность удара 0,02 с. Чему равна средняя сила удара молотка?
Скорость молотка перед ударом, равная 5 м/с, после удара равна 0, продолжительность удара 0,02 с. Чему равна средняя сила удара молотка?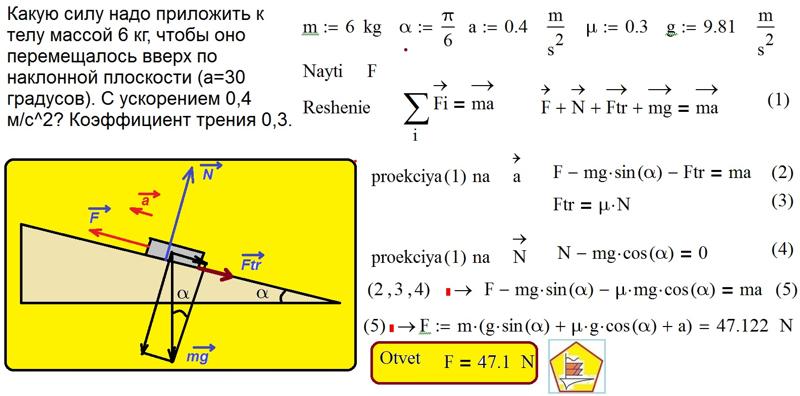 рисунок). Брусок скользит без трения по закрепленной наклонной плоскости, составляющей угол 30° с горизонтом. Чему равно ускорение бруска?
рисунок). Брусок скользит без трения по закрепленной наклонной плоскости, составляющей угол 30° с горизонтом. Чему равно ускорение бруска?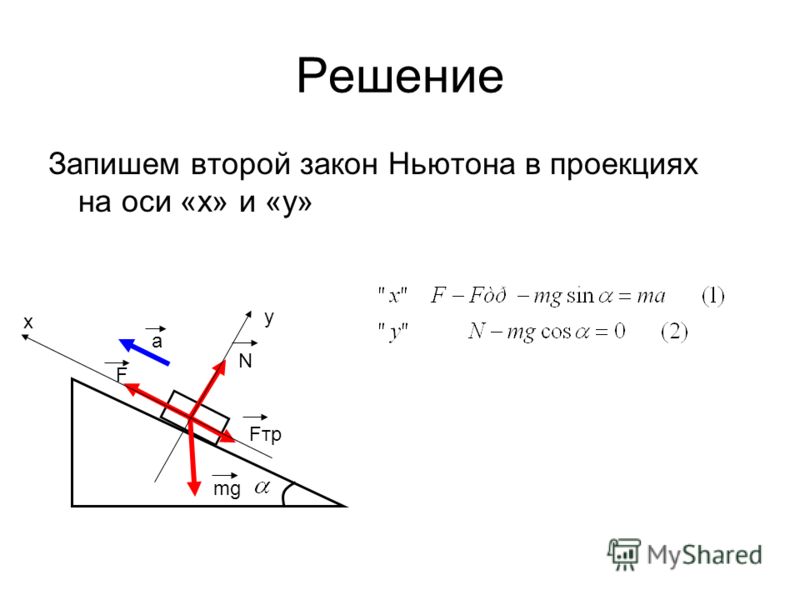 4
4 4,0 км/с2
4,0 км/с2
 Ее скорость при этом меняется в соответствии с уравнением v=20-3t, где все величины выражены в СИ. Коэффициент трения шайбы о лед равен…
Ее скорость при этом меняется в соответствии с уравнением v=20-3t, где все величины выражены в СИ. Коэффициент трения шайбы о лед равен…
 Система отсчёта, связанная с автомобилем,
тоже будет инерциальной, если автомобиль
Система отсчёта, связанная с автомобилем,
тоже будет инерциальной, если автомобиль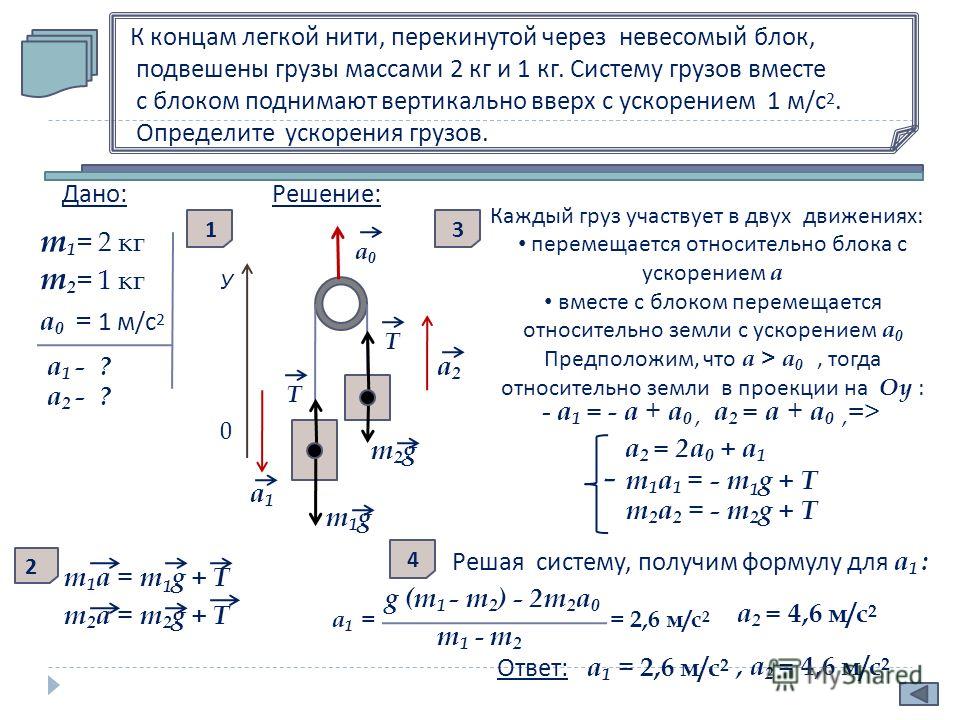 Известно, что масса Земли примерно в 81 раз больше массы Луны.
Вдоль какой стрелки (1 или 2) направлена и чему равна по модулю сила,
действующая на Землю со стороны Луны?
Известно, что масса Земли примерно в 81 раз больше массы Луны.
Вдоль какой стрелки (1 или 2) направлена и чему равна по модулю сила,
действующая на Землю со стороны Луны? При удалении кометы
от Солнца на расстояние 200 млн км сила притяжения, действующая на комету
При удалении кометы
от Солнца на расстояние 200 млн км сила притяжения, действующая на комету Коэффициент
трения между грузом и стенкой равен 0,4. С каким минимальным ускорением
надо передвигать стенку влево, чтобы груз не соскользнул вниз?
Коэффициент
трения между грузом и стенкой равен 0,4. С каким минимальным ускорением
надо передвигать стенку влево, чтобы груз не соскользнул вниз?
Leave A Comment