Задание 3 ЕГЭ по математике (профиль) часть 5
Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на площади треугольников, параллелограмма, ромба, трапеции и прямоугольника. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
27617. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
27623. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
27589. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30º. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
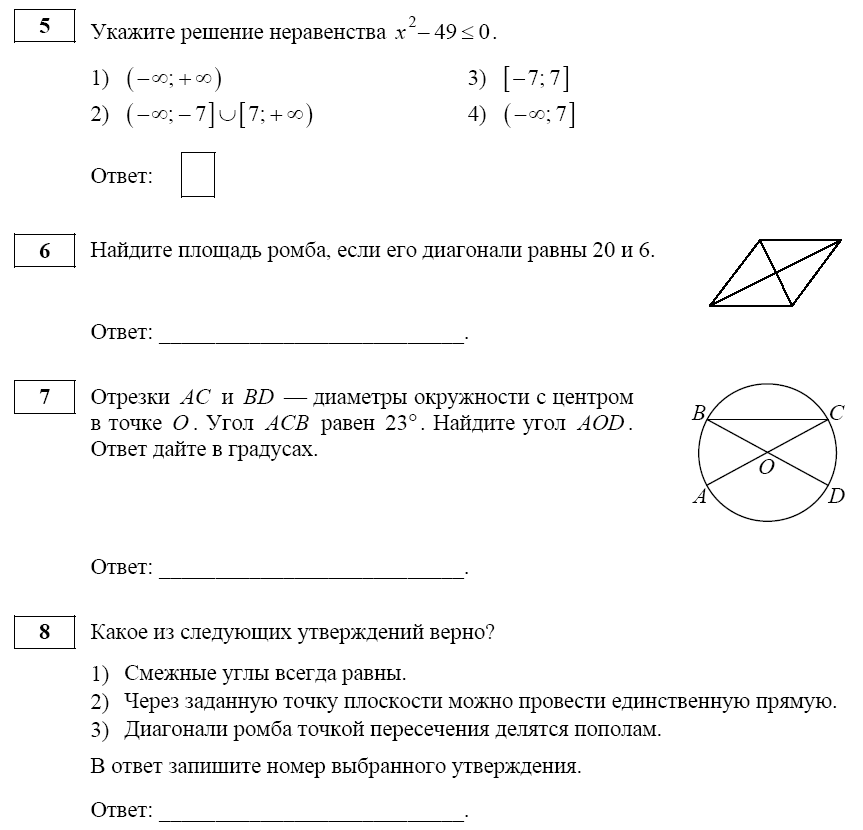
27590. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150º. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.
Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.
27591. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30º.
27620. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30º. Найдите боковую сторону треугольника, если его площадь равна 25.
27621. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150º. Найдите боковую сторону треугольника, если его площадь равна 10.
27619. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
27592. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
27618. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
Найдите меньший катет.
27624. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
319056. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.
319057. Площадь параллелограмма ABCD равна 176. Точка E – середина стороны CD. Найдите площадь треугольника ADE.
Точка E – середина стороны CD. Найдите площадь треугольника ADE.
27613. Найдите площадь ромба, если его высота равна 2, а острый угол 30º.
27614. Найдите площадь ромба, если его диагонали равны 4 и 12.
27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
27605. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
27582. Найдите площадь квадрата, если его диагональ равна 1.
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10.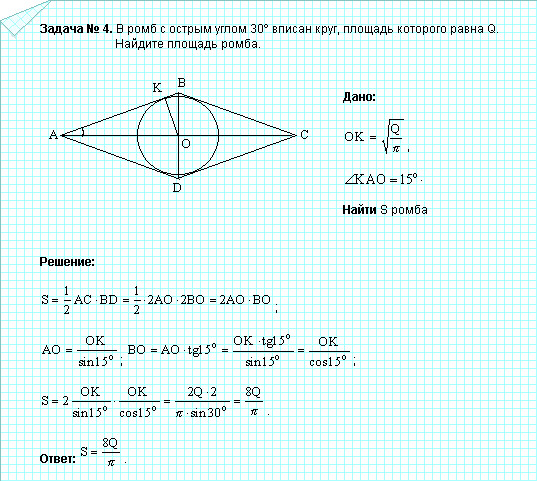 Найдите площадь трапеции.
Найдите площадь трапеции.
27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150º. Найдите площадь трапеции.
27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45º.
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне.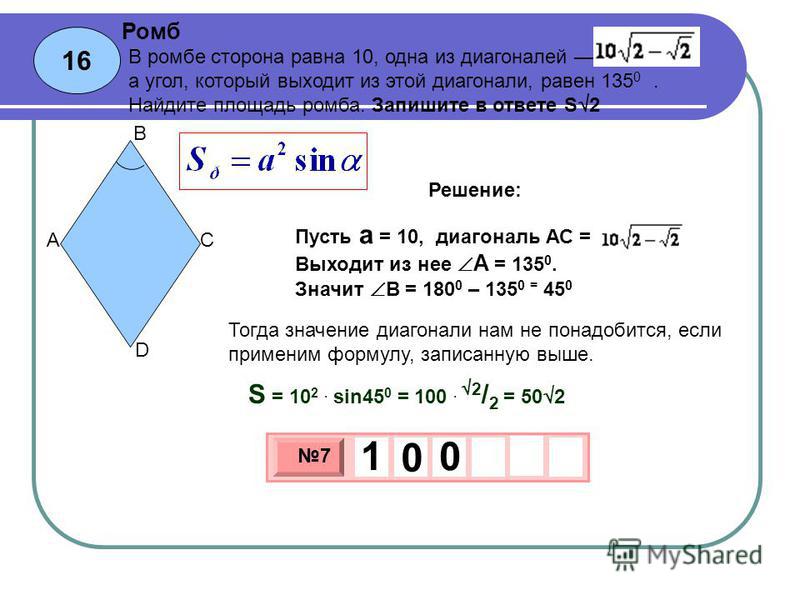 Ответ выразите в градусах.
Ответ выразите в градусах.
317338. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
319058. Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABDE.
27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Понравилось это:
Нравится Загрузка…
Зачетная работа по геометрии 8 класс по теме «Площади» | Материал для подготовки к ЕГЭ (ГИА) по геометрии (8 класс) на тему:
Опубликовано 02.12.2018 — 22:56 — Шаповалова Елена Дмитриевна
Зачетная работа состоит из 20 задач
Скачать:
Предварительный просмотр:
Зачет № 1
- Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 0,5 и 2.
- Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 9 и 225.

- Найдите площадь параллелограмма, если две стороны равны 12 и 11, а угол между ними 300.
- Найдите площадь параллелограмма, если две стороны равны 9 и 14, а угол между ними 300.
- Найдите площадь ромба, если его стороны равны 6, а один из углов 1500.
- Найдите площадь ромба, если его стороны равны 27, а один из углов 1500.
- Найдите площадь треугольника, если две стороны равны 16 и 12, а угол между ними 300.
- Основания трапеции 36 и 9, высота – 2. Найдите площадь трапеции.
- Найдите площадь прямоугольника, если его периметр равен 42 и одна из сторон на 3 см больше другой.
- Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3 : 20.
- Найдите периметр прямоугольника, если его площадь равна 16, а отношение соседних сторон равно 1 : 4.
- Найдите площадь ромба, если его высота равна 6, а острый угол 300.
- Найдите площадь ромба, если его диагонали равны 13 и 6.
- Основания трапеции равны 13 и 3, площадь равна 128.
 Найдите её высоту.
Найдите её высоту. - Основание трапеции равно 4, высота равна 11, а площадь равна 110. Найдите второе основание трапеции.
- Найдите площадь прямоугольной трапеции, основания которой равны 14 и 26, большая боковая сторона составляет с основанием угол 450.
- Площадь прямоугольного треугольника равна 224. Один из его катетов равен 28. Найдите другой катет.
- Площадь ромба равна 48. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.
- Стороны параллелограмма равны 5 и 10. Высота, опущенная на первую сторону, равна 3. Найдите высоту, опущенную на вторую сторону.
- Стороны параллелограмма равны 32 и 164. Высота, опущенная на меньшую сторону, равна 48. Найдите высоту, опущенную на большую сторону.
По теме: методические разработки, презентации и конспекты
Зачетные работы по геометрии в 7 классе по учебнику Атанасян Л.С.
Зачетные работы для аттестации учащихся по итогам 1,2,3,4 четверти. Данные работы можно использовать вместо зачета по иокончанию изучения главы в курсе геометрии. …
…
Зачетные работы по геометрии для 9 класса
Зачетные работы по темам: «Метод координат», «Соотношение между сторонами и углами треугольника», «Длина окружности и площадь круга»….
Методическая разработка для учителей математики по геометрии «Использование зачетных работ по геометрии для повторения изученного материала»
В этой разработке предлагаются вопрсы и задачи для учащихся по геометрии для повторения изученной главы. Цель: проверка знаний и умений в простой и доступной форме, повторение пройденного перед контро…
Зачетная работа по геометрии по теме «Простейшие задачи в координатах.Уравнение прямой и окружности.»
Зачетная работа представлена в двух вариантах и рассчитана на один урок. Она проверяет на практике знание учащимися простейших формул по теме «Простейшие задачи в координатах…
Зачетная работа по геометрии 11 кл. по теме «Простейшие задачи в координатах»
Дан один вариант,по аналогии можно составить 2 вариант. Работа проверяет знания по всем вопросам темы. Время работы — 45 минут…
Работа проверяет знания по всем вопросам темы. Время работы — 45 минут…
Зачетная работа по геометрии по тем «Прямоугольник, параллелограмм, ромб, квадрат»
Зачетная работа проводится по билетам. В билете три вопроса из устной части (на определение, на свойства, на построение чертежа к задаче) и три задачи, аналогичных представленным в практической …
Зачетная работа по геометрии в 9 классе » Подготовка к ОГЭ»
Цель работы — повторение материала по геометрии при подготовки к ОГЭ, выявление так называемых «слабых» мест и своевременная ликвидация пробелов….
Поделиться:
Расширенная справка по геометрии
Студенты, нуждающиеся в помощи по продвинутой геометрии, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по продвинутой геометрии. С обязательными концепциями изучения и соответствующими практическими вопросами прямо у вас под рукой, вы получите много помощи по продвинутой геометрии в кратчайшие сроки.
Получите помощь сегодня с нашей обширной коллекцией важной информации Advanced Geometry.
С обязательными концепциями изучения и соответствующими практическими вопросами прямо у вас под рукой, вы получите много помощи по продвинутой геометрии в кратчайшие сроки.
Получите помощь сегодня с нашей обширной коллекцией важной информации Advanced Geometry.
Вы когда-нибудь задавались вопросом: «Когда мне когда-нибудь понадобится это знать?» во время изучения курса геометрии? Как оказалось, изучение концепций геометрии на самом деле очень важно во многих профессиях и может применяться даже в самых простых проектах, связанных с образом жизни, таких как создание террасы или развешивание рамок для картин. Это правда, что для некоторых изучение и понимание концепций геометрии может быть очень сложным, и курсы Advanced Geometry выводят эту сложность на совершенно новый уровень. Будь то в старшей школе или в колледже, инструменты обучения Varsity Tutors Learn by Concept могут помочь упростить сложное содержание углубленной геометрии для вас, независимо от вашего возраста или уровня образования.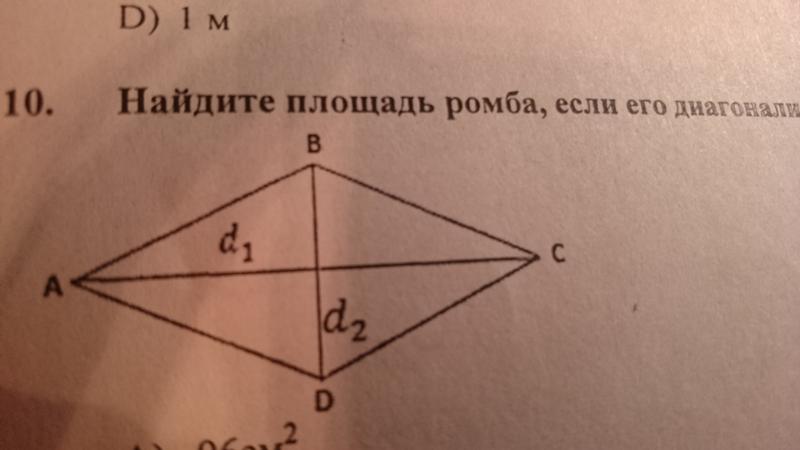
Инструмент «Изучение по понятиям» разбивает основные понятия расширенной геометрии на три основных предмета, включая координатную геометрию, плоскую геометрию и объемную геометрию. Вы можете начать бесплатное занятие по продвинутой геометрии прямо с основных предметов, чтобы оценить, какой контент требует вашего внимания больше всего. Например, если вы обнаружите, что вам нужна помощь с четырехугольниками в плоской геометрии, вы можете выбирать между подтемами воздушные змеи, ромбы и трапеции. После того, как вы выбрали одну из этих подтем, вы можете углубиться еще глубже.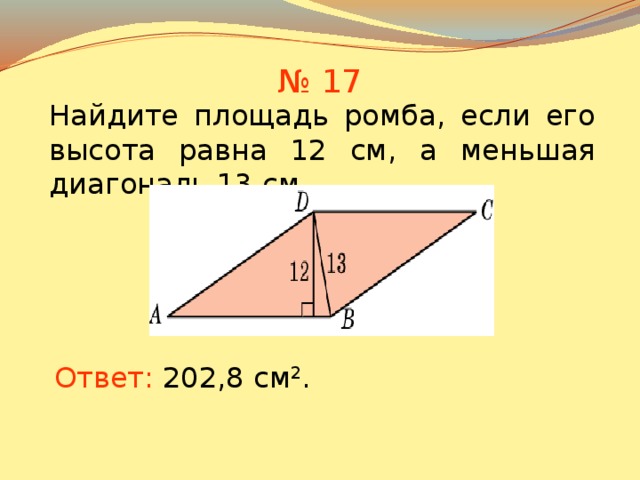
Интерактивная программа Advanced Geometry содержит примеры вопросов по каждому предмету или подтеме. Эти примеры вопросов представлены в формате множественного выбора. Представлено несколько ответов с несколькими вариантами ответов, за которыми следует правильный ответ и подробное объяснение того, почему этот ответ был лучшим выбором. Подробные пояснения показывают формулы и все действия, когда это необходимо, что делает средство обучения эффективным ресурсом для самостоятельного изучения.
Другие бесплатные средства обучения университетских преподавателей, которые помогают в изучении концепций продвинутой геометрии, включают карточки, которые очень эффективны при запоминании формул, упражнение «Вопрос дня», которое обеспечивает быстрый ежедневный обзор с новым вопросом каждый день и практические тесты. . Эти средства обучения дополняют друг друга, а также являются эффективными и действенными инструментами сами по себе. Средства обучения делают обучение увлекательным, даже если вы имеете дело со сложными предметами, такими как продвинутая геометрия!
Расширенная геометрия
Координатная геометрия
Графики
Как построить график функции
Как построить логарифм
Как построить график квадратичной функции
Как построить график двухшагового неравенства
Как построить график экспоненциальной функции
Как построить график упорядоченной пары
Как построить график комплексных чисел
Как построить график обратной вариации
Трансформация
Как найти преобразование для уравнения аналитической геометрии
Плоская геометрия
Четырехугольники
Воздушные змеи
Как найти площадь воздушного змея
Как найти длину диагонали воздушного змея
Ромбы
Как найти площадь ромба
Как найти длину диагонали ромба
Трапеции
Как найти площадь трапеции
Как найти длину диагонали трапеции
Твердотельная геометрия
Конусы
Как найти площадь поверхности конуса
Тетраэдры
Как найти диагональ тетраэдра
Как найти длину ребра
Как найти площадь поверхности тетраэдра
Формула, вывод и примеры решения
Ромб — это особый тип параллелограмма, который имеет огромное значение.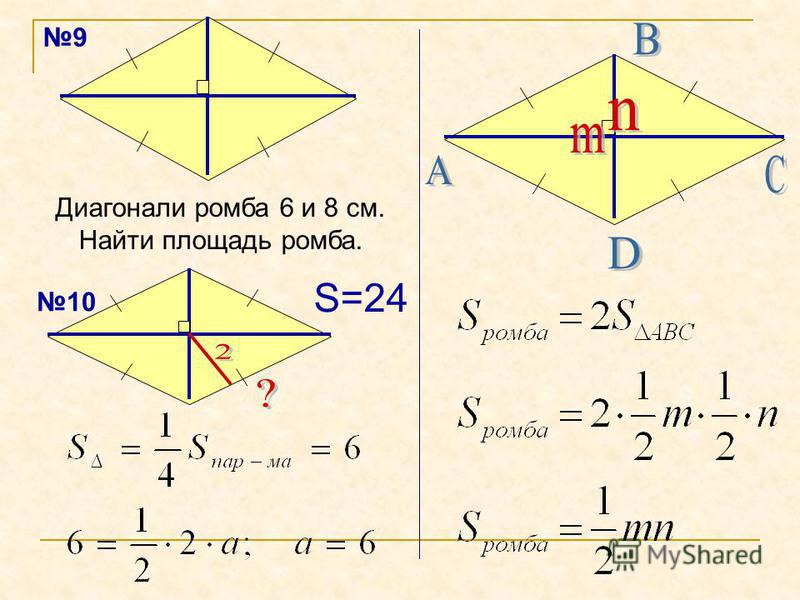 В ромбе все четыре стороны равны и противолежащие пары прямых конгруэнтны, также в ромбе противоположные углы равны. Ромб часто путают с квадратом, но ромб сильно отличается от квадрата. Здесь объясняется, почему ромб не считается квадратом. Площадь ромба — это пространство, занимаемое границами ромба в двумерном пространстве. Площадь ромба можно рассчитать с помощью различных методов, некоторые из которых обсуждаются в этой статье.
В ромбе все четыре стороны равны и противолежащие пары прямых конгруэнтны, также в ромбе противоположные углы равны. Ромб часто путают с квадратом, но ромб сильно отличается от квадрата. Здесь объясняется, почему ромб не считается квадратом. Площадь ромба — это пространство, занимаемое границами ромба в двумерном пространстве. Площадь ромба можно рассчитать с помощью различных методов, некоторые из которых обсуждаются в этой статье.
Площадью ромба считается пространство, ограниченное ромбом в двумерной плоскости. Это зависит от размеров ромба. Она измеряется в квадратных единицах, таких как квадратные метры, квадратные сантиметры и т. д. Площадь ромба измеряется с помощью приведенных ниже формул
Площадь ромба Формула
Площадь ромба можно найти с помощью различных методов, некоторые из них перечислены в таблице ниже
| Формулы для поиска площади Rhombus | |
|---|---|
| IF BASE и HOISH | A = B × H |
, если диаг. | |
| , если диаг. If Base and Interior angle is given | A = b 2 × Sin(a) |
Where,
D = length of first diagonal
d = length of second diagonal
b = длина стороны ромба
h = высота ромба
a = мера внутреннего угла
Вывод формулы площади ромба
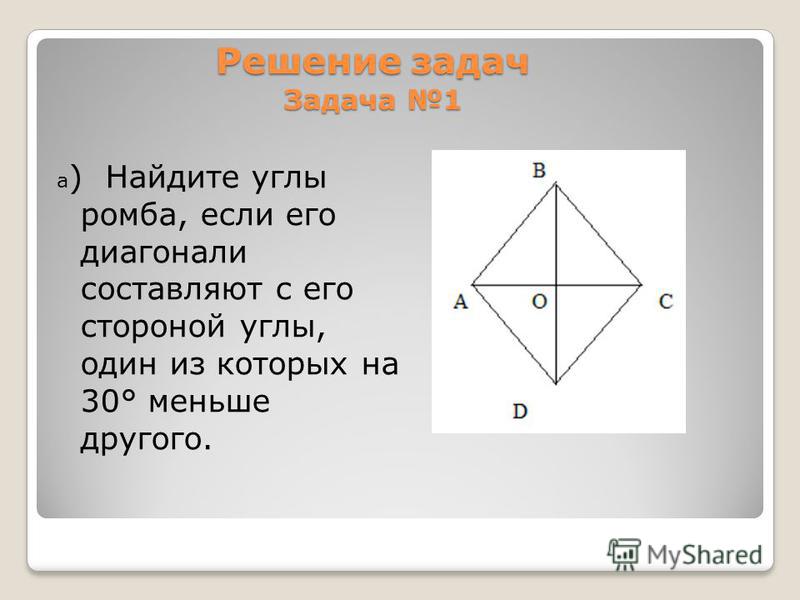
Рассмотрим ромб ABCD с точкой O как точкой пересечения двух диагоналей AC и BD.
Площадь ромба будет
Площадь = 4 × площадь △AOB
= 4 × (1/2) × АО × ОВ кв.ед. 1/2) d 1 × (1/2) d 2 кв.ед.
= 4 × (1/8) D 1 × D 2
= 1/2 D 1 × D 2
С. 2 д 1 × д 2 .
Как найти площадь ромба?
Площадь ромба – это полное пространство, покрытое или заключенное ромбом на двумерной плоскости. Площадь ромба можно рассчитать тремя различными способами: с использованием диагонали, с использованием основания и высоты и с помощью тригонометрии.
Площадь ромба можно рассчитать тремя различными способами: с использованием диагонали, с использованием основания и высоты и с помощью тригонометрии.
Different methods for finding area of Rhombus are given below
Area of Rhombus using DiagonalArea = (d 1 × d 2 )/2 sq. units
Where,
d 1 — длина диагонали 1
d 2 — длина диагонали 2
Пример 1. Найдите площадь ромба с диагоналями 16 м и 18 м.
Решение:
Область ромба с использованием базовой и высотой 55555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555.Диагональный 1, D 1 = 16 м
Диагональный 2, D 2 = 18 м
Площадь Rombus, A = (D 1 × D 2 ) / 2
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x 9021 × d 2 ) / 2
= × d 2 ) / 2
x .
(16 × 18) / 2
= 288 /2
= 144 м 2
Таким образом, площадь ромба составляет 144 м 2
Площадь ромба = b × h квадратных единиц
Где,
b — длина любой стороны ромба
h — высота ромба
Пример 2: Найдите площадь ромба с основанием 12 м и высотой 16 м.
Решение:
Площадь ромба с использованием тригонометрических соотношенийОснование, B = 12 м
Высота, H = 16 M
, A = B × H
= 12 × 16 M 2
A = 192 M 2
Таким образом, площадь ромба равна 192 м 2
Площадь ромба = b 2 × sin(A) кв.
единиц
A является мерой любого внутреннего угла
Пример 3. Найдите площадь ромба, если длина его стороны 12 м, а один из углов A равен 60°
Решение:
Сторона = s = 12 м
Угол A = 60 °
Площадь = S 2 × SIN (60 °)
A = 144 × √3/2
A = 72 адрес M 2
SED SED SET на примере 2
SETA Площадь ромба
Пример 1: Вычислите площадь ромба (используя основание и высоту), если его основание равно 5 см, а высота 3 см.
Решение:
Дано,
Основание (b) = 5 см
Высота ромба (h) = 3 см
Теперь’
Площадь ромба (A) = B × H
= 5 × 3
= 15 см 2
Пример 2: Рассчитайте площадь ромба (с использованием диагонала), имея диагонали, равные 4CM и 3CM.
Решение:
Дано,
Длина диагонали 1 (d1) = 4 см
Длина диагонали 2 (d2) = 3 см д1 × д2
= 4 x3/2 = 6 см 2
Решение:
Сторона ромба (b) = 8 см
угол (a) = 30 градусов )
= (8) × sin(30)
= 64 × 1/2 = 32 см 2
Решение:
, дано
Область = 25 см 2
Высота ромба (H) = 10 см
,
Область ромба (a) = B
.25 = b × 10
= 2,5 см
Часто задаваемые вопросы по области ромба
Вопрос 1: Что мы подразумеваем под ромбом?
Ответ:
Ромб — это четырехугольник, у которого противоположные стороны параллельны и равны.
Кроме того, противоположные углы ромба равны, а диагонали делят друг друга пополам под прямым углом.
Вопрос 2: Приведите формулу нахождения площади ромба.
Ответ:
901 3: как вычислить периметр ромба?Для нахождения площади ромба используется данная формула:
A = ½ × d 1 × d 2
где, d 1 и d 2 — диагонали ромба
Решение:
Периметр ромба можно рассчитать по формуле
P= 4b единиц
, где b — сторона ромба.
Вопрос 4. Как найти площадь ромба, зная сторону и высоту? 9
A = основание × высота кв. ед. квадрата?
Ответ:
Нет, площадь ромба не равна площади квадрата. Площадь квадрата равна квадрату его стороны, а площадь ромба равна половине произведения диагонали 1 и диагонали 2.

 Найдите её высоту.
Найдите её высоту.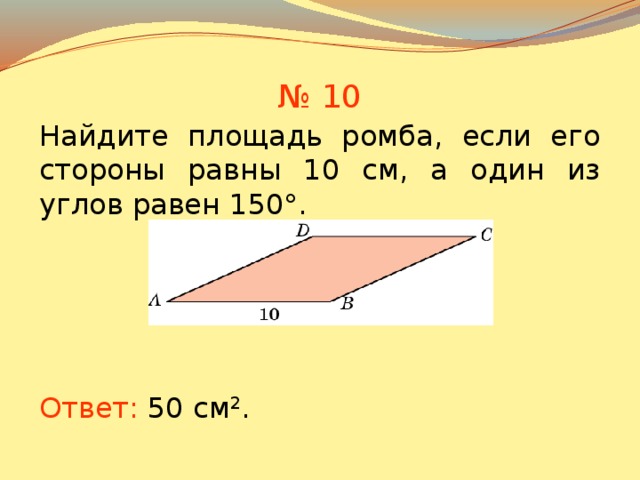 (16 × 18) / 2
(16 × 18) / 2 единиц
единиц
Leave A Comment