Пользуясь рисунком 14 а докажите что проекция вектора перемещения при: Пользуясь рисунком 14, а, докажите, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры ОАСВ.

Привет. помогите доказать. Вопрос 1 § 7 Физика 9 класс Перышкин – Рамблер/класс

Привет. помогите доказать. Вопрос 1 § 7 Физика 9 класс Перышкин – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Пользуясь рисунком 14, а, докажите, что проекция вектора перемещения при равноускоренном движении численно равна площади фигуры ОАСВ.

ответы

Проведем прямую из точки А и параллельную оси t, таким образом фигура ABCD будет состоять из двух фигур: прямоугольника О А К В ,

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных

     Среди предложений    21-29:  
      (21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Расстояние от точки до прямой. Что это такое? На плоскости и в пространстве

Поможем понять и полюбить математику

Начать учиться

Если вам понадобится узнать расстояние от дома до пиццерии, то вы без труда справитесь с задачей, ведь расстояние между точками — это длина отрезка, который соединяет эти точки. А что если нужно вычислить расстояние от дома до проспекта или улицы? В такой ситуации поможет знание темы «Расстояние от точки до прямой на плоскости».

Что называется расстоянием от точки до прямой?

Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на прямую. Перпендикуляр — это кратчайшее расстояние от точки до прямой.

Доказать это очень просто. Из точки M на прямую f мы опустим перпендикуляр MN и произвольную прямую MP, которая также называется наклонной. А по свойству мы помним, что наклонная всегда больше перпендикуляра, что и требовалось доказать.

Расстояние между точкой M и прямой f на плоскости обозначают так:

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Расстояние между параллельными прямыми

А если нужно вычислить расстояние между двумя параллельными улицами — какое математическое понятие поможет в этом случае? Конечно, вы уже догадались, что это расстояние между параллельными прямыми.

Расстоянием между параллельными прямыми называется расстояние от какой-либо прямой до другой прямой на плоскости.

Убедимся в верности этого утверждения — рассмотрим параллельные прямые m и n. На прямой m выберем две точки E и F, опустим из них перпендикуляры на прямую n, точки пересечения перпендикуляров с прямой n обозначим буквами G и H, а также соединим E и H отрезком.

Рассмотрим треугольники GEH и EFH: сторона EH — общая, (как накрест лежащие углы). Следовательно, по гипотенузе и острому углу. А из свойства равных треугольников мы знаем, что будут равны и соответствующие элементы, например, EG = FH.

Делаем вывод, что расстоянием между параллельными прямыми на плоскости является длина их общего перпендикуляра, причем выбор перпендикуляра может быть произвольным.

Расстояние между двумя прямыми m и n обозначается так: .

Решение задач

Применим полученные знания, решив несколько задач.

Задача 1

На клетчатой бумаге с размером клетки отмечены точки K, M и N. Чему равно расстояние от точки K до прямой MN?

Как вы помните, чтобы найти расстояние от точки до прямой, нужно из точки на прямую опустить перпендикуляр и вычислить его длину.

Ответ: 4 см.

Задача 2

Найдите расстояние от точки Q до прямой PR, пользуясь данными с чертежа.

Из чертежа видно, что отрезок QR перпендикулярен прямой PR, а значит QR — расстояние от точки Q до прямой PR. В прямоугольном треугольнике PQR отрезок QR лежит против угла в , а значит, равен половине гипотенузы, то есть 14 см.

Ответ: 14 см.

Задача 3

В равностороннем треугольнике PQR проведена биссектриса QS, а ST — расстояние от точки

S до прямой QR, равное 12 см. Чему равно расстояние от точки Q до прямой PR?

1. Поскольку — равносторонний, то , а так как по условию QS — биссектриса, то .

2. Рассмотрим , так как ST — расстояние от точки S до прямой QR, значит, — прямоугольный. А ST — катет, лежащий против угла в , следовательно, QS = 2ST = 24 см.

3. Так как — равносторонний, то QS не только биссектриса, но и высота , значит, .

Ответ: 24 см.

А если прямая на плоскости находится так далеко, что провести до нее перпендикуляр физически не получается — что делать в этом случае? Поможет формула расстояния от точки до прямой в координатах.

Пусть формула задана прямой f: ax + by + c = 0 и есть точка M с координатами , тогда формула расстояния от точки до прямой на плоскости выглядит следующим образом:

.

Задача 4

Найдите расстояние от точки M (36; 6) до прямой f: 6x + 2y − 12 = 0.

Нам не придется даже изображать прямую и точку, а тем более подбирать масштаб, чтобы поместился перпендикуляр, — достаточно воспользоваться формулой:

Конечно, без координат тоже можно вычислить, но вариант выше — самый рациональный и удобный.

На курсах по математике в онлайн-школе Skysmart мы всегда показываем разные способы решений, которые сохранят вам время на контрольной или экзамене. Выберите подходящий по уровню и цели обучения курс и начните заниматься в удовольствие!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Кристина Тоскина

К предыдущей статье

Сколько стоят занятия с репетитором

К следующей статье

Как подготовиться к ОГЭ по математике в 2023 году

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

12.3 Скалярный продукт

Вот вопрос, ответ на который оказывается очень полезным: Даны два вектора, чему равен угол между ними?

Может быть не сразу понятно, что вопрос имеет смысл, но это не трудно превратить в вопрос, который делает.

Так как векторы имеют нет позиции, мы, как обычно, вольны размещать векторы где угодно нравиться. Если два вектора расположены «хвост к хвосту», теперь разумное толкование вопроса: мы ищем меру наименьший угол между двумя векторами в плоскости, в которой они лежат. Рисунок 12.3.1 иллюстрирует ситуацию. 92)\кр &=2a_1b_1+2a_2b_2+2a_3b_3\cr |{\bf A}||{\bf B}|\cos\theta&=a_1b_1+a_2b_2+a_3b_3\cr \cos\theta&=(a_1b_1+a_2b_2+a_3b_3)/(|{\bf A}||{\bf B}|)\cr }$$ Итак, немного простой арифметики с координатами $\bf A$ и $\bf B$ позволяет вычислить косинус угла между ними. Если необходимо, мы можем использовать арккосинус, чтобы получить $\theta$, но во многих задач $\cos\theta$ оказывается всем, что нам действительно нужно.

В числителе дроби, которая дает нам $\cos\theta$, получается много, поэтому мы даем ему имя и более компактную запись: мы называем это скалярное произведение и запишите его как $${\bf A}\cdot{\bf B} = a_1b_1+a_2b_2+a_3b_3.$$ Это тот же самый символ, который мы используем для обычного умножения, но здесь никогда не должно быть никакой путаницы; вы можете сказать из контекста, были ли мы являются «перемножением» векторов или чисел. (Мы также можем использовать точку для скалярное умножение: $a\cdot{\bf V}=a{\bf V}$; опять же ясно что имеется в виду из контекста.)

Пример 12.3.1. Найдите угол между векторами ${\bf A}=\langle 1,2,1\rangle$ и ${\bf B}=\langle 3,1,-5\rangle$. Мы знаем это $\cos\theta={\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)= (1\cdot3 + 2\cdot1 + 1\cdot(-5))/(|{\bf A}||{\bf B}|)=0$, поэтому $\theta=\pi/2$, то есть векторы перпендикулярны. $\квадрат$

Пример 12.3.2. Найдите угол между векторами ${\bf A}=\langle 3,3,0\rangle$ и ${\bf B}=\langle 1,0,0\rangle$. Мы вычисляем $$\выравнивание{ \cos\theta &= (3\cdot1 + 3\cdot0 + 0\cdot0)/(\sqrt{9+9+0}\sqrt{1+0+0})\cr &= 3/\sqrt{18} = 1/\sqrt2\cr}$$ поэтому $\тета=\пи/4$. $\квадрат$

Пример 12.3.3. Некоторые частные случаи заслуживают рассмотрения: нахождение углов между ${\bf A}$ и ${\bf A}$; ${\bf A}$ и ${\bf -A}$; $ {\ бф А} $ и ${\bf 0}=\langle 0,0,0\rangle$.

$\ds ​​\cos\theta= {\bf A}\cdot{\bf A}/(|{\bf A}||{\bf A}|)=(a_1^2+a_2^2+a_3^2 )/ (\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{a_1^2+a_2^2+a_3^2})=1$, поэтому угол между ${\bf A}$ и собой равен нулю, что, конечно, правильно. 92})$, который не определен. С другой стороны, обратите внимание, что, поскольку ${\bf A}\cdot{\bf 0}=0$, выглядит сначала как будто $\cos\theta$ будет равно нулю, что, как мы видели, означает что векторы перпендикулярны; только тогда, когда мы замечаем, что знаменатель также равен нулю, если мы столкнемся с проблемами. Один из способов «исправить» это означает принятие соглашения о том, что нулевой вектор ${\bf 0}$ равен перпендикулярно всем векторам; то в общем случае можно сказать, что если ${\bf A}\cdot{\bf B}=0$, $\bf A$ и $\bf B$ перпендикулярны. $\квадрат$

Обобщая примеры, отметим следующие полезные факты:

1. Если $\bf A$ параллелен или антипараллелен $\bf B$, то ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=\pm1$, и наоборот, если ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=1$, $\bf A$ и $\bf B$ параллельны, а если ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=-1$, $\bf A$ и $\bf B$ антипараллельны. (Векторы параллельно если они указывают в одном направлении, антипараллельный если они направлены в разные стороны. )

2. Если $\bf A$ перпендикулярно $\bf B$, то ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=0$, и наоборот, если ${\bf A}\cdot{\bf B}/(|{\bf A}||{\bf B}|)=0$, тогда $\bf A$ и $\bf B$ перпендикулярны.

Имея два вектора, часто бывает полезно найти проекция одного вектора на другой, потому что это оказывается важным смысл во многих обстоятельствах. Точнее, учитывая ${\bf A}$ и ${\bf B}$ ищем вектор, параллельный $\bf B$, но с длиной определяется $\bf A$ естественным образом, как показано на рисунок 12.3.2. $\bf V$ выбран так, чтобы треугольник, образованный $\bf A$, $\bf V$ и ${\bf A}-{\bf V}$ является прямоугольным треугольником.

Рисунок 12.3.2. $\bf V$ — проекция $\bf A$ на $\bf B$.

Используя небольшую тригонометрию, мы видим, что $$ |{\bf V}|=|{\bf A}|\cos\theta= |{\bf A}|{{\bf A}\cdot{\bf B}\over|{\bf A}||{\bf B}|}= {{\bf A}\cdot{\bf B}\over|{\bf B}|}; $$ это иногда называют скалярная проекция $\bf A$ на $\bf B$ . Чтобы получить $\bfV$ умножаем эту длину на вектор длины один, параллельный $\bf В$: $$ {\bf V} = {{\bf A}\cdot{\bf B}\over|{\bf B}|}{{\bf B}\over|{\bf B}|}= {{\bf A}\cdot{\bf B}\over|{\bf B}|^2}{\bf B}.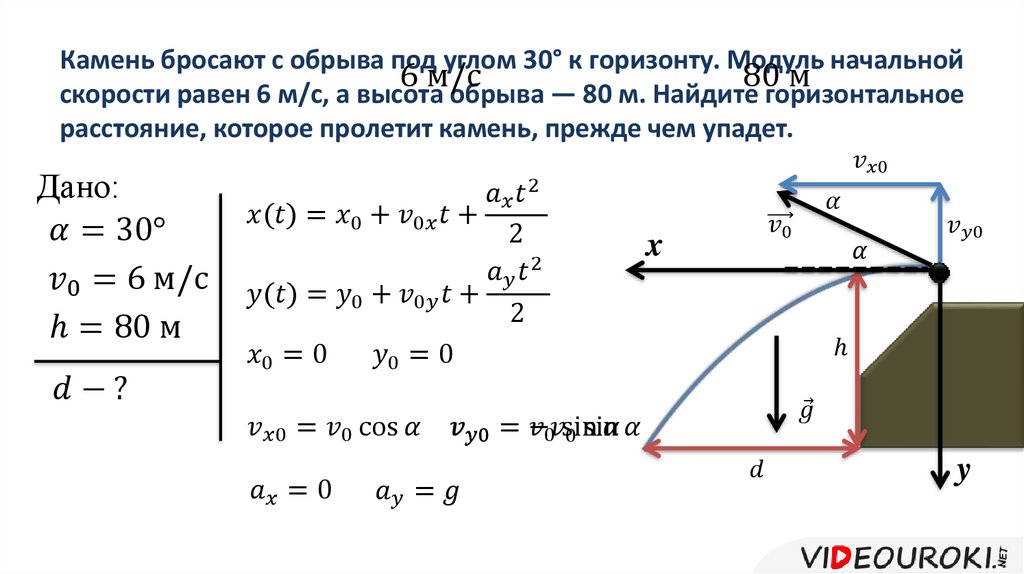 $$ Убедитесь, что вы понимаете, почему ${\bf B}/|{\bf B}|$ является вектором длина один (также называется 92}{\bf В}$$ антипараллелен $\bf B$, а его длина равна $$\left|{{\bf A}\cdot{\bf B}\over|{\bf B}|}\right|.$$ Таким образом, скалярная проекция $\bf A$ на $\bf B$ может быть положительным или отрицательным. Если он отрицательный, это означает, что вектор проекции антипараллелен к $\bf B$ и что длина вектора проекции равна абсолютное значение скалярной проекции. Конечно, вы также можете вычислить длину вектора проекции, как обычно, применяя формула расстояния до вектора.

Рисунок 12.3.3. $\bf V$ — проекция $\bf A$ на $\bf B$.

Обратите внимание, что фраза «проекция на $\bf B$» немного вводит в заблуждение. если понимать буквально; все, что дает $\bf B$, — это направление; в длина $\bf B$ не влияет на конечный вектор. В рис. 12.3.4, например, $\bf B$ короче, чем вектор проекции, но это вполне приемлемо.

Рисунок 12.3.4. $\bf V$ — проекция $\bf A$ на $\bf B$. 2$

2. ${\bf u}\cdot{\bf v} = {\bf v}\cdot{\bf u}$

3. ${\bf u}\cdot({\bf v}+{\bf w}) = {\bf u}\cdot{\bf v}+{\bf u}\cdot{\bf w}$

4. $(a{\bf u})\cdot{\bf v}=a({\bf u}\cdot{\bf v}) = {\ bf и} \ cdot (а {\ bf v}) $

$\qed$

Вы можете использовать Sage для вычисления скалярных произведений и связанных величин, таких как скалярная и векторная проекции.

Пример 12.3.1 Найдите $\langle 1,1,1\rangle\cdot\langle 2,-3,4\rangle$. (отвечать)

Пример 12.3.2 Найдите $\langle 1,2,0\rangle\cdot\langle 0,0,57\rangle$. (отвечать)

Пример 12.3.3 Найдите $\langle 3,2,1\rangle\cdot\langle 0,1,0\rangle$. (отвечать)

Пример 12.3.4 Найдите $\langle -1,-2,5\rangle\cdot\langle 1,0,-1 \rangle$. (отвечать)

Пример 12.3.5 Найдите $\langle 3,4,6\rangle\cdot\langle 2,3,4\rangle$. (отвечать)

Пример 12.3.6 Найдите косинус угла между $\langle 1,2,3\rangle$ и $\langle 1,1,1\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)

Пример 12.3.7 Найдите косинус угла между $\langle -1, -2, -3\rangle$ и $\langle 5,0,2\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)

Пример 12.3.8 Найдите косинус угла между $\langle 47,100,0\rangle$ и $\langle 0,0,5\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)

Пример 12.3.9 Найдите косинус угла между $\langle 1,0,1\rangle$ и $\langle 0,1,1\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)

Пример 12.3.10 Найдите косинус угла между $\langle 2,0,0\rangle$ и $\langle -1,1,-1\rangle$; используйте калькулятор, если необходимо, чтобы найти угол. (отвечать)

Пример 12.3.11 Найдите угол между диагональю куба и одной из сторон края, прилегающие к диагонали. (отвечать)

Пример 12.3.12 Найдите скалярную и векторную проекции $\langle 1,2,3\rangle$ на $\langle 1,2,0\rangle$. (отвечать)

Пример 12. 3.13 9\circ$ от горизонтали. Результирующая сила тянуть вагон горизонтально вдоль земля должна быть 10 фунтов. Какова величина необходимого заставить ${\bf F}$? (отвечать)

Пример 12.3.19 Используйте скалярное произведение, чтобы найти ненулевой вектор ${\bf w}$ перпендикулярно обоим ${\bf u}=\langle 1,2,-3\rangle$ и ${\bf v}=\langle 2,0,1\rangle$. (отвечать)

Пример 12.3.20 Пусть ${\bf x}=\langle 1,1,0 \rangle$ и ${\bf y}=\langle 2,4,2 \rangle$. Найдите единичный вектор, который перпендикулярен обоим $\bf x$ и $\bf y$. (отвечать) 92$. Чем этот результат лучше известный как?

Пример 12.3.25 Докажите, что диагонали ромба пересекаются под прямым углом.

Пример 12.3.26 Предположим, что ${\bf z}=|{\bf x}| {\bf у} + |{\bf у}| {\ бф х} $ где $\bf x$, $\bf y$ и $\bf z$ — ненулевые векторы. Доказывать что $\bf z$ делит пополам угол между $\bf x$ и $\bf y$.

Пример 12.3.27 Докажите теорему 12.3.5.

Глава 4.

Основы кинематики твердых тел со связями Йи Чжан
с
Сьюзан Фингер
Стефанни Беренс

Содержание

4.1 Степени свободы твердого тела

4.1.1 Степени свободы твердого тела на плоскости

Определены степени свободы (DOF) твердого тела как количество независимых движений, которые он имеет. Рисунок 4-1 изображено твердое тело на плоскости. Определить степень свободы этого тела мы должны рассмотреть, сколькими различными способами можно перемещать планку. В двумерная плоскость, такая как этот экран компьютера, есть 3 степени свободы. Бар может быть переведено по оси x , переведено вдоль оси и , а повернулся на вокруг своего центра масс.

Рисунок 4-1 Степени свободы твердого тела на плоскости

4.1.2 Степени свободы твердого тела в пространстве

Незакрепленное твердое тело в космосе имеет шесть степеней свободы: три поступательных движения вдоль x , y и z осей и три вращательных движения вокруг х , и и оси и соответственно.

Рисунок 4-2 Степени свободы твердого тела в пространстве

4.2 Кинематические ограничения

Два или более твердых тела в космосе вместе называются твердыми телами . система кузова . Мы можем воспрепятствовать движению этих независимых жестких тела с кинематическими связями . Кинематическая ограничения — это ограничения между твердыми телами, которые приводят к уменьшение степеней свободы системы твердых тел.

Термин «кинематическая пара» на самом деле относится к кинематические связи между твердыми телами. Кинематические пары делятся на младшие пары и высшие пары, в зависимости от того, как тела соприкасаются.

4.2.1 Нижние пары в планарных механизмах

В планарных механизмах есть два типа нижних пар: вращательные пары и призматические пары.

Твердое тело на плоскости совершает только три независимых движения — два поступательный и один вращательный — поэтому введение либо вращательной пары или призматическая пара между двумя твердыми телами удаляет две степени свобода.

Рисунок 4-3 Плоская вращающаяся пара (R-пара)

Рисунок 4-4 Плоская призматическая пара (P-пара)

4.2.2 Нижние пары в пространственных механизмах

Есть шесть видов нижних пар в категории пространственных механизмов. Типы: сферическая пара, плоская пара, цилиндрическая пара, вращающаяся пара, призматическая пара и винтовая пара.

Рисунок 4-5 Сферическая пара (S-пара)

Сферическая пара удерживает два сферических центра вместе. Два твердые тела, связанные этой связью, смогут повернуть относительно осей x , y и z , но не будет относительного перевода по любому из этих оси. Следовательно, сферическая пара лишает три степени свободы в пространственный механизм. степеней свободы = 3 .

Рисунок 4-6 Плоская пара (E-пара)

Пара плоскостей удерживает вместе поверхности двух твердых тел. Чтобы визуализировать это, представьте книгу, лежащую на столе, где она может двигаться. в любом направлении, кроме как от стола. Два твердых тела, соединенных такая пара будет иметь два независимых поступательных движения в плоскость и вращательное движение вокруг оси, перпендикулярной к самолету. Следовательно, плоская пара удаляет три степени свобода пространственного механизма. В нашем примере книги не будет. в состоянии подняться со стола или повернуться в стол. ГРИП = 3.

Рисунок 4-7 Цилиндрическая пара (C-пара)

Цилиндрическая пара удерживает две оси двух твердых тел выровнены. Два твердых тела, являющиеся частью такой системы, будут имеют независимое поступательное движение вдоль оси и относительное вращательное движение вокруг оси. Следовательно, цилиндрическая пара удаляет четыре степени свободы от пространственного механизма. Степень свободы = 2.

Рисунок 4-8 Вращающаяся пара (R-пара)

Вращающаяся пара удерживает оси двух твердых тел. вместе. Два твердых тела, скрепленные вращательной парой, имеют независимое вращательное движение вокруг общей оси. Следовательно, вращающаяся пара убирает пять степеней свободы в пространственном механизм. Степень свободы = 1.

Рисунок 4-9 Призматическая пара (P-пара)

Призматическая пара удерживает две оси двух твердых тел на одной линии и не допускать относительного вращения. Два твердых тела, ограниченные этим видом связи сможет иметь независимое поступательное движение вдоль оси. Следовательно, призматическая пара удаляет пять степеней свобода пространственного механизма. ГРИП = 1.

Рисунок 4-10 Винтовая пара (H-пара)

Пара винтов удерживает две оси двух твердых тел на одной линии и допускает относительное винтовое движение. Два твердых тела, ограниченные винтовая пара движение, составляющее поступательное движение вдоль оси и соответствующее вращательное движение вокруг оси. Следовательно, винтовая пара убирает пять степеней свободы в пространстве. механизм.

4.3 Закрепленные твердые тела

Твердые тела и кинематические связи являются основными компонентами механизмы. Ограниченная система твердых тел может быть кинематической цепью, механизмом, конструкцией или ничем из этого. Влияние кинематических связей на движение твердых тел имеет два внутренних аспекта: геометрический и физический. аспекты. Другими словами, мы можем анализировать движение ограниченного твердые тела из их геометрических взаимосвязей или с помощью второго закона Ньютона.

Механизм – это система твердых тел со связями, в которой один из тела является каркасом. Степени свободы важны при рассмотрении системы жесткого тела с ограничениями это механизм. Это менее важно, когда система представляет собой структуры или когда она не имеет определенного движения.

Вычисление степеней свободы системы твердых тел происходит прямо вперед. Любое неограниченное твердое тело имеет шесть степеней свободы. пространство и три степени свободы на плоскости. Добавление кинематики связи между твердыми телами соответственно уменьшат Степени свободы системы твердых тел. Мы обсудим больше на эта тема для планарных механизмов в следующем разделе.

4.4 Степени свободы планарных механизмов

4.4.1 Уравнение Грюблера

Определение степеней свободы механизма — количество независимых относительных движений между твердыми телами. Например, на рис. 4-11 показаны несколько случаев твердое тело, ограниченное разного рода парами.

Рисунок 4-11 Твердые тела, ограниченные различными типами плоских пар

На рис. 4-11а твердое тело ограничено вращательной парой, которая допускает только вращательное движение. движение вокруг оси. Имеет одну степень свободы, поворачивается точка А. Две потерянные степени свободы — это поступательные движения вдоль 9Оси 0201 x и и . Единственный способ, которым твердое тело может перемещение — это вращение вокруг фиксированной точки A.

На рис. 4-11b твердое тело ограничено призматической парой, которая позволяет только поступательное движение. В двух измерениях он имеет одну степень свобода, перемещаясь по оси x . В этом примере тело утратило способность вращаться вокруг какой-либо оси, и оно не может двигаться вдоль оси y .

На рис. 4-11c твердое тело ограничено высшей парой. Имеет две степени свобода: перемещение по криволинейной поверхности и поворот вокруг мгновенная точка контакта.

В общем случае твердое тело на плоскости имеет три степени свободы. Кинематические пары — это ограничения на твердые тела, которые уменьшают степени свободы механизма. На рис. 4-11 показаны три вида пар в планарных механизмах. Эти пары уменьшают количество степеней свободы. Если мы создадим нижнюю пару (рис. 4-11а,б), количество степеней свободы уменьшается до 2. Аналогично, если мы создадим высшую пару (рис. 4-11в), количество степеней свободы уменьшено до 1.

Рисунок 4-12 Кинематические пары в планарных механизмах

Следовательно, мы можем написать следующее уравнение:

(4-1)

Где

F = общее количество степеней свободы в механизме

n = количество ссылок (включая рама)

l = количество нижних пар (одна степень свободы)

ч = количество старших пар (две степени свободы)

Это уравнение также известно как уравнение Грюблера 9. 0012 .

Пример 1

Посмотрите на фрамугу над дверью на рис. 4-13а. Открытие и закрывающий механизм показан на рис. 4-13b. Давайте посчитаем его степень свободы.

Рисунок 4-13 Механизм транца

n = 4 (звено 1,3,3 и кадр 4), l = 4 (в точках A, B, C, D), h = 0

(4-2)

Примечание: D и E функционируют как одна призматическая пара, поэтому они только считаются одной нижней парой.

Пример 2

Рассчитайте степени свободы механизмов, показанных на рис. 4-14b. Рисунок 4-14a представляет собой приложение механизма.

Рисунок 4-14 Самосвал

n = 4, l = 4 (в точках A, B, C, D), h = 0

(4-3)

Пример 3

Рассчитайте степени свободы механизмов, показанных на рис. 4-15.

Рисунок 4-15 Расчет степеней свободы

Для механизма на рис. 4-15а

п = 6, л = 7, ч = 0

(4-4)

Для механизма на рис. 4-15b

п = 4, л = 3, ч = 2

(4-5)

Примечание: Вращение ролика не влияет на взаимосвязь входного и выходного движения механизма. Следовательно, свобода валика учитываться не будет; Это называется пассивный или резервный степень свободы. Представьте, что ролик приварен к звену 2 при подсчете градусов свободы механизма.

4.4.2 Критерий Куцбаха

Количество степеней свободы механизма также называется Мобильность устройства. мобильность количество входных параметров (обычно пара переменные), которые должны контролироваться независимо, чтобы устройство в определенную позицию. Критерий Куцбаха , которое аналогично уравнению Грюблера, вычисляет мобильность .

Для управления механизмом количество независимых входов движения должны равняться числу степеней свободы механизма. Например, транец на рис. 4-13а имеет одну степень свободы, поэтому ему нужен один независимый вход движения, чтобы открыть или закрыть окно. То есть вы просто толкаете или тянете стержень 3 для управления окном.

Чтобы увидеть еще один пример, механизм на рис. 4-15а также имеет 1 степень свободы. Если независимый вход применяется к звену 1 ( например, , двигатель установлен на шарнире A для привода звено 1), механизм будет иметь заданное движение.

4.5 Конечное преобразование

Конечное преобразование используется для описания движения точки на твердое тело и движение самого твердого тела.

4.5.1 Конечное плоское вращательное преобразование

Рисунок 4-16 Точка на плоском твердом теле, повернутом на угол

Предположим, что точка P на твердом теле совершает поворот описывающий круговой путь от P ₁ до P ₂ вокруг начала системы координат. Мы можем описать это движение оператором вращения Р ₁₂ :

(4-6)

где

(4-7)

4.

5.2 Конечный планарный поступательный Трансформация

Рисунок 4-17 Точка на плоском твердом теле, смещенная на расстояние

Предположим, что точка P на твердом теле проходит через перевод, описывающий прямой путь от P ₁ до P ₂ с изменением координат (x, y). Мы можем описать это движение с оператором перевода T ₁₂ :

(4-8)

где

(4-9)

4.5.3 Объединение конечных плоских перемещений

Рисунок 4-18 Конкатенация конечных плоских перемещений в пространстве

Предположим, что точка P на твердом теле совершает поворот описывающий круговой путь от P ₁ до P ₂ ‘ вокруг начала системы координат, затем перевод, описывающий прямой путь от P ₂ ‘ до Р ₂ . Мы можем представить эти два шага как

(4-10)

и

(4-11)

Мы можем объединить эти движения, чтобы получить

(4-12)

где D ₁₂ — оператор плоского общего смещения . :

(4-13)

4.5.4 Планарное преобразование твердого тела

Мы обсудили различные преобразования для описания перемещения точки твердого тела. Могут ли эти операторы быть применительно к перемещениям системы точек, такой как твердая тело?

Мы использовали однородную матрицу-столбец 3 x 1 для описания вектора представляющий одну точку. Выгодная особенность планара 3 х 3 поступательные, вращательные и общие матричные операторы смещения заключается в том, что их можно легко запрограммировать на компьютере для управления 3 x n матрица из n векторов-столбцов, представляющих n точек твердого тела. Поскольку расстояние каждой частицы твердого тела от любой другой точка твердого тела постоянна, векторы, определяющие положение каждой точки твердого тела должно претерпевать такое же преобразование, когда твердое тело тело движется и задана правильная ось, угол и/или перемещение представлять его движение. (Сандор и Эрдман 84). Например, общее плоское преобразование за три очка A, B, C на жестком кузове можно изобразить к

(4-14)

4.5.5 Преобразование пространственного вращения

Мы можем описать оператор пространственного вращения для вращательного преобразование точки относительно единичной оси u , проходящей через начало системы координат. Предположим, угол поворота точки примерно u есть , оператор вращения будет выражен как

(4-15)

где

u _x , u _y , u _z являются ортографическими проекция единичной оси u на x , y , и оси и соответственно.

с = грех

с =

v = 1 —

4.5.6 Пространственное поступательное преобразование

Предположим, что точка P на твердом теле проходит через перевод, описывающий прямой путь от P ₁ по P ₂ с заменой координат (x, y, z) мы можем описать это движение с оператором перевода T :

(4-16)

4.

5.7 Матрица пространственного перемещения и вращения для оси Через происхождение

Предположим, что точка P на твердом теле вращается под углом перемещение относительно единичной оси u , проходящей через начало координат сначала систему координат, а затем перевод D и по и . Этот состав этого вращательного преобразование, и это трансляционное преобразование является винтом движение. Соответствующий ему матричный оператор, винт оператор , является конкатенацией оператора перевода в уравнении 4-7 и оператора поворота в уравнении 4-9.

(4-17)

4.6 Матрица преобразования между твердыми телами

4.6.1 Матрица преобразования между двумя Arbitray Твердые тела

Для системы твердых тел можно установить локальную декартову система координат для каждого твердого тела. Матрицы преобразования используется для описания относительного движения между твердыми телами.

Например, два твердых тела в пространстве имеют локальные координаты системы x ₁ y ₁ z ₁ и х ₂ у ₂ z ₂ . Пусть точка P будет прикреплен к корпусу 2 в месте (x ₂ , y ₂ , я ₂ ) в локальной системе координат тела 2. Чтобы найти расположение P относительно локальной системы координат тела 1, мы знаем, что точка x ₂ y ₂ z ₂ можно получить из x ₁ y ₁ z ₁ с помощью комбинируя перемещение L _x1 по оси x и вращение z вокруг z ось. Мы можем вывести матрицу преобразования следующим образом:

(4-18)

Если твердое тело 1 закрепить в виде рамы, На этом теле может быть создана глобальная система координат. Следовательно приведенное выше преобразование можно использовать для отображения локальных координат указать в глобальных координатах.

4.6.2 Кинематические ограничения между двумя жесткими Кузова

Приведенная выше матрица преобразования является конкретным примером для двух несвязанные твердые тела. Матрица преобразования зависит от относительное положение двух твердых тел. Если соединить два жестких тела с кинематической связью, их степени свободы уменьшатся. Другими словами, их родственник движение будет задано в некоторой степени.

Предположим, мы свяжем два твердых тела с помощью вращающейся пары, как показано на рис. 4-19. Мы можем по-прежнему запишите матрицу преобразования в той же форме, что и уравнение 4-18.

Рисунок 4-19 Относительное положение точек на зависимых телах

Отличие в том, что L _x1 является константой теперь, потому что вращающаяся пара фиксирует начало системы координат x ₂ y ₂ z ₂ относительно системы координат х ₁ у ₁ у ₁ . Тем не менее, ротация г все еще является переменной. Таким образом, кинематические ограничения задают матрица преобразования в некоторой степени.

4.6.3 Обозначение Денавита-Хартенберга

Обозначение Денавита-Хартенберга (Denavit & Hartenberg 55) широко используется при преобразовании систем координат рычажных механизмов и механизмов роботов. Может быть используется для представления матрицы преобразования между ссылками, как показано на Рисунок 4-20.

Рисунок 4-20 Нотация Денавита-Хартенберга

На этом рисунке

• z _i-1 и z _i — оси двух вращательных пар;
• _и угол между осями x _i-1 и x _i ;
• d _i — расстояние между началом системы координат х _i-1 y _i-1 z _i-1 и подножие обыкновенного перпендикуляр;
• a _i — расстояние между двумя футами общего перпендикуляра;
• _и угол между осями z _i-1 и z _i ;

Матрица преобразования будет T _(i-1)i

(4-19)

Приведенную выше матрицу преобразования можно обозначить как T(a _i , _и , _и , д _и ) для удобства.

4.6.4 Применение матриц преобразования к связям

Рычажный механизм состоит из нескольких связанных твердых тел. Как механизм, рычажный механизм должен иметь раму. Матричный метод может быть используется для вывода кинематических уравнений рычажного механизма. Если все ссылки образуют замкнутый цикл, конкатенация всех матрицы преобразования будут единичной матрицей. Если механизм имеет н ссылки, мы будем иметь:

Т ₁₂ Т ₂₃ …Т _(n-1)n = I

(4-20)

Содержание

Полное оглавление

1 Введение в механизмы

2 Механизмы и простые машины

3 Подробнее о машинах и механизмах

4 Базовая кинематика жестких тел со связями

4.1 Степени свободы твердого тела

4.1.1 Степени свободы твердого тела на плоскости

4.1.2 Степени свободы твердого тела в пространстве

4.2 Кинематические ограничения

4.2.1 Нижние пары в планарных механизмах

4.2.2 Нижние пары в пространственных механизмах

4.