Из формулы (5) мы видим, что неизменная суммарная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=\pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
\[v_x=\pm {\omega }_0A\left(6\right).\]
В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $\frac{E}{2}$ находятся в противофазе друг с другом, частота их колебаний равна $2{\omega }_0$.
\[{E_k =\frac{E}{2}\left[1-{\cos 2({\omega }_0t+\varphi )\ }\right]\left(7\right).\ }\] \[E_p=\frac{E}{2}\left[1+{cos 2({\omega }_0t+\varphi )\ }\right]\left(8\right).\]
И так, выражения (7) и (8) показывают, что кинетическая и потенциальная энергии колебательной системы совершают гармонические колебания вокруг их общего значения $\frac{E}{2}$ с удвоенной частотой 2${\omega }_0$, тогда как полная энергия системы остается постоянной.
Ответ. $E=0,9Дж$
Читать дальше: понятие силы.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
1.3. Сохранение энергии при гармонических колебаниях
Умножим уравнение (1.18) гармонических колебаний на скорость изменения переменной x:
|
|
|
(1.28) |
Каждое из слагаемых можно представить как соответствующую производную:
так что уравнение (1.28) записывается в виде:
|
|
(1. |
Отсюда следует, что величина в скобках не зависит от времени, то есть сохраняется в процессе колебаний:
|
|
(1.30) |
Для выяснения физического смысла сохраняющейся величины применим эти соотношения к пружинному маятнику, когда
Видим, что уравнение (1.30) можно записать в виде суммы кинетической энергии груза и потенциальной энергии деформированной (сжатой или растянутой) пружины:
|
|
(1. |
Таким образом, найденный закон сохранения есть не что иное, как закон сохранения полной энергии системы.
Аналогично, для электромагнитного контура переменная
и
В этом случае соотношение (1.30) принимает вид:
|
|
(1.32) |
Первый член — это энергия магнитного поля в катушке, а второй — энергия электрического поля в конденсаторе. Снова мы получили, что сохраняется полная энергия системы.
Возвращаясь к общей форме (1.30) закона сохранения энергии и подставляя сюда общее решение (1.23), получаем законы изменения во времени кинетической
|
|
(1. |
Отсюда следует, что
-
кинетическая и потенциальная энергии — периодические функции времени с периодом, равным половине периода колебаний;
-
кинетическая и потенциальная энергии колеблются в противофазе: когда кинетическая энергия достигает максимума, значение потенциальной энергии минимально и наоборот;
-
в колебательной системе энергия периодически «перекачивается» из одной формы в другую, а полная энергия Е = К + П сохраняется;
-
полная энергия колебаний пропорциональна квадрату их амплитуды и квадрату частоты.
Видео 1.9 Сохранение энергии при почти гармонических колебаниях – маятник Галилея.
Сказанное проиллюстрировано на рис. 1.11, на котором показаны изменения кинетической и потенциальной энергий для пружинного маятника и электромагнитного контура.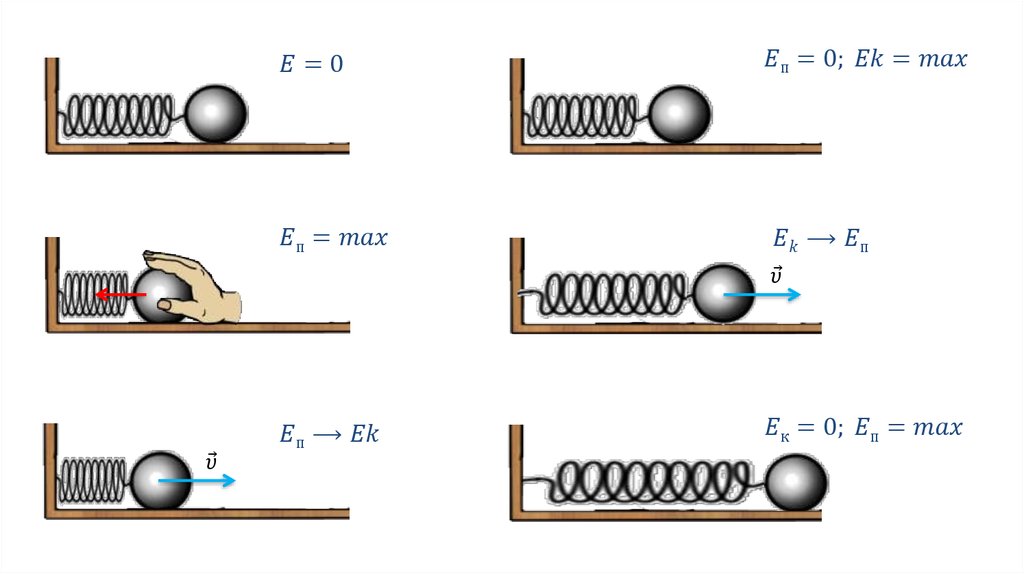
Рис. 1.11. Изменения во времени различных форм энергии в колебательной системе:
1 – пружинный маятник; 2 – электромагнитный колебательный контур
Видео 1.10 Cохранение энергии при механических колебаниях — маятник Максвелла
Видео 1.11 Cохранение энергии (и не только) при механических колебаниях — баллистический маятник
Видео-урок: Механическая энергия маятника
Стенограмма видео
В этом видео наша тема — механическая энергия маятника. Мы увидим, как энергии которые составляют механическую энергию, изменяющуюся с течением времени, когда маятник качается назад и вперед. Мы научимся их вычислять энергий, а также увидим, как интерпретировать графики энергии маятника через некоторое время.
Раз уж мы начали, давайте сначала
Вспомним немного о движении маятника. Мы знаем, что вообще маятник
состоит из груза, иногда называемого грузом, прикрепленного к концу фиксированного рычага.
длина, где эта рука может быть сплошным стержнем или отрезком шнура. Мы знаем, что если мы переместим
маятник отклонится от того, что мы могли бы назвать его положением равновесия, как только мы отпустим
маятник, он вернется в это положение, а затем пройдет мимо него, пока не исчезнет.
так же далеко от равновесия на этой стороне, как и здесь, и в этот момент
качается вниз через свое положение равновесия и так далее, и так далее. Если предположить, что нет
потери на трение в любом месте этого процесса, то груз будет продолжать двигаться назад
и далее до бесконечности.
Мы знаем, что вообще маятник
состоит из груза, иногда называемого грузом, прикрепленного к концу фиксированного рычага.
длина, где эта рука может быть сплошным стержнем или отрезком шнура. Мы знаем, что если мы переместим
маятник отклонится от того, что мы могли бы назвать его положением равновесия, как только мы отпустим
маятник, он вернется в это положение, а затем пройдет мимо него, пока не исчезнет.
так же далеко от равновесия на этой стороне, как и здесь, и в этот момент
качается вниз через свое положение равновесия и так далее, и так далее. Если предположить, что нет
потери на трение в любом месте этого процесса, то груз будет продолжать двигаться назад
и далее до бесконечности.
Если мы подумаем о скорости
маятник качается на этих разных моментальных снимках во времени, мы знаем, что в крайнем
положения слева и справа, в эти моменты скорость маятника
равен нулю. Но тогда, в любом случае, как
маятник возвращается в положение равновесия, к тому времени, когда он достигает этого
положение, его скорость является неким максимальным значением, самым высоким, которое он когда-либо получит. Сразу тогда, мы можем видеть, что
когда дело доходит до кинетической энергии этого маятника во времени, эта энергия
изменения. Когда маятник так высоко, как он
когда-либо получает, то эта энергия равна нулю. И когда это так низко, как никогда
достигает того, что мы назвали положением равновесия, эта энергия достигает максимума. Итак, это история о кинетике.
энергия маятника, которую мы можем вспомнить, равна половине его массы, умноженной на его
скорость в квадрате.
Но тогда, в любом случае, как
маятник возвращается в положение равновесия, к тому времени, когда он достигает этого
положение, его скорость является неким максимальным значением, самым высоким, которое он когда-либо получит. Сразу тогда, мы можем видеть, что
когда дело доходит до кинетической энергии этого маятника во времени, эта энергия
изменения. Когда маятник так высоко, как он
когда-либо получает, то эта энергия равна нулю. И когда это так низко, как никогда
достигает того, что мы назвали положением равновесия, эта энергия достигает максимума. Итак, это история о кинетике.
энергия маятника, которую мы можем вспомнить, равна половине его массы, умноженной на его
скорость в квадрате.
Но мы также можем рассмотреть
гравитационная потенциальная энергия маятника. Глядя на эту связь, мы
известно, что масса 𝑚 маятника фиксирована.

Мы сможем увидеть это яснее, если постройте график энергии по вертикальной оси и времени по горизонтальной. Допустим, наш маятник удерживается в этой позиции, а затем отпущенный в момент времени 𝑡 равен нулю. Итак, самые первые данные указывают на наш график покажет, что происходит в этот момент. Если мы подумаем о кинетике энергии маятника в этот момент, мы сказали, что скорость маятника равна нулю, а значит, его кинетическая энергия тоже должна быть равна нулю. На нашем графике мы можем начать создать кривую зависимости кинетической энергии от времени. И первая точка на этой кривой будет в истоке.
Точно так же мы можем построить
гравитационная потенциальная энергия маятника во времени. В отличие от кинетической энергии, при этом
В начальный момент гравитационная потенциальная энергия имеет максимальное значение. Если мы сделаем кривую зависимости GPE от времени
оранжевым, то можно сказать, что первая точка данных этой кривой находится здесь. Итак, мы видим, как эти два
энергии маятника исходят. Мы знаем, однако, что как только мы
отпустите боб, он начнет опускаться, пока не достигнет этого положения. В течение этого интервала две вещи занимают
место. Во-первых, скорость боба увеличивается
и быстрее, пока не достигнет некоторого максимального значения. Во-вторых, высота боба.
опускается до тех пор, пока не достигнет своего минимального значения, высоты, которую мы назвали нулем.
Итак, мы видим, как эти два
энергии маятника исходят. Мы знаем, однако, что как только мы
отпустите боб, он начнет опускаться, пока не достигнет этого положения. В течение этого интервала две вещи занимают
место. Во-первых, скорость боба увеличивается
и быстрее, пока не достигнет некоторого максимального значения. Во-вторых, высота боба.
опускается до тех пор, пока не достигнет своего минимального значения, высоты, которую мы назвали нулем.
Теперь предположим, что наш маятник
достигает этого положения равновесия на этой отметке на нашей временной оси. Потому что его высота в этот момент
во времени равно нулю, как мы его определили, мы можем сказать, что оно больше не имеет
гравитационно потенциальная энергия. Начиная с выпуска
Боб, GPE пошел вот так. А то, что сейчас ноль на
этот момент времени говорит нам кое-что о кинетической энергии маятника.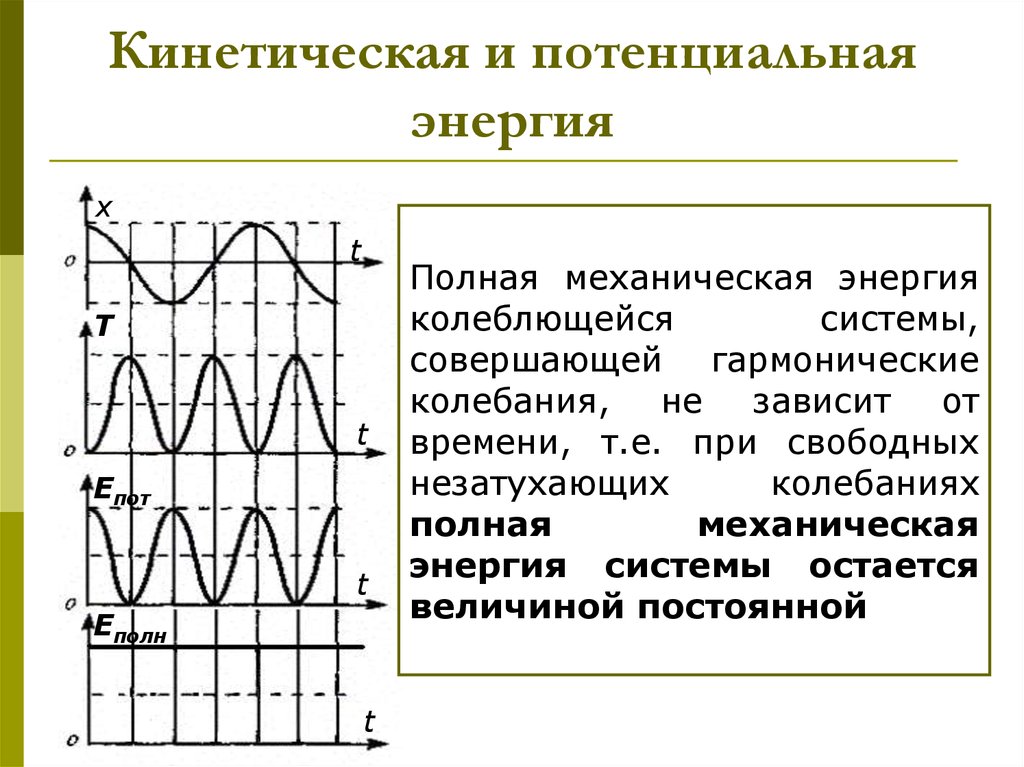 Это связано с тем, что энергия нашего
маятниковая система должна сохраняться во времени. То есть в любой момент, если мы добавим
вместе кинетическую энергию маятника и его гравитационную потенциальную энергию, что
сумма, которую называют механической энергией маятника, должна быть постоянной. То есть в любой момент времени, если
мы складываем вместе эти два значения, мы получаем тот же результат. Вот что это значит для энергии
системы, подлежащей консервации.
Это связано с тем, что энергия нашего
маятниковая система должна сохраняться во времени. То есть в любой момент, если мы добавим
вместе кинетическую энергию маятника и его гравитационную потенциальную энергию, что
сумма, которую называют механической энергией маятника, должна быть постоянной. То есть в любой момент времени, если
мы складываем вместе эти два значения, мы получаем тот же результат. Вот что это значит для энергии
системы, подлежащей консервации.
Возвращаясь к нашему графику, тогда, если
в этот момент времени потенциальная энергия гравитации равна нулю, то это должно
означают, что кинетическая энергия нашего маятника, которая сейчас имеет максимальное значение, равна
здесь. Таким образом, общая энергия нашего
система в данный момент времени такая же, как и в начале. То есть механическая энергия
наша система такая же. Теперь, как только наш маятник достигнет этого
положение, в котором его скорость максимальна, мы знаем, что он не остановится на этом, а
продолжайте подниматься, пока его высота не сравняется с исходной высотой. Можно сказать, что в тот миг
соответствует этой отметке на нашей временной оси. И как только Боб здесь, однажды
снова его скорость равна нулю, а высота возвращается к максимальному значению. А значит, его кинетическая энергия
возвращается к нулю, а его гравитационная потенциальная энергия возвращается к своему максимуму.
Теперь, как только наш маятник достигнет этого
положение, в котором его скорость максимальна, мы знаем, что он не остановится на этом, а
продолжайте подниматься, пока его высота не сравняется с исходной высотой. Можно сказать, что в тот миг
соответствует этой отметке на нашей временной оси. И как только Боб здесь, однажды
снова его скорость равна нулю, а высота возвращается к максимальному значению. А значит, его кинетическая энергия
возвращается к нулю, а его гравитационная потенциальная энергия возвращается к своему максимуму.
Пока маятник продолжает качаться
туда и обратно, этот цикл продолжается. И то, что мы видим, это то, что если мы
нужно было нанести на этот график механическую энергию маятника, то эта кривая
будет плоская линия, которая выглядит так. Он всегда равен сумме KE
и ГПО. А так как по закону сохранения энергии
эта сумма постоянна. Градиент механического
кривая энергии равна нулю. Учитывая этот график,
на самом деле это больше, чем говорит нам о движении маятника, помимо того, как его энергия
изменение с течением времени. Например, мы видели, что
рассматривая нашу кривую кинетической энергии, глядя на то, где эта кривая имеет минимум
а затем максимум, а затем минимум, мы можем вывести из этого соответствующее
положение маятника.
Градиент механического
кривая энергии равна нулю. Учитывая этот график,
на самом деле это больше, чем говорит нам о движении маятника, помимо того, как его энергия
изменение с течением времени. Например, мы видели, что
рассматривая нашу кривую кинетической энергии, глядя на то, где эта кривая имеет минимум
а затем максимум, а затем минимум, мы можем вывести из этого соответствующее
положение маятника.
Мы знаем, что при этих минимумах
значений кинетической энергии маятник находится на максимальной высоте, а затем на
максимальное значение кинетической энергии, оно возвращается к тому, что мы назвали его равновесием
позиция. Поэтому, когда мы двигались в наше время
ось от момента времени равна нулю до этого значения здесь наш маятник прошел
половина полного цикла. То есть он ушел от своего максимума.
высоты на одной стороне положения равновесия до максимальной высоты на
другой. Чтобы завершить один цикл, необходимо
тогда нужно сделать это в обратном порядке. И мы знаем, что если бы он завершился
этого цикла, он будет делать это за период времени, называемый периодом и представленный
столица 𝑇. Тогда на нашем графике мы видим
что этот интервал времени равен 𝑇, деленному на два, что составляет половину периода маятника.
период. И тогда, как мы считаем его
период, мы можем вспомнить, что это равно обратной частоте. Так, половина периода
колебания равны единице, умноженной на удвоенную частоту маятника.
Чтобы завершить один цикл, необходимо
тогда нужно сделать это в обратном порядке. И мы знаем, что если бы он завершился
этого цикла, он будет делать это за период времени, называемый периодом и представленный
столица 𝑇. Тогда на нашем графике мы видим
что этот интервал времени равен 𝑇, деленному на два, что составляет половину периода маятника.
период. И тогда, как мы считаем его
период, мы можем вспомнить, что это равно обратной частоте. Так, половина периода
колебания равны единице, умноженной на удвоенную частоту маятника.
И обратите внимание, что мы могли обнаружить
такие же отношения, глядя на GPE вместо KE. Для этой энергии, вместо того, чтобы искать
на интервале времени между минимальными значениями, мы смотрим на этот интервал между
максимальные значения. Синусоидальные изменения GPE и
Затем КЭ может дать нам информацию о периоде маятника и его частоте.
Теперь есть еще кое-что, что мы
можно увидеть гравитационную потенциальную энергию нашего маятника. Напомним, что в целом ГПО
тела в однородном гравитационном поле равна массе тела
умноженное на ускорение свободного падения, умноженное на высоту объекта над некоторым
стандартный уровень. На нашей диаграмме мы назвали это
максимальная высота ℎ ниже макс. И оказывается, мы можем
найдите это значение, используя другие параметры в этом сценарии. В частности, когда мы работаем с
маятник качается взад и вперед, нам часто говорят длину плеча маятника,
мы назовем это 𝑙. Кроме того, максимальный угловой
отклонение от равновесия может быть известно. Мы можем назвать этот угол 𝜃. Мы видим, что эта максимальная высота
достигнутое равно длине маятника за вычетом вот этого расстояния. Эта разница равна ℎ sub
Макс. И поэтому мы хотели бы решить для этого
длину, которую мы отметили.
Для этого. Рассмотрим этот прямоугольный треугольник, гипотенуза которой, как мы знаем, равна 𝑙. Зная, что наряду с углом 𝜃, говорит нам, что длина этого катета треугольника в 𝑙 умножена на потому что 𝜃. Итак, чтобы найти ℎ sub max, мы вычтем 𝑙 раз cos 𝜃 из общей длины нашего плеча маятника; это 𝑙. Возвращаясь к нашему уравнению для GPE, это означает, что мы можем заменить множитель ℎ на 𝑙 минус 𝑙, умноженный на cos 𝜃. И тогда, если мы вычтем один кратное 𝑙 из этого выражения, мы видим, что для маятника длины 𝑙 с максимальный угол отклонения 𝜃, гравитационная потенциальная энергия равна 𝑚 раз 𝑔 умножить на 𝑙 умножить на единицу минус кос 𝜃.
Зная все это о маятнике энергии, давайте теперь попрактикуемся с этими идеями на примере.
Какая из линий на графике правильно показывает, как гравитационная потенциальная энергия маятника по сравнению с что в его положении равновесия меняется со временем?
На этом графике мы видим гравитационные
потенциальная энергия в джоулях в зависимости от времени в секундах.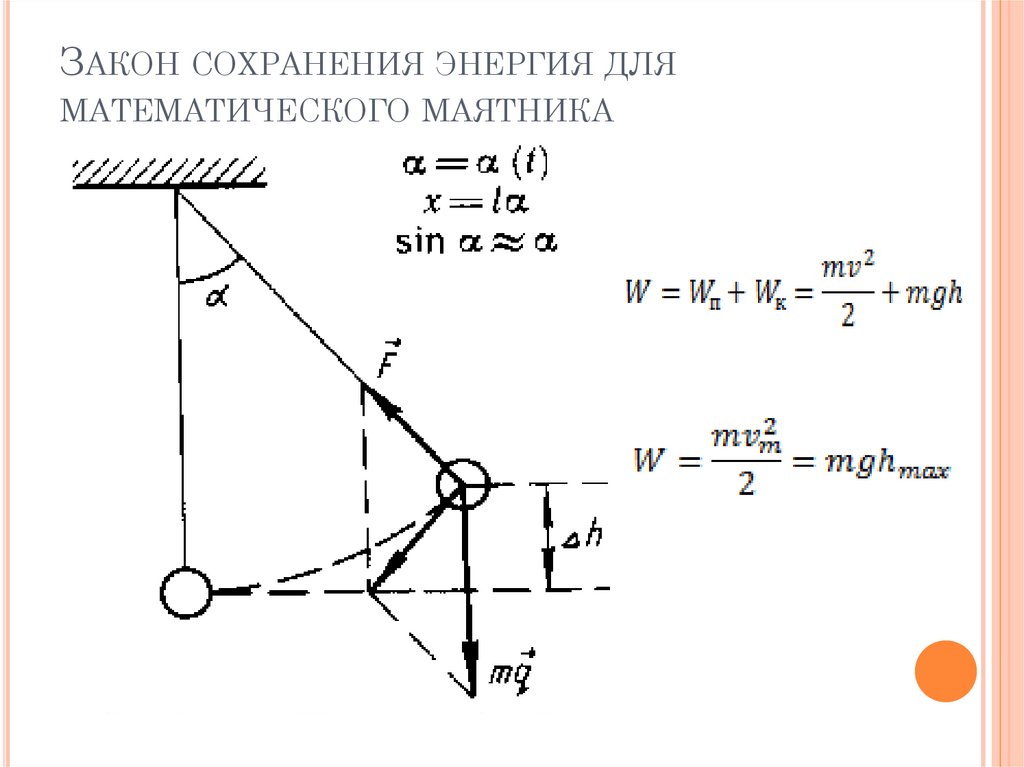 Существует ряд различных
линии на графике. Тут есть черный. Это ровная линия. Потом красный, желтый
один, синий, а здесь фиолетовый. Мы хотим знать, какая линия
правильно показывает, как гравитационная потенциальная энергия маятника по сравнению с
что в положении равновесия изменяется со временем. Так сказать, что это наш маятник,
и мы видим это здесь на трех разных моментальных снимках во времени. Центральное положение маятника
это то, что мы называем его положением равновесия. Вот где маятник
естественно движется, если его не беспокоить. Но тогда, если мы переместим его в
сторону, скажем здесь, а потом отпустим маятник, мы знаем, что он начнет это
возвратно-поступательное колебательное движение. А если представить отсутствие трения в
нашей системы, то это движение продолжается бесконечно.
Существует ряд различных
линии на графике. Тут есть черный. Это ровная линия. Потом красный, желтый
один, синий, а здесь фиолетовый. Мы хотим знать, какая линия
правильно показывает, как гравитационная потенциальная энергия маятника по сравнению с
что в положении равновесия изменяется со временем. Так сказать, что это наш маятник,
и мы видим это здесь на трех разных моментальных снимках во времени. Центральное положение маятника
это то, что мы называем его положением равновесия. Вот где маятник
естественно движется, если его не беспокоить. Но тогда, если мы переместим его в
сторону, скажем здесь, а потом отпустим маятник, мы знаем, что он начнет это
возвратно-поступательное колебательное движение. А если представить отсутствие трения в
нашей системы, то это движение продолжается бесконечно.
Если представить, что вся масса
маятника находится на его конце, называемом качающимся маятником, и ни один из них не находится в плече
который поддерживает боб, когда он качается вперед и назад, то в этом случае мы можем
понять гравитационную потенциальную энергию этого маятника, отслеживая
движение боба по мере его движения.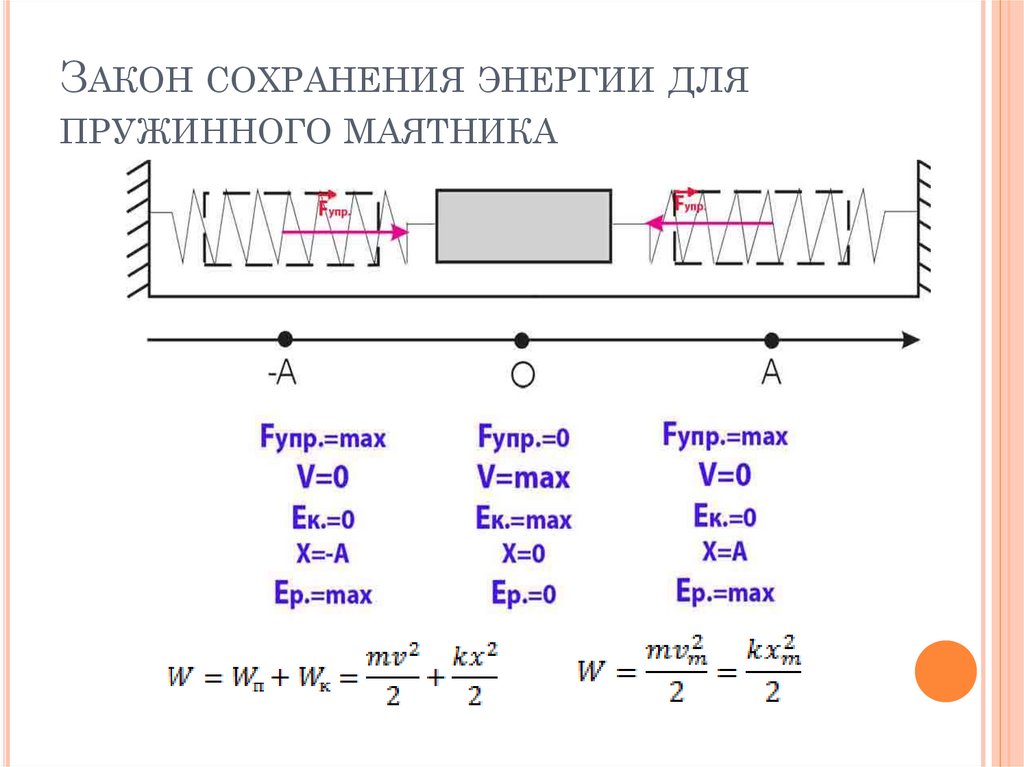 В общем случае GPE объекта в
однородное гравитационное поле равно массе этого объекта, умноженной на
ускорение силы тяжести, умноженное на высоту объекта над некоторой точкой отсчета. Для нашего маятника эта ссылка
уровень, мы можем сказать, проходит прямо через середину боба, когда он находится на своем
положение равновесия. Мы скажем, что эта высота
соответствует высоте нуля. Это определение важно
потому что это означает, что в моменты времени, когда наш маятник находится в равновесии
положение, его гравитационная потенциальная энергия равна нулю.
В общем случае GPE объекта в
однородное гравитационное поле равно массе этого объекта, умноженной на
ускорение силы тяжести, умноженное на высоту объекта над некоторой точкой отсчета. Для нашего маятника эта ссылка
уровень, мы можем сказать, проходит прямо через середину боба, когда он находится на своем
положение равновесия. Мы скажем, что эта высота
соответствует высоте нуля. Это определение важно
потому что это означает, что в моменты времени, когда наш маятник находится в равновесии
положение, его гравитационная потенциальная энергия равна нулю.
И поэтому какая бы строка на нашем
график правильно показывает, что GPE должен достигать горизонтальной оси. Мы видим, что соблюдение этого
Условие исключает две из возможных линий, черную и фиолетовую.
один. Ни одна из этих линий не пересекает
Горизонтальная ось.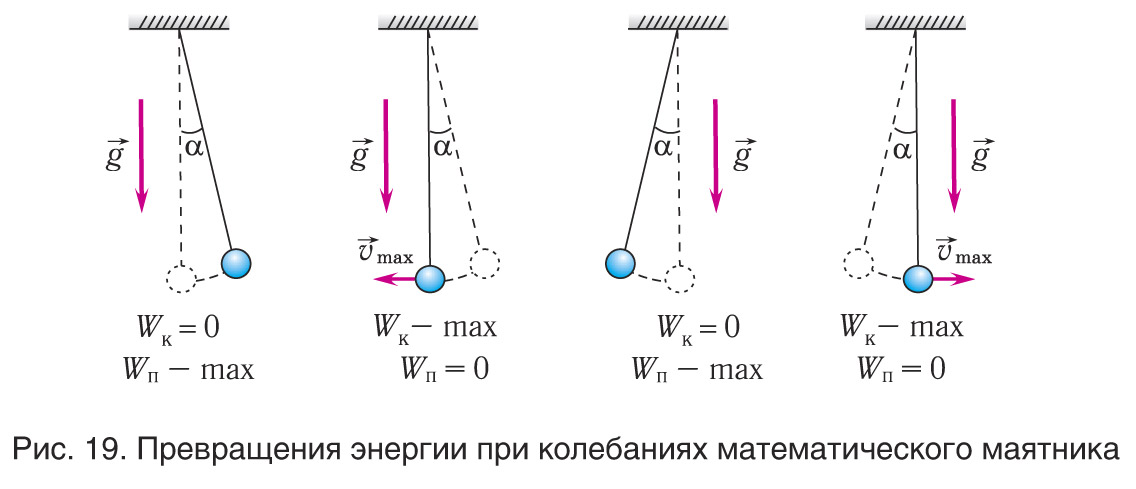 И мы видим, что они терпят неудачу для
Еще одна причина. Обратите внимание, что они показывают нам константу
гравитационная потенциальная энергия с течением времени, тогда как на самом деле мы знаем, что высота
наш маятник, двигаясь вверх и вниз, меняет гравитационный потенциал
энергии этой системы. По ряду причин мы не будем
выберите черную линию или фиолетовую линию в качестве нашего ответа.
И мы видим, что они терпят неудачу для
Еще одна причина. Обратите внимание, что они показывают нам константу
гравитационная потенциальная энергия с течением времени, тогда как на самом деле мы знаем, что высота
наш маятник, двигаясь вверх и вниз, меняет гравитационный потенциал
энергии этой системы. По ряду причин мы не будем
выберите черную линию или фиолетовую линию в качестве нашего ответа.
Учитывая еще раз наш боб в
это положение равновесия, мы сказали, что в этой точке гравитационный потенциал
энергия маятника равна нулю. Вопрос в том, как это
количество GPE относится к GPE системы в другое время? Другими словами, это минимум
значение, максимальное значение или где-то посередине? Наш набросок показывает нам, что в каждый
момент, кроме времени, когда груз находится в этом положении равновесия, высота
значение маятника, как мы его определили, будет положительным. И, следовательно, поскольку 𝑔 и 𝑚
как положительные, во все эти моменты гравитационная потенциальная энергия
маятник тоже будет положительным. Это показывает нам, что нулевые точки
мы ожидаем, что на нашей линии должны быть минимумы, то есть нижние точки гравитационного
потенциальная энергия этого маятника.
И, следовательно, поскольку 𝑔 и 𝑚
как положительные, во все эти моменты гравитационная потенциальная энергия
маятник тоже будет положительным. Это показывает нам, что нулевые точки
мы ожидаем, что на нашей линии должны быть минимумы, то есть нижние точки гравитационного
потенциальная энергия этого маятника.
Теперь, если мы пойдем и посмотрим на синий
линии, мы видим, что это имеет максимальные значения в нуле, в то время как желтая линия показывает нам
нулевые значения между максимальным и средним значениями линии. Это только красная линия, которая делает
имеют нулевые значения, если эти значения соответствуют нижним точкам на кривой,
удовлетворяет этому условию. И так, это наш ответ. Это красная линия на этом графике
который правильно показывает, как гравитационная потенциальная энергия маятника сравнивается
к тому, что в его положении равновесия меняется со временем.
Подведем итог тому, что у нас есть узнали о механической энергии маятника. На этом уроке мы увидели, что когда качающийся маятник находится в положении равновесия, то его гравитационный потенциал энергия равна нулю, а его кинетическая энергия достигает максимального значения. И тогда, когда качается маятник находится на максимальной высоте, его кинетическая энергия равна нулю, а его УГД достигает максимальное значение.
Далее мы видели, что механический
энергия маятника, то есть сумма его кинетического и гравитационного потенциала
энергия постоянна, и когда мы смотрим на график зависимости энергии маятника от времени,
из этого графика мы можем понять период маятника 𝑇 и его частоту
𝑓. И, наконец, мы увидели, что для
маятник массой 𝑚 и длиной плеча 𝑙 сдвинулся на угол 𝜃 от положения равновесия
положение, гравитационная потенциальная энергия этого маятника равна 𝑚 раз
𝑔 умножить на 𝑙, умноженное на единицу минус косинус 𝜃. Это краткое изложение механического
энергия маятника.
Это краткое изложение механического
энергия маятника.
Сайт физического кабинета
Движение маятника — классический пример сохранения механической энергии. Маятник состоит из массы (известной как груз ), прикрепленной веревкой к точке поворота. Когда маятник движется, он описывает дугу окружности, периодически двигаясь вперед и назад. Если пренебречь сопротивлением воздуха (которое действительно было бы небольшим для боба аэродинамической формы), на маятник действуют только две силы. Одна сила — гравитация. Сила тяжести действует вниз и действует на маятник. Однако гравитация является внутренней силой (или консервативной силой) и, таким образом, не служит для изменения общего количества механической энергии груза. Другая сила, действующая на груз, называется силой натяжения. Натяжение — это внешняя сила, и если бы оно действительно действовало на маятниковый груз, то оно действительно способствовало бы изменению полной механической энергии груза. Однако сила натяжения не совершает работы, так как она всегда действует в направлении, перпендикулярном движению груза. Во всех точках траектории маятника угол между силой натяжения и направлением его движения равен 90 градусов. Таким образом, сила натяжения не совершает работы над грузом.
Однако сила натяжения не совершает работы, так как она всегда действует в направлении, перпендикулярном движению груза. Во всех точках траектории маятника угол между силой натяжения и направлением его движения равен 90 градусов. Таким образом, сила натяжения не совершает работы над грузом.
Поскольку внешние силы не совершают работу, полная механическая энергия маятника сохраняется. Сохранение механической энергии продемонстрировано на анимации ниже. Обратите внимание на столбцы KE и PE гистограммы; их сумма является постоянной величиной.
Обратите внимание, что падающее движение боба сопровождается увеличением скорости. Когда боб теряет высоту и PE, он набирает скорость и KE; однако сумма двух форм механической энергии сохраняется.
Чтобы проверить свое понимание принципа сохранения, используйте высоты и скорости, указанные в таблице ниже, чтобы заполнить оставшиеся ячейки в различных точках на траектории груза массой 0,200 кг. Используйте выпадающие меню, чтобы проверить свою работу.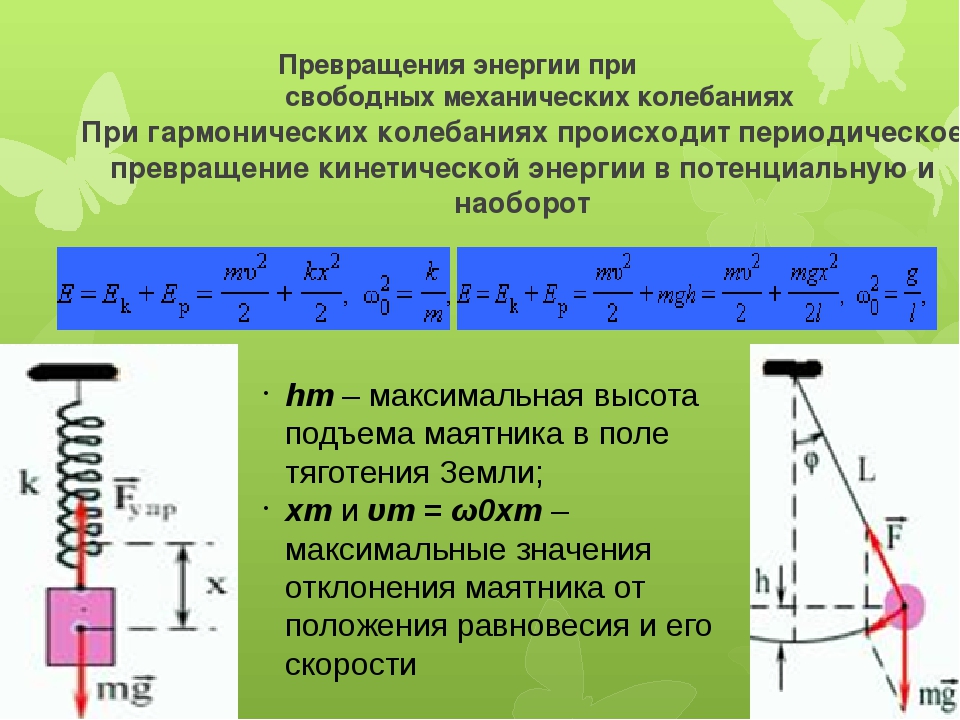

 29)
29) 31)
31) 33)
33)
Leave A Comment