По графику скорости найдите скорость через 10 с после начала движения: а) скорость через 10 с после начала движения;б) ускорение;в) перемещение тела за 10 с...

«Расчет пути и времени движения». 7-й класс

Цели урока:

Обучающая – формирование знаний и умений учащихся по расчету пути и времени движения, научить решить графические задачи.

Воспитывающая – овладение умением аккуратно оформлять физические задачи, аккуратно строить графики.

Развивающая – развитие обобщенных знаний и целостного представления о физическом движении.

Оборудование: персональные компьютеры,

Ход урока:

I. Организационный момент.(Приветствие учителя, доклад дежурного)

II. Повторение пройденного материала. Откройте Microsoft Office Word опорные конспекты № 1,2,3,4.

III. Актуализация имеющихся знаний . Откройте тетради, напишите число, классная работа, проверочная работа. Проверка знаний с помощью компьютера.

Откройте “вопросы к уроку ” на рабочем столе персонального компьютера, прочитайте вопросы и ответы напишите в тетрадях. Щелкните слово “Вопросы” и проверьте ответы , оцените и поставьте оценки в тетрадь.

Вопросы:

Изменение с течением времени положения тела относительно других тел. (Механическое движение)
Линия по которой движется тело. (Траектория)
Длина траектории, по которой движется тело в течение некоторого промежутка времени. (Пройденный путь)
Какими физическим величинами характеризуется механическое движение.
(Путь-s, скорость- ?, время-t)
Если тело за равные промежутки времени проходит одинаковые пути, то движение называется. (Равномерным движением)
Изменяется ли скорость при равномерном движении. (Скорость остается постоянной)

IV. Изучение нового материала.

Учитель: Назовите физические величины, которые характеризуют механическое движение?

Ученики:

Путь-s

Скорость- ?

Время-t

Учитель: От чего зависит путь ?

Ученики: От скорости движения и времени движения.

Учитель: А что можно сказать о скорости при равномерном движении?

Ученики: Скорость при равномерном движении остается величиной постоянной.

Учитель: От чего зависит путь при постоянной скорости?

Ученики: При постоянной скорости путь зависит от времени.

Учитель: Запишите эту формулу зависимости. ?=st и расположите их в треугольнике.

Чтобы найти s нужно ? умножить на t (Запомни: они стоят рядом) !

Чтоб найти ? нужно s делить на t,

(Запомни : s находится на верху, а t-внизу, подобно дроби)!

Чтоб найти t нужно s делить на ?,

(Запомни : s находится на верху, а ? -внизу, подобно дроби)!

Запишите эти формулы:

s=vt, v=s/t, t=s/v.
По формуле s=vt видно- чем больше время, тем больше пройденный путь и наоборот, чем меньше время тем меньше пройденный путь.
Сделаем вывод: пройденный путь при равномерном прямолинейном движении прямо пропорционален времени.
Давайте рассмотрим задачу:
Открываем таблицу №16 “Скорости движения в живой природе”
Лисица : v=10 м/с ;
Муха комнатная: v= 5 м/с;

Дельфин: v=20 м/с;
Напишите уравнение движения этих животных:
1.s=10t 2. s= 5t 3. s= 20t

t, c 0 2
s, м 0 6

V. Закрепление нового материала:
Учитель: Мы с вами убедились, что график наглядно характеризует движение. По данному графику скорость какого тела больше? (Обоснуйте свой ответ)

Ученики: Скорость второго тела больше, так как пройденный путь за одинаковое время тоже больше.

2. Учитель: График какой физической величины вы видите? Что можете сказать об этой величины?

v,м/с

Ученики: Мы видим график скорости тела. Скорость постоянная и равна 5 м/с.

3. Учитель: График какой физической величины вы видите? Что можете сказать об этой величине?

Ученики: Мы видим график изменения скорости тела, тело сначала движется , увеличивая скорость от 0 до 10 м/с, потом движется с постоянной скоростью 10 м/с и продолжает движение , уменьшая скорость от 10 м/с до 0.

4. Решение задач под руководством учителя. (График дан на доске). Найдите скорость движения тела и пройденный путь телом за 2 часа.
а). Записываем данные задачи по графику, (то есть читаем график движения)
б) находим пройденный путь телом за 2 часа.
в) Постройте график равномерного движения тела, если оно имеет скорость 3 м/с.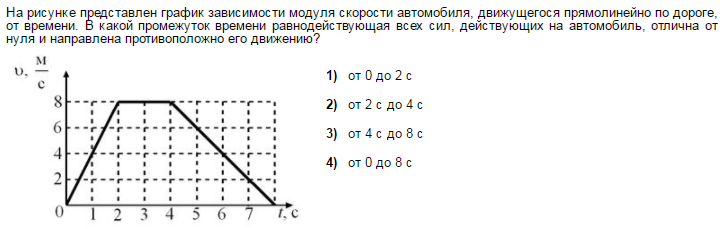

t, c 0 2
s, м 0 6
(в дальнейшем данные будем задавать устно)

V. Самостоятельная работа. (по уровням сложности)
За решение задач первого уровня – оценка “3”.
За решение задач первого, второго уровней– оценка “5”.

1-й уровень.
По графику определите скорость движения тела и пройденный путь за 5 с.

2.Постройте график равномерного движения тела, если оно имеет скорость 2 м/с.

По графику скорости равномерного движения определите скорость 10 движения тела через 3 с. после начала движения и найдите путь , пройденный телом за 2 с.

2. Постройте график равномерного движения тела, если оно имеет скорость 3 м/с.

V. Подведение итогов урока и комментирование оценок.
VI. Домашнее задание.
§16, упр.9(4,5-для всех), упр.9(4,5,6-для сильных)
Равноускоренное прямолинейное движение, ускорение, определение пути и перемещения по графику скорости
Равноускоренное движение
Ускорение
Уравнение скорости и график скорости при равноускоренном прямолинейном движении

Определение пути и перемещения по графику скорости
Задачи
п.1. Равноускоренное движение
Если тело начинает двигаться из состояния покоя, оно набирает скорость не мгновенно, а в течение некоторого времени. Аналогично происходит при торможении: тело останавливается не сразу, а теряя скорость постепенно.
Движение, во время которого скорость тела за любые равные промежутки времени увеличивается на одну и ту же величину, называют равноускоренным.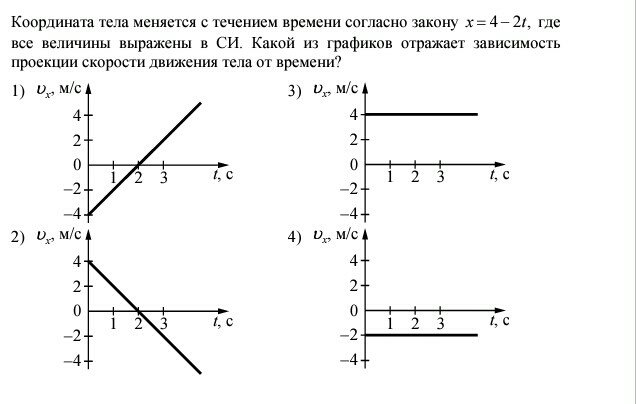
Примеры равноускоренного движения:
скатывание велосипеда с горки, скатывание санок с горки;

старт и торможение автомобиля, автобуса, трамвая, поезда;
падение на землю камня, ракеты, метеорита.
Это интересно
Время разгона от 0 до 100 км/ч – одна из основных характеристик современных автомобилей.
Марка автомобиля Время разгона, с
Nissan GTR Nismo 2,9
BMW M5 F90 2,8
Porsche 918 Spyder 2,6
п.2. Ускорение
Ускорение – это векторная величина, которая равна отношению изменения скорости тела к интервалу времени, за которое это изменение произошло: $$ \overrightarrow{a}=\frac{\overrightarrow{v}-\overrightarrow{v_0}} {t} $$ где $\overrightarrow{v_0}$ — начальная скорость тела, $\overrightarrow{v}$ — скорость тела в момент времени $t$.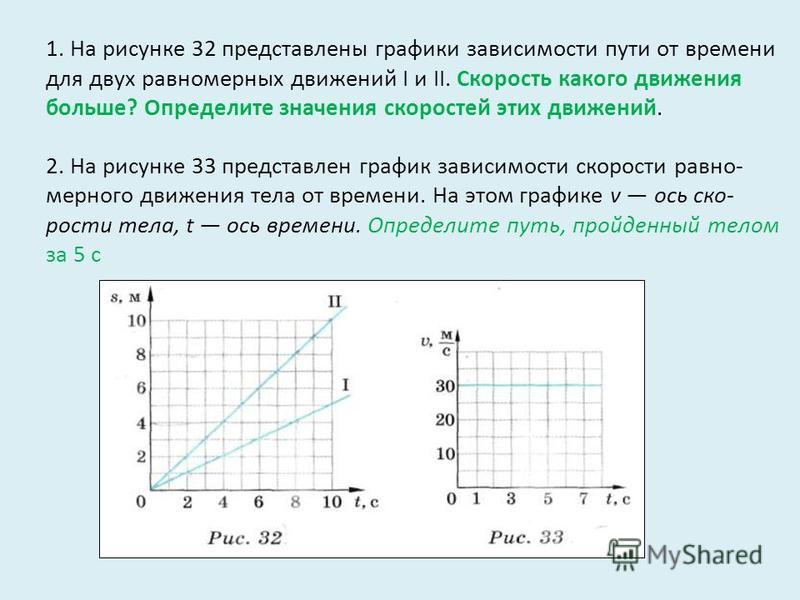
В системе СИ (см. §2 данного справочника) скорость измеряется в метрах в секунду, а время – в секундах. Поэтому:
Единицей ускорения в системе СИ является метр на секунду в квадрате (1 м/с²) – ускорение равноускоренного прямолинейного движения, при котором тело за 1 с увеличивает скорость на 1 м/с.
При описании прямолинейного движения мы переходим от векторов к проекциям на ось ОХ (см. §8 данного справочника).
При равноускоренном прямолинейном движении проекция ускорения равна: $$ a_x=\frac{v_x-v_{0x}}{t} $$ где $v_{0x}$ — проекция начальной скорости, $v_x$ — проекция скорости в момент времени $t$.
п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении
Для проекции скорости на ось ОХ в произвольный момент времени можем записать: $$ v_x(t)=v_{0x}+a_x t $$ Сравним полученное уравнение с уравнением прямой $y(x)=kx+b $ (см. §38 справочника по алгебре для 7 класса).
В уравнении скорости роль углового коэффициента $k$ играет проекция ускорения $a_x$, а роль свободного члена $b$ – начальная скорость $v_{0x}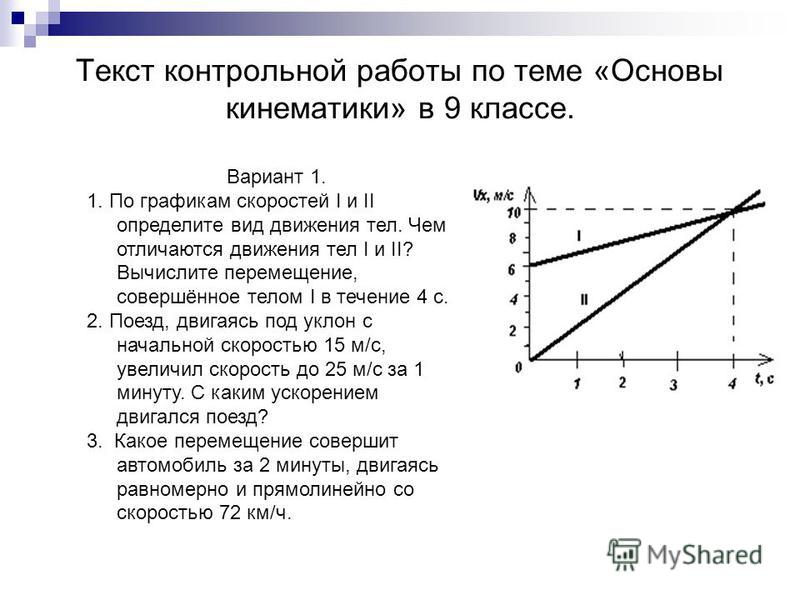$. 2},\ \ v_x(t)=20-5t $$ Проекция ускорения при торможении отрицательна. Скорость станет равна 0 через 4 с после начала торможения, автомобиль остановится.
Опишем полностью движение на всех участках: $$ v_x(t)= \begin{cases} 4t,\ \ 0\leq t\lt 5\\ 20,\ \ 5\leq t\lt 15\\ 20-5t,\ \ 15\leq t\leq 19 \end{cases} $$ И построим график:

Участок AB соответствует разгону автомобиля от 0 до 20 м/с, участок BC — равномерному движению со скоростью 20 м/с, участок CD — торможению от 20 м/с до 0.
п.4. Определение пути и перемещения по графику скорости
В §10 данного справочника мы рассматривали неравномерное прямолинейное движение, которое можно разбить на отдельные равномерные участки. Для такого движения путь равен сумме модулей площадей участков, определенных по графику скорости. А перемещение также равно сумме площадей, но уже с учетом знака.
Этот подход можно расширить на любое прямолинейное движение.
Пусть график скорости при прямолинейном движении разбит на $n$ участков, площади которых легко определить (треугольники, прямоугольники, трапеции). Тогда:
Весь пройденный путь равен сумме модулей площадей всех участков: $$ s=|s_1|+|s_2|+…+|s_n| $$ Величина перемещения по оси ОХ равна сумме площадей всех участков с учетом знака: $$ \triangle x=s_1+s_2+…s_n $$ Конечная координата равна: $x_к=x_0+\triangle x$
Пример определения пути и перемещения по графику скорости
Для построенного выше графика скорости автомобиля получаем следующие участки:
1) ΔABE, его площадь равна $$ s_1=\frac12 AE\cdot BE=\frac12\cdot 5\cdot 20=50\ (м) $$ 2) прямоугольник EBCF, его площадь равна $$ s_2=EF\cdot BE=10\ cdot 20=200\ (м) $$ 3) ΔCFD, его площадь равна $$ s_2=\frac12 FD\cdot GF=\frac12\cdot 4\cdot20=40\ (м) $$ Весь пройденный путь: $$ s=s_1+s_2+s_3=50+200+40=290\ (м) $$ Скорость автомобиля все время оставалась положительной (направление движения не менялось), поэтому величина перемещения равна пройденному пути: $$ \triangle x=s=290\ (м) $$
п.5. Задачи
Задача 1. За 1 мин автобус увеличил скорость с 28,8 км/ч до 72 км/ч.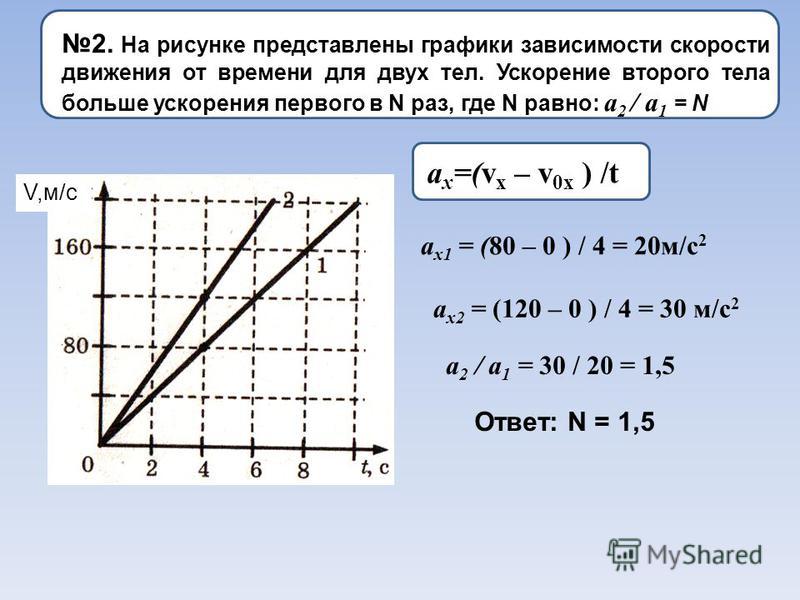 2}\right) $$ Уравнение зависимости скорости от времени: \begin{gather*} v(t)=v_0+at\\ v(t)=10+0,25t \end{gather*} График:

Скорость достигает значения $v=20\ м/с$ в момент времени $t=40\ с$.
Значит, время движения 40 с.
Путь по графику скорости равен площади четырехугольника ABCD. \begin{gather*} S_{ABCD}=S_{ABE}+S_{AECD}=\frac12 AE\cdot EB+AE\cdot AD=\frac12\cdot 40\cdot 10+40\cdot 10=200+400=600\ (м)\\ s=600\ м \end{gather*} Найденное значение пути совпадает с условием задачи. Все параметры движения найдены верно.
Ответ: 0,25 м/с²; 40 c
На графиках зависимости скорости от времени все времена t указаны в секундах, а все скорости v указаны в м/с. а. От наибольшего к наименьшему ранжируйте графики с точки зрения наибольшей скорости за 10 секунд. б. Расположите графики от большего к меньшему по наибольшему ускорению. в. От большего к меньшему ранжируйте графики по наибольшему расстоянию, пройденному за 10 секунд.
Глава 4, задача 25A
На графиках зависимости скорости от времени все времена t указаны в с, а все скорости v в м/с.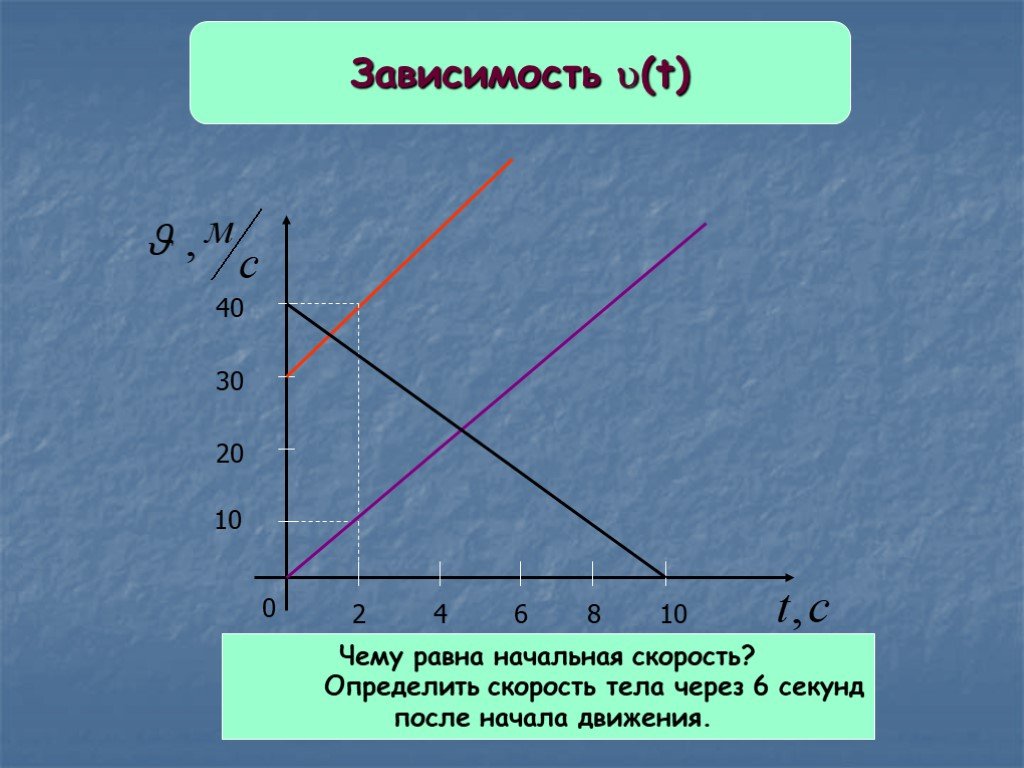
а. От наибольшего к наименьшему ранжируйте графики с точки зрения наибольшей скорости за 10 секунд.
б. Расположите графики от большего к меньшему по наибольшему ускорению.
в. От большего к меньшему ранжируйте графики по наибольшему расстоянию, пройденному за 10 секунд.
В рейтинге: Графики скорости в заданное время от наибольшей к наименьшей.
Ранг графика с точки зрения наибольшей скорости за 10 секунд: A=C, B .
Дано:
Данные графики показаны ниже:

Дано время 10 секунд.
Расчет:
На графике A,
Через 10 секунд значения скорости v=30 мс
На графике B,
Через 10 секунд значения скорости v=3 мс На 10-й секунде значения скорости v=10 мс
Вывод:
Следовательно, ранг графика по наибольшей скорости на 10-й секунде: A=C, B
Ранг: Приведенные графики в терминах наибольшего ускорения от наибольшего к наименьшему.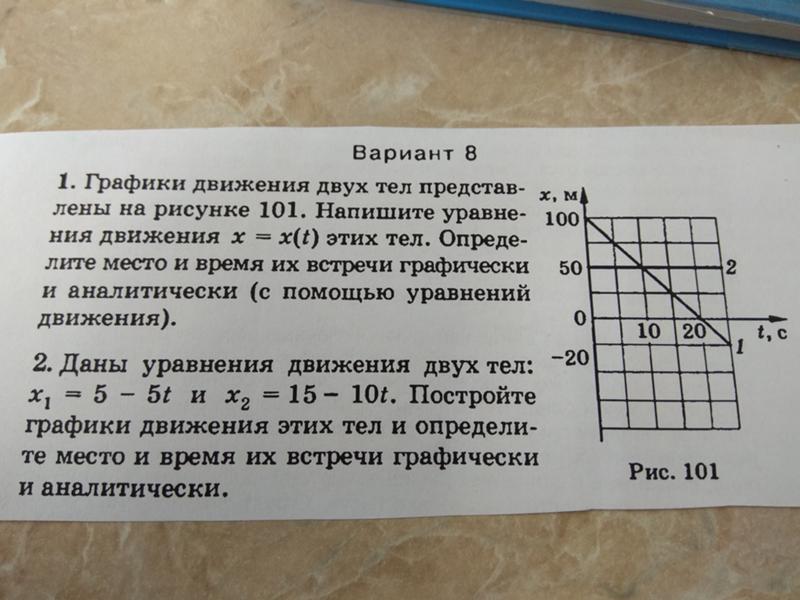
Ранжирование графиков по наибольшему ускорению: C,A=B .
Приведено:
. Показанные графики приведены ниже:
Используемая формула:
в графиках скорости в зависимости от времени, ускорение определено,
A = ΔVΔT
, где
A = ΔVΔt
, где
A = ΔVΔT
, где
A = ΔVΔT
, где
A = ΔVΔT
. изменение скорости
Δt = временной интервал
Расчет:
Из графика A,
ΔV = 0
Следовательно,
A = 0
Из графика B,
ΔV = 0
. Следовательно,
A = 0
. Из графика C,
ΔV = 10 мс
ΔT = 10 S
Следовательно,
A = 1MS2
Заключение:
Ранг графиков в терминах наибольшего ускорения-C, A = B
. Ранжировать: Графики с точки зрения наибольшего расстояния, пройденного за заданное время, от наибольшего к наименьшему.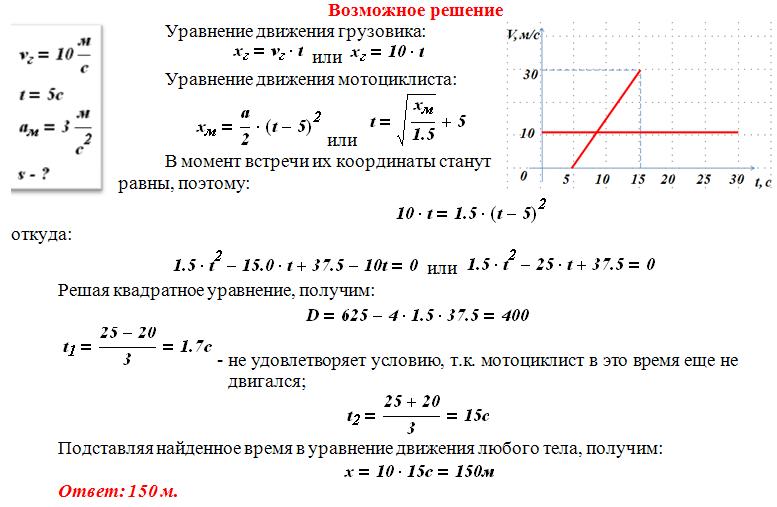
Ранжирование графиков по наибольшему пройденному расстоянию: A, C, B.
Дано:
Данные графики показаны ниже:

Заданное время равно 10 секундам.
Используемая формула:
Расстояние, пройденное объектом на графике скорость-время, равно площади под кривой.
d= Площадь под кривой
Расчет:
Из графика-A,
Площадь, охватываемая графиком, имеет прямоугольную форму.
Следовательно,
d=30×10
d=300 м
Из графика-B,
Площадь, охваченная графиком, имеет прямоугольную форму.
Следовательно,
d=3×10
d=30 м
Из графика-C:
Площадь, охваченная графиком, имеет треугольную форму.
Следовательно,
d=12×10×10
d=50 м
Вывод:
Ранжирование графиков по наибольшему пройденному расстоянию: A, C0 80 9 0 10 9 0 9 .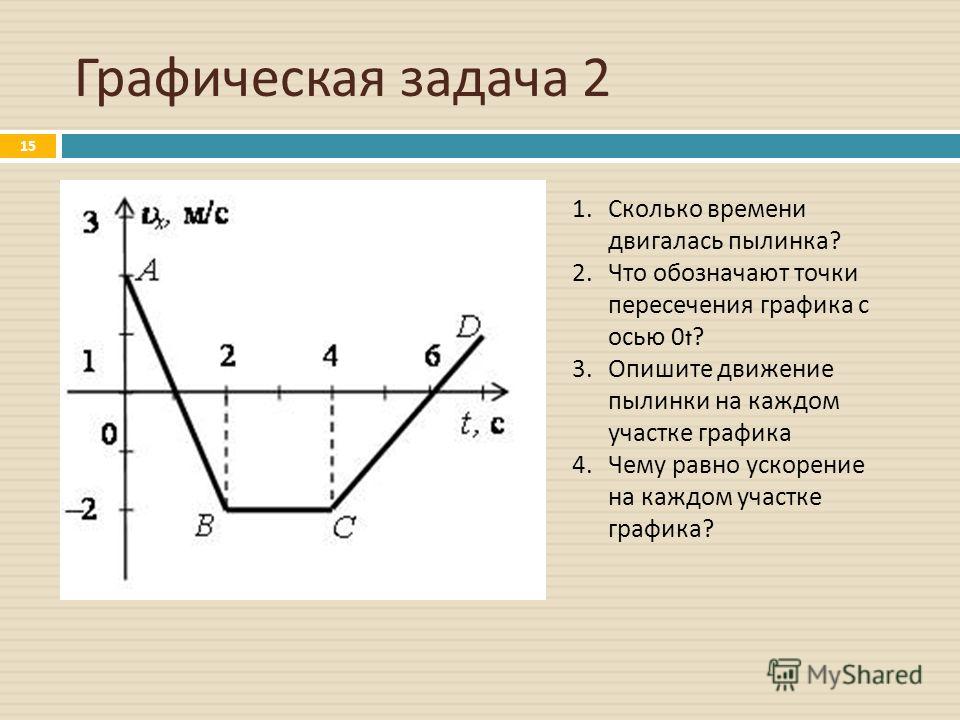 0181 chevron_left
Previous
Chapter 4, Problem 24A

Next
Chapter 4, Problem 26A
Conceptual Physics: The High School Physics Program
9th Edition
ISBN: 9780133647495
Автор: Пол Г. Хьюитт
Издатель: Prentice Hall
Бесполезно? См. похожие книги
Концептуальная физика: программа по физике для старших классов
Линейное движение. 25A
График скорости и времени — GCSE Maths
Введение
Что такое график скорости во времени?

Как нарисовать график скорость-время
Рабочие листы графиков скорости и времени
Как интерпретировать график скорость-время
Распространенные заблуждения
Практикуйте вопросы по графику скорости и времени
График скорости и времени Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застрял
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое график скорости во времени?

Как нарисовать график скорость-время
Рабочие листы графиков скорости и времени
Как интерпретировать график скорость-время
Распространенные заблуждения
Практикуйте вопросы по графику скорости и времени
График скорости и времени Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застрял
Здесь мы узнаем о графике скорость-время, включая рисование и чтение графиков скорость-время.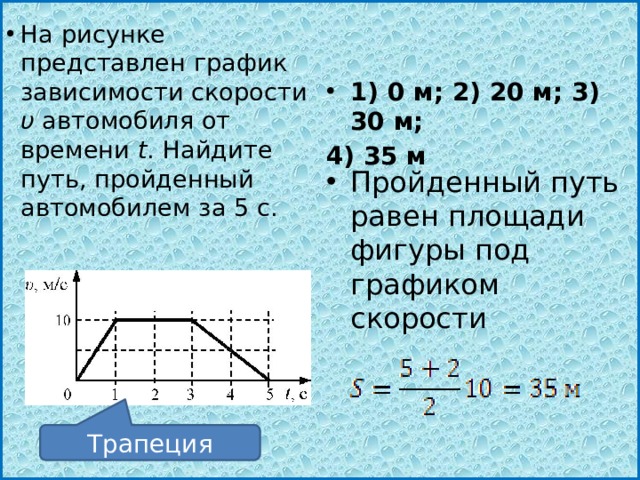 Мы также узнаем, как найти ускорение и пройденное расстояние по графику зависимости скорости от времени.
Существуют также рабочие листы с графиком скорости и времени , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое график скорость-время?
График скорость-время — это график, показывающий движение объекта в зависимости от времени.
Их также можно назвать графиками скорость-время.
Единицы измерения скорости, используемые для графика зависимости скорости от времени, могут различаться, но наиболее распространенными являются километры в час (км/ч), метры в секунду (м/с) и мили в час (миль в час).
Напр.
Этот график зависимости скорости от времени показывает скорость объекта в метрах в секунду за 10-секундный период.
Объект ускорялся из состояния покоя с постоянной скоростью в течение 4 секунд, пока не достиг скорости 10 м/с.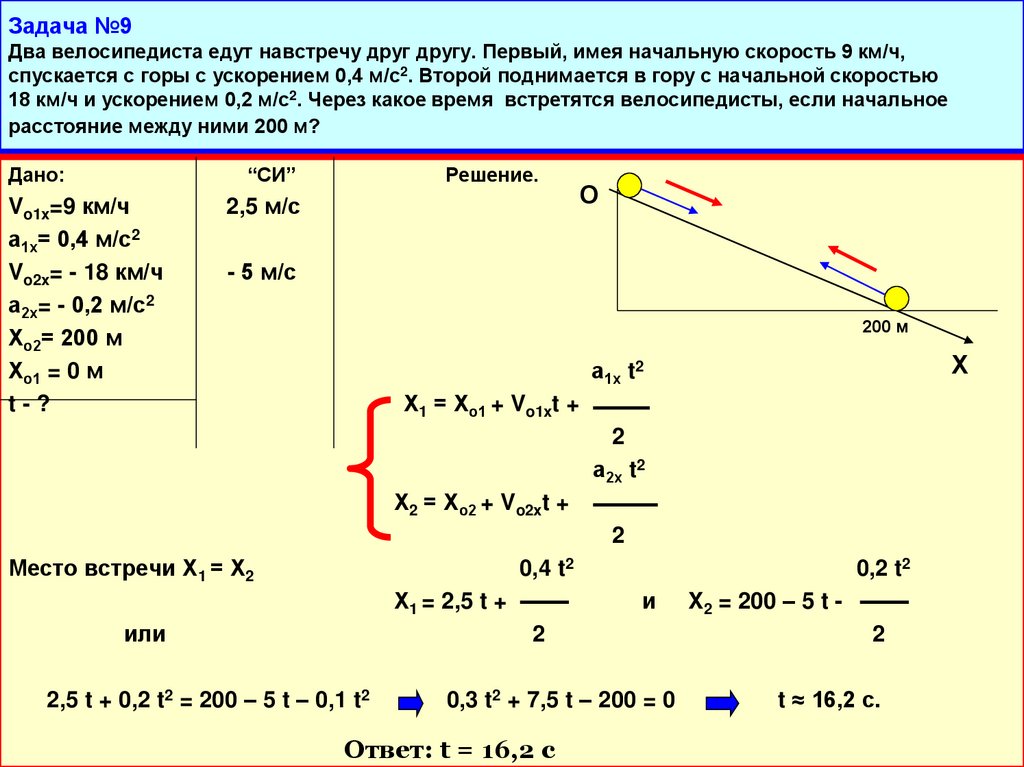 Затем он продолжал двигаться со скоростью 10 м/с еще 5 секунд, а затем замедлился до состояния покоя за 1 секунду. (Замедление — это когда объект замедляется.)
Прямая линия с номером \bf{1} показывает постоянное ускорение . Это ускорение можно рассчитать, найдя градиент линии.
Ускорение — скорость изменения скорости во времени. Вот формула
\text{Ускорение} = \frac{\text{изменение скорости}}{\text{изменение во времени}}
Горизонтальная линия с номером \bf{2} показывает объект, движущийся с постоянной скоростью.
Прямая с номером \bf{3} имеет отрицательный уклон, поэтому показывает замедление (объект замедляется).
Общее расстояние , которое переместил объект, можно найти путем вычисления площади под графиком скорость-время .
Средняя скорость может быть рассчитана путем деления общего пройденного расстояния на общее время .
Что такое график скорость-время?
Как нарисовать график скорость-время
Чтобы нарисовать график скорость-время:
Начертите горизонтальную ось для времени и вертикальную ось для скорости.
Используйте информацию о скорости объекта для построения точек на графике.
Соедините точки отрезками прямой линии.
Объясните, как построить график скорость-время
Рабочий лист графика скорости и времени
Получите бесплатный рабочий лист графика скорости, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Рабочий лист с графиком скорости и времени
Получите бесплатный рабочий лист с графиком скорости и времени, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Связанные уроки по скорости изменения
График скорости и времени является частью нашей серии уроков для поддержки пересмотра скорости изменения . Возможно, вам будет полезно начать с основного урока скорости изменений, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки в этой серии включают в себя:
Скорость изменения
График расстояния и времени
Примеры графика скорость-время
Пример 1: построение графика скорость-время
График скорость-время показывает скорость автомобиля в течение первых 10 секунд пути.
После первых 10 секунд автомобиль сохраняет скорость в течение 20 секунд. Затем он замедляется с постоянной скоростью и останавливается еще через 15 секунд.
Заполните график зависимости скорости от времени движения автомобиля.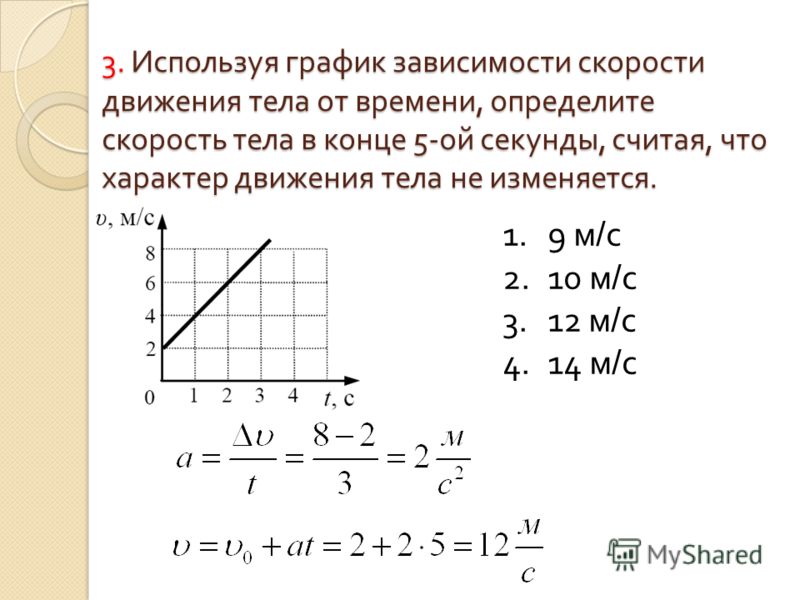
Начертите горизонтальную ось для времени и вертикальную ось для скорости.
Оси на графике уже начерчены и помечены, поэтому сразу переходите к шагу 2. Первая часть пути нарисована. Мы видим, что машина ехала 10 секунд, стартовав из состояния покоя и разогнавшись до скорости 12 м/с.
2 Используйте информацию о скорости объекта для построения точек на графике.
Автомобиль сохраняет скорость в течение 20 секунд, поэтому нам нужно нанести точку на той же высоте по вертикали, 12 м/с, когда время равно 30 секундам. Затем мы должны нанести точку через 45 секунд со скоростью 0 \ м/с \ (10+20+15=45).
3 Соедините точки отрезками прямой линии. т.р.
Пример 2: построение графика зависимости скорости от времени
Объект ускоряется из состояния покоя с постоянной скоростью в течение 5 секунд и достигает скорости 8 м/с. Объект сохраняет эту скорость еще 6 секунд.
Нарисуйте график зависимости скорости движения объекта от времени.
Начертите горизонтальную ось для времени и вертикальную ось для скорости.
Объект достигает максимальной скорости 8 м/с, а общее время движения объекта составляет 11 секунд.
Используйте информацию о скорости объекта для построения точек на графике.
Объект начинает движение из состояния покоя, достигает скорости 8 м/с за 5 секунд и остается со скоростью 8 м/с до 11 секунд

Точки графика в точках (0,0), \ (5,8) и (11 ,8).
Соедините точки отрезками прямой линии.
Пример 3: построение графика скорость-время
В 12:00 поезд едет со скоростью 60 \ км/ч. Он поддерживает эту скорость в течение 15 минут, а затем начинает замедляться с постоянной скоростью в течение 5 минут, пока не достигнет скорости 30 км/ч. Затем он поддерживает эту скорость еще 20 минут.
Нарисуйте график зависимости скорости движения поезда от времени.
Начертите горизонтальную ось для времени и вертикальную ось для скорости.
Горизонтальная ось должна начинаться в 12:00 и заканчиваться в 12:40.

Вертикальная ось должна иметь максимальную скорость 60 км/ч.
Используйте информацию о скорости объекта для построения точек на графике.
Точки графика в точках (12:00,60), \ (12:15,60), \ (12:20,30) и (12:40,30).
Соедините точки отрезками прямой линии.
Как интерпретировать график скорость-время
Чтобы интерпретировать график скорость-время:
Найдите любые соответствующие точки на графике скорость-время.
Проверьте необходимую информацию.
Используйте соответствующий процесс для следующего.
Период постоянной скорости – ищите, где линия горизонтальна.
Ускорение – найти уклон линии.
Пройденное расстояние за период времени – найти площадь под графиком.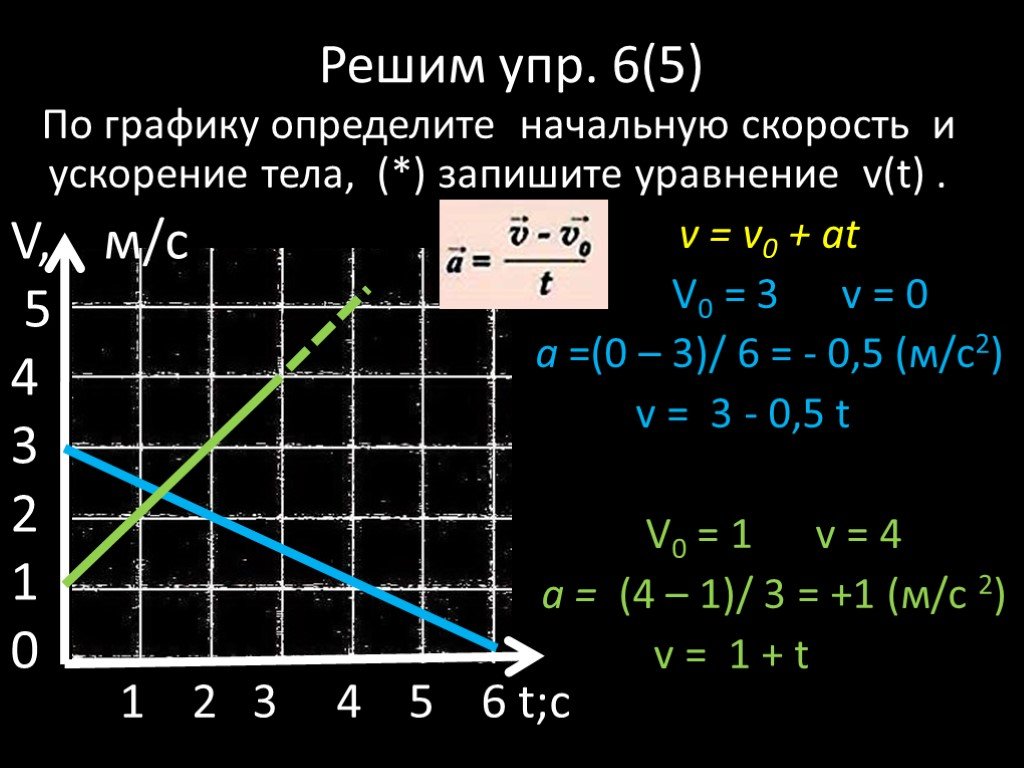
Средняя скорость – разделить общую площадь на общее время.
Объясните, как интерпретировать график скорость-время
Интерпретация примеров графика скорость-время
Пример 4: определение ускорения по графику скорость-время
График скорость-время показывает скорость объекта за 16-секундный период.
Найдите ускорение объекта.
Найдите любые соответствующие точки на графике скорость-время.
Объект разгоняется из состояния покоя до скорости 12 м/с за 16 секунд

Прямая линия проходит от (0,0) до (16,12).
Проверьте необходимую информацию.
Требуется ускорение объекта.
Используйте соответствующий процесс для следующего.
Ускорение – найти уклон линии. 92
Пример 5: определение замедления по графику скорость-время
График скорость-время показывает скорость автомобиля.
Найдите замедление автомобиля на последнем участке пути.
Найдите любые соответствующие точки на графике скорость-время.
Автомобиль замедляется между (1,5,60) и (3,0)
Проверьте необходимую информацию.
Требуется замедление, так что это вопрос ускорения. 9{2}.
Пример 6: определение общего расстояния и средней скорости по графику скорость-время
График скорость-время показывает движение объекта.
Найдите общее пройденное расстояние и среднюю скорость объекта на всем его пути.
Найдите любые соответствующие точки на графике скорость-время.
График скорость-время состоит из точек (0,0), \ (3,10), \ (7,10) и (9,0)
Проверьте необходимую информацию.
Требуется общее расстояние и средняя скорость.
Используйте соответствующий процесс для следующего.
Пройденное расстояние за период времени – найти площадь под графиком.

Средняя скорость – разделить общую площадь на общее время.

Общее расстояние можно найти, найдя площадь под графиком.

Форма графика — трапеция, поэтому можно использовать формулу площади трапеции или разделить фигуру на прямоугольник и два треугольника.

Общее пройденное расстояние 65\м.

Среднюю скорость объекта можно найти, используя

\text{средняя скорость}= \frac{\text{общее расстояние}}{\text{общее время}}=\frac{65}{9} =7,22 \ м/с \ (2 dp)
Распространенные заблуждения
Пройденное расстояние равно скорости, умноженной на время
Распространенной ошибкой при определении пройденного расстояния является простое умножение скорости объекта на затраченное время. Это работает только в том случае, если объект двигался с постоянной скоростью в течение всего этого периода времени.
Пройденное расстояние не будет указано, если объект в это время ускорялся. Важно найти площадь под графиком, чтобы найти расстояние.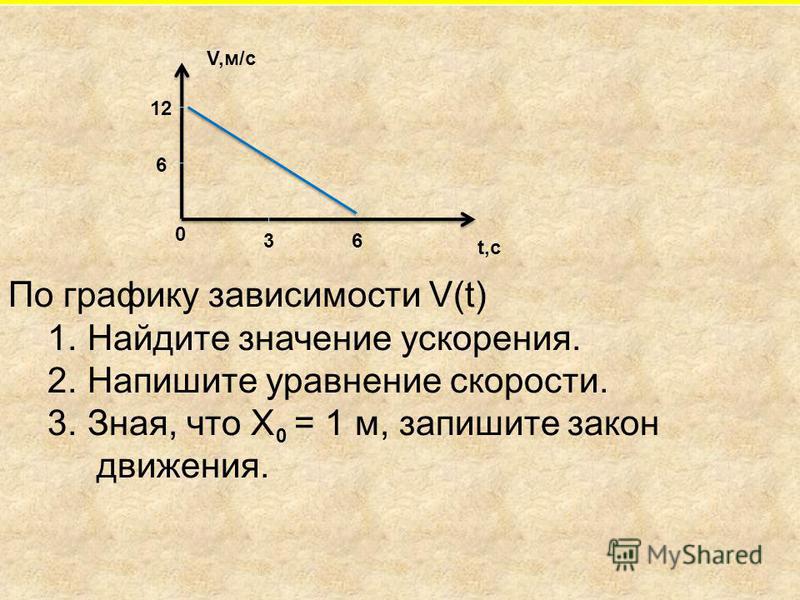
Шкала времени
Время всегда отсчитывается по горизонтальной оси, но следует соблюдать осторожность при использовании шкалы. Помните, что в одной минуте 60 секунд, а в одном часе 60 минут. Это означает, что шкалу можно разделить разными способами.
Практические вопросы по графику скорости и времени
Объект, ускоряющийся
Объект, движущийся с постоянной скоростью
Объект, замедляющийся
Объект, находящийся в мгновенном состоянии покоя
время, поэтому объект будет двигаться с постоянной скоростью.
Умножить максимальную скорость на общее время
Найти уклон линии
Найти площадь под графиком скорость-время
9{2}.
240 \ км
360 \ км
150 \ км
120 \ км
Форма графика — трапеция, поэтому можно использовать формулу площади трапеции или разделить фигуру на прямоугольник и два треугольники.

\text{Площадь}=\frac{1}{2}\times (1+3) \times 120=240
График скорость-время Вопросы GCSE
1. График скорость-время показывает первую часть пути на автомобиле. 9{2}
(1)

(c)

Горизонтальная линия, проведенная от (6,15) до (14,15)
(1)
Линия, проведенная от (14,75) 0)
(1)
(D)
Попытка использовать область трапеции или разрыв в отдельных треугольниках и прямоугольника
(1)
Расстояние 187,5 \ М. 2. График скорость-время показывает скорость поезда между 12:00 и 13:30.

а) Найдите общее расстояние, пройденное поездом за это время.

(b) Найдите среднюю скорость поезда с 12:00 до 13:30.

(5 баллов)
Показать ответ
(a)
Попытка разбить форму на трапеции, треугольники, прямоугольники и т. д.
(1)
. Расстояние между 12:30 и найдено км
(1)
Общее расстояние 67,5\км
(1)

(b)
Ответ на (a) \div 1.5
(1)
45 \ км/ч
(1)
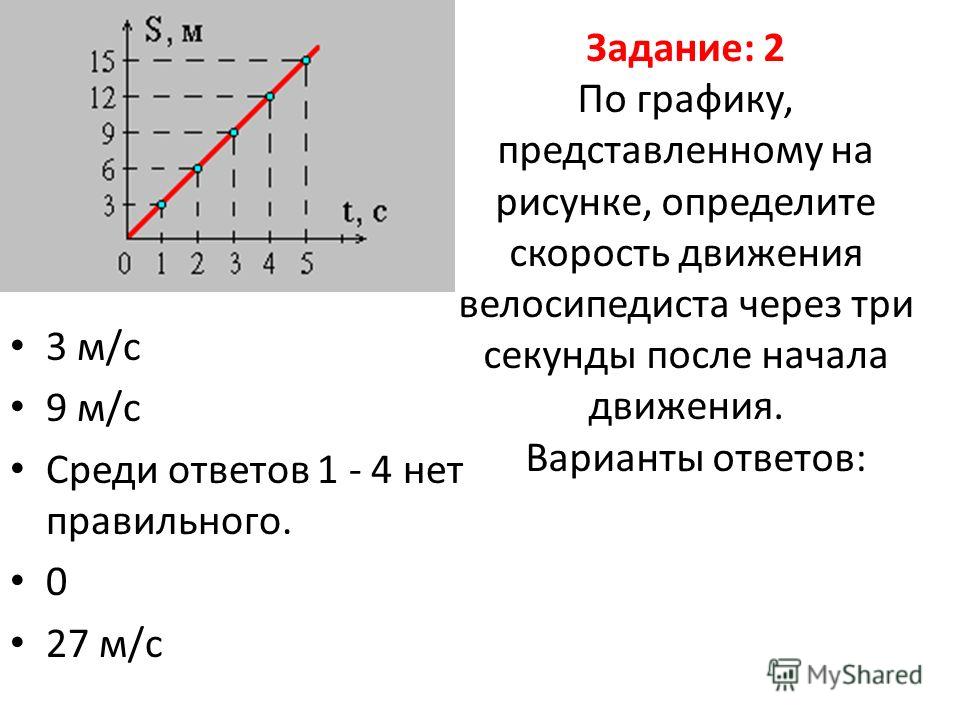
3.