Физика-9
Физика-9 В.Н.Блинов, г. Энгельс.Вариант 1
Ф. и. _________________________________
Класс __________
Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать материальной точкой иглу швейной машины в следующих случаях:
а) игла падает со стола _________ ;
б) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
3. Определите координату пешехода, взяв за тело отсчета:
а) дерево:
x = ________ ,
б) дорожный указатель:
x = _______ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1
x = _____ , s2x = ______ ,
s2x = _____ , s2y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела: v1x = __________,
v2x = __________ ;
б) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны
положения двух маленьких шариков в начальный
момент времени и их скорости. Запишите уравнения
движения этих тел:
Запишите уравнения
движения этих тел:
x1 = ___ ,
x2 = _____ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Ф. и. _________________________________
Класс __________
Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать космонавта материальной точкой в следующих случаях:
а) космонавт перемещается в космическом корабле ____ ;
б) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного
прямолинейного движения
называется_________________величина, равная _______________
__________________________ к промежутку времени
_____________________________________________________ .
Скоростью равномерного
прямолинейного движения
называется_________________величина, равная _______________
__________________________ к промежутку времени
_____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а) дерево:
x = ____________ ,
б) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1x = ___ , s2x = ___ ,
s1y = ___ , s2y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты
двух движущихся тел для определенных моментов
времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела:
v1x = ______________,
v2x = ______________ ;
б) расстояние l между телами в момент времениt = 4 с:
l = __________________.
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x1 = ___________ ,
x2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде
пловец плывет со скоростью 2 м/с. Когда он
плывет по реке против течения, его скорость
относительно берега равна 0,5 м/с вниз по
течению.
v = ____________ .
Вариант 3
Ф. и. _________________________________
Класс __________
Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать поезд материальной точкой в следующих случаях:
а) поезд въезжает на станцию ________________;
б) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а) дерево:
x = ________ ,
б) дорожный указатель:
x = _______ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1x = _____ , s2x = ______ ,
s1y = _____ , s2y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела:
v1x = __________,
v2x = __________;
б) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x1 = ______ ,
x2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Ф. и. _________________________________
Класс __________
Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать автомобиль материальной точкой в следующих случаях:
а) автомобиль движется по шоссе _____________;
б) автомобиль въезжает в гараж ______________?
2. Скорость тела
относительно ______________ системы координат равна
_________ сумме скорости ________ относительно ________ и
скорости ____________ относительно ___________.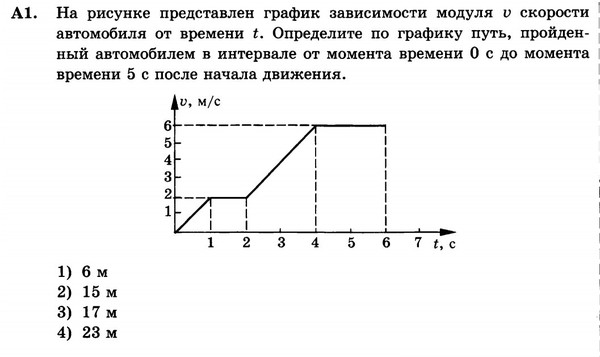
3. Определите координату пешехода, взяв за тело отсчета:
а) дерево:
x = ________ ,
б) дорожный указатель:
x = _______ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1x = ______ , s2x = ______ ,
s1y = ______ , s2y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела:
v1x = __________,
v2x = __________ .
б) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x1 = ______ ,
x2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
Вариант 1
Ф. и. _________________________________
Класс __________
Тест № 2. Прямолинейное
неравномерное движение
Прямолинейное
неравномерное движение
1. Чтобы найти среднюю
скорость тела при неравномерном движении, надо
_________________________________________
______________________________________________________.
2. Если при равноускоренном движении скорость
тела за 2 с изменилась на 4 м/с, то за
последующие 3 с она изменится на _________ .
3. В некоторый момент времени скорость тела
равна 10 м/с. Чему будет равна скорость через
3 с, если проекция вектора ускорения ax = –2 м/с2? v = ___________.
4. Автомобиль трогается с места с ускорением 2 м/с2.
Каково его перемещение за 5 с? Какую скорость он
наберет за это время?
s = ___________, v = ___________.
5. На рисунке даны графики проекций скоростей движения двух тел. Найдите проекцию вектора ускорения каждого тела:
ax1 = ___________ ,
ax2 = ___________ .
6. По уравнениям движения определите начальную координату тела и проекции векторов начальной скорости и ускорения:
а) x = –5 + 2t + 5t2, x0 = ______, v0x = ______, ax = ________,
б) x = –2t + 2t2, x0 = ______, v0x = ______, ax = ________.
7. На рисунке показаны положения двух человек в момент времени t = 0, а также их начальные скорости и ускорения. Запишите уравнения движения.
x1 = ______,
x2 = ______ .
8. Пользуясь условием предыдущего вопроса, постройте графики проекций скоростей двух тел и найдите проекции скоростей тел в момент времени t = 1 с:
v1x = ________ ,
v2x = ________ .
9. По графику зависимости vx(t) постройте график зависимости ax(t).
10. Сравнитe модули средних скоростей двух тел (поставьте один из знаков: <, >, =).
Вариант 2
Ф.
и. _________________________________
Класс __________
Тест № 2. Прямолинейное неравномерное движение
1. Равноускоренным называется
движение, при котором скорость тела
___________________________________________.
2. Если при равноускоренном движении скорость
тела за 3 с изменилась на 6 м/с, то изменение
скорости на 4 м/с произойдет за _____________.
3. Чему равна начальная скорость тела при
равноускоренном движении, если в момент времени t = 4 с
проекция скорости равна 12 м/с, а проекция
вектора ускорения ax = 2 м/с2?
v = ___________.
4. Стартующая ракета за 10 с набрала скорость
100 м/с. С каким ускорением двигалась ракета?
Каково ее перемещение за это время?
a = ___________, s = ___________.
5. На рисунке даны графики проекций скоростей движения двух тел. Найдите проекцию вектора ускорения каждого тела:
ax1 = ___________ ,
ax2 = ___________ .
6. По уравнениям движения определите начальную координату тела и проекции векторов начальной скорости и ускорения:
а) x = 10t + 10t2, x0 = ______, v0x = ______, ax = ________,
б) x = 4t – 2t2, x0 = ______, v0x = ______, ax = ________.
7. На рисунке показаны положения двух человек в момент времени t = 0, а также их начальные скорости и ускорения. Запишите уравнения движения.
x1 = ______,
x2 = ______ .
8. Пользуясь условием предыдущего вопроса, постройте графики проекций скоростей двух тел и найдите проекции скоростей тел в момент времени t = 2 с:
v1x = ________ ,
v2x = ________ .

9. По графику зависимости vx(t) постройте график зависимости ax(t).
10. Сравнитe модули средних скоростей двух тел (поставьте один из знаков: <, >, =).
Вариант 3
Ф. и. _________________________________
Класс __________
Тест № 2. Прямолинейное неравномерное движение
1. Мгновенной скоростью
тела называется ______________________________________________________.
2. Если при равноускоренном движении скорость
тела за 4 с изменилась на 8 м/с, то за
следующуе секунду она изменится на _________ .
3. Чему равна начальная скорость тела, если в
момент времени t = 2 c проекция скорости
равна 10 м/с, а проекция вектора ускорения ax = –2 м/с2? v0 = ___________.
4. Бегун со старта первые 4 м пробежал за 1 с. С
каким ускорением движется бегун? Какую скорость
он наберет за первую секунду?
a = ___________, v = ___________.
5. На рисунке даны графики проекций скоростей движения двух тел. Найдите проекцию вектора ускорения каждого тела:
ax1 = ___________ ,
ax2 = ___________ .
6. По уравнению движения определите начальную координату тела и проекции векторов начальной скорости и ускорения:
а) x = 4 – 4t – 4t2, x0 = ______, v0x = ______, ax = ________,
б) x = 10t + 2t2, x0 = ______, v0x = ______, ax = ________.
7. На рисунке показаны
положения двух человек в момент времени t = 0,
а также их начальные скорости и ускорения. Запишите уравнения движения.
Запишите уравнения движения.
x1 = ______,
x2 = ______ .
8. Пользуясь условием предыдущего вопроса, постройте графики проекций скоростей двух тел и найдите проекции скоростей тел в момент времени t = 1 с.
v1x = ________ , v2x = ________ .
9. По графику зависимости vx(t) постройте график зависимости ax(t).
10. Сравнитe модули средних скоростей двух тел (поставьте один из знаков: <, >, =).
Вариант 4
Ф.
и. _________________________________
Класс __________
Тест № 2. Прямолинейное неравномерное движение
1. Ускорением тела при его
равноускоренном движении называется величина,
равная _____________________________ .
2. Если при равноускоренном движении скорость
тела за 2 с изменилась на 6 м/с, то изменение
скорости на 9 м/с произойдет за _________ .
3. В начальный момент времени скорость тела
равна 1 м/с. Чему будет равна скорость тела
через 4 с, если проекция вектора ускорения ax = 2 м/с2? v = ___________.
4. Катер, трогаясь с места, за 2 с набирает
скорость 16 м/с. С каким ускорением движется
катер? Чему равно его перемещение за это время?
a = ___________, s = ___________.
5. На рисунке даны графики проекций скоростей движения двух тел. Найдите проекцию вектора ускорения каждого тела:
ax1 = ___________ ,
ax2 = ___________ .
6. По уравнению движения определите начальную координату тела и проекции векторов начальной скорости и ускорения:
а) x = – 8t – 10t2, x0 = ______, v0x = ______, ax = ________,
б) x = 8 + 8t2, x0 = ______, v0x = ______, ax = ________.
7. На рисунке показаны положения двух человек в момент времени t = 0, а также их начальные скорости и ускорения. Запишите уравнения движения.
x1 = ______,
x2 = ______ .
8. Пользуясь условием предыдущего вопроса, постройте графики проекций скоростей двух тел и найдите проекции скоростей тел в момент времени t = 2 с.
v1x = ________ ,
v2x = ________ .
9. По графику зависимости vx(t) постройте график зависимости ax(t).
10. Сравнитe модули средних скоростей двух тел (поставьте один из знаков: <, >, =).
Тест 1 равномерное движение вариант 4. Равномерное прямолинейное движение — тест
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 2x = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
а
v 1x = __________,
v 2x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1
= ___ ,
x 2 = _____
font-size:10.0pt;font-family:» arial cyr>.
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ___ , s 2x = ___ ,
s 1y = ___ , s 2y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = ______________,
v 2x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8.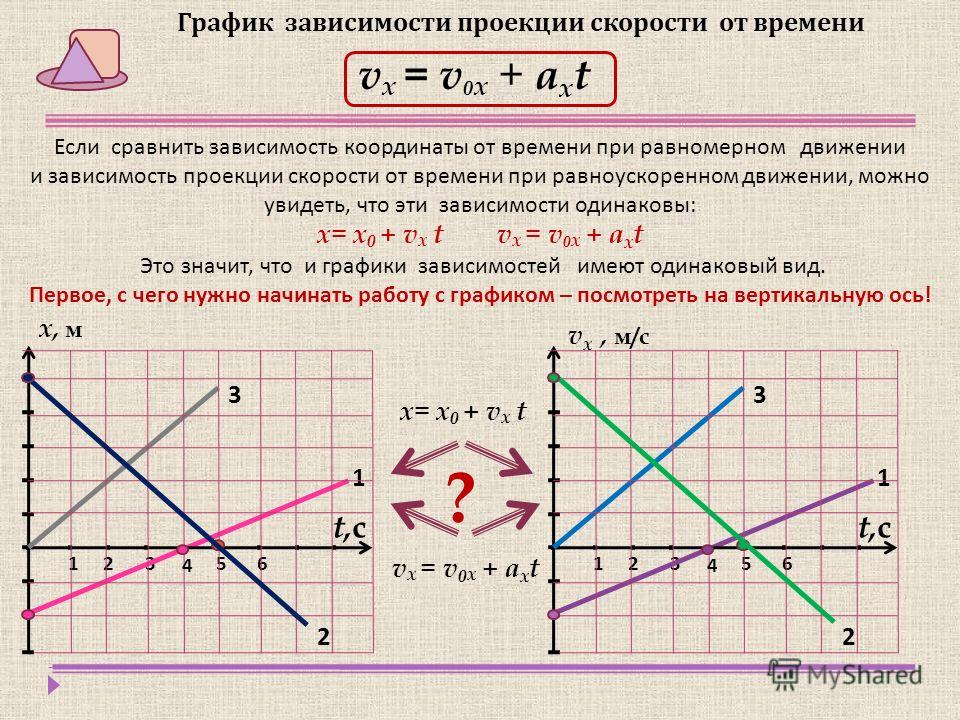 На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1
= ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
.
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .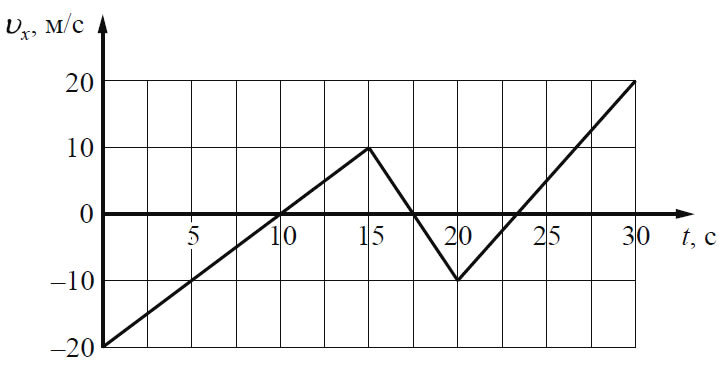
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 1y = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .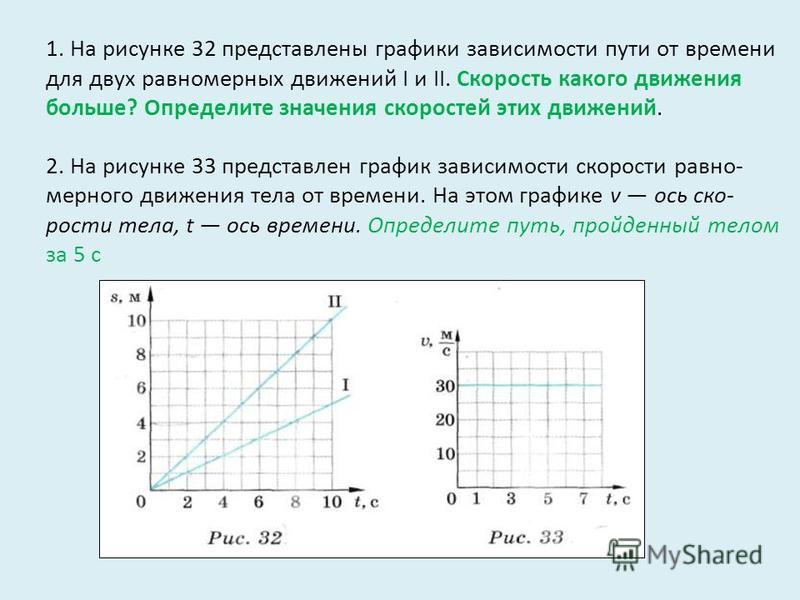
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .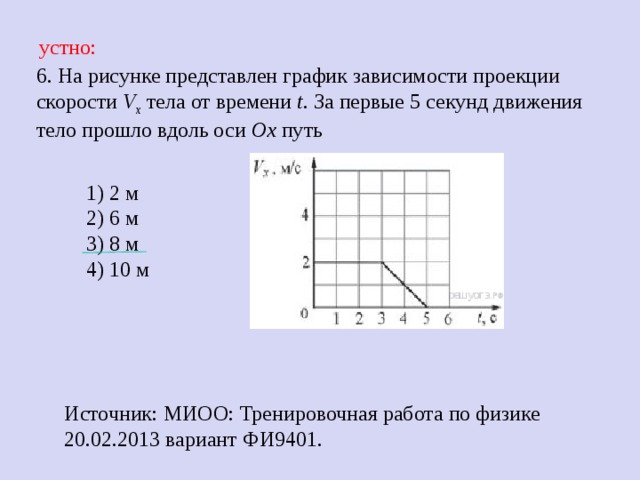
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ______ , s 2x = ______ ,
s 1y = ______ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно — мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
ВСЕРОССИЙСКИЙ ФЕСТИВАЛЬ ПЕДАГОГИЧЕСКОГО ТВОРЧЕСТВА
2016/2017 УЧЕБНОГО ГОДА
Автор: Петренко Надежда Федоровна,
учитель физики высшей квалификационной категории.
Образовательная организация: Муниципальное бюджетное общеобразовательное учреждение Городского округа Балашиха
«Средняя общеобразовательная школа № 7 с углубленным изучением отдельных предметов»
Адрес: 143980, Московская обл., Г. о. Балашиха,
мкр. Железнодорожный, ул. Октябрьская, д. 7.
Октябрьская, д. 7.
Дата 2013-2014 уч. год
МБОУ СОШ №7 с УИОП Г.о. Балашиха Московской обл.
Физика – 10 класс.
Урок №4. Тема: «Равномерное прямолинейное движение Решение задач»
Равномерное прямолинейное движение — ТЕСТ
Вариант I
Часть 1
А) троллейбус движется по прямой улице. К каждой следующей остановке он прибывает через равные интервалы времени и через равные интервалы отбывает от них
Б) автомобиль движется по дороге и проходит за любые равные промежутки времени одинаковые расстояния
В каком случае движение тела является равномерным?
Что такое скорость прямолинейного равномерного движения?
Физическая величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная произведению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная отношению промежутка времени к перемещению, которое совершило тело за этот промежуток времени.
Отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Тело движется прямолинейно равномерно так, что направление вектора скорости противоположно направлению оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
Выберите формулу координаты прямолинейного равномерного движения
2) 3) 4)
5; 2 2) 2; -5 3) -5; 2 4) 0; 2
3086100266065I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости второго тела на ось ОХ
–1,0 м/с
2) 1,0 м/с
3) — 0,5 м/с
4) 0,5 м/с
2971800188595Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите путь, пройденный телом за первые 8 секунд движения.
Определите путь, пройденный телом за первые 8 секунд движения.
Координата тела меняется с течением времени согласно формуле. Чему равна координата этого тела через 5 с после начала движения?
1) 28 м 2) 12 м 3) — 4 м 4) — 12 м Часть 2
Тело Вид движения
А) первое 1) покоится
Часть 3
Уравнения движения двух тел имеют вид:; . Найдите место и время встречи тел графически и аналитически.
Равномерное движение
Вариант II
Часть 1
К каждому из заданий 1 – 8 даны 4 варианта ответа, из которых только один правильный.
Рассмотрим два вида движения тел:
А) поезд метрополитена движется по прямолинейному пути. Он прибывает на каждую следующую станцию и отправляется от нее через одинаковые промежутки времени
Б) спутник движется по окружности вокруг Земли и за любые равные промежутки времени проходит одинаковые расстояния
В каком случае движение тела не является равномерным?
1) только в А 2) только в Б 3) в А и в Б 4) ни в А, ни в Б
Что характеризует скорость прямолинейного равномерного движения?
направление движения тела
отношение перемещения ко времени, за которое это перемещение совершено.
быстроту изменения координаты
произведение перемещения и времени, за которое это перемещение совершено.
Тело движется прямолинейно равномерно так, что направление вектора скорости совпадает с направлением оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
отрицательна 4) может быть, как положительной, так и отрицательной.
Выберите формулу скорости прямолинейного равномерного движения
2) 3) 4)
Уравнение движения имеет вид. Определите начальную координату и скорость
0; — 3 2) — 3; 0 3) 0; 3 4) 3; 0
2628900186055I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости третьего тела на ось ОХ
– 0,5 м/с
2) 2,5 м/с
3) — 2,5 м/с
4) 0,5 м/с
2514600227330Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени.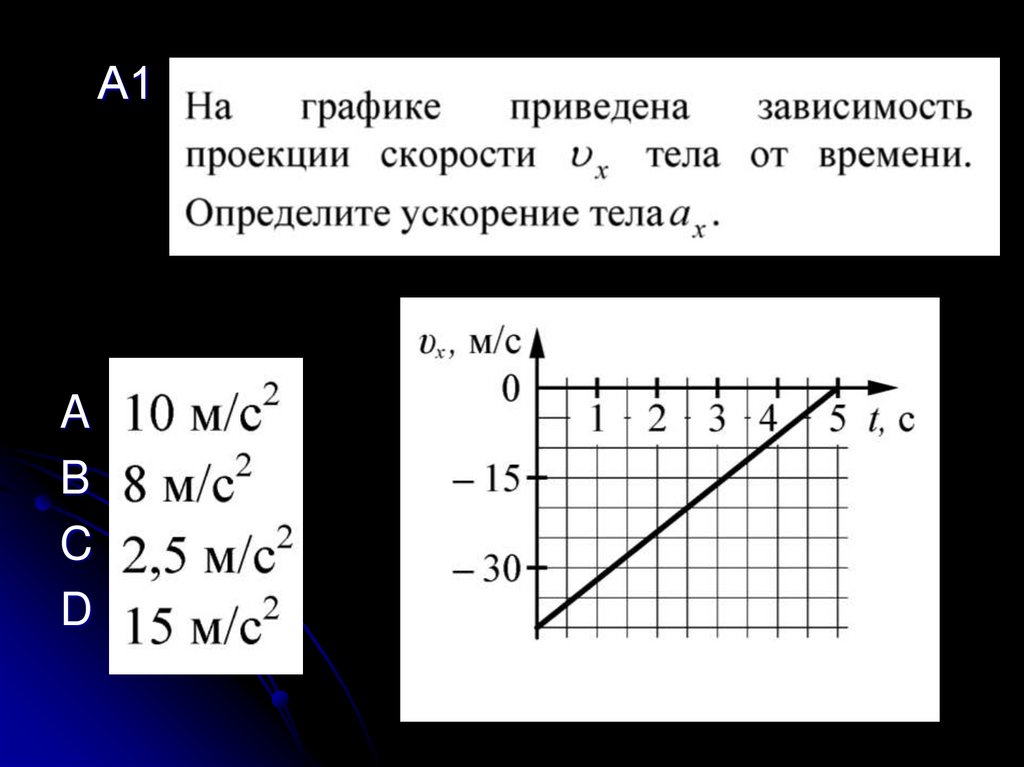 Определите перемещение тела за первые 8 секунд движения.
Определите перемещение тела за первые 8 секунд движения.
1) 4 м 2) 8 м 3) 16 м 4) 0 м
Координата тела меняется с течением времени согласно формуле. Через сколько секунд координата тела станет равной нулю?
1) 2 с 2) 5 с 3) 10 с 4) 4 с
Часть 2
В задании 9 требуется указать последовательность цифр, соответствующих правильному ответу.
Уравнения движения тел имеют вид:; ; . Как и в каком направлении движутся тела?
К каждой позиции первого столбика подберите соответствующую позицию второго столбика. Цифры могут повторяться.
Тело Вид движения
А) первое 1) покоится
Б) второе 2) равномерно по оси
В) третье 3) равномерно против оси
Часть 3
Задание 10 представляет собой задачу, полное решение которой необходимо записать.
Уравнения движения двух тел имеют вид: ; . Найдите место и время встречи тел графически и аналитически.
Ответы
N 1 2 3 4 5 6 7 8 9 10
Вариант I 2 1 2 2 3 1 3 4 231 10 с; 30 мВариант II 1 2 1 3 1 4 4 1 321 10 с; 50 м
с. 1
1
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 2 x = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
7. По графикам движения определите:
а
v 1 x = __________,
v 2 x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1 = ___ ,
x 2 = _____ .
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ___ , s 2 x = ___ ,
s 1 y = ___ , s 2 y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
а ) проекцию скорости каждого тела:
v 1 x = ______________,
v 2 x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1 = ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 1 y = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
М
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ______ , s 2 x = ______ ,
s 1 y = ______ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
с. 1
Движение свободного падения: объяснение, обзор и примеры
Свободное падение и движение снаряда описывают объекты, которые движутся по воздуху и на которые действует только сила тяжести. В этом посте мы опишем этот тип движения, используя как графики, так и кинематические уравнения. Поскольку движение снаряда включает два измерения, эти проблемы могут быть сложными. Мы объясним множество примеров, чтобы вы могли увидеть, как решать различные типы движения снаряда.
Что мы просматриваем
Свободное падение 92. Применение свободного падения к кинематическим уравнениям При анализе движения свободного падения мы можем применить те же кинематические уравнения, что и для движения на земле. Затем мы можем использовать эти уравнения для определения таких свойств, как расстояние, время и скорость.
Затем мы можем использовать эти уравнения для определения таких свойств, как расстояние, время и скорость.
Как найти расстояние падения объекта в свободном падении
Если объект находится в свободном падении, мы можем использовать кинематические уравнения, чтобы найти расстояние, на которое он падает за определенное время. Обычно вы будете использовать следующее кинематическое уравнение для расчета пройденного пути: 92 + 2ad
В этом случае необходимо знать конечную скорость v_f объекта. Затем вы можете решить уравнение для расстояния d.
Как найти время для объекта в свободном падении
Количество времени, в течение которого объект находится в свободном падении, зависит от его скорости и расстояния, на которое он падает. Как и в случае с расстоянием, есть два уравнения, которые вы можете использовать, чтобы найти время, в зависимости от того, что вы знаете.
Если известны начальная и конечная скорости объекта, то проще всего вычислить время с помощью кинематического уравнения:
| Формула для определения времени по скорости v_f=v_i+at |
Это уравнение можно решить для времени.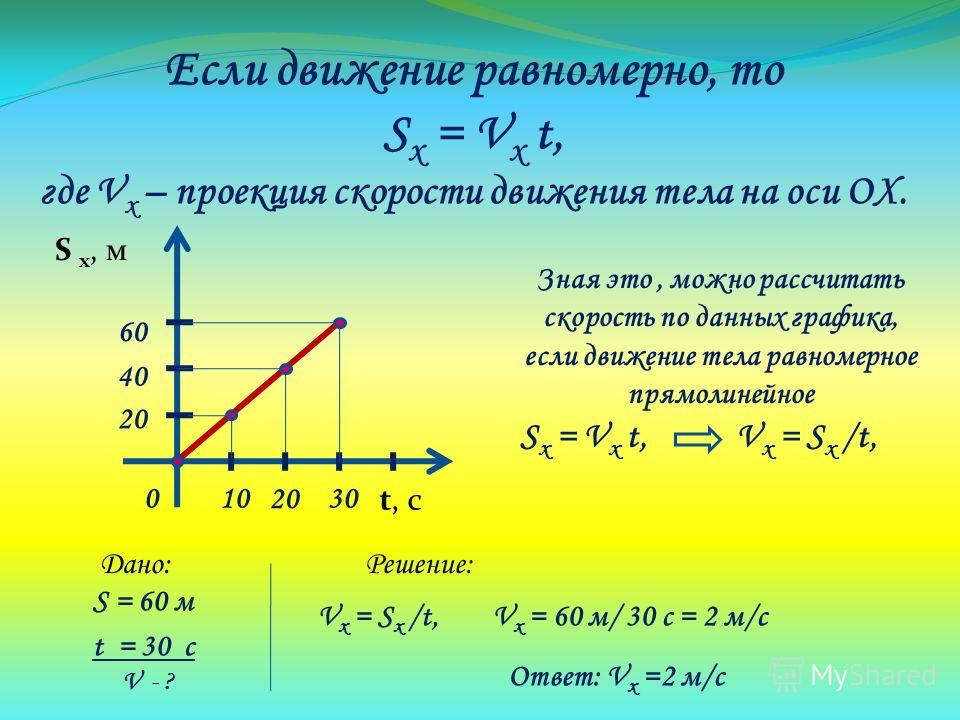 Затем вам нужно будет только подставить значения скоростей и ускорений под действием силы тяжести.
Затем вам нужно будет только подставить значения скоростей и ускорений под действием силы тяжести.
Другой способ найти время, если вы не знаете конечную скорость объекта, состоит в использовании уравнения:
| Формула для нахождения времени с использованием расстояния 2 |
Обратите внимание, что в этом уравнении есть два члена, которые включают время t. Если начальная скорость не равна нулю, это может затруднить решение этого уравнения для времени. Если вы используете это уравнение, вам может понадобиться использовать квадратную формулу для определения времени.
Как найти конечную скорость объекта в свободном падении
Конечная скорость объекта в свободном падении зависит от количества времени, в течение которого он падает. Из-за ускорения свободного падения скорость будет увеличиваться каждую секунду на 92 + 2ad
Это уравнение требует, чтобы вместо этого вы знали расстояние, на которое падает объект.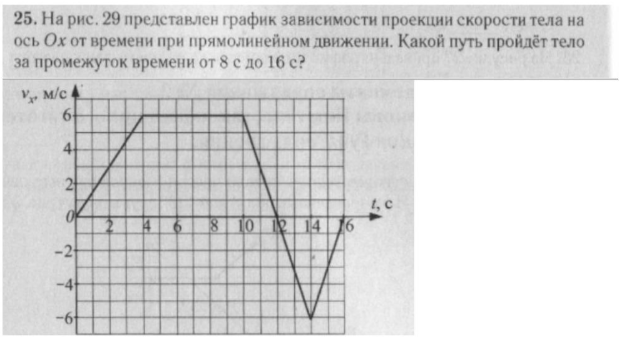 Если вы используете это уравнение для нахождения конечной скорости, помните, что в этом уравнении конечная скорость возводится в квадрат. Это означает, что вам нужно будет извлечь квадратный корень в качестве последнего шага для определения конечной скорости.
Если вы используете это уравнение для нахождения конечной скорости, помните, что в этом уравнении конечная скорость возводится в квадрат. Это означает, что вам нужно будет извлечь квадратный корень в качестве последнего шага для определения конечной скорости.
В следующем разделе мы применим методы, которые вы только что изучили, для решения некоторых задач, связанных со свободным падением. 92
d=122,625\текст{м}
Следовательно, высота здания составляет около 123\text{ м}.
Пример 2. Как найти конечную скорость объекта с начальной скоростью
В другом примере объект в свободном падении имеет начальную скорость вниз 2\text{ м/с} и падает с расстояния 45 \текст{ м}. Какова конечная скорость объекта?
В этом сценарии нам дана начальная скорость объекта v_i и расстояние d. Мы также знаем, что ускорение равно 92}
v_f=29,78\текст{ м/с}
Таким образом, конечная скорость объекта составляет около 30\text{ м/с}.
Помимо использования физических уравнений, мы также можем представить движение свободного падения с помощью графиков движения. Графики положение-время, графики скорость-время и графики ускорения-время могут многое рассказать нам о движении объекта во времени. Хотите более подробный обзор графиков движения? Посмотрите этот пост в блоге!
График положение-время для объекта в свободном падении
С точки зрения положения, многие объекты в свободном падении начинаются в высоком положении или на высоте над землей и движутся вниз. Объекты в свободном падении ускоряются под действием силы тяжести. Следовательно, график зависимости положения от времени при свободном падении должен быть кривым. Это означает, что объекты в свободном падении начинают с низкой скорости и постепенно ускоряются, что представлено крутой нисходящей кривой на графике.
График скорости и времени для объекта в свободном падении 92.
 Как показано на графике ниже, график зависимости ускорения от времени представляет собой постоянную отрицательную линию. Движение снаряда
Как показано на графике ниже, график зависимости ускорения от времени представляет собой постоянную отрицательную линию. Движение снаряда Снаряд — это объект, запускаемый или подбрасываемый в воздух, на который затем действует только сила тяжести. Движение снаряда во многом похоже на движение свободного падения, однако снаряды могут также перемещаться по горизонтали в дополнение к падению вертикально вниз.
Примеры движения снарядаТочная траектория или траектория движения снаряда зависит от того, как он будет запущен. Однако все снаряды следуют по кривой траектории, как на изображении ниже:
Если вы играете или смотрите спортивные состязания, вы, вероятно, уже наблюдали движение снаряда. Движение снаряда описывает дугу баскетбольного мяча при штрафном броске, летящего мяча в бейсболе или волейбольного мяча, переброшенного через сетку.
Горизонтальная составляющая скорости Для анализа движения снаряда мы должны разделить движение на горизонтальную и вертикальную составляющие. Горизонтальная составляющая скорости снаряда не зависит от вертикальной составляющей скорости. Поскольку гравитация действует вертикально, на снаряды не действуют горизонтальные силы. Это означает, что горизонтальная составляющая скорости снаряда остается постоянной на протяжении всего полета. 9{\circ} угол. Чему равна горизонтальная составляющая скорости снаряда?
Горизонтальная составляющая скорости снаряда не зависит от вертикальной составляющей скорости. Поскольку гравитация действует вертикально, на снаряды не действуют горизонтальные силы. Это означает, что горизонтальная составляющая скорости снаряда остается постоянной на протяжении всего полета. 9{\circ} угол. Чему равна горизонтальная составляющая скорости снаряда?
Нам потребуется использовать тригонометрические тождества для определения компонентов скорости. Мы можем визуализировать компоненты в виде треугольника, где гипотенуза — начальная скорость, а стороны — горизонтальная, v_{ix}, и вертикальная, v_{iy}, составляющие скорости.
Косинус определяется как прилежащая сторона треугольника, деленная на гипотенузу. Поскольку горизонтальная составляющая примыкает к углу, мы можем использовать косинус, чтобы найти горизонтальную составляющую скорости: 9{\ круг})
v_{ix}=4\text{ м/с}
Следовательно, горизонтальная составляющая начальной скорости равна 4\text{ м/с}.
Нужно проверить свои триггерные идентификаторы? Попробуйте этот ресурс от Академии Хана.
Вертикальная составляющая скоростиНа вертикальную составляющую скорости снаряда будет влиять гравитация, которая действует вертикально на объект, заставляя его ускоряться вниз. Поэтому вертикальная составляющая скорости будет изменяться на протяжении всего полета снаряда. Мы можем вычислить вертикальную составляющую скорости в определенный момент времени методом, аналогичным вычислению горизонтальной составляющей. 9{\ круг})
v_{iy}=6.9\text{ м/с}
Решение вопросов о движении снарядовДавайте применим то, что мы узнали, к некоторым примерам движения снарядов!
Пример 1. Определение дальности полета снаряда
В этом примере снаряд выпущен горизонтально со скоростью 5\text{ м/с} со скалы высотой 60\text{ м}. На каком расстоянии от основания скалы приземлится снаряд?
В этом сценарии нам задана начальная горизонтальная скорость v_{ix}=5\text{ м/с} и вертикальное изменение положения d_y=-60\text{ м}. {\circ}. Какова максимальная высота снаряда? 92)}
{\circ}. Какова максимальная высота снаряда? 92)}
d_y=18.7\text{м}
Следовательно, снаряд достигнет максимальной высоты около 18,7\text{ м} .
Для получения дополнительных примеров и объяснения решения этих типов задач движения снаряда посмотрите это видео на YouTube от профессора Дэйва.
Заключение Понимание свободного падения и движения снаряда позволит вам решить некоторые из самых сложных задач, с которыми вы столкнетесь в начальной физике. На все снаряды действует только сила тяжести, а вертикальная и горизонтальная составляющие движения не зависят друг от друга. Это позволяет нам применить наши кинематические уравнения для определения времени полета, скорости и смещения снаряда в каждом направлении.
[Решено] Скорость снаряда на максимальной высоте составляет половину
- 60º
- 15º
- 30 °
- 45 °
Вариант 1: 60 0003
. (Shift 1) Тест на основе памяти
1,3 миллиона пользователей
100 вопросов
100 баллов
90 минут
CONCEPT :
- Угол проекции: Угол между начальной скоростью тела относительно горизонтальной плоскости, через которую брошено тело, известен как угол проекции.
- Должен быть определен угол проекции, при котором максимальная высота снаряда равна горизонтальной дальности.
- Тело можно спроецировать двумя способами:
- Горизонтальная проекция — Когда телу придается начальная скорость только в горизонтальном направлении.
- Угловой выступ- Когда тело брошено с начальной скоростью под углом к горизонтальному направлению.

- Максимальная высота снаряда: Когда снаряд достигает нулевой вертикальной скорости, называется максимальной высотой.
- Из этой точки вертикальная составляющая вектора скорости будет направлена вниз.
- Горизонтальным перемещением снаряда называется дальность полета снаряда 92}θ }}{{2g}}\)
где H — максимальная высота, v o = начальная скорость, g = ускорение свободного падения, θ = угол начальной скорости от горизонтали плоскости (радианы или градусы).
РАСЧЕТ :
Учитывая, что v = u/2
На максимальной высоте вертикальная составляющая скорости исчезает и присутствует только горизонтальная составляющая
т.е. данной задачи, v = u/2
\(\следовательно \frac{u}{2} = u\cos θ \to \cos θ = \frac{1}{2}\)
θ = 60°
Правильно вариант 60°.





 и. _________________________________
и. _________________________________

 и. _________________________________
и. _________________________________

Leave A Comment