Площадь поверхности цилиндра – формула полной и боковой площади поверхности
4.6
Средняя оценка: 4.6
Всего получено оценок: 9392.
4.6
Средняя оценка: 4.6
Всего получено оценок: 9392.
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.
Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr2 + πr2 = 2πr2.
Боковая поверхность цилиндра
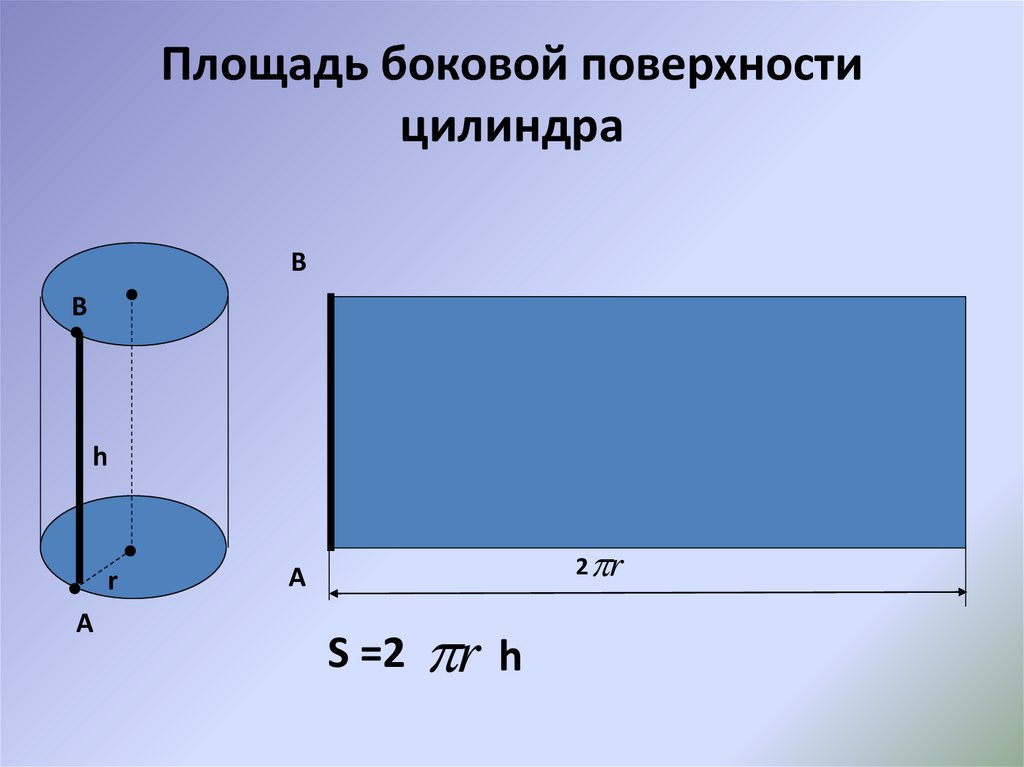
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника.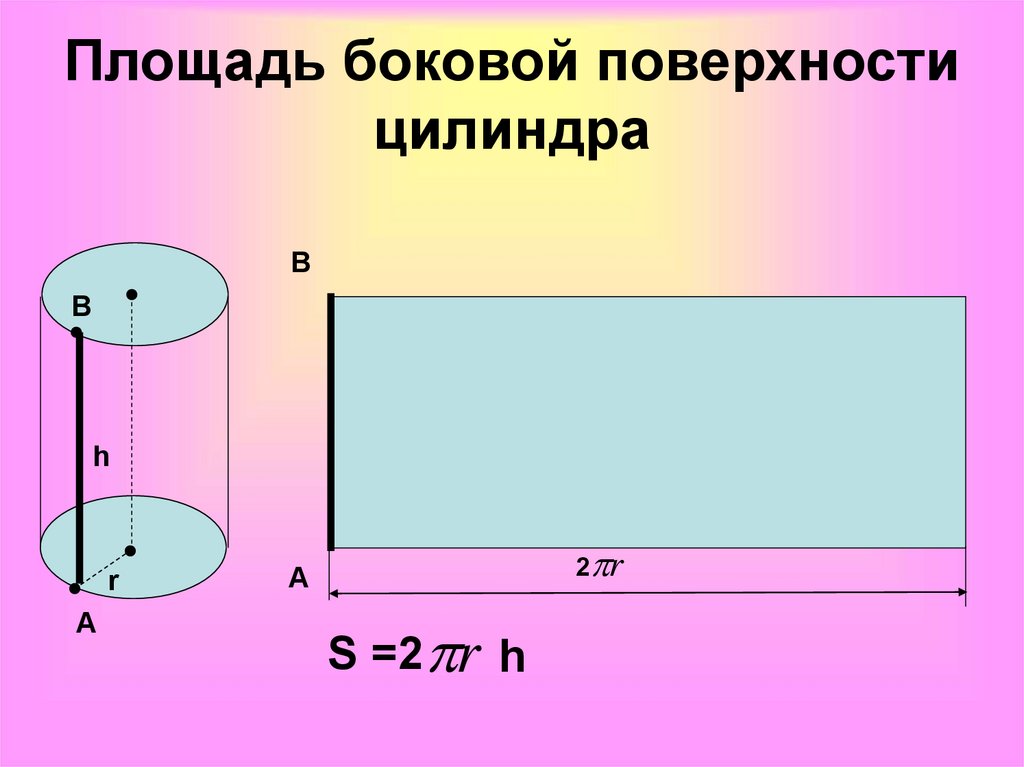
Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
Sбок. = 2πrh
r – радиус цилиндра, h – высота цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.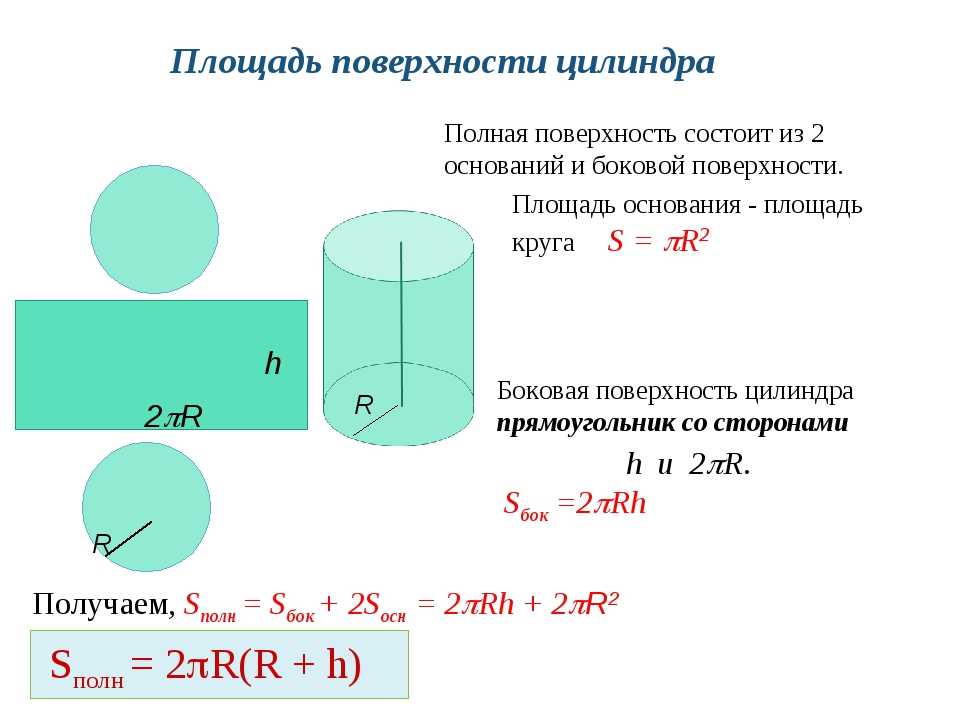
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь боковой поверхности рассчитывается по формуле: Sбок. = 2πrh
Sбок. = 2 * 3,14 * 2 * 3
Sбок. = 6,28 * 6
Sбок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr
S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
S = 376,8
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок.
= 2πrh следует, что высота равна:
h = Sбок./2πr
Значение радиуса получаем из формулы: d = 2r
h = 24π / (2π * 0,5d)
h = 24π / (2π * 0,5 * 3)
h = 8
Высота цилиндра равна 8.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Dark Spyro
5/5
Татьяна Матвиенко
5/5
Юрий Евдокимов
5/5
Михаил Чепурной
5/5
Дмитрий Новиков
5/5
Дилноза Саипова
4/5
Darya Simonova
5/5
Тамара Иванова
5/5
Татьяна Немчинова
5/5
Рамиль Сагиров
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 9392.
А какая ваша оценка?
Как найти площадь поверхности цилиндра: боковую, основания, полную
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
ru Математика Геометрия Нахождение площади поверхности цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см.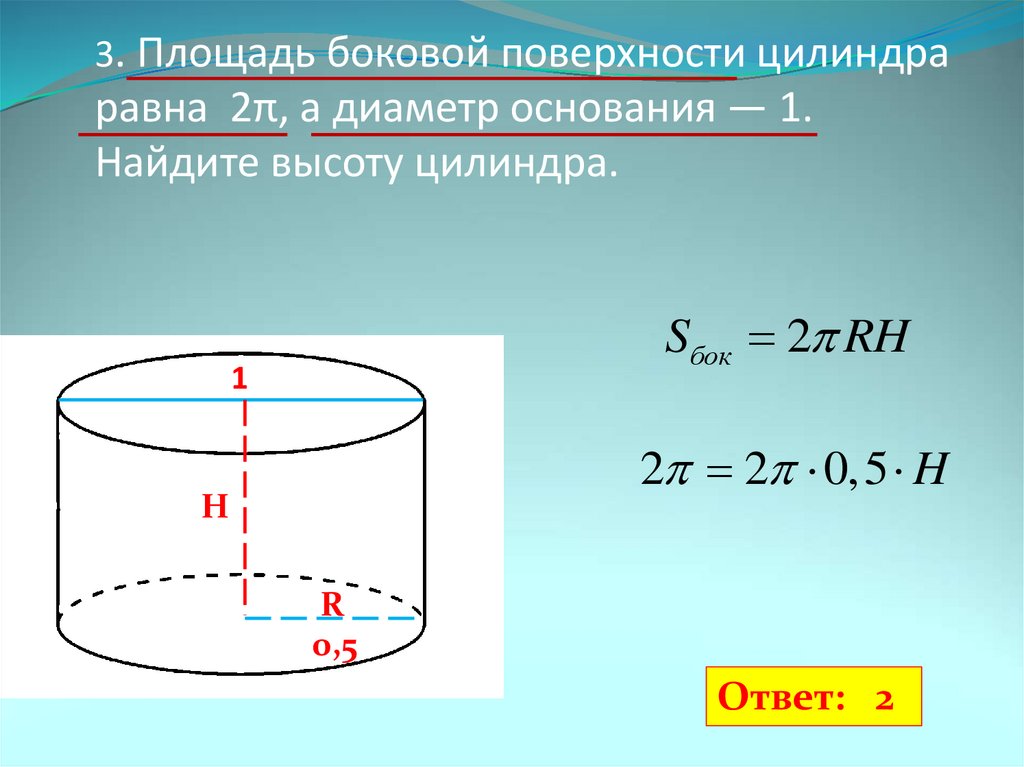
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Площадь поверхности цилиндра
Горячая математика Поскольку
цилиндр
тесно связана с
призма
, формулы их
площадь поверхности
относятся к.
Вспомните формулу площади боковой поверхности призмы. п час а общая площадь поверхности п час + 2 Б . Поскольку основанием цилиндра является окружность, подставляем 2 π р для п и π р 2 для Б где р это радиус основания цилиндра.
Итак, формула для площадь боковой поверхности цилиндра л . С . А . «=» 2 π р час .
Пример 1:
Найдите площадь боковой поверхности цилиндра с радиусом основания
3
дюймов и высотой
9дюймы.
л . С . А . «=» 2 π ( 3 ) ( 9 ) «=» 54 π дюймы 2
≈ 169,64 дюймы 2
Общая формула для общая площадь поверхности цилиндра
Т
.
С
.
А
.
«=»
2
π
р
час
+
2
π
р
2
.
Пример 2:
Найдите площадь полной поверхности цилиндра с радиусом основания 5 дюймов и высотой 7 дюймы.
Т . С . А . «=» 2 π ( 5 ) ( 7 ) + 2 π ( 5 ) 2 «=» 120 π дюймы 2 ≈ 376,99 дюймы 2
Площадь поверхности цилиндра
, написанный
Малкольм МакКинси
, проверенный на фактах.
где изогнутая стена встречается с конечными кругами, и изогнутая поверхность, протянувшаяся между двумя круглыми концами.
Вы сталкиваетесь с цилиндрами в повседневной деятельности, например, когда едите банку газировки, открываете металлическую банку с едой или шлепаете своих друзей цилиндрической лапшой для бассейна. Цилиндр математически представляет собой трехмерный объект, пару конгруэнтных окружностей, разделенных изогнутой поверхностью.
Цилиндр представляет собой трехмерное твердое тело, имеющее высоту ( h ) , ширину ( w ) ,0058 D ) и длина ( л ) . Поскольку он трехмерный, его площадь поверхности составляет , а не просто площадь (площадь обычно ассоциируется только с двумерными формами, такими как круг или прямоугольник).
Цилиндры обычно имеют стороны, перпендикулярные их концам, что делает их правильными цилиндрами .
Цилиндры тоже могут быть наклонными. Два их круглых конца могут не совпадать, поэтому стена или изогнутая поверхность наклоняются, как косой цилиндр известной Пизанской башни.
Площадь поверхности цилиндра
Когда мы говорим о площади поверхности цилиндра, мы имеем в виду две площади поверхности: площадь боковой поверхности и общую площадь поверхности . Общая площадь поверхности обычно называется площадью поверхности.
Если вас просят найти площадь поверхности цилиндра, то вы хотите найти площади двух концов и криволинейной поверхности.
Убедитесь, что вы понимаете связь между радиусом, диаметром и ππ, поскольку все они играют роль в определении площади поверхности правильного цилиндра.
Диаметр и радиус цилиндра определяются двумя окружностями, которые обычно считаются основаниями или верхом и низом цилиндра, хотя нет математической причины, по которой цилиндр мог бы стоять. Подумайте о цистернах в поезде; они представляют собой цилиндры «по бокам», их основания с обоих концов.
Все, что вы делаете при вычислении площади поверхности, это измеряете площадь двух кругов, высоту h цилиндра и используете π для их соотношения.
Площадь поверхности цилиндра формула
Формула площади поверхности цилиндра:
В этой формуле a — это общая площадь поверхности, r — это радиус окружностей. на обоих концах, h это высота, а 9{2}часть 2πr2). Если вы видите фразу «площадь основания цилиндра», автор имеет в виду верхний и нижний концы, а не изогнутую поверхность между ними.
Площадь всегда будет выражаться в квадратных единицах вытекающих из линейных единиц в задаче, поскольку любые две линейные меры, умноженные друг на друга, дают квадратные единицы.
Площадь боковой поверхности цилиндра
Как упоминалось выше, существует также площадь боковой поверхности объекта. Боковая поверхность объекта определяется как площадь всех сторон объекта, исключая площадь его основания и вершины.
Для цилиндра площадь боковой поверхности — это изогнутая поверхность, соединяющая основание и вершину.
Формула площади боковой поверхности
Формула для расчета площади боковой поверхности аналогична приведенной выше формуле площади поверхности, но поскольку мы не учитываем верх или основание, мы должны удалить эту часть формулы. Формула площади боковой поверхности:
Как найти площадь поверхности цилиндра
Возьмите картонный цилиндр из сердцевины рулона бумажных полотенец. Представьте, что это диаметром 1,7 дюйма , длиной 11 дюймов .
Зная, что картонная трубка 1,7 дюймов в ширину и 11 дюймов в длину, если бы мы закрыли концы, какова была бы его поверхность?
Здесь у нас не было радиуса, r ; Нам сказали диаметр, но, напоминав о взаимосвязи между частями кружков, мы помним:
, положив значения R и H в формулу, используя 3.14 для π :
для π :
9002 9 0002 9002 9 0002 9002 .
Leave A Comment