Площадь шара площадь сферы: Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Шар, сфера и их части

      Введем следующие определения, связанные с шаром, сферой и их частями.

      Определение 1. Сферой с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   равно   r   (рис. 1).

      Определение 2. Шаром с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   не превосходит   r   (рис. 1).

Рис.1

      Таким образом, сфера с центром в точке   O   и радиусом   r   является поверхностью шара с центром в точке   O   и радиусом   r.

      Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).

      Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

      Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями   (рис. 2).

Рис.2

      Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

      Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

      Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

      Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.

      Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

      Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

Рис.3

      Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

      Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.

Рис.4

      По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

Рис.5

      Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).

Рис.6

      Высотой шарового сектора называют высоту его сферического сегмента.

      Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.

Площади сферы и ее частей. Объемы шара и его частей

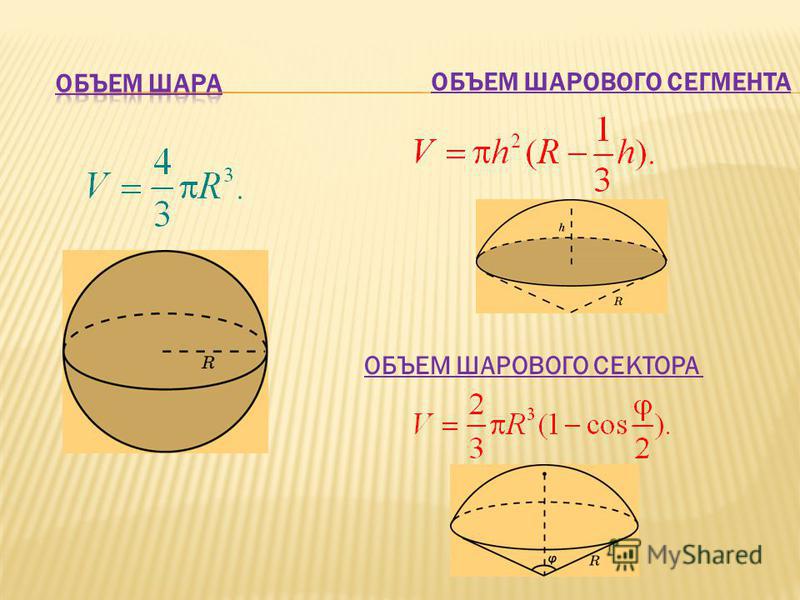
      В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)

2 + (z — z₀)² = R²

3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φy = y₀ + R · sin θ · sin φz = z₀ + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары

пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность

и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними. Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Как найти объём шара. Геометрия, 11 класс: уроки, тесты, задания.

1.	Отношение радиусов и объёмов двух шаров Сложность: лёгкое	1
2.	Шар, вписанный в куб Сложность: лёгкое	1
3.	Два шаровых сегмента Сложность: лёгкое	1
4.	Oбъём шарового сегмента по формуле Сложность: лёгкое	1
5.	Цилиндр, вписанный в шар Сложность: лёгкое	2
6.	Конус, вписанный в шар Сложность: лёгкое	1
7.	Вычисление объёма шара с использованием площади сферической поверхности Сложность: лёгкое	1
8.	Площадь сферы Сложность: лёгкое	2
9.	Объём шарового сегмента Сложность: среднее	3
10.	Шар касается плоскости Сложность: среднее	2
11.	Площадь поверхности шара, вписанного в цилиндр Сложность: среднее	2
12.	Cумма объёмов трёх шаров Сложность: среднее	2
13.	Шар, вписанный в конус Сложность: среднее	3
14.	Цилиндрическое отверстие в шаре Сложность: сложное	4
15.	Толщина плёнки мыльного пузыря Сложность: сложное	4
16.	Цилиндр наибольшего объёма Сложность: сложное	6

Площадь сферы

На этом уроке мы поговорим о формуле для вычисления площади поверхности сферы. Узнаем, какой многогранник называется описанным около сферы. А также решим несколько задач на применение формулы для вычисления площади сферы.

Прежде чем приступить к рассмотрению данной темы, давайте вспомним, что такое сфера.

Итак, сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Причём, данная точка называется центром сферы, а данное расстояние – радиусом сферы.

Ранее вы уже познакомились с понятием касательной плоскости к сфере, её свойством, а также с признаком касательной плоскости к сфере.

Вспомним их. Итак, плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

Свойство касательной плоскости к сфере: радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Признак касательной плоскости к сфере: если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Перейдём к рассмотрению вопроса о нахождении площади сферы.

В отличие от боковых поверхностей цилиндра и конуса сферу нельзя развернуть так, чтобы получилась плоская фигура.

Поэтому для сферы не подходит способ определения и вычисления площади поверхности с помощью развертки.

Для определения площади сферы воспользуемся понятием описанного многогранника.

Определение:

Многогранник называется описанным около сферы (шара), если сфера касается всех его граней.

При этом сфера называется вписанной в многогранник.

Говорят, что сфера касается грани многогранника, если плоскость грани является касательной к сфере и точка касания принадлежит грани. Понятно, что центр О сферы с радиусом , вписанной в многогранник, находится на расстоянии, равном радиусу  сферы, от каждой из плоскостей, содержащих грани многогранника.

На экране вы видите примеры описанных около сферы многогранников.

Тетраэдр, куб и октаэдр называются описанными около сферы. В свою очередь, сфера называется вписанной в многогранник. Обратите внимание, плоскость каждой грани многогранника является касательной к сфере.

Рассмотрим последовательность описанных около данной сферы многогранников. То есть пусть около сферы описан многогранник, который имеет  граней.

Будем неограниченно увеличивать число  граней так, чтобы при этом наибольший размер каждой грани многогранника стремился к нулю.

Наибольшим размером грани мы будем называть наибольшее расстояние между двумя точками грани. Например, если грань является прямоугольником, то её наибольший размер равен диагонали. Представим себе, что количество граней многогранника стало бесконечно много. Тогда площадь поверхности многогранника будет приближаться к площади сферы.

За площадь сферы можно принять предел последовательности площадей поверхностей этих многогранников при стремлении к нулю наибольшего размера каждой грани, который равен . Существование этого предела мы докажем при изучении объема шара.

Таким образом, площадь сферы можно вычислить по формуле , где  – радиус сферы.

Задача: найдите площадь сферы, радиус которой равен  см.

Решение: запишем формулу для вычисления площади сферы.

По условию задачи радиус сферы равен  см. Подставим длину радиуса в формулу. Получим, что площадь сферы равна . Запишем ответ.

Задача: площадь сферы равна  см². Найдите радиус сферы.

Решение: запишем формулу для вычисления площади сферы.

И выразим из неё радиус. Получили, что радиус сферы можно вычислить по формуле: . Не забудем записать ответ.

Задача: площадь сечения сферы, проходящего через её центр, равна  см². Найдите площадь сферы.

Решение: запишем формулу для вычисления площади сферы.

Рассмотрим внимательно рисунок.

Напомним, что сечение сферы плоскостью есть окружность. Так как по условию задачи сечение сферы проходит через её центр, то сечение будет иметь радиус равный радиусу сферы .

Площадь сечения (окружности) вычисляется по формуле . Отсюда, найдём радиус  (см).

Подставим найденный радиус в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

Запишем ответ.

Задача: около сферы описан куб с ребром, равным  см. Вычислите площадь сферы.

Решение: запишем формулу для вычисления площади сферы.

Напомним, что многогранник называется описанным около сферы, если сфера касается всех его граней.  

При этом плоскость каждой грани куба является касательной к сфере. А по свойству касательной плоскости к сфере: радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Значит, диаметр нашей сферы равен длине ребра куба  (см). Отсюда, радиус сферы равен  (см).

Подставим радиус сферы в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

Не забудем записать ответ.

Итоги:

На этом уроке мы вспомнили формулу для вычисления площади поверхности сферы. Узнали, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.

 

Сфера. Уравнение сферы. Площадь сферы и шара

1. Сфера . 11 класс.

2. ДЗ учить формулы ц+ к+ с+ ш № 582,584 циркуль доклады-2

Зачерпни воду,
и луна окажется в твоей руке…
Китайская мудрость
ДЗ
учить формулы ц+ к+ с+ ш
№ 582,584
циркуль
доклады-2
Определение сферы!
Сферой называется поверхность, состоящая из всех
точек пространства, расположенных на данном
расстоянии (R) от данной точки (центра — точки О).
dО
R
т. О – центр сферы
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.
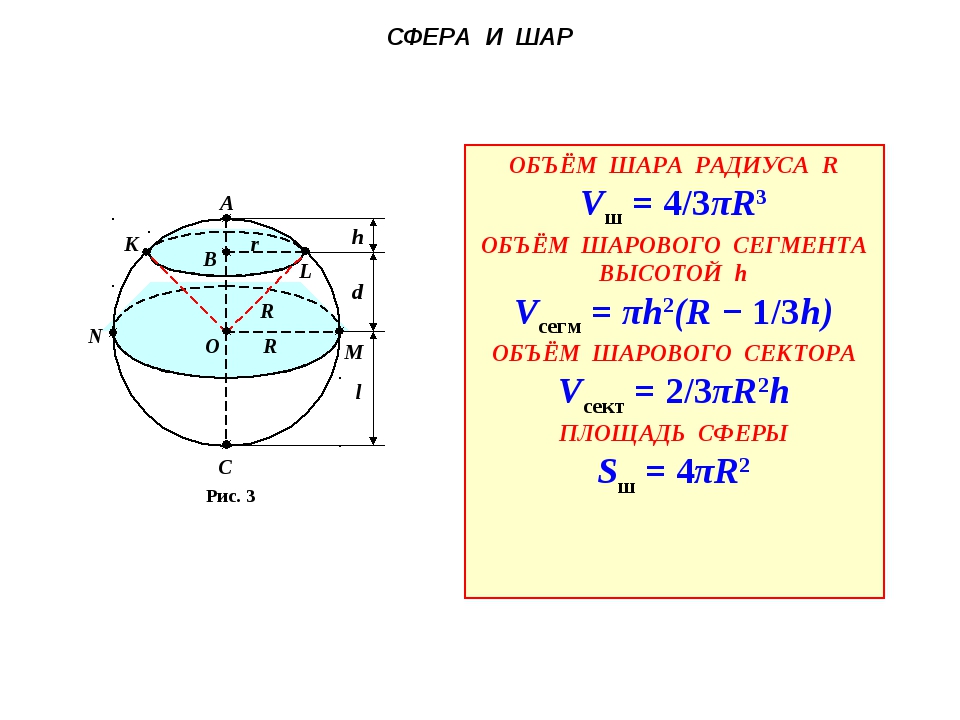
d – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через центр.
Уравнение
сферы !
R = (x–x0)2+(y–y0)2+(z–z0)2
CM
M(x;y;z)
I
I
z
I
I
I
C(x0;y0;z0)
I
I
I
y
x
R2
2+(y–y )2+(z–z )2
(x–x
)
=
0
0
0
Задача 1
Зная координаты центра С(0;-3;9) и радиус сферы
R=1,5, запишите уравнение сферы!
Решение:
Так как уравнение сферы с радиусом R и
центром в точке С(х0;у0;z0) имеет вид
(х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты
центра данной сферы С(0;-7;1,3) и радиус
R=1,5, то уравнение данной сферы
x2 + (y+7)2 + (z-1,3)2=2,25
Ответ: x2 + (y+7)2 + (z-9)2=2,25
Уравнение сферы
Центр
r
C(1;-2;-5)
r=2
C(-5;3;0)
C(-1;0;0)
r=5
r= 8
C(0;-2;-8)
C(0;0;0)
r= 2
r=3
C(3; 2;0)
C(-7; 5;-1)
r = 0,3
r = 2,5
5
r= 2
C(0;-4;9)
Уравнение сферы
Центр
r
Найди ошибки:
(x–1)2+(y+2)2+(z+5)2 = 4
C(1;-2;-5)
r=2
(x+5)2+(y–3)2 + z2 = 25
C(-5;3;0)
(x +
— 1 )2 + y 2 + z 2 = 8
C(-1;0;0)
r=5
r= 8
x2 +(y+2)2 +(z+8)2 = 2
C(0;-2;-8)
C(0;0;0)
r= 2
r=3
x 2 + y 2 + z 2= 9
(x–3 )2+(y–2)2 + z 2 = 0,09
0,9
C(3; 2;0)
(x+7)2+(y–5)2 +(z+1)2 = 2,5 C(-7; 5;-1)
1
2
2
2
C(0;-4;9)
x +(y+4) + (z+4) = 6 4
r = 0,3
r = 2,5
5
r= 2
Площадь сферы и шара
Сферу нельзя развернуть на плоскость.
Площадь сферы радиуса R:
Sсф=4πR2
Sшара=4 Sкруга
т.е.: площадь поверхности шара
равна учетверенной площади
большего круга
Задача 2
Найти площадь поверхности сферы,
радиус которой равен 6 см.
Дано:
сфера
R = 6 см
Найти:
Sсф = !
Решение:
1. Sсф = 4πR2
2. Sсф = 4π 62 = 144π ( см2)
Ответ: 144π см2
Задача 3
Найти площадь поверхности шара, площадь
центрального сечения которого равна 6.
Найти площадь поверхности шара, площадь
центрального сечения которого равна 0,8.
Найти площадь поверхности шара, площадь
центрального сечения которого равна 30,5.
№ 4 Вершины треугольника АВС лежат на сфере радиуса 13
см. Найдите расстояние от центра сферы до плоскости
треугольника, если АВ=6см, ВС=8см, АС=10см.
102=82+62 ABC прямоуголь ный
А
С
O1
А
В
O
O1
В
С
№ 5 Все стороны ромба, диагонали которого равны 15см и
20см, касаются сферы радиуса 10см. Найдите расстояние от
плоскости сферы до плоскости ромба.
D
F
M
K
C
O1
A
N
P
B
D
O
K
M
C
A
P
N
B
Итоги урока:
Сегодня мы вспомнили:
определение и уравнение сферы;
некоторые сведения из планиметрии;
Познакомились с :
сечениями сферы и шара;
площадью поверхности сферы и шара;
интересными научными фактами о сфере и шаре.
Применяли на практике знания и
оценивали свои действия.
Спасибо за работу!
Спасибо за работу!

Площадь сфера и шар. Шар и сфера, объем шара, площадь сферы, формулы

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr 3 ,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

Объём шарового сегмента можно найти по формуле:

V = πh 2 (R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.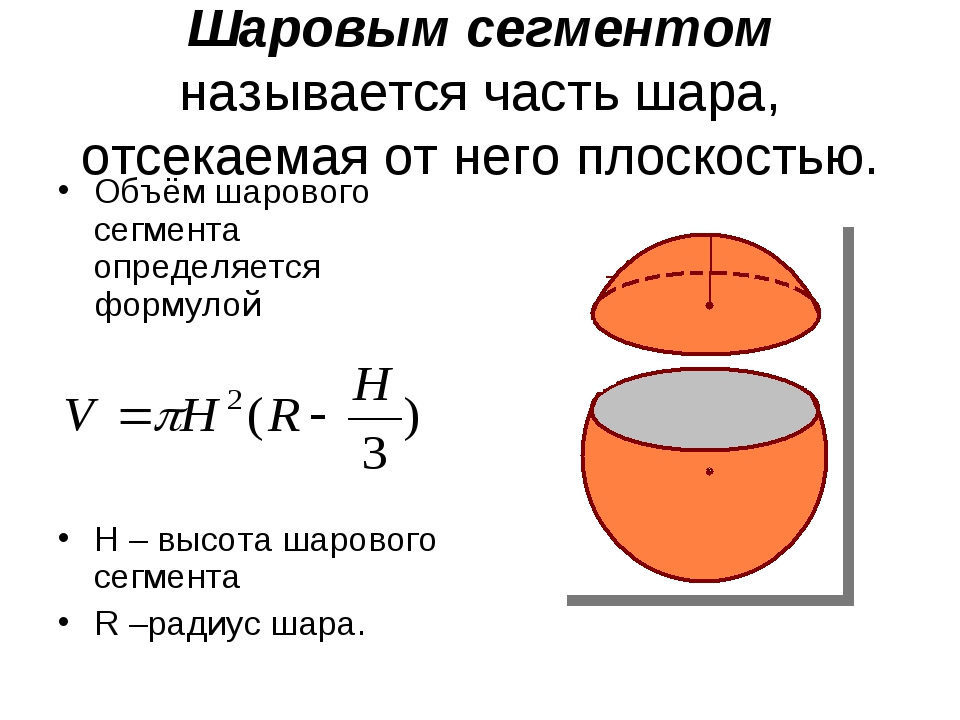

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR 2 H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr 3 ,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

Объём шарового сегмента можно найти по формуле:

V = πh 2 (R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR 2 H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Для получения грамотного ответа на вынесенный в заголовок вопрос читателю статьи потребуется хорошенько напрячь свои способности к абстрактному мышлению и как следует углубиться в определённые разделы математики, что ему доводилось изучать в школе. А для стимуляции воображения нелишним будет напомнить, что «Образование есть то, что остаётся после того, когда забывается всё, чему нас учили» (авторство фразы приписывается А.Эйнштейну).

Небольшое погружение в один из разделов математики

Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений. Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении.

Одно из таких базовых понятий — это геометрическая точка . Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.

Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».

Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы». Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!

Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).

Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т. д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).

Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.

Резюме

И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.

Сфера — это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.

Сфера: понятие в геометрии

Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние — это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).

На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка — центр сферы.

Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.

Сфера и шар: в чем разница и в чем сходство?

Часто школьники путают эти две фигуры, которые внешне похожи друг на друга, но обладают совершенно разными физическими свойствами. Сфера и шар в первую очередь отличаются своей массой: сфера — это бесконечно тонкий слой, шар же — это объемное тело конечной плотности, которая одинакова во всех его точках, ограниченных сферической поверхностью. То есть шар обладает конечной массой и является вполне реальным объектом. Сфера — это фигура идеальная, не имеющая массы, которая в действительности не существует, но она является удачной идеализацией в геометрии при изучении ее свойств.

Примерами реальных объектов, форма которых практически соответствует сфере, являются новогодняя игрушка в виде шарика для украшения елки или мыльный пузырь.

Что касается сходства между рассматриваемыми фигурами, то можно назвать следующие их признаки:

• обе они обладают одинаковой симметрией;
• для обеих формула площади поверхности является одинаковой, более того, они обладают равной площадью поверхности, если их радиусы равны;
• обе фигуры при равных радиусах занимают одинаковый объем в пространстве, только шар его заполняет полностью, а сфера лишь ограничивает своей поверхностью.

Сфера и шар равного радиуса приведены на рисунке ниже.

Заметим, что шар, так же как и сфера, является телом вращения, поэтому его можно получить, если вращать вокруг диаметра круг (не окружность!).

Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S — двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан — это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R 2 .

Геометрические свойства сферы

Из приведенного описания этой фигуры можно самостоятельно догадаться об этих свойствах. Они следующие:

• Любая прямая, которая пересекает сферу и проходит через ее центр, является осью симметрии фигуры. Поворот сферы вокруг этой оси на любой угол переводит ее в саму себя.
• Плоскость, которая пересекает рассматриваемую фигуру через ее центр, делит сферу на две равные части, то есть является плоскостью отражения.

Площадь поверхности фигуры

Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:

S = 4*pi*R 2 , где pi ≈ 3,1416.

Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:

Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.

Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:

Ω = S/R 2 = 4*pi*R 2 /R 2 = 4*pi стерадиан.

Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.

Поверхность планеты Земля

Формулу сферы можно применить для определения на которой мы живем. Перед тем как приступать к вычислениям, следует сделать пару оговорок:

• Во-первых, Земля не обладает идеальной сферической поверхностью. Ее экваториальный и полярный радиусы равны 6378 км и 6357 км соответственно. Отличие между этими цифрами не превышает 0,3%, поэтому для расчета можно взять средний радиус 6371 км.
• Во-вторых, рельеф является трехмерным, то есть на ней имеются впадины и горы. Эти характерные особенности планеты приводят к увеличению ее площади поверхности, тем не менее, в расчете их учитывать не будем, поскольку даже самая большая гора, Эверест, составляет 0,1% от земного радиуса (8,848/6371).

Используя формулу сферы, получаем:

S = 4*pi*R 2 = 4*3,1416*6371 2 ≈ 510,066 млн. км 2 .

Россия, по официальным данным, занимает площадь 17,125 млн км 2 , что составляет 3,36% от поверхности планеты. Если же учесть, что к суше относятся лишь 150,387 млн км 2 , тогда площадь нашей страны составит 11,4% от всей территории, не покрытой водой.

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

Сфера , как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами наблюдается и в некоторых других аспектах:

• Все точки шара находятся на одинаковом расстоянии от центра, при этом тело ограничено поверхностью (сферой, которая является пустой внутри). Иными словами, сфера полая. Обычно для простоты понимания приводят простой пример с воздушным и бильярдным шаром. Оба этих предмета называют шарами, однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.
• Сфера имеет свою площадь, но при этом у нее нет объема. Шар же наоборот: его объем можно вычислить, в то время как у него нет площади. Кто-то может сказать, что это главный признак отличия, но он проявляется только в том случае, если необходимо производить какие-то расчеты (сложные геометрические формулы). Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри.
• Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра. Радиусом может называться любой отрезок, соединяющий точку на сфере с ее центром. Все эти отрезки равны между собой. Что касается шара, то лежащие внутри него точки удалены от центра меньше, чем на радиус (как раз из-за ограничивающей его сферы).

Выводы сайт

1. Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
2. Сфера имеет площадь и не имеет объем, шар же наоборот.
3. Третье отличие – это измерение радиуса двух геометрических тел.

Как найти радиус сферы формула. Шар и сфера, объем шара, площадь сферы, формулы

Определение.

Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара :

V =	4	π R 3 =	1	π D 3
	3		6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4π R 2 = π D 2

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :

(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m

Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R 2 — m 2 ,

Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2π Rh

Примечание . Это часть урока с задачами по геометрии (раздел стереометрия, задачи о сфере). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом на форуме . В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».

Задача
В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы.

Решение .
Площадь сферы найдем по формуле:

Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы (180-60) / 2 = 60 , то есть все углы равны).

Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть

Таким образом площадь сферы

S = 4π(√3/3 l) 2
S = 4/3πl 2

Ответ : площадь сферы равна 4/3πl 2 .

Задача

Емкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость?

Решение .
Площадь поверхности фигуры будет равна половине площади сферы и площади сечения сферы.
Поскольку нам известна длина окружности основания, найдем ее радиус:
L = 2πR
Откуда
R = L / 2π
R = 46 / 2π
R = 23 / π

Откуда площадь основания равна
S = πR 2
S = π (23/π) 2
S = 529 / π

Площадь сферы найдем по формуле:
S = 4πr 2

Соответственно площадь полусферы
S = 4πr 2 / 2
S = 2π (23/π) 2
S = 1058 / π

Общая площадь поверхности фигуры равна:
529 / π + 1058 / π = 1587 / π

Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров)
1587 / π * 300 / 10 000 = 47,61 / π граммов ≈ 15,15 г

Задача

Решение. Рiшення .

	Для пояснения решения прокомментируем каждую из приведенных формул Воспользуемся формулой нахождения поверхности шара и запишем ее для первого шара, предположив, что его радиус равен R 1 Площадь поверхности второго шара запишем с помощью точно такой же формулы, предположив, что его радиус равен R 2 Найдем соотношение их площадей, разделив первое выражение на второе. Сократим полученную дробь. Нетрудно заметить, что соотношение площадей двух шаров равно соотношению квадратов их радиусов. По условию задачи это соотношение равно m/n Из полученного равенства найдем соотношение радиусов шаров путем извлечения квадратного корня. Полученное равенство запомним Воспользуемся формулой нахождения объема шара и запишем ее для первого шара с радиусом R 1 Объем второго шара запишем с помощью той же самой формулы, подставив в нее радиус R 2	Для пояснення рішення прокоментуємо кожну з приведених формул Скористаємося формулою знаходження поверхні кулі і запишемо її для першої кулі, передбачивши, що його радіус рівний R 1 Площу поверхні другої кулі запишемо за допомогою точний такої ж формули, передбачивши, що його радіус рівний R 2 Знайдемо співвідношення їх площ, розділивши перше вираження на друге. Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n З отриманої рівності знайдемо співвідношення радіусів куль шляхом витягання квадратного кореня. Отриману рівність запам»ятаємо Скористаємося формулою знаходження об»єму кулі і запишемо її для першої кулі з радіусом R 1 Об»єм другої кулі запишемо за допомогою тієї ж самої формули, підставивши в неї радіус R 2
	8. Разделим объемы первого и второго шара друг на друга 9. Сократим получившуюся дробь. Заметим, что соотношение объема двух шаров равно соотношению кубов их радиусов. Учтем выражение, полученное нами ранее в формуле 4 и подставим его. Поскольку корень квадратный — это число в степени 1/2, преобразуем выражение 10. Раскроем скобки и запишем полученное соотношение в виде пропорции. Ответ получен .	8. Розділимо об»єми першої і другої кулі один на одного 9. Скоротимо дріб, що вийшов. Відмітимо, що співвідношення об»єму двох куль дорівнює співвідношенню кубів їх радіусів. Врахуємо вираження, отримане нами раніше у формулі 4 і підставимо його. Оскільки корінь квадратний — це число в мірі 1/2, перетворимо вираження 10. Розкриємо дужки і запишемо отримане співвідношення у вигляді пропорції. Відповідь отримана .

Площадь искривленной поверхности, которую нельзя развернуть на плоскость, вычисляют так. Разбивают поверхность на такие куски, которые уже достаточно мало отличаются от плоских. Потом находят площади этих кусков, как если бы они были плоскими (например, заменяя их проекциями на плоскости, от которых поверхность мало отклоняется). Сумма их площадей и даст приближенно площадь поверхности. Так поступают на практике: площадь поверхности купола получается как сумма площадей покрывающих его кусков листового металла (рис. 17.5). Еще

лучше это видно на примере земной поверхности. Она искривлена — примерно сферическая. Но участки, небольшие в сравнении с размерами всей Земли, измеряют как плоские.

Вычисляя плоскость сферы, описывают вокруг нее близкую к ней многогранную поверхность. Ее грани будут приближенно представлять куски сферы, а ее площадь дает приближенно площадь самой сферы. Ее дальнейшее вычисление основано на следующей лемме.

Лемма. Объем многогранника Р, описанного вокруг сферы радиуса R, и площадь его поверхности связаны соотношением

Замечание: Аналогичным соотношением связаны площадь многоугольника Q, описанного вокруг круга радиуса и его периметр (рис. 17.6):

Опишем вокруг сферы какой-либо многогранник Р. Пусть у него граней Разобьем Р на пирамиды с общей вершиной в центре О и с гранями в основаниях (рис. 17.7).

Каждая такая грань лежит в касательной плоскости сферы и, значит, перпендикулярна радиусу сферы в точке касания. Значит, этот радиус есть высота пирамиды Поэтому ее объем будет:

где — площадь грани Сумма этих площадей дает площадь поверхности многогранника Р, а сумма объемов пирамид — его объем Поэтому

Теорема (о площади сферы). Площадь сферы радиуса R выражается формулой:

Пусть дана сфера радиуса R. Возьмем на ней П точек, не лежащих в одной полусфере, и проведем через них касательные плоскости к сфере. Эти плоскости ограничат многогранник описанный вокруг сферы. Пусть — объем многогранника — площадь его поверхности, V — объем шара, ограниченного рассматриваемой сферой, и S — ее площадь.

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Шар

Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.

Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.

Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.

Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.

Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.

Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.

Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

Калькулятор сфер

Форма сферы

r = радиус
В = объем
A = площадь поверхности
C = окружность
π = пи = 3,1415926535898
√ = квадратный корень

Использование калькулятора

Этот онлайн-калькулятор рассчитает 3 неизвестных значения сферы для любой 1 известной переменной, включая радиус r, площадь поверхности A, объем V и длину окружности C. 3 \]

\ [V \ около 4.{1/3} \]

\ [r = \ sqrt {\ frac {A} {4 \ pi}} \]

\ [r \ приблизительно 0,2821 \ sqrt {A} \]

\ [r = \ frac {C} {2 \ pi} \]

\ [r \ приблизительно 0,1592C \]

Окружность сферы

\ [C = 2 \ pi r \]

\ [C \ около 6.{1/3} \]

\ [C = \ sqrt {\ pi A} \]

\ [C \ приблизительно 1.77245 \ sqrt {A} \]

Расчет сфер:

Используйте следующие дополнительные формулы наряду с формулами выше.

• Зная радиус сферы, вычислите объем, площадь поверхности и длину окружности.
  Дано r найти V, A, C
• Зная объем сферы, вычислите радиус, площадь поверхности и длину окружности.
  Для данного V найти r, A, C
• Зная площадь поверхности сферы, вычислите радиус, объем и длину окружности.
  Дано A найти r, V, C
• По окружности сферы вычислить радиус, объем и площадь поверхности.
  Для данного C найти r, V, A

Площадь поверхности сферы

Греческий математик Архимед обнаружил, что площадь поверхности из сфера такая же, как и площадь боковой поверхности цилиндр имеющий тот же радиус, что и сфера, и высоту, равную длине диаметра сферы.

Площадь боковой поверхности цилиндра равна 2 π р час где час знак равно 2 р .

Площадь боковой поверхности цилиндра знак равно 2 π р ( 2 р ) знак равно 4 π р 2 .

Следовательно, площадь поверхности сферы радиуса р равно 4 π р 2 .

Пример :

Найдите площадь поверхности сферы радиуса 5 дюймы.

S .А . знак равно 4 π ( 5 ) 2 знак равно 100 π дюймы 2 ≈ 314.16 дюймы 2

Площадь поверхности сферы

Напомним наш последний раздел доказательства. После вращения полукруга вокруг оси xxx мы получим площадь поверхности сферы, и если мы разрежем только частичный участок с параллельными основаниями, новая площадь поверхности будет продемонстрирована на изображении ниже:

На изображении боковая поверхность секции окрашена в голубой цвет с двумя круглыми основаниями разного радиуса.Чтобы лучше визуализировать высоту секции, эта секция будет повернута на 90 градусов, как показано ниже:

Теперь внутри секции есть 2 переменных угла, ∠a \ angle a∠a и ∠b \ angle b∠b, которые появляются как неотъемлемые границы разрезаемой секции.

Из заключения доказательства площадь поверхности сечения (A ‘) (A’) (A ‘) может быть рассчитана как

A ′ = 2πr2∫absin⁡ (t) dt = 2πr2 [−cos⁡ (t) ∣ab] = (2πr) r [cos⁡ (a) −cos⁡ (b)].яркий] \\ & = (2 \ pi r) r \ big [\ cos (a) — \ cos (b) \ big]. \ end {align} A ′ = 2πr2∫ab sin (t) dt = 2πr2 [−cos (t) ∣ab] = (2πr) r [cos (a) −cos (b)].

Рассматривая прямоугольные треугольники с радиусом rrr (толстый красный) на изображении, очевидно, что rrr является стороной гипотенузы для обоих. В результате вертикальные стороны могут быть вычислены как r × cos⁡ (a) r \ times \ cos (a) r × cos (a) и r × cos⁡ (b) r \ times \ cos (b) r × cos (b) для левого и правого треугольников соответственно.

Следовательно, высота секции равна h = (r × cos⁡ (a)) — (r × cos⁡ (b)) = r [cos⁡ (a) −cos⁡ (b)] h = \ big ( r \ times \ cos (a) \ big) — \ big (r \ times \ cos (b) \ big) = r \ big [\ cos (a) — \ cos (b) \ big] h = (r × cos (a)) — (r × cos (b)) = r [cos (a) −cos (b)].

Подстановка этого члена в предыдущее уравнение дает

A ′ = (2πr) r [cos⁡ (a) −cos⁡ (b)] = 2πrh.A ‘= (2 \ pi r) r \ big [\ cos (a) — \ cos (b) \ big ] = 2 \ pi rh. A ′ = (2πr) r [cos (a) −cos (b)] = 2πrh.

Ясно, что это формула для боковой поверхности цилиндра с радиусом rrr и высотой hhh!

Это означает, что площадь боковой поверхности сечения сферы равна площади боковой поверхности цилиндра с радиусом rrr и высотой h, h, h, как показано на изображении, и это верно для любого уровня рассматриваемой сферы.□ _ \ квадрат □

Площадь поверхности сферы — объяснения и примеры

Сфера — одна из важных трехмерных фигур в геометрии. Напомним, сфера — это трехмерный объект, каждая точка которого находится на одинаковом расстоянии (одинаковом расстоянии) от фиксированной точки, известной как центр сферы. Диаметр сферы делит ее на две равные половины, называемые полусферами.

Площадь поверхности сферы — это мера области, покрытой поверхностью сферы.

Из этой статьи вы узнаете, как найти площадь поверхности сферы, используя формулу площади поверхности сферы .

Как найти площадь поверхности сферы?

Как и у круга, расстояние от центра сферы до поверхности называется радиусом. Площадь поверхности сферы в четыре раза больше площади круга того же радиуса.

Формула площади поверхности сферы

Формула площади поверхности сферы определяется как:

Площадь поверхности сферы = 4πr ² квадратных единиц …………….(Формула площади поверхности сферы)

Для полусферы (половины сферы) площадь поверхности определяется выражением;

Площадь поверхности полусферы = ½ × площадь поверхности сферы + площадь основания (круга)

= ½ × 4π r ² + π r ²

Поверхность полусферы = 3πr ² …………………. (Формула площади поверхности полусферы)

Где r = радиус данной сферы.

Давайте решим несколько примеров задач о площади поверхности сферы.

Пример 1

Вычислите площадь поверхности сферы радиусом 14 см.

Решение

Дано:

Радиус, r = 14 см

По формуле

Площадь поверхности сферы = 4πr ²

При замене получаем

SA = 4 x 3,14 x 14 x 14

= 2461,76 см ² .

Пример 2

Диаметр бейсбольного мяча составляет 18 см.Найдите площадь поверхности мяча.

Решение

Дано,

Диаметр = 18 см ⇒ радиус = 18/2 = 9 см

Бейсбольный мяч имеет сферическую форму, следовательно,

Площадь поверхности = 4πr ²

= 4 x 3,14 x 9 x 9

SA = 1017,36 см ²

Пример 3

Площадь поверхности сферического объекта составляет 379,94 м ² . Каков радиус объекта?

Решение

Дано,

SA = 379.94 м ²

Но, площадь поверхности сферы = 4πr ²

⇒ 379,94 = 4 x 3,14 xr ²

⇒ 379,94 = 12,56r ²

Разделите обе стороны на 12,56, а затем найти квадрат результата

⇒ 379,94 / 12,56 = r ²

⇒ 30,25 = r ²

⇒ r = √30,25

= 5,5

Следовательно, радиус сферического тела равен 5,5 м. .

Пример 4

Стоимость кожи 10 долларов за квадратный метр.Найти стоимость изготовления 1000 футбольных мячей радиусом 0,12 м.

Решение

Сначала найдите площадь поверхности шара

SA = 4πr ²

= 4 x 3,14 x 0,12 x 0,12

= 0,181 м ²

Стоимость изготовления шара = 0,181 м ² x 10 долларов США за квадратный метр

= 1,81 доллара США

Таким образом, общая стоимость изготовления 1000 шаров = 1,81 доллара США x 1000

= 1810 долларов США

Пример 5

Радиус Земли равен Говорят, что это 6 371 км.Какова площадь поверхности Земли?

Решение

Земля — ​​это сфера.

SA = 4πr ²

= 4 x 3,14 x 6,371 x 6,371

= 5,098 x 10 ⁸ км ²

Пример 6

Вычислить площадь поверхности твердой полусферы радиус 10 см.

Решение

Дано:

Радиус, r = 10 см

Для полусферы площадь поверхности определяется как:

SA = 3πr ²

Заменить.

SA = 3 x 3,14 x 10 x 10

= 942 см ²

Итак, площадь поверхности сферы составляет 942 см ² .

Пример 7

Площадь поверхности твердого полусферического объекта составляет 150,86 футов ² . Какой диаметр полушария?

Решение

Дано:

SA = 150,86 футов ² .

Площадь поверхности сферы = 3πr ²

⇒ 150.86 = 3 x 3,14 xr ²

⇒ 150,86 = 9,42 r ²

Разделим обе части на 9,42, чтобы получить,

⇒ 16,014 = r ²

r = √16,014

= 4

Следовательно, радиус составляет 4 фута, но диаметр в два раза больше радиуса.

Итак, диаметр полусферы составляет 8 футов.

Пример 8

Вычислите площадь поверхности сферы, объем которой составляет 1 436,03 мм ³ .

Решение

Поскольку, мы уже знаем, что:

Объем сферы = 4/3 πr ³

1,436,03 = 4/3 x 3,14 xr ³

1,436,03 = 4,19 r ³

Разделим обе стороны на 4,19

r ³ = 343

r = ³ √343

r = 7

Итак, радиус сферы равен 7 мм.

Теперь вычислите площадь поверхности сферы.

Площадь поверхности сферы = 4πr ²

= 4 x 3.14 x 7 x 7

= 615,44 мм ² .

Пример 9

Вычислить площадь поверхности глобуса радиусом 3,2 м

Решение

Площадь поверхности сферы
= 4π r ²
= 4π (3,2) ²
= 4 × 3,14 × 3,2 × 3,2
= 128,6 м ²

Следовательно, площадь поверхности земного шара составляет 128,6 м ² .

Предыдущий урок | Главная страница | Следующий урок

Площадь поверхности сферы

Сфера — это трехмерное пространство, например, в форме футбольного мяча.Сфера — это тело, ограниченное поверхностью, каждая точка которой находится на одинаковом расстоянии (то есть на одинаковом расстоянии) от фиксированной точки, называемой центром или началом сферы.

Подобно кругу в трех измерениях, все точки от центра постоянны. Расстояние от центра до любых точек на границе известно как радиус

сферы . Максимальное прямое расстояние через сферу известно как диаметр сферы. Половина сферы называется полусферой.

Мы можем найти общую площадь поверхности сферы, используя следующую формулу:

SA = 4 π r ²
где r — радиус.

ПРИМЕЧАНИЕ. Значение

π невозможно рассчитать точно, поэтому площадь поверхности сферы является лишь приблизительной.

Площадь поверхности сферы по диаметру = πd ²

где d — диаметр сферы.

Пример 1 : Какова общая площадь поверхности сферы с радиусом 5.5 метров?
Решение:
Учитывая, что:
r = 5.5
Площадь поверхности сферы:
SA = 4 × π × r ²
SA = 4 × π × (5.5) ²
SA = 4 × 3,14 × 30,25
SA = 379,94
Таким образом, площадь поверхности сферы составляет 379,94 м ² .

Пример 2 : Сферический шар имеет площадь поверхности 2464 см ² .Найдите радиус шара с точностью до 2 десятичных знаков, используя π = 3,142.
Решение:
SA = 4 × π × r ²
Чтобы найти r, нам нужно выделить его из приведенного выше уравнения:
r ² = SA / (4π)
r ² = 2464 / (4 × π)
r ² = 196,054
r = √ (196,054)
r = 14,00 см

Найти пример 3 : площадь поверхности шара радиусом 18 см.[ π = 3,14 ]
Решение:
r = 18 см
Площадь поверхности сферы определяется как:
SA = 4 × π × r ²
SA = 4 × π × 18 ²
SA = 4 × π × 342
SA = 4069,44 см ²

Площадь поверхности сферы 4069,44 см2.

Пример 4 : Найдите площадь поверхности сферы, радиус которой равен r = 11 см.
Решение:
Формула для расчета площади поверхности сферы имеет следующий вид:
SA = 4 × π × r ²
SA = 4 × 3,14 × 11 ²
SA = 1519,76
Площадь поверхности сферы 1519,76 см ² .

Пример 5 : Полусфера имеет радиус 8,3 см. Найдите его площадь без основания.
Решение:
г = 8.3 см
Площадь поверхности полусферы без основания определяется по следующей формуле:

SA = 2 × π × r ²
SA = 2 × π × 8,3 ²
SA = 432,62
Следовательно, площадь поверхности полушария составляет 432,62 см ² .

Пример 6 : Найти площадь поверхности сферы с радиусом 6 см?
Решение:
SA = 4 × π × r ²
SA = 4 × π × 6 ²
SA = 4 × π × 36
SA = 452 см ²

Онлайн-калькулятор площади поверхности

Определение объема и площади поверхности сферы

Результаты обучения

• Найдите объем и площадь поверхности сферы

Сфера — это форма баскетбольного мяча, похожая на трехмерный круг.Как и в случае с кругом, размер сферы определяется ее радиусом, который представляет собой расстояние от центра сферы до любой точки на ее поверхности. Формулы для объема и площади поверхности сферы приведены ниже.
Отображение происхождения этих формул, как мы это делали для прямоугольного твердого тела, выходит за рамки этого курса. Мы аппроксимируем [латекс] \ pi [/ latex] с помощью [latex] 3.14 [/ latex].

Объем и площадь поверхности сферы

Для шара радиусом [латекс] r \ text {:} [/ latex]

, пример

Сфера имеет радиус [латекс] 6 [/ латекс] дюймов.Найдите его 1. объем и 2. площадь поверхности.

Решение
Шаг 1 одинаков для 1. и 2., поэтому мы покажем его только один раз.

Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и подпишите это с данной информацией.

1.
Шаг 2. Определите , что вы ищете.	объем сферы
Шаг 3.{3} [/ латекс] [латекс] V \ приблизительно 904,32 \ text {кубические дюймы} [/ латекс]
Шаг 6. Проверка: Еще раз проверьте свои вычисления на калькуляторе.
Шаг 7. Ответьте на вопрос.	Объем [латекс] составляет приблизительно 904,32 [/ латекс] кубических дюймов.

2.
Шаг 2. Определите , что вы ищете.	площадь поверхности куба
Шаг 3.{2} [/ латекс] [латекс] S \ около 452,16 [/ латекс]
Шаг 6. Проверка: Еще раз проверьте свои вычисления на калькуляторе
Шаг 7. Ответьте на вопрос.	Площадь поверхности [латекс] составляет приблизительно 452,16 [/ латекс] квадратных дюймов.

, пример

Земной шар имеет форму шара радиусом [латекс] 14 [/ латекс] сантиметров.Найдите его 1. объем и 2. площадь поверхности. Округлите ответ до ближайшей сотой.

Показать решение

Решение

Шаг 1. Прочтите о проблеме. Нарисуйте фигуру дать информацию и обозначить ее.

1.
Шаг 2. Определите , что вы ищете.	объем сферы
Шаг 3.{3} [/ латекс]
Шаг 5. Решить.	[латекс] V \ прибл. 11 488,21 [/ латекс]
Шаг 6. Проверка: Мы предоставляем вам проверить ваши расчеты.
Шаг 7. Ответьте на вопрос.	Объем [латекс] составляет приблизительно 11 488,21 [/ латекс] кубических дюймов.

2.
Шаг 2. Определите , что вы ищете.{2} [/ латекс]
Шаг 5. Решить.	[латекс] S \ приблизительно 2461,76 [/ латекс]
Шаг 6. Проверка: Мы предоставляем вам проверить ваши расчеты.
Шаг 7. Ответьте на вопрос.	Площадь поверхности [латекса] составляет приблизительно 2461,76 [/ латекс] квадратных дюймов.

Площадь поверхности сферы

Площадь поверхности сферы — Math Open Reference

Определение: Количество квадратных единиц, которые точно покрывают поверхность сферы.

Попробуй это Перетащите оранжевую точку, чтобы настроить радиус сферы и обратите внимание на изменение области.

Площадь поверхности сферы определяется формулой Где r — радиус сферы. На рисунке выше перетащите оранжевую точку, чтобы изменить радиус сферы. и обратите внимание, как формула используется для расчета площади поверхности.

Эта формула была открыта более двух тысяч лет назад греческим философом Архемедом. Он также понял, что площадь поверхности сферы в точности равна площади изогнутой стенки описываемой им сферы. цилиндр, который является наименьшим цилиндром, который может содержать сферу.См. Площадь поверхности цилиндра.

Если вы знаете площадь

Переставив приведенную выше формулу, вы можете найти радиус: где а — площадь поверхности.

Интересные факты

1. Для данного объема сфера — это форма с наименьшей площадью поверхности. Вот почему он так часто появляется в природе, как капли воды, пузыри и планеты.
2. Площадь поверхности сферы ровно в четыре раза больше площади круга того же радиуса.Вы можете увидеть это в формуле площади, так как площадь круга равна а площадь поверхности шара равна

Что стоит попробовать

1. • На рисунке выше нажмите «скрыть детали».
   • Перетащите оранжевую точку, чтобы изменить размер сферы.
   • Рассчитать объем сферы
   • Нажмите «показать подробности», чтобы проверить свой ответ.
2. • На рисунке выше нажмите «Сброс», затем снимите флажок «Показать радиус».
   • Перетащите оранжевую точку, чтобы изменить размер сферы.
   • Вычислить радиус сферы из объема
   • Нажмите «показать радиус», чтобы проверить свой ответ.

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.