Площадь поверхности правильной треугольной призмы равна 19 какой будет: Площадь поверхности правильной треугольной призмы равна

Задания №13 и №16 (призма)

Практикум №5 по решению
стереометрических задач
(базовый уровень)
Задания №13 и №16
(призма)

3. Содержание

• Задача №1
• Задача №2
• Задача №3
• Задача №4
• Задача №5
• Задача №6
• Задача №7
• Задача №8
• Задача №9
• Задача №10
• Задача №11
• Задача №12
• Задача №13
• Задача №14
•Задача №15
• Задача №16
• Задача №17
• Задача №18
• Задача №19
• Задача №20
• Задача №21
•Для сам. решения

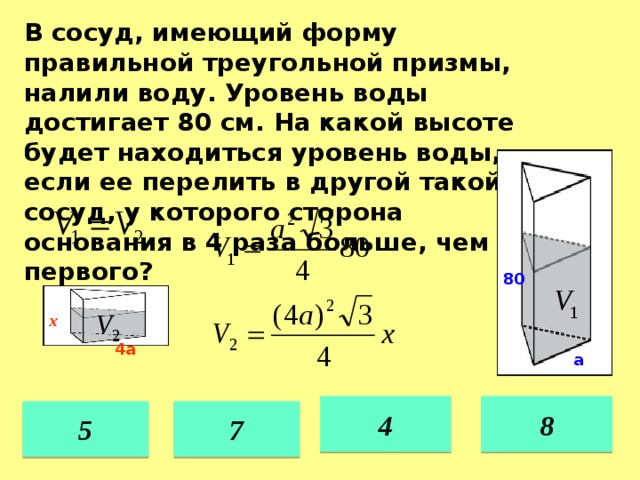
4. Задача №1

В сосуд, имеющий форму правильной треугольной призмы,
налили воду. Уровень воды достигает 80 см. На какой высоте
будет находиться уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона основания в 4 раза больше,
чем у первого? Ответ выразите в см.
Решение.
Объем призмы равен произведению площади ее
основания на высоту
. Поэтому
,а
значит, при увеличении стороны а в 4 раза
знаменатель увеличится в 16 раз, то есть высота
уменьшится в 16 раз и будет
равна 5 см.

5. Задача №2

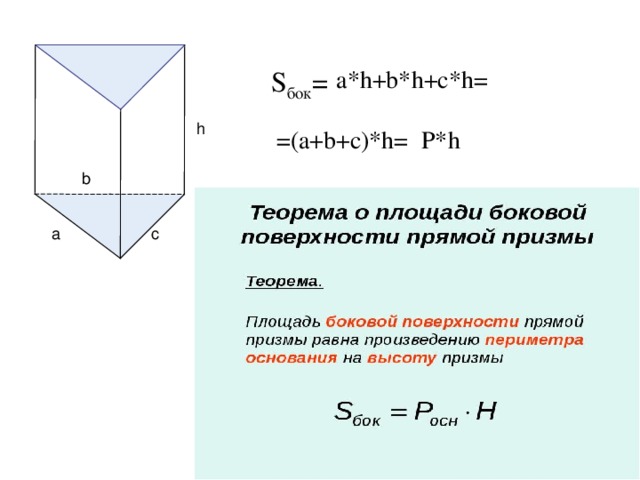
Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой
равна 5, а высота – 10.
Решение.
площадь боковой поверхности фигуры равна сумме
площадей всех боковых граней

6. Задача №3

Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями,
равными 6 и 8, и боковым ребром, равным 10.
Решение.

7. Задача №8

В основании прямой призмы лежит ромб с диагоналями,
равными 6 и 8. Площадь ее поверхности равна 248.
Найдите боковое ребро этой призмы.
Решение.

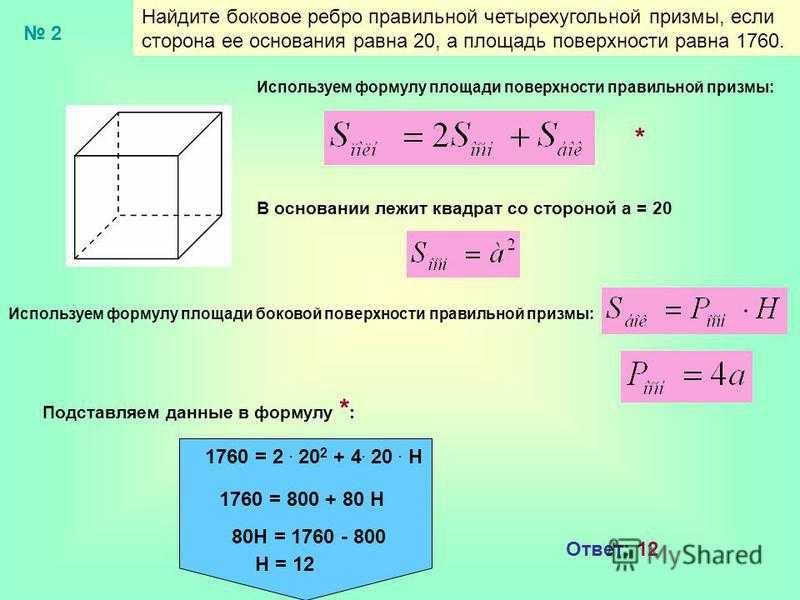
8. Задача №4

Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 20, а
площадь поверхности равна 1760.
Решение.
Площадь поверхности правильной четырехугольной
призмы выражается через сторону ее основания а
и боковое ребро Н как
Подставим значения а и S:

9. Задача №5

Через среднюю линию основания треугольной призмы,
объем которой равен 32, проведена плоскость,
параллельная боковому ребру. 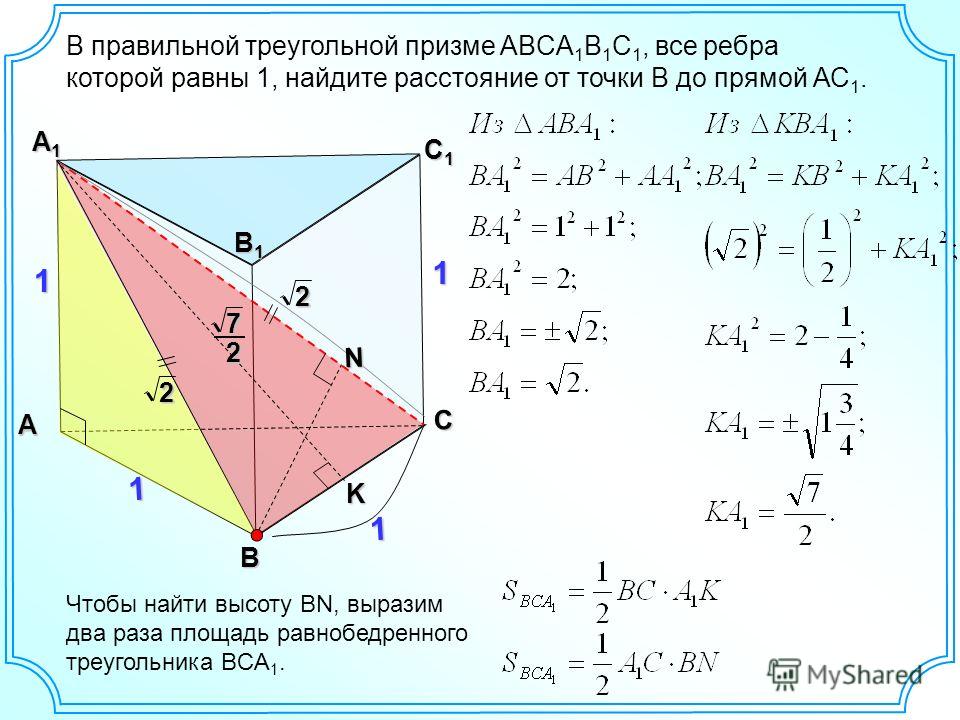Найдите объем
отсеченной треугольной призмы.
Площадь основания отсеченной части
меньше площади основания всей
призмы в 4 раза (т.к. и высота и
основание треугольника уменьшились в
2 раза). Высота осталась прежней,
значит, объем уменьшился в 4 раза.
Ответ: 8.

10. Задача №6

Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру.
Объем отсеченной треугольной призмы равен 5.
Найдите объем исходной призмы.
Решение.
Площадь основания отсеченной части
меньше площади основания всей призмы в 4
раза (т.к. и высота и основание треугольника
уменьшились в 2 раза). Высоты обеих частей
одинаковы, поэтому объем отсеченной части в
4 раза меньше объема целой призмы, который
равен 20.

11. Задача №10

Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру.
Площадь боковой поверхности отсеченной треугольной
призмы равна 8. Найдите площадь боковой
поверхности исходной призмы.
Решение.
Площадь боковой поверхности призмы равна произведению
периметра основания на высоту боковой грани.
Высота боковой грани у исходной призмы и отсеченной призм
совпадает. Поэтому площади боковых граней относятся как
периметры оснований. Треугольники в основании исходной и
отсеченной призм подобны, все их стороны относятся как 1:2.
Поэтому периметр основания отсеченной призмы вдвое меньше
исходного. Значит, площадь боковой поверхности исходной призмы
равна 16.

12. Задача №7

От треугольной призмы, объем которой равен 6, отсечена
треугольная пирамида плоскостью, проходящей через
сторону одного основания и противоположную вершину
другого основания. Найдите объем оставшейся части.
Решение.
Объем
призмы
больше
объема
пирамиды с такой же площадью
основания и высотой в 3 раза. Объем
оставшейся части составляет тогда две
трети исходного, он равен 4.

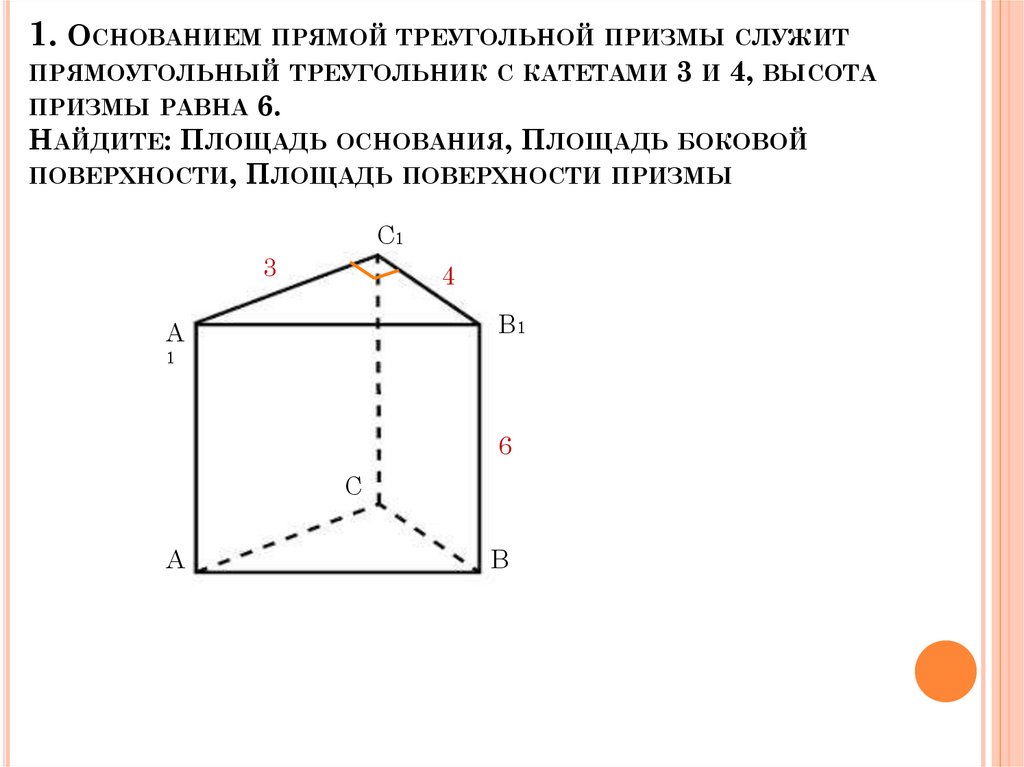
13. Задача №9

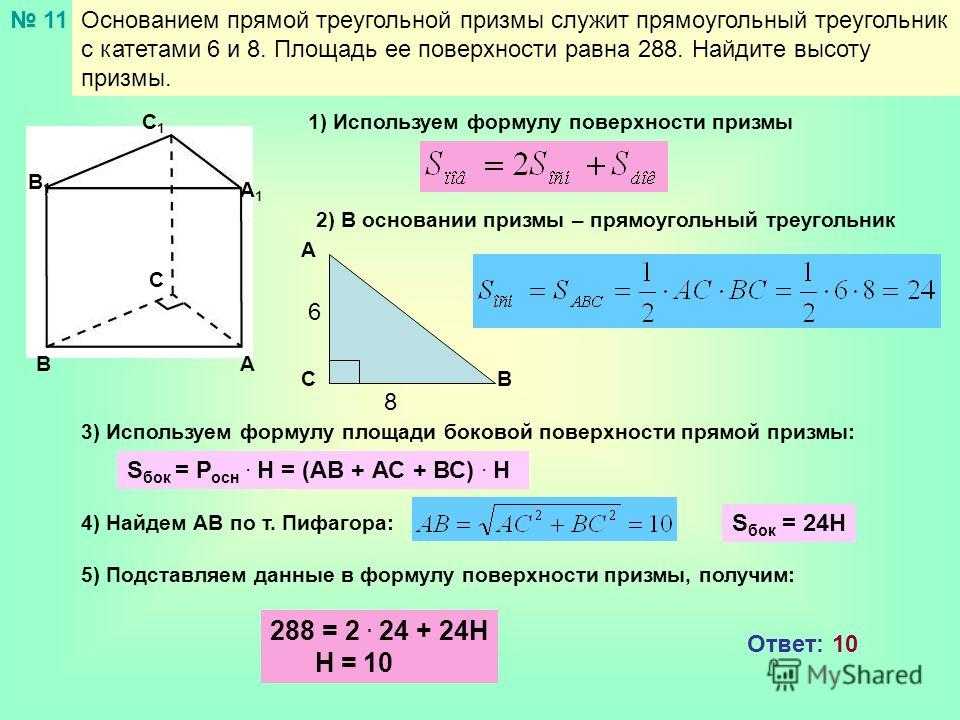
Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 6 и 8, высота
призмы равна 10. Найдите площадь ее поверхности.
Решение.
Третья сторона треугольника в основании равна 10

14. Задача №11

Плоскость, проходящая через три точки A, B и С, разбивает
правильную треугольную призму на два многогранника.
Сколько рёбер у многогранника, у которого больше вершин?
Решение.
Плоскость делит призму на две призмы:
треугольную, имеющую 6 вершин и
четырёхугольную, имеющую 8 вершин.
Четырёхугольная призма имеет по 4
ребра в каждом из оснований и 4
боковых ребра, всего 12 рёбер.

15. Задача №12

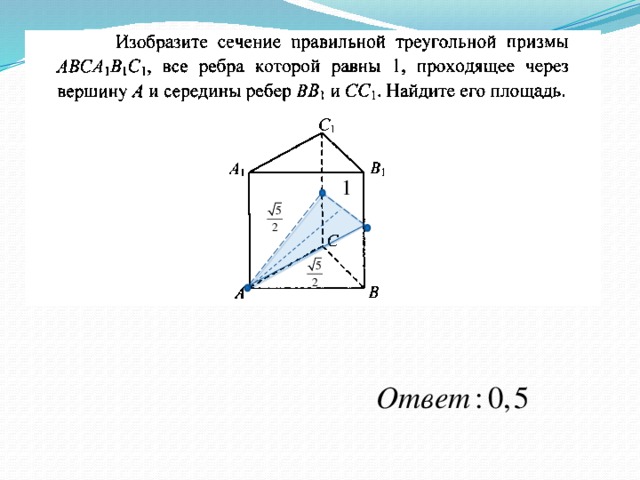
Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 3, а высота этой призмы равна
4√3. Найдите объём призмы ABCA1B1C1.
Решение.
Объём правильной треугольной призмы
вычисляется по формуле:

16. Задача №13

Площадь поверхности правильной треугольной призмы
равна 6. Какой будет площадь поверхности призмы,
если все ее ребра увеличить в три раза?
Решение.
Площади подобных тел относятся как
квадрат коэффициента подобия.
Поэтому если все ребра увеличить в три
раза, площадь поверхности увеличится в 9
раз. Значит , она станет равна 54.

17. Задача №14

Найдите объем многогранника, вершинами которого
являются точки А, В, С, А1 правильной треугольной
призмы АВСА1В1С1, площадь основания которой равна
2, а боковое ребро равно 3.
Требуется
найти
объём
пирамиды,
основание и высота которой совпадают с
основанием и высотой данной треугольной
призмы. Поэтому

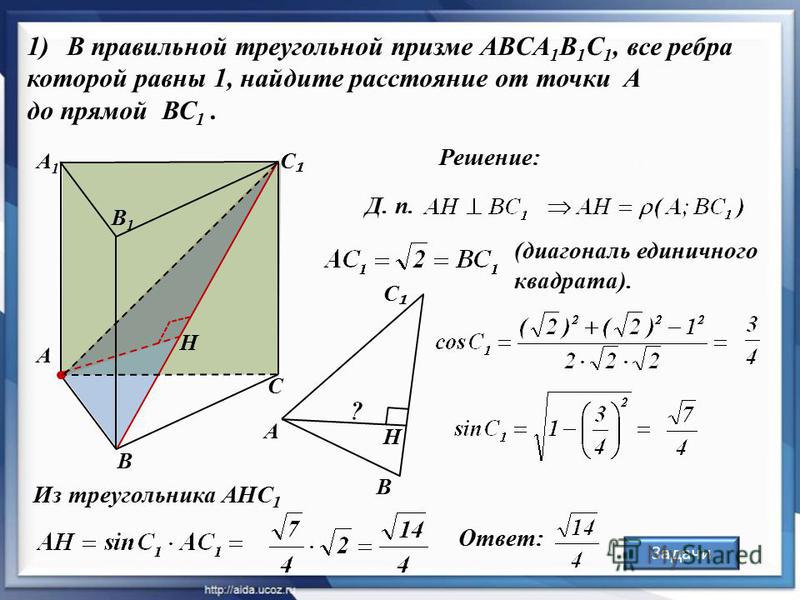
18. Задача №15

Найдите объем многогранника, вершинами которого
являются точки А, В, С, А1, С1 правильной треугольной
призмы АВСА1В1С1, площадь основания которой равна
3, а боковое ребро равно 2.
Искомый объём многогранника равен разности
объёмов призмы АВСА1В1С1 и пирамиды
ВА1В1С1, основания и высоты которых совпадают.

19. Задача №16

Найдите объем многогранника, вершинами которого являются
точки А,В,С,D,E,F,A1 правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 , площадь основания которой
равна 4, а боковое ребро равно 3.
Основание пирамиды такое же, как
основание
правильной
шестиугольной
призмы, и высота у них общая. Поэтому

20. Задача №17

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 1. Найдите расстояние между точками В и Е.
Длина большей диагонали правильного
шестиугольника равна его удвоенной
стороне. Поэтому

21. Задача №18

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 1. Найдите угол DАВ. Ответ дайте в градусах.
В правильном шестиугольнике углы
между сторонами равны120° значит,

22. Задача №19

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все
ребра равны 8. Найдите угол между прямыми FA и D1E1. Ответ
дайте в градусах.
Отрезки D1E1, DE и AB лежат на
параллельных прямых, поэтому искомый
угол между прямыми FA и E1D1 равен
углу между прямыми FA и AB.
Поскольку ∟FAB между сторонами
правильного шестиугольника равен
120°, смежный с ним угол между
прямыми FA и AB равен 60°.

23. Задача №20

В правильной треугольной призме АВСА1В1С1 , все ребра
которой равны 3, найдите угол между прямыми АА1 и ВС1.
Ответ дайте в градусах.
Отрезки A1A и BB1 лежат на параллельных
прямых, поэтому искомый угол между
прямыми A1A и BC1 равен углу между
прямыми BB1 и BC1.
Боковая грань CBB1C1 — квадрат, поэтому
угол между его стороной и диагональю равен
45°.

24. Задача №21

Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 3, а высота этой призмы
равна 4√3. Найдите объём призмы ABCA1B1C1.

25. Задача №22 задания №16 в ЕГЭ

В правильной треугольной призме ABCA1B1C1 стороны
оснований равны 2, боковые рёбра равны 5. Найдите площадь
сечения призмы плоскостью, проходящей через середины
рёбер AB, AC, A1B1 и A1C1.
Противоположные
стороны
сечения
являются
соответственно
средними
треугольников, лежащих в основании, и
прямоугольников, являющихся боковыми
гранями
призмы.
Значит,
сечение
представляет собой прямоугольник со
сторонами 1и 5, площадь которого равна 5.

26. Задача №23

В правильной четырёхугольной
призме ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1 равна
17. Найдите площадь сечения призмы плоскостью, проходящей
через точки A, A1 и C.
Диагональное сечение прямой призмы —
прямоугольникАА1С1С.
Диагонали
правильной
четырёхугольной
призмы
равны: ВD1=А1С. По теореме Пифагора
получаем:

27. Задача №24

В основании прямой призмы лежит прямоугольный
треугольник, один из катетов которого равен 2, а
гипотенуза равна √53. Найдите объём призмы, если её
высота равна 3.

28. Задача №25

Найдите объем правильной шестиугольной
призмы, стороны основания которой равны 1, а
боковые ребра равны √3.
Площадь правильного шестиугольника
со стороной а, лежащего в основнии,
задается формулой:

29. Задача №26

Найдите объем правильной шестиугольной призмы, все
ребра которой равны √3.
Объем призмы равен произведению площади
основания на высоту. Высотой правильной призмы
является ее боковое ребро. Основание призмы —
правильный шестиугольник. Площадь правильного
шестиугольника со стороной а вычисляется по
формуле

30. Задача №27

В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите
расстояние между точками А и Е1.
По теореме Пифагора
Угол между сторонами правильного
шестиугольника равен 120°. По теореме
косинусов

31. Задача №28

В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите
тангенс угла АD1D.
Рассмотрим прямоугольный ΔАD1D катет
которого является большей диагональю
основания. Длина
большей
диагонали
правильного шестиугольника равна его
удвоенной стороне: АD=2. Т.к.
D1D =1 имеем:

32. Задача №29

В треугольной призме две боковые грани
перпендикулярны. Их общее ребро равно 10 и отстоит
от других боковых ребер на 6 и 8. Найдите площадь
боковой поверхности этой призмы.

33. Задача №30

Через среднюю линию основания треугольной призмы, площадь
боковой поверхности которой равна 24, проведена плоскость,
параллельная боковому ребру. Найдите площадь боковой
поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной
призмы вдвое меньше соответствующих
площадей боковых граней исходной
призмы. Поэтому площадь боковой
поверхности отсеченной призмы вдвое
меньше площади боковой поверхности
исходной, т.е равна 12.

34. Задача №31

Найдите объем призмы, в основаниях которой лежат
правильные шестиугольники со сторонами 2, а боковые
ребра равны 2√3 и наклонены к плоскости основания
под углом 30° .
Объем призмы V = Soc.·h = Soc.·Lsinα
где S– площадь основания, а L – длина ребра,
составляющего с основанием угол α. Площадь
правильного
шестиугольника
со
стороной a равна

35. Задача №32

Правильная четырехугольная призма описана около цилиндра,
радиус основания и высота которого равны 1. Найдите площадь
боковой поверхности призмы.
Высота
призмы
равна
высоте
цилиндра, а сторона ее основания
равна
диаметру
цилиндра.
Тогда
площадь боковой поверхности

36. Задача №33

Найдите площадь боковой поверхности правильной треугольной
призмы, описанной около цилиндра, радиус основания
которого равен √3 , а высота равна 2.
Сторона правильного Δ:

37. Задача №34

Найдите площадь боковой поверхности правильной треугольной
призмы, вписанной в цилиндр, радиус основания которого
равен 2√3 , а высота равна 2.

38. Задача №35

Найдите площадь боковой поверхности правильной
шестиугольной призмы, описанной около цилиндра, радиус
основания которого равен √3 , а высота равна 2.
Задачи
для самостоятельного
решения

40. Задача Решите самостоятельно

1) В сосуд, имеющий форму правильной треугольной призмы,
налили 2700 см³ воды и погрузили в воду деталь. При этом
уровень воды поднялся с отметки 20 см до отметки 33 см.
Найдите объем детали. Ответ выразите в см³. Ответ:1755

41. Задача №1 Решите самостоятельно

1) В сосуд, имеющий форму правильной треугольной призмы,
налили воду. Уровень воды достигает 27 см. На какой высоте
будет находиться уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона основания в 3 раза
больше, чем у первого? Ответ выразите в см.
2) В сосуд, имеющий форму правильной треугольной призмы,
налили воду. Уровень воды достигает 180 см. На какой высоте
будет находиться уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона основания в 6 раз больше,
чем у первого? Ответ выразите в см.

42. Задача №2 Решите самостоятельно

1) Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой равна 5, а
высота – 2.
Ответ: 60
2) Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой равна 3, а
высота – 10.
Ответ:
3) Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой равна 6, а
высота – 3.
Ответ:

43. Задача №3 Решите самостоятельно

1) Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями,
равными 3 и 4, и боковым ребром, равным 3. Ответ:42
2) Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями,
равными 9 и 40, и боковым ребром, равным 55. Ответ:
3) Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями,
равными 20 и 21, и боковым ребром, равным 44.
Ответ:

44. Задача №4 Решите самостоятельно

1) Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 3, а
площадь поверхности равна 66.
Ответ:
2) Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 12, а
площадь поверхности равна 576.
Ответ:
3) Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 10, а
площадь поверхности равна 1080.
Ответ:

45. Задача №5 Решите самостоятельно

1) Через среднюю линию основания треугольной
призмы, объем которой равен 52, проведена
плоскость, параллельная боковому ребру. Найдите
объем отсеченной треугольной призмы. Ответ: 13
2) Через среднюю линию основания треугольной
призмы, объем которой равен 90, проведена
плоскость, параллельная боковому ребру. Найдите
объем отсеченной треугольной призмы. Ответ:

46. Задача №6 Решите самостоятельно

1) Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру.
Объем отсеченной треугольной призмы равен 23,5.
Найдите объем исходной призмы. Ответ: 94
2) Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру.
Объем отсеченной треугольной призмы равен 16,5.
Найдите объем исходной призмы. Ответ:

47. Задача №7 Решите самостоятельно

1) От треугольной призмы, объем которой равен 12,
отсечена треугольная пирамида плоскостью, проходящей
через сторону одного основания и противоположную
вершину другого основания. Найдите объем оставшейся
части.
Ответ:8
2) От треугольной призмы, объем которой равен 84,
отсечена треугольная пирамида плоскостью, проходящей
через сторону одного основания и противоположную
вершину другого основания. Найдите объем оставшейся
части.
Ответ:

48. Задача №8 Решите самостоятельно

1) В основании прямой призмы лежит ромб с диагоналями,
равными 16 и 30. Площадь ее поверхности равна 2588.
Найдите боковое ребро этой призмы.
Ответ:
2) В основании прямой призмы лежит ромб с диагоналями,
равными 15 и 36. Площадь ее поверхности равна 2100.
Найдите боковое ребро этой призмы.
Ответ:
3) В основании прямой призмы лежит ромб с диагоналями,
равными 21 и 28. Площадь ее поверхности равна 1568.
Найдите боковое ребро этой призмы.
Ответ:

49. Задача №9 Решите самостоятельно

1) Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 5 и 12, высота
призмы равна 8. Найдите площадь ее поверхности.
2) Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 7 и 24, высота
призмы равна 15. Найдите площадь ее поверхности.
3) Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 5 и 12, высота
призмы равна 4. Найдите площадь ее поверхности.

50. Задача №10 Решите самостоятельно

1) Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру.
Площадь боковой поверхности отсеченной треугольной
призмы равна 10. Найдите площадь боковой поверхности
исходной призмы. Ответ: 20
2) Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру.
Площадь боковой поверхности отсеченной треугольной
призмы равна 22. Найдите площадь боковой поверхности
исходной призмы. Ответ:

51. Задача №13 Решите самостоятельно

1) Площадь поверхности правильной треугольной призмы
равна 12. Какой будет площадь поверхности призмы,
если все ее ребра увеличить в 6 раз? Ответ:432
2) Площадь поверхности правильной треугольной призмы
равна 10. Какой будет площадь поверхности призмы,
если все ее ребра увеличить в 2 раза? Ответ:
3) Площадь поверхности правильной треугольной призмы
равна 6. Какой будет площадь поверхности призмы,
если все ее ребра увеличить в 9 раз? Ответ:

52. Задача №14 Решите самостоятельно

1) Найдите объем многогранника, вершинами которого
являются точки А, А1, В1, С1 правильной
треугольной призмы АВСА1В1С1, площадь основания
которой равна 8, а боковое ребро равно 3. Ответ: 8
2) Найдите объем многогранника, вершинами которого
являются точки В, А1, В1, С1 правильной
треугольной призмы АВСА1В1С1, площадь основания
которой равна 2, а боковое ребро равно 3. Ответ:

53. Задача №15 Решите самостоятельно

1) Найдите объем многогранника, вершинами которого
являются точки А, В, А1, В1, С1 правильной
треугольной призмы АВСА1В1С1, площадь основания
которой равна 3, а боковое ребро равно 5. Ответ:
2) Найдите объем многогранника, вершинами которого
являются точки А, В, С, А1, В1 правильной
треугольной призмы АВСА1В1С1, площадь основания
которой равна 7, а боковое ребро равно 3. Ответ:

54. Задача №16 Решите самостоятельно

1) Найдите объем многогранника, вершинами которого
являются точки А,В,С,D,E,F,В1 правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 , площадь основания которой
равна 9, а боковое ребро равно 4.
Ответ:
2) Найдите объем многогранника, вершинами которого являются
точки А,В,С,D,E,F, D1 правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 , площадь основания которой
равна 4, а боковое ребро равно 6.
Ответ:

55. Задача №17 Решите самостоятельно

1) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 40. Найдите
расстояние между точками А и D .
Ответ: 80
2) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите
расстояние между точками А и D.
Ответ:
3) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 15. Найдите
расстояние между точками А и D.
Ответ:

56. Задача №18 Решите самостоятельно

1) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 43. Найдите
угол А1В1Е1. Ответ дайте в градусах.
Ответ: 60
2) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите
угол ВАD. Ответ дайте в градусах.
Ответ:
3) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 36. Найдите
угол D1С1F1. Ответ дайте в градусах.
Ответ:

57. Задача №19 Решите самостоятельно

1) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите
угол между прямыми AВ и С1D1. Ответ дайте в градусах.
Ответ:
2) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны 2. Найдите
угол между прямыми СD и E1F1. Ответ дайте в градусах.
Ответ:
3) В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите угол
между прямыми DЕ и В1С1. Ответ дайте в градусах. Ответ:

58. Задача №20 Решите самостоятельно

1) В правильной треугольной призме АВСА1В1С1 , все ребра
которой равны 3, найдите угол между прямыми ВВ1 и АС1.
Ответ дайте в градусах. Ответ:45
2) В правильной треугольной призме АВСА1В1С1 , все ребра
которой равны 1, найдите угол между прямыми АА1 и ВС1.
Ответ дайте в градусах. Ответ:
3) В правильной треугольной призме АВСА1В1С1 , все ребра
которой равны 4, найдите угол между прямыми СС1 и АВ1.
Ответ дайте в градусах. Ответ:

59. Задача №24 Решите самостоятельно

1) В основании прямой призмы лежит прямоугольный
треугольник, один из катетов которого равен 3, а
гипотенуза равна √34. Найдите объём призмы, если
её высота равна 6.

60. Задача №25 Решите самостоятельно

1) Найдите объем правильной шестиугольной призмы,
стороны основания которой равны 8, а боковые ребра
равны √0,75.
Ответ:144
2) Найдите объем правильной шестиугольной призмы,
стороны основания которой равны 9, а боковые ребра
равны √27.
Ответ:
3) Найдите объем правильной шестиугольной призмы,
стороны основания которой равны 5, а боковые ребра
равны √0,75.
Ответ:

61. Задача №26 Решите самостоятельно

1) Найдите объем правильной шестиугольной призмы,
все ребра которой равны 1√3. Ответ:
2) Найдите объем правильной шестиугольной призмы,
все ребра которой равны 5√3.
Ответ:
3) Найдите объем правильной шестиугольной призмы,
все ребра которой равны 8√3.
Ответ:

62. Задача №27 Решите самостоятельно

1) В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 14. Найдите
расстояние между точками D и F1. 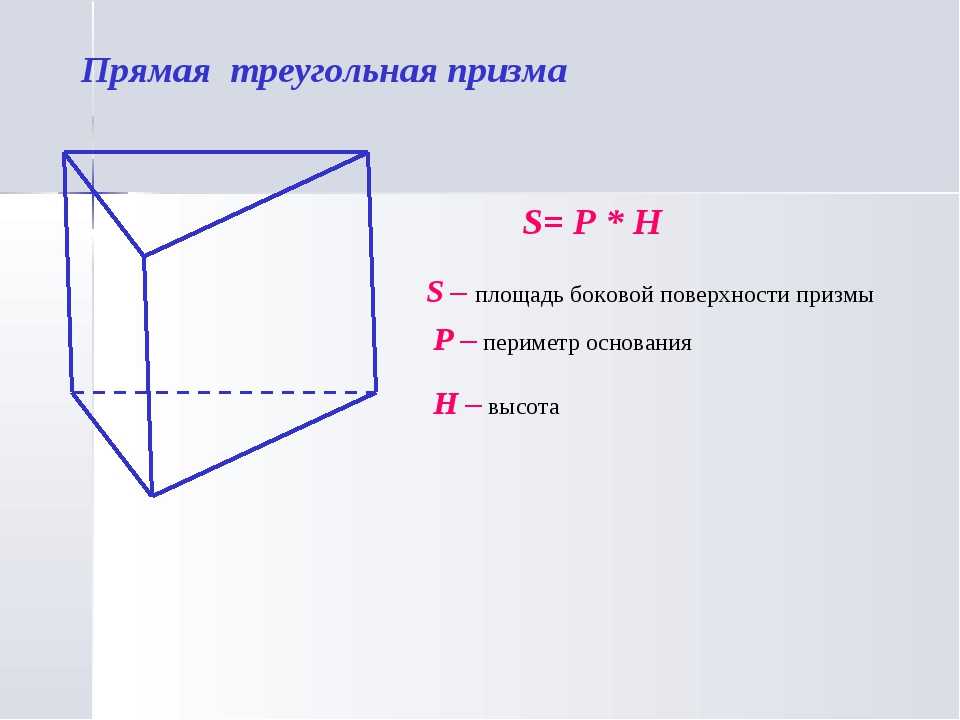Ответ: 28
2) В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 48. Найдите
расстояние между точками D и В1. Ответ:
3) В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 6. Найдите
расстояние между точками С и А1. Ответ:

63. Задача №28 Решите самостоятельно

1) В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 19. Найдите тангенс
угла АD1D.
Ответ:2
2) В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 31. Найдите тангенс
угла А1DD1.
Ответ:
3) В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 22. Найдите тангенс
угла А1DD1.
Ответ:

64. Задача №29 Решите самостоятельно

1) В треугольной призме две боковые грани перпендикулярны.
Их общее ребро равно 15 и отстоит от других боковых ребер
на 8 и 15. Найдите площадь боковой поверхности этой
призмы.
2) В треугольной призме две боковые грани перпендикулярны.
Их общее ребро равно 5 и отстоит от других боковых ребер на
10 и 24. Найдите площадь боковой поверхности этой призмы.
3) В треугольной призме две боковые грани перпендикулярны.
Их общее ребро равно 8 и отстоит от других боковых ребер на
9 и 12. Найдите площадь боковой поверхности этой призмы.

65. Задача №30 Решите самостоятельно

1) Через среднюю линию основания треугольной призмы, площадь
боковой поверхности которой равна 38, проведена плоскость,
параллельная боковому ребру. Найдите площадь боковой поверхности
отсеченной треугольной призмы.
Ответ:19
2) Через среднюю линию основания треугольной призмы, площадь
боковой поверхности которой равна 84, проведена плоскость,
параллельная боковому ребру. Найдите площадь боковой поверхности
отсеченной треугольной призмы.
Ответ:
3) Через среднюю линию основания треугольной призмы, площадь
боковой поверхности которой равна 30, проведена плоскость,
параллельная боковому ребру. Найдите площадь боковой поверхности
отсеченной треугольной призмы.
Ответ:

66. Задача №31 Решите самостоятельно

1) Найдите объем призмы, в основаниях которой лежат
правильные шестиугольники со сторонами 3, а боковые ребра
равны 12√3 и наклонены к плоскости основания под углом 30°.
Ответ: 243
2) Найдите объем призмы, в основаниях которой лежат
правильные шестиугольники со сторонами 6, а боковые ребра
равны 9√3 и наклонены к плоскости основания под углом 30° .
Ответ: 729
3) Найдите объем призмы, в основаниях которой лежат
правильные шестиугольники со сторонами 8, а боковые ребра
равны 10√3 и наклонены к плоскости основания под углом 30° .

67. Задача №32 Решите самостоятельно

1) Правильная четырехугольная призма описана около
цилиндра, радиус основания и высота которого равны 16.
Найдите площадь боковой поверхности призмы.
2) Правильная четырехугольная призма описана около
цилиндра, радиус основания и высота которого равны 11.
Найдите площадь боковой поверхности призмы.
3) Правильная четырехугольная призма описана около
цилиндра, радиус основания и высота которого равны 23,5.
Найдите площадь боковой поверхности призмы.

68. Задача №33 Решите самостоятельно

1) Найдите площадь боковой поверхности правильной
треугольной призмы, описанной около цилиндра, радиус
основания которого равен √75 , а высота равна 4. Ответ:360
2) Найдите площадь боковой поверхности правильной
треугольной призмы, описанной около цилиндра, радиус
основания которого равен √0,12 , а высота равна 2. Ответ:
3) Найдите площадь боковой поверхности правильной
треугольной призмы, описанной около цилиндра, радиус
основания которого равен √243 , а высота равна 3. Ответ:

69. Задача №34 Решите самостоятельно

1) Найдите площадь боковой поверхности правильной
треугольной призмы, вписанной в цилиндр, радиус основания
которого равен 8√3 , а высота равна 6. Ответ:432
2) Найдите площадь боковой поверхности правильной
треугольной призмы, вписанной в цилиндр, радиус основания
которого равен 2√3 , а высота равна 3. 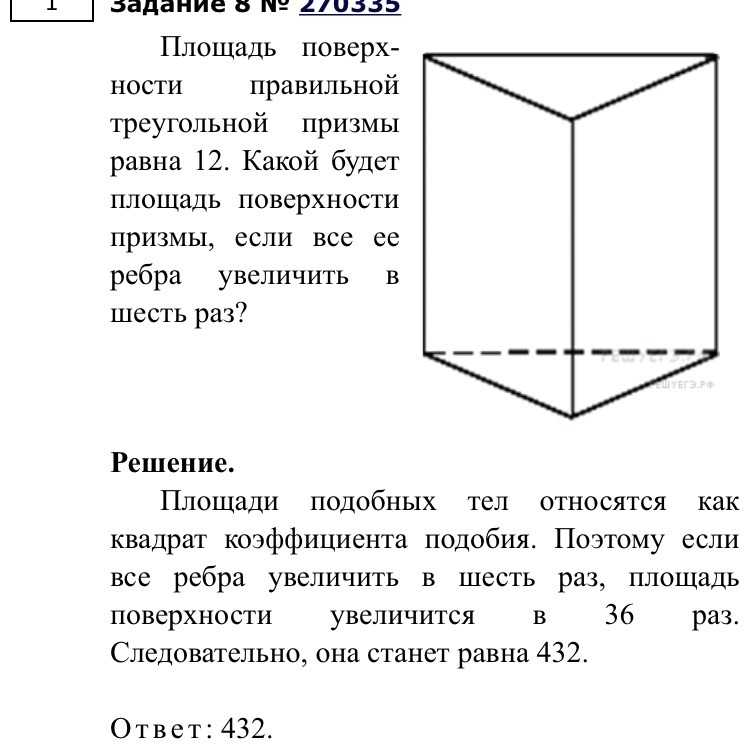Ответ:
3) Найдите площадь боковой поверхности правильной
треугольной призмы, вписанной в цилиндр, радиус основания
которого равен 3√3 , а высота равна 7. Ответ:

70. Задача №35 Решите самостоятельно

1) Найдите площадь боковой поверхности правильной
шестиугольной призмы, описанной около цилиндра, радиус
основания которого равен √27 , а высота равна 1. Ответ:
2) Найдите площадь боковой поверхности правильной
шестиугольной призмы, описанной около цилиндра, радиус
основания которого равен √0,27 , а высота равна 4. Ответ:
3) Найдите площадь боковой поверхности правильной
шестиугольной призмы, описанной около цилиндра, радиус
основания которого равен √147 , а высота равна 2. Ответ:

71. Используемые ресурсы

• Шаблон подготовила учитель русского языка и литературы
Тихонова Надежда Андреевна
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
«Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ.
Режим доступа: http://mathb.reshuege.ru
Автор и источник заимствования неизвестен
http://mathforum.org/dr.math/faq/formulas/images/prism.gif
http://birmaga.ru/dostc/«Призма»c/107240_html_m4a191404.png

«Призма» — Геометрия, 10 класс

Результаты авторизованых пользователей

Название теста	Дата	Результат	Пользователь
География / Тест с ответами “Русская равнина” 8 класс	03-07-2023 05:34:03 am	14/20	Юлия Шехурдина
География / Тест с ответами “Русская равнина” 8 класс	03-07-2023 04:03:04 am	10/20	Никита Меньшиков
История / Тест с ответами: “Внешняя политика России в 1725-1762 гг.”	03-06-2023 08:37:20 pm	16/20	__cheesecake__
Медицина / Тест с ответами: “Личная гигиена”	03-06-2023 01:55:40 pm	1/20	Elena Gogotishvili
Литература / Тест с ответами: “Скворцы” А. Куприн	03-06-2023 12:03:57 pm	16/20	Vanya Tsimbal

Все результаты

#1. Если основаниями прямой призмы являются правильные многоугольники, то она

A. наклонная

A. наклонная

B. пятиугольная

B. пятиугольная

C. правильная

C. правильная

#2. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 16 и отстоит от других боковых ребер на 9 и 12. Найдите площадь боковой поверхности этой призмы

A. 678

A. 678

B. 576

B. 576

C. 288

C. 288

#3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы

A. 30

A. 30

B.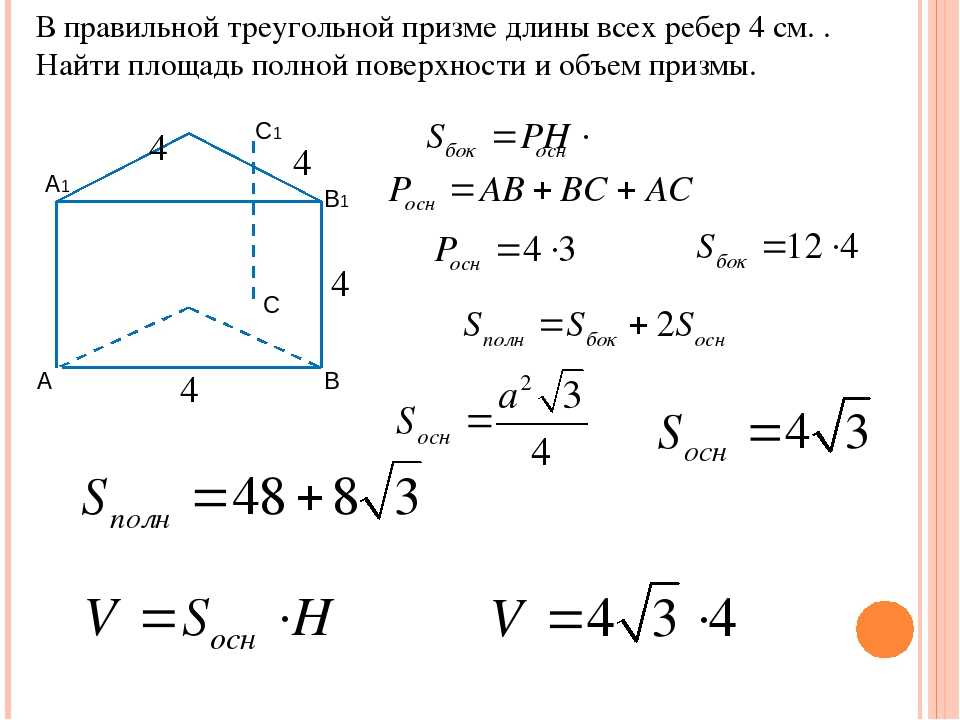 60

B. 60

C. 120

C. 120

#4. Расстояние между плоскостями оснований призмы называется

A. высотой

A. высотой

B. диагональю

B. диагональю

C. ребром

C. ребром

#5. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы

A. 32

A. 32

B. 16

B. 16

C. 8

C. 8

#6. В сосуд, имеющий формулу правильной треугольной призмы, налили 1300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали

A. 132 см3

A. 132 см3

B.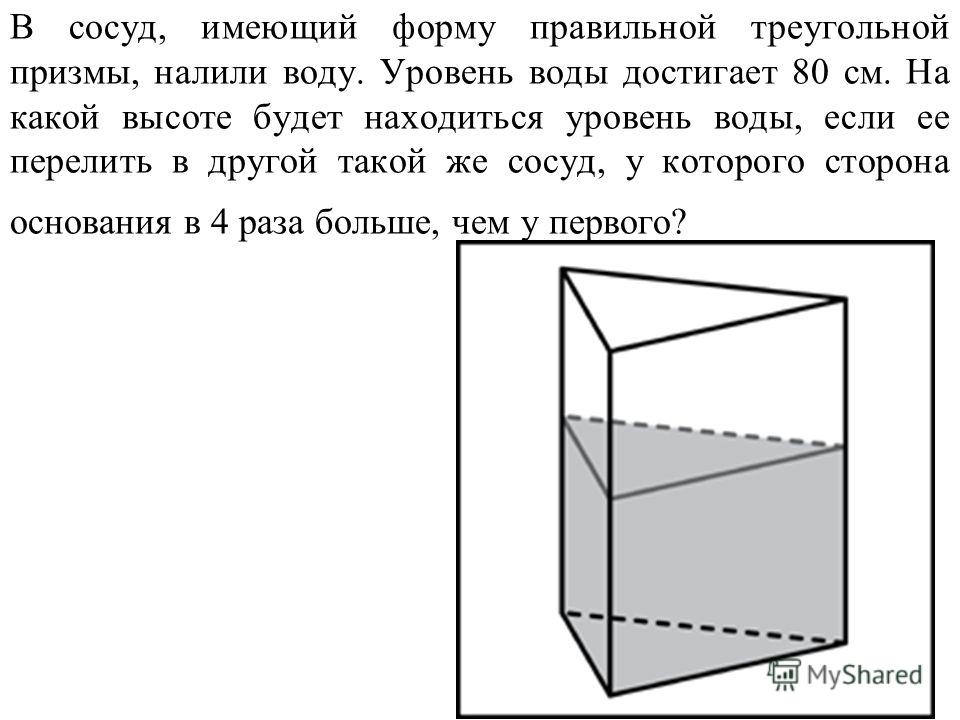 156 см3

B. 156 см3

C. 188 см3

C. 188 см3

#7. Грани многогранника параллельны и равны, так ли это

A. нет

A. нет

B. да

B. да

C. отчасти

C. отчасти

#8. В сосуд, имеющий формулу правильной треугольной призмы, налили 1300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали

A. 132 см3

A. 132 см3

B. 156 см3

B. 156 см3

C. 188 см3

C. 188 см3

#9. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота – 10

A. 160

A. 160

B. 180

B. 180

C. 220

C. 220

#10. Найдите боковое ребро правильной четырехугольной призмы, если сторона её основания равна 15, а площадь поверхности равна 930

A. 16

A. 16

B. 8

B. 8

C. 32

C. 32

#11. Не существует призмы, у которой все грани

A. треугольники

A. треугольники

B. квадраты

B. квадраты

C. прямоугольники

C. прямоугольники

#12. Боковые грани правильной треугольной призмы являются квадратами. Выбери правильное утверждение для данной призмы

A. Косинус угла между боковыми диагоналями призмы равна 0,75.

A. Косинус угла между боковыми диагоналями призмы равна 0,75.

B.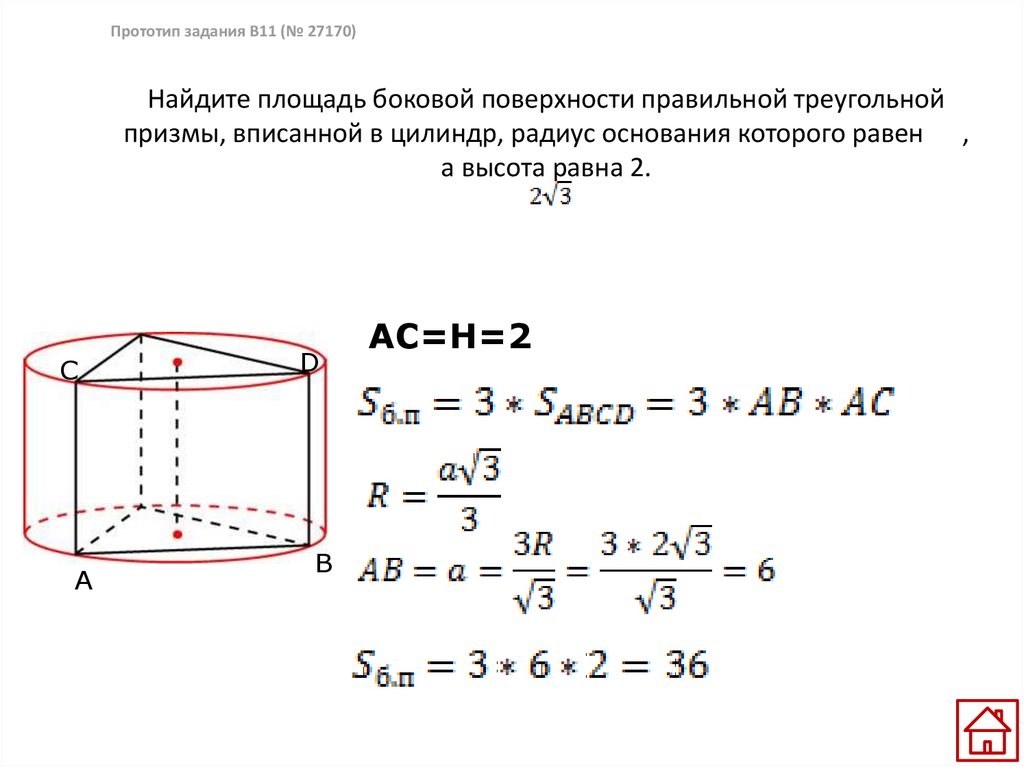

Косинус угла между боковыми диагоналями призмы равна 7,5.

B. Косинус угла между боковыми диагоналями призмы равна 7,5.

C. Двугранные углы при боковых ребрах прямые.

C. Двугранные углы при боковых ребрах прямые.

#13. Расстояние между плоскостями оснований призмы называется

A. высотой

A. высотой

B. диагональю

B. диагональю

C. ребром

C. ребром

#14. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота – 10

A. 160

A. 160

B. 180

B. 180

C. 220

C. 220

#15. Не существует призмы, у которой все грани

A. треугольники

A. треугольники

B. квадраты

B. квадраты

C. прямоугольники

C. прямоугольники

#16. Боковая поверхность призмы состоит из

A. треугольников

A. треугольников

B. ромбов

B. ромбов

C. параллелограммов

C. параллелограммов

#17. Могут ли диагонали призмы быть не равными

A. нет

A. нет

B. зависит от задачи

B. зависит от задачи

C. да

C. да

#18. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота – 8

A. 576

A. 576

B. 144

B. 144

C. 288

C. 288

#19. Если в основании призмы лежит параллелограмм, то она является

A. правильной призмой

A. правильной призмой

B. правильным многоугольником

B. правильным многоугольником

C. параллелепипедом

C. параллелепипедом

#20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объём отсеченной треугольной призмы равен 19,5. Найдите объем исходной призмы

A. 39

A. 39

B. 78

B. 78

C. 156

C. 156

Показать результаты

Оцените тест после прохождения!

Нажмите на звезду, чтобы оценить!

Средняя оценка 1 / 5. Количество оценок: 1

Оценок пока нет. Поставьте оценку первым.

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

Помощь в написании работы

Калькулятор площади поверхности треугольной призмы

Создано Луцией Заборовской, доктором медицинских наук, кандидатом наук

Отредактировано Стивеном Вудингом

Последнее обновление: 12 ноября 2022 г.

Содержание:

• Как использовать площадь поверхности треугольника призменный калькулятор?
• Как рассчитать площадь поверхности треугольной призмы?
• Как рассчитать боковую поверхность треугольной призмы?
• Часто задаваемые вопросы

Калькулятор площади поверхности треугольной призмы предлагает вам 4 различных способа расчета всех запросов , связанных с площадью поверхности призмы! Давай, попробуй; наши образцы фотографий и подробные инструкции делают все проще, чем когда-либо ! 🔺

Следуйте нашей короткой статье:

• Откройте для себя различных треугольных граней призмы ;
• Узнайте о площади боковой поверхности треугольной призмы; …и, наконец,
• Узнайте, как найти площадь треугольной призмы .

Вы готовы? Поехали!

🙋 Любите треугольные призмы? У нас есть дополнительные инструменты, связанные с ними: универсальный калькулятор треугольной призмы и специальный объем калькулятора треугольной призмы.

Как использовать площадь поверхности треугольной призмы калькулятор?

Этот раздел представляет собой пошаговую инструкцию о том, как найти площадь поверхности треугольной призмы с помощью нашего удобного инструмента; взгляните на математическую задачу, которую вы хотите решить, и соберите следующую информацию:

1. Определяем тип треугольной грани

💡 Треугольная грань является основанием нашей призмы

. Каждая призма имеет две треугольные грани (обе имеют форму треугольника).

Найдите всю информацию о треугольном лице, которая присутствует в вашем запросе:

1. Если даны только две стороны треугольника , это обычно означает, что ваше треугольное лицо является прямоугольным треугольником (треугольник с прямым углом = 90° между двумя его сторонами).

   • Вам нужно выбрать опцию ◣ прямоугольный треугольник (эта опция служит площадью поверхности калькулятора прямоугольной треугольной призмы )
   • Вы можете ввести любые две заданные стороны треугольника – будьте внимательны и проверьте, какие из них касаются прямого угла (a, b), а какие нет (c).

2. Если вам дали все три стороны треугольника – вы счастливчик!

   • Выберите вариант ▲ 3 стороны ; затем
   • Введите все три стороны, где хотите (a, b, c).

3. Если вам дадут две стороны и угол между ними

   • Выберите ▲ 2 стороны + угол между

4. Если даны 2 угла и только одна сторона между ними

   • Выберите ▲ 2 угла + сторона между опция

2. Введите все данные, указанные в вашем запросе

Мы даем вам более 15 единиц на выбор! Помните, что для всегда выбирайте единицу измерения, указанную в запросе и , не бойтесь их смешивать ; наш калькулятор позволяет и это!

💡 Длина — это высота всей треугольной призмы — часто это самое длинное заданное значение.

3. Ваши результаты здесь 🎉

На этом этапе вы также можете выбрать из множества единиц измерения площади – выберите ту, которая лучше всего соответствует вашим потребностям.

Как рассчитать площадь поверхности треугольной призмы?

Еще раз, мы должны спросить вас о данных, приведенных в вашем запросе — выберите правильный вариант расчетов на основе треугольного основания вашей призмы .

◣ прямоугольный треугольник

Вам, наверное, даны только две стороны основания треугольника; к сожалению, площадь поверхности прямоугольной треугольной призмы требует, чтобы мы знали площадь треугольной грани (основания) :

Площадь основания = (a × b) / 2

Вы должны помнить, что:

• a, b — это стороны, которые касаются прямого угла (также называемые ножками или катетами 0)
• c сторона, которая не касается прямого угла ( гипотенуза ).

💡 Третью сторону прямоугольного треугольника можно вычислить по теореме Пифагора: a² + b² = c² .
Если вам нужна помощь, перейдите к калькулятору теоремы Пифагора.

После того, как мы вычислили базовую площадь, мы можем перейти к фактическому вычислению поверхности .

Вот самая основная формула для поверхности треугольной призмы, которую мы можем использовать:

Площадь = длина × (a + b + c) + (2 × площадь основания)

или

Площадь = длина × Периметр основания + (2 × площадь основания)

💡 Периметр основания — это сумма всех сторон основания призмы (a+b+c).

▲ 3 стороны

Как и в предыдущем примере, нам сначала нужно узнать базовую площадь .

Это можно рассчитать по формуле Герона:

Площадь основания = 0,25 × √[(a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)] ,

где a, b, c стороны треугольного основания

Использовались те же уравнения, что и в предыдущем примере:

Площадь = Длина × (a + b + c) + (2 × Базовая площадь)

или

Площадь = длина × периметр основания + (2 × площадь основания)

▲ 2 стороны + угол между

Теперь пришло время, когда все становится сложнее.

Вы можете рассчитать площадь такого треугольника, используя формулу тригонометрии:

Площадь основания = 0,5 × a × b × sin(Angle γ)

В этом конкретном случае наш калькулятор площади треугольной призмы использует следующее формула в сочетании с законом косинусов :

Площадь = длина × (a + b + √( b² + a² - (2 × b × a × cos(угол γ)))) + a × b × sin(угол γ)

▲ 2 угла + сторона между

Мы погружаемся еще глубже в математические секреты! 😱

Вот формула площади треугольника, которую нам нужно использовать:

Площадь = = a² × sin(Угол β) × sin(Угол γ) / (2 × sin(Угол β + Угол γ))

В данном конкретном случае мы используем закон синусов.

А вот площадь поверхности треугольной призмы, которая нам нужна:

Площадь = (Длина × (a + a × (sin(Угол γ) / sin(Угол γ + Угол β)) + a × (sin(Угол β) / sin(Угол γ+Угол β)))) + a × ((a × sin(Угол γ)) / sin(Угол γ + Угол β)) × sin(Угол β)

❗ Обязательно используйте калькулятор преобразования углов, если ваши углы указаны в других единицах измерения чем градусов .

Как рассчитать боковую поверхность треугольной призмы?

Этот расчет чрезвычайно прост! Вы можете:

• Если известны все стороны треугольного основания , умножьте их значения на длину призмы:

  Боковая поверхность треугольной призмы = длина × (a + b + c)

• Если известна общая площадь поверхности , вычтите поверхность треугольных граней из общей площади поверхности призмы:

  Боковая поверхность = Общая поверхность треугольной призмы - (2 × Поверхность треугольного основания)

Часто задаваемые вопросы

Как рассчитать боковую поверхность треугольной призмы, зная длину и периметр?

Если известны длина призмы и периметр ее основания, можно определить площадь ее боковой поверхности, умножив периметр на на длину .

Чему равна площадь боковой поверхности треугольной призмы длиной 10 см и периметром основания 10 см?

Ответ: 100 см² . Вы можете получить этот ответ следующим образом:

1. Найдите периметр основания (в данном примере 10 см).
2. Измерьте длину призмы (10 см).
3. Умножить периметр основания призмы на ее длину.
4. 10 см умножить на 10 см равно 100 см² .

Мы также можем записать эти шаги в виде следующей математической формулы:

площадь поперечного сечения = периметр основания × длина призмы

Какова формула для общей площади поверхности треугольной призмы?

Общая площадь поверхности треугольной призмы равна сумме площадей всех ее граней: трех боковых граней (прямоугольники) и двух оснований (треугольники). Самая общая формула для площади поверхности любой призмы:

Общая площадь = боковая площадь + 2 × площадь основания

Это зависит от данных, которые вы получили, чтобы определить как боковую площадь, так и базовая площадь.

Люция Заборовска, доктор медицинских наук, кандидат наук

Тип треугольника

Длина призмы (L)

Площадь поверхности призмы

Площадь основания

Боковая поверхность

Проверьте 23 аналогичные калькуляторы 3D геометрии 📦

Площадь гемисферекубейбейка.

а = длина стороны а
b = длина стороны b = основание нижнего треугольника b
c = длина стороны c
h = высота призмы
H = высота нижнего треугольника
В = объем
A _tot = общая площадь поверхности = все стороны
A _lat = площадь боковой поверхности = все прямоугольные стороны
A _верх = площадь верхней поверхности = верхний треугольник
A _бот = площадь нижней поверхности = нижний треугольник

Треугольная призма представляет собой твердую геометрическую фигуру с треугольником в основании. Это трехсторонняя призма, в которой основание и вершина представляют собой равные треугольники, а остальные 3 стороны — прямоугольники.

Калькулятор Использование

Этот калькулятор позволяет найти объем, площадь поверхности и высоту треугольной призмы. Расчеты площади поверхности включают верхнюю, нижнюю, боковые стороны и общую площадь поверхности. Высота вычисляется по известному объему или площади боковой поверхности.

Единицы: Единицы показаны для удобства, но не влияют на расчеты. Ответы будут одинаковыми, будь то футы, футы ² , футы ³ , или метры, м ² , м ³ , или любые другие единицы измерения.

Значащие цифры: Выберите количество значащих цифр или оставьте значение авто, чтобы калькулятор определял точность чисел.

Треугольная призма Формулы для высоты и длин сторон треугольника a, b и c:

Объем треугольной призмы Формула

Находит трехмерное пространство, занимаемое треугольной призмой.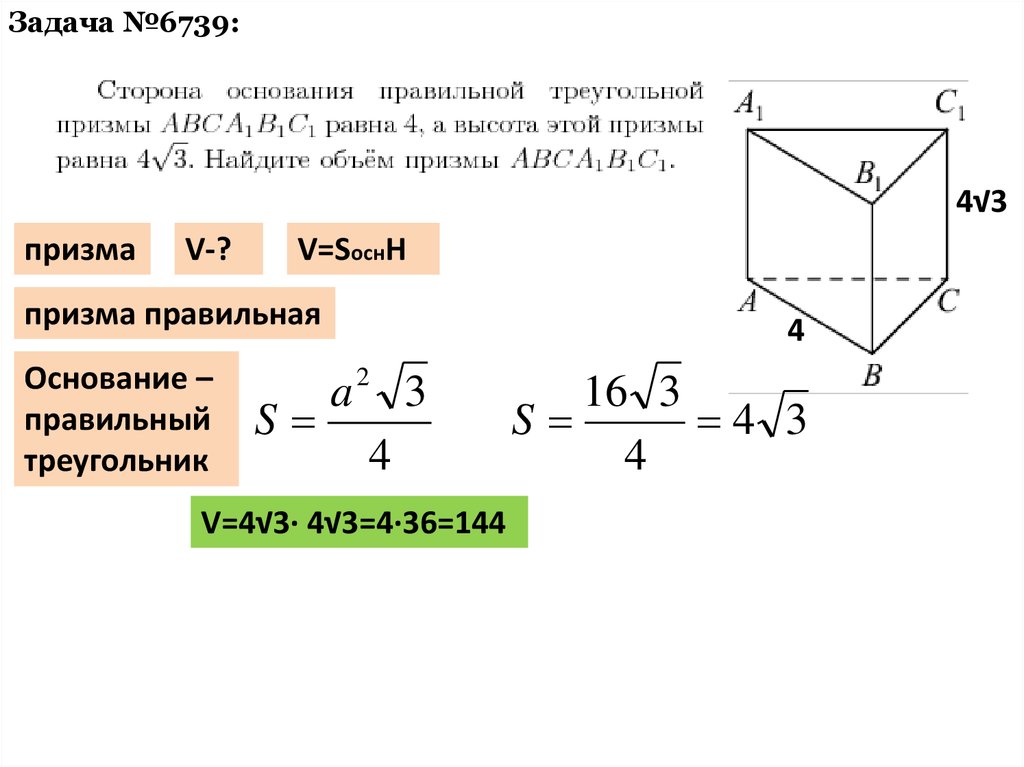

\[ V = \dfrac{1}{4}h \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ V = \ dfrac{1}{4}h \sqrt{(c+a-b)(a+b-c)} \\\times \sqrt{(a+b+c)(b+c-a)} \]

Площадь верхней поверхности a Треугольная призма Формула

Находит площадь треугольной поверхности в верхней части призмы. Это та же площадь, что и площадь нижней поверхности.

\[ A_{top} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ A_{top} = \dfrac{1}{4} \sqrt{\begin{align}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+ b-c)\end{align}} \]

Площадь нижней поверхности треугольной призмы Формула

Находит площадь треугольной поверхности в нижней части призмы. Это та же площадь, что и площадь верхней поверхности.

\[ A_{bot} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]

\[ A_ {bot} = \ dfrac {1} {4} \ sqrt {\ begin {align} (a + & b + c) (b + c-a) \\ & \ times (c + a-b) (a + b-c) \ end { выровнено}} \]

Площадь боковой поверхности треугольной призмы Формула

Находит общую площадь трех прямоугольных сторон призмы. Площадь боковой поверхности можно представить как общую площадь поверхности призмы за вычетом двух треугольных площадей вверху и внизу призмы.

\[ A_{широта} = h (a+b+c) \]

Общая площадь поверхности треугольной призмы Формула

Находит общую площадь всех сторон треугольной призмы. Общая площадь поверхности призмы включает площадь верхней и нижней треугольных сторон призмы, а также площадь всех трех прямоугольных сторон.

\[ A_{tot} = A_{top} + A_{bot} + A_{lat} \]

Формула высоты треугольной призмы в единицах объема

Находит высоту треугольной призмы путем решения формулы объема для высоты. Высота h рассчитывается исходя из объема V и длин сторон a, b и c.

\[ h = \dfrac{4V}{\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} \]

\[ h = 4V \div \left[ \, \sqrt{(c+a-b)(a+b-c)} \\\times \sqrt{(a+b+c)(b+c-a)} \, \right] \]

Формула высоты треугольной призмы через площадь боковой поверхности

Определение высоты треугольной призмы путем решения формулы площади боковой поверхности для высоты.