Площадь полной поверхности конуса равна
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-11-20
Здесь представлены задачи с конусами, условие связано с его площадью поверхности. В частности в некоторых задачах стоит вопрос об изменении площади при увеличении (уменьшении) высоты конуса или радиуса его основания. Теория для решения задач в предыдущей статье. Рассмотрим следующие задачи:
27135. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Площадь боковой поверхности конуса равна:
Подставляем данные:
Ответ: 3
75697. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз, а радиус основания останется прежним?
Площадь боковой поверхности конуса:
Образующая увеличивается в 36 раз. Радиус остался прежним, значит длина окружности основания не изменилась.
Значит площадь боковой поверхности изменённого конуса будет иметь вид:
Таким образом, она увеличится в 36 раз.
*Зависимость прямолинейная, поэтому эту задачу без труда можно решить устно.
Ответ: 36
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?
Площадь боковой поверхности конуса равна:
Радиус уменьшается в 1,5 раза, то есть:
Получили, что площадь боковой поверхности уменьшилась в 1,5 раза.
Ответ: 1,5
27159. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на Пи.
Полная поверхность конуса:
Необходимо найти радиус:
Известна высота и образующая, по теореме Пифагора вычислим радиус:
Таким образом:
Полученный результат разделим на Пи и запишем ответ.
Ответ: 144
76299. Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Формула полной поверхности конуса:
Сечение проходит через середину высоты параллельно основанию.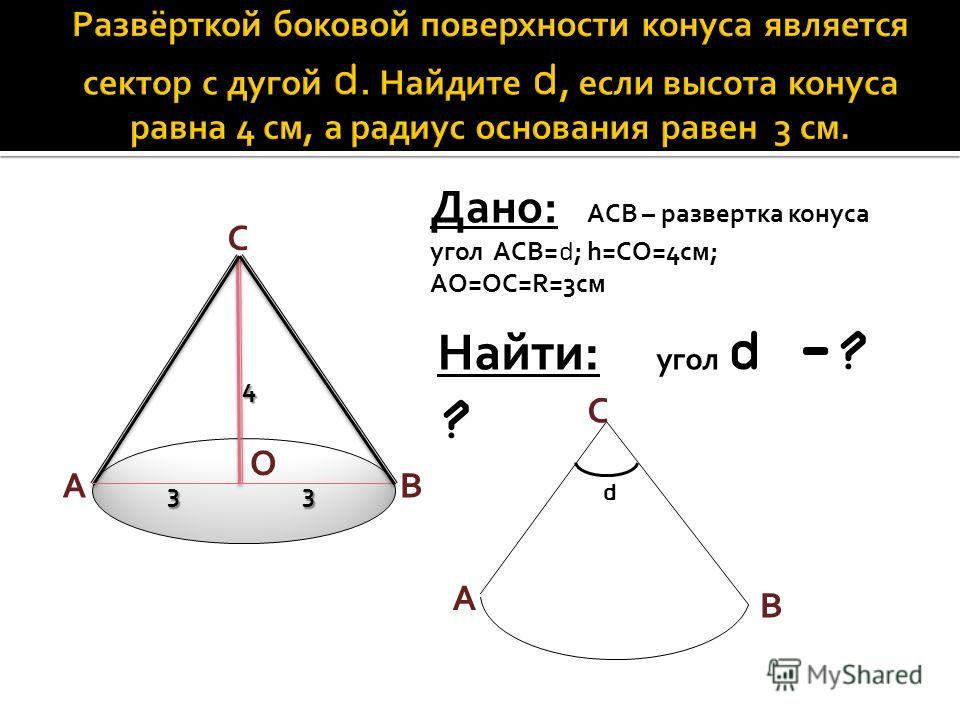 Значит радиус основания и образующая отсеченного конуса будут в 2 раза меньше радиуса и образующей исходного конуса. Запишем чему равна площадь поверхности отсечённого конуса:
Значит радиус основания и образующая отсеченного конуса будут в 2 раза меньше радиуса и образующей исходного конуса. Запишем чему равна площадь поверхности отсечённого конуса:
Получили, что она будет в 4 раза меньше площади поверхности исходного, то есть 108:4 = 27.
Ответ: 27
*Так как исходный и отсечённый конус являются подобными телами, то также можно было воспользоваться свойством подобия:
27167. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на Пи.
Формула полной поверхности конуса:
Радиус известен, необходимо найти образующую.
По теореме Пифагора:
Таким образом:
Результат разделим на Пи и запишем ответ.
Ответ: 24
Задача. Площадь боковой поверхности конуса в четыре раза больше площади основания. Найдите чему равен косинус угла между образующей конуса и плоскостью основания.
Площадь основания конуса равна:
Площадь боковой поверхности:
Исходя из условия можем записать:
Искомый угол – это угол между образующей и радиусом.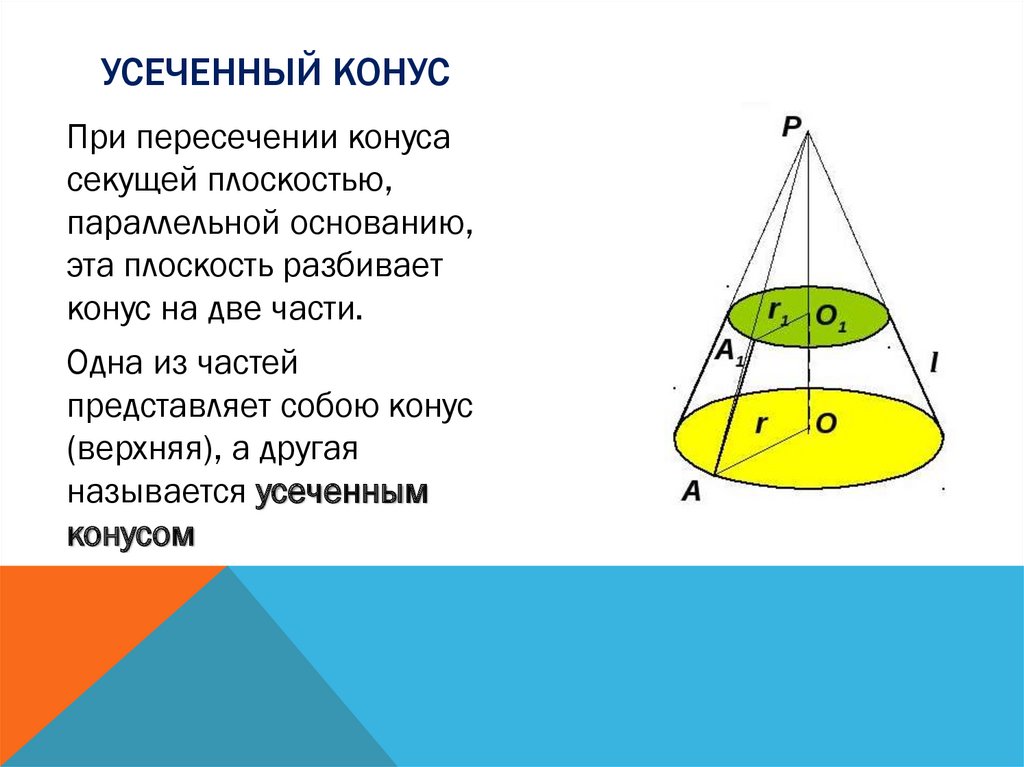 Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе (в данном случае указанный катет – это радиус, гипотенуза – это образующая):
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе (в данном случае указанный катет – это радиус, гипотенуза – это образующая):
То есть косинус будет равен:
Ответ: 0,25
Решить самостоятельно:
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? Посмотреть решение
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. Посмотреть решение.
27161. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
*Делитесь с друзьями информацией о сайте через социальные сети.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2Площадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Поверхность конуса — Математика — Экзамены, ЕГЭ, ОГЭ
ВАРИАНТ 1
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 8 раз?
Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности, деленную на π.
Радиус основания конуса равен 12, высота равна 16. Найдите площадь полной поверхности конуса, деленную на π.
Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Длина окружности основания конуса равна 7, образующая равна 2. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 2
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 11 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 19 раз?
Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности, деленную на π .
Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 28, высота равна 21. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 5, а диаметр основания — 24. Найдите образующую конуса.
Длина окружности основания конуса равна 7, образующая равна 2. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 3
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 9 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 15 раз?
Высота конуса равна 36, образующая равна 45. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 12, высота равна 16. Найдите площадь полной поверхности конуса, деленную на π.
Найдите площадь полной поверхности конуса, деленную на π.
Площадь полной поверхности конуса равна 84. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 15, а диаметр основания — 16. Найдите образующую конуса.
Длина окружности основания конуса равна 8, образующая равна 8. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 4
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 22 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 28 раз?
Высота конуса равна 21, образующая равна 35. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 16, высота равна 12. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 148. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 12, а диаметр основания — 10. Найдите образующую конуса.
Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 5
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 35 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 40 раз?
Высота конуса равна 24, образующая равна 26. Найдите площадь его полной поверхности, деленную на π.
Радиус основания конуса равен 72, высота равна 21. Найдите площадь полной поверхности конуса, деленную на π.
Площадь полной поверхности конуса равна 36. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 30, а диаметр основания — 80. Найдите образующую конуса.
Длина окружности основания конуса равна 8, образующая равна 4. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 6
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 40 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 30 раз?
Высота конуса равна 40, образующая равна 50. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 24, высота равна 18. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 100. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 40, а диаметр основания — 60. Найдите образующую конуса.
Длина окружности основания конуса равна 7, образующая равна 8. Найдите площадь боковой поверхности конуса
Найдите площадь боковой поверхности конуса
ВАРИАНТ 7
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 20 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 2 раза?
Высота конуса равна 28, образующая равна 35. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 24, высота равна 7. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 144. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 6, а диаметр основания — 16. Найдите образующую конуса.
Длина окружности основания конуса равна 4, образующая равна 2. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 8
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 2,5 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 37 раз?
Высота конуса равна 15, образующая равна 17. Найдите площадь его полной поверхности, деленную на π .
Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 60, высота равна 32. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 192. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 8, а диаметр основания — 12. Найдите образующую конуса.
Длина окружности основания конуса равна 2, образующая равна 5. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 9
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 24 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 10 раз?
Высота конуса равна 16, образующая равна 34. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 24, высота равна 45. Найдите площадь полной поверхности конуса, деленную на π .
Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 200. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Длина окружности основания конуса равна 4, образующая равна 5. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 10
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 39 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 11 раз?
Высота конуса равна 30, образующая равна 34. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 15, высота равна 36. Найдите площадь полной поверхности конуса, деленную на π.
Площадь полной поверхности конуса равна 96. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.
Длина окружности основания конуса равна 3, образующая равна 8. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 11
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 2 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 23 раза?
Высота конуса равна 32, образующая равна 40. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 12, высота равна 9. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 88. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 96, а диаметр основания — 56. Найдите образующую конуса.
Длина окружности основания конуса равна 2, образующая равна 3. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 12
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 18 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 20 раз?
Высота конуса равна 48, образующая равна 50. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 8, высота равна 15. Найдите площадь полной поверхности конуса, деленную на π.
Площадь полной поверхности конуса равна 80. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 64, а диаметр основания — 96. Найдите образующую конуса.
Длина окружности основания конуса равна 2, образующая равна 7. Найдите площадь боковой поверхности конуса.
Найдите площадь боковой поверхности конуса.
ВАРИАНТ 13
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 28 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 22 раза?
Высота конуса равна 15, образующая равна 25. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 4, высота равна 3. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 92. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 30, а диаметр основания — 32. Найдите образующую конуса.
Длина окружности основания конуса равна 6, образующая равна 3. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 14
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 19 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 21 раз?
Высота конуса равна 24, образующая равна 30. Найдите площадь его полной поверхности, деленную на π.
Найдите площадь его полной поверхности, деленную на π.
Радиус основания конуса равен 45, высота равна 24. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 52. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 25, а диаметр основания — 120. Найдите образующую конуса.
Длина окружности основания конуса равна 8, образующая равна 3. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 15
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 25 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 4 раза?
Высота конуса равна 8, образующая равна 10. Найдите площадь его полной поверхности, деленную на π.
Радиус основания конуса равен 25, высота равна 60.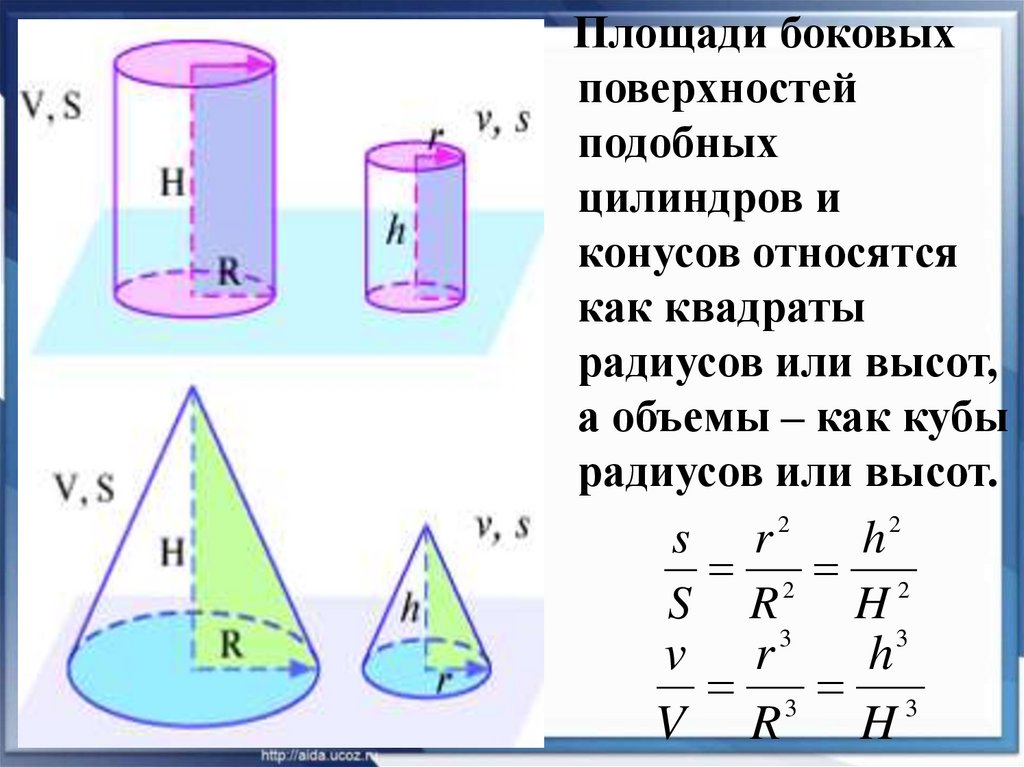 Найдите площадь полной поверхности конуса, деленную на π .
Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 40. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 48, а диаметр основания — 40. Найдите образующую конуса.
Длина окружности основания конуса равна 7, образующая равна 6. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 16
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 41 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 31 раз?
Высота конуса равна 8, образующая равна 17. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 40, высота равна 30. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 16. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 60, а диаметр основания — 126. Найдите образующую конуса.
Длина окружности основания конуса равна 8, образующая равна 6. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 17
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 26 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 13 раз?
Высота конуса равна 24, образующая равна 25. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 15, высота равна 20. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 124. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 32, а диаметр основания — 120. Найдите образующую конуса.
Длина окружности основания конуса равна 4, образующая равна 4. Найдите площадь боковой поверхности конуса.
ВАРИАНТ 18
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 32 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 33 раза?
Высота конуса равна 3, образующая равна 5. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 21, высота равна 28. Найдите площадь полной поверхности конуса, деленную на π .
Площадь полной поверхности конуса равна 176. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 54, а диаметр основания — 144. Найдите образующую конуса.
Длина окружности основания конуса равна 6, образующая равна 4.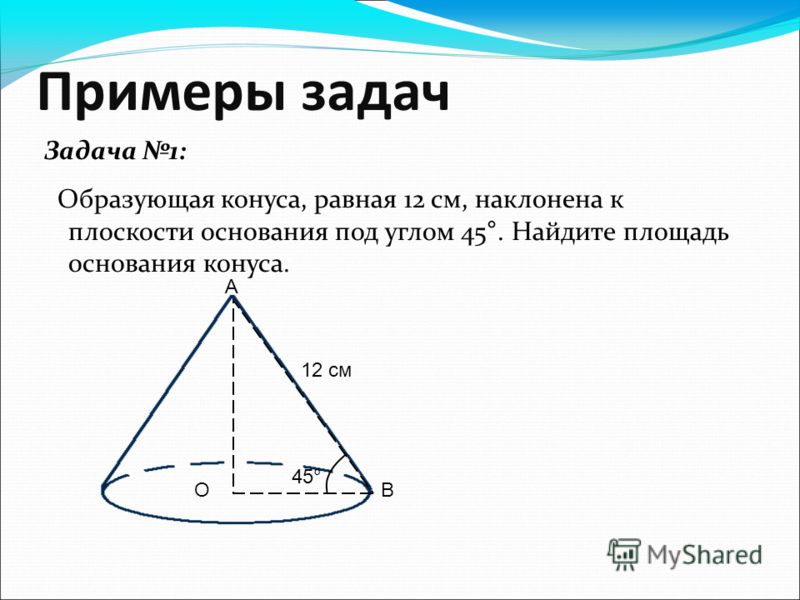 Найдите площадь боковой поверхности конуса.
Найдите площадь боковой поверхности конуса.
ВАРИАНТ 19
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 16 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 34 раза?
Высота конуса равна 12, образующая равна 13. Найдите площадь его полной поверхности, деленную на π .
Радиус основания конуса равен 12, высота равна 9. Найдите площадь полной поверхности конуса, деленную на π.
Площадь полной поверхности конуса равна 128. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Высота конуса равна 7, а диаметр основания — 48. Найдите образующую конуса.
Длина окружности основания конуса равна 2, образующая равна 8. Найдите площадь боковой поверхности конуса.
Площадь поверхности конуса
Площадь поверхности конуса — это общая площадь, занимаемая поверхностями конуса. Конус представляет собой геометрическую фигуру объемной формы, которая имеет плоскую грань и криволинейную поверхность с заостренным концом. Форма конуса получается вращением прямоугольного треугольника вокруг его перпендикуляра. Заостренный конец конуса называется вершиной или вершиной. Расстояние по перпендикуляру между центром основания и вершиной конуса называется высотой, а наклонная высота — это расстояние от вершины конуса до любой точки на окружности основания. Нормальный конус также называют прямым круговым конусом. В этой статье обсуждается площадь прямого кругового конуса. Конусы для мороженого, дорожные конусы, воронки, шляпы на день рождения и т. д. — вот некоторые примеры конусов, которые мы видим в нашей повседневной жизни.
Конус представляет собой геометрическую фигуру объемной формы, которая имеет плоскую грань и криволинейную поверхность с заостренным концом. Форма конуса получается вращением прямоугольного треугольника вокруг его перпендикуляра. Заостренный конец конуса называется вершиной или вершиной. Расстояние по перпендикуляру между центром основания и вершиной конуса называется высотой, а наклонная высота — это расстояние от вершины конуса до любой точки на окружности основания. Нормальный конус также называют прямым круговым конусом. В этой статье обсуждается площадь прямого кругового конуса. Конусы для мороженого, дорожные конусы, воронки, шляпы на день рождения и т. д. — вот некоторые примеры конусов, которые мы видим в нашей повседневной жизни.
Какова площадь поверхности конуса?
Площадь поверхности конуса визуализируется как площадь, занимаемая конусом, когда он разрезается. Он образован круглым основанием и изогнутой поверхностью. Площадь поверхности конуса зависит от радиуса его основания и высоты конуса. Кроме того, объем конуса зависит от его радиуса и высоты.
Кроме того, объем конуса зависит от его радиуса и высоты.
Площадь поверхности конуса Формула
Площадь поверхности конуса определяется как площадь, занимаемая границей или поверхностью конуса. Конус имеет два типа площадей поверхности, а именно: криволинейную площадь поверхности и общую площадь поверхности.
Площадь криволинейной поверхности конуса
Криволинейная поверхность конуса определяется как площадь криволинейной части конуса, т. е. площадь конуса без основания. Она также известна как площадь боковой поверхности конуса. Формула для CSA (площадь криволинейной поверхности) конуса задается следующим образом:
Общая площадь поверхности конуса
, где
« r » — радиус основания конуса, а
« l » — наклонная высота. конуса.
Общая площадь поверхности конуса определяется как общая площадь, занимаемая конусом в трехмерном пространстве, т. е. площадь криволинейной поверхности и площадь круглой база. Формула для TSA (общая площадь поверхности) конуса представлена следующим образом:
е. площадь криволинейной поверхности и площадь круглой база. Формула для TSA (общая площадь поверхности) конуса представлена следующим образом:
, где
« r » — радиус основания конуса, а
« l » — высота наклона. конуса.
Расчет площади поверхности конуса
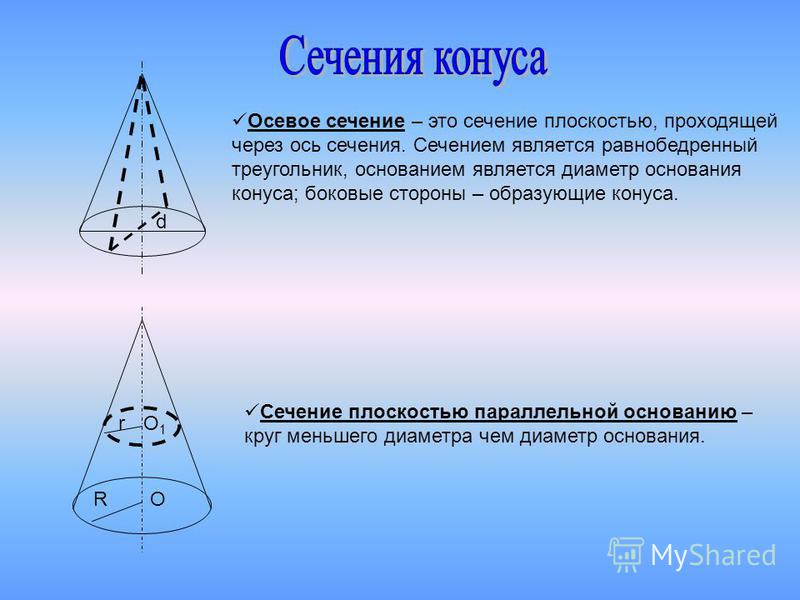
Чтобы увидеть фигуру, образованную поверхностью конуса, возьмите бумажный конус и разрежьте его по наклонной высоте. Теперь отметьте A и B как две конечные точки и O как точку пересечения двух линий. Теперь, если мы его откроем, он будет выглядеть как сектор круга.
Итак, чтобы найти площадь криволинейной поверхности конуса, нужно найти площадь сектора.
Площадь сектора по длине дуги = (длина дуги × радиус)/ 2 = ((2πr) × l)/2 = πrl.
CSA конуса = πrl квадратных единиц
Общая площадь поверхности конуса (T) = площадь основания + площадь криволинейной поверхности
Поскольку основание представляет собой круг, площадь основания = πr 2
⇒ T = πr 2 + πrl = πr(r + l)
TSA конуса = πr (r + l) квадратных единиц
Также узнайте об усеченной части тут конус.
Связь между площадью поверхности конуса и его высотой
Учитывая наклонную высоту, высоту и радиус конуса, они образуют прямоугольный треугольник, где наклонная высота — это гипотенуза, основание — радиус основания, а высота — высота прямоугольного треугольника.
Используя теорему Пифагора, получаем l 2 = r 2 +h 2
Таким образом, наклонная высота конуса (l) = √(r 9 0071 2 + ч 2 )
Итак, заменив величину наклона в формулах площади поверхности конуса, получим
Как найти площадь поверхности конуса?Площадь криволинейной поверхности (S) = πr√(r 2 + h 2 ) квадратных единиц
Общая площадь поверхности (T) = πr 2 + πr√(r 2 + h 2 ) квадратных единиц
Давайте рассмотрим пример, чтобы увидеть, как найти площадь поверхности конуса, используя его формулу.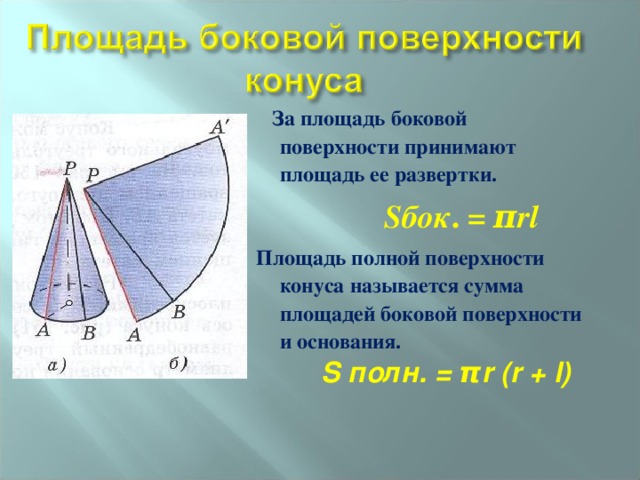
Пример. Найдите общую площадь поверхности конуса, если его радиус равен 5 дюймам, а высота наклона равна 12 дюймам. (Используйте π = 3,14)
Шаг 1: Запишите размеры данного конуса. Здесь наклонная высота конуса равна 12 дюймам, а его радиус равен 5 дюймам.
Шаг 2: Мы знаем, что общая площадь поверхности конуса = πr (r + l). Итак, подставьте значение заданных размеров в уравнение = (3,14) × 5 × (5 + 12) = 266,9 кв. дюйма
Шаг 3: Следовательно, общая площадь поверхности конуса равна 266,9 квадратных дюймов.
Решенные примеры на площади поверхности конуса
Пример 1. Найдите общую площадь поверхности конуса, если его радиус равен 15 см, а высота наклона равна 10 см. (Используйте π = 3,14)
Решение:
Приведенные данные,
Радиус конуса (r) = 15 см
Наклонная высота (l) = 10 см
Мы это знаем,
Общая площадь поверхности конуса = πr (r + l) квадратных единиц
= (3,14) × 15 × (15 + 10)
= 1177,5 кв.
см
Следовательно, общая площадь поверхности конуса равна 1 177,5 кв. см.
Пример 2: Какова высота конуса, если его радиус равен 14 единицам, а площадь криволинейной поверхности равна 1100 квадратных единиц? (Используйте π = 22/7)
Решение:
Приведенные данные,
Радиус конуса (r) = 14 единиц
Пусть наклонная высота конуса равна «l», а высота конуса — «h».
Мы знаем, что
Площадь криволинейной поверхности конуса = πrl квадратных единиц
⇒ 1100 = (22/7) × 14 × l
⇒ 44 × l = 1100
⇒ l = 1100/44 = 25 единиц
Мы это знаем,
наклон высота (l) = √(h 2 + r 2 )
⇒ h = √(l2 – r2)
= √(25 2 – 14 2 ) = √429 = 20,71 ед.
Таким образом, высота конуса составляет 20,71 ед.
Пример 3: Определите наклонную высоту конуса, если общая площадь поверхности конуса составляет 525 кв. см, а радиус равен 7 см. (Используйте π = 22/7)
см, а радиус равен 7 см. (Используйте π = 22/7)
Решение:
Приведены данные,
Радиус конуса (r) = 7 см
Общая площадь поверхности конуса = 525 кв. см
et sl муравьиная высота конуса будет “ л».
Мы знаем, что
Общая площадь поверхности конуса = πr (r + l) квадратных единиц
⇒ (22/7) × 7 × (7 + l) = 525
⇒ 22 × (7 + l) = 525
⇒ 7 + l = 25
⇒ l = 18 см
Следовательно, наклонная высота конуса равна 18 см.
Пример 4. Вычислите площадь боковой поверхности конуса, радиус которого 24 дюйма, а высота 7 дюймов. (Используйте π = 3,14)
Решение:
Приведенные данные,
Радиус конуса (r) = 24 дюйма
Высота конуса (h) = 7 дюймов.
Мы знаем, что
наклонная высота (l) = √(h 2 + r 2 )
l = √(7 2 + 24 2 ) = √(625) = 25 дюймов
Мы знаем, что
Площадь криволинейной поверхности конуса = πrl квадратных единиц
= 3,14 × 24 × 25
= 1884 кв.
в
Следовательно, площадь криволинейной поверхности конуса равна 1884 кв.
Часто задаваемые вопросы о площади поверхности конуса
Вопрос 1: Что произойдет с площадью криволинейной поверхности конуса, если его высоту удвоить?Ответ:
Вопрос 2. Как найти площадь поверхности конуса?Площадь криволинейной поверхности конуса напрямую зависит от радиуса его основания.
Площадь криволинейной поверхности = πrl
Если радиус конуса удвоить, площадь его криволинейной поверхности также удвоится.
CSA = π(2r)(l)
= 2πrl
= 2 × площадь исходной криволинейной поверхности
Ответ:
Площадь поверхности con можно рассчитать двумя способами:
CSA = πrl
TSA = πrl(r+l)
где
r радиус конуса
l высота наклона конуса
90 017 Вопрос 3: Напишите способы расчета наклонной высоты конус.

Ответ:
Вопрос 4: Напишите формулу базовой поверхности конуса.Наклонная высота конуса определяется по формуле
где «r» радиус и «h» высота конуса.
Ответ:
Вопрос 5: Что мы подразумеваем под площадью поверхности конуса?Поверхность основания конуса круглая и формула основания поверхности конуса πr 2 квадратных единиц.
Ответ:
Площадь поверхности конуса — это область, занимаемая поверхностью конуса в трехмерном пространстве. Его можно рассчитать, найдя сумму боковой площади и площади основания конуса.
Связанные ресурсы
9 0026
- Площадь поверхности цилиндра
- Площадь поверхности сферы
- Площадь поверхности куба
- Площадь поверхности куба

 см
см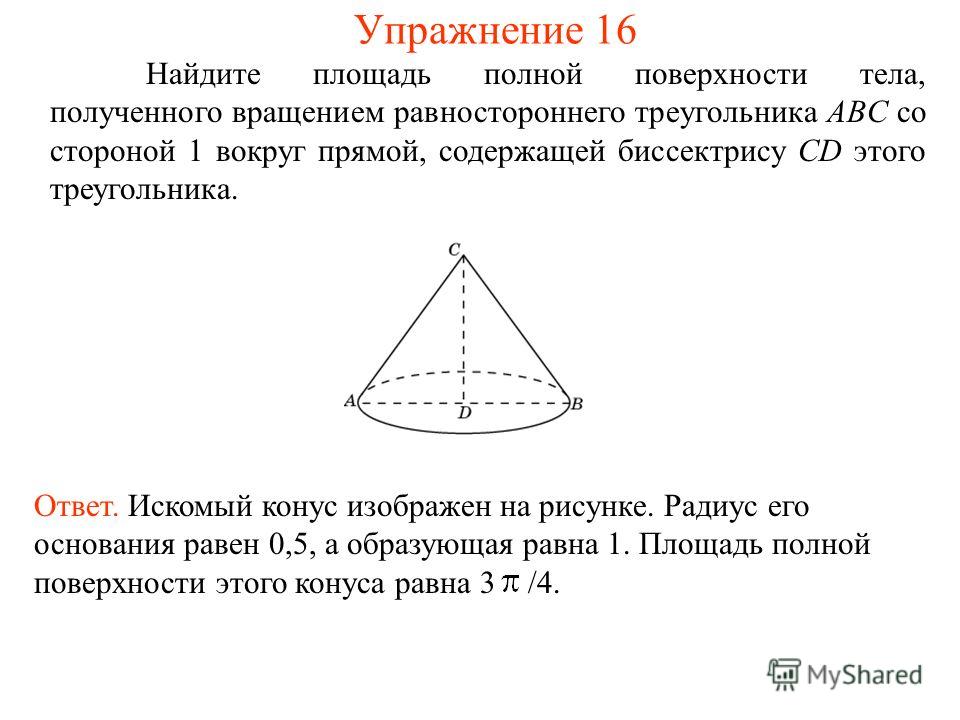 в
в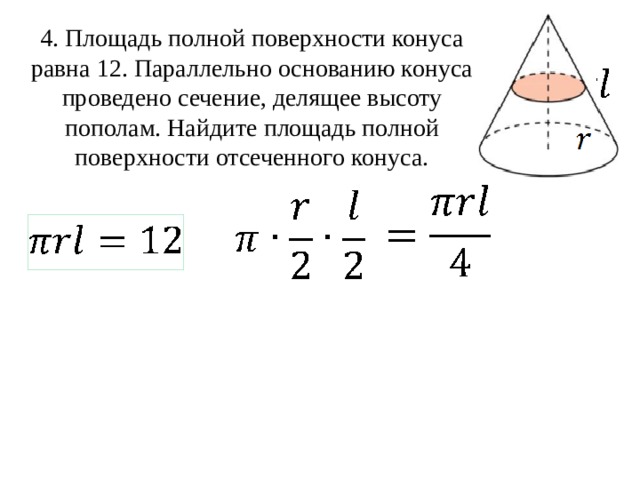 Это отличный способ связаться с другими лидерами в вашем районе И в Иллинойсе. Мероприятие состоится в субботу, 29 апреля., с 9:00 до 12:30. Основные темы включают Поддержка учителей, Циклы коучинга и Социально-эмоциональное обучение с помощью математики. Регистрация БЕСПЛАТНА для членов ICTM и 35 долларов США для нечленов. Все подробности смотрите на сайте нашей коучинговой мини-конференции!
Это отличный способ связаться с другими лидерами в вашем районе И в Иллинойсе. Мероприятие состоится в субботу, 29 апреля., с 9:00 до 12:30. Основные темы включают Поддержка учителей, Циклы коучинга и Социально-эмоциональное обучение с помощью математики. Регистрация БЕСПЛАТНА для членов ICTM и 35 долларов США для нечленов. Все подробности смотрите на сайте нашей коучинговой мини-конференции! 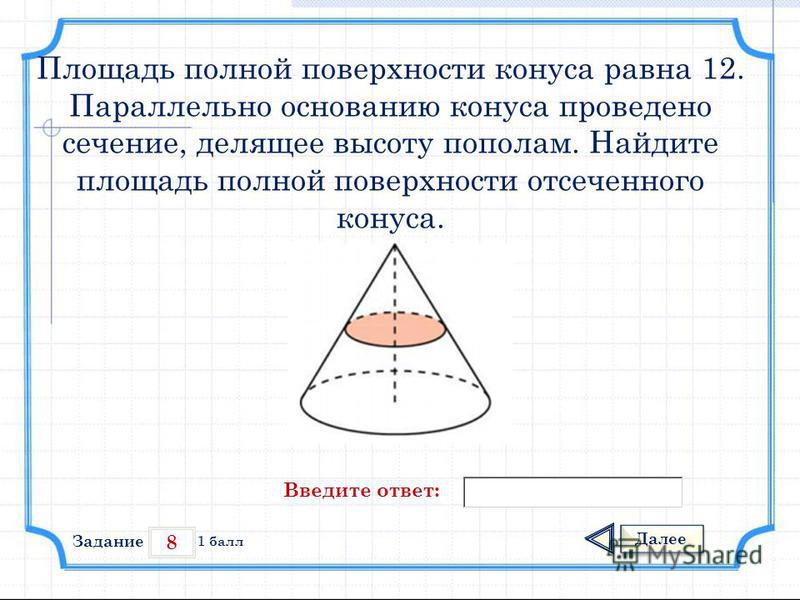 12-15). Время встречи будет 7-8:30pm (CT). Члены ICTM получат часы IL PD. Нажмите здесь, чтобы зарегистрироваться. Вопросы? Свяжитесь с Джастином Бреннаном по адресу justin[email protected].
12-15). Время встречи будет 7-8:30pm (CT). Члены ICTM получат часы IL PD. Нажмите здесь, чтобы зарегистрироваться. Вопросы? Свяжитесь с Джастином Бреннаном по адресу justin[email protected].

Leave A Comment