Площадь круга
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке»).
Все, что требуется в таких заданиях — это найти радиус окружности R. Затем можно вычислить площадь круга по формуле S = πR2. Из этой формулы также следует, что для решения достаточно найти R2.
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R2 = AB2 = AC2 + BC2 = 22 + 22 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R2 = AB2 = AC2 + BC2 = 12 + 22 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
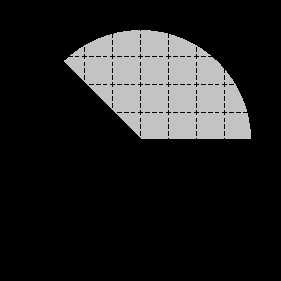
Задача. Найти площадь S закрашенного сектора. В ответе укажите S/π.
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · Sкруга.
Остается найти Sкруга — площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC — прямоугольный. По теореме Пифагора имеем: R2 = AB2 = AC2 + BC2 = 22 + 22 = 8.
Теперь находим площади круга и сектора: Sкруга = πR2 = 8π;S = 0,25 · Sкруга = 2π.
Наконец, искомая величина равна S/π = 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010—2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:

Пусть исходный круг имеет площадь Sкруга
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
- Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40 : 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64 : 8 = 8.
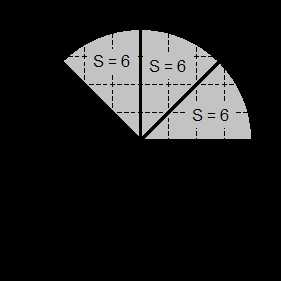
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48 : 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
Смотрите также:
- Задача B5: площадь сектора
- Задача B5: площадь закрашенного сектора
- Схема Бернулли. Примеры решения задач
- Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
- Тригонометрические функции
- ЕГЭ-2014 по математике и открытый банк задач
www.berdov.com
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | |
| Дуга | Часть окружности, расположенная между двумя точками окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Сектор | Часть круга, ограниченная двумя радиусами | |
| Сегмент | Часть круга, ограниченная хордой | |
| Правильный многоугольник | Выпуклый многоугольник, у которого все стороны равны и все углы равны | |
Около любого правильного многоугольника можно описать окружность |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |
Часть окружности, расположенная между двумя точками окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Сектор |
Часть круга, ограниченная двумя радиусами |
| Сегмент |
Часть круга, ограниченная хордой |
| Правильный многоугольник |
Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
Следовательно,
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
Следовательно,
В случае, когда величина α выражена в в радианах, получаем
Следовательно,
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Площадь круга — формулы, примеры расчетов
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. 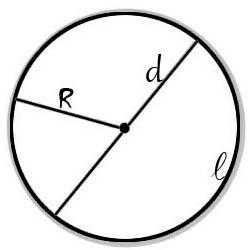
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
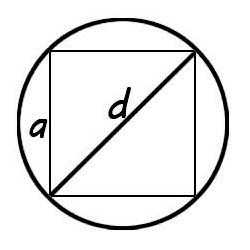
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
И после подставим все в основную формулу площади круга описанного вокруг квадрата: Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Площадь круга
Площадь круга — это численная характеристика, характеризующая размер плоскости, ограниченной линией окружности. Вычислить площадь круга можно с помощью числа Пи и радиуса окружности, или с помощью других известных исходных данных.
Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь круга или проверить уже выполненные вычисления.
1
Площадь круга через радиус
r — радиус
… подготовка …
2
Площадь круга через диаметр
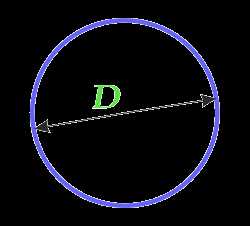
D — диаметр
… подготовка …
3
Площадь круга по длине окружности

— длина окружности
… подготовка …
4
Площадь круга через вписанный в круг квадрат
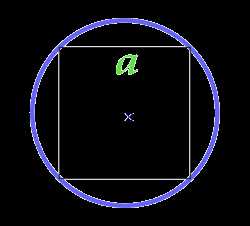
a — сторона
… подготовка …
5
Площадь круга вписанного в квадрат
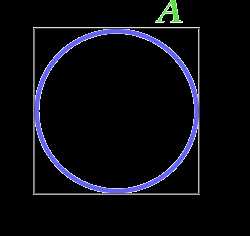
A — сторона
… подготовка …
6
Площадь круга описанного около произвольного треугольника
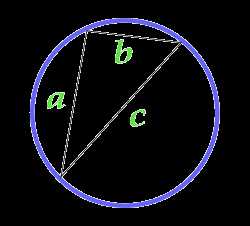
Данная формула применима только, если вокруг треугольника можно описать круг, то есть все три вершины треугольника должны лежать на линии окружности. Треугольник в данном случае может быть любым.
Для вычисления площади круга, предварительно рассчитаем полупериметр треугольника
a — сторона
b — сторона
c — сторона
… подготовка …
7
Площадь круга описанного около равностороннего треугольника
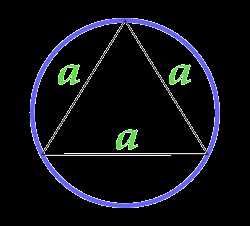
a — сторона
… подготовка …
8
Площадь круга описанного около равностороннего треугольника, вычисляемая по высоте треугольника
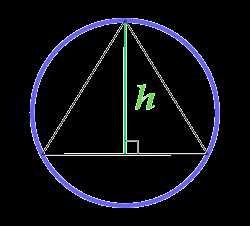
h — высота
… подготовка …
9
Площадь круга описанного около равнобедренного треугольника
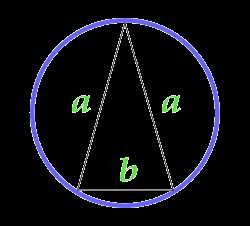
a — сторона
b — основание
… подготовка …
10
Площадь круга описанного около прямоугольного треугольника
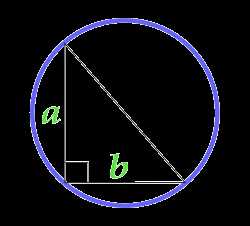
a — сторона
b — сторона
… подготовка …
11
Площадь круга вписанного в равнобедренный треугольник
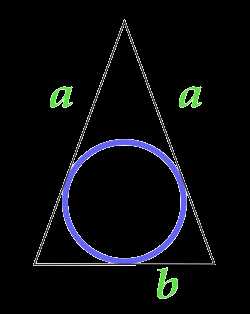
a — сторона
b — основание
… подготовка …
12
Площадь круга вписанного в равнобедренный треугольник, вычисляемая по боковым сторонам треугольника и углу между ними
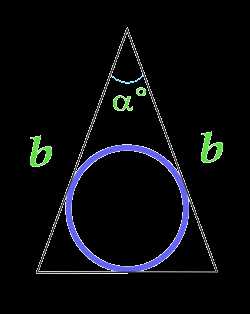
b — сторона
α — угол между сторонами
… подготовка …
13
Площадь круга вписанного в прямоугольный треугольник
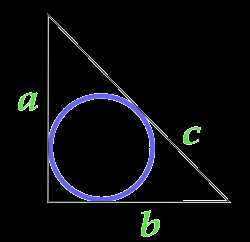
a — сторона
b — сторона
c — сторона
… подготовка …
14
Площадь круга вписанного в прямоугольный треугольник, вычисляемая по стороне и углу

b — сторона
α — угол при основании
… подготовка …
15
Площадь круга вписанного в равносторонний треугольник
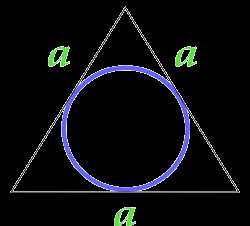
a — сторона
… подготовка …
16
Площадь круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании
b — сторона
α — угол при основании
… подготовка …
17
Площадь круга описанного около равнобедренной трапеции, рассчитанная по боковым сторонам трапеции, ее диагонали и основанию
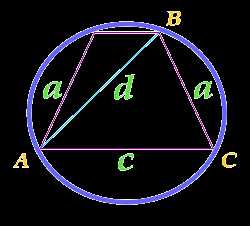
Для вычисления площади круга, предварительно рассчитаем полупериметр треугольника ABC
a — сторона
c — сторона
d — диагональ
… подготовка …
18
Площадь круга описанного около прямоугольника
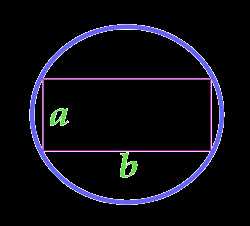
a — сторона
b — сторона
… подготовка …
19
Площадь круга описанного около правильного многоугольника
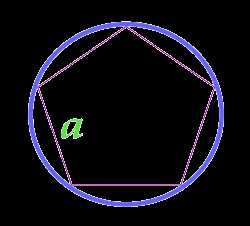
a — сторона
N — количество сторон многоугольника
… подготовка …
20
Площадь круга описанного около правильного шестиугольника
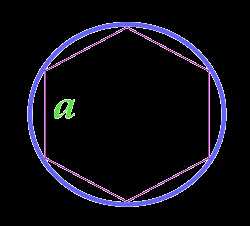
a — сторона
… подготовка …
Определения
Круг – это геометрическая плоская фигура, ограниченная линией состоящей из множества точек равноудаленных от одной точки – центра круга. Кривая замкнутая линия проведенная через равноудаленные точки, образует окружность.
Диаметр круга – это отрезок в виде прямой линии, проходящей через центр окружности и соединяющий две точки лежащие на окружности.
Радиус круга – это прямой отрезок соединяющий центр окружности с любой точкой лежащей на окружности.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
doza.pro
Окружность, круг, сегмент, сектор. Формулы и свойства
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность — окружность, радиус которой равна единице.
Определение. Круг — часть плоскости, ограничена окружностью.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:L = πD
2. Формула длины окружности через радиус:L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:S = πr2
2. Формула площади круга через диаметр:S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x — a)2 + (y — b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:AQ ∙ BQ = CQ ∙ DQ
2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды
 1. Длина хорды через центральный угол и радиус:
1. Длина хорды через центральный угол и радиус:AB = 2r sin α2
 2. Длина хорды через вписанный угол и радиус:
2. Длина хорды через вписанный угол и радиус:AB = 2r sin α
Основные свойства хорд
 1. Две одинаковые хорды стягивают две одинаковые дуги:
1. Две одинаковые хорды стягивают две одинаковые дуги:если хорды AB = CD, то
дуги ◡ AB = ◡ CD
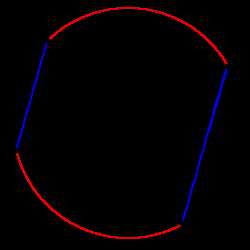 2. Если хорды параллельные, то дуги между ними будут одинаковые:
2. Если хорды параллельные, то дуги между ними будут одинаковые:если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
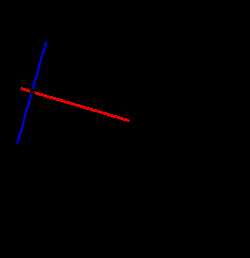 3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:если OD ┴ AB, то
AC = BC
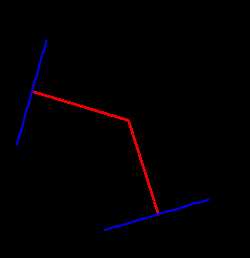
 4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:AQ ∙ BQ = DQ ∙ QC
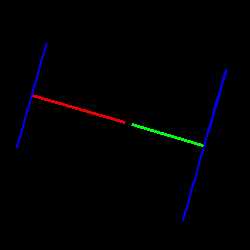
 5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.если хорды AB = CD, то
ON = OK
 6. Чем больше хорда тем ближе она к центру.
6. Чем больше хорда тем ближе она к центру.если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
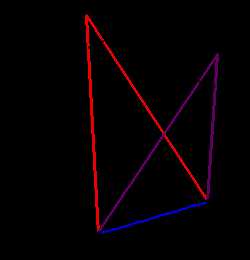 1. Все вписанные углы, которые опираются на одну дугу — равны.
1. Все вписанные углы, которые опираются на одну дугу — равны. 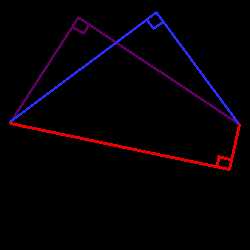 2. Вписанний угол, который опирается на диаметр будет прямым (90°).
2. Вписанний угол, который опирается на диаметр будет прямым (90°).  3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
3. Вписанный угол равен половине центрального угла, что опирается на ту же дугуβ = α2
 4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.α + β = 180°
Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
 Формула длины дуги через центральный угол (в градусах):
Формула длины дуги через центральный угол (в градусах):l = πr180°∙ α
Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
 Формула. Формула площади сектор через центральный угол (в градусах)
Формула. Формула площади сектор через центральный угол (в градусах)S = πr2360°∙ α
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.
ru.onlinemschool.com
Формула площади круга через диаметр или радиус или длину окружности.
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр
L — длина окружности
О — центр круга
π ≈ 3.14
Формула площади круга если известна длина окружности, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
- Подробности
- Автор: Сергей Кондратов
www-formula.ru
Найти площадь круга онлайн калькулятор.
Общая теория для вычисления площади круга.
Интересно, круг и окружность – это одно и то же? Оказывается, нет! В чем же их разница? Все станет ясно из определений.
Окружность – это такая фигура, которая состоит из множества всех точек плоскости и эти точки находятся от некоторой заданной точки О на определенном расстоянии. Точка О называется центром окружности. А отрезок, который соединяет центр с какой-либо точкой окружности, называется радиусом окружности. Отрезок, который соединяет две точки окружности и проходит через ее центр называется диаметром окружности. Диаметр окружности равен двум радиусам.
Круг же– это плоская фигура, ограниченная окружностью.
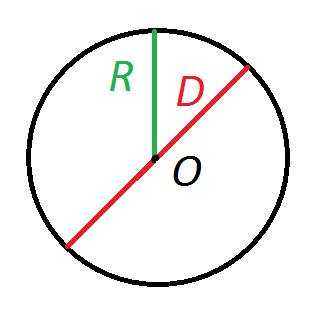
Рисунок №1: Окружность
На рисунке №1 представлена окружность с центром О, радиусом R и диаметром D.
Длина окружности L радиуса R вычисляется по формуле:
Площадью S плоской фигуры, к которым относится и круг, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади круга:
1. Площадь круга равна произведению квадрата радиуса на число :
2. Площадь круга равна четверти произведения квадрата диаметра на число :
3. Площадь круга возможно вычислить при известной длине окружности по формуле:
Число π= 3,14.
Пример 1: Вычислить площадь круга с радиусом R=4.
Решение:
Для нахождения площади круга воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 2: Найти радиус окружности с площадью S=144.
Решение:
Для нахождения радиуса окружности воспользуемся формулой вычисления площади круга:
Выразим из данной формулы радиус окружности:
Таким образом, имеем следующее:
Ответ:
Пример 3: Вычислить площадь круга с диаметром D = 10 см.
Решение:
Для нахождения площади круга воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Найти диаметр окружности с площадью S = 121 см2.
Решение:
Для нахождения диаметра окружности воспользуемся формулой вычисления площади круга:
Выразим из данной формулы диаметр окружности:
Таким образом, имеем следующее:
Ответ:
Пример 5: Вычислить площадь круга, если длина окружности L = 28.
Решение:
Для нахождения площади круга воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти длину окружности с площадью S = см2.
Решение:
Для нахождения длины окружности воспользуемся формулой вычисления площади круга:
Выразим из данной формулы длину окружности:
Таким образом, имеем следующее:
Ответ:
ktoreshit.ru

Leave A Comment