Подготовка к ЕГЭ. Задачи на сплавы. | Материал для подготовки к ЕГЭ (ГИА) по алгебре (11 класс) на тему:

Задачи на сплавы.

1.1. Первый сплав содержит 10% меди, второй  — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

2. Первый сплав содержит 5% меди, второй  — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

3. Первый сплав содержит 5% меди, второй  — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 13% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

4. Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

5. Первый сплав содержит 5% меди, второй  — 14% меди. Масса второго сплава больше массы первого на 8 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

6. Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

7. Первый сплав содержит 5% меди, второй  — 11% меди. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

8. Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 6 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

9. Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

2.1. Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

2. Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

3. Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

4. Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

5. Имеется два сплава. Первый сплав содержит 5% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

6. Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

7. Имеется два сплава. Первый сплав содержит 5% никеля, второй  — 20% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

8. Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

9. Имеется два сплава. Первый сплав содержит 5% никеля, второй  — 25% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Задачи на сплавы.

Проценты переводим в десятичную дробь.

Количество вещества = масса сплава • на десят. дробь.

1.1.Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение.

                                 Масса сплава        % содержание      Кол-во никеля                            

1-ый сплав                          х                 10%=0,1                     0,1х

2-ой сплав                         200-х           30%=0,3               0,3(200-х)=60-0,3х

3-ий сплав                         200              25% =0,25            0,25•200=50

Складываем количество никеля 1 и 2 сплавов и приравниваем к количеству 3 сплава.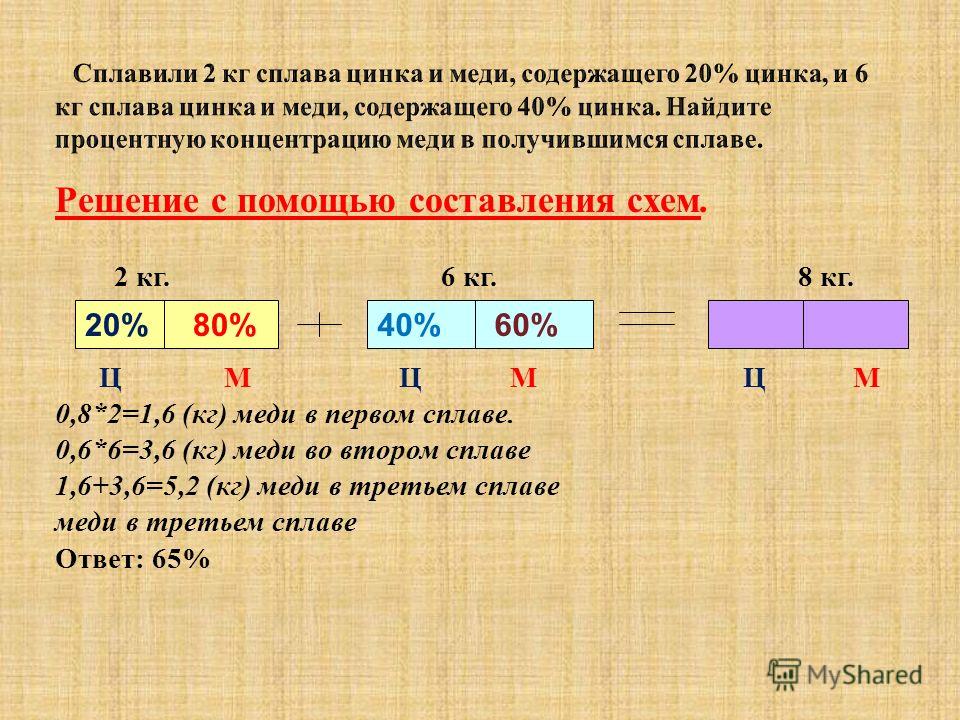

Уравнение:

0,1x+60-0,3x=50

 0,2x=10

 x=50 — масса 1-го сплава

Тогда 200-50=150 –  масса 2-го сплава

Разница 150-50=100

ОТВЕТ: 100

2.1.Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение.

                                          Масса сплава      % содержание              Кол-во меди

1-ый сплав                               x                       10%=0,1                           0,1x

2-ой сплав                                x+3                   40%=0,4                          0,4(x+3)

3-ий сплав                               2x+3                  30%=0,3                         0,3(2x+3)

Уравнение:

0,1x+0,4(x+3)=0,3(2x+3)

0,1x=0,3

 x=3

Масса 3-го сплава равна 2•3+3=9

ОТВЕТ: 9.

ОТВЕТЫ К ЗАДАЧАМ НА СПЛАВЫ.

1

2

3

4

5

6

7

8

9

1

100

27

9

12

24

6

13

8

10

2

9

90

45

120

75

105

50

35

100

Решутест. Продвинутый тренажёр тестов

Решутест. Продвинутый тренажёр тестов
  • Главная
  • ЕГЭ
  • Математика профильная
  • Текстовые задачи
  • Сплавы и смеси

Решил заданий

Не решил заданий

Осталось заданий

История решения
4188 — не приступал 9265 — не приступал 5478 — не приступал 7867 — не приступал 5402 — не приступал 3465 — не приступал 1186 — не приступал 7199 — не приступал 3437 — не приступал 7235 — не приступал 9919 — не приступал 9650 — не приступал 2353 — не приступал 1285 — не приступал 1145 — не приступал 1309 — не приступал 7508 — не приступал 1169 — не приступал

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Раскрыть Скрыть

№1

В сосуд, содержащий 5 литров 26 — процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?

№2

В сосуд, содержащий 6 литров 30 — процентного водного раствора некоторого вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора?

№3

Смешали 8 литров 40 — процентного водного раствора некоторого вещества с 12 литрами 25 — процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

№4

Смешали 4 литра 10 — процентного водного раствора некоторого вещества с 11 литрами 40 — процентного водного раствора этого же вещества.

Сколько процентов составляет концентрация получившегося раствора?

№5

Первый сплав содержит 5% меди, второй — 11% меди. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

№6

Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

№7

Смешали некоторое количество 21 — процентного раствора некоторого вещества с таким же количеством 13 — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

№8

Смешали некоторое количество 16 — процентного раствора некоторого вещества с таким же количеством 18 — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

№9

Имеется два сплава. Первый сплав содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?

№10

Имеется два сплава. Первый сплав содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 125 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?

№11

Имеются два сосуда. Первый содержит 40 кг, а второй — 25 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 20% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 23% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

№12

Имеются два сосуда. Первый содержит 100 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 64% кислоты.

Если же смешать равные массы этих растворов, то получится раствор, содержащий 72% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

№13

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

№14

Смешав 14 — процентный и 82 — процентный растворы кислоты и добавив 10 кг чистой воды, получили 22 — процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50 — процентного раствора той же кислоты, то получили бы 42 — процентный раствор кислоты. Сколько килограммов 14 — процентного раствора использовали для получения смеси?

№15

Смешав 24 — процентный и 70 — процентный растворы кислоты и добавив 10 кг чистой воды, получили 40 — процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50 — процентного раствора той же кислоты, то получили бы 45 — процентный раствор кислоты. Сколько килограммов 24 — процентного раствора использовали для получения смеси?

№16

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили раствор 36-процентный кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

№17

Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?

№18

Смешав 76-процентный и 78-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 76-процентного раствора использовали для получения смеси?

Так твой прогресс будет сохраняться.

Регистрация

Мы отправили код на:

Изменить

Получить код повторно через 00:00

Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных

Ништяк!

Решено верно

Браво!

Решено верно

Крутяк!

Решено верно

Зачёт!

Решено верно

Чётко!

Решено верно

Бомбезно!

Решено верно

Огонь!

Решено верно

Юхууу!

Решено верно

Отпад!

Решено верно

Шикарно!

Решено верно

Блестяще!

Решено верно

Волшебно!

Решено верно

Один сплав содержит в 3 раза больше меди, чем серебра.

Другой содержит в 5 раз больше серебра, чем меди. Сколько каждого из них нужно использовать, чтобы получить 14 кг, в которых вдвое больше с РЕШЕНИЕ: Один сплав содержит в 3 раза больше меди, чем серебра. Другой содержит в 5 раз больше серебра, чем меди. Сколько каждого из них нужно использовать, чтобы получить 14 кг, в которых в два раза больше с

Алгебра -> Настраиваемые средства решения задач Word -> Смеси -> РЕШЕНИЕ: Один сплав содержит в 3 раза больше меди, чем серебра. Другой содержит в 5 раз больше серебра, чем меди. Сколько каждого из них нужно использовать, чтобы получить 14 кг, в которых в два раза больше с Войти

Реклама: более 600 задач по алгебре на edhelper.com


Задачи Word: MixturesWord

РешателиРешатели

УрокиУроки

Архив ответовОтветы

    

  • Щелкните здесь, чтобы увидеть ВСЕ задачи на Mixture Word Problems
Вопрос 1059590: Один сплав содержит в 3 раза больше меди, чем серебра. Другой содержит в 5 раз больше серебра, чем меди. Сколько каждого из них нужно использовать, чтобы получить 14 кг, в которых меди вдвое больше, чем серебра?
3c+s
5s+c
2c+s=14 кг
Ответ от ikleyn(47643)    (Показать источник):

Вы можете разместить это решение на ВАШЕМ сайте!
.
Один сплав содержит в 3 раза больше меди, чем серебра. Другой содержит в 5 раз больше серебра, чем меди.
Сколько каждого из них нужно использовать, чтобы получить 14 кг, в которых меди вдвое больше, чем серебра?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Это стандартная задача смеси/сплава в нестандартной постановке.


Первое, что я сделаю, это переформулирую его в СТАНДАРТНУЮ формулировку.
Делается это в три строки:


     Первый сплав состоит из 25% серебра.

     Второй сплав , или % серебра.
     Полученный сплав содержит , или % серебра.


Теперь пусть «x» будет количеством первого сплава, который нужно смешать, в килограммах,
и пусть «y» будет количеством первого сплава, который нужно смешать, в килограммах. 


Тогда ваши уравнения

x + y = 14, (1) (на общую сумму)
 "=" (2) (для содержания серебра)


Упростим систему (1), (2). Для этого умножьте обе части (2) на 12. Вы получите

 х + у = 14, (1')
3x + 10y = 56. (2')

Чтобы решить эту систему, выразите x = 14-y из (1') и подставьте его в (2'). Вы получите одно уравнение для "y"

3(14-у) + 10у = 56.

С этого момента выполните задание самостоятельно.

Существует целая куча уроков, посвященных различным типам проблем со смесями.
    — Задачи о смесях
    — Еще Задачи о смесях
    — Решение типовых задач о смесях на растворы
    — Текстовые задачи о смесях для растворов антифриза
    — Текстовые задачи о смесях для сплавов
    — Типовые задачи о смесях из архива
на этом сайте .

Прочтите их и станьте экспертом в решении задач на смешение слов.

Кроме того, на этом сайте у вас есть бесплатный онлайн-учебник по АЛГЕБРЕ-I.
    — АЛГЕБРА-I — ВАШ ОНЛАЙН-УЧЕБНИК.

Упомянутые уроки являются частью этого учебника в разделе « Словесные задачи » по теме « Задачи на смесь «.

Учебник содержит множество других решаемых текстовых задач, а также много других интересных и полезных вещей.



В шаре из сплава медь и олово находятся в соотношении 86:14. В сфере из другого сплава медь и цинк находятся в соотношении 58:42. Найдите соотношение олова и цинка в сфере, полученной путем плавления двух сфер.A.1:3B.2:3C.3:4D.3:5

Дата последнего обновления: 07 марта 2023 г. : 277.2k

•

Просмотров сегодня: 3.60k

Ответить

Подтверждено

277.2k+ views

Подсказка: Для решения данной задачи сначала используйте соотношение металлов, используемых в обоих сплавах сфер. Преобразуйте это соотношение в части и сложите их, чтобы найти части, присутствующие в сфере, образовавшейся после плавления обоих, и окончательно найдите соотношение данных металлов с помощью частей металлов в конечной сфере.

Полный пошаговый ответ:
Учитывая, что
Соотношение меди и олова в первом сплаве 86:14.
Соотношение меди и цинка во втором сплаве 58:42.
Превратим их в части из целого.
Для первой сферы:
Общее количество деталей $ = 86 + 14 = 100$
У нас есть 86 частей меди из 100 имеющихся частей.
Также у нас есть 14 частей олова из 100 деталей в наличии.
Для второй сферы:
Общее количество деталей $ = 58 + 42 = 100$
У нас есть 58 частей меди из 100 имеющихся частей.
Так же у нас есть 42 части цинка из 100 частей присутствующих.
Теперь, учитывая, что обе сферы расплавляются, образуя новую сферу.
Для новой сферы:
Общее количество деталей $ = 100 + 100 = 200 $
Частей меди в этих 200 частях $ = 86 + 58 = 144 $
Олова, присутствующего в 200 частях, составляет 14 частей.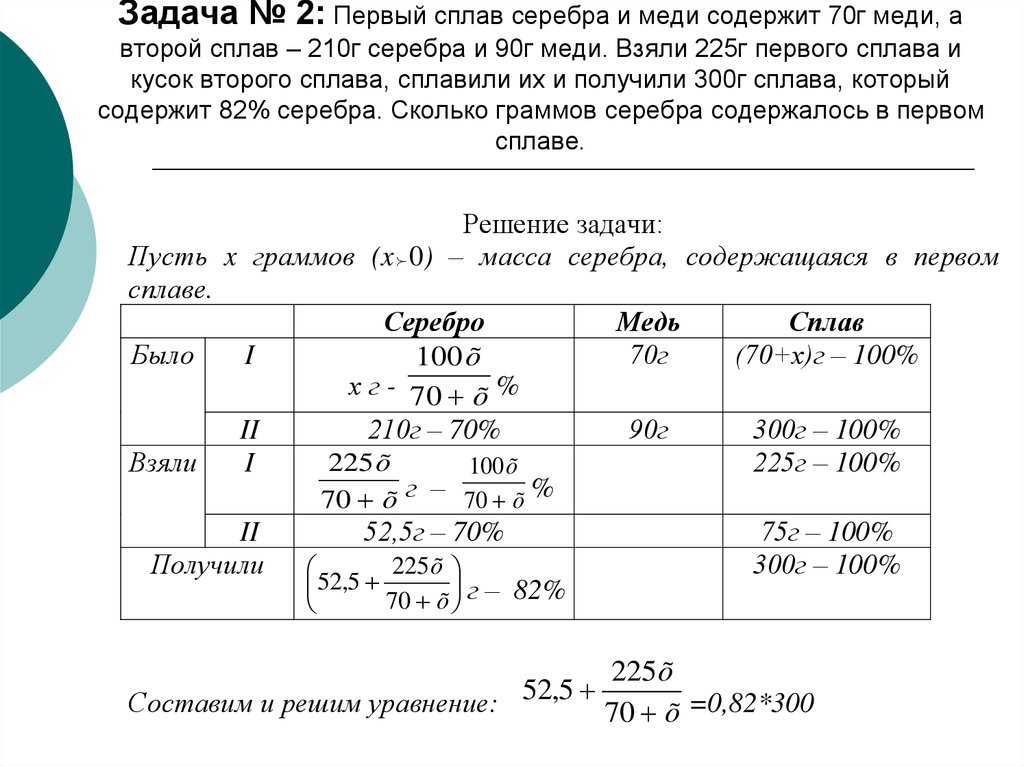
Количество частей цинка, содержащихся в этих 200 частях, равно 42.
Теперь, когда у нас есть части каждого металла в расплавленной сфере, давайте найдем соотношение олова и цинка.
Соотношение олова и цинка такое же, как и соотношение их частей, присутствующих в расплавленной сфере.
$ = \dfrac{{14}}{{42}}$
Еще больше упростим соотношение.
$ = \dfrac{1}{3}$
Следовательно, соотношение олова и цинка в сфере, полученной путем плавления двух сфер, составляет 1:3.
Итак, вариант А — правильный ответ.

Примечание Для решения таких задач учащиеся должны использовать формулы, связанные с отношением и пропорцией. Данную проблему также можно выяснить, найдя индивидуальное процентное содержание необходимых металлов в обеих сферах, а затем объединив их, но метод, используемый здесь, является основным и более простым для понимания. Соотношение — это основное математическое понятие, которое используется для сравнения двух или более величин, выраженных в одних и тех же единицах.