Период формула через скорость: Период, радиус и скорость

Длина волны — формулы, измерение, определение

Покажем, как применять знание физики в жизни

Начать учиться

Морские волны — далеко не все примеры волн. И длина волны — это не серферская характеристика, а вполне себе физическая величина. Сегодня разберемся, что такое волна и как ее охарактеризовать.

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

• Например, радиоволны, Wi-Fi и свет.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10⁸ м/с.

И источники у них разные.

Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

Морская волна — продольная или поперечная?

На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.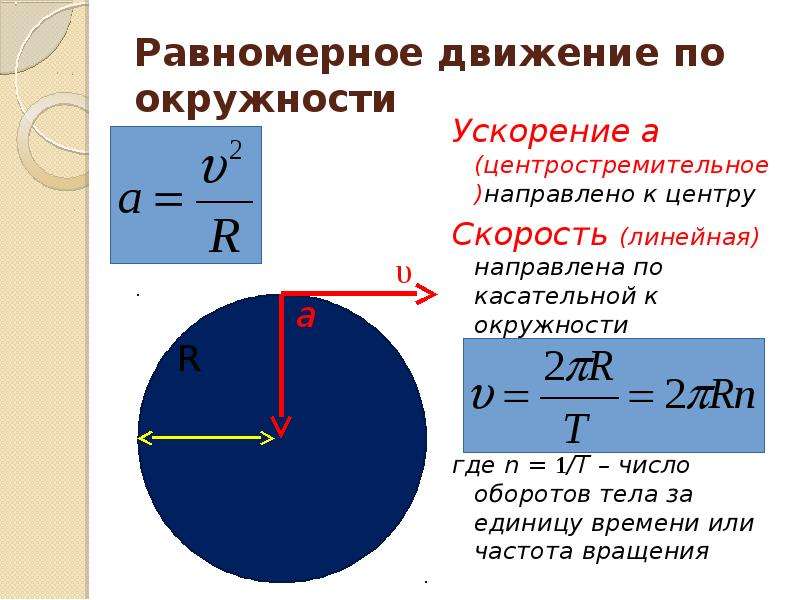

Полезные подарки для родителей

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

• λ — длина волны [м]

Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны T = t/N T — период [с] t — время [с] N — количество колебаний [—]

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.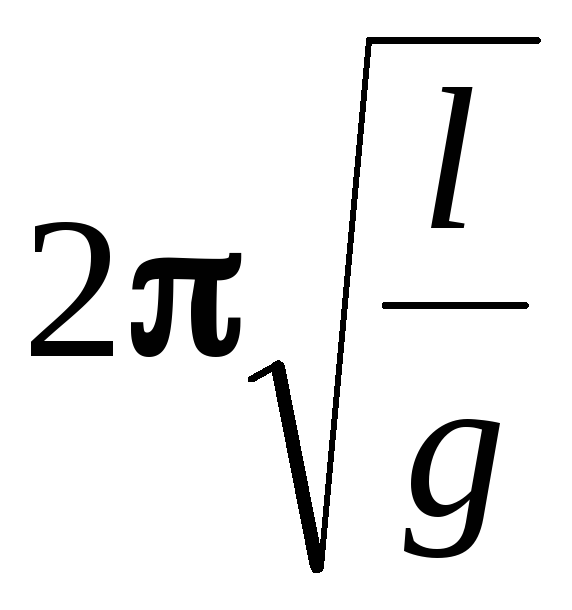

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Формула скорости 𝑣 = S/t 𝑣 — скорость [м/с] S — путь [м] t — время [с]

Переходя к волнам, можно провести следующие аналогии:

• путь — длина волны
• время — период

А для скорости даже аналогия не нужна — скорость и в Африке скорость.

Формула скорости волны 𝑣 = λ/T 𝑣 — скорость [м/с] λ — длина волны [м] T — период [с]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

1. Возьмем формулу скорости:

𝑣 = λ/T



2. Нам известна длина волны, но не дан период. Период вычисляется по формуле:

T = t/N

T = 40/10 = 4 с



3. Теперь подставляем величины в формулу

𝑣 = λ/T

𝑣 = ¼ = 0,25 м/с

Ответ: 𝑣 = 0,25 м/с

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник

резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты ν = N/t ν — частота [Гц] t — время [с] N — количество колебаний [—]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Карина Хачатурян

К предыдущей статье

181.8K

Сила трения

К следующей статье

Сила тяжести

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Формула периода колебаний математического маятника

Формула периода колебаний математического маятника

Математический маятник

Определение

Математический маятник — это частный случай физического маятника, масса которого находится в одной точке.

Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.

Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.

Формула для периода колебаний математического маятника

Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($\overline{F}$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис. 2}{R}=mg\frac{R}{l}\ \to v=R\sqrt{\frac{g}{l}}\left(4\right).\]

Полученную скорость подставим в формулу (1), имеем:

\[T=\frac{2\pi R}{R\sqrt{\frac{g}{l}}}\to \] \[T=2\pi \sqrt{\frac{l}{g}}\left(5\right).\]

Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.

Используя зависимость периода колебаний математического маятника от ускорения свободного падения, определяют величину данного ускорения. Для этого измеряют длину маятника, рассматривая большое количество колебаний, находят период $T$, затем вычисляют ускорение свободного падения.

Примеры задач с решением

Пример 1

Задание. Как известно, величина ускорения свободного падения зависит от широты. 2}$

Пример 2

Задание. Каким будет период колебаний математического маятника, если точка его подвеса движется вертикально вниз 1) с постоянной скоростью? 2) с ускорением $a$? Длина нити этого маятника равна $l.$

Решение. Сделаем рисунок.

1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:

\[T_1=2\pi \sqrt{\frac{l}{g}}\left(2.1\right).\]

2) Ускорение точки подвеса маятника можно рассматривать как появление дополнительной силы, равной $F=ma$, которая направлена против ускорения. То есть, если ускорение направлено вверх, то дополнительная сила направлена вниз, значит, она складывается с силой тяжести ($mg$). Если точка подвеса движется с ускорением, направленным вниз, то дополнительная сила вычитается из силы тяжести.

Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:

\[T_2=2\pi \sqrt{\frac{l}{a_p}}\left(2. 2\right),\]

где:

\[a_p=g-a\ \left(2.3\right),\]

тогда:

\[T_1=2\pi \sqrt{\frac{l}{g-a}}.\]

Ответ. 1) $T_1=2\pi \sqrt{\frac{l}{g}}$; 2) $T_1=2\pi \sqrt{\frac{l}{g-a}}$

Читать дальше: формула периода колебаний пружинного маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Наборы задач по круговому движению и гравитации

Наборы задач || Обзор физики || Устаревший набор задач
 

У нас есть 18 готовых наборов задач по теме Круговое движение и Гравитация. Эти наборы задач сосредоточены на использовании законов движения Ньютона и всемирного тяготения для математического анализа ситуаций, связанных с круговым движением или движением спутника.

Щелкните ссылку, чтобы открыть общедоступный набор задач. Если вы являетесь студентом системы отслеживания задач, откройте задание по ссылке на доске заданий системы отслеживания задач.

Набор задач CG1: Линейная скорость

Используйте уравнение v = 2•π•R/T для определения скорости, радиуса или периода. Включает 4 задачи.

 
Набор задач CG2: Центростремительное ускорение 1

Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение с радиусом окружности и периодом. Включает 7 задач.

 
Набор задач CG3: Центростремительное ускорение 2

Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение со скоростью вращения. Включает 7 задач.

 
Набор задач CG4: Центростремительная сила

Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение с центростремительной силой. Включает 5 задач.

 
Набор задач CG5: Круговое движение и анализ силы 1

Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по вертикальным окружностям. Большинство проблем включают в себя строительные леса. Включает 7 задач.

 
Набор задач CG6: круговое движение и анализ силы 2

Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по горизонтальным кругам. Включает 5 задач.

 
Набор задач CG7: Круговое движение и анализ силы 3

Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по кругу. Включает 7 задач.

 
Набор задач CG8: круговое движение и анализ силы 4

Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по кругу. Включает 7 задач.

 
Набор задач CG9: Гравитационная сила 1

Используйте закон всемирного тяготения Ньютона для расчета силы притяжения между двумя объектами с известной массой и расстоянием между ними. Включает 7 задач.

 
Набор задач CG10: Гравитационная сила 2

Используйте закон всемирного тяготения Ньютона для расчета силы притяжения между двумя объектами с известной массой и расстоянием между ними. Включает 5 задач.

 
Набор задач CG11: Гравитационная сила 3 ​​

Используйте закон всемирного тяготения Ньютона в качестве пропорционального аргумента и в качестве инструмента решения проблем для некоторых сложных сценариев. Включает 4 задачи.

 
Набор задач CG12: Напряженность гравитационного поля

Используйте уравнение для напряженности гравитационного поля, чтобы вычислить значение g при различных условиях.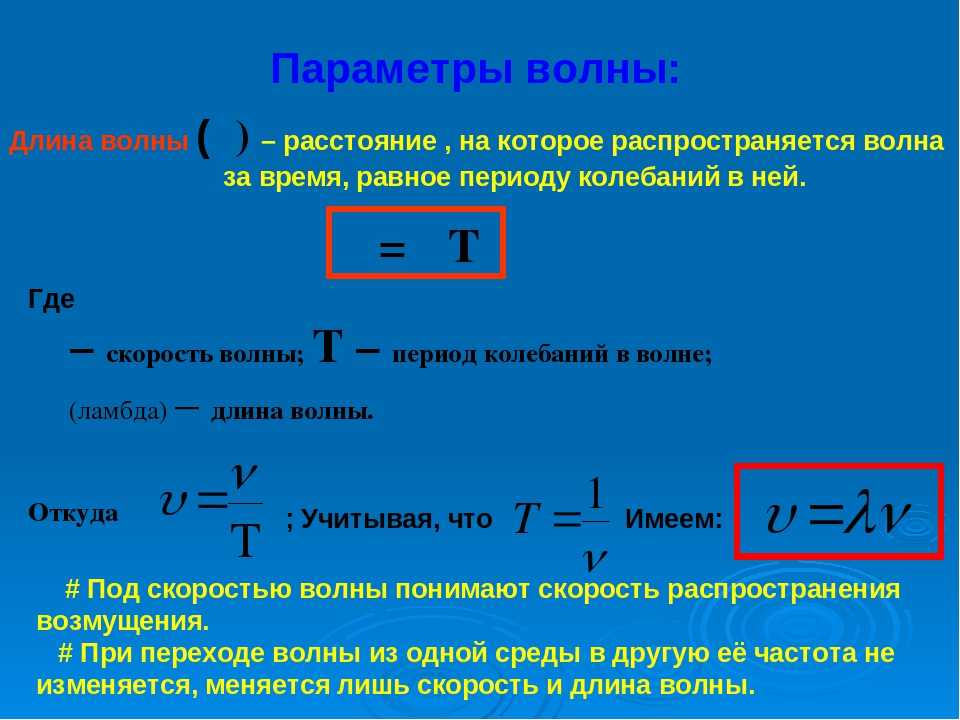 Включает 6 задач.

 
Набор задач CG13: Орбитальная скорость

Используйте уравнение для орбитальной скорости, чтобы связать радиус орбиты, период обращения и массу центрального тела. Включает 8 задач.

 
Набор задач CG14: Орбитальное ускорение

Соотнесите орбитальный период и орбитальный радиус с орбитальным ускорением. Включает 6 задач.

 
Набор задач CG15: Математика движения спутников

Используйте уравнения орбитального движения, чтобы связать радиус орбиты, орбитальную скорость, период обращения и массу центрального тела. Включает 4 задачи.

 
Набор задач CG16: Третий закон Кеплера 1

Используйте третий закон Кеплера для анализа данных периода-орбитального радиуса, чтобы определить неизвестный период или радиус орбиты. Включает 4 задачи.

 
Набор задач CG17: Третий закон Кеплера 2

Используйте третий закон Кеплера, чтобы связать период обращения, радиус обращения и массу центрального тела. Включает 7 задач.

 
Набор задач CG18: Третий закон Кеплера 1

Объедините третий закон Кеплера с навыками пропорционального рассуждения, чтобы определить неизвестный период или радиус орбиты. Включает 5 задач.

Период и частота — макеты

Авторы: Стивен Хольцнер и

Обновлено: 26 марта 2016 г. Купить на Amazon

При описании того, как все движется по кругу, вы не просто используете радианы; Вы также можете указать время, которое требуется. Время, за которое объект совершает полный оборот, называется период его движения.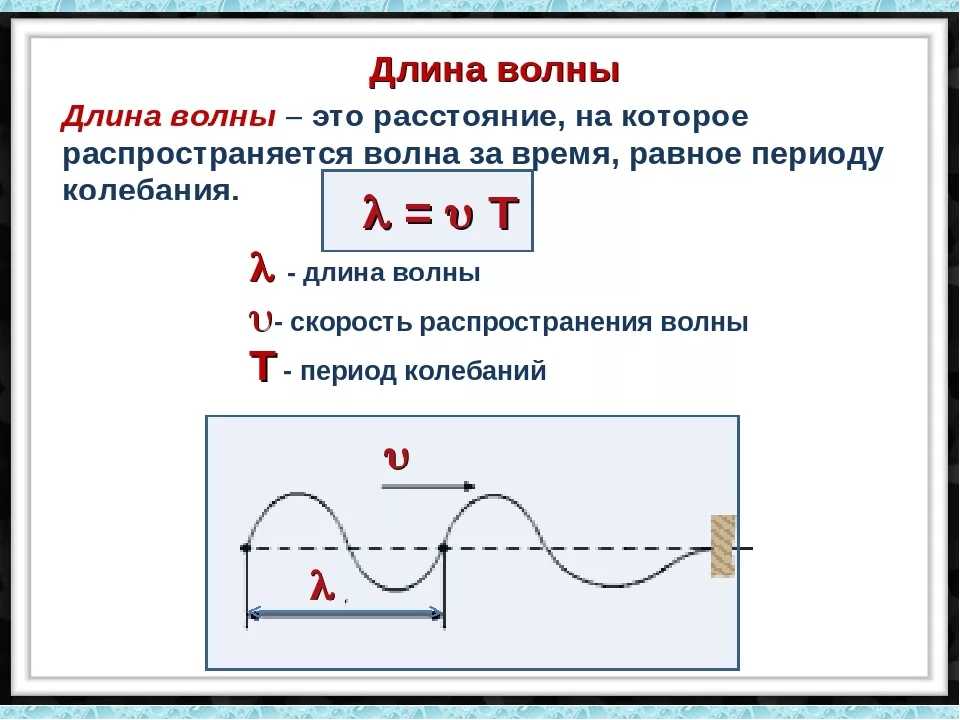 Обычно период измеряется в секундах, но его можно измерять и в других единицах времени, включая миллисекунды, минуты и годы.

Если объект движется со скоростью v , , то время, необходимое для прохождения круга — расстояние, которое он проходит по окружности, 2π r — будет

Обратите внимание на символ радиуса окружности: r . Это половина диаметра круга, который равен 9.0174 д . Итак, r = d /2. Обратите также внимание на символ периода: T . С помощью этого уравнения, учитывая скорость объекта на орбите и радиус окружности, вы можете рассчитать период объекта.

Другим измерением, которое вы встретите в задачах по физике, является частота . В то время как период — это время, за которое объект совершает оборот по кругу, частота — это количество кругов, которые объект делает за единицу времени. Частота, f , подключается к периоду так:

Частота чаще всего измеряется в единицах циклов в секунду (cps), которые также называются Герцами (Гц).