Периметр трапеции формула через площадь – ТРАПЕЦИЯ формулы площади и периметра, средняя линия трапеции

2. Формулы длины сторон через высоту и углы при нижнем основании

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

Формулы всех четырех сторон трапеции:

3.

a — нижнее основание

b — верхнее основание

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

Формулы длины сторон трапеции:

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Все формулы площади трапеции. Найти онлайн

Формулы площади трапеции

Внимание! Десятичную дробь надо писать с точкой, а не с запятой!

Трапеция — четырехугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами.

Площадь трапеции через основания и высоту

\(a\) — основание

\(b\) — основание

\(h\) — высота

\(a =\)    \(b =\)    \(h =\)

Площадь трапеции через высоту и среднюю линию

\(h\) — высота

\(m\) — средняя линия трапеции

\(h =\)    \(m =\)

Площадь трапеции через четыре стороны

\(a, b, c, d\) — стороны

\(a =\)   \(b =\)  

\(c =\)   \(d =\)

Площадь трапеции через диагонали и угол между ними

\(d_1, d_2\) — диагонали

\(\alpha\) — угол между диагоналями \(d_1\) и \(d_2\)

\(d_1 =\)    \(d_2 =\)    \(\alpha = \)

Для равнобедренной трапеции

Площадь равнобедренной трапеции через радиус вписанной окружности и угол

\(r\) — радиус вписанной окружности

\(\alpha\) — угол

\(r =\)    \(\alpha =\)

www.100formul.ru

Формулы периметра, Периметр

Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра. Стандартное обозначение периметра в математике — буква P

Периметр треугольника

P = a + b + c

Периметр квадрата

Пусть длина стороны квадрата равна a. Квадрат имеет четыре равных стороны, поэтому периметр квадрата есть P = a + a + a +a или:

P = 4 ⋅ a

Периметр прямоугольника

Пусть длины сторон прямоугольника равны a иb.
Длина всех его сторон есть P = a + b + a + b или:

P = 2 ⋅ a + 2 ⋅ b

Периметр параллелограмма

Пусть длины сторон параллелограмма равны a и b
Длина всех его сторон есть P = a + b + a + b, поэтому периметр параллелограмма есть:

P = 2 ⋅ a + 2 ⋅ b

Как видно, периметр параллелограмма равен периметру прямоугольника.

Периметр ромба

P = 4 ⋅ a

Периметр равнобедренной трапеции

Пускай длины параллельных сторон трапеции a и b, а длины двух других сторон равна c(Как известно, равнобедренная трапеция имеет две равные стороны).

P = a + b + c + c = a + b + 2 ⋅ c

Периметр равностороннего треугольника

Как известно, равносторонний треугольник имеет 3 равные стороны. Если длина стороны равна a, тогда формула нахождения периметра есть P = a + a + a

P = 3 ⋅ a

Длина окружности(периметр круга)

Обозначим длину окружности буквой l.

$l = d \cdot \pi = 2\cdot r \cdot \pi$

Где:
$\pi = 3,14$
r радиус круга (окружности)
d диаметр круга.

Правильный многоугольник

$P = 2nb\sin\frac{\pi}{n}$

n число ребер(вершин).
$\pi = 3,14159265359$

www.math10.com

Формулы периметра трапеции и примеры применения

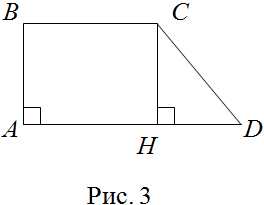
Обозначим . Опустим высоту из вершины :

Так как , то , то есть

Далее рассмотрим треугольник , он прямоугольный, – гипотенуза. Найдем ее по теореме Пифагора:

Подставляя в последнее равенство известные значения катетов, получим

(см)

Периметр данной прямоугольной трапеции найдем по формуле

В данном случае она примет вид:

Подставляя длинны сторон трапеции в последнее равенство, получим

(см)

ru.solverbook.com

Формула периметра трапеции

Периметр трапеции равен сумме длин всех четырех сторон

Трапе́ция (от др. -греч. τράπέζιου — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого произвольная пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции

Периметр произвольной трапеции

Периметр произвольной трапеции, в которой AB=a, BC=b, CD=c, AD=d, имеет вид:

\[ \LARGE P_{ABCD} = a + b + c + d \]

где:
P — периметр трапеции
a, b, c, d — стороны трапеции

Периметр равнобокой трапеции

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

Периметр произвольной трапеции, в которой AB=CD=a, BC=b, AD=c, имеет вид:

\[ \LARGE P_{ABCD} = 2 \cdot a + b + c \]

где:
P — периметр трапеции
a, b, c, d — стороны трапеции

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны: ∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны: AC = BD

3. Одинаковые углы между диагоналями и основаниями: ∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции, поэтому умножив ее на два, можно подставить ее вместо оснований в формулу периметра: \( P = 2 \cdot m + c + d \).

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Как найти периметр трапеции равнобедренной и прямоугольной

Прежде, чем приступить к расчету периметра трапеции, необходимо дать определение понятиям «периметр» и «трапеция», а так же изучить виды трапеций.

Периметр – это сумма длин всех сторон геометрической фигуры.

Так же в литературе имеется определение, согласно которому периметр – это длина линии, ограничивающей прямоугольную фигуру.

Трапеция – четырехугольник, две стороны которого параллельны (основания трапеции), а две другие стороны.

Виды трапеций

• равнобедренная;
• прямоугольная.

Если боковые стороны трапеции равны, трапеция называется равнобедренной.

В случае, когда одна из боковых сторон оказывается перпендикулярной основаниям – трапеция прямоугольная.

Определение периметра равнобедренной трапеции

Периметр равнобедренной трапеции определяется по формуле:

Периметр ABCD = a+b+c+d=2*a+b+d , где   a, c – длина боковых сторон; b, d – длина сторон, являющихся основаниями.

Таким образом, если стороны равнобедренной трапеции равны –  а=с=4см, b=5см, d=6см, периметр составит 19 см.: Периметр ABCD = 2*4+5+6=19 см.

Определение периметра прямоугольной трапеции

Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:

Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.

• опустим высоту из вершины С, высота CH = AB = 5см;
• исходя из рисунка 3, AH = BC = 7 см;
• HD = AD – AH = 10 – 7 = 3 см;
• далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
• подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же,  для определения длины различных сторон трапеции могут помочь следующие формулы:

• формула расчета длины основания через среднюю линию;
• формулы длин сторон через высоту и угол при нижнем основании трапеции;
• формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
• формулы длин сторон равнобедренной трапеции через площадь.

Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.

kakumno.ru

Все формулы средней линии трапеции

Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия

1. Формула средней линии трапеции через основания

b — верхнее основание

a — нижнее основание

m— средняя линия

Формула средней линии, (m ):