Задание № 1. Планиметрия. ЕГЭ. Математика. 3
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
7. Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11. Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 1. Планиметрия.
Планиметрия.
95. Найдите высоту ромба, сторона которого равна √3, а острый угол равен 60°.
Ответ: 1,5
96. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Ответ: 48
97. Найдите большую диагональ ромба, сторона которого равна √3, а острый угол равен 60°.
Ответ: 3
98. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Ответ: 10
99. В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите ее периметр.
Ответ: 69
100. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Ответ: 23
101. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Найдите среднюю линию этой трапеции.
Ответ: 10
102. Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
Ответ:15
103. Основания трапеции относятся как 2:3, а средняя линия равна 5. Найдите меньшее основание.
Ответ: 4
104. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Ответ: 20
105. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Ответ: 0,5
106. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Ответ: 12
107. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50°? Ответ дайте в градусах
Ответ: 115
108. Средняя линия трапеции равна 28, а меньшее основание равно 18.
Ответ: 38
109. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Ответ: 15
110. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Ответ: 9
111. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Ответ: 42
112. В трапеции АВСD основание AB равно 10. Средняя линии EF пересекается с диагональю
Ответ: 7
113. Основания равнобедренной трапеции равны 5 и 17, а ее периметр равен 42. Найдите площадь трапеции.
Ответ: 88
114. Основания равнобедренной трапеции равны 10 и 40.
Ответ: 0,6
115. Найдите площадь прямоугольной трапеции, основания которой равны 7 и 3, большая боковая сторона составляет с основанием угол 45°.
Ответ: 20
116. Радиус окружности, вписанной в правильный треугольник равен 2/√3. Найдите сторону этого треугольника.
Ответ: 4
117. Периметр треугольника равен 70, а радиус вписанной окружности равен 4. Найдите площадь этого треугольника.
Ответ: 140
118. Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
Ответ: 0,25
120 Периметр правильного шестиугольника равен 30. Найдите диаметр описанной окружности.
Ответ: 10
121. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен √3.
Ответ: 2
122. Найдите сумму углов выпуклого семиугольника. Ответ дайте в градусах.
Ответ: 900°
123. Угол между двумя соседними сторонами правильного многоугольника равен 168°. Найдите число вершин многоугольника. (без рисунка)
Ответ: 30
124. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Ответ: 50
125. Площадь круга равна 1/π. Найдите длину его окружности.
Ответ: 2
126. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
Ответ: 2
127. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Ответ: 22
128. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Ответ: 24
 Найдите периметр треугольника.
Найдите периметр треугольника.Ответ: 22
130. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Ответ: 6
131. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Ответ: 6
132. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Ответ: 2
133. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
Ответ: 25
134. Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружности, вписанной в этот треугольник.
Ответ: 1
135. Боковые стороны равнобедренного треугольника равны 5, основание 6.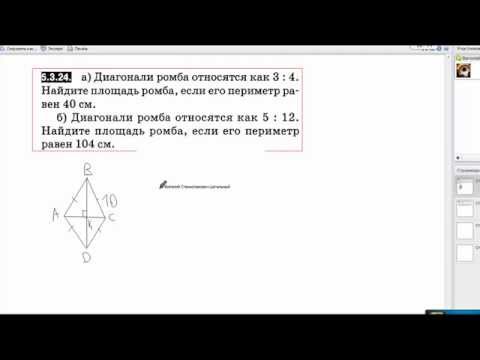 Найдите радиус вписанной окружности.
Найдите радиус вписанной окружности.
Ответ: 1,5
136. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Ответ: 7
137. В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
Ответ: 36
138. В треугольнике ABC угол A равен 44°, угол С равен 62°. На продолжении стороны AB за точку B отложен отрезок BD, равный стороне BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
Ответ: 37
Главная
119. Острый угол ромба равен 30°. Радиус вписанной окружности этого ромба равен 2. Найдите сторону ромба.
Ответ: 8
139. Найдите диагональ квадрата, если его площадь равна 2.
Ответ: 2
140. Найдите площадь прямоугольника, если его периметр равен 26, а одна сторона на 3 больше другой.
Ответ: 40
141. Диагональ параллелограмма образует с двумя его сторонами углы 26° и 34°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
Ответ: 120
142. В треугольнике ABC угол C равен 90°, AC=4, BC=3. Найдите радиус окружности, описанной около этого треугольника.
Ответ: 2,5
143. Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма.
Ответ: 1,5
144. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Ответ: 5
145. Площадь параллелограмма ABCD равна 153.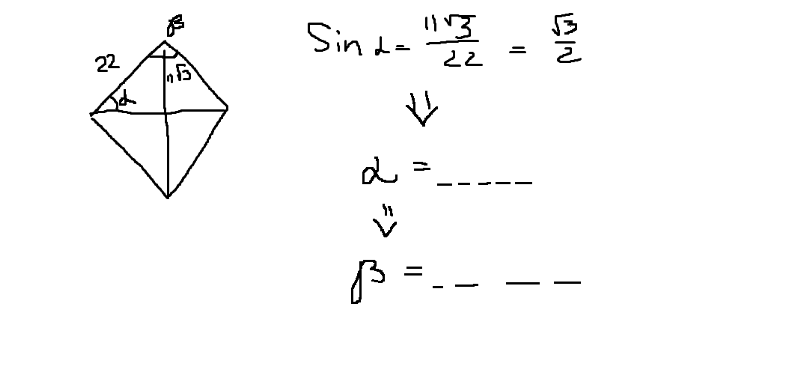 Найдите площадь параллелограмма, вершинами которого являются середины сторон данного параллелограмма.
Найдите площадь параллелограмма, вершинами которого являются середины сторон данного параллелограмма.
Ответ: 76,5
146. Площадь параллелограмма ABCD равна 40. Точка E— середина стороны AB. Найдите площадь треугольника ADE.
Ответ: 10
147. Площадь параллелограмма ABCD равна 20. Точка H — середина стороны АD. Найдите площадь трапеции AHCB.
Ответ: 15
148. Дан треугольник ABC, DE – средняя линия. Найдите площадь треугольника ACB, если площадь треугольника DEC равна 3.
Ответ: 12
149. Дан треугольник ABC, FE – средняя линия. Найдите площадь трапеции ACEF, если площадь треугольника ABC равна 20.
Ответ: 15
150. Сторона правильного треугольника равна √3. Найдите радиус окружности, описанной около этого треугольника.
Ответ: 1
151. Радиус окружности, описанной около правильного треугольника, равен √3. Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
Ответ: 3
152. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
Ответ: 4,5
153. Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.
Ответ: 2
154. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Ответ: 2
155. Радиус окружности, вписанной в правильный треугольник равен 5, Найдите высоту этого треугольника.
Ответ: 15
156. Сторона правильного треугольника равна √3. Найдите радиус окружности, вписанной в этот треугольник.
Ответ: 0,5
Тема 9. Планиметрия — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 9. Планиметрия1. Треугольник Сумма внутренних углов: . Площадь треугольника:
где p – полупериметр треугольника, . , где r – радиус вписанной окружности, R – радиус описанной окружности. Центр вписанной окружности – точка пересечения биссектрис; центр описанной окружности – точка пересечения серединных перпендикуляров. Теорема косинусов: a2=b2+c2-2bccosA. Теорема синусов: . Свойство медиан: AO:OM=2:1. Свойство биссектрис: CA:AD=CB:BD. Свойства средней линии: EF||AB, .
Прямоугольный треугольник a и b – катеты, c – гипотенуза. Теорема Пифагора: a2+b2=c2. Свойство высоты, опущенной на гипотенузу: Свойство медианы, опущенной на гипотенузу: . Равнобедренный треугольник
Медиана, высота и биссектриса, проведенные к основанию, совпадают. Высоты, проведенные к боковым сторонам, равны; медианы, проведенные к боковым сторонам, равны; биссектрисы углов при основании равны.
Равносторонний треугольник Медиана, биссектриса и высота, проведенные к каждой из сторон, совпадают. . Признаки равенства треугольников Два треугольника равны, если выполняется одно из условий: 1) две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника; 2) сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны; 3) стороны одного треугольника равны соответствующим сторонам другого треугольника. Признаки подобия треугольников Два треугольника подобны, если выполняется одно из условий: 1) две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны; 2) два угла одного треугольника равны двум углам другого треугольника; 3) стороны одного треугольника пропорциональны сторонам другого треугольника. Пример 1. Площадь равнобедренного остроугольного треугольника равна 12, а длина высоты, опущенной на боковую сторону, . Найдите угол при основании. Решение: Пусть длина боковой стороны равна b. Тогда . С другой стороны, . Отсюда или . По условию задачи угол – острый, а потому равен 300. Сумма углов треугольника равна . Т.о. и . Ответ: 750. Замечание. При решении задачи использован «метод площадей». Он состоит в том, что площадь треугольника выражается через разные элементы. В первом случае — через сторону и опущенную на нее высоту, а другом – через две стороны и угол между ними. Пример 2. Один из катетов прямоугольного треугольника в два раза больше другого. Высота, опущенная на гипотенузу, равна 12. Найдите площадь треугольника. Решение: Пусть в угол B прямой, AB=2BC, а BH – высота. Треугольники ABC и AHB подобны, т.к. один из углов у каждого из них прямой, а угол A у этих треугольников общий. Треугольники ABC и BHC подобны, поскольку оба являются прямоугольными и имеют общий угол C. В каждом из перечисленных треугольников один из катетов в два раза больше другого. Следовательно, , AH=2BH=24. Т.о. AC=AH+HC=24+6=30. Найдем площадь треугольника ABC: . Ответ: 180. Пример 3. Гипотенуза прямоугольного треугольника равна 5, а опущенная на нее высота 2. Найдите катеты. Решение: Пусть CH – высота, опущенная на гипотенузу AB. Обозначим отрезок HB через x. Тогда AH=5-x. Рассмотрим прямоугольные треугольники ACH и CHB. . Треугольники подобны по двум углам. Из подобия треугольников следует, что , откуда x2-5x+4=0. Корни полученного квадратного уравнения x1=1, x2=4. Пусть HB=1, тогда AH=5-1=4. Из свойства высоты, опущенной на гипотенузу, имеем и BC2=1•5=5, . Аналогично, если HB=4, то . Заметим, что, зная AH и BH, катеты можно также найти по теореме Пифагора. Ответ: . Пример 4. Решение: Пусть BC=MC=x. . По теореме косинусов для : , откуда . По теореме косинусов для ; . Ответ: 6. 2. Окружность и кругДлина окружности: ; площадь круга: . Длина дуги окружности: ; площадь сектора: (– центральный угол). Углы, вписанные в окружность: 1. углы, опирающиеся на одну хорду и лежащие по одну сторону от неё, равны; 2. сумма углов, опирающихся на одну хорду и лежащих от нее по разные стороны, равна ; 3. центральный угол, опирающийся на хорду, в два раза больше острого угла, вписанного в окружность и опирающегося на ту же хорду; 4. Свойство хорд: AK•KB=CK•KD. Свойство секущих: AD•AE=AF•AG=AB2 . Свойство касательных: AB=AC.
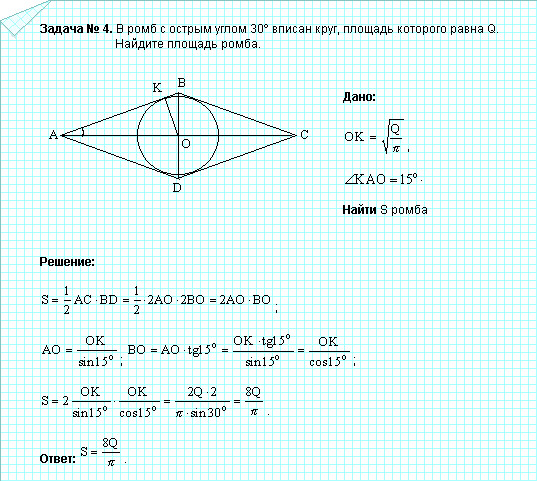
Пример 5. В окружность вписан равносторонний треугольник ABC со стороной . Найдите площадь треугольника AOC, где O – центр окружности. Решение: Угол ABC, отпирающийся на хорду AC, равен 600. Центральный угол . Стороны AO и OC являются радиусами окружности. Поскольку треугольник равносторонний, то радиус описанной окружности находим как . И, наконец, . Ответ: . Пример 6. В равнобедренный треугольник ABC с основанием AC вписана окружность. Она касается стороны AB в точке E, причем AE составляет 3/5 боковой стороны. Решение: Обозначим буквами F и H точки касания окружности со сторонами BC и AC. По условию задачи BH=6. Положив AB=5x, имеем AE=3x, EB=2x. По свойству секущих AH=AE=3x. Рассмотрим прямоугольный треугольник ABH. По теореме Пифагора 25x2=9x2+36, откуда 16x2=36 и x=3/2. Периметр треугольника ABC равен . Ответ: 24. Пример 7. Хорды AB и BC окружности радиуса 4 равны и образуют угол 600. Найти площадь части круга, лежащей внутри угла BAC. Решение: Фигура, площадь которой требуется найти, состоит из сектора круга, соответствующего углу AOC, и двух равных треугольников AOB и AOC. (см. пример 4). Площадь сектора равна . Площадь каждого из треугольников . Найдем площадь заданной фигуры: . Ответ: . 3. Четырехугольник
Сумма внутренних углов: . Площадь выпуклого четырехугольника: . Свойство четырехугольника, описанного около окружности: a+c=b+d. Параллелограмм – четырехугольник, у которого противолежащие стороны параллельны: AD||BC, AB||CD. Равенство противолежащих сторон и углов: AD=BC=a, AB=CD=b; . . . Свойства диагоналей: . Площадь параллелограмма: . Ромб – четырехугольник, у которого все стороны равны: . Свойства диагоналей: ; , (диагонали взаимно перпендикулярны и являются биссектрисами углов). Площадь: . Прямоугольник – четырехугольник, у которого все углы прямые: . Прямоугольник является параллелограммом. Около любого прямоугольника можно описать окружность. Свойства диагоналей: . Площадь: S=a•b. Квадрат – прямоугольник, все стороны которого равны. Квадрат также является ромбом и обладает всеми его свойствами. Длина диагонали: . Площадь: . Около квадрата можно описать окружность радиуса . В квадрат можно вписать окружность радиуса . Трапеция – четырехугольник, у которого ровно одна пара противолежащих сторон параллельна: AD||BC. AD=a и BC=b – основания трапеции; AB и CD – боковые стороны; CH=h – высота. . Свойства средней линии: MN||AD, . Площадь: . Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основаниям. Равнобокая (или равнобедренная) трапеция – трапеция, у которой боковые стороны равны: AB=CD. Около равнобокой трапеции можно описать окружность. Равенство углов при основании и диагоналей: . Пример 8. Площадь прямоугольника равна 12, а его стороны относятся как 1 : 3. Найти периметр прямоугольника. Решение: Пусть меньшая из сторон равна x, тогда длина большей 3x. Т.о. стороны прямоугольника равны 2 и 6, а периметр 2•2 + 2•6 = 16. Ответ: 16. Пример 9. Периметр прямоугольника равен 32, а площадь 48. Чему равен угол, образованный его диагоналями? Решение: Пусть стороны прямоугольника равны a и b. По условию задачи: 2a+2b=32, откуда a+b=16 и ab=48. Найдем длину диагонали. Для этого возведем равенство a+b=16 в квадрат. (a+b)2=162; a2+2ab+b2=256; a2+2•48+b2=256; d2=a2+b2=256-2•48=160. Поскольку для любого четырехугольника (в т.ч. и для параллелограмма) верно равенство , где – угол между диагоналями, то , откуда . Ответ: 3/5. Пример 10. Высоты параллелограмма, проведенные из тупого угла, равны 3 и , а угол между ними равен 450. Решение: Пусть в параллелограмме ABCD проведены высоты BH=3 и BF=. Рассмотрим четырехугольник HBFD. Углы и в нем прямые, а угол – по условию задачи. Т.о. . В параллелограмме ABCD . Рассмотрим прямоугольный треугольник AHB. Найдем его гипотенузу: . Аналогично вычислим гипотенузу прямоугольного треугольника BFC: . Периметр параллелограмма равен . Ответ: . Пример 11. Площадь ромба равна 24, а одна из его диагоналей равна 6. Найдите периметр ромба. Решение: Пусть в ромбе ABCD диагональ BD=6. Тогда площадь ромба равна , откуда AC=8. Найдем сторону ромба. Для этого рассмотрим треугольник AOB. Он является прямоугольным (см. свойства ромба). Его катеты равны , (см. Периметр ромба равен 4•5=20. Ответ: 20. Пример 12. Основания равнобокой трапеции равны 6 и 12, а высота равна 3. Чему равна диагональ трапеции? Решение: В трапеции, которую обозначим ABCD, проведем высоты BE и CF. Поскольку EBCF – прямоугольник, EF=BC=6. Прямоугольные треугольники ABF и DCF равны, т.к. и AB=DC. Таким образом, AE=FD. Поскольку AE+EF+FD=AD и AE+6+FD=12, то 2FD=6 и FD=3. Рассмотрим прямоугольный треугольник DBE. Его катеты BE=3, DE=12-3=9. По теореме Пифагора найдем гипотенузу треугольника: BD2=32+92=90; . Ответ: . Пример 13. В прямоугольной трапеции меньшая боковая сторона равна 8, диагонали 10 и 17. Чему равна большая боковая сторона? Решение: Меньшая боковая сторона AB прямоугольной трапеции ABCD перпендикулярна основаниям и равна по длине высоте CH (т. На чертеже AC=10 и BD=17. Рассмотрим прямоугольный треугольник ABC и найдем длину его катета . Аналогично найдем длину катета AD в прямоугольном треугольнике . Поскольку ABCH – прямоугольник, то BC=AH. AD=AH+HD, 15=6+HD, откуда HD=9. Длину стороны CD найдем как длину гипотенузы прямоугольного треугольника . Ответ: . 4. МногоугольникСумма внутренних углов многоугольника с n вершинами (n-угольника) равна (1). Сумма внешних углов n-угольника равна (2). Число диагоналей n-угольника . Правильный многоугольник – многоугольник, у которого равны все стороны и внутренние углы. O – центр вписанной и описанной окружностей; R – радиус описанной окружности – лежит на биссектрисе угла; r – радиус вписанной окружности – лежит на серединном перпендикуляре к стороне. Внешний угол равен центральному углу . Внутренний угол . Пример 14. Сколько сторон имеет правильный многоугольник, если наименьший угол, образованный его диагоналями, равен 400. Решение: Наименьший угол, образованный диагоналями многоугольника – это центральный угол. Если n – число сторон многоугольника, то: ; т.о. n=9. Ответ: 9. Пример 15. Найти площадь правильного восьмиугольника со стороной 1. Решение: Восьмиугольник можно разбить на 8 равных равнобедренных треугольников с вершиной и основанием 1. Боковая сторона такого треугольника является радиусом описанной окружности R. Площадь каждого из треугольников равна . Чтобы найти R, воспользуемся теоремой косинусов. В соответствии с ней: , откуда . Т.о. . Площадь восьмиугольника . Ответ: . Задачи для самостоятельного решения1) Углы треугольника пропорциональны числам 3, 5, 7. Найдите эти углы. 2) Углы треугольника образуют арифметическую прогрессию. Чему равен наибольший угол, если величина наименьшего 200? 3) Два внешних угла треугольника равны 1200 и 1600. Чему равен третий внешний угол? 4) Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 15, а один из острых углов равен 600. Чему равна длина меньшего катета? 5) Один из углов прямоугольного треугольника равен 300, а высота, проведенная к гипотенузе, равна 9. Найдите длину гипотенузы. 6) В треугольнике ABC проведена высота BH, причем AH=3. Найдите длину стороны BC, если . 7) Найдите гипотенузу равнобедренного прямоугольного треугольника, если его площадь равна 18. 8) Гипотенуза прямоугольного треугольника равна 13, а катеты относятся как 2 : 3. Чему равна площадь треугольника? 9) Один из катетов прямоугольного треугольника равен 9, а другой относится к гипотенузе, как 4 : 5. Чему равна площадь треугольника? 10) Катеты прямоугольного треугольника равны log49 и log316. Чему равна площадь треугольника? 11) Высота равнобедренного треугольника, равна 15, а боковая сторона больше основания на 1. Чему равно основание? 12) Найдите боковую сторону равнобедренного треугольника, если его основание равно 18, а площадь 108. 13) Найдите боковую сторону равнобедренного треугольника, если основание равно 10 см, а медиана, проведённая к основанию, равна 3 см. 14) Величины углов треугольника относятся как 1 : 1 : 2, а большая из сторон равна 15. Чему равна высота, проведенная к этой стороне? 15) Площадь равнобедренного треугольника равна , а углы при основании 300. 16) В треугольнике ABC проведена медиана AM. . Чему равна сторона AC? 17) Основание треугольника равно 22, боковые стороны 13 и 19. Чему равна медиана, опущенная на основание? 18) Две стороны треугольника равны 11 и 7, а медиана, опущенная на третью сторону 6. Найдите длину третьей стороны. 19) В треугольнике ABC медиана AM равна 6 и образует со стороной AC, равной 8, угол 300. Найдите площадь треугольника. 20) В треугольнике ABC к стороне BC=12 проведена медиана AM=7 и образует с этой стороной угол 300. Найдите площадь треугольника. 21) Площадь треугольника ABC равна 12. Из вершины B проведена медиана BD, длина которой равна 3. Найдите сторону AC, если . 22) Площадь правильного треугольника равна 64. Найдите его периметр. 23) В треугольнике ABC на сторонах AB и AC взяты точки M и N такие, что . 24) Площадь треугольника ABC равна 48. Точка D лежит на стороне AC, деля ее в отношении AD:DC=1:7. Найдите площадь треугольника ABD. 25) Сторона треугольника равна 2, а прилегающие к ней углы 300 и 450. Найдите его площадь. 26) Один из катетов прямоугольного треугольника равен 6, а противолежащий ему угол . Найдите площадь круга, описанного около треугольника. 27) Площадь правильного треугольника равна . Чему равен радиус описанной около него окружности? 28) Высота правильного треугольника равна 18. Найдите диаметр вписанной в него окружности. 29) Точка касания с вписанной окружностью делит гипотенузу треугольника в отношении 2 : 3. Расстояние от прямого угла треугольника до центра окружности равно . Найдите периметр треугольника. 30) Катеты прямоугольного треугольника равны 16 и 30. 31) Один катет прямоугольного треугольника равен 15, проекция другого катета на гипотенузу равна 16. Чему равен радиус вписанной в треугольник окружности? 32) Радиус вписанной в треугольник окружности равен , радиус описанной около него окружности . Чему равна площадь треугольника, если один из его углов равен . 33) На диаметре круга построен треугольник, вписанный в этот круг. Площадь круга равна , одна из сторон треугольника 30. Чему равна площадь круга, вписанного в треугольник? 34) Радиус окружности равен 6. Перпендикуляр, опущенный из точки окружности на диаметр, делит его в отношении 1 : 3. Найдите длину перпендикуляра. 35) Найдите величину острого угла, который опирается на дугу, равную 2/5 окружности. Ответ дайте в градусах. 36) Найдите величину тупого угла, который опирается на дугу, равную 1/7 окружности. Ответ дайте в радианах. 37) Радиус окружности равен 5. Найдите длину дуги окружности, соответствующей центральному углу 1080. 38) Радиус окружности равен 20. Найдите Величину центрального угла, которому соответствует дуга окружности длины . 39) Хорда окружности, стягивающая дугу 900, равна . Чему равна длина окружности? 40) Радиус окружности равен 13. На каком расстоянии от центра окружности находится хорда длины 24. 41) Из точки окружности радиуса R проведены две хорды длины . Чему равен косинус угла между этими хордами? 42) По разные стороны от центра окружности проведены две параллельные хорды длин 12 и 16. Чему равен радиус окружности, если расстояние между хордами равно 14? 43) Найти площадь прямоугольника, если его диагональ равна , а одна из сторон 18. 44) В прямоугольнике ABCD биссектриса угла BAD пересекает сторону BC в точке M и делит ее на отрезки BM=6, MC=4. 45) Площадь параллелограмма равна 120, а его высоты 8 и 12. Найдите периметр параллелограмма. 46) Высоты параллелограмма равны 4 и 8. Большая высота опущена на сторону, равную 6. Найти другую сторону параллелограмма. 47) Углы между стороной ромба и его диагоналями относятся как 5 : 4. Найдите тупой угол ромба. 48) Как изменится площадь ромба, если одну из его диагоналей уменьшить на 10%, а другую увеличить на 20%? 49) Сторона ромба равна 5, а одна из диагоналей 6. Чему равна его площадь? 50) Разница между радиусами окружностей, описанной около квадрата и вписанной в квадрат, составляет . Чему равна сторона квадрата? 51) Боковая сторона равнобокой трапеции равна , высота и большее из оснований, соответственно, 4 и 9. Найдите длину средней линии трапеции. 52) Средняя линия трапеции ABCD делит ее на две трапеции со средними линиями, равными 5 и 9. 53) Трапеция, средняя линия которой равна , равновелика (т.е. равна по площади) равностороннему треугольнику со стороной 12. Найти высоту трапеции. 54) В равнобокой трапеции тупой угол равен 1200 и меньшее основание равно боковой стороне и равно 6. Найдите площадь трапеции. 55) В равнобедренной трапеции основания равны 4 и 6, боковая сторона равна 5. Чему равна сумма длин диагоналей? 56) В равнобедренной трапеции разность длин оснований равна длине боковой стороны. Чему равен тупой угол трапеции? 57) Высота равнобокой трапеции равна 40, боковая сторона 41, средняя линия 45. Чему равно большее основания трапеции? 58) В прямоугольной трапеции боковые стороны равны 4 и 5, меньшее из оснований 5. Чему равна площадь трапеции? 59) В прямоугольнике перпендикуляр, опущенный на диагональ, делит прямой угол на две части в отношении 3 : 1. 60) Периметр ромба равен 52, а сумма длин диагоналей 34. Чему равна его площадь? 61) Диагонали ромба равны 26 и . Чему равен синус острого угла ромба? 62) В равнобокой трапеции боковая сторона равна 7, диагональ 8, а средняя линия 4. Найдите меньшее основание. 63) В окружность радиуса 6 вписан прямоугольник. Найдите большую сторону прямоугольника, если угол между его диагоналями составляет 600. 64) В круг вписан прямоугольник со сторонами 2 и 6. Найдите площадь круга. 65) Равнобедренная трапеция вписана в окружность радиуса 6. Ее диагональ составляет угол 300 с большим основанием и перпендикулярна боковой стороне. Найдите периметр трапеции. 66) Периметр равнобедренной трапеции, описанной около окружности, равен 60. Найдите длину средней линии трапеции. 67) Основания равнобокой трапеции равны 12 и 20. 68) В трапецию вписана окружность. Расстояние от центра этой окружности до вершины верхнего основания равно 15; до вершины нижнего 20. Чему равна площадь трапеции? 69) Четырехугольник ABCD вписан в окружность. BC=4, CD=5, . Чему равна диагональ BD? 70) Окружность, вписанная в ромб, разбивает его диагональ на отрезки длины 9, 16, 9. Найдите площадь ромба. 71) Сторона вписанного в окружность правильного треугольника равна 6. Чему равна площадь квадрата, вписанного в ту же окружность? 72) Во сколько раз площадь круга больше площади вписанного в него квадрата? 73) Какой правильный многоугольник имеет внутренний угол 1440? 74) Сколько диагоналей можно провести в многоугольнике, если сумма его внутренних углов равна ? 75) Чему равна площадь круга, описанного около правильного шестиугольника со стороной 2? 76) Дан правильный восьмиугольник ABCDEFKM. 77) Найдите радиус окружности, описанной около правильного девятиугольника A1A2…A9, если периметр треугольника A1OA4 равен . Ответы1) 360, 600, 840; 2) 1000; 3) 1000; 4) 15; 5) ; 6) ; 7) ; 8) 39; 9) 54; 10) 2; 11) 16; 12) 15; 13) ; 14) 7,5; 15) 2; 16) ; 17) 12; 18) 14; 19) 24; 20) 21; 21) 10; 22) ; 23) 4; 24) 6; 25) ; 26) ; 27) ; 28) 3; 29) 24; 30) 17; 31) 5; 32) ; 33) ; 34) ; 35) 720; 36) ; 37) ; 38) 900; 39) ; 40) 5; 41) 1/8; 42) 10; 43) ; 44) 60; 45) 50; 46) 12; 47) 1000; 48) увеличится на 8%; 49) 24; 50) ; 51) 7; 52) 11; 53) 108; 54) ; 55) 14; 56) 1200; 57) 54; 58) 26; 59) 450; 60) 120; 61) ; 62) 2; 63) ; 64) ; 65) 30; 66) 15; 67) ; 68) 600; 69) ; 70) 845/6; 71) 24; 72) ; 73) десятиугольник; 74) 54; 75); 76) 4; 77) 6. |
Четырехугольники: Ромб
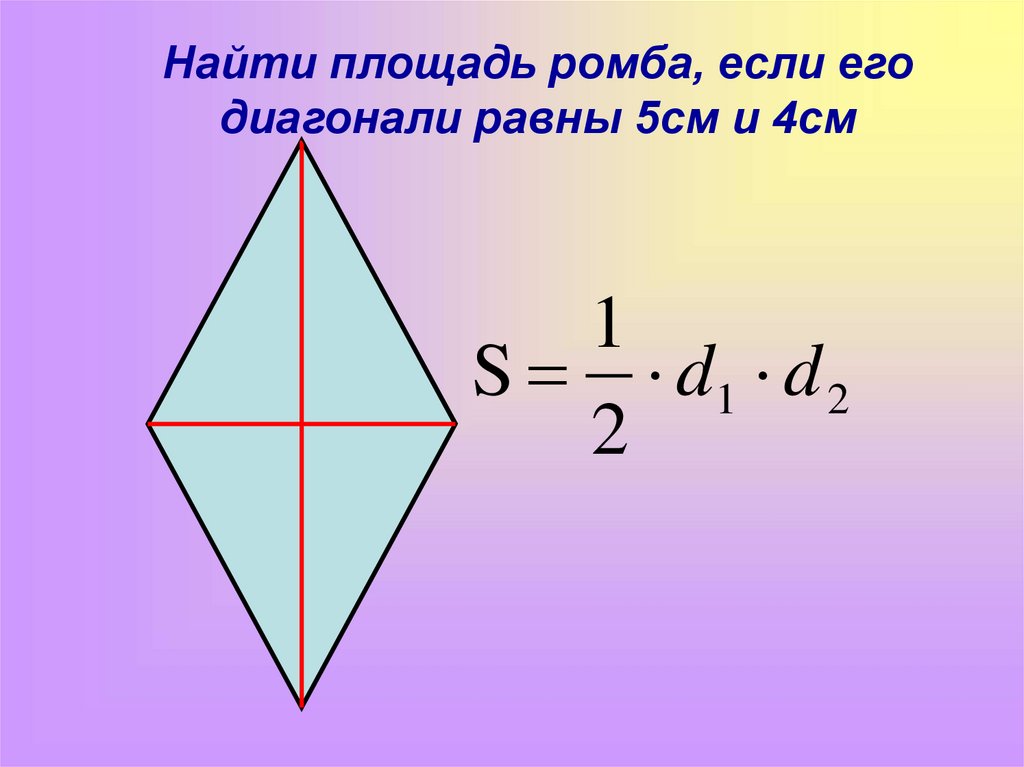
Периметр ромба равен 100, а его площадь равна 600. Какова длина большей диагонали ромба?
Неверно. [[фрагмент]] В задаче говорится, что периметр ромба равен 100, поэтому его стороны имеют длину $100 \div 4 = 25$$ единиц. Таким образом, гипотенуза каждого прямоугольного треугольника равна 25. Этот ответ, 60, делает одну сторону каждого треугольника $$$60 \div 2 = 30$$ единиц длины. Но это длиннее гипотенузы, что делает его невозможным треугольником — гипотенуза прямоугольного треугольника должна быть самой длинной стороной прямоугольного треугольника.
Неверно.
[[фрагмент]]
В задаче говорится, что периметр ромба равен 100, поэтому его стороны имеют длину $100 \div 4 = 25$$ единиц. Таким образом, гипотенуза каждого прямоугольного треугольника равна 25.
Этот ответ, 50, также делает одну сторону каждого треугольника $$$50 \div 2 = 25$$ единиц длины. Но так как это равно длине гипотенузы, это невозможный треугольник. Гипотенуза прямоугольного треугольника _должна_ быть длиннее любого из катетов по отдельности.
Гипотенуза прямоугольного треугольника _должна_ быть длиннее любого из катетов по отдельности.
Вы также можете получить этот ответ, просто исключив другие варианты ответов.
Если бы одна из диагоналей имела длину 50 (ответ D), то один из катетов прямоугольного треугольника был бы равен 25. Но поскольку периметр ромба равен 100, гипотенузы этих прямоугольных треугольников равны 25. Гипотенуза должна всегда быть длиннее катетов прямоугольного треугольника, поэтому 50 — это слишком много. Это означает, что вы также можете исключить 60. D и E больше нет!
Если длина большей диагонали равна 30 (ответ B), длина стороны каждого треугольника составляет $30 \div 2 = 15$$ единиц.
$$\hspace{0,5 дюйма} \displaystyle A = \frac{bh}{2} = 150$$
$$\hspace{0,5 дюйма} \displaystyle A = \frac{15h}{2} = 150$$
$$\hspace{0.5in} 15ч = 300$$
$$\hspace{0,5 дюйма} ч = 20$$
Таким образом, длина других катетов должна быть 20 единиц, а длина всей другой диагонали — 40 единиц. Но 30 должно было быть _длиннее_ по диагонали, так что 30 слишком мало. Это означает, что вы также можете устранить 20. А и Б больше нет! В качестве возможного ответа остается только С.
Это означает, что вы также можете устранить 20. А и Б больше нет! В качестве возможного ответа остается только С.
Неверно. [[фрагмент]] Этот ответ, 30, делает одну сторону каждого треугольника $$30 \div 2 = 15$$ единицами длины. $$\hspace{0,5 дюйма} \displaystyle A = \frac{bh}{2} = 150$$ $$\hspace{0,5 дюйма} \displaystyle A = \frac{15h}{2} = 150$$ $$\hspace{0.5in} 15ч = 300$$ $$\hspace{0,5 дюйма} ч = 20$$ Таким образом, длина других катетов должна быть 20 единиц, а длина всей другой диагонали — 40 единиц. Но диагональ 30 должна была быть _длиннее_, так что это не может быть правильным.
Неверно.
[[фрагмент]]
Этот ответ, 20, делает одну сторону каждого треугольника $$20 \div 2 = 10$$ единицами длины.
$$\hspace{0,5 дюйма} \displaystyle A = \frac{bh}{2} = 150$$
$$\hspace{0,5 дюйма} \displaystyle A = \frac{10h}{2} = 150$$
$$\hspace{0,5 дюйма} 5ч = 150$$
$$\hspace{0,5 дюйма} ч = 30$$
Это означает, что другие стороны должны иметь длину 30 единиц, а вся другая диагональ — 60 единиц. Но 20 должно было быть _большей_ диагональю, так что это не может быть правильным.
Но 20 должно было быть _большей_ диагональю, так что это не может быть правильным.
Верно!
Ромб – это параллелограмм, у которого четыре стороны равны. Кроме того, диагонали ромба перпендикулярны друг другу. При начертании они разбивают ромб на четыре конгруэнтных прямоугольных треугольника.
Используйте стратегию __Reverse Pluging In__, чтобы определить, какой вариант ответа дает правильные значения периметра и площади ромба на основе этих треугольников.
Этот ответ, 40, делает одну сторону каждого треугольника $$40 \div 2 = 20$$ единиц длины. Нарисуйте этот ромб вместе с его диагоналями, которые образуют четыре конгруэнтных прямоугольных треугольника.

Поскольку площадь ромба равна 600, площадь каждого треугольника равна $600 \div 4 = 150$$. Используйте формулу площади $$A = \frac{bh}{2}$$, чтобы написать уравнение, а затем найти $$h$$.
$$\hspace{0,5 дюйма} \displaystyle \frac{bh}{2} = 150$$
$$\hspace{0,5 дюйма} \displaystyle \frac{20h}{2} = 150$$
$$\hspace{0.5in} 10h = 150$$
$$\hspace{0,5 дюйма} ч = 15$$
Таким образом, остальные ноги должны быть длиной 15 единиц.
Наконец, если катеты прямоугольного треугольника имеют длину 15 и 20 единиц, то треугольник представляет собой треугольник 3:4:5 (увеличенный в 5 раз), поэтому его гипотенуза должна быть $$5\cdot5 = 25$$ единиц. длинный. Таким образом, каждая сторона ромба имеет длину 25 единиц, а это означает, что периметр ромба равен $$25 \cdot 4 = 100$$, что и требовалось.
Используйте формулу площади $$A = \frac{bh}{2}$$, чтобы написать уравнение, а затем найти $$h$$.
$$\hspace{0,5 дюйма} \displaystyle \frac{bh}{2} = 150$$
$$\hspace{0,5 дюйма} \displaystyle \frac{20h}{2} = 150$$
$$\hspace{0.5in} 10h = 150$$
$$\hspace{0,5 дюйма} ч = 15$$
Таким образом, остальные ноги должны быть длиной 15 единиц.
Наконец, если катеты прямоугольного треугольника имеют длину 15 и 20 единиц, то треугольник представляет собой треугольник 3:4:5 (увеличенный в 5 раз), поэтому его гипотенуза должна быть $$5\cdot5 = 25$$ единиц. длинный. Таким образом, каждая сторона ромба имеет длину 25 единиц, а это означает, что периметр ромба равен $$25 \cdot 4 = 100$$, что и требовалось.
20
30
40
50
60
Продолжить
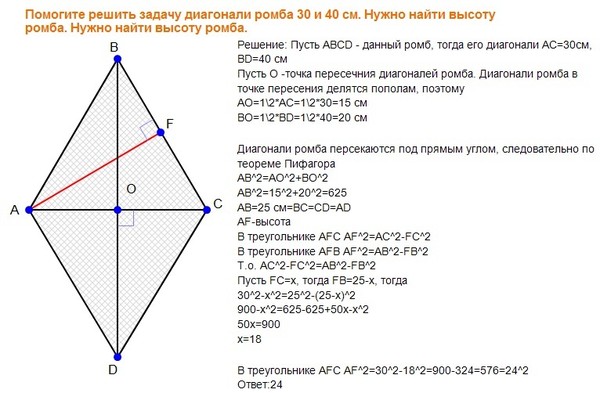
в ромбе, если диагонали 30 см и 40 см Найдите свой периметр …
Прыжки до
- Теорема Пифагора. Упражнение 12.
- Рациональные и иррациональные числа
- Сложные проценты
- Расширения
- Факторизация
- Одновременные линейные уравнения
- Задачи на одновременные линейные уравнения
- Квадратные уравнения
- Индексы
- Логарифмы
- Треугольники
- Теорема о средней точке
- Теорема Пифагора
- Прямолинейные фигуры
- Теоремы о площади
- Круг
- Измерение
- Тригонометрические отношения
- Тригонометрические отношения и стандартные углы
- Координатная геометрия
- Статистика
Главная >
ML Aggarwal Solutions
Класс 9
Математика
>
Глава 12. {2}=625
\end{выровнено}
{2}=625
\end{выровнено}
Извлечение квадратного корня с обеих сторон
ВС = 25 см
Итак, сторона ромба а = 25 см.
Периметр = 4a = 4×25 = 100 см
Следовательно, периметр ромба равен 100 см.
Связанные вопросы
Ниже приведены длины сторон треугольников. Определите, какие из них прямоугольные. В случае …
Ножка лестницы длиной 10 м, прислоненной к вертикальному колодцу, находится на расстоянии 6 м от основания стены. Фи…
В прямоугольном треугольнике, если гипотенуза равна 20 см, а отношение двух других сторон равно 4:3, найти…
Для поездки в город B из города A существует маршрут через город C такой, что AC ⊥ CB, AC = 2x км и CB =…
АВС равнобедренный треугольник, в котором стороны АВ = АС = 12 см, а ВС = 8 см.

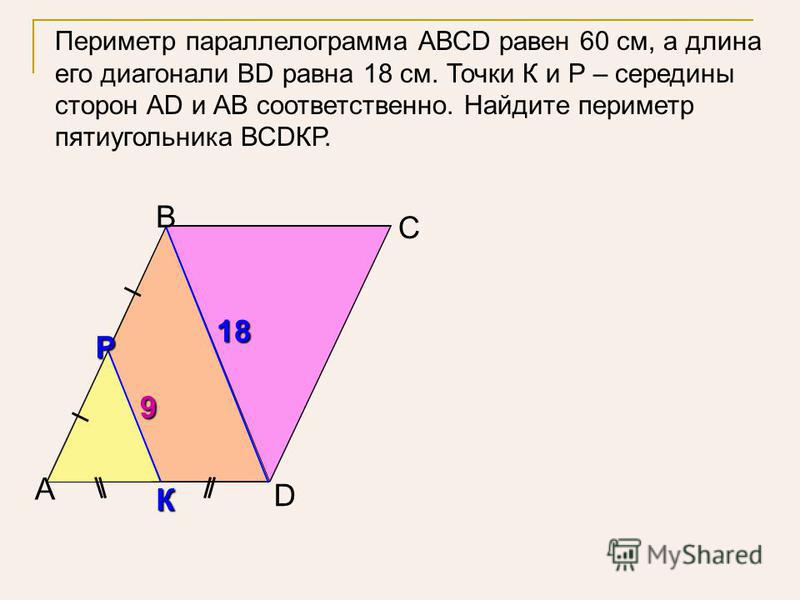


 В треугольнике ABC проведена медиана CM, причем треугольник BCM – равнобедренный с основанием BM. . Найдите сторону BC.
В треугольнике ABC проведена медиана CM, причем треугольник BCM – равнобедренный с основанием BM. . Найдите сторону BC. углы, опирающиеся на диаметр – прямые.
углы, опирающиеся на диаметр – прямые. Найдите периметр треугольника, если его высота равна 6.
Найдите периметр треугольника, если его высота равна 6.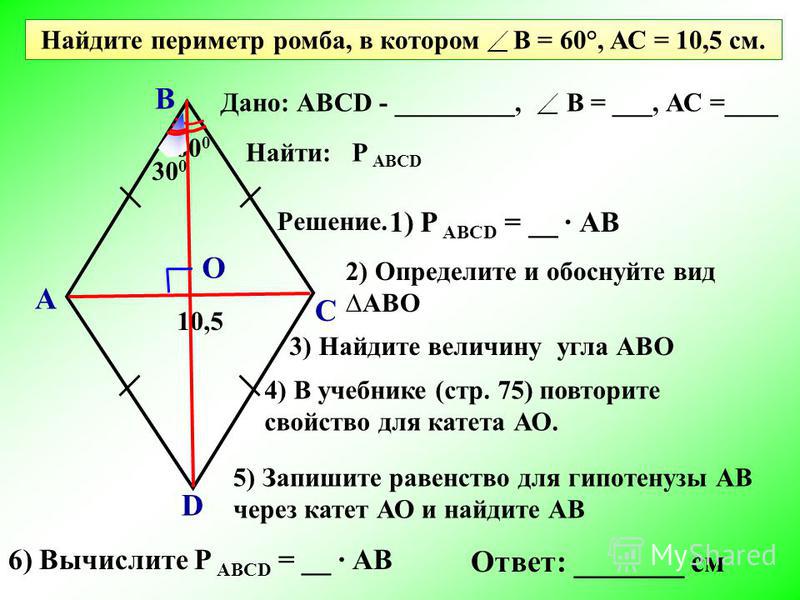
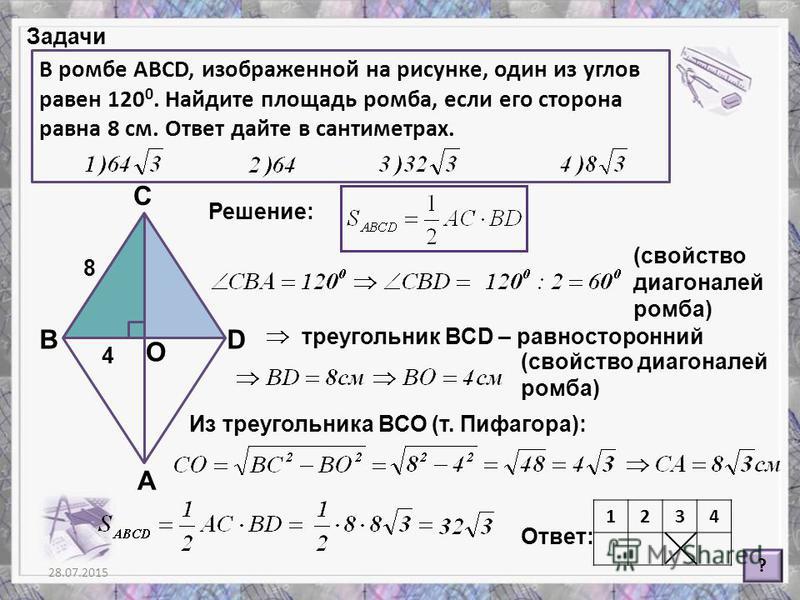 Ромб является параллелограммом. В любой ромб можно вписать окружность.
Ромб является параллелограммом. В любой ромб можно вписать окружность.
 Площадь прямоугольника равна x•3x=12, откуда x=2.
Площадь прямоугольника равна x•3x=12, откуда x=2.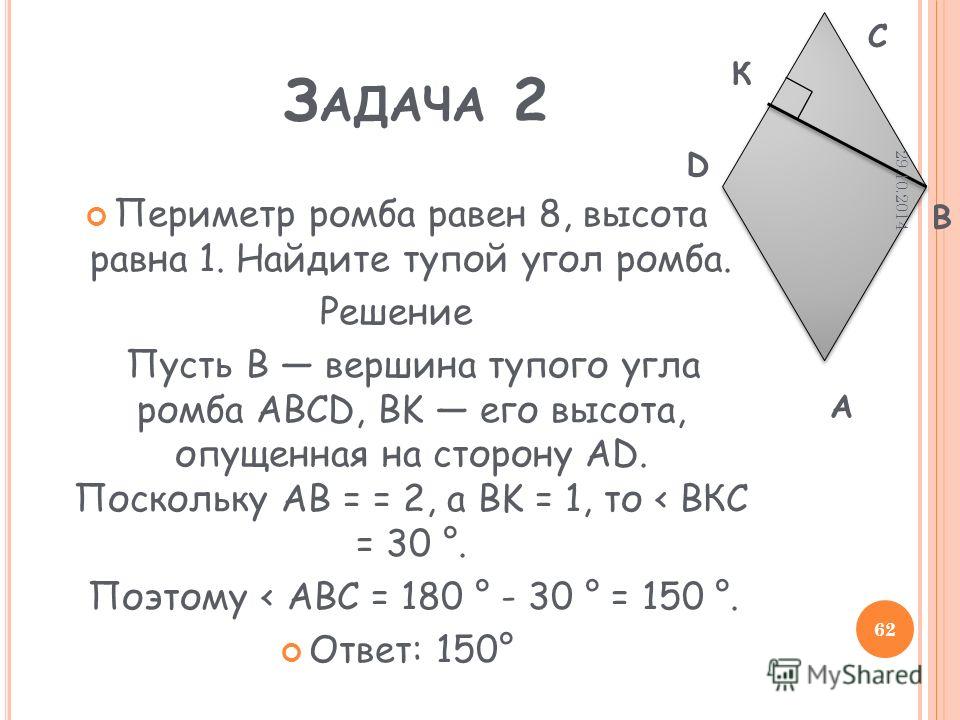 Найти периметр параллелограмма.
Найти периметр параллелограмма. свойства параллелограмма). По теореме Пифагора найдем гипотенузу: .
свойства параллелограмма). По теореме Пифагора найдем гипотенузу: . к. ABCH – прямоугольник), т.е. AB=CH=8.
к. ABCH – прямоугольник), т.е. AB=CH=8.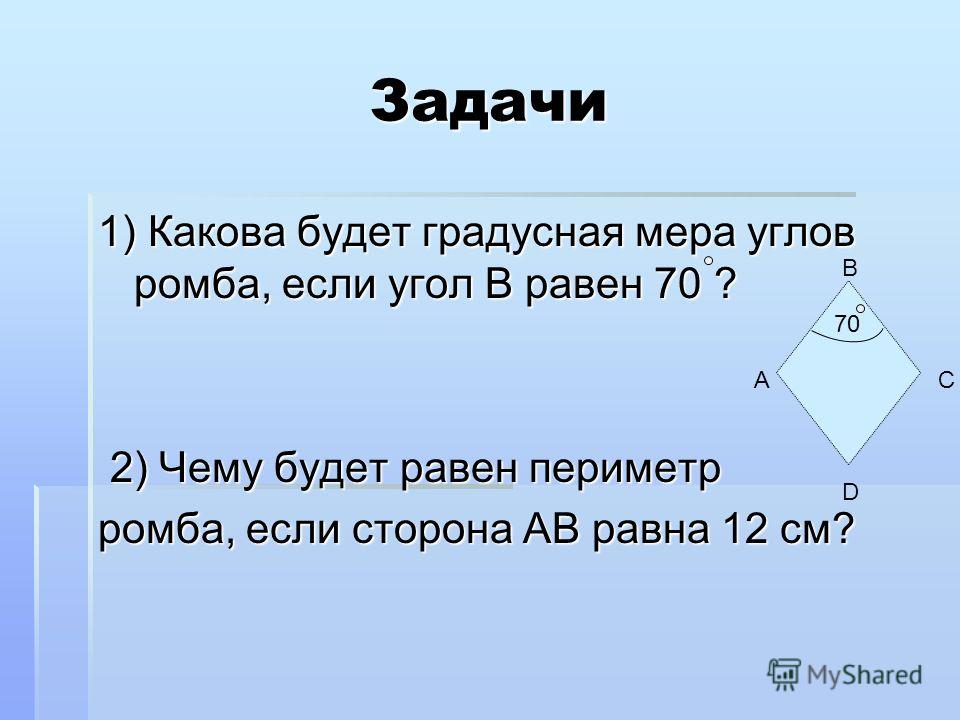

 Найдите высоту, опущенную на основание.
Найдите высоту, опущенную на основание. Найдите площадь треугольника AMN.
Найдите площадь треугольника AMN. Найдите радиус описанной около него окружности.
Найдите радиус описанной около него окружности.
 Чему равна площадь прямоугольника?
Чему равна площадь прямоугольника?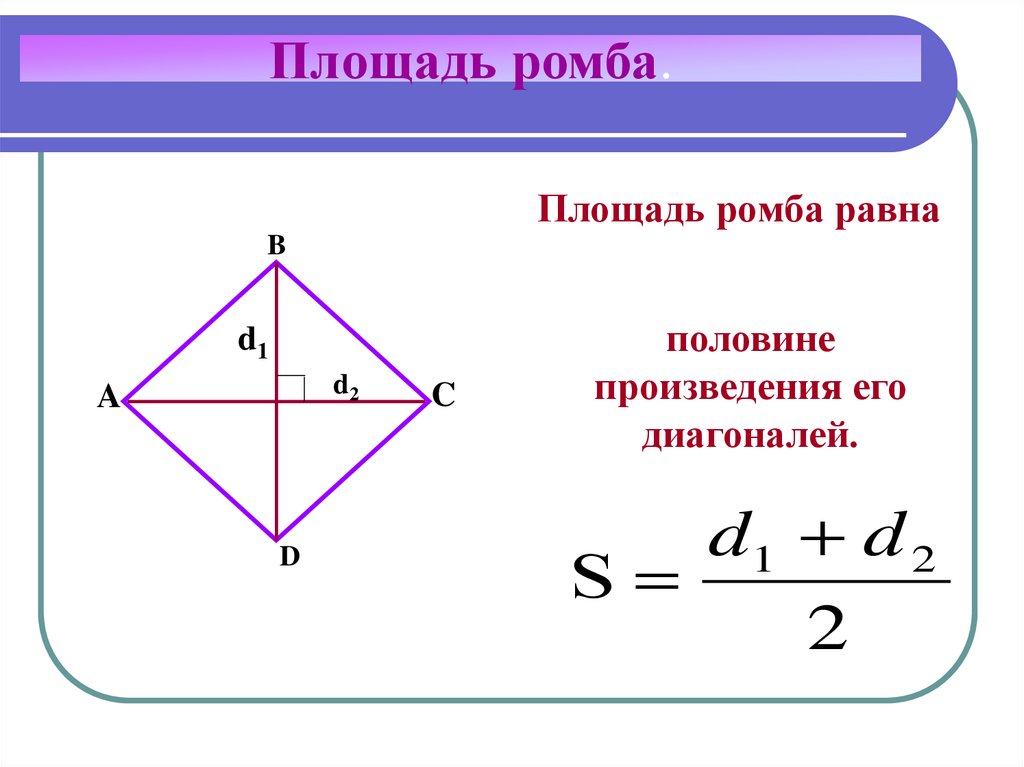 Найдите большее основание ABCD.
Найдите большее основание ABCD. Чему равен угол между этим перпендикуляром и другой диагональю?
Чему равен угол между этим перпендикуляром и другой диагональю? Центр описанной около окружности трапеции лежит на ее большем основании. Чему равна диагональ трапеции?
Центр описанной около окружности трапеции лежит на ее большем основании. Чему равна диагональ трапеции? Найдите радиус описанной около него окружности, если площадь треугольника ABE равна .
Найдите радиус описанной около него окружности, если площадь треугольника ABE равна .
Leave A Comment