В каком случае проекция скорости движения будет отрицательной? Равна нулю? Помогите
Азот массой 5 г нагревается от 20 С при постоянном давлении 150кПА. После нагрева объём газа оказался равным V=12 л. Найти:1)количество теплоты,получе … нное азотом;2)работу,совершённую газом;3)приращение внутренней энергии.
На горизонтальном дне бассейна, имеющего глубину h = = 2,0 м, лежит плоское зеркало. Луч света, преломившись на поверхности воды, отражается от зеркал … а и выходит в воздух. Расстояние от точки вхождения луча в воду до точки выхода отраженного луча из воды равно L = 1,5 м. Определить угол падения луча α.
Фотон с энергией ε = 0,25 МэВ рассеялся под углом α = = 120° на первоначально покоившемся свободном электроне. Определить кинетическую энергию электро … на отдачи.
Який опір провідника, якщо при різниці потенціалів на його кінцях 1 В сила струму в ньому становить 1 А ?а) 1 Дж; б) 1 Ом; в) 1 Вт.
на горизонтальном дне бассейна, имеющего глубину h =
= 2,0 м, лежит плоское зеркало.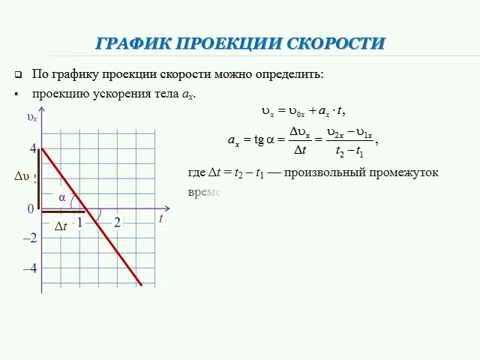
Який опір провідника, якщо при різниці потенціалів на його кінцях 1 В сила струму в ньому становить 1 А ?а) 1 Дж; б) 1 Ом; в) 1 Вт.
Яку фізичну величину позначають буквою l ?а) напругу; б) електричний опір; а) силу струму.
Знайдіть потужність, що споживає лампочка, на цоколі якої написано: 3,5 В , 0,38 А.а) 13,5 Вт; б) 3,78 Вт; в) 0,98 Вт.
Энергия конденсатора электроемкостью 10 ПФравна 800 нДж. Вычислите напряжение междуобкладками конденсатора.
с вертолета сбрасываются два груза так, чтобы два самолета без начальной скорости выходили из первого с опозданием на 1 секунду.Расстояние между груза … ми через 2 секунды после начала движения первого груза.
В каком случае скорость будет положительной? отрицательной? 7 класс
Найдите линейную скорость Земли при её орбитальном движений.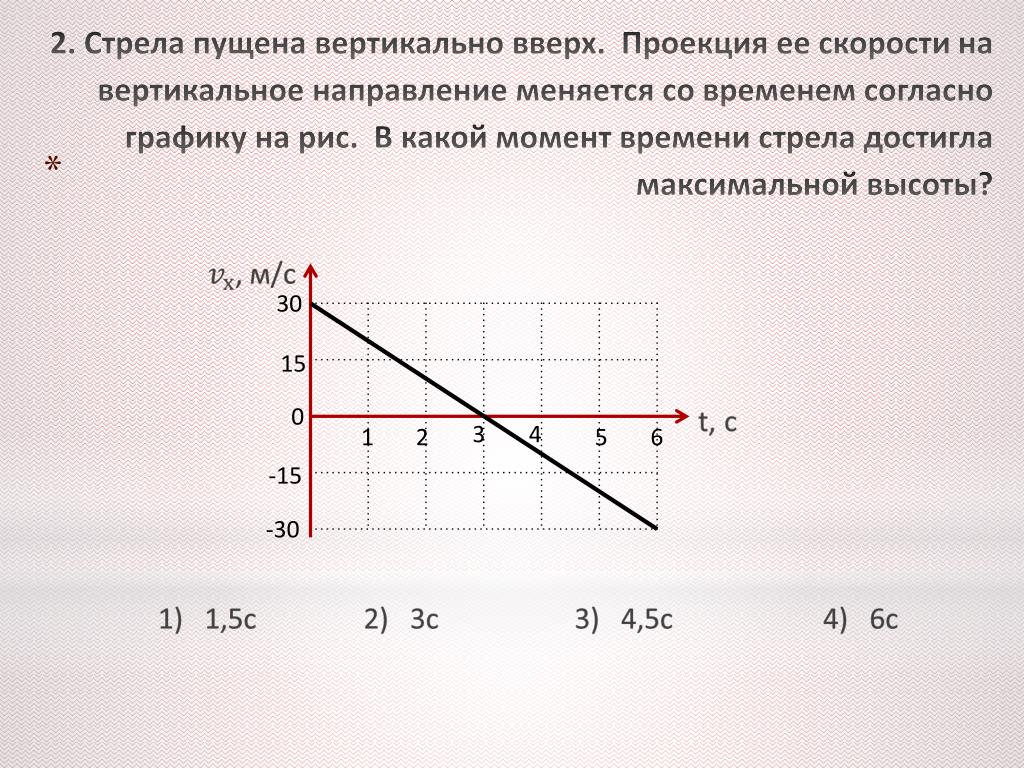 8 км.
8 км.
Проводники сопротивлением 3 Ом и 4 Ом соединены параллельно. Если через сопротивление 3 Ом протекает ток 0,2 А, то через сопротивление 4 Ом протекает … ток… (в а)
При повышении температуры диффузия происходит быстрее, потому что
A. Увеличивается скорость движения молекул
B. Уменьшаются промежутки между молекулам
… и
C. Уменьшается скорость движения молекул
D. Изменяются размеры молекул
2. При превращении 3 кг воды при 200С в лед при 00С, выделяется количество теплоты (с=4200Дж/кг*С; λ=3,4*105Дж/кг)
A. 1270кДж
B. 127 кДж
C. 1,27МДж
D. 12,7кДж
3. Если при снятии нагрузки кристалл после деформации возвращается в исходное состояние, то такая деформация называется…
A. возвращаемой
B. упругой
C. недеформируемой
D. кристаллической
4. Индуктивность катушки колебательного контура увеличивалась в 4 раза. При этом период колебаний
A. Увеличится в 4 раза.
B. Уменьшится в 2 раза
C. Не изменится
D. Увеличится в 2 раза.
5. Спектральным анализом называется:
A. способ возбуждения атома
B.
сделать первое задание по литию № 19
Ізольована металева пластина освітлюється світлом з довжиною хвилі 450 нм. До якого потенціалу зарядиться пластинка при тривалому освітленні, якщо роб … ота виходу електронів дорівнює 2 еВ?
Два одинаковых маленьких металлических шарика заряжены положительными зарядами 2q и 4q.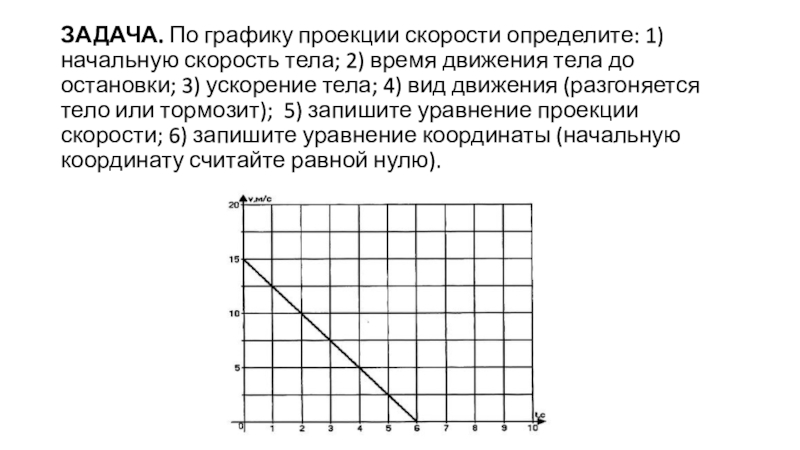 Шарики привели в соприкосновение и развели их. Каким стал заря
… д каждого шарика?
А. q. Б. 2q. В. 3q. Г. 6q.
Шарики привели в соприкосновение и развели их. Каким стал заря
… д каждого шарика?
А. q. Б. 2q. В. 3q. Г. 6q.
БУДЬ ЛАСКА (20 балів) Знайти як зміниться зображення предмета, який вміщено перед збиральною лінзою на відстані 7,5 см, якщо відомо, що фокусна відста … нь лінзи 0,2 м
Задача на силу Ампера. Сила тока в проводнике 2А, длина активной части проводника 0,3м, магнитное поле, действует на проводник с силой 0,2Н. Определит … е индукцию магнитного поля, если линия индукции поля и ток взаимно перпендикулярны.
Вычислить силу тока на втором резисторе, если: R1=5 Ом, R2=3 Ом, R3=9Ом, R4=12 Ом, U3= 200В. Ответ:
Какое количество теплоты потребуется для того, чтобы нагреть воду массой 15 кг от 10 до 90 градусов Цельсия? Ответ выразите в кДж а)7400, б)4800, с)17 … 5 д)5040, е)501
Скорость движения в физике
Скорость является одной из основных характеристик механического движения. Она выражает саму суть движения, т.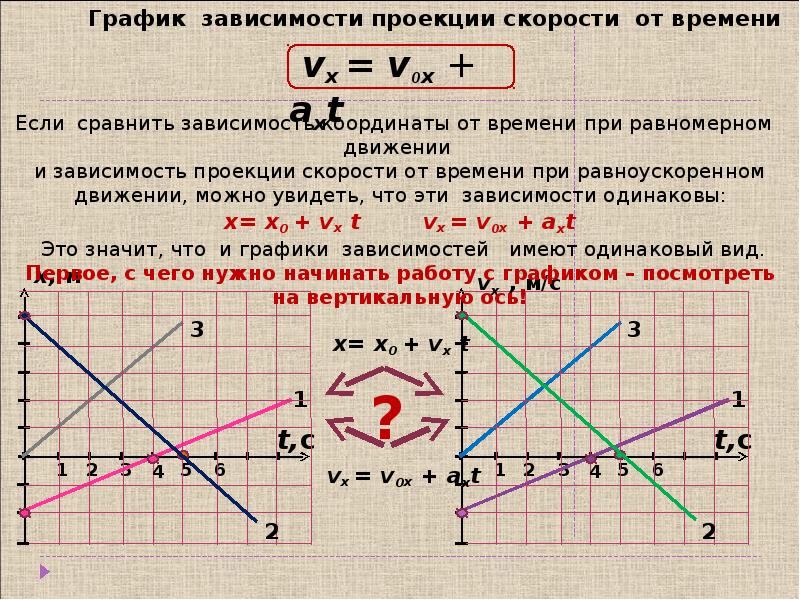 е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с.
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по траектории движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
Отрицательная скорость
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета.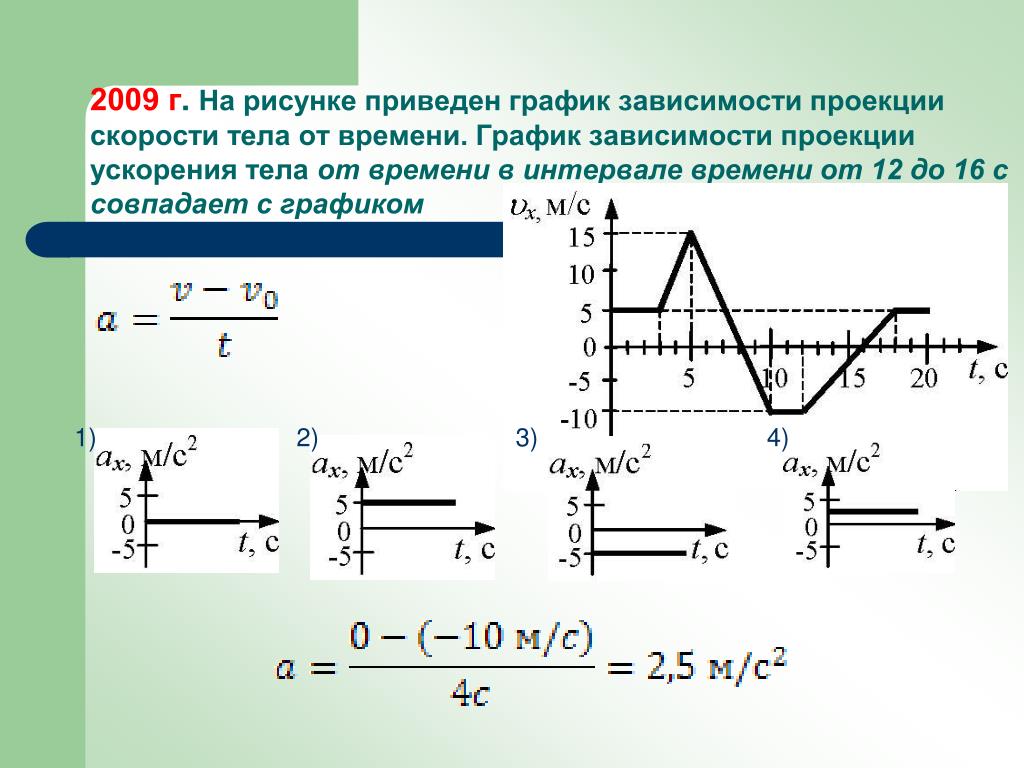 На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
В случае неравномерного движения говорят о средней скорости:
Примеры решения задач по теме «Скорость»
| Понравился сайт? Расскажи друзьям! | |||
| posted Oct 15, 2009, 1:24 AM by Дмитрий Белозёров
[
updated Dec 23, 2014, 6:24 AM
] |
Из курса физики седьмого класса мы помним, что механическое движение тела – это его перемещение во времени относительно других тел. Исходя из таких сведений, мы можем предположить необходимый набор инструментов для расчета движения тела. Во-первых, нам необходимо нечто, относительно чего мы будем производить наши расчеты. Далее, нам потребуется условиться, каким образом мы будем определять положение тела относительно этого «нечто». И наконец, нужно будет как-то фиксировать время. Таким образом, для того, чтобы рассчитать, где будет находиться в конкретный момент тело, нам понадобится система отсчета. Система отсчета в физикеСистемой отсчета в физике называют совокупность тела отсчета, системы координат, связанной с телом отсчета, и часы или иной прибор для отсчета времени. При этом всегда следует помнить, что всякая система отсчета условна и относительна. Всегда можно принять другую систему отсчета, относительно которой любое движение будет иметь совершенно другие характеристики. Относительность – это вообще немаловажный аспект, который следует учитывать практически при любых расчетах в физике. Например, во многих случаях мы далеко не в любой момент времени можем определить точные координаты движущегося тела. В частности, мы не можем расставить наблюдателей с часами на каждых ста метрах вдоль железнодорожного пути от Москвы до Владивостока. В таком случае мы рассчитываем скорость и местоположение тела приближенно в течение какого-то отрезка времени. Нам не важна точность до одного метра при определении местоположения поезда на пути в несколько сотен или тысяч километров. Для этого в физике существуют приближения. Одним из таких приближений является понятие «материальная точка». Материальная точка в физикеМатериальной точкой в физике обозначают тело, в случаях, когда его размерами и формой можно пренебречь. При этом считается, что материальная точка имеет массу исходного тела. Например, при расчете времени, которое понадобится самолету, чтобы долететь из Новосибирска до Новополоцка, нам не важны размеры и форма самолета. Практически всякое тело можно считать материальной точкой либо когда расстояние, преодолеваемое телом велико в сравнении с его размерами, либо когда все точки тела двигаются одинаково. Например, автомобиль, проехавший несколько метров от магазина до перекрестка, вполне сравним с этим расстоянием. Но даже в такой ситуации его можно считать материальной точкой, потому что все части автомобиля перемещались одинаково и на равное расстояние. А вот в случае, когда нам надо разместить тот же автомобиль в гараже, его уже никак не сочтешь материальной точкой. Придется учитывать его размеры и форму. Это тоже примеры, когда необходимо учитывать относительность, то есть относительно чего мы производим конкретные расчеты.
Для того, чтобы определить положение тела, которое совершило некоторое перемещение, можно графически приставить вектор перемещения к начальному положению тела. В этом случае вычисления будут производиться не с самим векторами, а с их проекциями на координатные оси и с их модулями. Эти величины которые будут представлять собой некоторые числа, положительные или отрицательные, но не будут иметь направления. Рассмотрим следующую задачу Необходимо определить координату движущегося тела, по известной начальной координате и известному вектору перемещения.
Определить координаты катеров по отношению к пристани и расстояние между ними. Построим координатную ось Ох, параллельно прямой вдоль которой двигаются катера. Спроецируем начала и концы векторов перемещений s1 и s2 на ось Ох, получим отрезки sx1 и sx2. Эти отрезки будут являться проекциями данных векторов. Проекция вектора на ось, будет положительной, если вектор сонаправлен с осью, и отрицательной, если вектор направлен в противоположную оси сторону. В нашем случае sx1 положительная проекция, а sx2 отрицательная проекция. Проекция вектора, будет равна разности координат конца и начала вектора. В нашем случае имеем: Теперь выразим из этих уравнений координаты x1 и x2. Расстояние между двумя катерами будет равно модулю разности их координат, Мы получили формулы для вычисления координат точек и расстояния между ними. Из условия задачи, катера встретились на расстоянии 100 км от пристани. х0 – точка встречи. Следовательно расстояние от х0 до пристани(начала координат) 100 км. х0=100 км. Так как мы выбрали ось Ох параллельно векторам перемещений катеров. По условию у нас даны числа 50 км и 60 км, это и есть модули векторов соответствующий перемещений.
В итоге получаем,
Ответ: х1=160 км, х2=50 км, l=110 км.
Довольно часто в физике приходится иметь дело с прямолинейным равномерным движением. Задача нахождения перемещения при равномерном прямолинейном движении довольно проста. По определению скорость равномерного прямолинейного движения – постоянная векторная величина, которая равна отношению перемещения тела за некий промежуток времени к величине этого промежутка: v(->) = s(->) /t, откуда следует,что перемещение s(->) = v(->) * t . где v(->) – скорость (векторная величина), s(->) – перемещение (векторная величина), t – время. При работе с векторными величинами для нахождения числовых значений величин применяют значения проекций конкретных величин на оси. В случае равномерного прямолинейного движения направления векторов скорости и перемещения совпадают, поэтому можно смело использовать в расчетах модульные значения. Тогда формула принимает вид: s = v*t Но такая формула известна уже давно, и в ней под буквой s понимали путь, пройденный телом. Так что же такое s – путь или модуль перемещения? Как характеризуется перемещение тела при прямолинейном равномерном движении?Дело в том, что при равномерном и прямолинейном движении модуль вектора перемещения за некий промежуток времени будет равен пройденному телом пути за тот же промежуток времени. Это утверждение можно подтвердить рисунком. Если изобразить векторно скорость движения тела в зависимости от времени, то модуль такого перемещения при равномерном прямолинейном движении будет в любой момент времени совпадать с путем, пройденным за это время телом. Если же направление тела будет меняться, то пройденный путь будет больше значения модуля перемещения. Поэтому принятое нами равенство справедливо только для случаев, когда тело двигается равномерно и прямолинейно. Можно изобразить данную ситуацию графически. Для этого проведем из точки 0 оси скорости и времени. (Рис. 1)Если применить проекции значений скорости и времени на оси, то тогда мы увидим, что скорость, как величина постоянная является прямой, проходящей параллельно оси времени. И если мы проведем перпендикуляры от временной оси в начальный и конечный моменты времени к линии скорости, то получим прямоугольник, площадь которого и будет равна перемещению за данный промежуток времени. Рис. 1 Стороны этого прямоугольника будут равны все тем же значениям v и t. Таким образом, мы видим, что и при построении проекций векторных величин, принятое нами выше равенство сохраняет свою справедливость. В случае же, когда мы имеем в расчетах дело с двумя телами, двигающимися равномерно и прямолинейно, при этом совпадают направления их движения, то расчеты также можно производить, применяя приведенную выше формулу. Если же два тела двигаются равномерно и прямолинейно, а направления их движения противоположны, но расположены вдоль одной оси, то можно по-прежнему использовать в расчетах значения их модулей. Но необходимо будет брать значение величин для одного тела со знаком минус в зависимости от того, направление какого из тел мы примем за положительное.
Хотите провести эксперимент? Да запросто. Возьмите длинную линейку, положите ее горизонтально и приподнимите один конец. У вас получится наклонная плоскость. А теперь возьмите монетку и положите на верхний конец линейки. Монетка начнет скользить вниз по линейке, проследите, как будет двигаться монетка с одинаковой скоростью или нет. Вы заметите, что скорость монетки будет постепенно возрастать. И изменение скорости будет напрямую зависеть от угла наклона линейки. Чем угол наклона круче, тем большую скорость будет набирать монетка к концу пути. Изменение скорости монеткиМожно попытаться узнать, как меняется скорость монетки за каждый одинаковый промежуток времени. Такое движение тела, когда его скорость за любые равные промежутки времени меняется одинаково, а тело при этом движется по прямой линии, называется в физике прямолинейным равноускоренным движением. Под скоростью в данном случае понимается скорость в каждый конкретный момент времени. Такая скорость называется мгновенной скоростью. Мгновенная скорость тела может меняться по-разному: быстрее, медленнее, может возрастать, а может уменьшаться. Для того чтобы охарактеризовать это изменение скорости, вводят величину, называемую ускорением. Понятие ускорения: формулаУскорение это физическая величина, показывающая, насколько изменилась скорость тела за каждый равный промежуток времени. Если скорость меняется одинаковым образом, то ускорение будет величиной постоянной. a = (v — v_0 )/ t, где a ускорение, v конечная скорость, v_0 начальная скорость, t время. Измеряется ускорение в метрах на секунду в квадрате (1 м/с2). Немного странная на первый взгляд единица очень легко объясняется: ускорение= скорость/время=(м/с)/с , откуда и выводится такая единица. Ускорение величина векторная. Оно может быть направлена либо в ту же сторону, что и скорость, если скорость возрастает, либо в противоположную сторону, если скорость уменьшается. Пример второго варианта это торможение. Если, например, автомобиль тормозит, то скорость его уменьшается. Тогда ускорение будет являться отрицательной величиной, и направлено оно будет не по ходу движения автомобиля, а в обратную сторону. В случаях, когда скорость у нас меняется от нуля до какой-либо величины, например, при старте ракеты, либо в случае, когда скорость наоборот уменьшается до нуля, например, при торможении поезда до полной остановки, можно использовать в расчетах только одно значение скорости.
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле: Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t. То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.
Графиком уравнения Vx=V0x+ax*t будет прямая линия. Расположение этой лини в системе координат будет определяться значениями ax b V0x. График проекции скорости тела при нулевой начальной скоростиНа следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел нулевую скорость, и двигалось равноускоренно и прямолинейно с ускорением ax=1,5 м/(с^2) в течение 40 секунд. Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость. График проекции скорости тела при торможенииЕсли бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол. Ниже представлен график такой ситуации. Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Попытаемся вывести формулу для нахождения проекции вектора перемещения тела, которое двигается прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к графику зависимости проекции скорости прямолинейного равноускоренного движения от времени. График зависимости проекции скорости прямолинейного равноускоренного движения от времениНиже на рисунке представлен график, для проекции скорости некоторого тела, которое движется с начальной скорость V0 и постоянным ускорением а. Если бы у нас было равномерное прямолинейное движение, то для вычисления проекции вектора перемещения, необходимо было бы посчитать площадь фигуры под графиком проекции вектора скорости. Теперь докажем, что и в случае равноускоренного прямолинейного движения проекция вектора перемещения Sx будет определяться таким же образом. То есть проекция вектора перемещения будет равняться площади фигуры под графиком проекции вектора скорости. Найдем площадь фигуры ограниченную осью оt, отрезками АО и ВС, а также отрезком АС.
Выделим на оси ot малый промежуток времени db. Проведем через эти точки перпендикуляры к оси времени, до их пересечения с графикос проекции скорости. Отметим точки пересечения a и c. За этот промежуток времени скорость тела поменяется от Vax до Vbx. Если взять этот промежуток достаточно малым, то можно считать что скорость остается практически неизменной, а следовательно мы будем иметь на этом промежутке дело с равномерным прямолинейным движением. За промежуток t3=3*t1, это тело совершит перемещение S3=9*S1 и т.д., для любого натурального n. Это конечно же будет выполняться, при условии, что время должно отсчитываться от одного и того же момента. На следующем рисунке хорошо представлена эта зависимость.
При увеличении промежутка времени, который отсчитывается от начал движения, в целое число раз по сравнению с t1, модули векторов перемещений будут возрастать как ряд квадратов последовательных натуральных чисел. Помимо этой закономерности, из представленного выше рисунка можно установить еще одну, следующую закономерность:
За последовательные равные промежутки времени, модули векторов перемещений, совершаемых телом, будут относиться между собой как ряд последовательных нечетных чисел. Стоит отметить, что такие закономерности будут верными только в равноускоренном движении.
Представьте себе электричку. Она едет тихонько по рельсам, развозя пассажиров по дачам. И вдруг сидящий в последнем вагоне хулиган и тунеядец Сидоров замечает, что на станции «Сады» в вагон входят контролеры. Билет, естественно, Сидоров не купил, а штраф платить ему хочется еще меньше. Относительность движения безбилетника в поездеИ вот, чтобы его не поймали, он быстренько совершает перемещение при прямолинейном равномерном движении в другой вагон. Контролеры, проверив билеты у всех пассажиров, движутся в том же направлении. Сидоров опять переходит в следующий вагон и так далее. И вот, когда он достигает первого вагона и идти дальше уже некуда, оказывается, что поезд как раз доехал до нужной ему станции «Огороды», и счастливый Сидоров выходит, радуясь тому, что проехал зайцем и не попался. Что мы можем извлечь из этой остросюжетной истории? Мы можем, без сомнения, порадоваться за Сидорова, а можем, кроме того, обнаружить еще один небезынтересный факт. В то время, как поезд за пять минут проехал пять километров от станции «Сады» до станции «Огороды», заяц Сидоров за это же время преодолел такое же расстояние плюс расстояние, равное длине поезда, в котором он ехал, то есть около пяти тысяч двухсот метров за те же пять минут. Получается, что Сидоров двигался быстрее электрички. Впрочем, такую же скорость развили и следующие за ним по пятам контролеры. Учитывая, что скорость поезда была около 60 км/ч впору выдать им всем несколько олимпийских медалей. Однако, конечно же, никто такой глупостью заниматься не будет, потому что все понимают, что невероятная скорость Сидорова была развита им только лишь относительно неподвижных станций, рельсов и огородов, и обусловлена эта скорость была передвижением поезда, а вовсе не невероятными способностями Сидорова. Относительно же поезда Сидоров двигался вовсе и не быстро и не дотягивает не то что до олимпийской медали, но даже до ленточки от нее. Вот тут-то мы и сталкиваемся с таким понятием как относительность движения. Понятие относительности движения: примерыОтносительность движения не имеет определения, так как не является физической величиной. Относительность механического движения проявляется в том, что некоторые характеристики движения, такие как скорость, путь, траектория и так далее, относительны, то есть зависят от наблюдателя. В различных системах отсчета эти характеристики будут различны. Кроме приведенного примера с гражданином Сидоровым в поезде, можно взять практически любое движение любого тела и показать, насколько оно относительно. Идя на работу, вы двигаетесь вперед относительно дома и в то же время передвигаетесь назад относительно автобуса, на который опоздали. Вы стоите на месте относительно плеера в кармане и несетесь с огромной скоростью относительно звезды по имени Солнце. В этом и заключается понятие относительности движения.
С древнейших времен движение материальных тел не переставало волновать умы ученых. Так, например, сам Аристотель считал, что если на тело не действуют никакие силы, то такое тело всегда будет находиться в покое. И лишь только спустя 2000 лет итальянский ученый Галилео Галилей смог исключить из формулировки Аристотеля слово «всегда». Галилей понял, что пребывание тела в состоянии покоя не является единственным следствием отсутствия внешних сил. Тогда Галилей заявил: тело, на которое не действуют никакие силы, будет либо находиться в покое, либо двигаться равномерно прямолинейно. То есть, движение с одинаковой скоростью по прямой траектории, с точки зрения физики, равнозначно состоянию покоя. Что есть состояние покоя?В жизни этот факт наблюдать очень сложно, поскольку всегда имеет место сила трения, которая не дает предметам и вещам покидать свои места. Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой. И в самом деле, на тело действую только две силы: сила тяжести и сила реакции опоры. Но расположены они на одной прямой и направлены друг против друга. Таким образом, по принципу суперпозиции, мы имеем, что общая сила, действующая на такое тело равна нулю. Однако это идеальный случай. В жизни сила трения проявляет себя почти во всех случаях. Галилей сделал важное открытие, приравняв состояние покоя и движение с постоянной скоростью по прямой линии. Но этого было недостаточно. Оказалось, что условие это выполняется не во всех случаях. Ясность в этот вопрос внес Исаак Ньютон, обобщивший исследования Галилея и, таким образом, сформулировавший Первый Закон Ньютона. Первый закон Ньютона: формулируем самиСуществуют две формулировки первого закона Ньютона современная и формулировка самого Исаака Ньютона. В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон. Современная формулировка звучит следующим образом: «Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго». Инерциальные системы отсчетаИнерциальными называют системы отсчета, в которых выполняется закон инерции. Закон же инерции заключается в том, что тела сохраняют свою скорость неизменной, если на них не действуют другие тела. Получается очень неудобоваримо, малопонятно и напоминает комичную ситуацию, когда на вопрос: “Где это «тут»?” отвечают: “Это здесь”, а на следующий логичный вопрос: “А где это «здесь»?” отвечают: “Это тут”. Масло масляное. Замкнутый круг. Формулировка самого Ньютона такова: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Однако на практике этот закон выполняется не всегда. Убедиться в этом можно элементарно. Когда человек стоит, не держась за поручни, в движущемся автобусе, и автобус резко тормозит, то человек начинает двигаться вперед относительно автобуса, хотя его не понуждает к этому ни одна видимая сила. То есть, относительно автобуса первый закон Ньютона в изначальной формулировке не выполняется. Очевидно, что он нуждается в уточнении. Уточнением и является введение инерциальных систем отсчета. То есть, таких систем отсчета, в которых первый закон Ньютона выполняется. Это не совсем понятно, поэтому попробуем перевести все это на человеческий язык. Инерциальные и неинерциальные системы отсчетаСвойство инерции любого тела таково, что до тех пор, пока тело остается изолированным от других тел, оно будет сохранять свое состояние покоя или равномерного прямолинейного движения. «Изолированным» — это значит никак не связанным, бесконечно удаленным от других тел. На практике это означает, что если в нашем примере за систему отсчета принять не автобус, а какую-то звезду на окраине Галактики, то первый закон Ньютона будет абсолютно точно выполняться для беспечного пассажира, не держащегося за поручни. При торможении автобуса он будет продолжать свое равномерное движение, пока на него не подействуют другие тела. Вот такие системы отсчета, которые никак не связаны с рассматриваемым телом, и которые никак не влияют на инертность тела, называются инерциальными. Для таких систем отсчета первый закон Ньютона в его исходной формулировке абсолютно справедлив. То есть закон можно сформулировать так: в системах отсчета, абсолютно никак не связанных с телом, скорость тела при отсутствии стороннего воздействия остается неизменной. В таком виде первый закон Ньютона легко доступен для понимания. Проблема заключается в том, что на практике очень сложно рассматривать движение конкретного тела относительно таких систем отсчета. Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле. Поэтому за такую систему отсчета условно часто принимают Землю, хотя она и связана с находящимися на ней телами и влияет на характеристики их движения. Но для многих расчетов такое приближение оказывается достаточным. Поэтому примерами инерциальных систем отсчета можно считать Землю для расположенных на ней тел, Солнечную систему для ее планет и так далее. Первый закон Ньютона не описывается какой-либо физической формулой, однако с помощью него выводятся другие понятия и определения. По сути, этот закон постулирует инертность тел. И таким образом выходит, что для инерциальных систем отсчета закон инерции и есть первый закон Ньютона. Еще примеры инерциальных систем и первого закона НьютонаТак, например, если тележка с шаром будет ехать сначала по ровной поверхности, с постоянной скоростью, а потом заедет на песчаную поверхность, то шар внутри тележки начнет ускоренное движение, хотя никакие силы на него не действуют (на самом деле, действуют, но их сумма равна нулю). Происходит это от того, что система отсчета (в данном случае, тележка) в момент попадания на песчаную поверхность, становится неинерциальной, то есть перестает двигаться с постоянной скоростью. Первый Закон Ньютона вносит важное разграничение между инерциальными и неинерциальными системами отсчета. Также важным следствием этого закона является тот факт, что ускорение, в некотором смысле, важнее скорости тела. Поскольку движение с постоянной скоростью по прямой линии суть нахождение в состоянии покоя. Тогда как движение с ускорением явно свидетельствуют о том, что либо сумма сил, приложенных к телу, не равно нулю, либо сама система отсчета, в которой находится тело, является неинерциальной, то есть движется с ускорением. Причем ускорение может быть как положительным (тело ускоряется), так и отрицательным (тело замедляется).
Второй закон Ньютона связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать. Элементарный опыт по второму закону НьютонаНачнем с практической части. Нагрузите чем-нибудь две сумки или два пакета. Один чуть-чуть, а второй очень сильно. Только пакеты берите покрепче. А теперь примерно с одинаковой силой по очереди резко поднимите оба пакета вверх. Вы увидите, что легкий пакет практически взлетит, а вот тяжелый перемещаться будет намного медленнее. А теперь другой опыт положите на землю футбольный мячик и пните его пару раз. Один раз легонько, а второй раз со всей силы. Понаблюдайте, как изменится скорость мяча после пинка. В первом случае он потихоньку откатится на небольшое расстояние, во втором улетит далеко и на весьма приличной скорости. Ну вот и все, с практической частью закончили. Теперь немного порассуждаем. Действие равнодействующей силыМы знаем, что скорость тела изменяется под действием приложенной к нему силы. Если на тело действуют несколько сил, то находят равнодействующую этих сил, то есть некую общую суммарную силу, обладающую определенным направлением и числовым значением. То есть, фактически, все случаи приложения различных сил в конкретный момент времени можно свести к действию одной равнодействующей силы. Таким образом, чтобы найти, как изменилась скорость тела, нам надо знать, какая сила действует на тело. Какое ускорение получает тело?В зависимости от величины и направления силы тело получит то или иное ускорение. Это четко видно в опыте с мячом. Когда мы подействовали на тело небольшой силой, мяч ускорился не очень сильно. Когда же сила воздействия увеличилась, то мяч приобрел гораздо большее ускорение. То есть, ускорение связано с приложенной силой прямо пропорционально. Чем больше сила воздействия, тем большее ускорение приобретает тело. От чего еще зависит ускорение, полученное телом в результате воздействия на него? Вспомним первую часть нашего опыта. Ускорение двух грузов у нас было ощутимо разным, хотя силу мы старались прикладывать одинаковую. А вот масса грузов у нас отличалась. И в случае с большей массой ускорение тела было небольшим, а в случае меньшей массы намного большим. То есть, второй вывод это то, что масса тела напрямую связана с ускорением, приобретаемым телом в результате воздействия силы. При этом, масса тела обратно пропорциональна полученному ускорению. Чем больше масса, тем меньше будет величина ускорения. Второй Закон Ньютона: формула и определениеИсходя из всего вышесказанного, приходим к тому, что можно записать второй закон Ньютона в виде следующей формулы: a =F / m , где a ускорение, F сила воздействия, m масса тела. Соответственно, второму закону Ньютона можно дать такое определение: ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела. Это и есть второй закон Ньютона.
В первом законе Ньютона говорится о поведении тела, изолированного от воздействия других тел. Второй закон говорит о прямо противоположной ситуации. В нем рассматриваются случаи, когда тело или несколько тел воздействуют на данное. Оба эти закона описывают поведение одного конкретного тела. Но во взаимодействии всегда участвуют минимум два тела. Что будет происходить с обоими этими телами? Как описать их взаимодействие? Анализом этой ситуации и занялся Ньютон после формулировки своих первых двух законов. Займемся и мы такими же изысканиями. Взаимодействие двух телМы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы. Такое может происходить среди по-разному воспитанных людей, но никак не в природе. Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо. Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие. Фактически, мы каждый день по многу раз пинаем очень и очень тяжелый мяч нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе. Соотношение сил во взаимодействии между теламиТак что из этих рассуждений видно, что при взаимодействии двух тел, не только первое действует на второе с некоторой силой, но и второе в ответ действует на первое также с некоторой силой. Возникает вопрос: а как соотносятся эти силы? Какая из них больше, какая меньше? Для этого необходимо проделать некоторые измерения. Потребуются два динамометра, но в домашних условиях их вполне могу заменить два безмена. Они измеряют вес, а вес это тоже сила, только выраженная в единицах массы в случае безмена. Поэтому, если у вас есть два безмена, то проделайте следующее. Один из них оденьте колечком на что-то неподвижное, например, на гвоздь в стене, а второй соедините с первым крючками. И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен. И хотя мы тянем только за один из них, окажется, что показания обоих, как на очной ставке, будут совпадать. Получается, что сила, с которой мы воздействуем вторым безменом на первый, равна силе, с которой первый безмен воздействует на второй. Третий закон Ньютона: определение и формулаСила действия равна силе противодействия. В этом и состоит суть третьего закона Ньютона. Определение его таково: силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. Третий закон Ньютона можно записать в виде формулы: F_1 = — F_2, Где F_1 и F_2 силы действия друг на друга соответственно первого и второго тела. Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.
Как вы думаете, одновременно ли долетят до земли, сброшенные с крыши перо, пластиковая бутылка и монета? Можно проделать такой опыт и убедиться, что монета приземлится первой, бутылка второй, а перо долго будет болтаться в воздухе и может вообще не долететь до земли, если его подхватит и унесет внезапный ветерок. Так ли свободно свободное падение тел?Соответственно, делаем вывод, что свободное падение тел не подчиняется какому-либо одному правилу, и все предметы падают на землю по-своему. Тут бы как говорится, и сказке конец, но некоторые физики на этом не успокоились и предположили, что на свободное падение тел может оказывать влияние сила сопротивления воздуха и, соответственно, такие результаты эксперимента нельзя считать окончательными. Они взяли длинную стеклянную трубку и поместили в нее перо, дробинку, деревянную пробку и монету. Потом они закупорили трубку, откачали из нее воздух и перевернули.2)/2 (если v_0 = 0), соответственно, где v конечная скорость, v_0 начальная скорость, s перемещение, t время, g ускорение свободного падения. Вывод, что свободное падение любых тел происходит одинаково, на первый взгляд кажется нелепым с точки зрения повседневного опыта. Но на самом деле все правильно и логично. Просто, незначительная на первый взгляд величина сопротивления воздуха для многих падающих тел оказывается довольно ощутимой, а потому очень сильно замедляет их падение.
Как нам уже известно, сила тяжести действует на все тела, которые находятся на поверхности Земли и вблизи неё. При этом не важно, находятся ли они в состоянии покоя или совершают движение. Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой. Суть движения вертикально вверхЕсли же подбросить некоторое тело вертикально вверх, и при этом считать что сопротивление воздуха отсутствует, то можно считать что оно тоже совершает равноускоренное движение, с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться. Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Как решать задачиКогда вы столкнетесь с задачами на движение тела вверх, при котором не учитывается сопротивление воздуха и другие силы, а считается, что на тело действует только сила тяжести, то так как движение равноускоренное, то можно применять те же самые формулы, что и при прямолинейном равноускоренном движении с некоторой начальной скорость V0.2)/2. Необходимо также учитывать, что при движении вверх вектор ускорения свободного падения направлен вниз, а вектор скорости вверх, то есть они разнонаправлены, а следовательно, их проекции будут иметь разные знаки. Например, если Ось Ох направить вверх, то проекция вектора скорости при движении вверх, будет положительна, а проекция ускорения свободного падения отрицательна. Это надо учитывать, подставляя значения в формулы, иначе получится совершенно неверный результат.
Все мы ходим по Земле потому, что она нас притягивает. Если бы Земля не притягивала все находящиеся на ее поверхности тела, то мы, оттолкнувшись от нее, улетели бы в космос. Но этого не происходит, и всем известно о существовании земного притяжения. Притягиваем ли мы Землю? Притягивает Луна!А притягиваем ли мы сами к себе Землю? Смешной вопрос, правда? Но давайте разберемся. Вы знаете, что такое приливы и отливы в морях и океанах? Каждый день вода уходит от берегов, неизвестно где шляется несколько часов, а потом, как ни в чем не бывало, возвращается обратно. Так вот вода в это время находится не неизвестно где, а примерно посредине океана. Там образуется что-то наподобие горы из воды. Невероятно, правда? Вода, которая имеет свойство растекаться, сама не просто стекается, а еще и образует горы. И в этих горах сосредоточена огромная масса воды. Просто прикиньте весь объем воды, который отходит от берегов во время отливов, и вы поймете, что речь идет о гигантских количествах. Но раз такое происходит, должна же быть какая-то причина. И причина есть. Причина кроется в том, что эту воду притягивает к себе Луна. Вращаясь вокруг Земли, Луна проходит над океанами и притягивает к себе океанические воды. Луна вращается вокруг Земли, потому что она притягивается Землей. Но, выходит, что она и сама при этом притягивает к себе Землю. Земля, правда, для нее великовата, но ее влияние оказывается достаточным для перемещения воды в океанах. Сила и закон всемирного тяготения: понятие и формулаА теперь пойдем дальше и подумаем: если два громадных тела, находясь неподалеку, оба притягивают друг друга, не логично ли предположить, что и тела поменьше тоже будут притягивать друг друга? Просто они намного меньше и сила их притяжения будет маленькой? Оказывается, что такое предположение абсолютно верно.2 . Возвращаясь к нашему исходному вопросу: «притягиваем ли мы Землю?», мы можем с уверенностью ответить: «да». Согласно третьему закону Ньютона мы притягиваем Землю ровно с такой же силой, с какой Земля притягивает нас. Силу эту можно рассчитать из закона всемирного тяготения. А согласно второму закону Ньютона воздействие тел друг на друга какой-либо силой выражается в виде придаваемого ими друг другу ускорения. Но придаваемое ускорение зависит от массы тела. Масса Земли велика, и она придает нам ускорение свободного падения. А наша масса ничтожно мала по сравнению с Землей, и поэтому ускорение, которое мы придаем Земле, практически равно нулю. Именно поэтому мы притягиваемся к Земле и ходим по ней, а не наоборот.
Одним из частных случаев всемирного тяготения является тот факт, что все тела притягиваются к Земле. Для нас, жителей планеты Земля, сила тяжести имеет огромное значение. Сила, с которой тело некоторой массы m будет притягиваться к Земле, согласно закону всемирного тяготения будет вычисляться по следующей формуле: Где Мз — масса земли, Но значение этой силы будет отличаться от значения силы тяжести которую мы вычисляем по формуле Fт =m*g.2). Отсюда можно выразить значение g. Как видите масса тела сократилась, а следовательно масса тела никак не влияет на ускорение свободного падения тел, которые находятся на Земле или вблизи её поверхности. А будет зависеть только от радиуса Земли, а точнее от расстояния от центра Земли, до центра данного тела массы m. Если мы например поднимем тело на некоторую высоту h, то расстояние между центрами Земли и тела увеличится, а следовательно должно измениться ускорение свободного падения тела. Так как расстояние в таком случае будет (Rз+h), то ускорение свободного падения на высоте h от поверхности Земли можно вычислить по формуле: Чем больше мы поднимем тело над Землей, тем будет меньше ускорение свободного падения. Следовательно, будет уменьшатся и сила тяжести которая действует на это тело. Чаще всего этим увеличением пренебрегают, так как расстояние, на которое поднимается тело от поверхности Земли, по сравнению с радиусом Земли пренебрежимо мало. Например, если человек массой 80 кг поднялся на гору высотой 3 км, то действующая на него сила тяжести уменишилась всего на 0.7 Н. Это очень мало, поэтому в таких случаях при расчетах берут вблизи поверхности земли значение ускорения свободного падения g=9,81. Применение формулы для других небесных телФормула, которую мы записали выше, подходит также для вычисления ускорения свободного падения на любых небесных объектах. То есть вместо радиуса и массы Земли необходимо подставить радиус и массу данного небесного объекта.
Мы знаем, что все тела притягиваются друг к другу. В частности, Луна, например, притягивается к Земле. Но возникает вопрос: если Луна притягивается к Земле, почему она вращается вокруг нее, а не падает на Землю? Для того чтобы ответить на этот вопрос, необходимо рассмотреть виды движения тел. Мы уже знаем, что движение может быть равномерным и неравномерным, но существуют и другие характеристики движения. В частности, в зависимости от направления различают прямолинейное и криволинейное движение. Прямолинейное движениеИзвестно, что тело двигается под действием приложенной к нему силы. Можно проделать несложный эксперимент, показывающий, как направление движения тела будет зависеть от направления приложенной к нему силы. Для этого потребуется произвольный предмет небольшого размера, резиновый шнур и горизонтальная или вертикальная опора. Привязывает шнур одним концом к опоре. На другом конце шнура закрепляем наш предмет. Теперь, если мы оттянем наш предмет на некоторое расстояние, а потом отпустим, то увидим, как он начнет двигаться в направлении опоры. Его движение обусловлено силой упругости шнура. Именно так Земля притягивает все тела на ее поверхности, а также летящие из космоса метеориты. Только вместо силы упругости выступает сила притяжения. А теперь возьмем наш предмет на резинке и толкнем его не в направлении к/от опоры, а вдоль нее. Если бы предмет не был закреплен, он бы просто улетел в сторону. Но так как его держит шнур, то шарик, двигаясь в сторону, слегка растягивает шнур, тот тянет его обратно, и шарик чуть меняет свое направление в сторону опоры. Криволинейное движение по окружностиТак происходит в каждый момент времени, в итоге шарик движется не по первоначальной траектории, но и не прямолинейно к опоре. Шарик будет двигаться вокруг опоры по окружности. Траектория его движения будет криволинейной. Именно так вокруг Земли двигается Луна, не падая на нее. Именно так притяжение Земли захватывает метеориты, которые летят близко от Земли, но не прямо на нее. Эти метеориты становятся спутниками Земли. При этом от того, каким был их первоначальный угол движения по отношению к Земле, зависит, как долго они пробудут на орбите. Если их движение было перпендикулярно Земле, то они могут находиться на орбите бесконечно долго. Если же угол был меньше 90˚, то они будут двигаться по снижающейся спирали, и постепенно все-таки упадут на землю. Движение по окружности с постоянной по модулю скоростьюЕще один момент, который следует отметить, это то, что скорость криволинейного движения по окружности меняется по направлению, но одинакова по значению. А это означает, что движение по окружности с постоянной по модулю скоростью происходит равноускорено. Так как направление движения меняется, значит, движение происходит с ускорением. А так как оно меняется одинаково в каждый момент времени, следовательно, движение будет равноускоренным. А сила притяжения является силой, которая обусловливает постоянное ускорение. Луна двигается вокруг Земли именно благодаря этому, но если вдруг когда-либо движение Луны изменится, например, в нее врежется очень крупный метеорит, то она вполне может сойти со своей орбиты и упасть на Землю. Нам остается лишь надеяться, что этот момент не наступит никогда.
Вы когда-нибудь соревновались, кто дальше кинет камень или снежок? Все мальчишки наверняка проходили через это. И все знают, что чтобы камень пролетел как можно дальше, надо кинуть его как можно сильнее. То есть нужно придать ему как можно большую скорость. Сила человеческой руки ограничена, и камень мы можем кинуть относительно недалеко. Намного большую скорость телам могут придать различные артиллерийские орудия. Снаряды могут преодолевать несколько километров и даже десятков километров. Однако всегда траекторией всех этих летящих тел является дуга, концом упирающаяся в землю. Бексонечно долгое вращение вокруг ЗемлиЕсли же пойти дальше и предположить, что мы можем придать телу намного большую скорость? Такую, что дуга, которую тело опишет, будет уже не упираться в землю, а проходить на некотором расстоянии вокруг всей Земли? Тогда получится, что мы получим тело, способное бесконечно долго вращаться вокруг Земли. Единственное, что будет мешать нам это сопротивление воздуха. Значит надо избавиться от него. Избавиться от сопротивления воздуха мы можем на большой высоте. На высоте свыше трехсот километров воздуха уже практически нет. Именно начиная с такой высоты, и запускают искусственные спутники Земли. Спутники вращаются вокруг Земли по различным орбитам, но все они не падают на Землю. Движение спутника — пример свободного паденияЭто происходит потому, что запущены они были со скоростью, достаточной для того, чтобы преодолеть земное притяжение. Как ни странно звучит, движение спутника вокруг Земли это пример свободного падения тела. Происходит оно с ускорением, как и положено свободно падающему телу, только ускорение это не увеличивает скорость тела по модулю, а изменяет по направлению. Поэтому спутники и движутся по орбите. Первая и вторая космическая скоростьСкорость, необходимая для того, чтобы тело начало вращаться по орбите вокруг Земли не падая, называется первой космической скоростью. Она составляет от 7,9 км/с. Чем больше высота тела над землей, тем величина этой скорости меньше. На высоте, например, 500 км эта скорость составляет уже 7,6 км/с. Это объясняется тем, что гравитационные силы уменьшаются с увеличением расстояния между телами. Первой космической скоростью обусловлено движение искусственных спутников земли. А есть ли такая скорость, которая позволит совсем вырваться из оков земного притяжения? Такая скорость есть и называется она второй космической скоростью. Она составляет 11,2 км/с. При такой скорости тела описывают вокруг Земли не дугу, а эллипс, и тело удаляется на расстояние, достаточное для полного освобождения от земного притяжения. Такую скорость развивают ракеты, которые уходят в космическое пространство прочь от Земли.
Проделаем несколько несложных преобразований с формулами. По второму закону Ньютона силу можно найти: F=m*a. Ускорение находится следующим образом: a=v⁄t . Таким образом получаем: F=m*v/t. Определение импульса тела: формулаВыходит, что сила характеризуется изменением произведения массы на скорость во времени. Если обозначить это произведение некой величиной, то мы получим изменение этой величины во времени как характеристику силы. Эту величину назвали импульсом тела. Импульс тела выражается формулой: p=m*v , где p импульс тела, m масса, v скорость. Импульс это векторная величина, при этом его направление всегда совпадает с направлением скорости. Единицей импульса является килограмм на метр в секунду (1 кг*м/с). Что же такое импульс тела: как понять?Попробуем по-простому, «на пальцах» разобраться, что такое импульс тела. Если тело покоится, то его импульс равен нулю. Логично. Если скорость тела изменяется, то у тела появляется некий импульс, который характеризует величину приложенной к нему силы. Если воздействие на тело отсутствует, но оно движется с некоторой скоростью, то есть имеет некий импульс, то его импульс означает, какое воздействие способно оказать данное тело при взаимодействии с другим телом. В формулу импульса входит масса тела и его скорость. То есть чем большей массой и/или скоростью обладает тело, тем большее воздействие оно может оказать. Это понятно и из жизненного опыта. Чтобы сдвинуть тело небольшой массы, нужна небольшая сила. Чем больше масса тела, тем большее придется приложить усилие. То же самое касается и скорости, которую сообщают телу. В случае же воздействия самого тела на другое, импульс также показывает величину, с которой тело способно действовать на другие тела. Эта величина напрямую зависит от скорости и массы исходного тела. Импульс при взаимодействии телВозникает еще один вопрос: что произойдет с импульсом тела при его взаимодействии с другим телом? Масса тела измениться не может, если оно остается целым, а вот скорость может измениться запросто. При этом скорость тела изменится в зависимости от его массы. В самом деле, понятно, что при столкновении тел с очень разными массами, скорость их изменится по-разному. Если летящий на большой скорости футбольный мяч врежется в неготового к этому человека, например зрителя, то зритель может упасть, то есть приобретет некоторую небольшую скорость, но точно не полетит как мячик. А все потому, что масса зрителя намного больше массы мяча. Но при этом сохранится неизменным общий импульс этих двух тел. Закон сохранения импульса: формулаВ этом и заключается закон сохранения импульса: при взаимодействии двух тел их общий импульс остается неизменным. Закон сохранения импульса действует только в замкнутой системе, то есть в такой системе, в которой нет воздействия внешних сил или их суммарное действие равно нулю. В реальности практически всегда на систему тел оказывается стороннее воздействие, но общий импульс, как и энергия, не пропадает в никуда и не возникает из ниоткуда, он распределяется между всеми участниками взаимодействия. Закон сохранения импульса для двух тел в виде формулы будет выглядеть следующим образом: (p_1′ ) +(p_2′ ) = (p_1 ) + (p_2 ), где левая часть уравнения это сумма импульсов тел после взаимодействия, а правая часть после взаимодействия. Уравнение говорит нам, что общий импульс (сумма импульсов) остается неизменнным.
Реактивное движение — это все же движение. А мы знаем, что чтобы происходило движение, необходимо воздействие некоторой силы. Тело либо само должно оттолкнуться от чего-нибудь, либо стороннее тело должно толкнуть данное. Это хорошо известно и понятно нам из жизненного опыта. От чего оттолкнуться в космосе?У поверхности Земли можно оттолкнуться от поверхности либо от находящихся на ней предметов. Для передвижения по поверхности используют ноги, колеса, гусеницы и так далее. В воде и воздухе можно отталкиваться от самих воды и воздуха, имеющих определенную плотность, и потому позволяющих взаимодействовать с ними. Природа для этого приспособила плавники и крылья. Человек создал двигатели на основе пропеллеров, которые во много раз увеличивают площадь контакта со средой за счет вращения и позволяют отталкиваться от воды и воздуха. А как быть в случае безвоздушного пространства? От чего отталкиваться в космосе? Там нет воздуха, там ничего нет. Как осуществлять полеты в космосе? Вот тут-то и приходит на помощь закон сохранения импульса и принцип реактивного движения. Разберем подробнее. Импульс и принцип реактивного движенияИмпульс это произведение массы тела на его скорость. Когда тело неподвижно, его скорость равна нулю. Однако тело обладает некоторой массой. При отсутствии сторонних воздействий, если часть массы отделится от тела с некоторой скоростью, то по закону сохранения импульса, остальная часть тела тоже должна приобрести некоторую скорость, чтобы суммарный импульс остался по-прежнему равным нулю. Причем скорость оставшейся основной части тела будет зависеть от того, с какой скоростью отделится меньшая часть. Чем эта скорость будет выше, тем выше будет и скорость основного тела. Это понятно, если вспомнить поведение тел на льду или в воде. Если два человека будут находиться рядом, а потом один из них толкнет другого, то он не только придаст тому ускорение, но и сам отлетит назад. И чем сильнее он толкнет кого-либо, тем с большей скоростью отлетит сам. Наверняка, вам приходилось бывать в подобной ситуации, и вы можете представить себе, как это происходит. Так вот, именно на этом и основано реактивное движение. Ракеты, в которых реализован этот принцип, выбрасывают некоторую часть своей массы на большой скорости, вследствие чего сами приобретают некоторое ускорение в противоположном направлении. Потоки раскаленных газов, возникающие в результате сгорания топлива, выбрасываются через узкие сопла для придания им максимально большой скорости. При этом, на величину массы этих газов уменьшается масса ракеты, и она приобретает некую скорость. Таким образом реализован принцип реактивного движения в физике. Принцип полета ракетыВ ракетах применяют многоступенчатую систему. Во время полета нижняя ступень, израсходовав весь свой запас топлива, отделяется от ракеты, чтобы уменьшить ее общую массу и облегчить полет. Количество ступеней уменьшается, пока не остается рабочая часть в виде спутника или иного космического аппарата. Топливо рассчитывают таким образом, чтобы его хватило как раз для выхода на орбиту. При посадках на космические тела рассчитывают количество топлива для посадки и на обратный путь, если он запланирован. |
Проектирование векторов на оси | LAMPA
Проектирование вектора на ось, когда задан угол между вектором и осью
Очень часто (а вернее — почти всегда) бывает так, что задан угол между вектором и осью, а также длина вектора, а на оси нет никаких обозначений координат. Тогда проекцию вектора ищут с помощью косинуса или синуса. Рассмотрим все на конкретном примере.
Пусть у нас есть вектор a⃗\vec{a}a⃗.
Из его начала проведем нужные нам оси XXX и YYY, на которые будем проектировать наш вектор.
Из конца вектора опускаем перпендикуляры на оси XXX и YYY.
Получается прямоугольник. Стороны этого прямоугольника и есть проекции вектора a⃗\vec{a}a⃗: axa_{x}ax и aya_{y}ay.
Видно, что у нас получился прямоугольный треугольник.
Его стороны как раз проекции нашего вектора. Наверняка вы помните (а тем, кто не помнит, я напоминаю), что в прямоугольном треугольнике
cosα=прилежащий катетгипотенуза\cos \alpha=\frac{\text{прилежащий катет}}{\text{гипотенуза}}cosα=гипотенузаприлежащий катет
sinα=противолежащий катетгипотенуза\sin \alpha=\frac{\text{противолежащий катет}}{\text{гипотенуза}}sinα=гипотенузапротиволежащий катет.
В нашем треугольнике то же самое:
cosα=axa\cos \alpha=\frac{a_{x}}{a}cosα=aax
sinα=aya\sin \alpha = \frac{a_{y}}{a}sinα=aay.
Или:
ax=a⋅cosαa_{x}=a\cdot \cos \alphaax=a⋅cosα;
ay=a⋅sinαa_{y}=a\cdot \sin \alphaay=a⋅sinα.
Итак:
Проекция на прилежащую ось — это умножение на косинус.
Проекция на противолежащую ось — это умножение на синус.
Что такое проекция скорости на ось х. Прямолинейное равномерное движение
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: v cp = v Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:
V x = v, то есть v > 0 Проекция перемещения на ось ОХ равна: s = vt = x – x 0 где x 0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения , то есть зависимость координаты тела от времени х = х(t), принимает вид:
Х = x 0 + vt Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v х = x 0 — vt
Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна
V = s 1 / t 1 = tg α где α – угол наклона графика к оси времени. Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости: tg α = v
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
Tg α 1 > tg α 2 следовательно, скорость тела 1 выше скорости тела 2 (v 1 > v 2). tg α 3 = v 3 Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х 0
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот.
Возьмем следующее координатное уравнение: x = x(t), y = y(t), z = z(t). В данном случае функция скорости будет спроецирована на три оси и будет иметь следующий вид: V(x) = dx / dt = x»(t), V(y) = dy / dt = y»(t), V(z) = dz / dt = z»(t). Отсюда следует, что для нахождения скорости необходимо брать производные. Сам же вектор скорости выражается уравнением такого вида: V = V(x) i + V(y) j + V(z) k. Здесь i, j, k являются единичными векторами координатных осей x, y, z соответственно. 2).
Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.
Векторы начальной скорости и ускорениямогут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.
Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.
График скорости
Из уравнения
следует, что графиком зависимости
проекции скорости равноускоренного
движения от времени является прямая.
Если проекция начальной скорости на
ось OX равна нулю, то прямая проходит
через начало координат.
Основные виды движения
а n = 0, a = 0 – прямолинейное равномерное движение;
а n = 0, a = const – прямолинейное равнопеременное движение;
а n = 0, a 0 – прямолинейное с переменным ускорением;
а n = const , a = 0 – равномерное по окружности
а n = const , a = const – равнопеременное по окружности
а n const , a const – криволинейное с переменным ускорением.
Вращательное движение твердого тела.
Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Равномерное движение по окружности
Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.
При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения.
Из подобия треугольников OAB и BCD следует
Если интервал
времени ∆t
мал, то мал и угол .
При малых значениях угла
длина хорды AB примерно равна длине дуги
AB, т.е.
.
Т.к.
,
,
то получаем
.
Поскольку
,
то получаем
Период и частота
Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодам обращения (Т ). Т.к. длина окружности равна 2 R , период обращения при равномерном движении тела со скоростью v по окружности радиусом R равняется:
Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:
(с -1)
Определение
Равномерное прямолинейное движение — это движение с постоянной скоростью, при котором ускорение отсутствует, а траектория движения представляет собой прямую линию.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: $\left\langle v\right\rangle =v$
Определение
Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела $\overrightarrow{S}$ за любой промежуток времени к значению этого промежутка t:
$$\overrightarrow{v}=\frac{\overrightarrow{S}}{t}$$
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
$$ \overrightarrow{S} = \overrightarrow{v} \cdot t $$
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: $v_x = v$, то есть $v $>$ 0$
Проекция перемещения на ось ОХ равна: $s = v_t = x — x0$
где $x_0$ — начальная координата тела, $х$ — конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени $х = х(t)$, принимает вид: $х = x_0 + v_t$
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля ($v $
Зависимость проекции скорости тела от времени показана на рис. 1. Так как скорость постоянна ($v = const$), то графиком скорости является прямая линия, параллельная оси времени Ot.
Рис. 1. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 2), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Рис. 2. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 3. Из графика видно, что проекция скорости на ось Ot численно равна тангенсу угла наклона графика к оси времени:
Рис. 3. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 4. Из рисунка видно, что
tg $\alpha $1 $>$ tg $\alpha $2, следовательно, скорость тела 1 выше скорости тела 2 (v1 $>$ v2).
tg $\alpha $3 = v3 $
Рис. 4. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0
Задача 1
Два поезда движутся на встречу друг другу по параллельным рельсам. Скорость первого поезда 10 метров в секунду, длина первого поезда 500 метров. Скорость второго поезда 30 метров в секунду, длина второго поезда 300 метров. Определить в течение какого времени второй поезд будет ехать мимо первого.
Дано: $v_1$=10 м/с; $v_2$=30 м/с; $L_1$=500 м; $L_2$=300 м
Найти: t — ?
Время, в течение которого поезда будут проходить мимо друг друга, можно определить, разделив общую длину поездов на их относительную скорость. Скорость первого поезда относительно второго определяется по формуле v= v1+v2 Тогда формула для определения времени принимает вид: $t=\frac{L_1+L_2}{v_1+v_2}=\frac{500+300}{10+30}=20\ c$
Ответ: второй поезд будет ехать мимо первого в течение 20 секунд.
Задача 2
Определить скорость течения реки и скорость катера в стоячей воде, если известно, что катер проходит расстояние 300 километров по течению за 4 часа, а против течения — за 6 часов.
Дано: $L$=300000 м; $t_1$=14400 с; $t_2$=21600 с
Найти: $v_p$ — ?; $v_k$ — ?
Скорость катера по течению реки относительно берега $v_1=v_k+v_p$, а против течения $v_2=v_k-v_p$ . Запишем закон движения для обоих случаев:
Решив уравнения относительно vp и vk, получаем формулы для расчета скорости течения реки и скорости катера.
Скорость течения реки: $v_p=\frac{L\left(t_2-t_1\right)}{2t_1t_2}=\frac{300000\left(21600-14400\right)}{2\times 14400\times 21600}=3,47\ м/с$
Скорость катера: $v_к=\frac{L\left(t_2+t_1\right)}{2t_1t_2}=\frac{300000\left(21600+14400\right)}{2\times 14400\times 21600}=17,36\ м/с$
Ответ: скорость течения реки равна 3,47 метров в секунду, скорость катера равна 17,36 метров в секунду.
Скорость является одной из основных характеристик . Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с .
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
Отрицательная скорость
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
ОПРЕДЕЛЕНИЕ
Равномерное движение – это движение с постоянной по модулю скоростью.
В случае неравномерного движения говорят о :
Примеры решения задач по теме «Скорость»
ПРИМЕР 1
| Задание | Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля. |
| Решение | Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. Воспользуемся определением средней скорости: Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить. Время, потраченное автомобилем на прохождение всего отрезка пути: где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути. Суммарное перемещение равно расстоянию между населенными пунктами, т.е. . Подставив эти соотношения в формулу для средней скорости, получим: Переведем скорости на отдельных участках в систему СИ: Тогда средняя скорость автомобиля: (м/с) |
| Ответ | Средняя скорость автомобиля равна 18,8 м/с |
ПРИМЕР 2
| Задание | Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля. |
| Решение | Сделаем рисунок. |
1. График зависимости скорости от времени при прямолинейном движении с постоянным ускорением
Самое простое из всех неравномерных движений — это прямолинейное движение с постоянным ускорением.
При движении с постоянным ускорением (a→=const→) скорость тела линейно зависит от времени:
v→=v→o+a→t.
В проекциях на ось \(Ox\) данные равенства имеют вид:
ax=const;
vx=vox+axt.
Построим графики зависимостей axt и vxt для случаев ax>0 и ax<0.
Примем vox>0.
Поскольку в обоих случаях ax=const, то графиком зависимости axt ускорения от времени в обоих случаях будет прямая, параллельная оси времени.
Только при ax>0 данная прямая будет лежать в верхней полуплоскости (рис. \(1\)), а при ax<0 — в нижней (рис. \(2\)).
Рис. \(1\)
Рис. \(2\)
Графиком зависимости скорости движения тела от времени vxt является прямая, пересекающая ось скорости в точке v0 и образующая с положительным направлением оси времени острый угол при ax>0 (рис. \(3\)) и тупой угол при ax<0 (рис. \(4\)).
Рис. \(3\)
Рис. \(4\)
График на рисунке \(3\) описывает возрастание проекции скорости vx. При этом модуль скорости тела также растёт. Данный график соответствует равноускоренному движению тела.
График на рисунке \(4\) показывает, что проекция vx скорости тела вначале положительна.
Она уменьшается и в момент времени t=tп становится равной нулю.
В этот момент тело достигает точки поворота, в которой направление скорости тела меняется на противоположное, и при t>tп проекция скорости становится отрицательной.
Из последнего графика также видно, что до момента поворота модуль скорости уменьшался — тело двигалось равнозамедленно.
При t>tп модуль скорости растёт — тело движется равноускоренно.
Для любого равнопеременного прямолинейного движения площадь фигуры между графиком vx и осью времени \(t\) численно равна проекции перемещения Δrx.
Рис. \(5\)
Согласно данному правилу, проекция перемещения Δrx при равнопеременном движении определяется площадью трапеции \(ABCD\) (рис. \(5\)). Эта площадь равна полусумме оснований трапеции, умноженной на её высоту:
S=AB+DC2⋅AD.
В результате:
Δrx=vox+vx2⋅Δt.
Из данной формулы получим формулу для среднего значения проекции скорости:
vxср=ΔrxΔt=vox+vx2.
При движении с постоянным ускорением данное отношение выполняется не только для проекций, но и для векторов скорости:
vcp→=vo→+v→2.
Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.
Снаряд Движение Спорт Наука Степень физического воспитания
Q4 E Пример 15 — Движение снаряда
Предлагаемое использование темы:
Математика / физика (уровень A / AS), спортивные науки (степень 1/2)
Введение
Снаряд — это тело, падающее в свободном падении, на которое действуют только силы тяжести (9,81 мс²) и сопротивление воздуха. Объект должен быть сброшен с высоты, брошен вертикально вверх или под углом, чтобы считаться снарядом.Путь, по которому летит снаряд, известен как траектория. Если бы гравитации не было, снаряд летел бы по постоянной прямой. Однако наличие силы тяжести вынуждает снаряды двигаться по параболической траектории, таким образом, сила тяжести ускоряет объекты вниз.
Факторы, влияющие на траекторию:
a) Угол проекции
b) Скорость проекции
c) Относительная высота проекции
Для анализа движения снаряда оно делится на два компонента: горизонтальное движение и вертикальное движение.Перпендикулярные компоненты движения независимы друг от друга, т.е. горизонтальное и вертикальное движения снаряда независимы. Горизонтальное движение объекта не имеет внешних сил, действующих на него (за исключением сопротивления воздуха, которое обычно не учитывается). Из-за отсутствия горизонтальных сил снаряд остается в движении с постоянной горизонтальной скоростью, преодолевая равные расстояния за равные периоды времени. Таким образом, горизонтального ускорения не происходит. Однако степень вертикальной скорости уменьшается под действием силы тяжести.Сила тяжести действует на начальную вертикальную скорость копья, уменьшая скорость до нуля. Вертикальная скорость, равная нулю, представляет собой вершину траектории, что означает, что снаряд достиг максимальной высоты. Во время полета снаряда вниз вертикальная скорость увеличивается за счет действия силы тяжести.
Начальная скорость (Vi) снаряда, выпущенного под углом к горизонтали, имеет как горизонтальную (Vh), так и вертикальную (Vv) составляющие.При расчете горизонтального движения ускорение принимается равным 0 мс², поскольку в горизонтальном направлении нет сил. Таким образом, отсутствие ускорения означает, что начальная горизонтальная скорость и конечная горизонтальная скорость одинаковы. Ускорение при вертикальном движении составляет 9,81 мс², поскольку сила тяжести является единственной силой в вертикальном направлении. Это значение является постоянным независимо от веса, размера и т. Д. Проецируемого объекта. Если объект выпущен и приземляется на одной и той же высоте, то начальная скорость и конечная скорость будут одинаковыми, с той лишь разницей, что конечная скорость будет в противоположном направлении.Пиковая высота, достигаемая объектом, может быть найдена, если принять высоту пика как конечную скорость, которая равна 0 мс‾¹, так как, когда объект достигает своей максимальной высоты, вертикальная скорость равна 0 мс. Если объект падает с высоты, начальная скорость (u) равна 0 мс‾¹, и по ней может быть рассчитана конечная скорость.
Законы постоянного ускорения можно использовать для определения горизонтальной и вертикальной составляющих снаряда. Эти уравнения могут применяться только к горизонтальному и вертикальному движениям снаряда — они не могут применяться к результирующему движению.Используются три уравнения:
- v = u + при
- v² = u² + 2as
- с = ut + ½at²
Где:
u = начальная скорость (мс‾¹)
v = конечная скорость (мс‾¹)
a = ускорение (мс‾²)
t = время (с)
с = смещение (м)
Объективы
- Для сравнения движения снаряда при пяти различных метаниях копья с помощью программного обеспечения Quintic.
- Для расчета пройденного расстояния, начальной скорости и угла выброса копья
Методы
Видео были откалиброваны и оцифрованы с помощью программного обеспечения Quintic.
Данные были экспортированы в файл Excel, где они использовались для расчета всех переменных метания копья. Графики были составлены с использованием этой информации. Неподвижные изображения были взяты из видео, чтобы обозначить различные этапы упражнения.
Используемые функции программного обеспечения Quintic:
- Модуль одноточечной оцифровки
- Фильтр Баттерворта
- Калибровка
- Интерактивный график и дисплеи данных
- Экспорт данных
- Захват нескольких изображений
Результаты
Каждый из метаний копья был проанализирован с использованием одноточечной оцифровки.Каждый кадр с момента выпуска до конца ролика был оцифрован. Используя результаты оцифровки, были рассчитаны такие значения, как расстояние броска, время броска и максимальная высота, достигнутая копьем.
Рисунок 1: Последовательность нескольких изображений метания Javelin |
Таблица 1: Результаты пяти метаний копья
График 1: Начальная скорость метания копья
График 1 показывает начальные скорости всех бросков.Начальная скорость метания копья определяет высоту и длину траектории, при условии, что все остальные факторы остаются постоянными. Бросок 2 имел самую высокую начальную среднюю скорость 28,13 мс, а остальные имели несколько более низкие средние значения 21,48 мс, 19,70 мс, 22,11 мс и 20,87 мс для бросков 1-5 соответственно.
Зная начальное значение скорости, можно определить горизонтальное и вертикальное значения. Горизонтальная скорость копья остается постоянной в течение всего времени полета из-за отсутствия внешних сил, действующих на горизонтальное движение.С другой стороны, вертикальная скорость постоянно меняется из-за силы тяжести. Таблица 1 показывает, что для всех бросков конечная вертикальная скорость больше начальной и имеет отрицательное значение. Это происходит из-за того, что копье выпущено с высоты. Если объект проецируется и приземляется на одной и той же высоте, то начальная скорость и конечная скорость совпадают. Однако, если объект проецируется с высоты и приземляется ниже этой высоты, конечная скорость будет больше начальной скорости и в противоположном направлении.Все броски имеют отрицательную конечную скорость, так как все копья выпущены с высоты. Бросок 2 имеет большую конечную вертикальную скорость, чем остальные, -19,55 мс‾¹. Это связано с тем, что он прошел большее расстояние и достиг большей высоты, поэтому сила тяжести действовала на копье в течение более длительного периода времени, прежде чем он ударился о землю. Тремя основными переменными, которые влияют на метание копья, являются начальная скорость, угол выпуска и высоты выпуска копья. Одной из этих переменных недостаточно, чтобы обеспечить хороший бросок.Из расчетов в таблице 1, бросок 2 считается самым успешным, так как он прошел самое большое расстояние 82,37 м. В этом броске можно увидеть тенденцию по сравнению с другими. Бросок 2 имеет наименьший угол выброса (40,65 °), самую высокую начальную скорость (28,13 м‾¹) и запускается с максимальной высоты (2,38 м). Все это вместе приводит к броску на самую дальнюю дистанцию.
График 2: угол выпуска и расстояние выброса
Форма траектории снаряда определяется углом проекции.Оптимальный угол вылета снаряда, выпущенного на уровне земли, составляет 45º. Если относительная высота выступа увеличивается, угол выпуска должен уменьшаться. И наоборот, если относительная высота выступа уменьшается, угол выпуска должен увеличиваться. Оптимальный угол выпуска при метании копья составляет 34-36º. Однако этот угол не принимает во внимание внешние факторы, такие как ветер, и поэтому его необходимо изменять в соответствии с минимизацией или максимизацией его воздействия. Если ветер дует против полета копья, то угол выпуска следует немного уменьшить, а при метании в попутный ветер угол выпуска должен быть больше.
Рисунок 2: Угол выпуска метания копья
График 2 и рисунок 1 показывают углы выпуска пяти метаний копья в возрастающем порядке по сравнению с метанным расстоянием. Бросок с наименьшим углом (бросок 2, 40,65 °), безусловно, достиг самой длинной дистанции (82,37 м). Остальные броски не следуют той же схеме, при этом наибольший угол выпуска занимает второе место по длине.Это связано с тем, что угол выпуска — только один из факторов, влияющих на расстояние выброса, и хотя угол выпуска может быть не близок к оптимальному, другие факторы могут быть более точными, что дает хороший результат. Увеличение угла выпуска может привести к увеличению расстояния
График 3 и рисунок 2 показывают разную высоту, на которой были выпущены копья. Бросок 2, у которого была самая длинная дистанция, 82,37 м, имел самую высокую точку сброса 2,38 м. Остальные броски выполняются с высотой 1.80 м, 1,96 м, 2,02 м и 1,68 м соответственно.
График 3: освобожденная высота и выброшенное расстояние
Высота, на которой выпущено копье, влияет на оптимальный угол выпуска. Чем больше высота, тем меньше должен быть угол, чтобы увеличить расстояние метания. Высота выпуска может в основном определяться естественным ростом спортсмена и может выдерживать более высоких спортсменов с небольшим преимуществом над своими конкурентами.Поэтому метателям копья часто приходится определять собственный оптимальный угол выпуска в соответствии со своим ростом. Обычно, когда скорость снаряда и угол выброса остаются постоянными, чем выше высота полета, тем больше время полета. Следовательно, чем больше время полета, тем больше расстояние.
Рисунок 3: Высота от земли
График 4: Угол вылета копья
График 4 сравнивает высоту выпуска с углом выпуска.Можно было бы ожидать, что с увеличением высоты угол уменьшается. Оптимальный угол выпуска от уровня земли — 45º; таким образом, все броски должны производиться под углом менее 45 °. Только три метателя имеют угол выброса менее 45 °, бросок 2, при котором копье выпущено на 2,38 м над землей под углом 40,65 °, бросок 4, при котором копье выпущено на высоте 2,02 м над землей под углом 43,41 °. и бросок 5, который выпустил копье на 1,68 м над землей под углом 43.63º. Два других броска имели углы чуть выше 45 °, составляющие 45,55 ° и 45,58 ° для бросков 1 и 3 соответственно. Уменьшение угла их выпуска может увеличить дальность метания копья.
Заключение:
Понимание того, как работает движение снаряда, очень полезно для определения того, как лучше всего двигать объект. Что касается метания копья, то умение рассчитывать различные переменные помогает спортсмену разработать лучшую технику для него лично, чтобы метать самую длинную дистанцию.Часто, глядя на метательное движение объекта, можно выявить ошибки на других этапах техники. Например, начальная скорость копья может использоваться как показатель количества движения, созданного во время подготовительной фазы действия. Часто низкая начальная скорость является результатом потери импульса во время этой фазы, и поэтому необходимо изменить методику, чтобы улучшить начальную скорость. То же самое и с другими видами спорта, такими как толкание ядра, баскетбол, вбрасывание в футбол и многие другие.
Расстояние до снаряда можно также рассчитать, используя начальную скорость, угол выброса и высоту выброса, по следующему уравнению:
Расстояние = Vi * cos Θ [Vi * sin Θ + √ ((Vi² * sin² Θ) + (2 * h * g)) / g]
Где:
Vi = начальная скорость (мс‾¹)
Θ = угол выпуска (град)
h = высота выпуска (м)
g = ускорение свободного падения (9.81 мс²)
технологий фотографии | Системы, типы и факты
Технология фотографии , оборудование, методы и процессы, используемые при производстве фотографий.
Наиболее широко используемый фотографический процесс — это черно-белая система негатив-позитив (рис. 1). В камере объектив проецирует изображение фотографируемой сцены на пленку, покрытую светочувствительными солями серебра, такими как бромид серебра.Затвор, встроенный в линзу, пропускает свет, отраженный от сцены в течение заданного времени, создавая невидимое, но проявляющееся изображение в сенсибилизированном слое, таким образом экспонируя пленку.
Во время проявления (в темной комнате) кристаллы соли серебра, на которые попал свет, превращаются в металлическое серебро, образуя видимый осадок или плотность. Чем больше света достигает заданной области пленки, тем больше соли серебра становится проявляющейся и тем плотнее серебряный осадок, который там образуется.Таким образом, изображение с различными уровнями яркости дает изображение, в котором эти яркости перевернуты по тонам — негатив. Яркие детали объекта записываются как темные или плотные области на проявленной пленке; темные части объекта записываются как области с низкой плотностью; т.е. серебра у них мало. После проявления пленка обрабатывается фиксирующей ванной, которая растворяет всю непроявленную соль серебра и тем самым предотвращает последующее потемнение таких неэкспонированных участков. Наконец, смывка удаляет все растворимые соли из эмульсии пленки, оставляя постоянное негативное серебряное изображение внутри слоя желатина.
При повторении этого процесса получается положительное изображение. Обычная процедура — увеличение: негатив проецируется на чувствительную бумагу, содержащую эмульсию галогенида серебра, аналогичную той, которая используется для пленки. Экспозиция от источника света увеличителя снова дает скрытое изображение негатива. После проявки и обработки на бумаге появляется позитивное серебряное изображение. При контактной печати негативная пленка и бумага помещаются лицом к лицу в тесном контакте и освещаются рассеянным светом, проходящим через негатив.Плотные (черные) части негативного изображения приводят к тому, что бумага мало экспонируется, и, следовательно, появляются светлые области изображения; тонкие участки негатива пропускают больше света и оставляют темные области на отпечатке, таким образом воссоздая значения яркости исходной сцены.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасОсновные функции камеры
В своей простейшей форме камера представляет собой светонепроницаемый контейнер, содержащий объектив, затвор, диафрагму, устройство для удержания (и смены) пленки в правильной плоскости изображения и видоискатель, позволяющий камеру, чтобы навести на желаемую сцену.
Объектив проецирует перевернутое изображение сцены перед камерой на пленку в плоскости изображения. Изображение будет резким только в том случае, если пленка расположена на определенном расстоянии за объективом. Это расстояние зависит от фокусного расстояния объектива ( см. Ниже Характеристики и параметры линз) и расстояния до объекта перед объективом. Для фотографирования близких и удаленных объектов все камеры, кроме самых простых, имеют регулировку фокусировки, которая изменяет расстояние между объективом и плоскостью пленки, чтобы объекты на выбранном расстоянии создавали резкое изображение на пленке.В некоторых камерах регулировка фокусировки достигается перемещением только переднего элемента или внутренних элементов объектива, что фактически изменяет фокусное расстояние.
Затвор состоит из набора металлических створок, установленных внутри или за линзой, или системы жалюзи, расположенных перед пленкой. Его можно заставить открываться на заданное время, чтобы экспонировать пленку для изображения, сформированного линзой. Время экспозиции — один из двух факторов, контролирующих количество света, попадающего на пленку.Другой фактор — это диафрагма объектива, или апертура, отверстие с регулируемым диаметром. Сочетание раскрытия диафрагмы и времени выдержки составляет фотографическую выдержку. Чтобы получить изображение на пленке, точно записывающее все градации тонов объекта, эта экспозиция должна соответствовать яркости (яркости) объекта и чувствительности или светочувствительности пленки. Экспонометры, встроенные в большинство современных фотоаппаратов, измеряют яркость объекта и настраивают затвор или диафрагму объектива для получения правильно экспонированного изображения.
Основные типы камер
Самый простой тип камеры, часто используемый случайными любителями, имеет большинство функций, перечисленных в предыдущем разделе — объектив, затвор, видоискатель и систему крепления пленки. Светонепроницаемый контейнер традиционно имел коробчатую форму. Современные эквиваленты — карманные фотоаппараты, принимающие легко загружаемые картриджи с пленкой или диски с пленкой. Обычно установка фиксированного затвора дает примерно 1 / 50 -секундную выдержку; объектив постоянно настроен на резкую запись всех объектов более чем на пять футов (1.5 метров) от камеры. Возможна встроенная вспышка. Несмотря на простоту использования, такие камеры при дневном свете могут снимать только неподвижные или медленно движущиеся объекты.
Глоссарий кинематографических терминов
Защитная пленка: Фотопленка, основа которой является огнестойкой или медленно горящей в соответствии с определением ANSI и различными правилами пожарной безопасности. В настоящее время термины «безопасная пленка на основе», «пленка на ацетатной основе» и «пленка на основе полиэстера» являются синонимами «защитная пленка».«
Частота дискретизации: Частота, с которой аналоговый сигнал измеряется и преобразуется в цифровые данные.
Насыщенность: Термин, используемый для описания яркости или чистоты цвета. Когда изображения на цветной пленке проецируются с надлежащей яркостью и без постороннего света, цвета, которые кажутся яркими, глубокими, насыщенными и неразбавленными, называются «насыщенными».
Разрешение сканирования: Число пикселей, полученных с оригинального негатива камеры.Сканирование пленки имеет три популярных разрешения: полное (4K), половинное (2K) и четверть (1K).
Сканер (пленочный сканер): Устройство, используемое для оцифровки пленочных изображений. Каждый кадр фильма дает отдельный файл цифрового изображения.
Сцена: Отрезок фильма, изображающий отдельную ситуацию или инцидент.
SD: Видео стандартной четкости.
Коррекция вторичного цвета: Выбор и изменение определенных частей цветового спектра или объектов без влияния на общий цветовой баланс сцены.
Чувствительность: Степень чувствительности пленки к свету.
Сенситометр: Прибор, с помощью которого фотоэмульсия подвергается градуированной серии световых воздействий с контролируемым спектральным качеством, интенсивностью и продолжительностью. В зависимости от того, различаются ли экспозиции по яркости или продолжительности, прибор можно назвать шкалой интенсивности или сенситометром шкалы времени.
Сенситометрическая кривая: См. «Характеристическая кривая.«
Сенситометрия: Изучение реакции фотоэмульсий на свет.
Мастера разделения: Три отдельных черно-белых мастер-позитива, изготовленных из одного цветного негатива; один содержит красную запись, другой — зеленую запись, а третий — синюю запись.
Детали теней: Комбинация трех других атрибутов изображения: скорость носка, скорость уровня черного и низкий контраст носка. Улучшение любого из атрибутов должно привести к улучшению деталей в тенях; хотя может быть трудно описать детали в тенях, когда фильм имеет преимущество в одной из категорий, но недостаток в других.
Резкость: Визуальное ощущение резкости лезвия. Ясность.
Короткий шаг (см. Шаг перфорации): Шаг перфорации отрицательного материала, который несколько короче шага положительного материала, чтобы избежать проскальзывания при контактной печати.
Плечо: Участок характеристической кривой с высокой плотностью, наклон которой изменяется при постоянных изменениях экспозиции. Для негативных пленок наклон уменьшается, и дальнейшие изменения экспозиции (log H) в конечном итоге не приводят к увеличению плотности, поскольку достигается максимальная плотность.Для обратных пленок наклон увеличивается.
Затвор: В театральной проекции, вращающееся устройство с двумя лопастями, используемое для прерывания действия источника света, пока пленка протягивается в проектор. Одно лезвие маскирует раскрытие, в то время как другое лезвие вызывает дополнительное прерывание света, увеличивая частоту мерцания до 48 циклов в секунду — уровень, который не вызывает возражений у зрителя при рекомендуемой яркости экрана в 16 фут-ламбертов (55 кандел на квадратный метр).В камере — вращающийся диск с удаленной секцией.
Галогениды серебра: Светочувствительное соединение, используемое в пленочных эмульсиях.
Пленка с одинарной перфорацией: Пленка с перфорацией только по одному краю.
Замедленная съемка: Процесс фотографирования объекта с более высокой частотой кадров, чем используется при проецировании, для увеличения временного элемента.
SMPTE: Акроним Общества инженеров кино и телевидения.
Мягкий: (1) Применяется к фотоэмульсии или проявителю с низким контрастом. (2) Применительно к освещению набора — рассеянный, давая плоскую сцену, в которой разница яркости между светлыми участками и тенями мала.
Отрицательный звук: Отрицательная запись фотографической звукозаписи.
Sound Positive: Позитивный отпечаток фотопленки для звукозаписи.
Источник: Тенденция к восприятию источника света как искусственного.Эта искусственность является результатом того, что свет кажется слишком ярким или слишком сильным на объекте, а затем очень быстро падает в интенсивности.
Кривая плотности специального красителя: График 1) общей плотности трех слоев красителя, измеренной как функция от длин волн, и 2) визуально нейтральной плотности объединенных слоев, измеренных аналогичным образом.
Спектральная чувствительность: Относительная чувствительность конкретной эмульсии к определенным полосам спектра в пределах диапазона чувствительности пленки.Иногда путают с Чувствительностью цвета.
Спектр: Диапазон лучистой энергии, в пределах которого существует видимый спектр с длинами волн от 400 до 700 мм.
Скорость: Может быть охарактеризована с точки зрения абсолютной чувствительности пленки или с точки зрения воспроизводимого черного изображения. Абсолютная чувствительность — это просто мера того, какой уровень света (экспозиции) начинает давать сигнал первой плотности в пленке — это известно как скорость схождения. Кинематографист также может интерпретировать скорость схождения пленки как широту недоэкспонирования или детализацию теней.
Чернота позитивного изображения D-max также может использоваться для определения скорости. Большинство кинематографистов описали бы фильм с более дымчатым черным цветом как более медленный, чем фильм с более черным черным, учитывая, что оба экспоната были одинаковыми. Уровень черного также связан с восприятием кинематографистом деталей в тенях.
Точка скорости: Точка, которая соответствует экспозиции, необходимой для получения определенной оптической плотности, обычно на 0,1 выше базовой + туман.
Соединение: Любой тип цемента или механического крепления, с помощью которого два отдельных отрезка пленки соединяются встык, так что они действуют как единый кусок пленки при прохождении через камеру, машину для обработки пленки или проектор.
Точечный измеритель: Люксметр, предназначенный для измерения света, отраженного от объекта.
Звездочка: Зубчатое колесо, используемое для транспортировки перфорированной кинопленки.
Статическое электричество: Электрическое поле, которое возникает в основном из-за наличия электрических зарядов на материалах.
Шаг: Увеличение или уменьшение экспозиции, обычно в 2 раза. То же, что и «Стоп», за исключением того, что остановка конкретно относится к диафрагме объектива.Пластырь ступенчатого планшета, используемый для сенситометрических снимков, как в «21-ступенчатом планшете».
Шаговый контактный принтер: Контактный принтер, в котором копируемая пленка и необработанный материал продвигаются с перерывами за кадром. Воздействие происходит только тогда, когда оба неподвижны.
Наличие: Общий термин для кинофильмов, особенно перед экспонированием.
Stop Down: Для уменьшения диаметра светопропускающего отверстия линзы путем регулировки ирисовой диафрагмы.
Stop Motion: Метод анимации, при котором видимое движение объектов получается на пленке путем экспонирования отдельных кадров и перемещения объекта для имитации непрерывного движения.
Сеть хранения данных (SAN): Высокоскоростная сеть, которая соединяет компьютерные запоминающие устройства, такие как жесткие диски и ленточные библиотеки, с серверами. SAN позволяет нескольким компьютерам получать доступ к централизованному пулу хранилища. Файлы можно обмениваться, копировать или быстро и эффективно перемещать по SAN.
Область прямой линии: Часть характеристической кривой, наклон которой не изменяется, поскольку скорость изменения плотности для данного изменения экспозиции бревна постоянна или линейна.
Subbing Layer: Клеевой слой, который связывает пленочную эмульсию с основой.
Субтрактивный цвет: Голубой, пурпурный и желтый, субтрактивные основные цвета, используемые пленкой для воспроизведения цвета.
Субтрактивное освещение: Этот метод обычно используется при съемке экстерьера при доступном освещении.При использовании больших флажков, бабочек или потолков удаляется свет от объекта, чтобы увеличить яркость освещения. Иногда это называют «отрицательной заливкой».
Субтрактивный процесс: Фотографический процесс, в котором используется один или несколько субтрактивных основных цветов, например голубой, пурпурный и желтый для управления красным, зеленым и синим светом.
Солнечный свет: Свет, достигающий наблюдателя непосредственно от Солнца. Отличаться от дневного света и света в крыше, которые включают непрямой свет облаков и преломляют атмосферу.
Super 16: Этот формат предлагает гораздо большую площадь изображения, чем у стандартных 16 мм, и обеспечивает более широкий формат 1,66: 1 по сравнению с телевизионным соотношением сторон 1,33: 1.
Super 8 мм: Раньше любительский формат, теперь популярный выбор для спецэффектов и обучения.
Super 35: Формат камеры 35 мм, который использует всю область кадра на пленке.
Supercoat: Защитное покрытие на пленке.
СУПЕР ПАНАВИЗИЯ: Подобно Panavision 35, но сфотографировано плоско на 65 мм.Отпечатки диаметром 70 мм обеспечивают соотношение сторон 2,25: 1 при 4-канальном звуке и соотношение 2: 1 при 6-канальном звуке.
Sweetening: Постпродакшн аудио, при котором устраняются незначительные проблемы со звуком. Музыка, повествование и звуковые эффекты смешаны с оригинальными звуковыми элементами.
Набухание: Увеличение размеров кинопленки из-за поглощения влаги при хранении и использовании в условиях высокой влажности. В условиях экстремальной влажности и последующего набухания пленки повышается подверженность истиранию поверхности пленки.
Синхронизация: Считается, что запись изображения и звукозапись «синхронизированы», когда они размещаются относительно друг друга на выпуске печати, поэтому при проецировании действие будет точно совпадать с сопровождающим звуком.
Синхронизация: Точное выравнивание звука и изображения для редактирования, проецирования и печати.
Синхронизатор: Механизм, использующий общий вращающийся вал, имеющий звездочки, которые, зацепляя перфорацию в пленке, одновременно пропускают соответствующие отрезки изображения и звуковой пленки, таким образом эффективно сохраняя синхронизацию двух (или более) пленок в процессе монтажа. .
Движение снаряда | Физика
1. Снаряд запускается с уровня земли с начальной скоростью 50,0 м / с под углом 30,0º над горизонтом. Через 3 секунды он поражает цель над землей. Каковы расстояния x и y от места запуска снаряда до места приземления?
2. Мяч бьет с начальной скоростью 16 м / с в горизонтальном направлении и 12 м / с в вертикальном направлении. а) С какой скоростью мяч ударяется о землю? б) Как долго мяч остается в воздухе? (c) Какая максимальная высота достигает мяча?
3.Мяч бросается горизонтально с вершины здания высотой 60,0 м и приземляется на расстоянии 100,0 м от основания здания. Не обращайте внимания на сопротивление воздуха. а) Как долго мяч находится в воздухе? б) Какой должна была быть начальная горизонтальная составляющая скорости? (c) Какова вертикальная составляющая скорости перед ударом мяча о землю? (d) Какова скорость (включая горизонтальную и вертикальную составляющие) мяча непосредственно перед тем, как он упадет на землю?
4. (a) Сорвиголова пытается перепрыгнуть на своем мотоцикле через линию припаркованных автобусов, проезжая по рампе 32 ° со скоростью 40 °.0 м / с (144 км / ч). Сколько автобусов он может очистить, если верх взлетной рампы находится на той же высоте, что и верхняя часть автобусов, а длина автобусов составляет 20,0 м? (b) Обсудите, что ваш ответ подразумевает допустимую погрешность в этом действии, то есть подумайте, насколько больше диапазон, чем горизонтальное расстояние, которое он должен пройти, чтобы пропустить конец последнего автобуса. (Пренебрегая сопротивлением воздуха.)
5. Лучник стреляет из стрелы в цель на расстоянии 75,0 м; прицел цели находится на той же высоте, что и высота выброса стрелы.(а) Под каким углом должна быть выпущена стрела, чтобы попасть в цель, если ее начальная скорость составляет 35,0 м / с? В этой части задачи явно покажите, как вы выполняете шаги, связанные с решением проблем с движением снаряда. (b) На полпути между лучником и целью находится большое дерево с нависающей горизонтальной веткой на 3,50 м над высотой выпуска стрелы. Пойдет стрелка над веткой или под веткой?
6. Регбист передает мяч 7,00 м через поле, где он пойман на той же высоте, что и оставил его руку.(a) Под каким углом был брошен мяч, если его начальная скорость составляла 12,0 м / с, если предположить, что использовался меньший из двух возможных углов? б) Какой другой угол дает такой же диапазон и почему бы его не использовать? (c) Сколько времени длился этот пропуск?
7. Проверьте дальность полета снарядов на Рисунке 5 (а) для θ = 45º и заданных начальных скоростей.
8. Проверьте дальность полета снарядов на Рисунке 5 (b) для начальной скорости 50 м / с при заданных начальных углах.
9. Пушка линкора может стрелять снарядом на максимальную дальность 32,0 км. (а) Рассчитайте начальную скорость снаряда. б) Какой максимальной высоты он достигает? (На самом высоком уровне оболочка составляет более 60% атмосферы — но сопротивление воздуха на самом деле не является незначительным, как предполагается, чтобы облегчить эту проблему.) (C) Океан не плоский, потому что Земля изогнута. Предположим, что радиус Земли равен 6.37 × 10 3 . На сколько метров ниже его поверхность будет в 32,0 км от корабля по горизонтальной линии, параллельной поверхности у корабля? Означает ли ваш ответ, что здесь существенна ошибка, связанная с предположением о плоской Земле в движении снаряда?
10.Стрела выпущена с высоты 1,5 м в сторону обрыва высотой H . Он выстреливается со скоростью 30 м / с под углом 60º над горизонтом. Через 4 секунды он приземляется на вершину обрыва. а) Какова высота обрыва? (б) Какая максимальная высота достигает стрелка на своей траектории? (c) Какова скорость удара стрелы непосредственно перед тем, как она упадет в обрыв?
11. В прыжке в длину с места человек приседает, а затем отталкивается ногами, чтобы посмотреть, как далеко он может прыгнуть.Предположим, что разгибание ног из положения приседа составляет 0,600 м, а ускорение, достигаемое из этого положения, в 1,25 раза превышает ускорение свободного падения, г . Как далеко они могут прыгнуть? Выскажите свои предположения. (Увеличенной дальности можно добиться, поворачивая руки в направлении прыжка.)
12. Мировой рекорд по прыжкам в длину — 8,95 м (Майк Пауэлл, США, 1991). Считается, что это снаряд, какова максимальная дальность, которую может получить человек, если у него скорость взлета 9.5 м / с? Выскажите свои предположения.
13. На скорости 170 км / ч теннисист отбивает мяч на высоте 2,5 м под углом θ ниже горизонтали. Линия обслуживания находится на расстоянии 11,9 м от сети, высота 0,91 м. Каков угол θ , при котором мяч просто пересекает сетку? Приземлится ли мяч в штрафную площадку, внешняя линия которой находится на расстоянии 6,40 м от сетки?
14. Футбольный квотербек движется прямо назад со скоростью 2,00 м / с, когда он делает пас игроку 18.0 м прямо по полю. (a) Если мяч брошен под углом 25º относительно земли и пойман на той же высоте, что и выпущен, какова его начальная скорость относительно земли? б) Сколько времени нужно, чтобы добраться до получателя? (c) Какова его максимальная высота над точкой выпуска?
15. Прицельные приспособления отрегулированы так, чтобы прицелиться высоко, чтобы компенсировать эффект силы тяжести, что эффективно обеспечивает точность прицела только на определенном расстоянии. (a) Если ружье прицеливается для поражения целей, находящихся на той же высоте, что и ружье, и 100.На расстоянии 0 м, как низко пуля попадет в цель на расстоянии 150,0 м? Начальная скорость пули — 275 м / с. (б) Обсудите качественно, как большая начальная скорость пули повлияет на эту проблему и каков будет эффект сопротивления воздуха.
16. Орел летит горизонтально со скоростью 3,00 м / с, когда рыба в его когтях, раскачиваясь, падает в озеро на 5,00 м ниже. Вычислите скорость рыбы относительно воды, когда она ударяется о воду.
17.Сова несет мышь к птенцам в гнезде. Его положение в то время составляет 4,00 м к западу и 12,0 м над центром гнезда диаметром 30,0 см. Сова летит на восток со скоростью 3,50 м / с под углом 30,0 ° ниже горизонтали, когда случайно уронила мышь. Достаточно ли повезло сове, что мышь попала в гнездо? Чтобы ответить на этот вопрос, вычислите горизонтальное положение мыши, когда она упала на 12,0 м.
18. Предположим, футболист отбивает мяч ногой с расстояния 30 м к воротам.Найдите начальную скорость мяча, если он только что пролетает над воротами на высоте 2,4 м над землей, учитывая, что начальное направление находится на 40º над горизонтом.
19. Может ли вратарь у своих ворот забить футбольный мяч в ворота соперника так, чтобы мяч не касался земли? Дистанция составит около 95 м. Вратарь может дать мячу скорость 30 м / с.
20. Линия штрафных бросков в баскетболе находится на расстоянии 4,57 м (15 футов) от корзины, что на 3,05 м (10 футов) над полом. Игрок, стоящий на линии штрафного броска, бросает мяч с начальной скоростью 7.15 м / с, выпуская его на высоте 2,44 м (8 футов) над полом. Под каким углом над горизонтом нужно бросить мяч так, чтобы он точно попал в корзину? Обратите внимание, что большинство игроков будут использовать большой начальный угол, а не прямой выстрел, потому что это допускает большую погрешность. Ясно покажите, как вы выполняете шаги, связанные с решением проблем с движением снаряда.
21. В 2007 году Майкл Картер (США) установил мировой рекорд в толкании ядра с броском 24,77 м. Какова была начальная скорость выстрела, если он выпустил его на высоте 2.10 м и бросил под углом 38,0º над горизонтом? (Хотя максимальное расстояние для снаряда на ровной поверхности достигается при 45 °, если пренебречь сопротивлением воздуха, фактический угол для достижения максимальной дальности меньше; таким образом, 38 ° даст большую дальность, чем 45 ° при толкании ядра.)
22. Баскетболист бежит со скоростью 5,00 м / с прямо к корзине, когда он прыгает в воздух, чтобы замочить мяч. Он сохраняет свою горизонтальную скорость. (а) Какая вертикальная скорость ему нужна, чтобы подняться на 0.750 м над уровнем пола? (b) На каком расстоянии от корзины (по горизонтали) он должен начать свой прыжок, чтобы достичь максимальной высоты одновременно с достижением корзины?
23. Футболист толкает мяч под углом 45 градусов. Без воздействия ветра мяч пролетел бы 60,0 м по горизонтали. а) Какова начальная скорость мяча? (b) Когда мяч приближается к своей максимальной высоте, он испытывает короткий порыв ветра, который снижает его горизонтальную скорость на 1,50 м / с. На какое расстояние мяч проходит по горизонтали?
24.{2} \ text {\ sin} {2 \ theta} _ {0}} {g} \\ [/ latex] для определения дальности полета снаряда на ровной поверхности путем нахождения времени t , при котором y становится ноль и подставив это значение t в выражение для x — x 0 , отметив, что R = x — x 0 .
26. Необоснованные результаты (a) Найдите максимальную дальность стрельбы суперпушки с начальной скоростью 4,0 км / с. б) Что неразумного в найденном вами диапазоне? (c) Является ли предпосылка необоснованной или имеющееся уравнение неприменимо? Поясните свой ответ.(d) Если такая начальная скорость может быть получена, обсудите влияние сопротивления воздуха, разрежения воздуха с высотой и кривизны Земли на дальность действия супер-пушки.
27. Создай свою задачу Представьте мяч, брошенный через забор. Составьте задачу, в которой вы вычисляете необходимую начальную скорость мяча, чтобы просто преодолеть забор. Среди вещей, которые нужно определить: высота ограждения, расстояние до ограждения от точки выброса мяча и высота, на которой мяч выпущен.Вы также должны подумать, можно ли выбрать начальную скорость для мяча и просто рассчитать угол, под которым он брошен. Также изучите возможность нескольких решений с учетом выбранных вами расстояний и высоты.
Быстрый отрицательный пробой во время грозы
События быстрого пробоя во время грозы, распространенной на NBE
Наблюдения были получены в Космическом центре Кеннеди, Флорида, во время грозы 24 августа 2016 года, расположенной на море. Наблюдения включают данные о массиве трехмерного картирования молний (LMA) 5,26 с массива картирования молний Космического центра Кеннеди с 10 станциями (KSCLMA), формы волны ОВЧ, зарегистрированные широкополосным интерферометром New Mexico Tech 27 (INTF), и формы сигналов, записанные плоской быстрой антенной (FA), которая измеряла изменение вертикального электрического поля у земли с постоянной затухания 100 мкс.
На рис. 1 показан обзор наблюдений LMA для шторма 24 августа и интересующих событий. На рисунке 1а показана полная продолжительность высот источников в зависимости от всемирного времени (UT) с источниками LMA, окрашенными в зависимости от времени. 10-минутный период бури (черная скобка на рис. 1a) расширен на рис. 1b, d – f, где источники LMA окрашены в соответствии с полярностью событий грозового разряда, причем красные источники указывают на положительный штормовой заряд. , а синие источники указывают отрицательный штормовой заряд 28,29,30 .NBE высокой мощности окрашены в черный цвет и обычно возникают ниже области верхнего положительного заряда на подветренной стороне шторма. Этот 10-минутный период отмечен увеличением частоты вспышек (примерно от 1 до 5 полностью проявившихся вспышек в минуту) и высоты возникновения вспышки (примерно от 8–10 до 10–15 км над средним уровнем моря (MSL)), так как а также увеличение количества случаев изолированного NBE (примерно с 1 до 15 мин -1 ) на высотах возникновения вспышки. Такие высокие начальные высоты NBE не являются чем-то необычным для штормов во Флориде 6,31 , но частота возникновения NBE является исключительной и резко контрастирует с предыдущими исследованиями 32 .
Один особенно высокоскоростной период NBE (~ 40 NBE в течение 1 минуты) длился с 09:58 до 09:59 UT, в течение которого NBE имели тенденцию группироваться в пространстве и времени (например, Stanley et al. 33 ). Кластер из десяти изолированных NBE, который имел место между основными областями отрицательного и верхнего положительного заряда в шторме нормальной полярности 34 , обозначен черной скобкой на рис. 1b и показан в развернутом виде на рис. 1c, где LMA размеры и цвет источников соответствуют мощности источника в дБВт.Десяти NBE предшествовали и следовали полностью проявившиеся вспышки (не показаны), т. Е. Отрицательная вспышка облака-земля закончилась за 3 с до начала первой NBE в кластере, и началась внутриоблачная вспышка нормальной полярности. 0,1 с после десятого (последнего) НБЭ в кластере. INTF сработал по сильному УКВ-излучению от каждого из десяти NBE. Как обсуждается в следующем разделе, данные INTF и FA показывают, что NBE 1 (рис. 2) был образован в результате распространяющегося вниз быстрого положительного пробоя, аналогичного тому, который был описан Rison et al. 8 . Напротив, такой же быстрый пробой, но направленный вверх и отрицательной полярности, дает NBE 2 и NBE 9 (рис. 3 и 4, соответственно). Полярность остальных семи NBE не могла быть определена, потому что вертикальная протяженность каждого события была слишком мала, чтобы определить однозначное направление распространения.
Рис. 2Данные интерферометра для NBE 1. a , c Центроиды излучения (круглые маркеры, окрашенные и измеренные в зависимости от мощности VHF) для NBE 1, построенные по высоте в зависимости отазимут, показывающий, что активность пробоя была в основном вертикальной. Каждый маркер обозначает среднее угловое положение 128 исходных решений в каждом окне 0,7 мкс, а полосы ошибок обозначают стандартные отклонения. b , d Наблюдения за центроидами излучения и быстрым изменением электрического поля (сферические) (черная форма волны), наложенные на форму волны УКВ (серый цвет), показывающие распространение источника УКВ вниз. Положительная сферическая форма волны указывает на направленный вниз ток, соответствующий NBE, возникающему ниже верхнего положительного заряда бури, и указывает на то, что развитие вниз было связано с пробоем положительной полярности.Пробой снизился на 600 м за 13 мкс, что соответствует скорости 5 × 10 7 м с −1 . e Полугодовой график зависимости мощности VHF от времени, показывающий быстрый экспоненциальный рост излучения (время нарастания τ = 0,21 мкс), совпадающий с быстрым ростом изменения электрического поля ( d ). Пиковый ток пробоя составил -75 кА.
Рис. 3Данные интерферометра для NBE 2. a , c Центроиды излучения (круглые маркеры, окрашенные и измеренные в зависимости от мощности VHF) для NBE 2, нанесенные на высоте против.азимут, показывающий, что активность пробоя была в основном вертикальной. Каждый маркер обозначает среднее угловое положение 128 исходных решений в каждом окне 0,7 мкс, а полосы ошибок обозначают стандартные отклонения. b , d Наблюдения за центроидами излучения и быстрым изменением электрического поля (сферические) (черная форма волны), наложенные на форму волны УКВ (серый цвет), показывая восходящее распространение источника УКВ. Положительная сферическая форма волны указывает на направленный вниз ток, соответствующий NBE, возникающему ниже верхнего положительного заряда шторма, и указывает, что восходящее развитие было связано с пробоем отрицательной полярности.Пробой поднялся на 600 м за 15 мкс, что соответствует скорости 4 × 10 7 м с −1 . e Полугодовой график зависимости мощности VHF от времени, показывающий быстрое экспоненциальное нарастание излучения (время нарастания τ = 0,24 мкс), совпадающее с быстрым нарастанием изменения электрического поля ( d ). Пиковый ток пробоя составил -47 кА.
Рис. 4Данные интерферометра для NBE 9. a , c Центроиды излучения (круглые маркеры, окрашенные и измеренные в зависимости от мощности VHF) для NBE 9, нанесенные на высоте против.азимут, показывающий, что активность пробоя была в основном вертикальной. Каждый маркер обозначает среднее угловое положение 128 исходных решений в каждом окне 0,7 мкс, а полосы ошибок обозначают стандартные отклонения. b , d Наблюдения за центроидами излучения и быстрым изменением электрического поля (сферические) (черная форма волны), наложенные на форму волны УКВ (серый цвет), показывая восходящее распространение источника УКВ. Положительная сферическая форма волны указывает на направленный вниз ток, соответствующий NBE, возникающему ниже верхнего положительного заряда шторма, и указывает, что восходящее развитие было связано с пробоем отрицательной полярности.Пробой поднялся на 400 м за 10 мкс, что соответствует скорости 4 × 10 7 м с −1 . e Полугодовой график зависимости мощности VHF от времени, показывающий быстрый экспоненциальный рост излучения (время нарастания τ = 0,23 мкс), совпадающий с быстрым ростом изменения электрического поля ( d ). Пиковый ток пробоя составлял -58 кА
Несмотря на различия в полярности пробоя и направлении распространения, NBE 1, 2 и 9 согласуются с NBE высокой мощности, обсуждаемыми в Rison et al. 8 , имеющий пиковую мощность VHF, оцененную LMA, равную 105, 12 и 43 кВт соответственно. Кроме того, изменяются заряд-момент (-320, -190 и -120 См), перенос заряда (-0,5, -0,3 и -0,3 Кл), пиковые токи (-75, -47 и -58 кА), и нарастание тока и — времена развертки (0,5, 0,4 и 0,4 мкс), полученные из моделирования сферических характеристик быстрого пробоя для NBE 1, 2 и 9, аналогичны Rison et al. 8 результат. Эти результаты приведены в таблице 1.
Таблица 1 Характеристики быстрого пробоя для NBE 1, 2 и 9Полярность быстрого пробоя
Быстрое изменение электрического поля, измеренное FA, было положительным для всех трех NBE, что указывает на ток. направленный вниз 35 .Затем полярность событий определяется из наблюдений INTF за направлением распространения пробоя. Для каждого NBE мы строим серию VHF-изображений с экспозицией 0,7 мкс 36,37 (также см. Методы), а затем определяем центр тяжести или самый яркий пиксель на каждом изображении, чтобы определить местоположение источника VHF-излучения. со временем. Чтобы минимизировать эффекты шума в каждом изображении длительностью 0,7 мкс, что соответствует 128 выборкам VHF, мы находим 128 положений центроидов, сдвигая каждое окно изображения на одну выборку (5.6 нс) и вычислите среднее значение для этих 128 местоположений. Результирующие карты центроидов для NBE 1, 2 и 9 показаны на рис. 2–4 соответственно, где круглые маркеры соответствуют среднему положению центроида за период времени 0,7 мкс, а полосы ошибок обозначают стандартное отклонение (SD). В частности, для НБЭ с отрицательным пробоем вверх, рис. 3a, c и 4a, c показаны центроиды NBE 2 и NBE 9, соответственно, по углу места по отношению к азимутальному углу, что указывает на то, что их развитие было преимущественно вертикальным, подобно положительному положительному разрушению NBE 1 на рис.2, и в других наблюдениях NBE 8,38 . Панели b, d каждого из рисунков показывают временное развитие NBE, совмещенное с совпадающими формами сигналов VHF (голубой) и FA (черный). Развитие NBE с отрицательным пробоем вверх по высоте в зависимости от времени аналогично таковому в примере с положительным пробоем вниз, причем оба указывают на локализованный источник или единичный фронт пробоя (хотя и с заметным разбросом в местах расположения эмиттеров). Измеренные скорости VHF и время нарастания также аналогичны для трех NBE, в диапазоне от 4 до 5 × 10 7 м с -1 и 0.21–0,24 мкс соответственно.
Характеристики источника NBE
На рисунке 5 показан пример изображений 0,7 мкс, используемых при определении результатов центроида в предыдущем разделе. Техника визуализации центроида отличается от таковой Rison et al. 8 тем, что он использует все функции взаимной корреляции антенных пар, а не только их пики 36 . Расположение центроидов одинаково для двух подходов, но отображение дает дополнительную информацию о пространственном распределении источника (см. Методы).Если источник локализован, т.е. находится в пределах углового разрешения INTF, то его местоположение хорошо определяется положением центроида. Для расширенных источников центроид не обязательно представляет местоположение источника.
Рис. 5Радиоизображения NBE 2. Изображения высоты в зависимости от азимута ( a ) идеального точечного источника в местоположении NBE 2 ( Az, , \ (E \ ell \) = 50 °, 23 ° ), называемая функцией рассеяния точки (PSF), b — e образцы изображений с интервалами 4 мкс в течение первых 15 мкс NBE 2, соответствующих его фазе быстрого отрицательного пробоя вверх (FNB), и f — i образцы изображений в течение последовательных интервалов 15 мкс.В каждом случае изображения имеют экспозицию 0,7 мкс, нормированную на пиковую амплитуду центроида. Центральный лепесток PSF показывает угловое разрешение трехантенной решетки и, вместе с боковыми лепестками, остается практически неизменным во время FNB, что согласуется с излучением УКВ от локализованного источника. После FNB центральный лепесток становится все более удлиненным, а боковые лепестки усиливаются и дезорганизуются, что свидетельствует о протяженных и / или множественных источниках излучения. j Стандартные отклонения (SD) центрального лепестка в плоскости проекции (cos α , cos β ) в зависимости от времени (красные, синие символы) по сравнению с SD функции PSF (серая линия), количественно показывая, что излучение должно быть локализовано во время FNB и все более нелокализовано и случайным после FNB
. В качестве примера на рис. 5 показаны последовательные изображения, полученные с NBE 2. Распределение интенсивности в каждом изображении нормализовано в диапазоне от 0 (темно-синий) до 1 (желтый).Для сравнения на рис. 5а показано смоделированное изображение идеального (бесшумного) точечного источника, расположенного под азимутальным углом ( Az ) и углом места \ ((E \ ell) \) 50 ° и 23 ° соответственно, аналогично расположение источников NBE 2. Диаграмма интенсивности идеального точечного источника называется функцией рассеяния точки (PSF) 37,39 INTF (см. Методы) и зависит от технических характеристик INTF, таких как ширина полосы, длина и ориентация базовой линии. PSF характеризуется ярким главным лепестком с угловым размером, который указывает разрешение INTF, и боковыми лепестками с меньшей интенсивностью.Обратите внимание, что верхний ряд изображений (рис. 5b – e) соответствует первым 15 мкс NBE 2, и изображения качественно похожи на PSF, имея один яркий главный лепесток сопоставимого размера и такую же яркую и морфологически похожую сторону доли. Это указывает на то, что первые 15 мкс NBE 2 соответствуют локализованному источнику, и что источники удачно расположены по центрам тяжести. Напротив, вторая строка (рис. 5f – i) соответствует последней (≥15 мкс) части NBE 2, и изображения выглядят существенно иначе, чем PSF, имея как более широкий главный лепесток, так и морфологически разные боковые лепестки, так как а также более интенсивное содержание в боковых лепестках.Такие изображения несовместимы с локализованным источником, и местоположения центроидов могут неточно отображать местоположения излучателей. Это отражается в увеличении неопределенности значений высоты через ~ 15 мкс на рис. 2–4, а также в увеличенных СД, показанных на рис. 5j.
УКВ-изображения для NBE 2 (рис. 5b – i) были подогнаны к двумерному гауссиану для определения их SD (см. Методы). Полученные значения показаны на рис. 5j, который ясно демонстрирует два различных режима активности.В течение первых 15 мкс NBE 2, т. Е. Стадии быстрого пробоя, SD в направлениях cos α и cos β (см. Методы проекции косинусной плоскости) ограничиваются значениями между 0,010 и 0,012, что делает источники соответствуют локализованному источнику, излучающему с угловым разрешением около 1,0 ° азимутального угла и 3,5 ° угла места. Часто источник неотличим от точечного (с обоими значениями SD ≈ 0,011, что соответствует угловому разрешению 1.6 ° и 3,8 ° по азимуту и углу места соответственно). В этом случае местоположения и развитие источников хорошо представлены значениями центроидов, которые показывают уменьшенный разброс при распространении (см. Рис. 2a, b, 3a, b и 4a, b). Примерно через 15 мкс (рис. 5f – i) SD заметно больше и демонстрируют значительно больший разброс значений в диапазоне от 0,012 до 0,022, что указывает на то, что угловая протяженность источника больше, чем у PSF, а вместо этого увеличивается до> 1,6 ° и> 5 ° по азимуту и углу места соответственно.Кроме того, существенно изменены боковые лепестки. Таким образом, последняя стадия представляет собой смесь локализованных и протяженных источников, центроиды которых не соответствуют локализованному источнику.
Поскольку первые 15 мкс NBE 2 соответствовали локализованному источнику, существуют четыре возможных модели для объяснения восходящего движения центроида NBE 2, изображенного на рис. 3d. Первая и самая простая модель — это точечный источник или отрицательный фронт пробоя, движущийся вверх по высоте, что является моделью, используемой для получения рис.6 (обсуждается ниже). Вторая правдоподобная модель — это модель протяженного источника, который растет вверх по высоте. В этом случае пробой отрицательной полярности вверх все еще необходим для объяснения движения центроида. Третья модель состоит из двух точечных источников, один из которых движется вверх по высоте с большей мощностью источника, а другой движется вниз по высоте с меньшей мощностью источника, так что общее изменение высоты центроида является положительным. Опять же, это потребовало бы пробоя отрицательной полярности вверх, чтобы объяснить движение центроида, но также указывало бы на то, что положительный пробой происходит одновременно с быстрым отрицательным пробоем.Кроме того, нижним пределом будет скорость быстрого отрицательного пробоя, определенная на рис. 3d. Четвертая модель представляет собой два стационарных точечных источника, разделенных высотой не менее 600 м. Если более высокий источник со временем излучает сильнее по сравнению с более низким источником, то движение центроида является очевидным эффектом. Этот сценарий физически неправдоподобен. Экспоненциальный рост (время нарастания 0,24 мкс) измеренной мощности ОВЧ требует, чтобы мощность ОВЧ более высокого (более сильно излучающего) источника увеличивалась в том же масштабе времени.Если более низкий источник также не увеличивается в той же шкале времени, то положение центроида вскоре определяется только более высоким источником (через 1,5 мкс мощность источника увеличивается в 500 раз). В этом случае движение центроида вверх должно происходить из-за распространения источника вверх, а не из-за двух стационарных источников. В качестве альтернативы, если и более высокая, и более низкая мощность источника увеличиваются в одном и том же масштабе времени, то весьма вероятно, что между двумя источниками существует электрическое соединение. Это позволяет предположить, что протяженный излучатель (> 600 м) уже существует в начале экспоненциального роста мощности VHF, что несовместимо с наблюдениями INTF, показывающими отсутствие разрядной активности перед событием.
Рис. 6Моделирование NBE 2. Смоделированные центроиды излучения (круглые маркеры, окрашенные и имеющие размер в зависимости от мощности VHF) вертикально распространяющегося точечного источника, имеющего те же амплитуды, высоты и скорость VHF, равные NBE 2. Каждый маркер обозначает среднее угловое положение 128 решений источника в каждом 0,7 Окно-мкс, а полосы ошибок обозначают стандартные отклонения. a , b Расположение центроидов без дополнительного шума, построенное по углу места в зависимости от азимута и высоте в зависимости отвремени, соответственно, и c , d то же самое, но с добавленным шумом перед вспышкой NBE 2, показывая, что результирующий разброс по углу места и азимуту частично, но не полностью, объясняется шумом перед вспышкой
С учетом вышеизложенного, для объяснения движения центроида локализованного источника, как показано на рис. 3 и 4. Как и NBE 2, NBE 9 также был получен путем быстрого пробоя вверх отрицательной полярности, в данном случае со скоростью 3.9 × 10 7 м с −1 (рис. 4г). Напротив, быстрый пробой NBE 1 развивался вниз, в том же направлении, что и ток, и поэтому имел положительную полярность (рис. 2d). В каждом случае пробой инициировался на высоте около 13,6 км и имел одинаковые вертикальные протяженность (400–600 м) и скорость распространения (несколько раз 10 7 м с −1 ). Особенности начального быстрого пробоя во время NBE 1, 2 и 9 суммированы в таблице 1.
Моделирование быстрого пробоя
Для дальнейшего подтверждения того, что пробой развивается как быстро распространяющееся событие, мы моделируем изображения INTF распространяющейся идеальной точки. источника, принимая во внимание шум (до вспышки) при измерении INTF (см. Методы).В частности, начальные 15 мкс NBE 2 моделируются как быстрый (4,2 × 10 7 м с −1 ) монотонно восходящий точечный источник, который начинается на высоте 13,6 км и на расстоянии 32,6 км от INTF, который имеет та же мощность VHF на изображение, что и для фактической записи NBE 2. На рис. 6a, b показана модель без шума для быстрого пробоя NBE 2, а на рис. 6c, d — модель с добавленным шумом.
Сравнение рис. Фигуры 3c, d и 6c, d показывают, что разброс в местах расположения источников фактических измерений только частично объясняется шумом перед вспышкой.Поскольку наше моделирование монотонно восходящего точечного источника (рис. 6c, d) не полностью объясняет разброс в центроидах, который показан в наблюдениях (рис. 3c, d), возможно, что мы либо недооценили шум, либо скорость источника колеблется, или что пространственно распределенная каскадная последовательность активности ответственна за быстрый отрицательный пробой, наблюдаемый для NBE 2 (и NBE 9), и, возможно, также отвечает за быстрый положительный пробой NBE 1 и другие быстрые положительные пробои , учитывая сходство между быстрым отрицательным и быстрым положительным срывом.Несмотря на это, положения центроидов во время начального пробоя NBE 2 (рис. 3c, d) соответствуют быстрому пробою, распространяющемуся вверх, который переносит ток, противоположный направлению его распространения, переносящий отрицательный заряд вверх в верхнюю область положительного заряда (вставка на рис. 1d), и поэтому имеет отрицательную полярность.
Расширения — Общество офтальмологических фотографов
«Создание увеличения» очень похоже на создание контактной печати, основное отличие состоит в том, что для печати будет выбран один негатив.Вместо того, чтобы помещать негатив в контакт с бумагой для печати, он будет помещен в держатель негативов увеличителя и спроецирован на бумагу, которая будет удерживаться на месте увеличивающим мольбертом.
Настройка увеличителя. Установите печатный станок на основание увеличителя. При использовании регулируемого мольберта установите лезвия в соответствии с размером печати. Отпечатки обычно печатаются с белым полем дюйма. Это достигается путем установки лезвий мольберта на полдюйма меньше, чем размеры бумаги.Скоростной мольберт настроен на определенный размер бумаги и позволяет печатать с полями ¼ дюйма.
Регулировка лезвий мольберта
Выберите негатив для печати. Поместите негатив стороной с эмульсией носителя вниз. Эмульсионная сторона может быть идентифицирована несколькими способами: эмульсионная сторона обычно является матовой стороной пленки, пленка обычно имеет тенденцию скручиваться к эмульсионной стороне, когда слова, напечатанные на краях пленки, могут быть прочитаны эмульсией находится далеко от вас, и когда маленькие стрелки на краях пленки указывают против часовой стрелки, эмульсия находится далеко от вас.Перевернув пленку в увеличителе, вы получите зеркальное отображение объекта.
Обычно легче работать с увеличением, когда изображение находится на бумаге лицевой стороной вверх. Когда негатив помещается в держатель верхом к вам, верх на мольберте будет от вас.
Отрицательный в отрицательном носителе
Отрегулируйте размер изображения, включив свет увеличителя с помощью переключателя фокусировки на таймере увеличителя. Откройте диафрагму на линзе увеличителя, поворачивая ее до тех пор, пока проецируемое изображение не станет самой яркой.Отрегулируйте высоту увеличителя так, чтобы проецируемое изображение было размером с область печати на мольберте. Приблизительно сфокусируйте увеличитель.
Обрежьте изображение, глядя на композицию на мольберте. Большинство ангиограмм будут распечатаны в полнокадровом режиме: то есть будет распечатан весь негатив. Просто отрегулируйте высоту увеличителя и фокусировку до тех пор, пока изображение не станет резким, и очень небольшая часть изображения попадет на створки мольберта, чтобы получить четкую границу.
Иногда, особенно с изображениями, отличными от ангиограмм, желательно распечатать только часть негатива.Сделав проецируемое изображение больше, чем область печати на мольберте, изображение можно обрезать так, чтобы напечатать только его часть. Этот метод может быть полезен для привлечения внимания к поражению в центре макулы или для выравнивания горизонта на живописной фотографии.
Критически сфокусируйте изображение с помощью лупы. Типы с большим увеличением, называемые фокусировщиками зерна, обеспечивают наиболее критическую фокусировку. Поместите лупу на мольберт и смотрите в окуляр, медленно поворачивая ручку фокусировки на увеличителе.Когда изображение (или зернистость) кажется резким, убедитесь, что изображение все еще покрывает всю область печати на мольберте. Изменение фокуса немного меняет размер изображения.
Фокусировка изображения
Всегда фокусируйте изображение с широко открытым объективом, чтобы изображение было самым ярким на мольберте. Во-первых, изображение будет ярче и его легче увидеть, но основная причина в том, что проецируемое изображение имеет гораздо меньшую глубину резкости при открытом объективе, что делает точку истинной фокусировки гораздо более очевидной.Как только изображение сфокусировано, объектив можно закрыть для экспонирования.
Сделайте тест-полоску. Процедура изготовления тест-полосок может быть почти идентична созданию тест-полоски из контактного листа, который мы рассмотрели в разделе «Создание контактной печати».
Закройте объектив до тех пор, пока изображение не станет наиболее темным, затем откройте объектив на два стопа (два «щелчка» кольца диафрагмы). Став опытным печатником, вы сможете оценить количество света, падающего на мольберт, и, возможно, сможете просто закрыть линзу до точки, при которой экспозиция печати будет составлять около 10 секунд.Но это требует значительной практики.
Установите таймер увеличителя на 2 секунды, как это делалось при контактной печати. Поместите в мольберт целый лист бумаги. Поместите кусок картона на бумагу так, чтобы на конце было около 1,5 дюймов. Нажмите кнопку экспозиции на таймере увеличителя, чтобы сделать экспозицию в две секунды. Слегка сдвиньте картон, открывая еще 1½ дюйма бумаги, и сделайте еще двухсекундную экспозицию. Повторяйте процесс до тех пор, пока не будет обнажена вся тест-полоска.
Есть много вариаций на эту тему.Например, нет необходимости использовать весь лист бумаги для тест-полосок. Полоска бумаги шириной 3 дюйма вполне может служить этой цели.
Открытие тест-полоски
После экспонирования обработайте тест-полоску, поместив ее в бумажный проявитель на 2 минуты при перемешивании, затем остановите ванну и закрепите, как это было сделано с контактной печатью.
Сделайте окончательный отпечаток. Выберите наилучшую экспозицию на тест-полоске, сделайте и установите таймер соответственно.Поместите лист бумаги в мольберт и нажмите кнопку экспонирования на таймере увеличителя. Обработайте бумагу как обычно. Как и в случае с контактной печатью, бумага должна оставаться в проявителе не менее 2 минут, чтобы получить насыщенный черный цвет. Бумага может оставаться в проявителе дольше, чтобы изображение стало темнее. Слишком раннее извлечение бумаги из проявителя приведет к получению неровных серых тонов вместо черного.
Локальный контроль экспозиции. Когда будет сделана полная печать, можно заметить, что почти все изображение имеет очень приятную плотность, одна небольшая область немного темная.Если бы экспозиция была уменьшена, чтобы выделить детали в темную область, остальная часть отпечатка будет слишком светлой. Вместо того, чтобы уменьшать яркость всего изображения, можно использовать небольшой кусок ленты или картона на конце провода, чтобы не допустить попадания света в темную область, не затрагивая остальную часть отпечатка.
Осветление — это название, данное этой локальной блокировке экспонирования для осветления определенной области отпечатка. Сделайте инструмент для уклонения, намотав небольшой кусок черной фотоленты на конец проволоки (подойдет и вешалка).Допустим, выдержка всего отпечатка составляет 10 секунд. Нажмите кнопку экспонирования. Во время экспонирования вставьте провод в световой тракт, заблокировав экспонирование слишком темной области. Заблокируйте его на секунду или две из десятисекундной экспозиции. Слегка перемещая инструмент для осветления и удерживая его на достаточном расстоянии от бумаги, вы получите размытые края, позволяющие осветленной области слиться с остальной частью отпечатка. Обработайте бумагу и оцените результаты. При необходимости скорректируйте время или место уклонения.
Горение — это противоположность уклонению. Весь отпечаток выглядит довольно хорошо, но есть одна небольшая область, которая слишком светлая. Увеличение экспозиции всего отпечатка, чтобы увидеть детали в светлой области, сделает остальную часть отпечатка слишком темной. Поэтому мы оставляем базовую экспозицию в покое и добавляем немного больше экспозиции в слишком светлую область. Для этого подойдет кусок картона с прорезанным отверстием.
Инструмент для записи
Давайте возьмем 10 секунд в качестве примера для базовой выдержки.Нажмите кнопку экспонирования и подождите, пока будет открыт весь отпечаток. После завершения экспонирования поместите картон между линзой и бумагой, рядом с линзой, но не касаясь ее, чтобы свет не падал на бумагу. Установите переключатель фокуса на таймере увеличителя и включите свет увеличителя. Быстро переместите картон, чтобы через отверстие на бумагу пролился дополнительный свет на область, которую вы хотите затемнить. Считайте две-три секунды. Перемещение отверстия во время прожига области отпечатка позволит краям выжженной области слиться с окружающими областями на отпечатке.
Контрастные фильтрымогут использоваться с бумагой для печати с переменным контрастом для увеличения или уменьшения контрастности отпечатка. Бумага с переменным контрастом обычно покрывается эмульсией с высокой и низкой контрастностью. Без фильтрации обе эмульсии открываются, и достигается «нормальный» контраст. Размещение желтого фильтра на световом пути выберет эмульсию с низким контрастом вместо эмульсии с высокой контрастностью, снизив контрастность отпечатка. Размещение фиолетового фильтра на пути света выбирает высококонтрастную эмульсию, повышая контраст изображения.
Контрастные фильтры продаются в наборах и производятся производителем бумаги в соответствии с конкретными эмульсиями. Для достижения наилучших результатов используйте набор фильтров, предназначенный для вашей бумаги.
Обзор векторов и снарядов — с ответами №2
Перейдите к:
Обзорная сессия Главная — Список темВекторы и снаряды — Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || # 1-9 || # 10-45 || # 46-55 || # 56-72
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
Часть B: множественный выбор
10.Если сложить два вектора смещения 6 метров и 8 метров (с разными направлениями), то результат может находиться в диапазоне от ___ метров до ___ метров.
а. 0, 48 | г. 1,33, 48 | г. 0, 14 | г. 2, 14 |
e. …бред какой то! Такого прогноза сделать нельзя. | |||
ф. … бред какой то! Можно сделать прогноз, но ни один из этих вариантов не верен. | |||
Ответ: D
Векторная сумма 6,0 метра и 8,0 метра будет наибольшей, если их сложить в одном направлении; что даст в результате 14 метров. Векторная сумма 6,0 метра и 8,0 метра будет наименьшей, если их сложить в противоположном направлении; что даст результат 2.0 метров. Анимация, изображающая различные результирующие 6,0 метра, добавленные к 8,0 метрам в различных направлениях, показана на отдельной странице. Смотрите анимацию.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
11. Три вектора добавляются согласно правилам сложения векторов. Четвертый вектор рисуется от хвоста первого вектора к голове последнего вектора.Этот четвертый вектор обозначается как ____.
а. равновесный | г. гипотенуза | г. в результате | г. ошибка |
Ответ: C
Результирующий результат представляет собой результат добавления двух или более векторов. На диаграмме сложения масштабированных векторов результат всегда тянется от хвоста первого вектора к голове последнего вектора.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
12. ИСТИНА или ЛОЖЬ:
Порядок добавления векторов повлияет на конечный результат.
Ответ: B
Порядок, в котором добавляются векторы, не влияет на величину или направление результирующего.A + B + C дает тот же результат, что и B + C + A, и тот же результат, что и A + C + B. Анимация, изображающая сложение пяти векторов в трех разных порядках, отображается на отдельной странице. . Смотрите анимацию.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
13. Вектор A направлен на север, а вектор B — на восток.Какая из следующих векторных диаграмм сложения лучше всего представляет сложение векторов A и B и последующий результат?
Ответ: E
Если используется метод «голова к хвосту» (иногда называемый методом треугольника), то хвост B должен быть нарисован, начиная с головы A. Обе диаграммы D и E показывают это. Затем полученный результат следует провести от хвоста A к голове B (что не показано на диаграмме D). Также существует метод параллелограмма для сложения векторов.В этом методе хвосты двух векторов помещаются вместе (как на диаграммах A и B). Затем следует нарисовать параллелограмм с двумя векторами, образующими смежные стороны параллелограмма. Результирующая проводится от хвостов векторов к противоположному углу параллелограмма. Это сделано неправильно на диаграммах A и B. Диаграммы C и F не похожи ни на один (точный) метод сложения векторов, известный человечеству.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
14.При добавлении вектора B к вектору A геометрически (или графически) с использованием метода «голова к хвосту» результат отрисовывается от ____ до ____.
а. голова А, хвост В | г. хвост А, голова Б | ||
г. голова Б, хвост А | г. хвост Б, голова А |
Ответ: B
Добавление вектора B к вектору A эквивалентно слову A + B.В таком случае сначала рисуется A, затем B рисуется с хвостом во главе A. Наконец, результат рисуется от хвоста первого вектора (A) до головы последнего вектора ( Б) .
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]Используйте следующие векторные диаграммы сложения для вопросов # 15- # 20.
15. Какое из следующих уравнений сложения векторов показано на диаграмме 1?
а. А + В = С | г. А + С = В | г. В + С = А | г. В + А = С |
e. С + В = А | ф.С + А = В | г. Ни один из этих |
16. Какое из следующих уравнений сложения векторов показано на диаграмме 2?
а. А + В = С | г. А + С = В | г. В + С = А | г.В + А = С |
e. С + В = А | ф. С + А = В | г. Ни один из этих |
17. Какое из следующих уравнений сложения векторов показано на диаграмме 3?
а. А + В = С | г.А + С = В | г. В + С = А | г. В + А = С |
e. С + В = А | ф. С + А = В | г. Ни один из этих |
18. Какое из следующих уравнений сложения векторов показано на диаграмме 4?
а.А + В = С | г. А + С = В | г. В + С = А | г. В + А = С |
e. С + В = А | ф. С + А = В | г. Ни один из этих |
Ответы на вопросы №15- №18:
15.В
16. А
17. E
18. G
Векторы добавляются методом «голова к хвосту», и результат протягивается от хвоста первого вектора к началу последнего вектора. Таким образом, если добавляются два вектора — скажем, B добавляется к A (как в A + B) — тогда сначала рисуется A, а хвост B помещается в начало A. Получившийся результат рисуется так, чтобы его хвост находился в хвосте вектора. A и его голова в начале B. Таким образом, когда хвосты двух векторов видны связанными, один из векторов является результирующим, а другой — первым добавляемым вектором.И когда головы двух векторов видны соединенными, один из векторов является результирующим, а другой — вторым добавляемым вектором. Эти принципы могут быть применены для ответа на поставленные выше вопросы.
Обратите внимание, что в вопросе 18 нет ни одного вектора, который проходит от хвоста одного вектора к началу другого вектора. Таким образом, результат не выводится. Можно сказать, что диаграмма показывает, что A + B + C = 0.
19. Рассмотрите величину и направление векторов A и B, как показано на Диаграмме 1 выше.Какая из следующих диаграмм представит B — A = R?
Ответ: B
Вычитание A из B эквивалентно добавлению отрицательного числа A к B. То есть B — A = B + (-A). Негатив вектора — это просто тот же вектор, нарисованный в противоположном направлении. Правильным ответом должна быть диаграмма, на которой сначала изображается буква B. Затем во главе B должен быть нарисован хвост вектора, указывающий в направлении, противоположном направлению A. Это показано на обеих диаграммах B и C.Затем полученный результат должен быть проведен от хвоста B к голове -A. Это не показано на диаграмме C.
20. Рассмотрите величину и направление векторов B и C, как показано на Диаграмме 2 выше. Какая из следующих диаграмм представит C — B = R?
Ответ: C
Вычитание B из C эквивалентно добавлению отрицательного числа B к C. То есть C — B = C + (-B). Негатив вектора — это просто тот же вектор, нарисованный в противоположном направлении.Правильным ответом должна быть диаграмма, на которой сначала нарисован C. Затем во главе C следует нарисовать хвост вектора, указывающий в направлении, противоположном направлению B. Это показано на обеих диаграммах B и C. Полученный результат затем следует провести от хвоста C к голове -B. Это не показано на диаграмме B.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]21.Векторная сумма (только звездная величина) 25,0 м, север + 18,0 м, восток ___ м.
а. 7,00 | г. 21,5 | г. 30,8 | г. 35,8 |
e. 43,0 | ф. 54,2 | г.949 | ч. Ни один из этих |
Ответ: C
Эти два вектора направлены под прямым углом друг к другу. В таких случаях векторная сумма может быть определена с помощью теоремы Пифагора. Результирующее (R) равно квадратному корню из суммы квадратов двух добавляемых векторов. То есть R = Sqrt (A 2 + B 2 ), где A и B — два вектора, которые складываются вместе.Таким образом,
R = Площадь [(25,0 м) 2 + (18,0 м) 2 ] = Площадь [(625 м 2 ) + (324 м 2 )] = Площадь (949 м 2 )R = 30,805 м = ~ 30,8 м
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]22. Векторная сумма (только звездная величина) 32,0 м, север + 41.0 м, запад ___ м.
а. 9.00 | г. 36,5 | г. 38,0 | г. 52,0 |
e. 73,0 | ф. 128 | г. 2,70 х 10 3 | ч.Ни один из этих |
Ответ: D
Как и в вопросе № 21 выше, эти два вектора направлены под прямым углом друг к другу. Теорема Пифагора может использоваться, чтобы определить результат их суммы. Результирующее (R) равно квадратному корню из суммы квадратов двух добавляемых векторов.
R = Sqrt (A 2 + B 2 )R = Sqrt [(32,0 м) 2 + (41,0 м) 2 ] = Sqrt [(1024 м 2 ) + (1681 м 2 )] = Sqrt (2705 м 2 )
R = 52.010 м = ~ 52,0 м
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
Используйте схему ниже, чтобы ответить на вопросы # 23- # 28. Каждый квадрат на диаграмме представляет собой площадь 20 х 20 метров.
23. Если человек идет от D к H, от G к C, то пройденное расстояние составляет ____ метров.
а. 128 | г. 180 | г. 401 | г. 460 |
e. 480 | ф. 533 | г. 620 | ч. Ни один из этих |
Ответ: F
Расстояние — это скалярная величина, и сложить три скаляра так же просто, как арифметически сложить три числа.Однако, поскольку первый из трех этапов этого путешествия не проходит через восток, запад, север или юг, для определения расстояния для этого этапа требуется использование теоремы Пифагора. То есть ходьба от D к H эквивалентна переходу на 140 метров на восток (7 квадратов) и 160 метров (8 квадратов) на юг. Таким образом, расстояние от D до H составляет 212,6 метра — Sqrt [(140 м) 2 + (160 м) 2 ]. Расстояние от H до G составляет 80 метров (4 квадрата), а от G до C — 240 метров (12 квадратов).Общее пройденное расстояние составляет 212,6 м + 80 м + 240 м = 532,6 м = ~ 533 м .
24. Если человек идет от D к H, от G к C, то величина смещения составляет ____ метров.
а. 128 | г. 180 | г. 401 | г. 460 |
e.480 | ф. 533 | г. 620 | ч. Ни один из этих |
Ответ: A
Смещение — это векторная величина, которая показывает, как далеко от нашего места находится объект в конце движения относительно начала движения. Смещение не зависит от пути, пройденного от начальной позиции до конечной позиции, а только от расстояния вектора, нарисованного от начала до конца.Результирующая для трех сегментов этого блуждания просто переносится из D в C. Расстояние этого результирующего результата находится с помощью теоремы Пифагора. Результирующий простирается на юг на 80 метров (4 квадрата) и на запад на 100 метров (5 квадратов). Результирующая величина имеет величину Sqrt [(80 м) 2 + (100 м) 2 ] или 128 метров.
25. Если человек идет от D к H, от G к C, то направление смещения составляет ___ градусов (при измерении против часовой стрелки с востока).
а. 39 | г. 51 | г. 53 | г. 217 |
e. 219 | ф. 231 | г. 233 | ч. Ни один из этих |
Ответ: E
Как обсуждалось в предыдущей задаче, результирующая тянется на юг на 80 метров (4 квадрата) и на запад на 100 метров (5 квадратов).Это показано на диаграмме справа. Эти две части результирующего вектора можно объединить с тригонометрической функцией для определения угла тета. Угол тета составляет примерно 38,7 градуса. Это не направление результирующего смещения, а просто угол между вектором смещения и западным направлением. Условие, используемое для выражения направления вектора, заключается в измерении угла поворота против часовой стрелки с востока. Итак, в данном случае направление 180 градусов + 38.7 градусов или ~ 219 градусов.
26. Если человек идет от H до E, от C до G, то пройденное расстояние составляет ____ метров.
а. 80. | г. 240. | г. 253 | г. 333 |
e. 493 | ф.560. | г. 640. | ч. Ни один из этих |
Ответ: E
Расстояние — это скалярная величина, и сложить три скаляра так же просто, как сложить отдельные расстояния трех ног так же просто, как сложить расстояния. арифметически. Задача упрощается тем, что первые два отрезка пути проходят по одному и тому же отрезку линии.Остановку в точке E можно не принимать во внимание, поскольку это просто точка на линии от точки H до точки C. То есть HE + EC = HC . Поскольку отрезок линии HC не простирается на восток, запад, север или юг, определение расстояния для этого отрезка требует использования теоремы Пифагора. То есть ходьба от H к C эквивалентна ходу на 240 метров на запад (12 квадратов) и 80 метров (4 квадрата) на север. Таким образом, расстояние от D до H составляет 253,0 метра — Sqrt [(240 м) 2 + (80 м) 2 ].Расстояние от H до E до C составляет 253 метра, а от C до G — 240 метров (12 квадратов). Общее пройденное расстояние составляет 253 м + 240 м = ~ 493 м .
27. Если человек идет от H к E, от C к G, то величина смещения составляет ____ метров.
а. 80. | г. 240. | г. 253 | г.333 |
e. 493 | ф. 560. | г. 640. | ч. Ни один из этих |
Ответ: A
Смещение — это векторная величина, которая показывает, как далеко от нашего места находится объект в конце движения относительно начала движения.Смещение не зависит от пути, пройденного от начальной позиции до конечной позиции, а только от расстояния вектора, нарисованного от начала до конца. Результирующая величина для трех сегментов этой прогулки просто вычерчивается от H до G. Расстояние этой результирующей составляющей просто 80 метров (4 квадрата) на север.
28. Если человек идет от H к E, от C к G, то направление смещения составляет ___ градусов (при измерении против часовой стрелки с востока).
а.0 | г. 18. | г. 72 | г. 90. |
e. 108 | ф. 162 | г. 342 | ч. Ни один из этих |
Ответ: D
Конечный пункт назначения G находится к северу от исходного местоположения.Таким образом, смещение направлено на север (на 90 градусов).
Используйте следующую схему для вопросов # 29- # 33. На схеме показано речное судно, начинающееся в позиции А на восточном берегу реки. Лодка направляется к позиции B (точка прямо через реку от точки A) со скоростью 3.8 м / с. Но из-за течения со скоростью 1,8 м / с лодка приземляется на западном берегу реки в точке C, расположенной ниже по течению от B. Ширина реки (d через ) составляет 86,4 метра.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
29. Величина результирующей скорости лодки ____ м / с.
а. 1,8 | г. 2,0 | г. 3,4 | г. 3,8 |
e. 4,2 | ф. 5,6 | г.11 | ч. Ни один из этих |
Ответ: E
Это случай, когда лодка пересекает реку с помощью своего двигателя.Мотор позволяет лодке преодолевать 3,8 метра в сторону противоположного берега каждую секунду. Река течет на юг, каждую секунду унося лодку вниз на 1,8 метра. Результирующая скорость — это просто векторная сумма этих двух отдельных скоростей. Поскольку эти две скорости расположены под прямым углом друг к другу, векторная сумма может быть определена с помощью теоремы Пифагора.
v результат 2 = (3,8 м / с) 2 + (1,8 м / с) 2v результат = Sqrt [(3.8 м / с) 2 + (1,8 м / с) 2 ]
v результат = 4,2 м / с
30. Направление результирующей скорости лодки ____ м / с.
а. 0 | г. 18. | г. 712 | г. 90. |
e.108 | ф. 162 | г. 342 | ч. Ни один из этих |
Ответ: H
Направление результирующей скорости — юго-восток. Это помещает вектор в третий квадрант с направлением где-то между 180 и 270 градусами. Точный угол можно определить, если угол тета определяется с помощью тригонометрии.Тета — это угол, который результирующая скорость (красный вектор на диаграмме справа) составляет относительно западного направления. Этот угол можно найти с помощью функции касательной. Работа показана справа.
Угол тета составляет 25,3 градуса. Фактическое направление, измеренное как угол поворота против часовой стрелки с учетом восточного направления, составляет 180 градусов плюс 25,3 градуса. Это будет 205,3 градуса .
31. Время, необходимое лодке для пересечения 86.Река шириной 4 м занимает ___ секунд.
а. 4,2 | г. 15 | г. 21 | г. 23 |
e. 48 | ф. Ни один из этих |
Ответ: D
Мотор позволяет лодке двигаться 3.8 метров в сторону противоположного берега каждую секунду. Длина пути от берега до берега составляет 86,4 метра. (Присутствие течения не влияет на ширину или расстояние от берега до берега.) Время перехода через реку можно рассчитать, исходя из ширины реки и скорости лодки, используя уравнение v = d / t. Преобразуя уравнение для решения относительно t, получаем
т = д / v t = (86,4 м) / (3,8 м / с) = ~ 23 с (без закругления 22,7 с)
32.Местоположение C — это место, где лодка в конечном итоге приземляется на противоположном берегу. Каково расстояние от точки B до точки C.
а. 37 | г. 41 | г. 78 | г. 86 |
e. 96 | ф.180 | г. 2,0 х 10 2 | ч. Ни один из этих |
Ответ: B
Расстояние, на котором точка C находится ниже по течению от точки B, математически связано со скоростью реки и временем перехода через реку. Расстояние можно рассчитать, умножив текущую скорость на время перехода через реку.
d ниже по течению = v река • td ниже по потоку = (1.8 м / с) • (22,7 с)
d ниже по потоку = ~ 41 м
33. Если течение в определенный день было в два раза большей скоростью, то время для перехода через реку было бы ____.
а. в два раза больше | г. вдвое меньше | ||
г. больше, но не в два раза больше | г.меньше, но не в два раза меньше исходного времени | ||
e. так же, как это было при скорости тока 1,8 м / с. | |||
Ответ: E
В этой ситуации, когда лодка движется прямо через реку, скорость течения направлена перпендикулярно скорости лодки. Эти две составляющие результирующего движения лодки не зависят друг от друга. Скорость лодки делает единственный вклад в способность лодки пересекать реку.Скорость реки несет лодку только на юг вниз по реке. Таким образом, изменение скорости реки не повлияет на время, необходимое лодке для пересечения реки.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
34. Объект совершает свободное падение. При падении объект ____.
а. скорость увеличивается | г. ускорение увеличивается |
г. оба эти | г. ни один из этих |
Ответ: A
Когда объект свободно падает, его скорость (а также скорость) изменяется примерно на 10 м / с каждую секунду.Это означает, что ускорение имеет постоянное значение 10 м / с / с. Объект имеет изменяющуюся скорость (или скорость) и постоянное ускорение, если скорость изменяется на одну и ту же величину («постоянную величину») в каждую последующую секунду его движения.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
35.Футбольный мяч подбрасывается в воздух под углом 45 градусов к горизонту. В самом верху траектории мяча его скорость равна _______.
а. полностью вертикальный | г. полностью горизонтально |
г. как вертикальный, так и горизонтальный | г. недостаточно информации, чтобы знать. |
Ответ: B
По мере того, как снаряд поднимается к своему пику, его горизонтальная скорость остается постоянной, а вертикальная скорость уменьшается.На пике его вертикальная скорость становится равной 0 м / с. В этот момент скорость полностью горизонтальна; у скорости нет вертикальной составляющей.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
36. Футбольный мяч подброшен в воздух под углом 45 градусов к горизонтали.На самом верху пути мяча его ускорение составляет _______. (Не обращайте внимания на сопротивление воздуха.)
а. полностью вертикальный | г. полностью горизонтально |
г. как вертикальный, так и горизонтальный | г. недостаточно информации, чтобы знать. |
Ответ: A
По мере того, как снаряд поднимается к своему пику, его горизонтальная скорость остается постоянной, а вертикальная скорость уменьшается.Это означает, что объект ускоряется по вертикали, а не по горизонтали. На пике и по всей траектории наблюдается вертикальное (нисходящее) ускорение. Фактически, снаряд — это объект, на который действует единственная сила тяжести. Эта сила вызывает ускорение в том же направлении, что и сила — вниз.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
37.Футбольный мяч подбрасывается в воздух под углом 45 градусов к горизонту. В самом верху траектории мяча действующая на него чистая сила равна _______. (Не обращайте внимания на сопротивление воздуха.)
а. полностью вертикальный | г. полностью горизонтально |
г. как вертикальный, так и горизонтальный | г.недостаточно информации, чтобы знать. |
Ответ: A
Снаряд — это объект, на который действует только сила тяжести. Поскольку никакие другие силы не действуют на объект, результирующая сила будет направлена вниз.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
38.В какой точке его пути горизонтальная составляющая скорости (v x ) снаряда наименьшая?
а. В тот момент, когда он брошен. | г. На полпути к вершине. | г. На вершине. |
г. По мере приближения к вершине. | e. То же самое на всем пути. | |
Ответ: E
По мере того, как снаряд поднимается к своему пику, его горизонтальная скорость остается постоянной, а вертикальная скорость уменьшается. Это означает, что объект ускоряется по вертикали, а не по горизонтали. При постоянной горизонтальной скорости нет точки на траектории, где значение v x меньше, чем в других точках.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
39.В какой точке его пути вертикальная составляющая скорости (v y ) снаряда наименьшая?
а. В тот момент, когда он брошен. | г. На полпути к вершине. | г. На вершине. |
г. По мере приближения к вершине. | e. То же самое на всем пути. | |
Ответ: C
По мере того, как снаряд поднимается к своему пику, его горизонтальная скорость остается постоянной, а вертикальная скорость уменьшается. Во время восходящего участка траектории v y непрерывно уменьшается, пока не станет равным 0 м / с на пике. Таким образом, v y настолько малы, насколько они когда-либо будут, когда они находятся на пике траектории.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
40.Самолет, который летит со скоростью 100 км / ч при боковом ветре урагана со скоростью 100 км / ч, имеет скорость (относительно земли) ____.
а. 0 км / ч | г. 100 км / ч | г. 141 км / ч | г. 200 км / ч |
Ответ: C
Когда объект, такой как самолет или лодка, движется в среде, которая движется относительно земли, скорость самолета или лодки (измеренная его спидометром) не будет такой же, как скорость, измеренная человеком. на земле ( путевая скорость ).Скорость относительно земли (т. Е. Результирующая скорость, полученная комбинацией скорости самолета и скорости ветра) может быть определена путем сложения скорости самолета и скорости ветра в виде векторов. В этом случае два вектора расположены под прямым углом, поэтому результирующую скорость можно определить с помощью теоремы Пифагора.
R 2 = (100 км / час) 2 + (100 км / час) 2R = SQRT ((100 км / час) 2 + (100 км / час) 2 )
R = 141 км / час
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
41.Самолет движется со скоростью 141 км / ч на северо-восток (45 градусов). Какова его составляющая скорость в северном направлении?
а. 41 км / ч | г. 100 км / ч | г. 110 км / ч | г. 141 км / ч |
Ответ: B
Чтобы определить компонент вектора в заданном направлении, должны применяться принципы векторного разрешения.Этот вектор скорости направлен под углом 45 градусов и имеет величину 141 км / ч. Вертикальный компонент (север) этого вектора может быть найден с помощью функции синуса.
v y = v * синус (тета)v y = (141 км / ч) * синус (45 градусов)
v y = 100 км / ч
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
42.Скатайте шар для боулинга с края стола. Когда он падает, его горизонтальная составляющая скорости ___.
а. уменьшается | г. остается неизменным | г. увеличивается |
Ответ: B
Как только мяч покидает край стола, он становится снарядом. При падении его горизонтальная скорость остается постоянной, а вертикальная — уменьшается.Это означает, что объект ускоряется по вертикали, а не по горизонтали. Фактически, снаряд — это объект, на который действует единственная сила тяжести. Эта сила вызывает ускорение в том же направлении, что и сила — вниз.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
43.Пуля выстреливается горизонтально и падает на землю за 0,5 секунды. Если бы он был запущен с удвоенной скоростью в том же направлении, он бы упал на землю через ____. (Предположим, что сопротивление воздуха отсутствует.)
а. менее 0,5 с. | г. более 0,5 с. | г. 0,5 с. |
Ответ: C
Как только пуля выходит из дула, она становится снарядом (при условии отсутствия сопротивления воздуха).При падении его горизонтальная скорость остается постоянной, а вертикальная — уменьшается. Сила тяжести действует на пулю, вызывая ее ускорение вниз. Движение пули в направлении вниз не зависит от движения в горизонтальном направлении. То есть любое изменение в горизонтальном аспекте его движения не повлияет на движение в вертикальном направлении. На время вертикального падения на землю не влияет горизонтальная скорость снаряда.Чтобы упасть на землю с этой высоты, все равно потребуется 0,5 секунды, независимо от горизонтальной скорости.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
44. Снаряд запускается под углом 15 градусов над горизонтом и падает на дальность. При такой же скорости под каким другим углом проецирования будет получено такое же расстояние вниз?
а.30 градусов. | г. 45 градусов. | г. 50 градусов. | г. 75 градусов | e. 90 градусов. |
Ответ: D
Для снарядов, выпущенных под углом, угол пуска в 45 градусов обеспечивает наибольшее горизонтальное смещение. Любые два угла запуска, которые отделены от 45 градусов на одинаковую величину (например, 40 градусов и 50 градусов, 30 градусов и 60 градусов и 15 градусов и 75 градусов), будут обеспечивать одинаковое горизонтальное смещение.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]
45. Два снаряда выстреливаются с одинаковой скоростью, но под разными углами. Один стреляет под углом 30 градусов, другой — под углом 60 градусов. Снаряд, который первым попадет в землю, будет выпущен (без учета сопротивления воздуха) ____.
а.30 градусов | г. 60 градусов | г. оба попали одновременно |
Ответ: A
Для снарядов, выпущенных под углом, угол пуска в 45 градусов обеспечивает наибольшее горизонтальное смещение. Углы пуска более 45 градусов приводят к большим вертикальным составляющим скорости; они дольше остаются в воздухе и поднимаются на большую высоту.Углы пуска менее 45 градусов приводят к небольшим вертикальным составляющим скорости; они не поднимаются так высоко и в конечном итоге за более короткое время падают на землю.
[# 10 | # 11 | # 12 | # 13 | # 14 | # 15 | # 16 | # 17 | # 18 | # 19 | # 20 | # 21 | # 22 | # 23 | # 24 | # 25 | # 26 | # 27 | # 28 | # 29 | # 30 | # 31 | # 32 | # 33 | # 34 | # 35 | # 36 | # 37 | # 38 | # 39 | # 40 | # 41 | # 42 | # 43 | # 44 | # 45]Перейдите к:
Обзорная сессия Главная — Список темВекторы и снаряды — Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || # 1-9 || # 10-45 || # 46-55 || # 56-72
Вам тоже может понравиться…
Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, которые включают встроенную обратную связь и инструкции. Если это то, что вы ищете, то вам также может понравиться следующее:- Блокнот калькулятора
Блокнот калькулятора включает в себя текстовые задачи по физике, организованные по темам. Каждая проблема сопровождается всплывающим ответом и аудиофайлом, в котором подробно объясняется, как подойти к проблеме и решить ее.Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.
Посещение: Панель калькулятора Главная | Блокнот калькулятора — Векторы и снаряды
- Minds On Physics Приложение серии
Minds On Physics Приложение («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно настроены улучшить свое концептуальное понимание физики. Каждый модуль этой серии посвящен отдельной теме и разбит на подтемы.


 Достаточно знать, какую скорость он развивает и расстояние между городами. В случае же, когда нам надо рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то тут уж никак не обойтись без точного знания формы и размеров того же самолета.
Достаточно знать, какую скорость он развивает и расстояние между городами. В случае же, когда нам надо рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то тут уж никак не обойтись без точного знания формы и размеров того же самолета.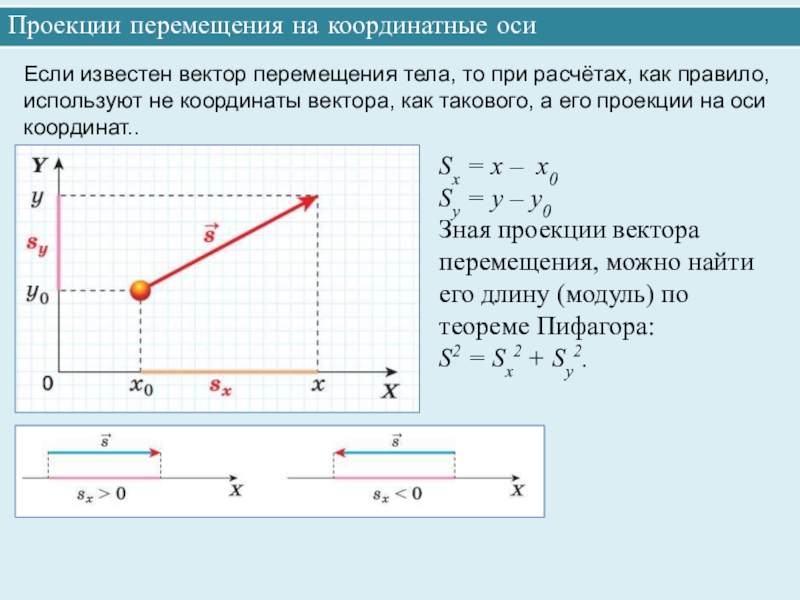 Но на практике часто встречаются задачи в которых необходимо вычислить положение тела, то есть записать его координаты в некоторой системе координат.
Но на практике часто встречаются задачи в которых необходимо вычислить положение тела, то есть записать его координаты в некоторой системе координат. Начало оси х=0 совместим с пристанью. За положительное направление примем направление на восток.
Начало оси х=0 совместим с пристанью. За положительное направление примем направление на восток.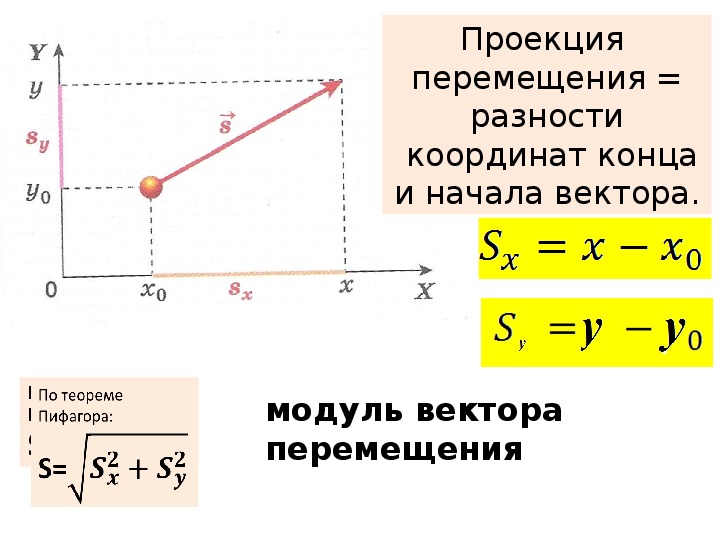 Длины отрезков sx1 и sx2 будут равны длинам векторов s1 и s2. Модуль каждой проекции будет равен модулю соответствующего ей вектора.
Длины отрезков sx1 и sx2 будут равны длинам векторов s1 и s2. Модуль каждой проекции будет равен модулю соответствующего ей вектора.
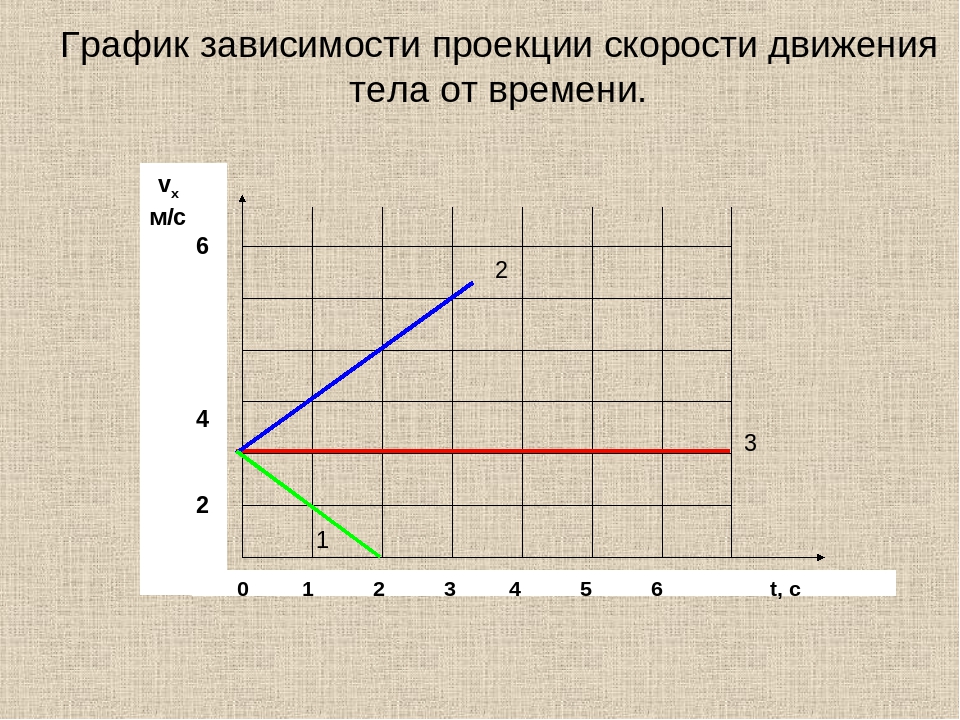

 В случае с линейкой и монеткой в домашних условиях это трудно проделать, но в условиях лаборатории можно зафиксировать, что при постоянном угле наклона скользящая монетка за каждую секунду изменяет свою скорость на одинаковую величину.
В случае с линейкой и монеткой в домашних условиях это трудно проделать, но в условиях лаборатории можно зафиксировать, что при постоянном угле наклона скользящая монетка за каждую секунду изменяет свою скорость на одинаковую величину.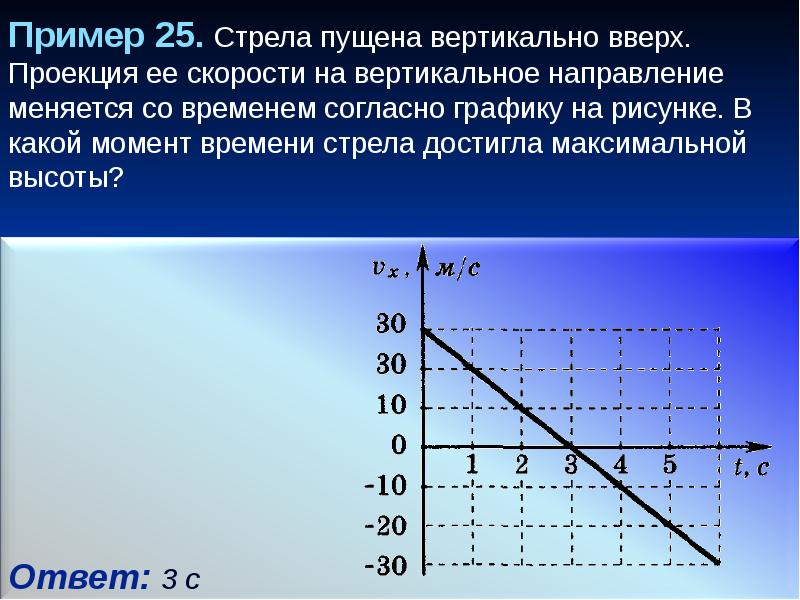 Так происходит в случае прямолинейного равноускоренного движения. Формула для ускорения выглядит следующим образом:
Так происходит в случае прямолинейного равноускоренного движения. Формула для ускорения выглядит следующим образом: Формула тогда примет вид: a =v /t для первого случая либо же: a = v_0 /t для второго.
Формула тогда примет вид: a =v /t для первого случая либо же: a = v_0 /t для второго. 2) в течение 4 секунд.
2) в течение 4 секунд.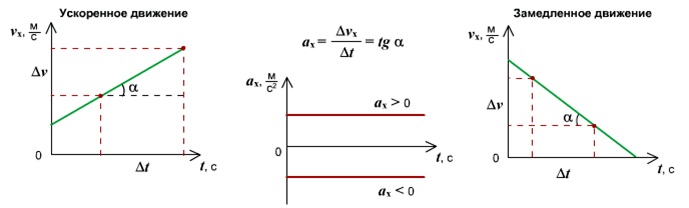
 2=4*S1.
2=4*S1. То есть они являются как бы неким своеобразным признаком равноускоренного движения. Если необходимо проверить, является ли движение равноускоренным, то можно проверить эти закономерности, и если они будут выполняться, то движение будет равноускоренным.
То есть они являются как бы неким своеобразным признаком равноускоренного движения. Если необходимо проверить, является ли движение равноускоренным, то можно проверить эти закономерности, и если они будут выполняться, то движение будет равноускоренным.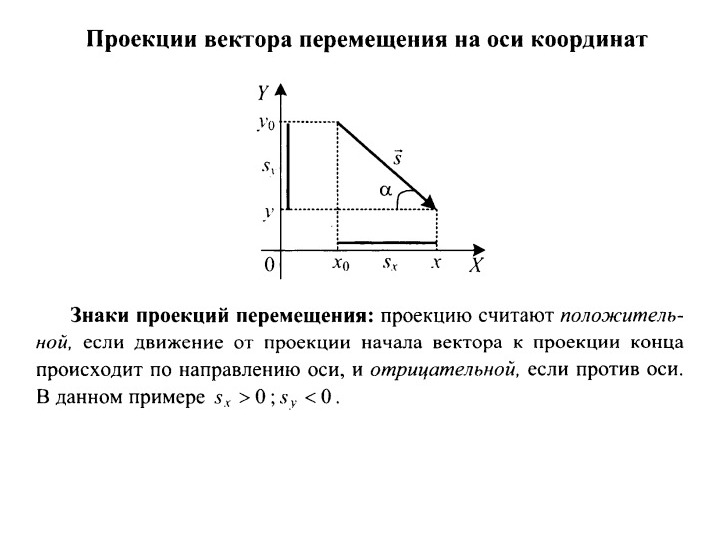

 Каждый ваш шаг будет гигантским расстоянием для молекулы асфальта и ничтожным для планеты Земля. Любое движение, как и все его характеристики всегда имеют смысл только относительно чего-либо еще.
Каждый ваш шаг будет гигантским расстоянием для молекулы асфальта и ничтожным для планеты Земля. Любое движение, как и все его характеристики всегда имеют смысл только относительно чего-либо еще.
Leave A Comment