Отрицательная проекция скорости – Скорость движения в физике

Скорость движения в физике

Скорость является одной из основных характеристик механического движения. Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.

Единицей измерения скорости в системе СИ является м/с.

Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по траектории движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).

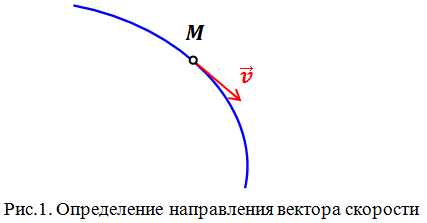
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.

Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).

Отрицательная скорость

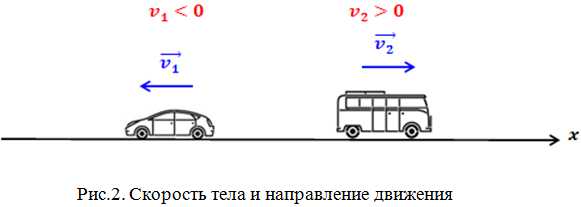
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.

Равномерное и неравномерно движение

В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.

В случае неравномерного движения говорят о средней скорости:

Примеры решения задач по теме «Скорость»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Почему и как существует отрицательная скорость?

Velocity — вектор. Скорость — его величина.
Позиция — это вектор. Длина (или расстояние ) — его величина.

Вектор указывает в направлении в пространстве. Отрицательный вектор (или, точнее, «отрицательный вектор») просто указывает противоположный путь.

Если я поеду из своего дома на свое рабочее место (а затем определив свое положительное направление таким образом), то моя скорость будет положительной, если я пойду на работу , но отрицательно, когда вернусь с работы. Это все о направлении, которое видно из того, как я определил свою положительную ось

Рассмотрим пример, когда я вернусь назад, чем там, где я начал. У меня, должно быть, была отрицательная чистая скорость, чтобы закончить движение назад (я заканчиваю в отрицательном положении ). Но только потому, что назад и вперед четко определяются как отрицательные и положительные направления, соответственно, прежде чем я начну.

Итак, существует ли отрицательная скорость? Ну, так как это всего лишь вопрос слов, описывающих событие, то да . Отрицательная скорость просто означает скорость в противоположном направлении, чем то, что было бы положительным.

Jon Custer

Точно так же время может быть положительным (завтра) и отрицательным (вчера).

immibis

@AndrejSlavejkov Velocity — вектор. Строго говоря, векторы не могут быть отрицательными. Но для 1D-вектора (который может указывать только два пути) вы можете называть одностороннее позитивное или вперед, а наоборот — отрицательным или обратным.

Floris

@AndrejSlavejkov вы путаете скорость и скорость. Скорость — это абсолютное расстояние (положительное), деленное на абсолютное время (положительное). Velocity — относительное расстояние (конец — старт), деленное на время. Поэтому, если вы двигаетесь к отрицательной оси, «конец» меньше «старта», а число, которое вы вычисляете, отрицательно. Если вам нравится, в качестве вектора вы записываете скорость = скорость * d i r e c t i o n → d я р е с T я о N → и знак направления может быть любым …

Shufflepants

Вам не хватает того, что говорят другие. Говоря о скорости, мы говорим не о скалярных числах. Мы говорим о векторах. Если мы выберем систему координат и разместим ваш дом в точке (0,0,0) и вашем рабочем месте (1,0,0), и вы будете путешествовать из своего дома на рабочее место по 1 единице в секунду, тогда ваша скорость (1,0,0). Если вы путешествуете со своего рабочего места в свой дом по 1 единице в секунду, ваша скорость равна (-1,0,0). Ваша концепция скорости кажется величиной скорости. И то и другое v 1 = ( 1 , 0 , 0 ) v 1 знак равно ( 1 , 0 , 0 ) а также v 2 = ( — 1 , 0 , 0 ) v 2 знак равно ( — 1 , 0 , 0 ) имеют величину +1, но v 1 = — v 2 v 1 знак равно — v 2 ,

Floris

@AndrejSlavejkov — Я рад, если мои комментарии помогли, но все, что я сделал, это повторить то, что сказал Стивен. Если бы это помогло вам, вы могли бы принять его ответ (небольшая галочка). Это даст ему заслуженную репутацию.

askentire.net

Проекции скорости и ускорения

Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.

Векторы начальной скорости и ускорения могут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.

Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.

График скорости

Из уравнения следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.

Основные виды движения

1. а_n = 0, a_t = 0 – прямолинейное равномерное движение;

2. а_n = 0, a_t = const – прямолинейное равнопеременное движение;

3. а_n = 0, a_t ¹ 0 –прямолинейное с переменным ускорением;

а_n = const, a_t = 0 –равномерное по окружности

5. а_n = const, a_t = const – равнопеременное по окружности

6. а_n ¹ const, a_t ¹ const – криволинейное с переменным ускорением.

Вращательное движение твердого тела.

Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.

Равномерное движение по окружности

Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.

При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения.

Из подобия треугольников OAB и BCD следует

Если интервал времени ∆t мал, то мал и угол a. При малых значениях угла a длина хорды AB примерно равна длине дуги AB, т.е. . Т.к. , , то получаем

Поскольку , то получаем

Период и частота

Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется

периодам обращения (Т). Т.к. длина окружности равна 2pR, период обращения при равномерном движении тела со скоростью v по окружности радиусом Rравняется:

Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:

(с^-1)

Кинематика вращательного движения

При вращении твердого тела вокруг неподвижной оси OO’ точка M этого тела с радиус-вектором за время Dt пройдет путь равный длине дуги DS, а радиус вектор повернется на угол Dj. Величина называется углом поворота радиус-вектора выбранной точки от некоторого начального положения или модулем углового перемещения.

Для указания направления вращения малым углам поворота приписывают направление: направлен по оси вращения так, чтобы рассматриваемое с его конца вращение происходило против часовой стрелки (правило правого винта). Если тело сделало N поворотов: . Средняя угловая скорость:

(11)

Мгновенная угловая скорость:

(12)

Направление связано с углом поворота правилом правого винта. Размерность – рад/с. Если тело делает n оборотов в сек, то его угловая скорость . Связь линейной и угловой скоростей: ;

или

(13)

в векторной форме:

(14)

Угловое ускорение вращающегося тела

Отношение называется средним угловым ускорением.

infopedia.su

Равномерное прямолинейное движение – FIZI4KA

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время \( t \) тело совершило перемещение \( \vec{s} \), то скорость его движения \( \vec{v} \) равна \( \vec{v}=\frac{\vec{s}}{t} \).

Единица скорости: \( [\,v\,]=\frac{[\,s\,]}{[\,t\,]} \); \( [\,v\,]=\frac{1\,м}{1\,с}=1\frac{м}{с} \). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: \( \vec{s}=\vec{v}t \). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Пусть \( \vec{s} \) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке \( x_0 \) — координата начальной точки перемещения, \( x \) — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: \( \vec{s}_x=x-x_0 \). С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. \( \vec{s}_x=\vec{v}_xt \). Откуда \( x-x_0=\vec{v}_xt \) или \( x=x_0+\vec{v}_xt \). Если начальная координата \( x_0 \) = 0, то \( x=\vec{v}_xt \).

Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае \( x>x_0 \). Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x<x_0 \).

4. Зависимость координаты от времени можно представить графически.

Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: \( x \) = 4 м/с · \( t \). Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

Для того чтобы её построить, необходимо иметь две точки: одна из них \( t \) = 0 и \( x \) = 0, а другая \( t \) = 1 с, \( x \) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

Если в начальный момент времени координата тела \( x_0 \) = 2 м, а проекция его скорости \( v_x \) = 4 м/с, то уравнение движения имеет вид: \( x \) = 2 м + 4 м/с · \( t \). Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой \( t \) = 0, \( x \) = 2 м (рис. 14).

В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) = 2 м – 4 м/с · \( t \). График зависимости координаты такого движения от времени представлен на рисунке 15.

Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

Кратко записать условие задачи.
Проанализировать ситуацию, описанную в условии задачи:
— выяснить, можно ли принять движущиеся тела за материальные точки;
— сделать рисунок, изобразив на нём векторы скорости;
— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.
Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
Решить задачу в общем виде.
Подставить в формулу значения величин и выполнить вычисления.
Проанализировать ответ.

Применим эту последовательность действий к приведённой выше задаче.

Дано: \( v_1 \) = 15 м/с \( v_2 \) = 12 м/с \( l \) = 270 м. Найти: \( t \) – ? \( x\) – ?

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

Система отсчёта связана с Землёй, ось \( Ox \) направлена в сторону движения первого тела, начало отсчёта координаты — т. \( O \) — положение первого тела в начальный момент времени.

Начальные условия: \( t \) = 0; \( x_{01} \) = 0; \( x_{02} \) = 270.

Уравнение в общем виде: \( \vec{s}=\vec{v}t \); \( x=x_0+v_xt \).

Уравнения для каждого тела с учётом начальных условий: \( x_1=v_1t \); \( x_2=l-v_2t \). В месте встречи тел \( x_1=x_2 \); следовательно: \( v_1t=l-v_2t \). Откуда \( t=\frac{l}{v_1+v_2}\cdot t \). Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: \( x \) = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — \( v_1 \) и скорости «Пежо» — \( v_2 \).

1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости \( v_1 \) и \( v_2 \).

1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости \( v_1 \), \( v_2 \) и \( v_3 \) движения этих тел.

1) \( v_1=v_2=v_3 \)
2) \( v_1>v_2>v_3 \)
3) \( v_1<v_2<v_3 \)
4) \( v_1=v_2 \), \( v_3<v_1 \)

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) \( x=1t \) (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Ответы

Равномерное прямолинейное движение

5 (100%) 2 votes

fizi4ka.ru

Ускорение тела в физике

Важно помнить, что ускорение – величина векторная. Говорить об ускорении можно, когда скорость изменяется как по величине, так и по направлению.

Единицей измерения ускорения в системе СИ является м/с .

Примеры ускоренного движения – разгон, торможение, падение, различные маневры.

Если скорость всегда направлена по касательной к траектории движения, и направление вектора скорости совпадает с направлением движения, то вектор ускорения в общем случае может составлять любой угол с вектором скорости. Так, при разгоне по прямолинейному участку пути направления векторов скорости и ускорения совпадают (угол между векторами скорости и ускорения ) (рис.1,а). При торможении на прямолинейном участке шоссе вектора скорости и ускорения противоположно направлены (угол между векторами скорости и ускорения ) (рис.1,б).

При равномерном движении по окружности вектор ускорения перпендикулярен вектору скорости (угол между векторами скорости и ускорения ) (рис.1,в). В более общем сложном случае движения по криволинейной траектории угол между векторами скорости и ускорения зависит от кривизны траектории и интенсивности разгона/торможения, т.е. может принимать любое значение (рис.1,г).

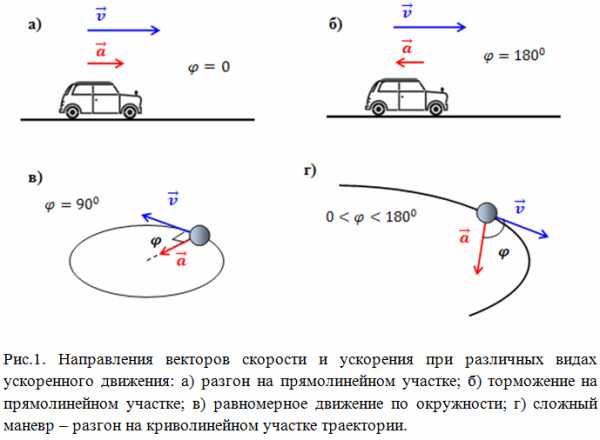
Ускорение может быть как положительным, так и отрицательным. Если , говорят об ускоренном движении, если , движение замедленное.

Примеры решения задач по теме «Ускорение»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Проекция скорости это — Чем отличаются понятия «скорость» и «проекция скорости»? — 22 ответа

В разделе ВУЗы, Колледжи на вопрос Чем отличаются понятия «скорость» и «проекция скорости»? заданный автором Алексей Поспелов лучший ответ это Скорость более общее понятие. А проекция рассматривает скорость вдоль направления, несовпадающего с направлением движенияНЕТ
Просветленный
(37445)
Да кто ж против-то? Тока я толкую о практических задачах. решаемых этим оперативным инструментом, а не о соотношениях между инструментами. Оно когда увлечёшься векторАми сильно, можно и про реальный процесс позабыть

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Чем отличаются понятия «скорость» и «проекция скорости»?

Ответ от Взрослеть[эксперт]
тем же что «вектор» и «проекция вектора на ось»

Ответ от черносотенный[гуру]
Проекция всегда «на что-нибудь». Например, «проекция на ось 0х» или «проекция на горизонтальную плоскость» . Проекция бывает только у векторных величин. У одной и той же векторной величины бесконечное число проекций, поэтому имеет смысл говорить только о конкретной проекции (т. е. проекции на конкретную плоскость или конкретную ось) .
Если с обеих концов вектора на ось или на плоскость опустить 2 отрезка. то концы этих отрезков образуют проекцию вектора на ось или на плоскость.
Чаще всего говорят об оргогональной проекции вектора — т. е. о случае, когда с концов вектора на ось (прямую) или плоскость опускают перпендикулярные этой оси или плоскости отрезки. Ортогональная проекция вектора на ось или плоскость равна произведению вектора на косинус угла между этим вектором и другим вектором (например, вектором оси 0х, 0у или 0z) или этим вектором и какой-то плоскостью.

Ответ от Невропатолог[гуру]
Скорость это числовое значение (скалярная величина) А проекция скорости это Ее направление (вектор)

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Равноускоренное движение на Википедии
Посмотрите статью на википедии про Равноускоренное движение

Ответить на вопрос:

22oa.ru

Проекция вектора скорости на оси координат

В векторной форме уравнения записываются легко и кратко. Но для практических вычислений нужно знать проекции вектора на оси координат выбранной системы отсчета.

Положение точки А (рис. 2.8) задается радиус-вектором . Спроецируем вектор на оси x, y, z.

Рис. 2.8

Понятно, что х, y, z зависят от времени t, т.е. x(t), y(t), z(t). Зная зависимость этих координат от времени (закон движения точки), можно найти в каждый момент времени скорость точки.


Иллюстрация зависимости дальности полета от угла бросания.

Проекция вектора скорости на ось x равна: . Здесь dx – проекция вектора перемещения на ось х.

Аналогично:

Модуль вектора скорости

Так как скорость величина векторная, то её можно представить с помощью единичных векторов i, j, k:

(2.3.6)

ens.tpu.ru