2. Отрезки АВ и CD лежат соответственно в параллельных плоскостях α и β… Зив Б.Г. 10 класс Геометрия. Самостоятельная работа 4. Вариант 3
2. Отрезки АВ и CD лежат соответственно в параллельных плоскостях α и β… Зив Б.Г. 10 класс Геометрия. Самостоятельная работа 4. Вариант 3 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
2.
Отрезки АВ и CD лежат соответственно в параллельных плоскостях α и β (рис. 14). Что можно сказать о взаимном расположении прямых AD и BC?
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Помогите решить контрольную работу
Решите уровнения:
а)4x — 12 = 18 — x
б)21x — 5(2x-7)=24 (Подробнее…)
ГДЗ
Привет! Помогите определить национальности. Модуль (Module) 1c № 1. ГДЗ Английский язык Spotlight 6 класс Ваулина.
a) Match the countries to the nationalities. Listen and check. What nationality are you?
b) Choose a flag and describe it (Подробнее. ..)
..)
ГДЗАнглийский языкSpotlight6 классВаулина Ю.Е.
1. ABCD — квадрат со стороной, равной √2, О — точка пересечения его… Геометрия 10 класс Зив Б.Г. Самостоятельная работа 7. Вариант 2
1. ABCD — квадрат со стороной, равной √2, О — точка пересечения его диагоналей, ОЕ — перпендикуляр к плоскости АВС, ОЕ = √3. Найдите (Подробнее…)
ГДЗГеометрияЗив Б. Г.10 класс
В основании прямой призмы АВСА1В1С1 лежит прямоугольный треугольник… 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 14. Вариант 2
(Подробнее…)
ГДЗГеометрияЗив Б. Г.10 класс
2. Основанием пирамиды PEFM служит равнобедренный треугольник… Геометрия Зив Б.Г. 10 класс. Самостоятельная работа 17. Вариант 2
2. Основанием пирамиды PEFM служит равнобедренный треугольник, EF = ЕМ, MF = 20√6. Боковое ребро РЕ равно 10 и перпендикулярно (Подробнее…)
ГДЗГеометрияЗив Б.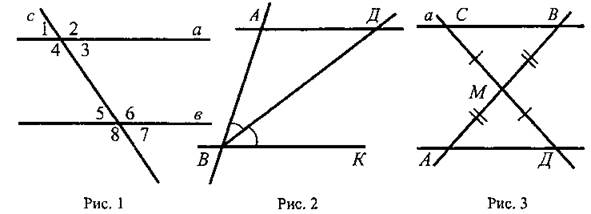
Формулировка параллельных прямых. Прямая линия. Параллельные прямые. Основные понятия. накрест лежащие углы равны, или
Эта статья о параллельных прямых и о параллельности прямых. Сначала дано определение параллельных прямых на плоскости и в пространстве, введены обозначения, приведены примеры и графические иллюстрации параллельных прямых. Далее разобраны признаки и условия параллельности прямых. В заключении показаны решения характерных задач на доказательство параллельности прямых, которые заданы некоторыми уравнениями прямой в прямоугольной системе координат на плоскости и в трехмерном пространстве.
Навигация по странице.
Параллельные прямые – основные сведения.
Определение.
Две прямые на плоскости называются параллельными , если они не имеют общих точек.
Определение.
Две прямые в трехмерном пространстве называются параллельными , если они лежат в одной плоскости и не имеют общих точек.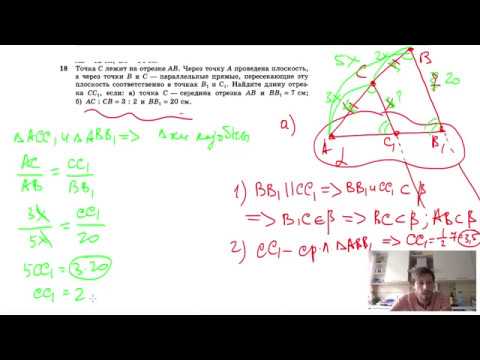
Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении параллельных прямых в пространстве очень важна. Поясним этот момент: две прямые в трехмерном пространстве, которые не имеют общих точек и не лежат в одной плоскости не являются параллельными, а являются скрещивающимися.
Приведем несколько примеров параллельных прямых. Противоположные края тетрадного листа лежат на параллельных прямых. Прямые, по которым плоскость стены дома пересекает плоскости потолка и пола, являются параллельными. Железнодорожные рельсы на ровной местности также можно рассматривать как параллельные прямые.
Для обозначения параллельных прямых используют символ «». То есть, если прямые а и b параллельны, то можно кратко записать а b .
Обратите внимание: если прямые a и b параллельны, то можно сказать, что прямая a параллельна прямой b , а также, что прямая b параллельна прямой a .
Озвучим утверждение, которое играет важную роль при изучении параллельных прямых на плоскости: через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.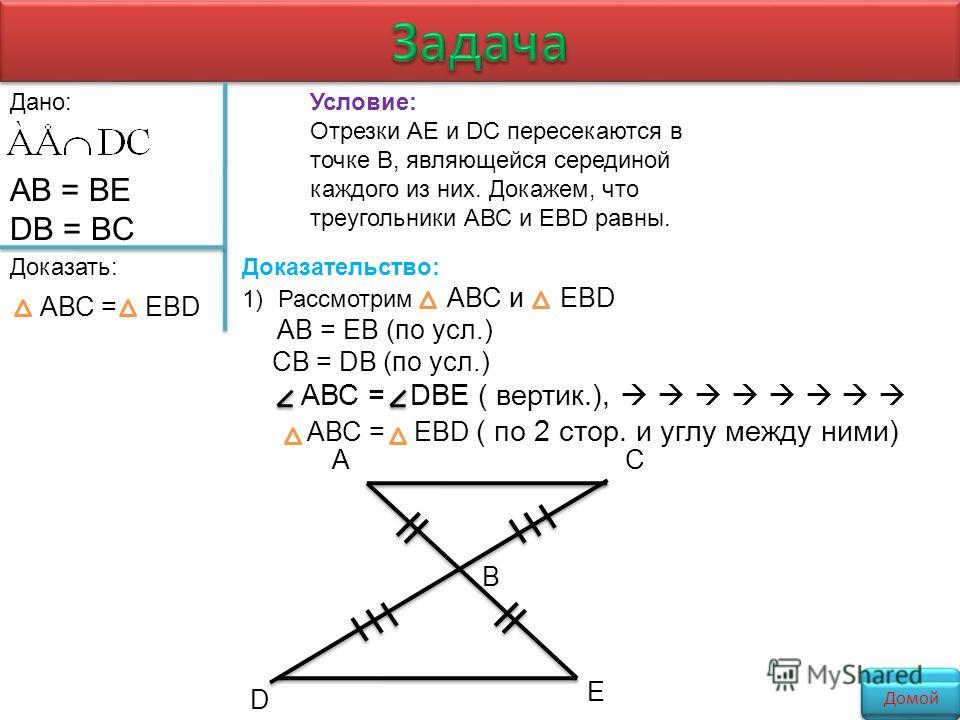
Для случая в пространстве справедлива теорема: через любую точку пространства, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Эта теорема легко доказывается с помощью приведенной выше аксиомы параллельных прямых (ее доказательство Вы можете найти в учебнике геометрии 10-11 класс, который указан в конце статьи в списке литературы).
Для случая в пространстве справедлива теорема: через любую точку пространства, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Эта теорема легко доказывается с помощью приведенной выше аксиомы параллельных прямых.
Параллельность прямых — признаки и условия параллельности.
Признаком параллельности прямых является достаточное условие параллельности прямых, то есть, такое условие, выполнение которого гарантирует параллельность прямых.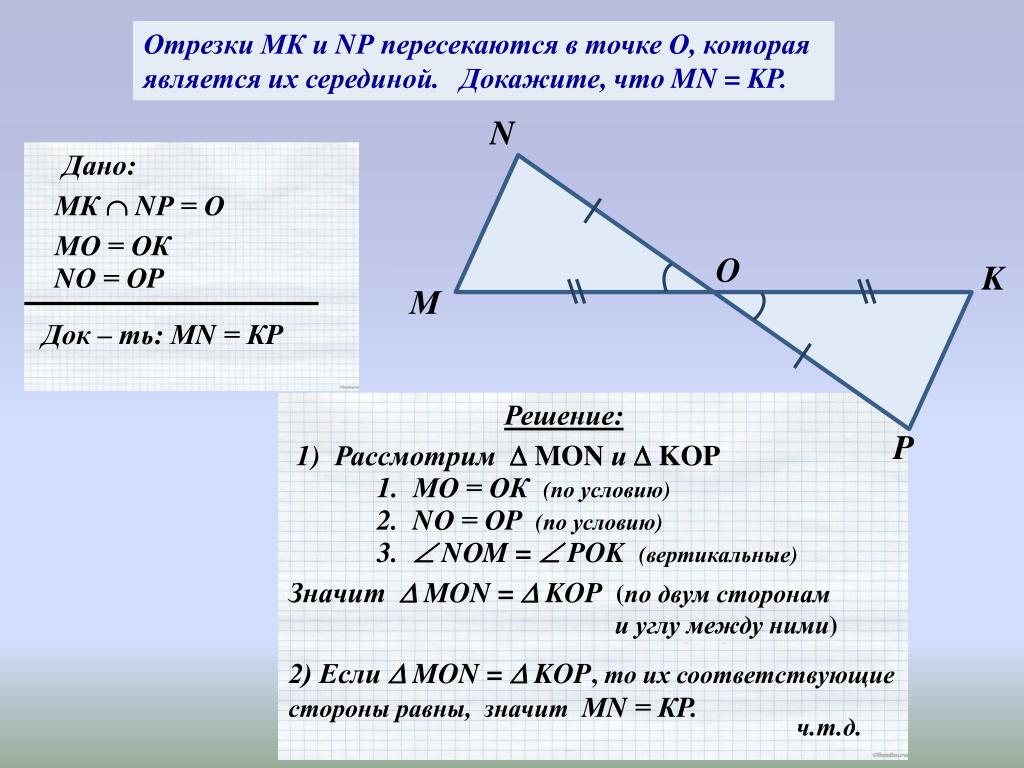 Иными словами, выполнение этого условия достаточно для того, чтобы констатировать факт параллельности прямых.
Иными словами, выполнение этого условия достаточно для того, чтобы констатировать факт параллельности прямых.
Также существуют необходимые и достаточные условия параллельности прямых на плоскости и в трехмерном пространстве.
Поясним смысл фразы «необходимое и достаточное условие параллельности прямых».
С достаточным условием параллельности прямых мы уже разобрались. А что же такое «необходимое условие параллельности прямых»? По названию «необходимое» понятно, что выполнение этого условия необходимо для параллельности прямых. Иными словами, если необходимое условие параллельности прямых не выполнено, то прямые не параллельны. Таким образом, необходимое и достаточное условие параллельности прямых – это условие, выполнение которого как необходимо, так и достаточно для параллельности прямых. То есть, с одной стороны это признак параллельности прямых, а с другой стороны – это свойство, которым обладают параллельные прямые.
Секущая прямая – это прямая, которая пересекает каждую из двух заданных несовпадающих прямых.
При пересечении двух прямых секущей образуются восемь неразвернутых . В формулировке необходимого и достаточного условия параллельности прямых участвуют так называемые накрест лежащие, соответственные и односторонние углы . Покажем их на чертеже.
Теорема.
Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180 градусам.
Покажем графическую иллюстрацию этого необходимого и достаточного условия параллельности прямых на плоскости.
Доказательства этих условий параллельности прямых Вы можете найти в учебниках геометрии за 7 -9 классы.
Заметим, что эти условия можно использовать и в трехмерном пространстве – главное, чтобы две прямые и секущая лежали в одной плоскости.
Приведем еще несколько теорем, которые часто используются при доказательстве параллельности прямых.
Теорема.
Существует аналогичное условие параллельности прямых в трехмерном пространстве.
Теорема.
Если две прямые в пространстве параллельны третьей прямой, то они параллельны. Доказательство этого признака рассматривается на уроках геометрии в 10 классе.
Проиллюстрируем озвученные теоремы.
Приведем еще одну теорему, позволяющую доказывать параллельность прямых на плоскости.
Теорема.
Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
Существует аналогичная теорема для прямых в пространстве.
Теорема.
Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
Изобразим рисунки, соответствующие этим теоремам.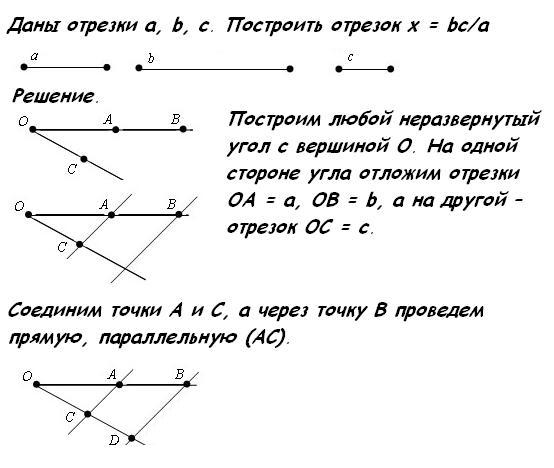
Все сформулированные выше теоремы, признаки и необходимые и достаточные условия прекрасно подходят для доказательства параллельности прямых методами геометрии. То есть, чтобы доказать параллельность двух заданных прямых нужно показать, что они параллельны третьей прямой, или показать равенство накрест лежащих углов и т.п. Множество подобных задач решается на уроках геометрии в средней школе. Однако следует отметить, что во многих случаях удобно пользоваться методом координат для доказательства параллельности прямых на плоскости или в трехмерном пространстве. Сформулируем необходимые и достаточные условия параллельности прямых, которые заданы в прямоугольной системе координат.
Параллельность прямых в прямоугольной системе координат.
В этом пункте статьи мы сформулируем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от вида уравнений, определяющих эти прямые, а также приведем подробные решения характерных задач.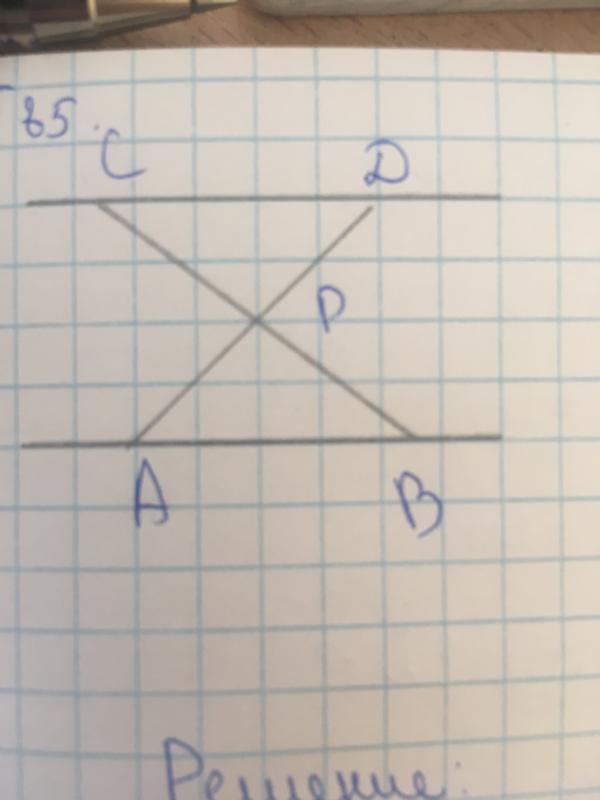
Начнем с условия параллельности двух прямых на плоскости в прямоугольной системе координат Oxy . В основе его доказательства лежит определение направляющего вектора прямой и определение нормального вектора прямой на плоскости.
Теорема.
Для параллельности двух несовпадающих прямых на плоскости необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, или нормальные векторы этих прямых были коллинеарны, или направляющий вектор одной прямой был перпендикулярен нормальному вектору второй прямой.
Очевидно, условие параллельности двух прямых на плоскости сводится к (направляющих векторов прямых или нормальных векторов прямых) или к (направляющего вектора одной прямой и нормального вектора второй прямой). Таким образом, если и — направляющие векторы прямых a
и b
, а и — нормальные векторы прямых a
и b
соответственно, то необходимое и достаточное условие параллельности прямых а
и b
запишется как , или , или , где t
— некоторое действительное число. В свою очередь координаты направляющих и (или) нормальных векторов прямых a
и b
находятся по известным уравнениям прямых.
В свою очередь координаты направляющих и (или) нормальных векторов прямых a
и b
находятся по известным уравнениям прямых.
В частности, если прямую a в прямоугольной системе координат Oxy на плоскости задает общее уравнение прямой вида , а прямую b — , то нормальные векторы этих прямых имеют координаты и соответственно, а условие параллельности прямых a и b запишется как .
Если прямой a соответствует уравнение прямой с угловым коэффициентом вида , а прямой b — , то нормальные векторы этих прямых имеют координаты и , а условие параллельности этих прямых примет вид . Следовательно, если прямые на плоскости в прямоугольной системе координат параллельны и могут быть заданы уравнениями прямых с угловыми коэффициентами, то угловые коэффициенты прямых будут равны. И обратно: если несовпадающие прямые на плоскости в прямоугольной системе координат могут быть заданы уравнениями прямой с равными угловыми коэффициентами, то такие прямые параллельны.
Если прямую a
и прямую b
в прямоугольной системе координат определяют канонические уравнения прямой на плоскости вида и , или параметрические уравнения прямой на плоскости вида и соответственно, то направляющие векторы этих прямых имеют координаты и , а условие параллельности прямых a
и b
записывается как .
Разберем решения нескольких примеров.
Пример.
Параллельны ли прямые и ?
Решение.
Перепишем уравнение прямой в отрезках в виде общего уравнения прямой: . Теперь видно, что — нормальный вектор прямой , а — нормальный вектор прямой . Эти векторы не коллинеарны, так как не существует такого действительного числа t , для которого верно равенство (). Следовательно, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, поэтому, заданные прямые не параллельны.
Ответ:
Нет, прямые не параллельны.
Пример.
Являются ли прямые и параллельными?
Решение.
Приведем каноническое уравнение прямой к уравнению прямой с угловым коэффициентом: . Очевидно, что уравнения прямых и не одинаковые (в этом случае заданные прямые были бы совпадающими) и угловые коэффициенты прямых равны, следовательно, исходные прямые параллельны.
Второй способ решения.
Сначала покажем, что исходные прямые не совпадают: возьмем любую точку прямой , например, (0, 1)
, координаты этой точки не удовлетворяют уравнению прямой , следовательно, прямые не совпадают. Теперь проверим выполнение условия параллельности этих прямых. Нормальный вектор прямой есть вектор , а направляющий вектор прямой есть вектор . Вычислим и : . Следовательно, векторы и перпендикулярны, значит, выполненяется необходимое и достаточное условие параллельности заданных прямых. Таким образом, прямые параллельны.
Теперь проверим выполнение условия параллельности этих прямых. Нормальный вектор прямой есть вектор , а направляющий вектор прямой есть вектор . Вычислим и : . Следовательно, векторы и перпендикулярны, значит, выполненяется необходимое и достаточное условие параллельности заданных прямых. Таким образом, прямые параллельны.
Ответ:
Заданные прямые параллельны.
Чтобы доказать параллельность прямых в прямоугольной системе координат в трехмерном пространстве пользуются следующим необходимым и достаточным условием.
Теорема.
Для параллельности несовпадающих прямых в трехмерном пространстве необходимо и достаточно, чтобы их направляющие векторы были коллинеарны.
Таким образом, если известны уравнения прямых в прямоугольной системе координат в трехмерном пространстве и нужно ответить на вопрос параллельны эти прямые или нет, то нужно найти координаты направляющих векторов этих прямых и проверить выполнение условия коллинеарности направляющих векторов. Другими словами, если и — направляющие векторы прямых a
заданных прямых имеют координаты и . Так как , то . Таким образом, выполнено необходимое и достаточное условие параллельности двух прямых в пространстве. Этим доказана параллельность прямых и .
Так как , то . Таким образом, выполнено необходимое и достаточное условие параллельности двух прямых в пространстве. Этим доказана параллельность прямых и .
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
- Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
Эта глава посвящена изучению параллельных прямых. Так называются две прямые на плоскости, которые не пересекаются. Отрезки параллельных прямых мы видим в окружающей обстановке — это два края прямоугольного стола, два края обложки книги, две штанги троллейбуса и т.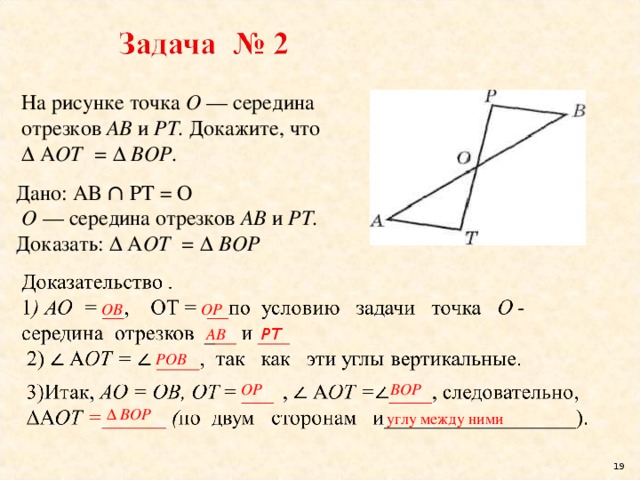 д. Параллельные прямые играют в геометрии очень важную роль. В этой главе вы узнаете о том, что такое аксиомы геометрии и в чём состоит аксиома параллельных прямых — одна из самых известных аксиом геометрии.
д. Параллельные прямые играют в геометрии очень важную роль. В этой главе вы узнаете о том, что такое аксиомы геометрии и в чём состоит аксиома параллельных прямых — одна из самых известных аксиом геометрии.
В п. 1 мы отмечали, что две прямые либо имеют одну общую точку, т. е. пересекаются, либо не имеют ни одной общей точки, т. е. не пересекаются.
Определение
Параллельность прямых а и b обозначают так: а || b.
На рисунке 98 изображены прямые а и b, перпендикулярные к прямой с. В п. 12 мы установили, что такие прямые а и b не пересекаются, т. е. они параллельны.
Рис. 98
Наряду с параллельными прямыми часто рассматривают параллельные отрезки. Два отрезка называются параллельными , если они лежат на параллельных прямых. На рисунке 99, а отрезки АВ и CD параллельны (АВ || CD), а отрезки MN и CD не параллельны. Аналогично определяется параллельность отрезка и прямой (рис. 99, б), луча и прямой, отрезка и луча, двух лучей (рис. 99, в).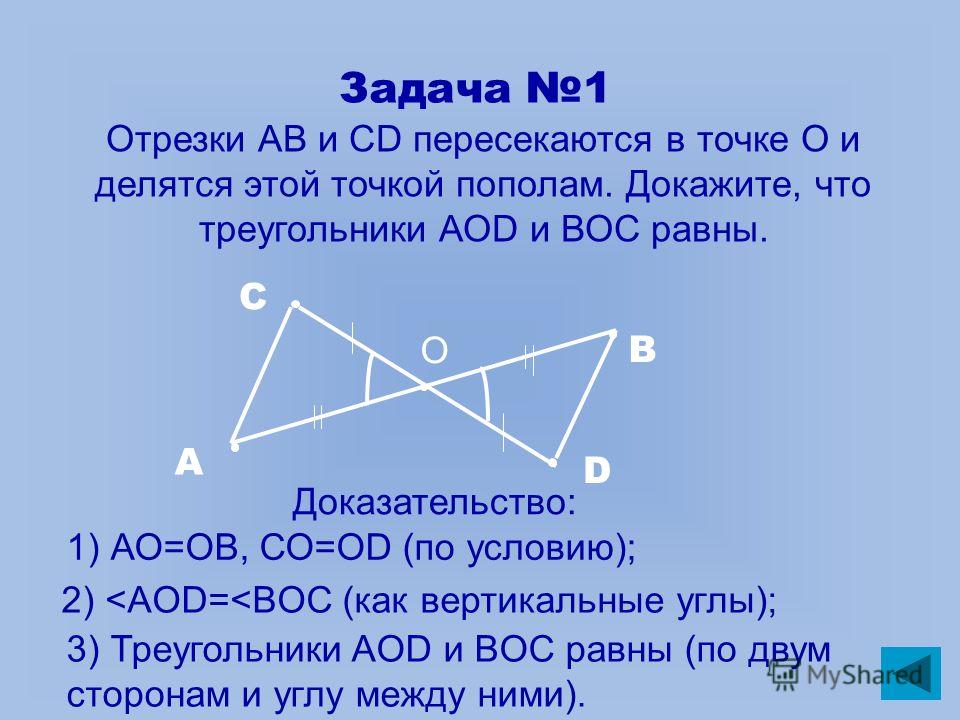
Рис. 99 Признаки параллельности двух прямых
Прямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы : 3 и 5, 4 и 6;
односторонние углы : 4 и 5, 3 и 6;
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Рис. 100
Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1 = ∠2 (рис. 101, а).
Докажем, что а || b. Если углы 1 и 2 прямые (рис. 101, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны.
Рис. 101
Рассмотрим случай, когда углы 1 и 2 не прямые.
Из середины О отрезка АВ проведём перпендикуляр ОН к прямой а (рис. 101, в). На прямой b от точки В отложим отрезок ВН 1 , равный отрезку АН, как показано на рисунке 101, в, и проведём отрезок ОН 1 . Треугольники ОНА и ОН 1 В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН 1 , ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Из равенства ∠3 = ∠4 следует, что точка Н 1 лежит на продолжении луча ОН, т. е. точки Н, О и Н 1 лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые а и b перпендикулярны к прямой HH 1 поэтому они параллельны. Теорема доказана.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1 =∠2 (рис. 102).
Рис. 102
Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.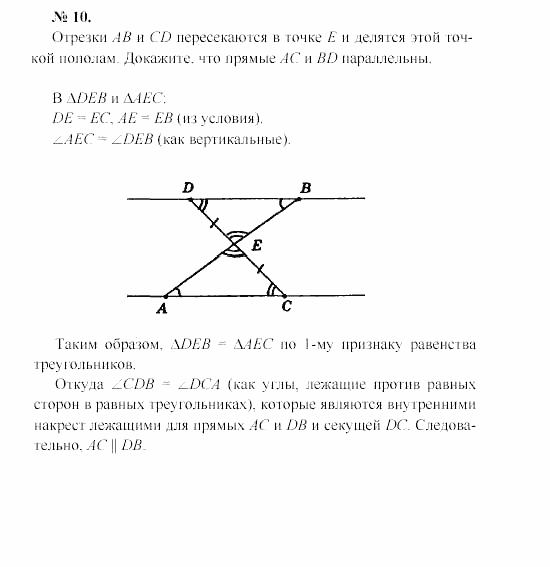
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1 + ∠4 = 180° (см. рис. 102).
Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.
Практические способы построения параллельных прямых
Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертёжного угольника и линейки.
Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертёжный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьёмся того, чтобы точка М оказалась на стороне угольника, и проведём прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами α и β, равны.
Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами α и β, равны.
Рис. 103 На рисунке 104 показан способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертёжной практике.
Рис. 104 Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скреплённые шарниром, рис. 105).
Рис. 105
Задачи
186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что а || b, если:
а) ∠1 = 37°, ∠7 = 143°;
б) ∠1 = ∠6;
в) ∠l = 45°, а угол 7 в три раза больше угла 3.
Рис. 106
187. По данным рисунка 107 докажите, что АВ || DE.
Рис. 107
188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АС и BD параллельны.
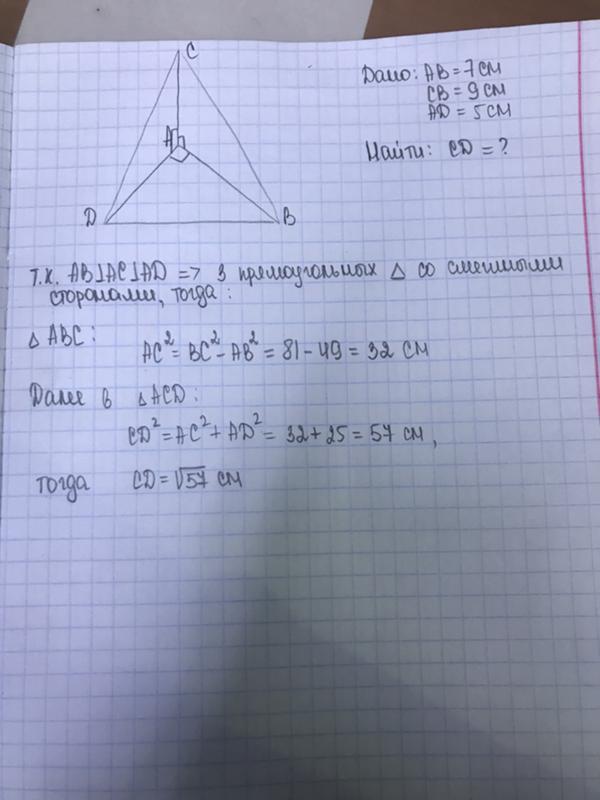
189. Используя данные рисунка 108, докажите, что ВС || AD.
Рис. 108
190. На рисунке 109 АВ = ВС, AD = DE, ∠C = 70°, ∠EAC = 35°. Докажите, что DE || АС.
Рис. 109
191. Отрезок ВК — биссектриса треугольника АВС. Через точку К проведена прямая, пересекающая сторону ВС в точке М так, что ВМ = МК. Докажите, что прямые КМ и АВ параллельны.
192. В треугольнике АВС угол А равен 40°, а угол ВСЕ, смежный с углом АСВ, равен 80°. Докажите, что биссектриса угла ВСЕ параллельна прямой АВ.
193. В треугольнике ABC ∠A = 40°, ∠B = 70°. Через вершину В проведена прямая BD так, что луч ВС — биссектриса угла ABD. Докажите, что прямые АС и BD параллельны.
194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертёжного угольника и линейки проведите прямую, параллельную противоположной стороне.
195. Начертите треугольник АВС и отметьте точку D на стороне АС. Через точку D с помощью чертёжного угольника и линейки проведите прямые, параллельные двум другим сторонам треугольника.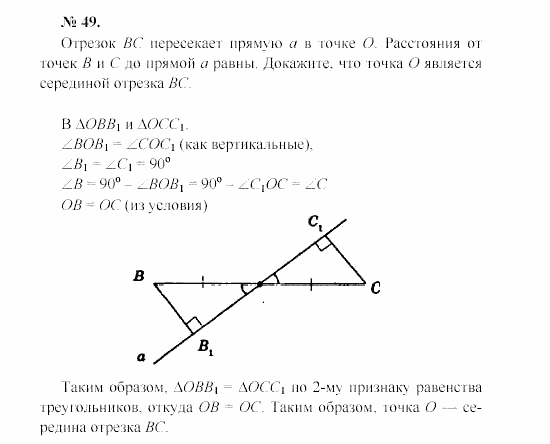
Определение 1
Прямую $с$ называют секущей для прямых $а$ и $b$, если она пересекает их в двух точках.
Рассмотрим две прямые $a$ и $b$ и секущую прямую $с$.
При их пересечении возникают углы, которые обозначим цифрами от $1$ до $8$.
У каждого из этих углов есть название, которое часто приходиться употреблять в математике:
- пары углов $3$ и $5$, $4$ и $6$ называются накрест лежащими ;
- пары углов $1$ и $5$, $4$ и $8$, $2$ и $6$, $3$ и $7$ называют соответственными ;
- пары углов $4$ и $5$, $5$ и $6$ называют односторонними .
Признаки параллельности прямых
Теорема 1
Равенство пары накрест лежащих углов для прямых $a$ и $b$ и секущей $с$ говорит о том, что прямые $a$ и $b$ – параллельны:
Доказательство .
Пусть накрест лежащие углы для прямых $а$ и $b$ и секущей $с$ равны: $∠1=∠2$.
Покажем, что $a \parallel b$.
При условии, что углы $1$ и $2$ будут прямыми, получим, что прямые $а$ и $b$ будут перпендикулярными относительно прямой $АВ$, а значит – параллельными. {\circ}$.
{\circ}$.
Согласно III-му признаку параллельности прямых $a \parallel b$. Утверждение доказано.
Пример 3
Дано : $\bigtriangleup ABC=\bigtriangleup ADB$.
Доказать : $AC \parallel BD$, $AD \parallel BC$.
Доказательство :
У рассматриваемых рисунков сторона $АВ$ – общая.
Т.к. треугольники $АВС$ и $ADB$ равны, то $AD=CB$, $AC=BD$, а также соответствующие углы равны $∠1=∠2$, $∠3=∠4$, $∠5=∠6$.
Пара углов $3$ и $4$ – накрест лежащие для прямых $АС$ и $BD$ и соответствующей секущей $АВ$, поэтому согласно I-му признаку параллельности прямых $AC \parallel BD$.
Пара углов $5$ и $6$ – накрест лежащие для прямых $AD$ и $BC$ и соответствующей секущей $АВ$, поэтому согласно I-му признаку параллельности прямых $AD \parallel BC$.
AB и С D пересечены третьей прямой MN , то образовавшиеся при этом углы получают попарно такие названия:
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренние накрест лежащие углы : 3 и 5, 4 и 6;
внешние накрест лежащие углы : 1 и 7, 2 и 8;
внутренние односторонние углы : 3 и 6, 4 и 5;
внешние односторонние углы : 1 и 8, 2 и 7.
Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.
Следовательно, ∠ 2 =∠ 8.
3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.
5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам , как углы вертикальные .
Из выше доказанного обоснования получаем обратные теоремы.
Когда при пересечении двух прямых произвольной третьей прямой получим, что:
1. Внутренние накрест лежащие углы одинаковы;
или 2. Внешние накрест лежащие углы одинаковые;
или 3. Соответственные углы одинаковые;
или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;
Сумма внутренних односторонних углов равна 2d = 180 0 ;
или 5. Сумма внешних односторонних равна 2d = 180 0 ,
то первые две прямые параллельны.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Сегменты Середины и лучи
Концепция линий проста, но большая часть геометрии связана с частями линий. Некоторые из этих частей настолько особенные, что имеют собственные имена и символы.
Некоторые из этих частей настолько особенные, что имеют собственные имена и символы.
Линейный сегмент
Отрезок линии — это соединенный кусок линии. Он имеет две конечные точки и называется по своим конечным точкам. Иногда для обозначения сегмента используется символ – написанный поверх двух букв. Это отрезок CD (рис. 1).
Рисунок 1 Сегмент линии.
Записывается CD (Технически CD относится к точкам C и D и всем точкам между ними, а CD без них относится к расстоянию от C до D . ) Обратите внимание, что CD является частью файла .
Постулат 7 (Постулат линейки): Каждая точка на линии может быть соединена ровно с одним действительным числом, называемым ее координата . Расстояние между двумя точками равно положительной разности их координат (рис. 2).
2).
Пример 1 : На рисунке 3 найдите длину QU .
Рисунок 3 Длина сегмента линии.Постулат 8 (Постулат сложения сегментов): Если B лежит между A и C в строке, то AB + BC = AC (рисунок 4).
Рисунок 4 Сложение длин отрезков.
Пример 2 : На рисунке 5 A находится между C и T . Найдите CT , если CA = 5 и AT = 8.
Рисунок 5 Сложение длин отрезков.
Поскольку A лежит между C и T , постулат 8 говорит вам, что
Средняя точка
Середина отрезка прямой является средней точкой или точкой, равноудаленной от конечных точек (рис. 6).
6).
Рисунок 6 Середина отрезка.
R является средней точкой QS , потому что QR = RS или потому что QR = ½ QS или RS = ½ QS3 Пример 3: На рисунке 7 найдите середину KR . Средняя точка KR будет равна ½ (24) или 12 пробелам либо из K , либо из R . Поскольку координата K равна 5, и она меньше, чем координата R (которая равна 29), чтобы получить координату средней точки, вы можете либо прибавить 12 к 5, либо вычесть 12 из 29. В любом случае вы определить, что координата середины равна 17. Это означает, что точка O является средней точкой KR , потому что KO = ИЛИ . Другой способ получить координату средней точки — найти среднее значение координат конечной точки. Теорема 4: Отрезок имеет ровно одну середину. Рэй Луч также является частью линии, за исключением того, что он имеет только одну конечную точку и всегда продолжается в одном направлении. Его можно представить как полулинию с конечной точкой. Он называется по букве своей конечной точки и любой другой точки луча. Символ →, написанный над двумя буквами, используется для обозначения этого луча. Это луч AB (рис. 8). Рисунок 8 Ray AB . Записывается как Это луч CD (рисунок 9). Рисунок 9 Ray CD . пишется как или Обратите внимание, что нестрелочная часть символа луча находится над конечной точкой. РУКОВОДЯЩАЯСЯ ПРАКТИКА, СТР. 77. 1. Возможный ответ: Предположение основано на наблюдении и не является верным до тех пор, пока оно не будет доказано в каждом случае. 2. Сентябрь. [PDF] Глава 2 Геометрические причины — г-н Грац mrgrazmath.weebly.com › загрузки › 2 › Chapter_2 A. прямой путь, который не имеет толщины и простирается навсегда. Б. Фигура, образованная двумя лучами с общим концом. C. плоская поверхность, не имеющая толщины … Geo.Ch3 — ГЛАВА 2 Решения Ключевые геометрические рассуждения… www.coursehero.com › файл › GeoCh3 Просмотр подготовки к экзамену — Geo.Ch3 из ENGL 101 в старшей школе Ланкастера, Ланкастер. ГЛАВА 2 Решения Ключевые геометрические рассуждения УПРАЖНЕНИЯ ВЫ ГОТОВЫ? PAGE 71 1. Bilder Alle anzeigen Alle anzeigen [PDF] Chapter 2: Reasoning and Proof — Clarkwork.com clarkhapwork. Миссис Тэкетт — Геометрия — Глава 2. Рассуждения и доказательства. Ответы Угловые отношения Домашнее задание Key.pdf · Ch 2 Test Review Key.pdf … [PDF] Геометрия. Глава 2 Учебное пособие Обоснование и доказательство www.lcps.org › lib4 › Centricity › Domain › G Ch3 SG ОТВЕТЫ Геометрия. Глава 2 Учебное пособие. Рассуждение и доказательство. Имя: УЧИТЬ … быть положительным, чтобы получить положительный ответ? … Ключевые термины: не требуется для полного кредита. [PDF] Рассуждения и доказательства — подготовка к главе 2 www.lancasterschools.org › cms › lib › centricity › домен › глава… 2-1 Индуктивные рассуждения и предположения – проверьте свое понимание . .. Расширьте 2-3 Лабораторная работа по геометрии: Биоусловные операторы — Упражнения. [PDF] ГЛАВА 2 Дедуктивное мышление — Classroom Web classweb. Чтобы найти среднее двух чисел, нужно найти их сумму и разделить на два. (5 + 29) ÷ 2 = 17. Координата средней точки равна 17, поэтому середина — это точка O .
Чтобы найти среднее двух чисел, нужно найти их сумму и разделить на два. (5 + 29) ÷ 2 = 17. Координата средней точки равна 17, поэтому середина — это точка O .
глава 2 ключ ответа на геометрическое мышление0003
 com равенство в доказательствах геометрии. Доказательство отношений сегментов (стр. 101–106). 2. 2. 1. 1.
com равенство в доказательствах геометрии. Доказательство отношений сегментов (стр. 101–106). 2. 2. 1. 1.

Leave A Comment