Задачи по планиметрии — 4ЕГЭ
Сборник задач по материалам открытого банка ФИПИ. Без ответов.
planim33.docx
planim33.pdf
1. Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.
3. Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
4. Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
5. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF— высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
6. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD— биссектриса внешнего угла при вер-шине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
7. В треугольнике ABC, CH -высота, AD -биссектриса, O -точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах.
8. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
9. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.
10. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
11. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
12. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.
13. Угол ACO равен 24°. Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
14. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
15. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
16. В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
17. Катеты равнобедренного прямоугольного треугольника равны √30T . Найдите радиус окружности, вписанной в этот треугольник.
18. Сторона ромба равна 1, острый угол равен 300. Найдите радиус вписанной окружности этого ромба.
19. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
20. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54°. Найдите n.
Найдите n.
21. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
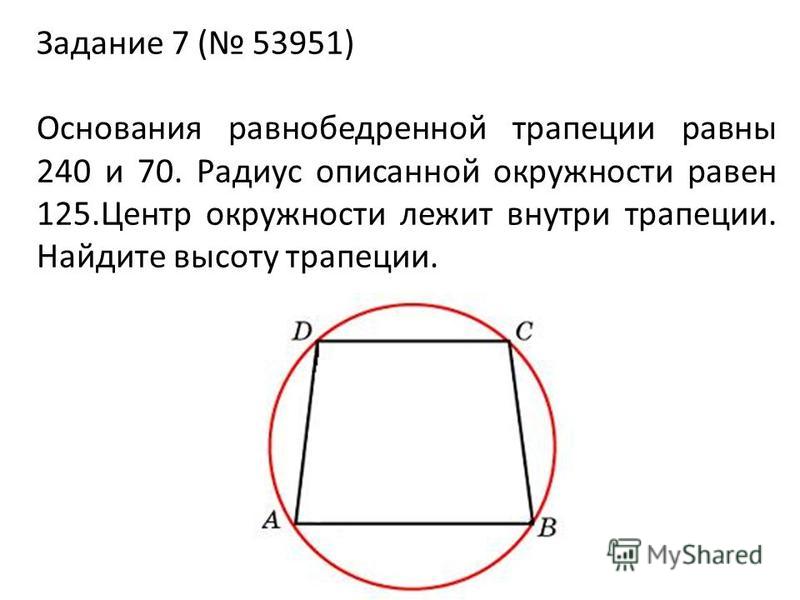
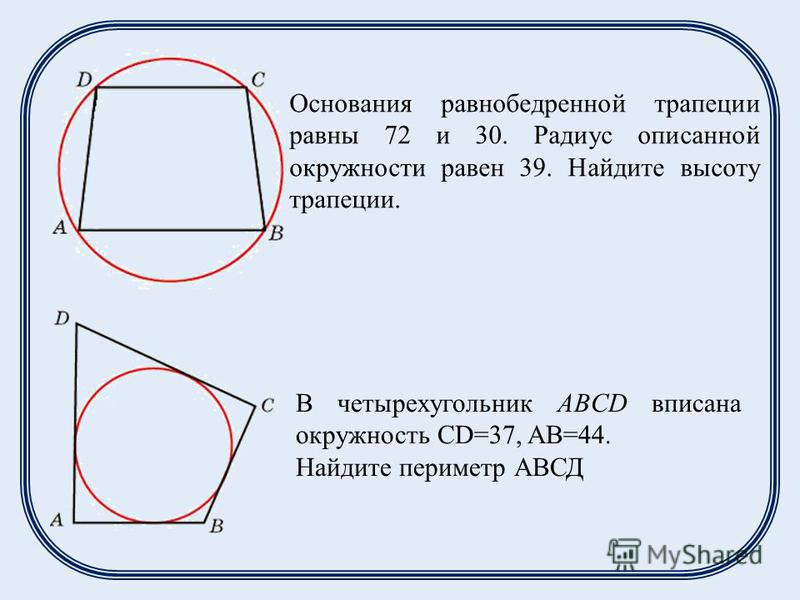
22. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
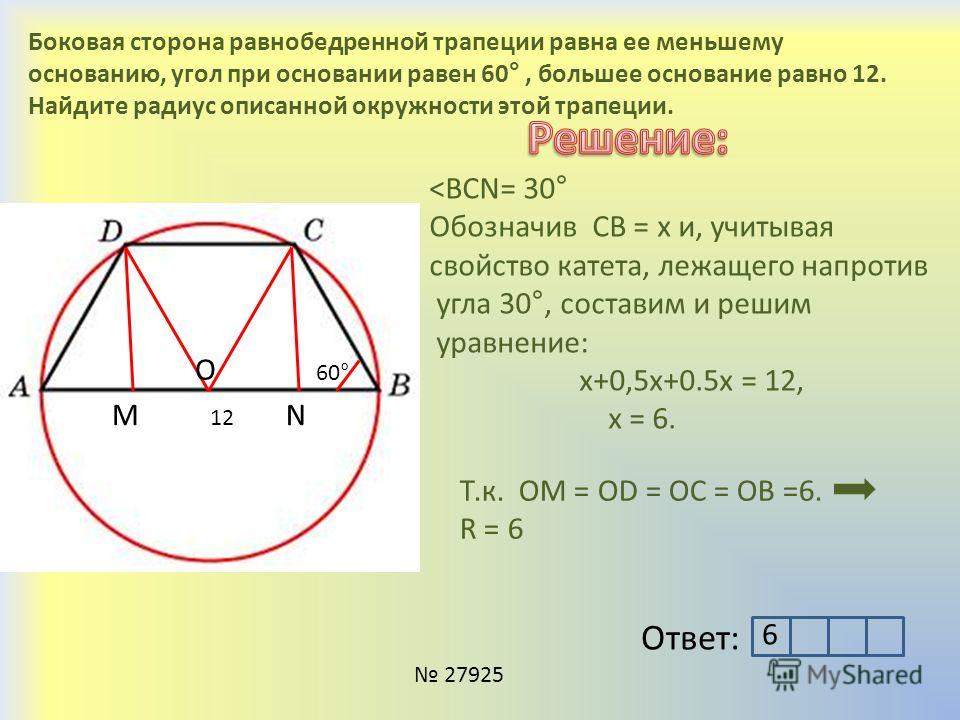
23. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
24. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника
25. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника.
26. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
27. Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника.
28. Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
Найдите больший угол треугольника ABC. Ответ дайте в градусах.
29. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
30. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.
31. Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.
32. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
33. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Вписанные многоугольники — презентация онлайн
1. Вписанные многоугольники
Многоугольник называется вписанным в окружность, есливсе его вершины принадлежат окружности.
 Окружность при этом
Окружность при этомназывается описанной около многоугольника.
Теорема 1. Около всякого треугольника можно описать
окружность. Ее центр является точкой пересечения серединных
перпендикуляров к сторонам треугольника.
Теорема
2.
Суммы
противоположных
четырехугольника, вписанного в окружность, равны 180о.
углов
2. Описанные многоугольники
Многоугольник называется описанным около окружности,если все его стороны касаются этой окружности.
Сама
окружность при этом называется вписанной в многоугольник
Теорема 3. В любой треугольник можно вписать
окружность. Ее центром будет точка пересечения биссектрис
этого треугольника.
Теорема
4.
Суммы
противоположных
сторон
четырехугольника, описанного около окружности, равны.
3. Вписанные и описанные треугольники
Теорема 5. Отношение стороны треугольника к синусупротиволежащего угла равно диаметру описанной окружности.
Теорема 6. Радиус R окружности, описанной около
правильного треугольника, выражается формулой R 2S , где
a b c
a, b, c – стороны треугольника S – его площадь.
Теорема 7. Радиус r окружности, вписанной в
треугольник, выражается формулой
a b c , где a, b, c –
стороны треугольника S – его площадь. r 4 S
4. Упражнение 1
Сторона равностороннего треугольника равна2 3 . Найдите радиус окружности, вписанной в
этот треугольник.
Ответ: 1.
5. Упражнение 2
Сторона равностороннего треугольника равна2 3 . Найдите радиус окружности, описанной
около этого треугольника.
Ответ: 2.
6. Упражнение 3
Гипотенуза прямоугольного треугольника равна10 см. Найдите радиус описанной окружности.
Ответ: 5.
7. Упражнение 4
Окружность, вписанная в равнобедренныйтреугольник, делит в точке касания одну из
боковых сторон на два отрезка, длины которых
равны 4 и 3, считая от вершины. Найдите
периметр треугольника.
Ответ: 20.
8. Упражнение 5
Одна сторона треугольника равна радиусуописанной
окружности.
Найдите
угол
треугольника, противолежащий этой стороне.
Ответ: 30о.
9. Упражнение 6
Сторона AB треугольника ABC равна 3 , угол Cравен 60о. Найдите радиус окружности,
описанной около этого треугольника.
Ответ: 1.
10. Упражнение 7
Найдите диагональ прямоугольника, вписанногов окружность радиуса 6.
Ответ: 12.
11. Упражнение 8
Найдите радиус окружности, описанной околоквадрата со стороной, равной 2 .
Ответ: 1.
12. Упражнение 9
Меньшая сторона прямоугольника равна 5 см.Угол между диагоналями равен 60о. Найдите
радиус описанной окружности.
Ответ: 5.
13. Упражнение 10
Около окружности радиуса, равного 2 , описанквадрат. Найдите радиус окружности,
описанного около этого квадрата.
Ответ: 2.
14. Упражнение 11
Сторона ромба равна 4, острый угол – 30о.Найдите радиус вписанной окружности.
Ответ: 1.
15. Упражнение 12
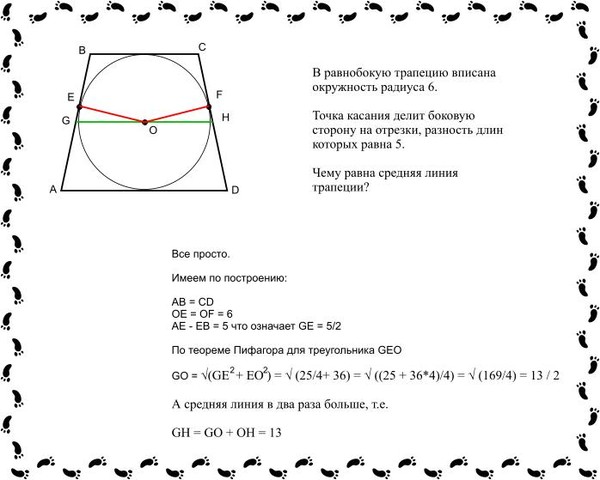
Боковые стороны трапеции, описанной околоокружности, равны 2 и 4. Найдите среднюю
линию трапеции.
Ответ: 3.
16. Упражнение 13
Около трапеции описана окружность. Периметртрапеции равен 20, средняя линия 5 см. Найдите
боковую сторону трапеции.
Ответ: 5.
17. Упражнение 14
Угол A четырехугольника ABCD, вписанного вокружность, равен 100о. Найдите угол C.
Ответ: 80о.
18. Упражнение 15
Два угла вписанного в окружностьчетырехугольника равны 80о и 60о. Найдите
больший из оставшихся углов.
Ответ: 120о.
19. Упражнение 16
В четырехугольник ABCD вписана окружность,AB = 11, CD = 17. Найдите периметр
четырехугольника.
Ответ: 56.
20. Упражнение 17
Периметр четырехугольника, описанного околоокружности, равен 20, две его стороны равны 4 и
5. Найдите большую из оставшихся сторон.
Ответ: 6.
21. Упражнение 18
В четырехугольник ABCD вписана окружность,AB = 11, BC = 10 и CD = 15. Найдите четвертую
сторону четырехугольника.
Ответ: 16.
22. Упражнение 19
Чему равна сторона правильногошестиугольника, вписанного в окружность
радиуса 5?
Ответ: 5.
23. Упражнение 20
Найдите сторону правильного шестиугольника,описанного около окружности, радиус которой
равен 2 3 .
Ответ: 3.
24. Упражнение 21
Сторона AB треугольника ABC равна 2 , радиусописанной окружности равен 1. Найдите угол C.
Ответ: 45о.
25. Упражнение 22
Боковая сторона равнобедренного треугольникаравна 2, угол при вершине равен 120о. Найдите
диаметр описанной окружности.
Ответ: 4.
26. Упражнение 23
Сторона BC треугольника ABC равна 8 , угол Aравен 45о. Найдите радиус окружности,
описанной около этого треугольника.
Ответ: 2.
27. Упражнение 24
Сторона AB треугольника ABC равна 10, радиусописанной окружности равен 10. Найдите угол C.
Ответ: 150о.
28. Упражнение 25
Боковые стороны равнобедренного треугольникаравны 40, основание равно 48. Найдите радиус
описанной окружности.
Ответ: 25.
29. Упражнение 26
В треугольнике ABC AC = 8, BC = 6, угол Cравен
90о.
Найдите
радиус
вписанной
окружности.
Ответ: 2.
30. Упражнение 27
Боковые стороны равнобедренного треугольникаравны 10, основание равно 12. Найдите радиус
вписанной окружности.
Ответ: 3.
31. Упражнение 28
Боковые стороны равнобедренного треугольникаравны 3 10 , основание равно 6. Найдите радиус
описанной окружности.
Ответ: 5.
32. Упражнение 29
Сторона AB треугольника ABC равна 10. Найдитерадиус описанной около этого треугольника
окружности, если противолежащий этой стороне
угол C равен 150о.
Ответ: 10.
33. Упражнение 30
Около окружности описана трапеция, периметркоторой равен 36. Найдите ее среднюю линию.
Ответ: 9.
34. Упражнение 31
В четырехугольнике ABCD, вписанном вокружность, угол A равен 75о, угол B равен 90о.
Найдите разность двух других углов.
Ответ: 15о.
35. Упражнение 32
Боковая сторона равнобедренной трапеции равнаее меньшему основанию, угол при основании
равен 60о, большее основание равно 10.
 Найдите
Найдитерадиус описанной окружности.
Ответ: 5.
36. Упражнение 33
Углы A, B и C четырехугольника ABCD относятсякак 2:3:4. Найдите угол D, если около данного
четырехугольника можно описать окружность.
Ответ: 90о.
37. Упражнение 34
Основания равнобедренной трапеции равны 8 и6, высота равна 7. Найдите радиус описанной
окружности.
Ответ: 5.
38. Упражнение 35
Периметр прямоугольной трапеции, описаннойоколо окружности, равен 20, ее большая боковая
сторона равна 6. Найдите радиус окружности.
Ответ: 2.
39. Упражнение 36
Три стороны описанного около окружностичетырехугольника относятся (в
последовательном порядке) как 1:2:3. Найдите
большую сторону этого четырехугольника, если
известно, что его периметр равен 24.
Ответ: 9.
40. Упражнение 37
Угол между стороной правильного n-угольника,вписанного в окружность, и радиусом этой
окружности, проведенным в одну из вершин
стороны, равен 72.
 Найдите n.
Найдите n.Ответ: 10.
41. Упражнение 38
Найдите диаметр окружности, вписанной вправильный шестиугольник со стороной 3 .
Ответ: 3.
42. Упражнение 39
Около окружности радиуса, равного 3 , описанправильный шестиугольник. Найдите радиус
окружности, описанного около этого
шестиугольника.
Ответ: 2.
43. Упражнение 40
К окружности, вписанной в треугольник АВС,проведены
три
касательные.
Периметры
отсеченных треугольников равны 3, 4, 5. Найдите
периметр данного треугольника.
Ответ: 12.
44. Упражнение 41
В треугольнике ABC AC = 8, BC = 6, угол Cравен
90о.
Найдите
радиус
описанной
окружности.
Ответ: 5.
45. Упражнение 42
В равнобедренном треугольнике боковыестороны делятся точками касания вписанной в
треугольник окружности в отношении 7:5, считая
от вершины, противоположной основанию.
Найдите периметр треугольника, если его
основание равно 10.

Ответ: 34.
46. Упражнение 43
Угол B четырехугольника ABCD, вписанного вокружность, равен 70о. Найдите угол D.
Ответ: 110о.
47. Упражнение 44
Меньшая сторона прямоугольника равна 36.Один из углов, образованных диагоналями 120о.
Найдите диаметр описанной окружности.
Ответ: 72.
48. Упражнение 45
Периметр правильного шестиугольника равен 36.Найдите диаметр описанной окружности.
Ответ: 12.
49. Упражнение 46
Трипоследовательные
стороны
четырехугольника, в который можно вписать
окружность, равны 6 см, 8 см и 9 см. Найдите
четвертую сторону.
Ответ: 7.
50. Упражнение 47
Сторона ромба равна 8 см, острый угол – 30о.Найдите радиус вписанной окружности.
Ответ: 2.
51. Упражнение 48
Боковые стороны трапеции, описанной околоокружности, равны 4 и 6. Найдите среднюю
линию трапеции.
Ответ: 5.
52. Упражнение 49
Основания равнобедренной трапеции равны 16 и12, радиус описанной окружности равен 10.

Найдите высоту трапеции.
Ответ: 14.
53. Упражнение 50
Угол между стороной правильного n-угольника,вписанного в окружность, и радиусом этой
окружности, проведенным в одну из вершин
стороны, равен 70. Найдите n.
Ответ: 9.
Математическая задача: Вычислить 46541 — математическая задача, планиметрия
Вычислить периметр и площадь прямоугольного треугольника, если a = 6 см, b = 8 см, c = 10 см.
Правильный ответ:
o = 24 смS = 24 см 2
Пошаговое объяснение:
a=6 см b=8+см c=10 см b+o=10 см b c=6+8+10=24 см
S=2a⋅ b=26⋅ 8=24=24 см2 Проверка решения: c2=a2+b2
=62+82
=10 см с2=с
Вы нашли ошибку или неточность? Не стесняйтесь
пишите нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Для решения этой математической задачи вам необходимо знать следующие знания:
- планиметрия
- прямоугольный треугольник
- площадь фигуры
- периметр 900 задача 900 0034
- практика для детей 12 лет
- Практика для 13-летних
- Трапеция
Прямоугольная трапеция ABCD с прямым углом в вершине A имеет стороны a, b, c и д. Вычислить длину окружности и площадь трапеции, если даны: a = 25 см, c = 10 см, d = 8 см - Вычислить 4424
Вычислить площадь треугольника ABC, если a = 10 см, c = 8 см, ta = 6 см . - Прямоугольный треугольник ABC
Вычислите периметр и площадь прямоугольного треугольника ABC. Если известны длины катетов, то гипотенузой будут 4 см, 5,5 см и 6,8 см.
Если известны длины катетов, то гипотенузой будут 4 см, 5,5 см и 6,8 см. - Равнобедренный треугольник
Вычислите площадь и периметр равнобедренного треугольника ABC с основанием AB, если a = 6 см, c = 7 см. - Сторона и диагональ
Найдите длину окружности и площадь прямоугольника, если даны данные: сторона a = 8 см, диагональ u = 10 см. - Описанный 22713
Вычислите длину окружности и площадь правильного десятиугольного многоугольника, если радиус описанного круга r = 20 см. - RT 10
Площадь прямоугольного треугольника 84 см 2 , а один из его катетов а=10 см. Вычислите периметр треугольника АВС. - Конус — S,V
Рассчитайте объем и площадь поверхности конуса, если его радиус r = 6 см, а сторона s = 10 см. - Алмаз и диагонали
Алмаз имеет диагонали f = 8 см и g = 6 см в длину. Какова длина периметра этого алмаза? (Рассчитайте!) - Прямоугольный треугольник
Вычислите недостающую сторону b и внутренние углы, периметр и площадь прямоугольного треугольника, если a=10 см, а гипотенуза c = 16 см.
- Основания
Основания равнобедренной трапеции ABCD имеют длину 10 см и 6 см. Его плечи образуют угол α = 50˚ с более длинным основанием. Вычислите длину окружности и площадь трапеции ABCD. - Четырехугольная пирамида
Вычислить поверхность четырехугольной пирамиды, имеющей прямоугольное основание с размерами a = 8 см, b = 6 см и высотой H = 10 см. - Равнобедренная трапеция
Основания равнобедренной трапеции относятся как 5:3. Руки имеют длину 5 см и высоту = 4,8 см. Вычислите длину окружности и площадь трапеции. - Высота стены
Рассчитайте поверхность и объем правильной четырехугольной пирамиды, если сторона a = 6 см, а высота стены v = 0,8 дм. - Рассчитать 16223
В прямоугольном треугольнике ABC известны следующие элементы: a = 10 см, высота до стороны c h = 9,23 см. Вычислить o, R (радиус вписанной окружности), r (радиус вписанной окружности). - Площадь прямоугольника
Вычислите площадь прямоугольника с диагональю u = 12,5 см и шириной b = 3,5 см. Используйте теорему Пифагора.
Используйте теорему Пифагора. - Равнобедренная трапеция
Вычислите длину окружности и площадь равнобедренной трапеции, если известны размеры оснований 8 и 12 см, а размер плеч 5 см. - планиметрия
- теорема Пифагора
- прямоугольный треугольник
- площадь фигуры 037 треугольник
- трапеция
- практика для 13-летних
- практика для 14-летних
- Трапеция RT
График имеет форму прямоугольной трапеции ABCD, где ABIICD с прямым углом в вершине B. Сторона AB имеет длина 36 м. Длины сторон АВ и ВС относятся как 12:7. Длины сторон AB и CD относятся как 3:2. Вычислить con - Трапеция — RR
Найти площадь прямоугольной трапеции ABCD с прямым углом при вершине A; a = 3 дм b = 5 дм c = 6 дм d = 4 дм - Диагональ BD
Найдите длину диагонали BD в прямоугольной трапеции ABCD с прямым углом при вершине A, когда /AD / = 8,1 см и угол DBA равен 42° - Равнобедренная 37621
В равнобедренной трапеции ABCD , даны основания AB = 20 см, CD = 12 см и длины плеч AD = BC = 8 см. Укажите его высоту и угол альфа при вершине A
Укажите его высоту и угол альфа при вершине A - Прямоугольная трапеция
В прямоугольной трапеции ABCD с прямыми углами при вершинах A и D со сторонами a = 12 см, b = 13 см, c = 7 см. Найдите углы бета и гамма и высоту v. - RT — вписанная окружность
В прямоугольном треугольнике длины сторон > а = 30см, b = 12,5см. Прямой угол лежит при вершине С. Вычислите радиус вписанной окружности. - Окружность 7052
Дана трапеция ABCD (AB || CD, AB перпендикулярно AD). Вычислите его окружность, если | АБ | = 20см, | компакт-диск | = 15см, | ОБЪЯВЛЕНИЕ | = 12см. Теорема Пифагора - Прямоугольная трапеция
Прямоугольная трапеция ABCD: /AB/ = /BC/ = /AC/. Длина медианы 6 см. Вычислите длину окружности и площадь трапеции. - Основания
Основания равнобедренной трапеции ABCD имеют длину 10 см и 6 см. Его плечи образуют угол α = 50˚ с более длинным основанием. Вычислите длину окружности и площадь трапеции ABCD. - Прямоугольный
Прямоугольный треугольник KLM с прямым углом при вершине L, углом бета при вершине K и углом альфа при вершине M. Угол при вершине M = 65°, сторона l = 17,5 см. Используйте теоремы Пифагора и тригонометрические функции для вычисления длин всех сторон и угла
Угол при вершине M = 65°, сторона l = 17,5 см. Используйте теоремы Пифагора и тригонометрические функции для вычисления длин всех сторон и угла - Трапеция
Вычислите площадь трапеции ABCD со сторонами |AB|= 50 см, |BC|=25 см, |CD|=10 см, |AD|=25 см.. - Прямоугольная трапеция
Вычислите площадь прямоугольная трапеция с прямым углом в точке A и если |AC| = 4 см, |ВС| = 3 см, а диагональ АС перпендикулярна стороне ВС. - Вычислить 60423
В прямоугольном треугольнике RST с прямым углом при вершине T известны длины двух сторон: s = 7,8 см и t = 13 см; вычислить третье лицо r. - Описанный 6568
В прямоугольном треугольнике ABC с прямым углом при вершине C дано: a = 17 см, Vc = 8 см. Вычислите длины сторон b, c, его площадь S, периметр o, длину радиусов окружностей треугольника, описанного R и вписанного в него r an - Равнобедренная трапеция

Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1
Математические задачи: Трапеция — вопрос № 58271, планиметрия, теорема Пифагора
Прямоугольная трапеция ABCD с прямым углом при вершине A имеет стороны a, b, c и d. Вычислите длину окружности и площадь трапеции, если даны: a = 25см, c = 10см, d = 8см
Правильный ответ:
o = 60 смS = 140 см 2
Пошаговое объяснение:
a=25 см c=10 см d=8 см 2 x=a−c=5 −10=15 см x2+d2 = b2 b=x2+d2
=152+82
=17 см o=a+b+c+d=25+17+10+8=60 см
S=2a+c⋅ d=225+10⋅ 8=140 см2
Нашли ошибку или неточность? Не стесняйтесь
пишите нам .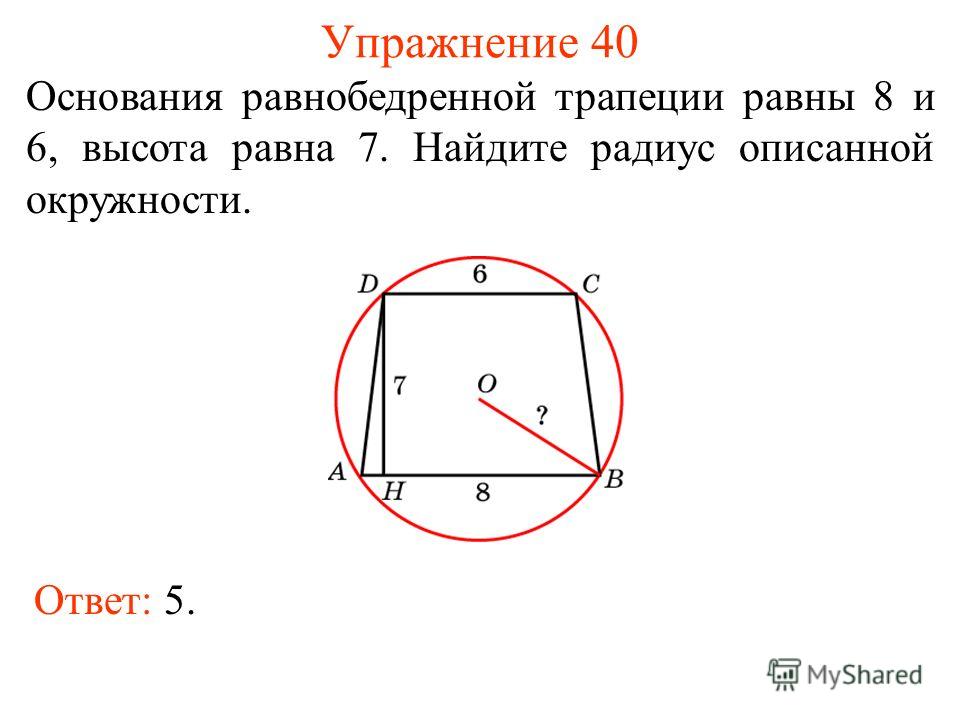 Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой задачи по математике необходимо знать следующие знания:
Уровень задачи:
Рекомендуем посмотреть это обучающее видео по этой математической задаче: видео1 видео2

 Если известны длины катетов, то гипотенузой будут 4 см, 5,5 см и 6,8 см.
Если известны длины катетов, то гипотенузой будут 4 см, 5,5 см и 6,8 см.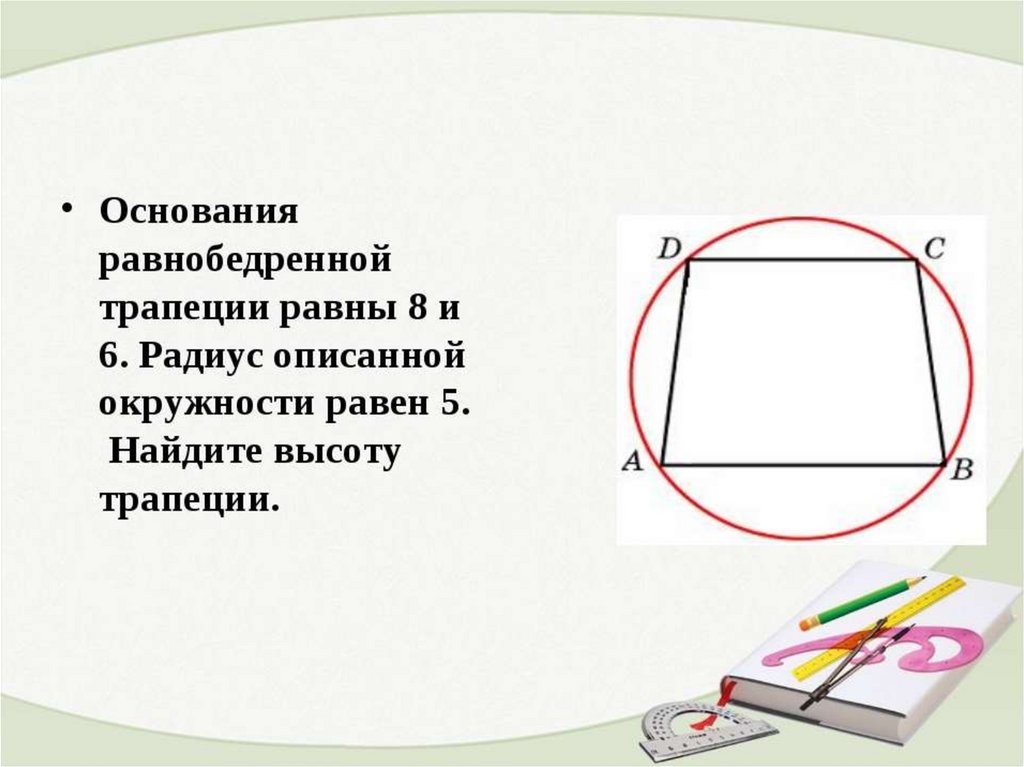
 Используйте теорему Пифагора.
Используйте теорему Пифагора.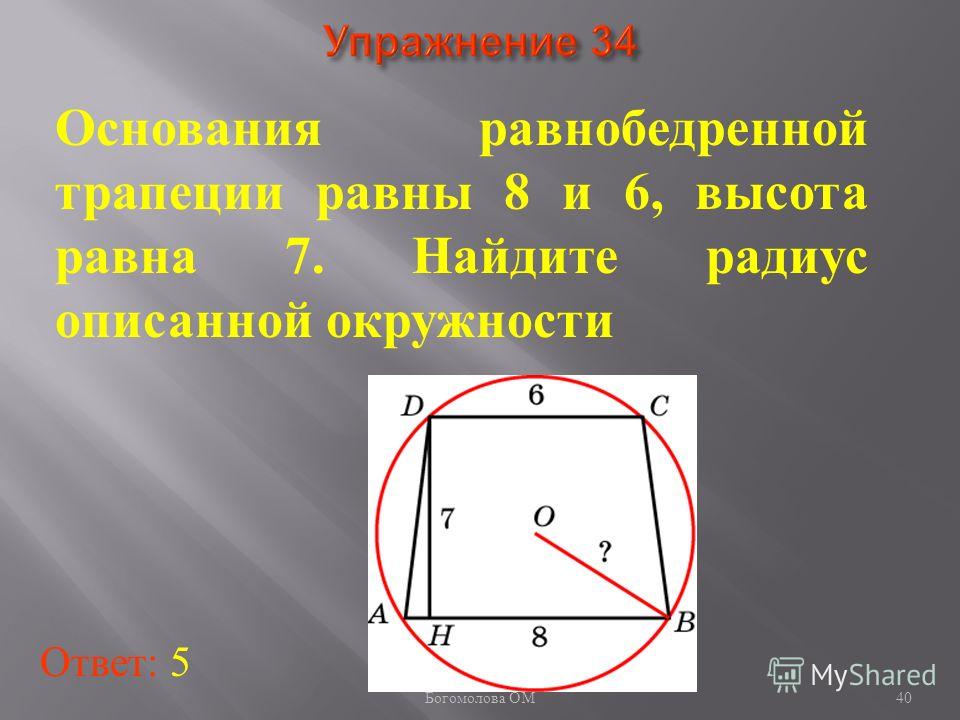 Укажите его высоту и угол альфа при вершине A
Укажите его высоту и угол альфа при вершине A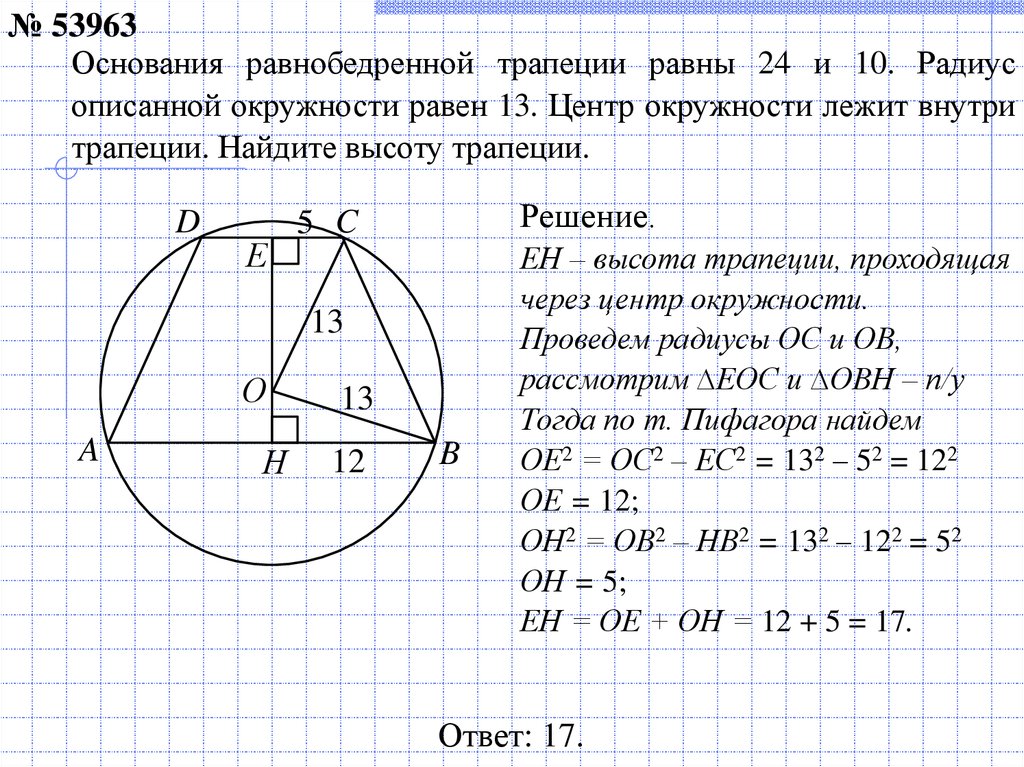 Угол при вершине M = 65°, сторона l = 17,5 см. Используйте теоремы Пифагора и тригонометрические функции для вычисления длин всех сторон и угла
Угол при вершине M = 65°, сторона l = 17,5 см. Используйте теоремы Пифагора и тригонометрические функции для вычисления длин всех сторон и угла
Leave A Comment