Задание 14 ЕГЭ по физике
Электричество. Закон сохранения электрического заряда,
закон Кулона, конденсатор, сила тока,
закон Ома для участка цепи, последовательное и параллельное соединение
проводников, работа и мощность тока,
закон Джоуля – Ленца
В. З. Шапиро
В задании 14 проверяются знания по теме «Постоянный электрический ток». Это задание базовому уровня. Задачи носят, в основном, расчетный характер. Их решение основывается на знаниях законов и закономерностей постоянного электрического тока, умении «читать» электрические схемы, работать с графическими зависимостями.
1. На графике показана зависимость силы тока I в проводнике от времени t. Определите заряд, прошедший через проводник за Δt = 60 с с момента начала отсчёта времени.
Ответ: _____________________ Кл.
Необходимая теория: Постоянный электрический ток
Используя зависимость силы тока от времени, электрический заряд можно определить как площадь геометрической фигуры под графиком.
Ответ: 180 Кл.
Секрет решения. Подобный прием нахождения значения физической величины через площадь под графиком применяется во многих разделах физики: в «Механике», «МКТ и термодинамике», «Электродинамике». Здесь важно правильно выделить геометрическую фигуру, так как иногда требуется найти площадь не всей фигуры, а только ее части. Как всегда, в расчетах требует особого внимания система единиц (СИ). Пренебрежение одним из перечисленных моментов приведет к потере «легкого» балла.
2. Пять одинаковых резисторов с сопротивлением 3 Ом соединены в электрическую цепь, через которую течёт ток I (см. рисунок). Идеальный вольтметр показывает напряжение 9 В. Чему равна сила тока I?
Ответ: __________________________ А.
Необходимая теория: Соединения проводников
Резисторы, подключенные к вольтметру, соединены между собой последовательно.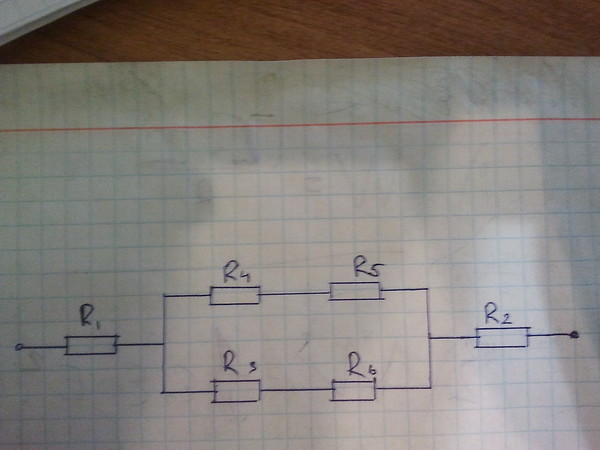 Отсюда следует, что сумма напряжений на каждом резисторе равна значению напряжения, которое показывает вольтметр. Запишем это в виде формулы Используя закон Ома, выразим значения напряжений и
Отсюда следует, что сумма напряжений на каждом резисторе равна значению напряжения, которое показывает вольтметр. Запишем это в виде формулы Используя закон Ома, выразим значения напряжений и
Здесь учтено, что в указанной точке (см. схему) ток I разделяется на две равные части из-за равенства сопротивлений в разветвленных частях цепи.
Деление силы тока на две равные части
Таким образом,
Подставляя численные значения, получим
Ответ: 2А.
Секреты решения. В задачах со схемами необходимо уметь выделять виды соединения проводников. После этого можно использовать известные закономерности для силы тока, напряжения и сопротивления. Ввиду того, что в задачах может быть большое количество проводников, решение в общем виде бывает громоздким, что может привести к математической ошибке. Поэтому лучше подставлять численные значения на ранних этапах решения.
3. На плавком предохранителе счётчика электроэнергии указано: «15 А, 380 В». Какова максимальная суммарная мощность электрических приборов, которые можно одновременно включать в сеть, чтобы предохранитель не расплавился?
Какова максимальная суммарная мощность электрических приборов, которые можно одновременно включать в сеть, чтобы предохранитель не расплавился?
Ответ: _________________________Вт.
Необходимая теория: Работа и мощность тока
Формулы для расчета мощности электрического тока имеют вид:
В зависимости от условия задачи, надо применять ту или иную формулу. Так как в задаче дается сила тока и напряжения, необходимо воспользоваться формулой
Подставляя численные значения, проведем расчет:
(Вт).
Ответ: 5700 Вт.
Секреты решения.
Формулы для расчета мощности лучше изучать как следствия формул для расчета работы тока или количества теплоты, выделяющейся в проводнике с током.
При делении этих формул на время t получим формулы для расчета мощности.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Публикация обновлена: 07.04.2023
404 Cтраница не найдена
Размер:
AAA
Цвет: C C C
Изображения Вкл. Выкл.
Обычная версия сайта
Контакты Версия для слабовидящих Версия для слабовидящих
структурное подразделение федерального государственного бюджетного образовательного учреждения высшего образования «Петербургский государственный университет путей сообщения Императора Александра I»
-
О техникуме
- Сведения об образовательной организации
- История
- Структура
- Руководство
- Лицензии
- Новости
- Фотогалерея
- Видеогалерея
- Контакты
- Противодействие коррупции
- Напишите нам
- Приемная комиссия
- Часто задаваемые вопросы
- Платное обучение
- Специальности
- Учебные корпуса
- Жилье иногородним
- Фотогалерея
- Видеогалерея
-
Студенту
- Расписание
- Консультации
- Государственная итоговая аттестация
- Система дистанционного обучения
- Учебно-методические материалы
- Библиотека
- Заочное отделение
- Демонстрационный экзамен
- Производственная практика
- Чемпионаты профессионального мастерства
- Региональный этап Чемпионата по профессиональному мастерству «Профессионалы» (10-28 апреля 2023 г.
 )
) - Общежитие
- Платное обучение
- Социальная поддержка
- Студенческая жизнь
- Спортивная жизнь
- Студенческое самоуправление
- Одежда обучающихся
- Единый государственный экзамен
- Коллективный договор
- Локальные нормативные акты
- Педагогический совет
- Профсоюзная организация
- Медицинский осмотр
- Система дистанционного обучения
- Контакты
- Главная
[Решено] Найти ток в каждой ветви данной сети, если
Найти ток в каждой ветви данной сети, если общий ток равен 2,55 А. Предыдущий документ EE 9 (состоялся: 29 октября 2020 г., вечер)
Предыдущий документ EE 9 (состоялся: 29 октября 2020 г., вечер)
Просмотреть все документы SSC JE EE >
- I 1 = 1,25 A, I 2 = 1,0 A
- I 1 = 1 А, I 2 = 1,55 А
- I 9I 1 = 1 А, I 2 = 1.55 A
Бесплатно
SSC JE: General Intelligence & Reasoning Бесплатный пробный тест
35,6 тыс. пользователей
20 вопросов
20 баллов
12 минут
Концепция:
Различные соединения сопротивления.
1.Последовательное соединение.
R eq = R 1 + R 2 + R 3
Если сопротивление N соединено последовательно, то
Ч экв = Р 1 + Р 2 + R 3
Если сопротивление N соединено последовательно, то 2 + Р 3 + —— + Р Н-1 9N \frac{1}{{{R_i}}}\)
Правило деления тока:
Ток в любой из параллельных ветвей равен отношению сопротивления противоположной ветви к общему сопротивлению, умноженному на общий ток.

\( {I_1} = \;\frac{{{R_2}}}{{{R_1} + {R_2}}}I\;\;\;\& \;\;\;{I_2} = \frac{{{R_1}}}{{{R_1} + {R_2}}}I\)
Расчет:
Здесь V = 10 В
R a = 2 Ом 9 0003
р b = 8 Ом
R c = 5 Ом
R x = R a + R b = 2 + 8 = 10 Ом 900 03
р у = р с + R = (5 + R) Ом
R eq = R x || R y =\( \frac{{{\rm{RxRy\;}}}}{{{\rm{Rx}} + {\rm{Ry}}}} = \;\frac{{10\ влево( {5 + R} \вправо)}}{{10 + 5 + R}} = \;\frac {{10\влево( {5 + R} \вправо)}}{{15 + R}}\ )
Поскольку V = IR eq
\( 10 = 2,55 \times \frac{{10\left( {5 + R} \right)}}{{15 + R}}\)
\( \;\;\frac{{15 + R}}{{5 + R}} = 2,55 \)
15 + R = 12,75 + 2,55R
1,55R = 2,25
R = 1,45 Ω
So R y = 5 + R = 5 + 1,45 = 6,45 Ω
Теперь, через правило деления тока
\( \;\;{I_1} = \;\frac{{{R_y}}} {{{R_x} + {R_y}}} \times I\)
=\( \frac{{6,45}}{{10 + 6,45\;}}\; \times 2,55\)
= \( \ frac{{6,45 \times 2,55}}{{16,45}} = 1\;A\)
\( {I_2} = \;\frac{{{R_x}}}{{{R_x} + {R_y}} }Я\)
= \( \frac{{10}}{{10 + 6,45}}2,55\)
= \( \frac{{10 \times 2,55}}{{16,45}} = 1,55\;A\)
Важные моменты
Правило разделения напряжения:
Напряжение на резисторе в последовательной цепи равно значению этого резистора, умноженному на общее напряжение на последовательных элементах, деленному на общее сопротивление последовательных элементов.
 .
.\( {V_{R1}} = \;\frac{{{R_1}}}{{{R_1} + {R_2}}}{V_s}\;\;\& \;\;{V_ {R2}} = \;\frac{{{R_2}}}{{{R_1} + {R_2}}}{V_s}\)
Уловка быстрого доступа:
Сопротивление R x = 10 Ом
Напряжение на R x равно 10 В В}{{{R_x} }} = \;\frac{{10}}{{10}} = 1\;A\)
Из приведенных ниже 4 вариантов только вариант (2) содержит I 1 = 1 Ампер.
Итак, вариант (2) правильный.
Скачать решение PDFПоделиться в WhatsApp
Последние обновления SSC JE EE
Последнее обновление: 23 февраля 2023 г.
Комиссия по отбору персонала выпустит уведомление SSC JE EE 2023 26 июля 2023 года. Последний день подачи заявок будет 16 августа 2023 года, а экзамен Paper I будет проведен в октябре 2023 года. Это соответствует календарю экзаменов. В 2022 году документ I SSC JE проводился с 14 ноября 2022 года по 16 ноября 2022 года.
 Кандидаты, которые сдадут экзамен, получат заработную плату в диапазоне от рупий до рупий. 35 400 / — до рупий. 1,12,400/-. Чтобы успешно пройти отбор, кандидаты могут обратиться к документам SSC JE EE за предыдущий год, чтобы оценить уровень экзамена.
Кандидаты, которые сдадут экзамен, получат заработную плату в диапазоне от рупий до рупий. 35 400 / — до рупий. 1,12,400/-. Чтобы успешно пройти отбор, кандидаты могут обратиться к документам SSC JE EE за предыдущий год, чтобы оценить уровень экзамена.Как использовать теорему Тевенина | EAGLE
Этот пост также доступен в: Немецкий (немецкий)
Узнайте, как использовать теорему Тевенина для расчета тока и напряжения на нагрузочном резисторе в линейной цепи.
Как рассчитать ток и напряжение нагрузки с помощью теоремы Тевенина — не усложняйте задачу
Существует множество методов анализа сложных электрических цепей. К ним относятся сеточный анализ, узловой анализ или законы цепей Кирхгофа. Проблема заключается в том, что при проектировании сети питания постоянного тока у вас будет нагрузка, значение которой будет меняться по мере развертывания процесса проектирования. Вместо того, чтобы пересчитывать ток и напряжение всей цепи каждый раз при изменении нагрузки, вы можете упростить этот процесс с помощью теоремы Тевенина.
 В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Thevenin для быстрого расчета тока и напряжения. Давай начнем.
В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Thevenin для быстрого расчета тока и напряжения. Давай начнем.Что такое Теорема Тевенина?
Как и все другие математические и научные теории/законы, Теорема Тевенина была изобретена самим человеком, Леоном Шарлем Тевенином. Тевенен был французским инженером-телеграфистом, родившимся в Мо, Франция. После службы в корпусе телеграфных инженеров в 1882 году он был назначен преподавателем-инспектором в Высшей школе телеграфии. Именно здесь он заинтересовался измерением электрических цепей. В то время он использовал два доступных метода — законы Кирхгофа и закон Ома.
Léon Charles Thévenin (Источник изображения)Пытаясь упростить анализ сложных схем для каждого инженера, Тевенин разработал свою знаменитую теорему Тевенина. Эта теорема сводит сложные схемы к упрощенным эквивалентным схемам Тевенина.

Теорема
Упрощенная эквивалентная схема Thevenin с одним источником напряжения и сопротивлением. (Источник изображения)Th e гласит, что можно взять любую линейную цепь, которая может содержать несколько ЭДС и резистивных составляющих, и упростить схему до одного источника напряжения и последовательного сопротивления, подключенного к нагрузке.
Зачем использовать теорему Тевенина?
В этом случае линейная цепь включает пассивные компоненты, такие как резисторы, катушки индуктивности и конденсаторы. Однако если вы работаете со схемой, включающей газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина подходила не для этого. Так зачем же использовать эту теорему для анализа линейных цепей?
- Эффективность . Теорема Тевенина обеспечивает простой метод анализа силовых цепей, которые обычно имеют нагрузку, значение которой изменяется в процессе анализа.
 Эта теорема обеспечивает эффективный способ расчета напряжения и тока, протекающих через нагрузку, без необходимости заново пересчитывать всю схему.
Эта теорема обеспечивает эффективный способ расчета напряжения и тока, протекающих через нагрузку, без необходимости заново пересчитывать всю схему. - Фокус . Теорема Тевенина также предоставляет эффективный способ сосредоточить анализ на определенной части схемы. Это позволяет вам рассчитать напряжение и ток на конкретной клемме, упростив остальную часть схемы с помощью эквивалента Thevenin.
Например, посмотрите на схему ниже. Здесь у нас есть резистор R2 в качестве нагрузки. Мы хотим рассчитать напряжение и ток, протекающие через этот резистор, без необходимости использовать трудоемкий метод анализа, такой как ток ответвления, ток сетки и т. д., каждый раз, когда значение нагрузочного резистора изменяется.
(Источник изображения)Чтобы упростить задачу, мы можем использовать теорему Тевенина для удаления сопротивления нагрузки и напряжения. Затем мы упрощаем остальную часть схемы, используя один источник напряжения и последовательное сопротивление.
(Источник изображения) В этой упрощенной схеме Thevenin два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенное напряжение и сопротивление будут работать так же, как наша исходная схема. Теперь у нас есть только две простые переменные для расчетов.
В этой упрощенной схеме Thevenin два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенное напряжение и сопротивление будут работать так же, как наша исходная схема. Теперь у нас есть только две простые переменные для расчетов.Теорема Тевенина в действии
Давайте рассмотрим пример схемы и рассчитаем ток, протекающий через нагрузочный резистор между двумя клеммами. Процесс анализа цепи постоянного тока с использованием теоремы Тевенина требует следующих шагов:
- Найдите сопротивление Thevenin, удалив все источники напряжения и нагрузочный резистор.
- Найдите напряжение Thevenin, подключив напряжения.
- Используйте сопротивление и напряжение Thevenin, чтобы найти ток, протекающий через нагрузку.
Вот пример схемы, с которой мы будем работать:
(Источник изображения)Шаг 1.
 Сопротивление тевенину
Сопротивление тевенинуСначала нам нужно удалить нагрузочный резистор 40 Ом, соединяющий клеммы A и B, вместе со всеми источниками напряжения. Это даст нам разомкнутую цепь при нулевом напряжении, в результате чего останутся только два резистора, соединенных последовательно.
(Источник изображения)Чтобы рассчитать общую устойчивость к тевенину, мы можем использовать следующий процесс:
Шаг 2 – Напряжение Thevenin
Затем мы можем использовать закон Ома для расчета полного тока, протекающего через цепь, следующим образом:
Поскольку эти резисторы соединены последовательно, они будут иметь одинаковые 0,33 ампера. Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:
Шаг 3 — Ток нагрузки
Теперь, когда у нас есть сопротивление и напряжение Thevenin, мы можем соединить нашу эквивалентную схему Thevenin с нашим исходным нагрузочным резистором, как показано ниже.

Отсюда мы можем использовать закон Ома для расчета полного тока, протекающего через нагрузочный резистор, следующим образом:
Готовы проверить свои навыки? Используйте теорему Тевенина, чтобы найти iload и vload для схемы ниже!
Запомните трехэтапный процесс:
- Найдите сопротивление Thevenin, удалив все источники напряжения и нагрузку.
- Найдите напряжение Тевенина, повторно подключив источники напряжения.
- Используйте сопротивление и напряжение Thevenin, чтобы найти полный ток, протекающий через нагрузку.
Будь проще
Планируете спроектировать силовую цепь постоянного тока? Скорее всего, вы будете включать нагрузку, значение которой изменится во время анализа схемы. Вместо того, чтобы пересчитывать всю схему каждый раз, когда вы меняете значение этой нагрузки, теперь у вас есть теорема Тевенина, облегчающая вашу работу.
Эта теорема позволяет вам взять любую сложную линейную цепь с различными резистивными компонентами и ЭДС и упростить ее до эквивалентной схемы Тевенина.

- Эффективность . Теорема Тевенина обеспечивает простой метод анализа силовых цепей, которые обычно имеют нагрузку, значение которой изменяется в процессе анализа.

 )
)
 .
. Кандидаты, которые сдадут экзамен, получат заработную плату в диапазоне от рупий до рупий. 35 400 / — до рупий. 1,12,400/-. Чтобы успешно пройти отбор, кандидаты могут обратиться к документам SSC JE EE за предыдущий год, чтобы оценить уровень экзамена.
Кандидаты, которые сдадут экзамен, получат заработную плату в диапазоне от рупий до рупий. 35 400 / — до рупий. 1,12,400/-. Чтобы успешно пройти отбор, кандидаты могут обратиться к документам SSC JE EE за предыдущий год, чтобы оценить уровень экзамена. В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Thevenin для быстрого расчета тока и напряжения. Давай начнем.
В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Thevenin для быстрого расчета тока и напряжения. Давай начнем.
 Эта теорема обеспечивает эффективный способ расчета напряжения и тока, протекающих через нагрузку, без необходимости заново пересчитывать всю схему.
Эта теорема обеспечивает эффективный способ расчета напряжения и тока, протекающих через нагрузку, без необходимости заново пересчитывать всю схему. В этой упрощенной схеме Thevenin два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенное напряжение и сопротивление будут работать так же, как наша исходная схема. Теперь у нас есть только две простые переменные для расчетов.
В этой упрощенной схеме Thevenin два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенное напряжение и сопротивление будут работать так же, как наша исходная схема. Теперь у нас есть только две простые переменные для расчетов.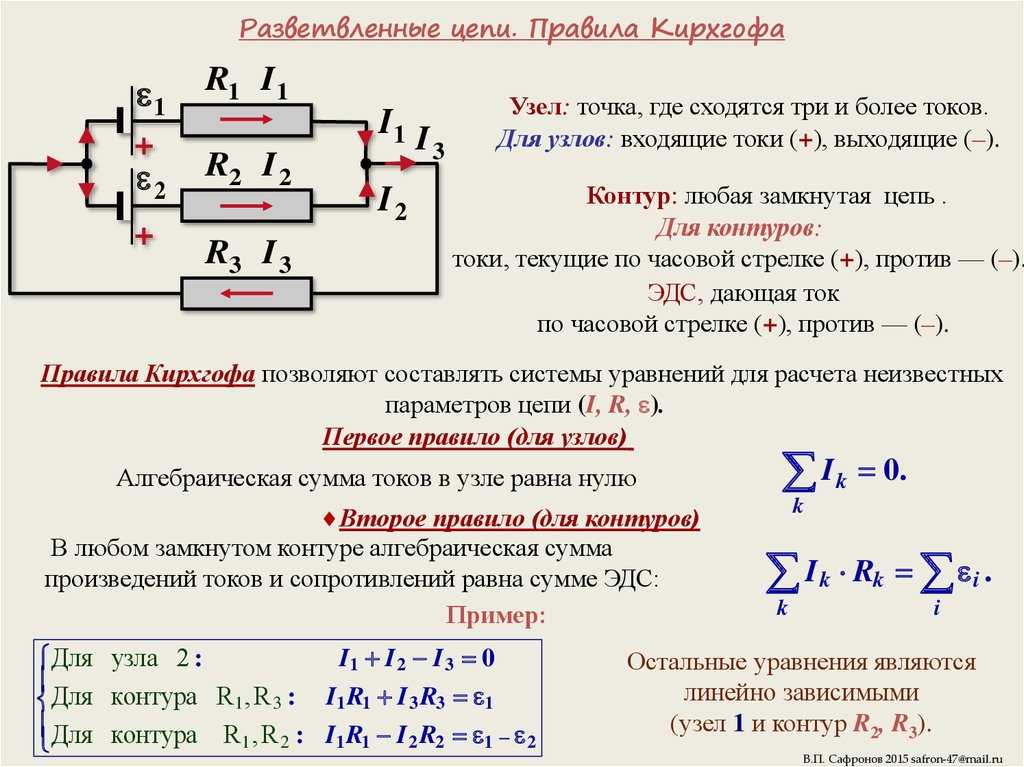 Сопротивление тевенину
Сопротивление тевенину
Leave A Comment