Определите скорость изменения тока в катушке с индуктивностью: №1155. Определите скорость изменения тока в катушке с индуктивностью 100 мГн, если в ней возникла ЭДС самоиндукции 80 В.

Явление самоиндукции — определение, формулы, примеры

Покажем, как применять знание физики в жизни

Начать учиться

Быть самостоятельным — это хорошо. Вот и электрический ток решил, что он сам со всем разберется. А нам в этой статье предстоит разобраться в явлении самоиндукции.

Магнитный поток

Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.

Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.

Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению:

• модуля вектора магнитной индукции ​B​,
• площади поверхности ​S​, которую пронизывает поток,
• и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).

Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла

​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Пятерка по физике у тебя в кармане!

Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.

Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.

Вот что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.


2. Направление тока различается при увеличении числа линий и при их уменьшении.


3. Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Самоиндукция

Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.

Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А]

Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.

Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.

Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:

• первая лампа загорится практически сразу,
• вторая лампа загорится с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС.

Поэтому электрические лампочки так часто перегорают при отключении света.

ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн]

Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.

Индуктивность

Индуктивность — это способность катушки, контура или проводника с током накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.

Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

Можно ли увеличивать индуктивность катушки?

Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.

Как работает катушка

Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.

Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.

Задачка раз

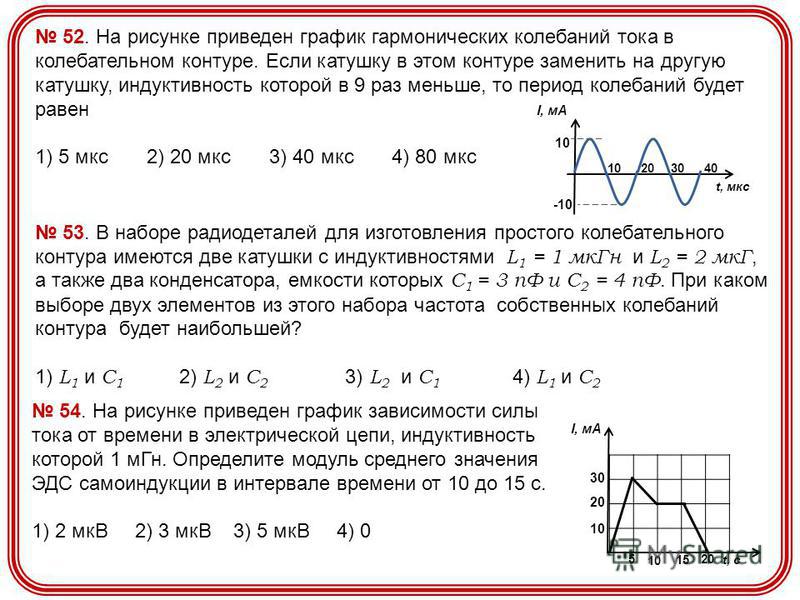
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.

Решение

За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:

Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.

Задачка два

По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб.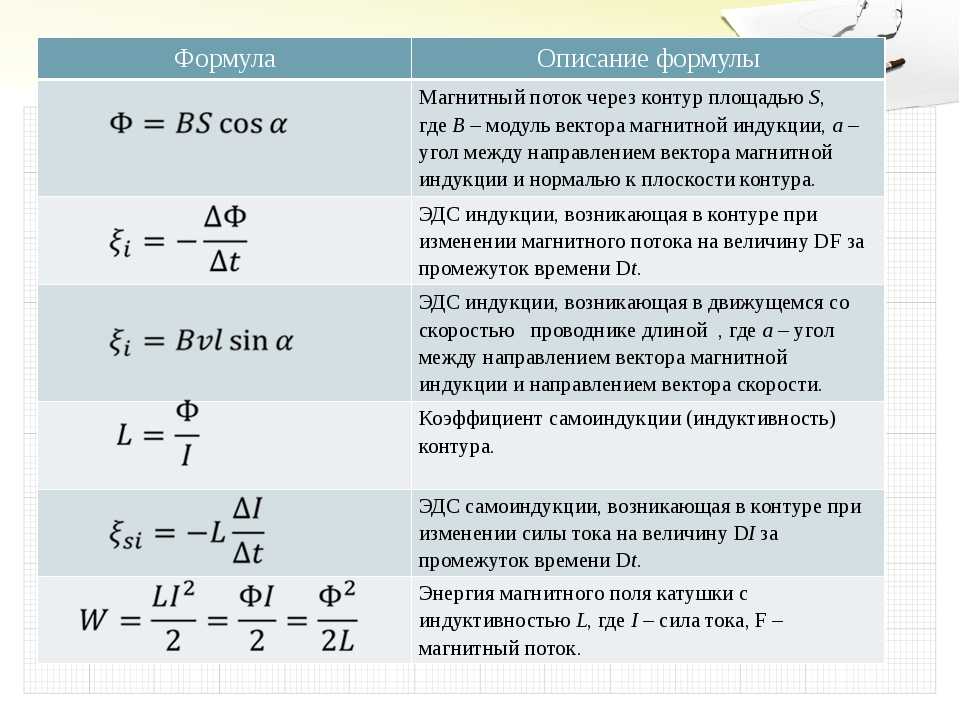 Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?

Решение

При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.

Отсюда индуктивность катушки равна:

Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:

Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.

Карина Хачатурян

К предыдущей статье

Закон Кеплера

К следующей статье

157.5K

Закон всемирного тяготения

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Электричество и магнетизм

Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле.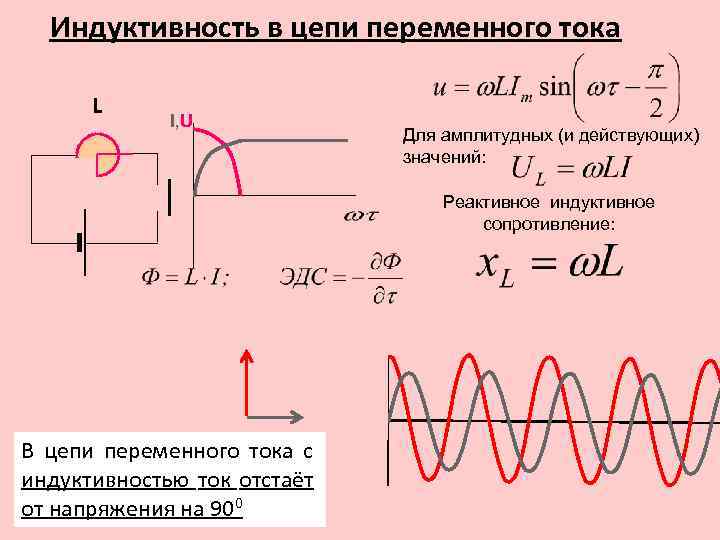 Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока

Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре

Введем коэффициент пропорциональности L

(8.16)

Коэффициент пропорциональности L называется индуктивностью контура. 

Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока.

 

Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.  

В системе СИ единицей измерения индуктивности является генри (Гн)

Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции. 

Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.

 

Видео 8. 13.  Закон Фарадея. Явление самоиндукции.

Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.

Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.  

Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени

(8.17)

Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков

,

что необходимо учитывать при дифференцировании

Подставляя это выражение в (8.17), получаем для неподвижного контура всреде

(8. 18)

 

Если же индуктивность контура не зависит от силы тока в нём, то имеем

(8.19)

Мы приходим к закону самоиндукции. В этом простейшем случае: 

В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи.

Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна

где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как

(8.20)

где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между  и I, получаем величину индуктивности длинного соленоида (рис. 8.31)

(8.21)

 

Рис. 8.31. Индуктивность соленоида 

При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.

Рассмотрим цепь, состоящую из сопротивления, индуктивности и источника тока (рис. 8.32).  

Рис. 8.32. Цепь, содержащая катушку, сопротивлении и источник постоянного тока

Рис. 8.33. Токи замыкания (1) и размыкания (2) цепи с индуктивностью  

Будем считать, что в сопротивление R уже включены соединенные с ним последовательно внутреннее сопротивление источника и сопротивление катушки. После того, как исчезнут экстра токи замыкания и размыкания и установится постоянный ток, сила тока в цепях, показанных на рис. 8.33, согласно закону Ома, будет равна

При разомкнутомключе ток не идет. Что будет, если ключ замкнуть, перебросив его из положения 1 в положение 2? 

Обозначим через I мгновенное значение силы тока в цепи:  (функция времени). Если учесть ЭДС самоиндукции, то в каждый момент времени по-прежнему справедлив закон Ома

(8.22)

Подставим в (8.22) выражение (8.19), предполагая, что индуктивность не зависит от тока. В результате применения закона Ома получаемдифференциальное уравнение для силы тока в цепи

(8.23)

Это уравнение легко интегрируется

или

откуда следует общее решение уравнения (8.23)

(8. 24)

Постоянную интегрирования сonst определяем из начального условия: в момент времени t = 0 (замыкание ключа) тока в цепи еще не было, то есть I(0) = 0. Тогда

Таким образом, зависимость от времени тока замыкания в цепи с индуктивностью имеет вид

(8.25)

Величина

имеет размерность времени и является характерным временем нарастания тока в цепи с индуктивностью. Сначала ток растет от нулевого значения линейно, затем скорость его роста начинает уменьшаться и ток асимптотически стремится к своему предельному значению

равному току в этой же цепи в отсутствие индуктивности. Практически предельное значение тока, учитывая реальную точность измерений силы тока, достигается за времена примерно равные  (рис. 8.34).

 

Рис. 8.34. Ток замыкания цепи с индуктивностью 

Рассмотрим теперь рис. 8.33-2. Сначала ключ находился в положении 1, и в цепи шел ток

При перебрасывании ключа в положение2 источник тока отключается от цепи, и ток I начинает уменьшаться. Закон Ома для замкнутого участка цепи имеет теперь вид

(8.26)

В отличие от (8.23) в разомкнутой цепи больше нет ЭДС  и действует только ЭДС самоиндукции. Уравнение (8.26) интегрируется еще легче

(8.27)

Учитывая, что начальный ток в цепи был равен

для зависимости от времени тока размыкания в цепи с индуктивностью получаем

(8. 28)

На рис 8.35 представлен опыт, иллюстрирующий явления при замыкании и размыкании цепи, содержащей индуктивность. В цепь питания большой катушки индуктивности включена электрическая лампа. При замыкании цепи ключом лампа загорается не сразу, поскольку ЭДС самоиндукции препятствует изменению тока (правило Э.Х. Ленца). При размыкании наблюдается яркая вспышка из-за того, что источником тока становится ЭДС самоиндукции катушки, которая при резком изменении силы тока обычно заметно больше ЭДС источника.

Рис. 8.35. Явления при замыкании и размыкании цепи, содержащей индуктивность

Видео 8.14. Явление самоиндукции. Токи при замыкании и размыкании цепи.

Пример. К источнику с внутренним сопротивлением 2 Ом подключают катушку индуктивностью 0,5 Гн и сопротивлением 8 Ом. Найти время T, в течение которого после замыкания цепи ток в катушке достигнет значения, отличающегося от максимального на .

Решение. В этой задаче полное сопротивление цепи равно

где r  — внутреннее сопротивление источника, а — сопротивление катушки. Согласно (8.25), ток в момент времени Т  равен

По условию задачи,

откуда

electromagnetism — Скорость изменения тока в индукторе

Я опишу, как сделать что-то, что действует так же, как индуктор, так что тогда это должно быть ясно.

Представьте, что у вас не было индуктора, и вы заменили его проводом. Тогда по проводу пойдет ток.

А теперь представьте, что там тонны маленьких батареек не подключены. Кто-то указывает в одну сторону, кто-то в другую. Теперь в батарее хранится столько энергии, что если вы пропускаете через нее ток слишком долго, батарея выходит из строя и умирает.

Итак, вы заменили индуктор проводом и кучей батарей, и мы скажем, что количество энергии, хранящейся в ваших батареях, пропорционально квадрату тока, проходящего через этот участок провода.

Представьте, что вы наняли кого-то, чтобы это произошло. Когда ток увеличивается, этому человеку придется подключить кучу батарей, обращенных в сторону, где ток течет в неправильном направлении (чтобы батареи могли получить питание), и ему нужно будет подключить достаточное количество батарей, чтобы они заряжались со скоростью, которая поддерживает в зависимости от того, сколько энергии они должны хранить для увеличения тока.

А что, если сила тока уменьшится, запасенная энергия должна будет уменьшиться, поэтому нанятому вами человеку придется подключить нужное количество батарей в том направлении, где они теряют энергию.

Это означает, что есть куча крошечных батареек, направленных в ту или иную сторону, и их количество связано с тем, как быстро меняется ток. И они подключены, чтобы получать или терять энергию, и они получают энергию, когда ток увеличивается, и они теряют энергию, когда ток уменьшается.

Итак, мы знаем, как работает такой элемент схемы. У него есть ток, и у него есть куча батарей, которые имеют накопленную энергию, пропорциональную квадрату тока, и что батареи могут быть подключены или не подключены, и могут быть подключены разные количества, и они могут быть подключены, чтобы питать себя или заряжать заряды, протекающие через них. Но чем больше у вас их подключено, тем больше текущих изменений. Достаточно, чтобы энергия всегда была пропорциональна квадрату тока.

Вот что такое индуктор. Энергия хранится в магнитном поле (у магнитных полей есть энергия, и удвоенное поле в четыре раза больше энергии). И поэтому, если энергия магнитного поля изменяется, эта энергия должна куда-то уйти или откуда-то прийти. И это идет на сборы или исходит от сборов.

Мы можем представить этот обмен энергией с помощью ЭДС (думаем об этом как о мощности на ток). И это потому, что он буквально работает над электрическими зарядами именно с той скоростью, которая уравновешивает энергию.

Итак, как работает ЭДС.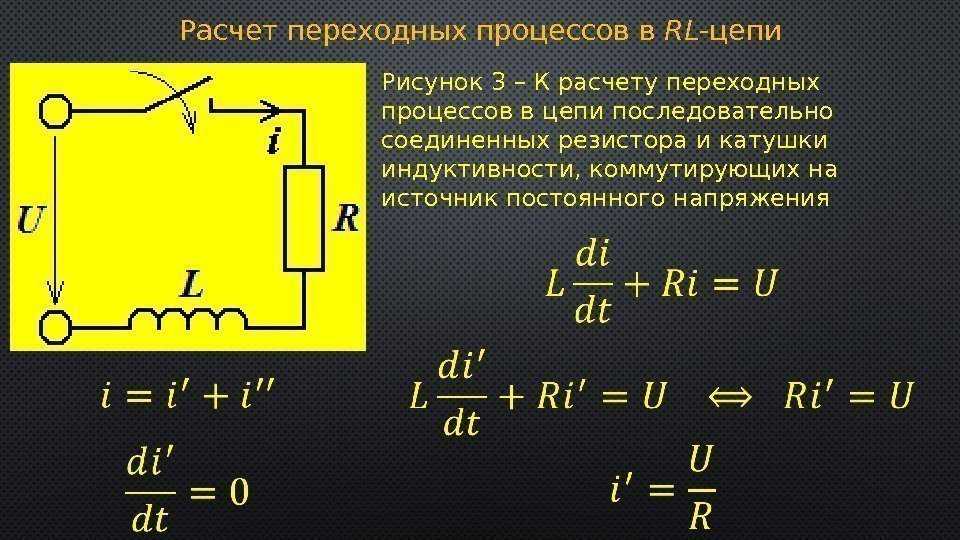 Он работает точно так же, как связка батареек. Таким образом, вы можете представить себе, что индуктор — это батарея, напряжение которой связано со скоростью изменения тока. Потому что изменение тока означает изменение магнитного поля, следовательно, изменение количества энергии в магнитном поле, и, следовательно, энергия должна откуда-то поступать, а энергия исходит от зарядов (или уходит куда-то).

Можно буквально представить, что есть аккумулятор, напряжение которого зависит от скорости изменения тока. И тому есть веская причина. Когда вы пропускаете ток через батарею в обратном направлении, вы заряжаете батарею. И вы возбуждаете индуктор. Большее магнитное поле в индукторе буквально имеет больше энергии.

Таким образом, циркулирующие электрические поля связаны с изменением магнитных полей и, следовательно, с направлением энергии в магнитные поля.

Таким образом, батарея питает заряды, которые текут к индуктору, и именно в индукторе энергия течет в индуктор (в его магнитное поле), когда ток увеличивается (и энергия течет от магнитного поля в индукторе к заряжается при уменьшении тока).

Итак, магнитные поля обладают энергией, и для их увеличения требуется энергия, а когда вы их уменьшаете, вы получаете энергию. Поскольку магнитное поле связано с током, изменяющийся ток связан с изменяющимся магнитным полем, поэтому энергия для этого исходит откуда-то из зарядов.

И как мы можем количественно оценить энергию, поступающую на заряды или поступающую от них? С э.д.с. И направление такое, чтобы сбалансировать энергию. Уменьшить энергию зарядов (например, подзарядить батарею).

И заметьте, что когда я говорю зарядить батарею, я имею в виду подзарядку перезаряжаемой батареи, я не говорю об изменении мощности. Вы можете себе представить, что есть тонны батарей, каждая из которых имеет фиксированное напряжение и каждая обращена определенным образом, и они подключаются при изменении тока, чтобы высасывать энергию, если ток увеличивается, и способ отдавать энергию, если ток уменьшается. и если изменение более быстрое, вы подключаете больше из них. Так что они действуют точно так же, как батареи, и мы вставляем их достаточно, чтобы правильно учитывать энергию, которая обменивается между зарядами и магнитным полем.

На самом деле вы можете думать обо всей электродинамике как о полях, обладающих энергией и импульсом, а там, где нет зарядов или токов, импульс и энергия текут по кругу, когда поля меняются, и даже когда поля находятся там (и да, энергия и импульс могут течь даже когда поля статичны, точно так же, как электрический ток может течь, даже если плотность электрического заряда не меняется). Так что обычно энергия и импульс полей просто перетекают. Но когда есть ток и есть заряд, тогда поля могут терять или набирать энергию, они могут терять или набирать импульс, и заряды уравновешивают это.

Таким образом, если ваша цепь не движется, ЭДС — это просто мощность на ток, поэтому для вашего заданного тока вы можете узнать, сколько ЭДС вам нужно для учета энергии, обменивающейся с магнитным полем. То же самое происходит и с конденсатором. Когда он заряжен, возникает электрическое поле, обладающее энергией. Напряжение на конденсаторе точно такое, какое необходимо, чтобы сбалансировать энергию, взятую от зарядов, и передать поле.

Итак ваша реальная батарея заряжает заряды и они идут по цепи и по мере приближения к конденсатору заряд уже там забирает энергию зарядов и запасает ее в усиленном электрическом поле. Вы можете думать об этом так, как если бы заряд ощущал силу электрического поля, куда уходит или откуда берется энергия? Она переходит в энергию полей. Итак, если энергия поля поступает в область, то либо равное количество энергии лучше вытекает, либо энергия поля там должна измениться, либо энергия должна тут же и там обмениваться зарядом.

ОК. Давайте будем честными о том, почему вы этого еще не знали, потому что это не ваша вина. В электростатике у вас были заряды, мгновенно воздействующие друг на друга, и у вас была потенциальная энергия. Но все это неверно. Это только приблизительно выполняется, когда вещи не двигаются. Более сложная реальность состоит в том, что в зарядах, а также в полях, разбросанных по всему пространству, есть энергия и импульс. И она течет вокруг, и ею можно обмениваться между зарядами, токами и полями.

Меняют ли поля свою энергию, потому что заряды меняют свою энергию? Или наоборот? Ни то, ни другое не совсем точно. Они должны произойти вместе. Энергосбережение говорит, что они происходят вместе. И тогда мы должны установить конкретные законы о том, как происходит взаимодействие между зарядами, токами и полями. Это взаимодействие диктует, как они оба должны измениться. Это не одно вызывает другое.

В нашем примере, когда вы заплатили кому-то за подключение батарей, казалось, что изменение тока вызвало другое. Представьте, что вы заплатили им, но они ничего не сделали, потому что знали, что магнитное поле хранит для них энергию.

Реальность такова, что заряды движутся таким образом, что напрасно или теряют энергию, а поля таковы, что обмениваются энергией без самих себя, так что поля теряют энергию или приобретают энергию именно там, где находятся эти заряды, и с точно правильной скоростью, чтобы уравновесить энергосбережение Но каждый просто взаимодействует так, как он это делает.

И импульс делает то же самое, за исключением того, что ток может участвовать в обмене импульсом без обмена энергией.

электромагнетизм — Как поддерживается/уменьшается скорость изменения тока в катушке индуктивности в цепи?

спросил 3 года 8 месяцев назад

Изменено 3 года, 8 месяцев назад

Просмотрено 243 раза

$\begingroup$

Рассмотрим идеальную цепь источника постоянного напряжения и катушки индуктивности, соединенных вместе с переключателем между ними. Когда переключатель замкнут в t = 0, ток начинает увеличиваться, что вызывает индуцированную ЭДС, которая, в свою очередь, приводит к неконсервативному электрическому полю, чтобы поддерживать нулевое электрическое поле внутри проводника (идеального) накапливаются электрические заряды, чтобы отменить неконсервативное поле, из-за которого на индукторе возникает напряжение (как оно определено для статических полей), но чистое электрическое поле равно нулю внутри идеального индуктора, из уравнения ЭДС = -L(di/dt), я понимаю, что ток должен изменение для существования ЭДС, но из аргумента, который я только что упомянул выше, я чувствую, что внутри нет электрического поля, и, следовательно, ток должен оставаться постоянным, что приводит к тому, что индуцированная ЭДС становится равной нулю (поскольку сейчас нет изменения тока) и также исчезает электрическое поле из-за накопленных зарядов на поверхности индуктора, так как же теперь поддерживается скорость изменения тока? Что заставляет его поддерживать именно то, что заставляет его существовать? Пожалуйста, дайте интуитивное объяснение того, как это происходит.

Я читал, что ЭДС индукции вызывает уменьшение скорости тока (в целом), но как, согласно аргументу, который я упомянул выше?

А что значит скорость изменения тока? Это увеличение скорости зарядов? Или увеличить количество зарядов?

Я знаю, что в моем объяснении есть ошибка, я наверняка что-то упускаю, поэтому, пожалуйста, помогите мне.

• электромагнетизм
• электрические цепи
• напряжение
• электромагнитная индукция
• индуктивность

$\endgroup$

0

$\begingroup$

внутри нет электрического поля и, следовательно, ток должен оставаться постоянным,

В случае идеального индуктора и идеального источника постоянного тока для увеличения тока не требуется наличия существенного результирующего макроскопического электрического поля в проводе. Существует сильное кулоновское поле батареи и поверхностные заряды, но внутри проводов это поле почти нейтрализуется индуцированным электрическим полем из-за носителей заряда в индукторе.

Конечно, на микроскопическом уровне описания должна быть какая-то небольшая ненулевая сила, которая ускоряет носители тока в направлении тока, чтобы заставить их двигаться быстрее. Таким образом, кулоновское поле батареи и поверхностных зарядов немного больше, чем индуцированное электрическое поле, поэтому на носителях заряда совершается некоторая суммарная работа по увеличению их кинетической энергии. Но эта ускоряющая сила в макроскопическом масштабе пренебрежимо мала, поскольку носители заряда чрезвычайно легки и (по предположению) отсутствует омическое сопротивление.

При расчете кинетической энергии подвижных электронов в индукторе она на много порядков меньше магнитной энергии, запасенной в индукторе. Таким образом, чистая сила (сумма кулоновских сил и сил индуцированного электрического поля), необходимая для их ускорения, пренебрежимо мала по сравнению с чистой кулоновской силой, и, таким образом, чистое электрическое поле считается фактически нулевым.