EF18831 | СПАДИЛО
ЕГЭ▿базовый уровень сложности▿ФИПИ(18831)
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
📜Теория для решения: Равномерное прямолинейное движение Перемещение и путь при равноускоренном прямолинейном движении
Введите ответ: Посмотреть решение
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с.
 В это время тело двигалось равноускоренно (с положительным ускорением).
В это время тело двигалось равноускоренно (с положительным ускорением). - От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка.
 Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
s1+ s2= 100 + 100 = 200 (м)
Ответ: 200Алиса Никитина | Просмотров: 757
Практика — Курсы ЕГЭ и ОГЭ
Тренировка предмета ЕГЭ Физика по теме 3.2 Неравномерное движение
Задание № 4975
Сложность 0
Зависимость координаты x тела от времени t имеет вид:
$x(t)=1+2t+3t^2$. Чему равна проекция скорости тела на ось Ox в момент времени t = 3 с при таком движении? (Ответ дайте в метрах в секунду.)
Чему равна проекция скорости тела на ось Ox в момент времени t = 3 с при таком движении? (Ответ дайте в метрах в секунду.)
Задание № 4822
Сложность 0
Тело брошено вертикально вверх с начальной скоростью 10 метров в секунду. Каков будет модуль скорости через секунду после броска?
Задание № 2264
Сложность 0
Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с постоянным ускорением, и догоняет грузовик на расстоянии 150 м от остановки. Чему равно ускорение мотоцикла?
Задание № 2258
Сложность 0
Тело массой 2 кг, брошенное с некоторой высоты вертикально вверх, упало на землю со скоростью 6 м/с. Потенциальная энергия тела относительно поверхности земли в момент броска была равна 20 Дж. С какой начальной скоростью бросили тело? Сопротивлением воздуха пренебречь.
Задание № 2256
Сложность 0
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. 2$. Через 2с его скорость будет равна.
2$. Через 2с его скорость будет равна.
Задание № 2247
Сложность 0
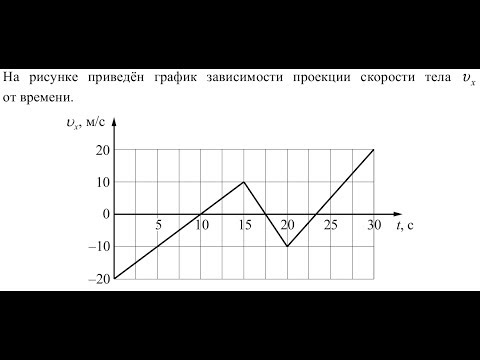
На рисунке показан график зависимости проекции $υ_x$ скорости тела от времени t. Какова проекция $a_x$ ускорения этого тела в интервале времени от 3 до 4 c?
Задание № 2246
Сложность 0
На рисунке показан график зависимости проекции $υ_x$ скорости тела от времени t. Какова проекция $a_x$ ускорения этого тела в интервале времени от 2 до 3 c?
Задание № 2245
Сложность 0
Мяч брошен вертикально вверх с начальной скоростью 20 м/с. Чему равно перемещение мяча за 3 с, считая от момента броска? Сопротивлением воздуха пренебречь.
Задание № 2244
Сложность 0
Дом стоит на краю поля. С балкона с высоты 5 м мальчик бросил камешек в горизонтальном направлении. Начальная скорость камешка 7 м/с, его масса 0,1 кг. Через 2 с после броска кинетическая энергия камешка равна
Задание № 2243
Сложность 0
Дом стоит на краю поля. С балкона с высоты 5 м мальчик бросил камешек в горизонтальном направлении.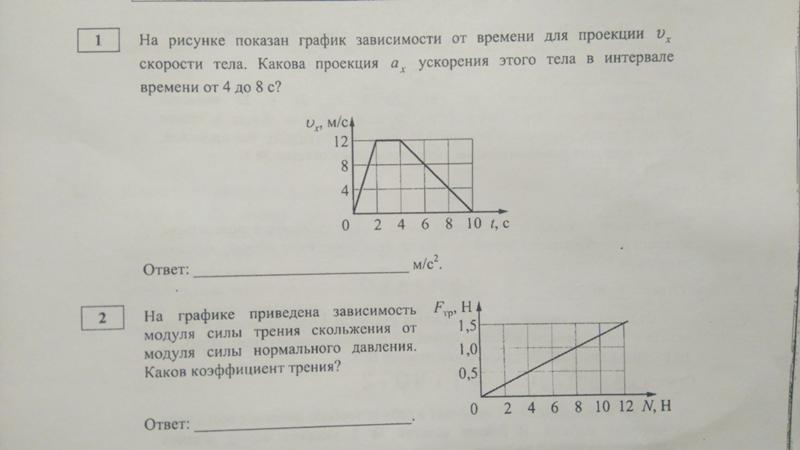 2$. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с?
2$. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с?
Задание № 2239
Сложность 0
На рисунке показан график зависимости проекции $υ_x$ скорости тела от времени t. Какова проекция $a_x$ ускорения этого тела в интервале времени от 4 до 6 c?
Задание № 2237
Сложность 0
На рисунке показан график зависимости от времени для проекции $υ_x$ скорости тела. Какова проекция $a_x$ ускорения этого тела в интервале времени от 0,5 до 1 c?
Задание № 2236
Сложность 0
На рисунке приведён график зависимости проекции скорости $υ_x$ от времени t для тела, движущегося прямолинейно по оси x. Определите проекцию ускорения тела $a_x$.
Задание № 2235
Сложность 0
На рисунке показан график зависимости от времени для проекции $υ_x$ скорости тела. Какой путь $S$ проехало тело в интервале времени от 4 до 8 c?
Задание № 2233
Сложность 0
На рисунке приведён график зависимости проекции скорости тела $υ_x$ от времени.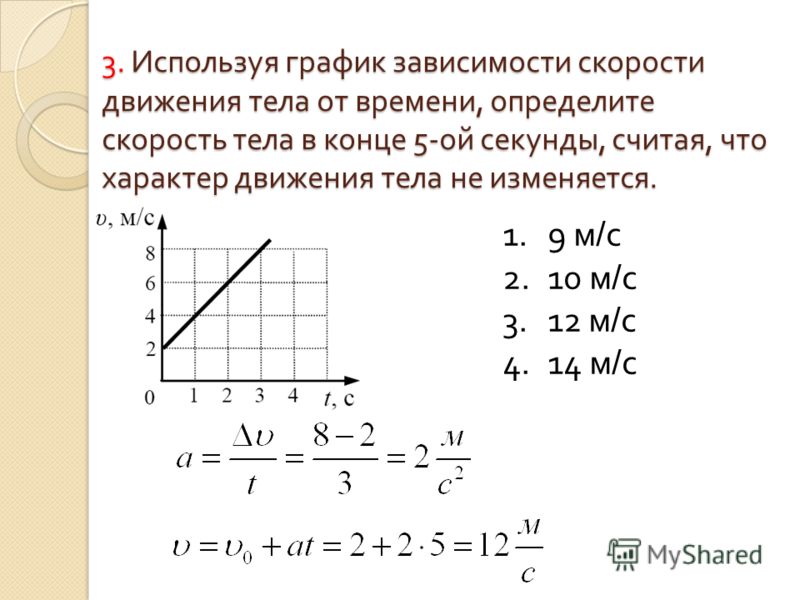 Определите проекцию ускорения этого тела $a_x$ в интервале времени от 15 до 20 с.
Определите проекцию ускорения этого тела $a_x$ в интервале времени от 15 до 20 с.
Задание № 2231
Сложность 0
Мяч падает с некоторой высоты вертикально вниз и после удара о землю отскакивает вверх с той же (по модулю) скоростью. Какой из приведённых графиков зависимости модуля скорости υ от времени соответствует указанному движению тела? Система отсчёта связана с Землёй. Сопротивление воздуха не учитывать.
Задание № 2230
Сложность 0
На рисунке приведён график зависимости проекции скорости тела $υ_x$ от времени. Найдите модуль ускорение тела в промежутке с 8 до 10 с.
Задание № 2227
Сложность 0
Камень, брошенный с крыши дома почти вертикально вверх со скоростью 10 м/с, упал на землю через 3 с после броска. С какой высоты брошен камень? Сопротивление воздуха не учитывать.
Задание № 2226
Сложность 0
Автомобиль движется по прямой улице. На графике представлена зависимость его скорости от времени. Найдите ускорение на участке от 0 до 10 секунд.
Задание № 2225
Сложность 0
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси x. Определите модуль ускорение тела.
Задание № 2223
Сложность 0
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Задание № 2222
Сложность 0
С аэростата, зависшего над Землёй, упал груз. Через 10с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Задание № 2218
Сложность 0
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от $t_1$=20 с до $t_2$=50 с.
Задание № 2201
Сложность 0
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через 1.5 секунду после броска модуль скорости тела будет равен
Кратчайший путь | Математика для гуманитарных наук
Результаты обучения
- Определение вершин, ребер и петель графа
- Определить степень вершины
- Определить и нарисовать как путь, так и цепь через граф
- Определить, подключен граф или нет
- Найдите кратчайший путь через граф с помощью алгоритма Дейкстры
Когда вы посещаете веб-сайт, такой как Google Maps, или используете свой смартфон, чтобы узнать дорогу от дома до дома вашей тети в Пасадене, вы обычно ищете кратчайший путь между двумя точками. Эти компьютерные приложения используют представления карт улиц в виде графиков с расчетным временем в пути в качестве весовых коэффициентов.
Эти компьютерные приложения используют представления карт улиц в виде графиков с расчетным временем в пути в качестве весовых коэффициентов.
Хотя часто можно найти кратчайший путь на небольшом графе методом угадывания и проверки, наша цель в этой главе — разработать методы для систематического решения сложных задач, следуя алгоритмам . Алгоритм — это пошаговая процедура решения проблемы. Алгоритм Дейкстры (произносится как дайк-стра) найдет кратчайший путь между двумя вершинами.
Алгоритм Дейкстры
1. Отметьте конечную вершину нулевым расстоянием. Обозначим эту вершину как текущую.
2. Найти все вершины, ведущие к текущей вершине. Вычислите их расстояния до конца. Поскольку мы уже знаем, на каком расстоянии от конца находится текущая вершина, потребуется просто добавить самое последнее ребро. Не записывайте это расстояние, если оно больше, чем ранее записанное расстояние.
3. Отметить текущую вершину как посещенную. Мы больше никогда не будем смотреть на эту вершину.
Мы больше никогда не будем смотреть на эту вершину.
4. Отметьте вершину с наименьшим расстоянием как текущую и повторите действия, начиная с шага 2.
ПРИМЕР
Предположим, вам нужно проехать из Такомы, штат Вашингтон (вершина T), в Якима, штат Вашингтон (вершина Y). Глядя на карту, кажется, что ехать через Оберн (A), а затем через Маунт-Рейнир (MR) может быть кратчайшим, но это не совсем ясно, поскольку эта дорога, вероятно, медленнее, чем ехать по главному шоссе через Норт-Бенд (NB). Ниже показан график времени в пути в минутах. Также показан альтернативный маршрут через Итонвилль (E) и Паквуд (P).
Шаг 1: Отметьте конечную вершину нулевым расстоянием. Расстояния будут записаны в [скобках] после имени вершины
Шаг 2: Для каждой вершины, ведущей к Y, мы вычисляем расстояние до конца. Например, NB — это расстояние 104 от конца, а MR — 96 от конца. Помните, что расстояния в данном случае относятся к времени в пути в минутах.
Шаг 3 и 4: Мы отмечаем Y как посещенную и отмечаем вершину с наименьшим записанным расстоянием как текущую. В этот момент P будет обозначаться текущим. Вернемся к шагу 2.
В этот момент P будет обозначаться текущим. Вернемся к шагу 2.
Шаг 2 (#2): Для каждой вершины, ведущей в P (и не ведущей в посещенную вершину), мы находим расстояние от конца. Так как Е равно 96 минут от P, и мы уже подсчитали, что P составляет 76 минут от Y, мы можем вычислить, что E составляет 96+76 = 172 минуты от Y. и обозначим вершину с наименьшим зарегистрированным расстоянием как текущую: MR. Вернемся к шагу 2.
Шаг 2 (#3): Для каждой вершины, ведущей в MR (и не ведущей в посещенную вершину), мы находим расстояние до конца. Единственная рассматриваемая вершина — это A, так как мы уже посетили Y и P. Добавление расстояния MR 96 к длине от A до MR дает расстояние 96+79 = 175 минут от A до Y.
Шаги 3 и 4 (#3): Мы помечаем MR как посещенную и обозначаем вершину с наименьшим зарегистрированным расстоянием как текущую: NB. Вернемся к шагу 2.
Шаг 2 (№4): Для каждой вершины, ведущей к NB, мы находим расстояние до конца. Мы знаем, что кратчайшее расстояние от NB до Y равно 104, а расстояние от A до NB равно 36, поэтому расстояние от A до Y через NB равно 104+36 = 140.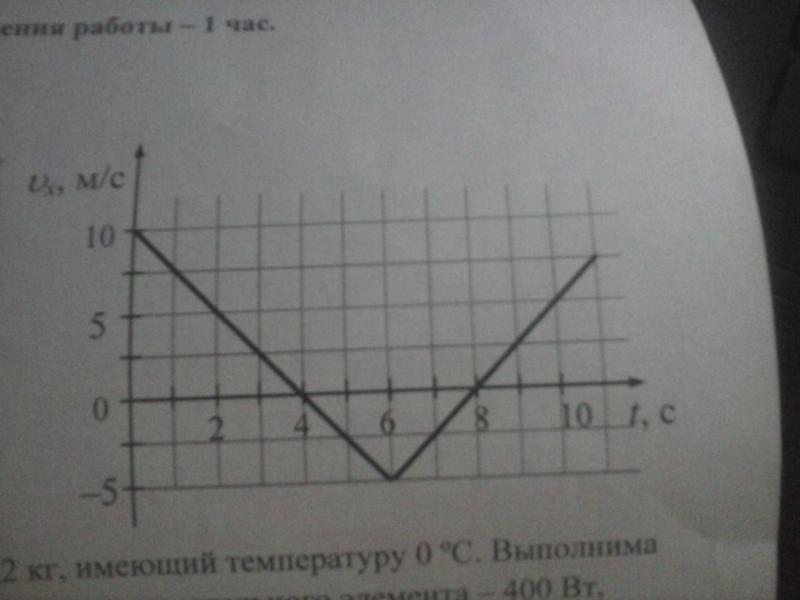 Так как это расстояние короче рассчитанного ранее расстояния от Y до А через MR, заменяем.
Так как это расстояние короче рассчитанного ранее расстояния от Y до А через MR, заменяем.
Шаги 3 и 4 (#4): Мы помечаем NB как посещенный и обозначаем A как текущий, так как теперь он имеет кратчайшее расстояние.
Шаг 2 (#5): T — единственная непосещаемая вершина, ведущая к A, поэтому мы вычисляем расстояние от T до Y через A: 20+140 = 160 минут.
Шаг 3 и 4 (#5): Мы отмечаем A как посещенный, а E — как текущий.
Шаг 2 (#6): Единственная непосещаемая вершина, ведущая к E, — это T. Вычисляя расстояние от T до Y через E, мы вычисляем 172+57 = 229минут. Поскольку это больше, чем существующее отмеченное время, мы не заменяем его.
Шаг 3 (#6): Мы отмечаем E как посещенный. Поскольку все вершины были посещены, мы закончили.
Отсюда мы знаем, что кратчайший путь от Такомы до Якимы займет 160 минут. Отслеживая, какая последовательность ребер дала 160 минут, мы видим, что кратчайший путь — это T-A-NB-Y.
Алгоритм Дейкстры является оптимальным алгоритмом , а это означает, что он всегда выдает фактический кратчайший путь, а не просто довольно короткий путь, если он существует. Этот алгоритм тоже эффективен , что означает, что его можно реализовать за разумное время. Алгоритм Дейкстры требует около V2 вычислений, где V — количество вершин в графе[1]. Граф со 100 вершинами потребует около 10 000 вычислений. В то время как это было бы много, чтобы сделать вручную, это не так уж много для компьютера. Именно благодаря этой эффективности GPS-устройство вашего автомобиля может вычислить направление движения всего за несколько секунд.
Этот алгоритм тоже эффективен , что означает, что его можно реализовать за разумное время. Алгоритм Дейкстры требует около V2 вычислений, где V — количество вершин в графе[1]. Граф со 100 вершинами потребует около 10 000 вычислений. В то время как это было бы много, чтобы сделать вручную, это не так уж много для компьютера. Именно благодаря этой эффективности GPS-устройство вашего автомобиля может вычислить направление движения всего за несколько секунд.
[1] Его можно ускорить за счет различных оптимизаций реализации.
Напротив, неэффективный алгоритм может попытаться перечислить все возможные пути, а затем вычислить длину каждого пути. Попытка перечислить все возможные пути может легко потребовать 1025 вычислений для вычисления кратчайшего пути всего с 25 вершинами; это 1 с 25 нулями после нее! Для сравнения, самый быстрый компьютер в мире все равно потратил бы более 1000 лет на анализ всех этих путей.
ПРИМЕР
Транспортной компании необходимо направить посылку из Вашингтона, округ Колумбия, в Сан-Диего, Калифорния. Чтобы свести к минимуму затраты, посылка сначала будет отправлена в их центр обработки в Балтиморе, штат Мэриленд, а затем отправлена в рамках массовых поставок между их различными центрами обработки и в конечном итоге окажется в их центре обработки в Бейкерсфилде, Калифорния. Оттуда он будет доставлен на небольшом грузовике в Сан-Диего.
Чтобы свести к минимуму затраты, посылка сначала будет отправлена в их центр обработки в Балтиморе, штат Мэриленд, а затем отправлена в рамках массовых поставок между их различными центрами обработки и в конечном итоге окажется в их центре обработки в Бейкерсфилде, Калифорния. Оттуда он будет доставлен на небольшом грузовике в Сан-Диего.
Время в пути в часах между их центрами обработки показано в таблице ниже. К каждому времени в пути было добавлено три часа для обработки. Найдите кратчайший путь из Балтимора в Бейкерсфилд.
| Балтимор | Денвер | Даллас | Чикаго | Атланта | Бейкерсфилд | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Хотя мы могли бы нарисовать график, мы также можем работать непосредственно с таблицей.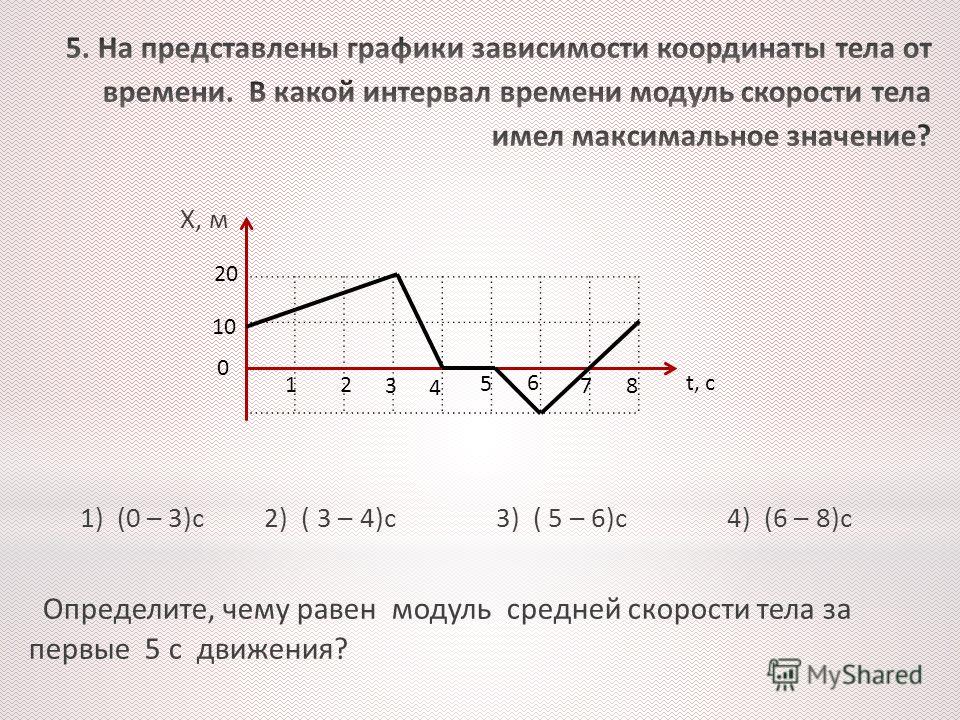
Шаг 1: Конечная вершина Бейкерсфилд помечается как текущая.
Шаг 2: Все города, связанные с Бейкерсфилдом, в данном случае Денвер и Даллас, рассчитываются по расстоянию; мы отметим эти расстояния в заголовках столбцов.
Шаг 3 и 4: Отметьте Бейкерсфилд как посещенный. Здесь мы делаем это, затеняя соответствующую строку и столбец таблицы. Мы помечаем Денвер как текущий, выделенный жирным шрифтом, так как это вершина с кратчайшим расстоянием.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго | Атланта | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#2): Для городов, связанных с Денвером, рассчитайте расстояние до конца.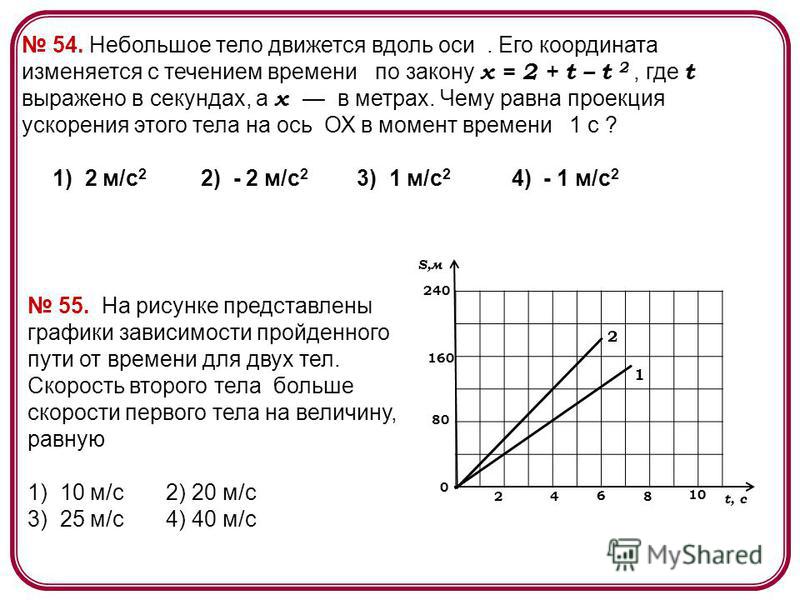
Шаг 3 и 4 (#2): Мы отмечаем Денвер как посещенный и помечаем Даллас как текущий.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [43] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#3): Для городов, связанных с Далласом, рассчитайте расстояние до конца.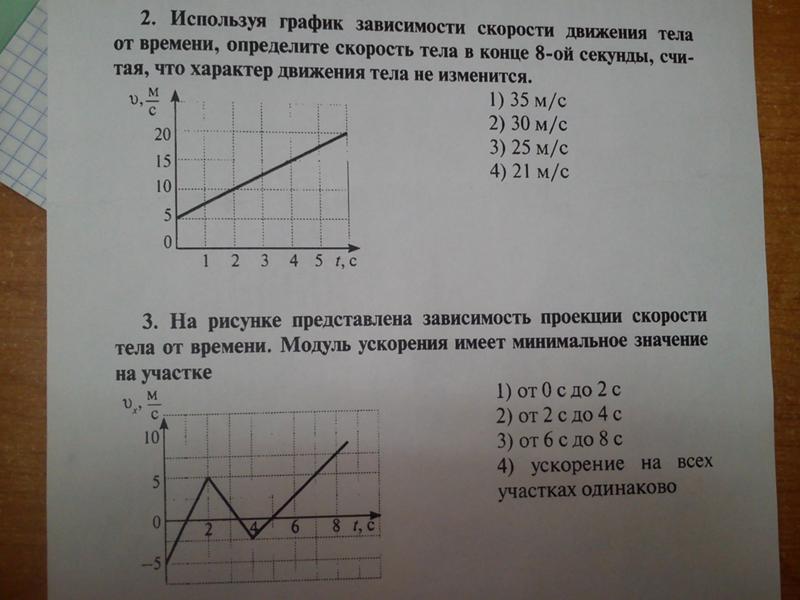 Для Чикаго расстояние от Чикаго до Далласа равно 18, а от Далласа до конца — 25, поэтому расстояние от Чикаго до конца через Даллас будет 18 + 25 = 43. Поскольку это больше, чем отмеченное в настоящее время расстояние для Чикаго, мы не заменяем его. Для Атланты мы вычисляем 15+25 = 40. Так как это меньше, чем текущее отмеченное расстояние для Атланты, мы заменяем существующее расстояние.
Для Чикаго расстояние от Чикаго до Далласа равно 18, а от Далласа до конца — 25, поэтому расстояние от Чикаго до конца через Даллас будет 18 + 25 = 43. Поскольку это больше, чем отмеченное в настоящее время расстояние для Чикаго, мы не заменяем его. Для Атланты мы вычисляем 15+25 = 40. Так как это меньше, чем текущее отмеченное расстояние для Атланты, мы заменяем существующее расстояние.
Шаг 3 и 4 (#3): Мы отмечаем Даллас как посещенный, а Чикаго как текущий.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [40] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#4): Балтимор и Атланта — единственные непосещаемые города, связанные с Чикаго.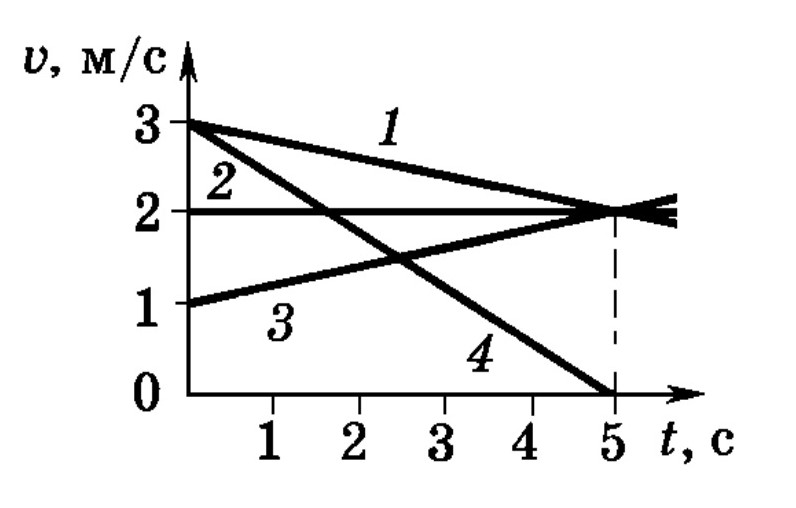 Для Балтимора мы вычисляем 15+37 = 52 и отмечаем это расстояние. Для Атланты мы вычисляем 14+37 = 51. Поскольку это больше, чем существующее расстояние 40 для Атланты, мы не заменяем это расстояние.
Для Балтимора мы вычисляем 15+37 = 52 и отмечаем это расстояние. Для Атланты мы вычисляем 14+37 = 51. Поскольку это больше, чем существующее расстояние 40 для Атланты, мы не заменяем это расстояние.
Шаг 3 и 4 (#4): Отметьте Чикаго как посещенный, а Атланту как текущий.
| Балтимор [52] | Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [40] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#5): Расстояние от Атланты до Балтимора равно 14.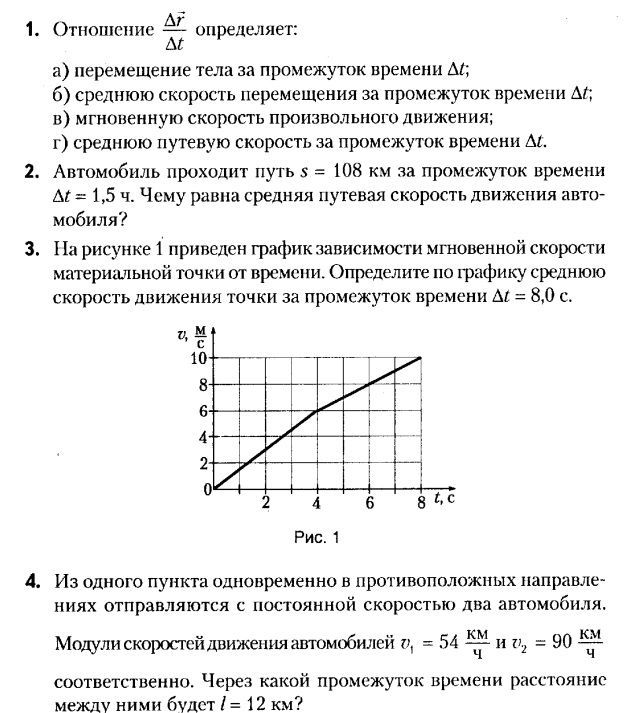 Прибавив это к расстоянию, уже рассчитанному для Атланты, мы получим общее расстояние 14+40 = 54 часа от Балтимора до Бейкерсфилда через Атланту. Так как это больше рассчитываемого в настоящее время расстояния, мы не заменяем расстояние для Балтимора.
Прибавив это к расстоянию, уже рассчитанному для Атланты, мы получим общее расстояние 14+40 = 54 часа от Балтимора до Бейкерсфилда через Атланту. Так как это больше рассчитываемого в настоящее время расстояния, мы не заменяем расстояние для Балтимора.
Шаг 3 и 4 (#5): Мы отмечаем Атланту как посещенную. Все города были посещены, и мы закончили.
Самый короткий маршрут из Балтимора в Бейкерсфилд займет 52 часа и пройдет через Чикаго и Денвер.
Попробуйте
- Найдите кратчайший путь между вершинами A и G на приведенном ниже графике.
В следующем видео обобщены темы, затронутые на этой странице.
Объяснение урока: Графики смещения и времени | Nagwa
В этом объяснении мы узнаем, как использовать графики смещения и времени и интерпретировать наклон кривой как скорость тела.
Начнем с того, что вспомним, что скаляр — это величина, которая имеет величину (размер), но не имеет направления, тогда как вектор — это величина, которая имеет как величину, так и направление. Это различие помогает нам понять разницу между расстоянием и смещением.
Определение: Расстояние
Расстояние является скалярной величиной. Расстояние, которое проходит объект, — это длина пути, который проходит объект от начальной точки своего движения до конечной точки своего движения.
Определение: Перемещение
Перемещение является векторной величиной. Смещение объекта имеет величину, равную кратчайшему расстоянию между необходимо указать начальную и конечную точки движения объекта, а также направление движения.
Таким образом, хотя расстояние, пройденное объектом, и его перемещение можно измерить, используя одни и те же единицы, например,
километров или
метров, смещение всегда должно иметь указанное направление
слишком. Кроме того, расстояния всегда положительны, а перемещения, связанные с движением по прямой (одномерное движение)
может быть положительным или отрицательным.
Кроме того, расстояния всегда положительны, а перемещения, связанные с движением по прямой (одномерное движение)
может быть положительным или отрицательным.
Параллельно определениям расстояния и смещения у нас есть следующие определения скорости и скорости.
Определение: Скорость
Скорость — это мера того, насколько быстро движется объект. Это скалярная величина. Скорость можно измерить как расстояние в единицу времени, например километров в час (км/ч) или метры в секунду (РС). Скорость объекта не говорит нам направление в который он путешествует.
Определение: Скорость
Скорость – это скорость изменения смещения. Это векторная величина. Скорость можно измерить как перемещение на единицу
времени. Единицы измерения те же, что и для скорости, но с указанием направления, например
километров в час в восточном направлении или
метров в секунду в положительном направлении движения.
Построив эти концепции, мы теперь в состоянии исследовать графики смещения-времени, которые являются нашей главной целью в этом объяснении. Мы можем представить движение объекта с помощью графика смещения во времени. Эти графики всегда имеют смещение от данная точка представлена на вертикальной оси, а время представлено на горизонтальной оси.
Легче всего узнать об этих графиках, изучив несколько конкретных примеров. На следующих трех графиках смещение объекта от заданной точки в метрах отображается в зависимости от времени в секунды.
На приведенном выше графике перемещение-время горизонтальная линия, начинающаяся с цифры 4 по вертикальной оси, показывает, что перемещение объект остается постоянным во времени на расстоянии 4 м от заданной точки.
На графике перемещение-время градиент представляет скорость. Тот факт, что градиент горизонтальной линии равен нулю показывает, что скорость равна нулю, а значит, объект неподвижен.
В общем случае любые горизонтальные участки графика перемещение-время представляют интервалы времени, для которых данный объект
стационарный.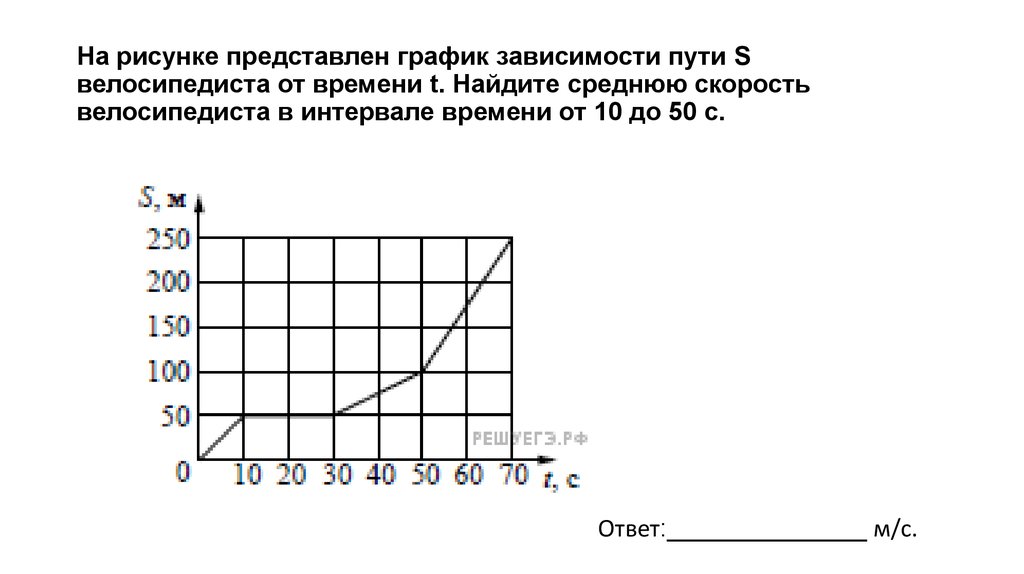
Наш второй график зависимости смещения от времени показывает движение объекта по прямой линии от начальной точки (положительное значение). направление движения), а затем обратно к исходной точке (отрицательное направление движения).
Здесь наклонная вверх прямая линия от начала координат до точки (20 100) говорит нам, что этот объект начинается в заданной точке, а затем проходит 100 метров прямо от эту точку в первые 20 секунд, как показано ниже.
Вспомните, что на графике перемещение-время градиент представляет собой скорость. Положительный градиент линии показывает, что смещение от начальной точки увеличивается с постоянной скоростью во времени, поэтому во время этот период объект движется с постоянной скоростью в положительном направлении. Скорость определяется градиентом, который равен время изменения смещения kenms=100−020−0=10020=5/.
Далее нисходящая прямая от (20,100) до (40,50) показывает
нам, что в следующие 40−20=20 секунд объект
меняет направление своего движения и проходит 100−50=50 метров прямо назад к исходной точке, как показано на рисунке. ниже.
ниже.
Отрицательный градиент линии показывает, что смещение от начальной точки уменьшается с постоянной скоростью с течением времени, поэтому в этот период объект движется с постоянной скоростью в отрицательном направлении. Скорость задается градиентом, который время изменения смещения, взятое мс=50−10040−20=−5020=−2,5/.
В общем, любые прямолинейные участки графика перемещение-время с восходящим или нисходящим уклоном представляют заданное движение объекта за промежутки времени, в течение которых он движется с постоянной скоростью. Наклон вверх (и, следовательно, положительный градиент) показывает положительную скорость; нисходящий наклон (и, следовательно, отрицательный градиент) показывает отрицательную скорость.
Наш третий график зависимости смещения от времени показывает движение объекта от его начальной точки по прямой линии в положительное направление.
На этот раз кривая от начала координат до (8,25) говорит нам, что этот объект начинается в данной точке и
затем проходит 25 метров прямо от этой точки в
8 секунд. Постоянно увеличивающийся градиент кривой показывает, что
смещение увеличивается с возрастающей скоростью с течением времени. Следовательно, скорость постоянно увеличивается, поэтому объект ускоряется.
Постоянно увеличивающийся градиент кривой показывает, что
смещение увеличивается с возрастающей скоростью с течением времени. Следовательно, скорость постоянно увеличивается, поэтому объект ускоряется.
В общем случае любые криволинейные участки графика перемещение-время отображают движение данного объекта в интервалах времени для чего он ускоряется или замедляется. Распространенное заблуждение состоит в том, что любые кривые на графике перемещение-время подразумевают что данный объект следует криволинейной траектории, но на самом деле они ничего не говорят нам о форме траектории.
Наконец, нам нужны две важные формулы, которые позволят нам вычислить среднюю скорость и среднюю скорость объекта после считывание некоторой релевантной информации с графиков перемещение-время.
Формула: Средняя скорость
Средняя скорость объекта равна общему пройденному расстоянию, деленному на затраченное время: средняя скоростьобщее расстояниепройденное время=.
Это скалярная величина, измеряемая как расстояние в единицу времени, например,
километров в час
(км/ч) или
метры в секунду
(РС).
Формула: Средняя скорость
Средняя скорость объекта равна смещению от начальной точки, деленному на затраченное время: средняя скорость, смещение от начальной точки, время =.
Поскольку перемещение является векторной величиной, средняя скорость также является векторной величиной и поэтому может быть положительной или отрицательной. Его величина, который является скаляром, измеряется как расстояние в единицу времени и поэтому всегда положителен.
Чтобы проиллюстрировать разницу между этими двумя величинами, мы можем вернуться к нашему второму графику перемещение-время выше.
Чтобы рассчитать среднюю скорость, нам нужно разделить общее пройденное расстояние на затраченное время. Объект путешествовал 100 м в первом 20 секунд и 50 м в следующие 20 секунд. Следовательно, его средняя скорость определяется следующим образом: средняя скоростьобщее расстояниепройденное времякэнмс==100+5020+20=15040=3,75/.
Чтобы вычислить среднюю скорость, нам нужно разделить полное перемещение от начальной точки на затраченное время.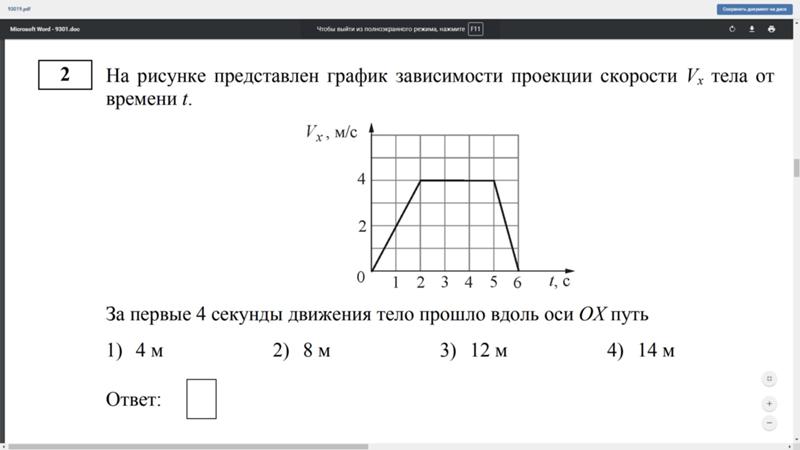 Объект
проехал 100 м в положительном направлении в первом
20 секунд и
50 м в отрицательном направлении в следующем
20 секунд. Следовательно, его средняя скорость определяется выражением
средняя скорость перемещения от начальной точки по времени мс==100−5020+20=5040=1,25/.
Объект
проехал 100 м в положительном направлении в первом
20 секунд и
50 м в отрицательном направлении в следующем
20 секунд. Следовательно, его средняя скорость определяется выражением
средняя скорость перемещения от начальной точки по времени мс==100−5020+20=5040=1,25/.
Обратите внимание, что первая и третья диаграммы смещения-время, приведенные выше, будут иметь среднюю скорость, равную по модулю их Средняя скорость.
На первом графике данный объект неподвижен, поэтому пройденное расстояние равно 0, как и величина смещение. Следовательно, при расчете средней скорости или среднего расстояния мы будем брать значение 0 и делить это по затраченному времени, что ясно дает ответ 0 в обоих случаях.
На третьем графике данный объект просто движется прямо от своей начальной точки в положительном направлении, поэтому его движение
имеет только одну стадию. Он проходит 25 м в
8 секунд, поэтому его средняя скорость равна
средняя скоростьобщее расстояниепройденное времяв мс==258=3,125/.
Опять же, величина его перемещения равна пройденному расстоянию, поэтому мы получили бы точно такой же результат, если бы подставили значения смещения от начальной точки и времени, учитываемые в формуле для средней скорости.
Давайте теперь рассмотрим пример, где мы можем попрактиковаться в вычислении средней скорости на основе информации, представленной в график перемещение-время.
Пример 1. Определение средней скорости движения по графику «перемещение-время»
График представляет зависимость между смещением частицы и временем, в течение которого она движется по прямой линии.
Заполните пропуск: Средняя скорость за всю поездку =/мс.
Ответ
Напомним, что средняя скорость объекта равна смещению от начальной точки, деленному на затраченное время: средняя скорость, смещение от начальной точки, время =.
Напомним также, что на графике перемещение-время градиент представляет собой скорость. Анализируя градиенты, показанные на
На графике выше видно, что движение частицы имеет три стадии.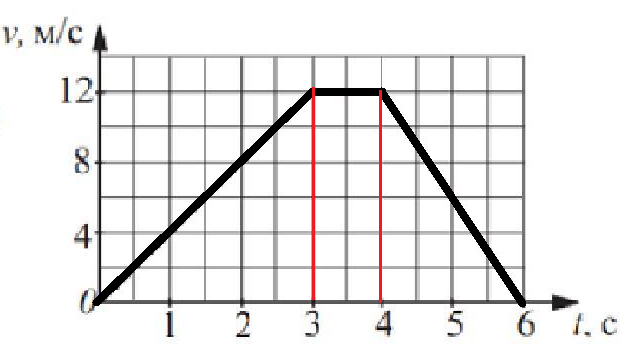
Во-первых, в интервале времени от 𝑡=0 до 𝑡=3 положительный градиент прямой от От (0,0) до (3,6) говорит нам, что частица имеет постоянную скорость, двигаясь непосредственно от начальной точки на 6 м в положительном направлении. Поэтому, изменение его водоизмещения за первые 3 секунды равно 6 м.
Секунда, в интервале времени от 𝑡=3 до 𝑡=5 горизонтальная прямая (с нулевым градиентом) из (3,6) в (5,6) говорит нам, что скорость частицы равна нулю и таким образом является стационарным. Следовательно, изменение его водоизмещения за эти 2 секунды 0,
В-третьих, в интервале времени от 𝑡=5 до 𝑡=10 положительный градиент прямой от От (5,6) до (10,16) говорит нам, что частица снова имеет постоянную скорость, двигаясь прямо от начальной точки еще на 16−6=10 м в положительном направлении. Следовательно, изменение его смещения в последние 5 секунд 10 м.
Чтобы рассчитать среднюю скорость за всю поездку, мы берем результаты для трех отдельных этапов и применяем формулу как
следует:
средняя скорость всего кругового перемещения от начальной точки за время, взятое мс==6+0+103+2+5=1610=1,6/.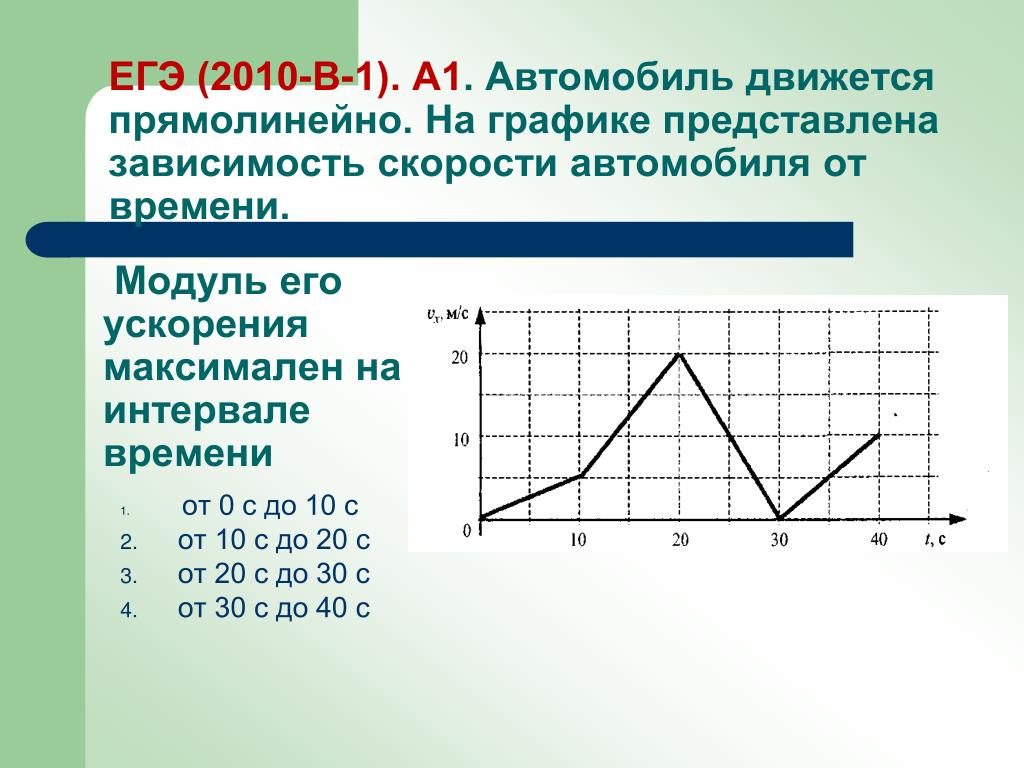
Мы заключаем, что последнее предложение вопроса должно звучать так: «Средняя скорость всего пути = 1,6 м/с».
В приведенном выше примере мы использовали график зависимости перемещения от времени, чтобы рассчитать среднюю скорость на всем пути. В следующем примере нам нужно будет рассчитать среднюю скорость на разных этапах пути.
Пример 2. Определение средней скорости на разных этапах пути
На этом графике перемещение-время показано движение велосипедиста по прямой дороге. Она едет по прямой 15 минут, а затем останавливается на 10 минут. Наконец, она возвращается к исходной точке. за 25 минут по прямой.
Рассчитайте среднюю скорость для каждого этапа пути в километров в час.
Ответ
Напомним, что средняя скорость объекта равна смещению от начальной точки, деленному на затраченное время: средняя скорость, смещение от начальной точки, время =.
В этом вопросе нас просят рассчитать среднюю скорость в километрах в час для каждого этапа движения велосипедиста. путешествие показано на приведенном выше графике перемещение-время. Напомним, что на графике перемещение-время градиент представляет
скорость, поэтому мы можем видеть, что это путешествие разбивается на три отдельных этапа: от 𝑂 до 𝐴,
затем от 𝐴 к 𝐵 и, наконец, от 𝐵 к 𝐶.
путешествие показано на приведенном выше графике перемещение-время. Напомним, что на графике перемещение-время градиент представляет
скорость, поэтому мы можем видеть, что это путешествие разбивается на три отдельных этапа: от 𝑂 до 𝐴,
затем от 𝐴 к 𝐵 и, наконец, от 𝐵 к 𝐶.
Однако обратите внимание, что на этом графике смещение от начальной точки в километров наносится на график в зависимости от времени, затраченного на минут . Это означает, что у нас есть выбор: вычислить три скорости в километрах в минуту, а затем преобразовать их в километры в час или переводя время в минут в часы до расчета скоростей в километров в час. Мы будем работать с первым методом в деталь.
Мы знаем, что этап пути из 𝑂 в 𝐴 занимает
15 минут. При этом положительный градиент прямой от
От (0,0) до (15,4) говорит нам, что за этот интервал времени велосипедист движется
прямо от своей начальной точки, проехав 4 км в положительном направлении. Этот этап путешествия показан ниже.
Этот этап путешествия показан ниже.
Следовательно, изменение перемещения велосипедиста за эти 15 минут составляет 4 км. Применив формулу, получаем следующее: средняя скорость от до перемещения от до времени nkmmmin𝑂𝐴=𝑂𝐴=415=0,2̇6/.
Чтобы преобразовать значение в километрах в минуту в километров в час, умножаем на 60 (количество минут в час). В этом случае мы получаем следующее: средняя скорость от tokmh𝑂𝐴=0.2̇6×60=16/.
Этап пути из 𝐴 в 𝐵 занимает 10 минут, и мы знаем, что велосипедист не находится в движении все время этот этап. Этот факт подтверждается горизонтальной прямой (с нулевым уклоном) из (15,4) к (25,4), говоря нам, что на этом этапе велосипедист имеет нулевую скорость и, следовательно, неподвижен. Этот этап путешествия показан ниже.
Следовательно, изменение перемещения велосипедиста за эти 25−15=10 минут равно 0. Так как мы вычисляем среднюю скорость по формуле
деля изменение смещения на затраченное время, это сразу означает, что средняя скорость велосипедиста от
𝐴 в 𝐵 равно 0.
Наконец, этап путешествия из 𝐵 в 𝐶 занимает 25 минут. Кроме того, отрицательный градиент прямой от (25,4)–(50,0) говорит нам, что за этот промежуток времени велосипедист движется прямо к ее исходной точке, проехав 4 км в отрицательном направлении направление. Этот этап путешествия показан ниже.
Таким образом, изменение перемещения велосипедиста за эти 50−25=25 минут равно −4 км. Применив формулу, получаем следующее: средняя скорость от до перемещения от до времени nkmmmin𝐵𝐶=𝐵𝐶=−425=−0,16/.
Чтобы преобразовать это значение в километры в час, мы умножаем его на 60, что дает нам следующее: средняя скорость от tokmh𝐵𝐶=−0,16×60=−9,6/.
Обратите внимание, что если бы мы сначала преобразовали время в минуты для различные этапы пути в часы, а затем выполняли вычисления скорости, мы получили бы следующие результаты.
Этап пути из 𝑂 в 𝐴 занимает
15 минут, что составляет 1560 = 0,25 часа, поэтому
средняя скорость от до перемещения от до времени, взятого nkmh𝑂𝐴=𝑂𝐴=40,25=16/.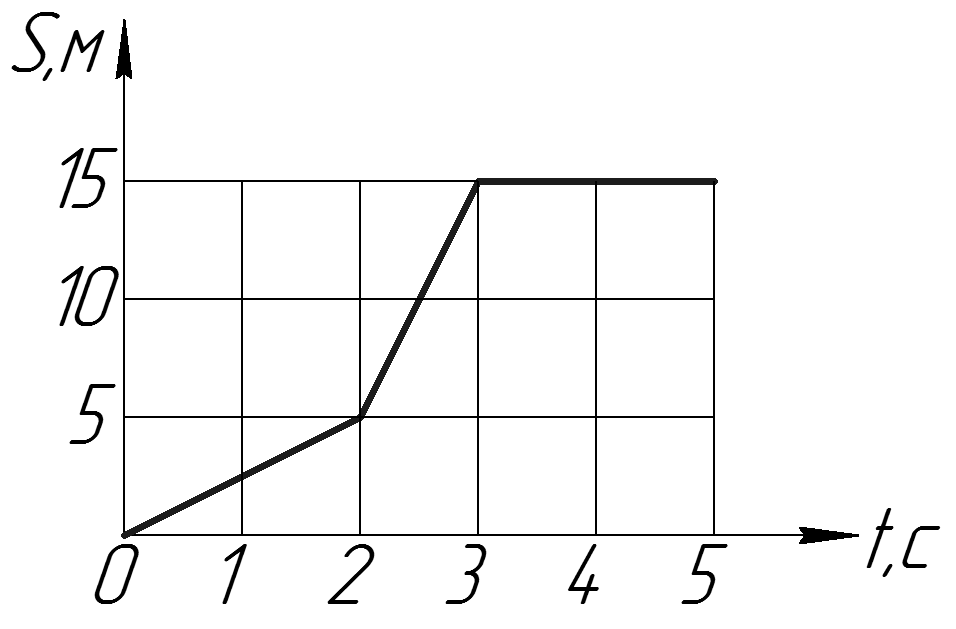
Этап пути из 𝐴 в 𝐵 занимает 10 минут, что составляет 1060 = 0,1̇6 часов. Однако по мере изменения смещения за это интервал времени равен 0, и мы вычисляем среднюю скорость, разделив изменение смещения на затраченное время, а затем преобразовав время от минут до часов по-прежнему дает среднюю скорость от 𝐴 до 𝐵 как 0,
Наконец, этап пути из 𝐵 в 𝐶 занимает 25 минут, т.е. 2560 = 0,41̇6 часов, поэтому средняя скорость от до перемещения от до времени nkmh𝐵𝐶=𝐵𝐶=−40,41̇6=−9,6/.
Как и ожидалось, все три средние скорости согласуются с нашими первоначальными результатами.
Теперь сравним среднюю скорость и среднюю скорость для данного путешествия.
Пример 3: определение средней скорости и средней скорости движения
Этот график смещения-времени показывает движение частицы по прямой линии. Он удаляется от начальной точки за 15 минут, а затем возвращается через 30 минут.
- Рассчитайте среднюю скорость на всем пути в километрах в час.

- Рассчитайте среднюю скорость на всем пути в километрах в час.
Ответ
В этом вопросе данное путешествие состоит из двух этапов, которые мы будем называть этапами туда и обратно.
Нас просят рассчитать среднюю скорость и среднюю скорость в километрах в час для целое путешествие. Однако обратите внимание, что на этом графике смещение от начальной точки в километрах построен в зависимости от времени, затраченного на минут . Поэтому мы преобразуем соответствующие времена в часов, прежде чем делать какие-либо расчеты, чтобы убедиться, что наши ответы имеют правильные единицы измерения.
Внешний этап занимает 15 минут, что составляет 1560 = 0,25 часа.
Вспомните, что на графике перемещение-время градиент представляет собой скорость. Наклоненная вверх прямая линия от (0,0) до
(15,12) говорит нам, что частица имеет постоянную скорость и движется прямо от своей начальной точки на
12 км в положительном направлении.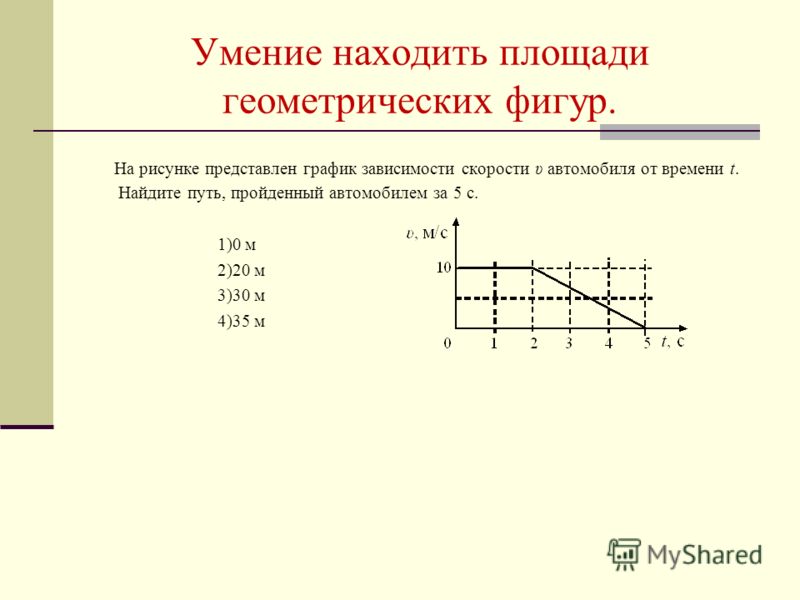 Следовательно, изменение его водоизмещения в первом
0,25 часа это 12 км.
Следовательно, изменение его водоизмещения в первом
0,25 часа это 12 км.
Этап возврата занимает 30 минут, что составляет 3060=0,5 часа.
Наклонная вниз прямая линия от (15,12) до (45,0) говорит нам, что частица имеет постоянную скорость, двигаясь прямо к исходной точке на 12 км в отрицательном направлении. Следовательно, изменение его смещения в остальные 0,5 часа составляет −12 км.
Часть 1
Для части 1 напомним, что средняя скорость объекта равна общему пройденному расстоянию, деленному на затраченное время: средняя скоростьобщее расстояниепройденное время=.
Частица прошла 12 км за первые 0,25 часа и 12 км за оставшиеся 0,5 часа. Отсюда его средняя скорость дается следующим: средняя скоростьобщее расстояниепройденное времякм/ч==12+120,25+0,5=240,75=32/.
Часть 2
Для части 2 напомним, что средняя скорость объекта равна смещению от начальной точки, деленному на затраченное время:
средняя скорость, смещение от начальной точки, время =.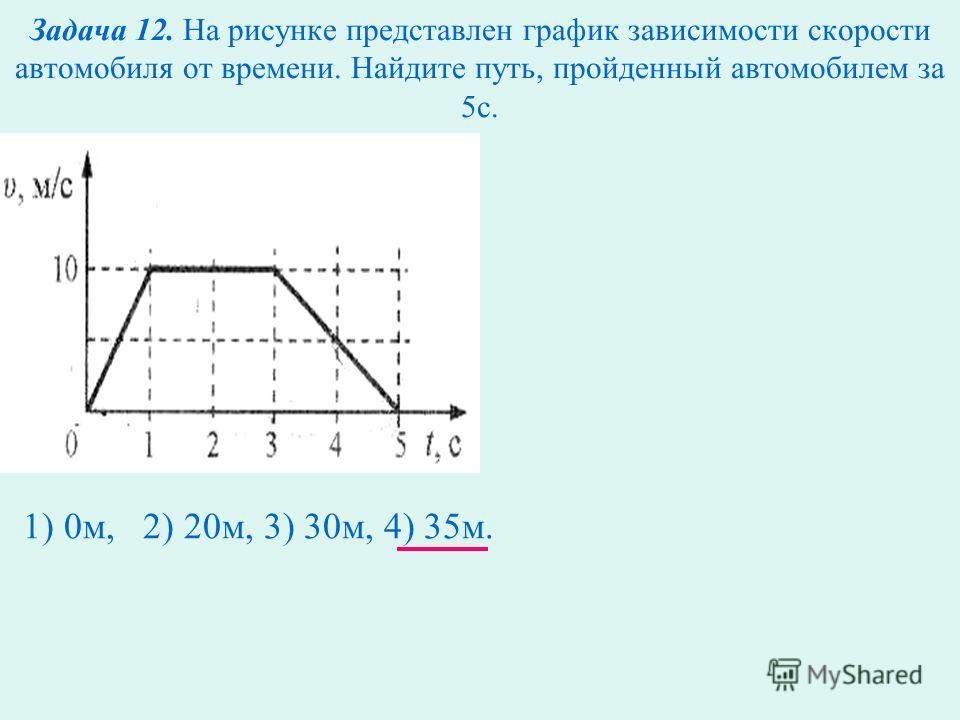
Частица прошла 12 км в положительном направлении в первом 0,25 часа и 12 км в отрицательном направлении в ближайшие 0,5 часа. Следовательно, его средняя скорость определяется следующим образом: средняя скорость перемещения от начальной точки по времени nkmh==12−120,25+0,5=00,75=0/.
Если мы задумаемся над частью 2, должно быть очевидно, почему мы получаем нулевой ответ. Ведь путешествие частицы началось и закончилось в одном и том же месте, поэтому его полное перемещение равно нулю. Разделение этого значения на время, необходимое для получения средней скорости, обязательно дает нулевой ответ.
В следующем примере мы покажем, как считывать информацию о градиенте с графика смещения во времени, чтобы вычислить время, когда объект находится в состоянии покоя.
Пример 4. Распознавание состояния покоя тела на графике смещения во времени
График перемещение-время, приведенный ниже, описывает движение объекта.
В какое время объект покоится (скорость равна нулю)?
Ответ
Вспомните, что на графике перемещение-время градиент представляет собой скорость. Если градиент равен нулю, то и скорость равна нулю. Это означает, что
объект неподвижен, что равносильно утверждению, что он находится в состоянии покоя.
Если градиент равен нулю, то и скорость равна нулю. Это означает, что
объект неподвижен, что равносильно утверждению, что он находится в состоянии покоя.
Только горизонтальные участки графика смещения-времени имеют нулевой градиент, поэтому они представляют интервалы времени, в течение которых данный объект находится в покое.
Изучив приведенный выше график смещения и времени, мы можем увидеть, что единственный горизонтальный участок происходит между моментами времени 𝑡=2 и 𝑡=3. Делаем вывод, что объект покоится в течение интервала времени 2𝑡3.
Мы также можем использовать графики смещения во времени, чтобы найти максимальную высоту, достигнутую снарядом. Вот пример такого типа.
Пример 5. Определение максимальной высоты при броске мяча
Это график зависимости перемещения от времени для мяча, который подброшен в воздух вертикально вверх и падает обратно в исходную точку.
- Найдите максимальную высоту, на которую поднялся мяч.

- Найдите момент, когда мяч достигнет максимальной высоты.
Ответ
Напомним, что на графиках перемещение-время всегда имеется перемещение из заданной точки, представленное на вертикальной оси, и время, представленное на горизонтальной оси. ось.
Часть 1
В этом случае мы знаем, что мяч брошен вверх, и его высота над землей отложена на вертикальной оси. Таким образом, мы можем вычислить максимальную высоту, достигнутую мяч, найдя самую высокую точку на кривой и прочитав по вертикальной оси. Как показано на диаграмме ниже, это значение равно 5 м.
Часть 2
Чтобы найти время, за которое мяч достигает максимальной высоты, мы считываем вниз от самой высокой точки к горизонтальной оси. Как показано выше, это значение равно 1 секунда.
Еще один способ решить эту проблему — понять, что когда мяч достигает максимальной высоты, он мгновенно останавливается (поскольку он закончил
поднимается и вот-вот начнет падать).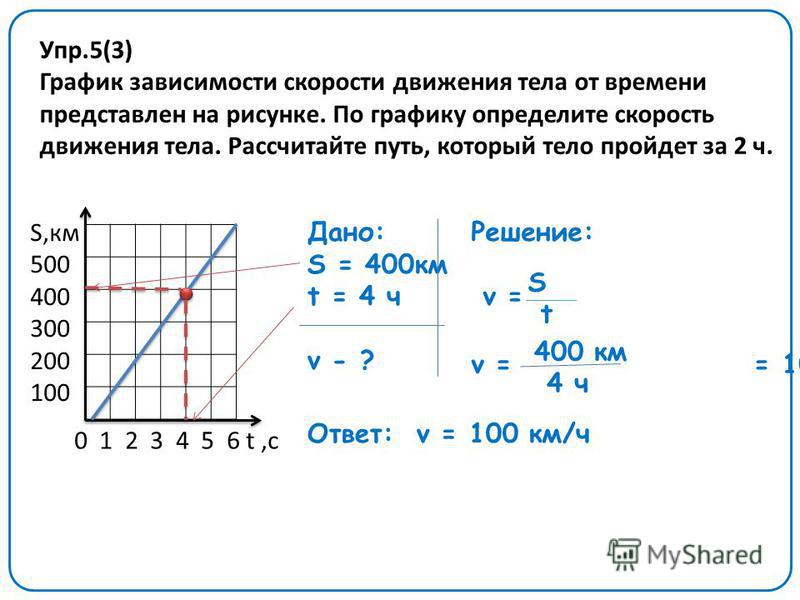
Вспомните, что на графике перемещение-время градиент представляет собой скорость. Если градиент равен нулю, то скорость равна нулю, а это означает, что данный объект находится в покое. Рассматривая график, мы видим, что на кривой есть только одна точка, где градиент равен нулю, а именно (1,5). Опять же, это подразумевает, что мяч достигает максимальной высоты 5 м после 1 секунда.
В нашем последнем примере мы научимся определять, когда скорость объекта положительна, используя график зависимости смещения от времени.
Пример 6. Выводы о скорости из графика «перемещение-время»
Этот график «перемещение-время» описывает движение объекта.
Какое из следующих утверждений верно?
- Скорость положительна на интервале времени 0𝑡2.
- Скорость положительна только на временном интервале 3𝑡4.
- Скорость положительна на временном интервале 1𝑡3.
- Скорость положительна только на временном интервале 0𝑡1.
- Скорость положительна в промежутках времени 0𝑡1 и 3𝑡4.

Ответ
Вспомните, что на графике перемещение-время градиент представляет скорость. Следовательно, чтобы определить, когда скорость положительна, нам нужно проверить заданный график смещения-времени, чтобы найти участки кривой, которые имеют положительный градиент.
В интервале времени 0𝑡1 кривая имеет восходящий наклон, поэтому градиент положительный.
При 𝑡=1 градиент равен 0.
В интервале времени 1𝑡3 кривая наклонена вниз, поэтому градиент отрицательный.
При 𝑡=3 градиент равен 0.
В интервале времени 3𝑡4 кривая имеет наклон вверх, поэтому градиент положительный.
Делаем вывод, что градиент положителен во временных интервалах 0𝑡1 и 3𝑡4. Следовательно, это время интервалы, для которых скорость положительна, поэтому правильный ответ — E.
Давайте закончим повторением некоторых ключевых понятий из этого объяснения.
Ключевые точки
- Расстояние является скалярной величиной.
 Расстояние, которое проходит объект, — это длина пути, который проходит объект от начальной точки своего движения до
конечной точки своего движения.
Расстояние, которое проходит объект, — это длина пути, который проходит объект от начальной точки своего движения до
конечной точки своего движения. - Перемещение является векторной величиной. Смещение объекта имеет величину, равную кратчайшему расстоянию между начальной и конечной точками необходимо указать движение объекта и направление движения.
- Средняя скорость объекта равна общему пройденному расстоянию, деленному на затраченное время: средняя скоростьобщее расстояниепройденное время=. Это скалярная величина, измеряемая как расстояние в единицу времени, например, километры в час. (км/ч) или метры в секунду (РС).
- Средняя скорость объекта равна смещению от начальной точки, деленному на время:
средняя скорость, смещение от начальной точки, время =.
Поскольку перемещение является векторной величиной, средняя скорость также является векторной величиной и поэтому может быть положительной или отрицательной.


 В это время тело двигалось равноускоренно (с положительным ускорением).
В это время тело двигалось равноускоренно (с положительным ускорением). Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.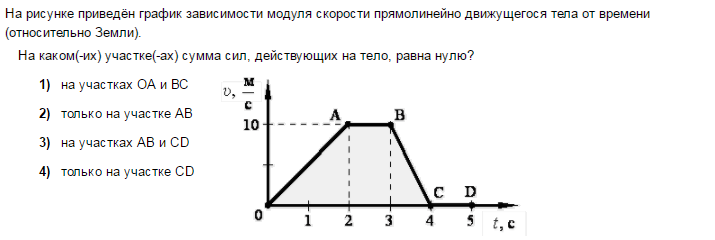

 Расстояние, которое проходит объект, — это длина пути, который проходит объект от начальной точки своего движения до
конечной точки своего движения.
Расстояние, которое проходит объект, — это длина пути, который проходит объект от начальной точки своего движения до
конечной точки своего движения.
Leave A Comment