Определить количество информации полученной вторым игроком: Какое количество информации получит второй игрок при игре в крестики- нолики на поле размером 8х8 клеток, после первого хода первого

В помощь студенту! — Тема 9

Количество информации как мера уменьшения неопределенности знаний

Информация и знания. Человек получает информацию из окружающего мира с помощью органов чувств, анализирует ее и выявляет существенные закономерности с помощью мышления, хранит полученную информацию в памяти. Процесс систематического научного познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и так далее). Таким образом, с точки зрения процесса познания информация может рассматриваться как знания.

Процесс познания можно наглядно изобразить в виде расширяющегося круга знания (такой способ придумали еще древние греки). Вне этого круга лежит область незнания, а окружность является границей между знанием и незнанием. Парадокс состоит в том, что чем большим объемом знаний обладает человек (чем шире круг знаний), тем больше он ощущает недостаток знаний (тем больше граница нашего незнания. мерой которого в этой модели является длина окружности) — рис. 1.

 

Рис. 1 Знание и незнание

Так, объем знаний выпускника школы гораздо больше, чем объем знаний первоклассника, однако и граница его незнания существенно больше. Действительно, первоклассник ничего не знает о законах физики и поэтому не осознает недостаточности своих знаний, тогда как выпускник школы при подготовке к экзаменам по физике может обнаружить, что существуют физические законы, которые он не знает или не понимает.

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.

Например, после сдачи экзамена по информатике вы мучаетесь неопределенностью, вы не знаете какую оценку получили. Наконец, экзаменационная комиссия объявляет результаты экзамена, и вы получаете сообщение, которое приносит полную определенность, теперь вы знаете свою оценку. Происходит переход от незнания к полному знанию, значит, сообщение экзаменационной комиссии содержит информацию.

Уменьшение неопределенности знаний. Подход к информации как мере уменьшения неопределенности знаний позволяет количественно измерять информацию, что чрезвычайно валено для информатики. Рассмотрим вопрос об определении количества информации более подробно на конкретных примерах.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий — монета окажется в одном из двух положений: «орел» или «решка».

Можно говорить, что события равновероятны, если при возрастающем числе опытов количества выпадений «орла» и «решки» постепенно сближаются. Например, если мы бросим монету 10 раз, то «орел» может выпасть 7 раз, а решка — 3 раза, если бросим монету 100 раз, то «орел» может выпасть 60 раз, а «решка» — 40 раз, если бросим монету 1000 раз, то «орел» может выпасть 520 раз, а «решка» — 480 и так далее.

В итоге при очень большой серии опытов количества выпадений «орла» и «решки» практически сравняются.

Перед броском существует неопределенность наших знаний (возможны два события), и, как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении (например, «орел»). Это сообщение приводит к уменьшению неопределенности наших знаний в два раза, так как до броска мы имели два вероятных события, а после броска — только одно, то есть в два раза меньше (рис. 2).

 

Рис. 2 Возможные и произошедшее события

В окружающей действительности достаточно часто встречаются ситуации, когда может произойти некоторое количество равновероятных событий. Так, при бросании равносторонней четырехгранной пирамиды существуют 4 равновероятных события, а при бросании шестигранного игрального кубика — 6 равновероятных событий.

Чем больше количество возможных событий, тем больше начальная неопределенность и соответственно тем большее количество информации будет содержать сообщение о результатах опыта.

Единицы измерения количества информации. Для количественного выражения любой величины необходимо определить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы — килограмм и так далее. Аналогично, для определения количества информации необходимо ввести единицу измерения.

За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность в два раза. Такая единица названа «бит».

Если вернуться к опыту с бросанием монеты, то здесь неопределенность как раз уменьшается в два раза и, следовательно, полученное количество информации равно 1 биту.

Минимальной единицей измерения количества информации является бит, а следующей по величине единицей является байт, причем

1 байт = 2³ бит = 8 бит

В информатике система образования кратных единиц измерения количества информации несколько отличается от принятых в большинстве наук. Традиционные метрические системы единиц, например Международная система единиц СИ, в качестве множителей кратных единиц используют коэффициент 10n, где п = 3, 6, 9 и так далее, что соответствует десятичным приставкам Кило (10³), Мега (10⁶), Гига (10⁹) и так далее.

Компьютер оперирует числами не в десятичной, а в двоичной системе счисления, поэтому в кратных единицах измерения количества информации используется коэффициент 2ⁿ.

Так, кратные байту единицы измерения количества информации вводятся следующим образом:

1 Кбайт = 2¹⁰ байт = 1024 байт;
1 Мбайт = 2¹⁰ Кбайт = 1024 Кбайт;
1 Гбайт = 2¹⁰ Мбайт = 1024 Мбайт.

Количество возможных событий и количество информации. Существует формула, которая связывает между собой количество возможных событий N и количество информации I:

N=2I

(1)

По этой формуле можно легко определить количество возможных событий, если известно количество информации. Например, если мы получили 4 бита информации, то количество возможных событий составляло:

N = 2⁴ = 16.

Наоборот, для определения количества информации, если известно количество событий, необходимо решить показательное уравнение относительно /. Например, в игре «Крестики-нолики» на поле 8×8 перед первым ходом существует 64 возможных события (64 различных варианта расположения «крестика»), тогда уравнение принимает вид:

64 = 2^I.

Так как 64 = 2⁶, то получим:

2⁶ = 2^I.

Таким образом, I = 6 битов, то есть количество информации, полученное вторым игроком после первого хода первого игрока, составляет 6 битов.

Алфавитный подход к определению количества информации

При определении количества информации на основе уменьшения неопределенности наших знаний мы рассматриваем информацию с точки зрения содержания, ее понятности и новизны для человека. С этой точки зрения в опыте по бросанию монеты одинаковое количество информации содержится и в зрительном образе упавшей монеты, и в коротком сообщении «Орел», и в длинной фразе «Монета упала на поверхность земли той стороной вверх, на которой изображен орел».

Однако при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от содержания информации и рассматривать ее как последовательность знаков (букв, цифр, кодов цветов точек изображения и так далее).

Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события). Тогда, если считать, что появление символов в сообщении равновероятно, по формуле (1) можно рассчитать, какое количество информации несет каждый символ.

Так, в русском алфавите, если не использовать букву ё, количество событий (букв) будет равно 32. Тогда:

32 = 2^I, откуда I = 5 битов.

Каждый символ несет 5 битов информации (его информационная емкость равна 5 битов). Количество информации в сообщении можно подсчитать, умножив количество информации, которое несет один символ, на количество символов.

Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на количество знаков.

Формула Шеннона

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если монета несимметрична (одна сторона тяжелее другой), то при ее бросании вероятности выпадения «орла» и «решки» будут различаться.

Формулу для вычисления количества информации в случае различных вероятностей событий предложил К. Шеннон в 1948 году. В этом случае количество информации определяется по формуле:

(2)

где I — количество информации;
N — количество возможных событий;
р_i — вероятность i-го события.

Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:

Р₁ = 1/2, р₂ = 1/4, р₃ = 1/8, р₄ = 1/8.

Тогда количество информации, которое мы получим после реализации одного из них, можно рассчитать по формуле (2):

I = -(l/2 log₂l/2 + l/4 log₂l/4 + l/8 log₂l/8 + l/8 log₂l/8) = (1/2 + 2/4 + 3/8 + 3/8) битов = 14/8 битов = 1,75 бита.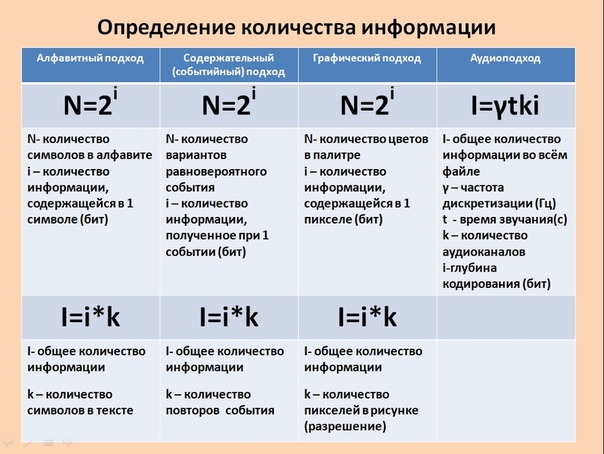

Этот подход к определению количества информации называется вероятностным.

Для частного, но широко распространенного и рассмотренного выше случая, когда события равновероятны (p_i= 1/N), величину количества информации I можно рассчитать по формуле:

(3)

По формуле (3) можно определить, например, количество информации, которое мы получим при бросании симметричной и однородной четырехгранной пирамидки:

I = log₂4 = 2 бита. Таким образом, при бросании симметричной пирамидки, когда события равновероятны, мы получим большее количество информации (2 бита), чем при бросании несимметричной (1,75 бита), когда события неравновероятны.

Количество информации, которое мы получаем, достигает максимального значения, если события равновероятны.

Выбор оптимальной стратегии в игре «Угадай число». На получении максимального количества информации строится выбор оптимальной стратегии в игре «Угадай число», в которой первый участник загадывает целое число (например, 3) из заданного интервала (например, от 1 до 16), а второй — должен «угадать» задуманное число. Если рассмотреть эту игру с информационной точки зрения, то начальная неопределенность знаний для второго участника составляет 16 возможных событий (вариантов загаданных чисел).

При оптимальной стратегии интервал чисел всегда должен делиться пополам, тогда количество возможных событий (чисел) в каждом из полученных интервалов будет одинаково и отгадывание интервалов равновероятно. В этом случае на каждом шаге ответ первого игрока («Да» или «Нет») будет нести максимальное количество информации (1 бит).

Как видно из табл. 1, угадывание числа 3 произошло за четыре шага, на каждом из которых неопределенность знаний второго участника уменьшалась в два раза за счет получения сообщения от первого участника, содержащего 1 бит информации. Таким образом, количество информации, необходимое для отгадывания одного из 16 чисел, составило 4 бита.

Таблица 1. Информационная модель игры «Угадай число»

Вопрос второго участника Ответ первого участника Неопределенность знаний (количество возможных событий) Полученное количество информации     16   Число больше 8? Нет 8 1 бит Число больше 4? Нет 4 1 бит Число больше 2? Да 2 1 бит Число 3? Да 1 1 бит

Определение количества информации.

Вероятностный подход. ЕГЭ

Похожие презентации:

Таблица умножения. Тренажер

Комбинаторика. Правила и формулы

Теорема Шеннона

Задачи 1-32 по математике

Теория игр

მენეჯერული სტატისტიკა. შერჩევა და შერჩევის განაწილება. თავი 7

Элементы теории функций комплексного переменного

Шаблон тренажера. Олімпіада з математики

Комплексные числа

ეკონომიკისა და ბიზნესის სტატისტიკა. მონაცემთა გაბნევის (გაფანტულობის) მახასიათებლები. თემა 3

ЕГЭ Определениеколичестваинформации( ) вероятностный подход( ) вероятностный подход Урок2 Существует формула, которая связывает между собой количество возможных событийN и количество информацииI:N = 2I По этой формуле можно легко определить количество возможных событий, если известно количество информации.

Например, если мы получили4 бита информации, то количество возможных событий составлялоN = 24 =16 Наоборот, для определения количества информации, если известно количество событий, необходимо решить показательное уравнение относительноI.

Решение задач 1.

Определить количество информации, полученной вторым игроком после первого хода первого игрока, в игре «крестики-нолики» на поле размером 8х8 клеток.

Решение: Перед первым ходом существует64 возможных события (64 различных варианта расположения «крестика»), тогда уравнениеN = 2I принимает вид: 64 = 2I Так как 64 = 26 , то26 = 2I .

Таким образом,I =6 битов , т.е.

количество информации, полученной вторым игроком после первого хода первого игрока, составляет 6 битов.

Ответ: 6 битов2.

В рулетке общее количество лунок равно 32.

Какое количество информации (с точки зрения вероятностного подхода) мы получаем в зрительном сообщении об остановке шарика в одной из лунок? 1) 8 битов 2) 5 битов 3) 2 бита 4) 1 бит Решение:N = 2I 32 = 2I т.к.

32=25 , то 25 = 2I, I = 5 Ответ: 5 битов 3.

Каково было количество возможных событий, если после реализации одного из них получено количество информации, равное 3 битам? Решение:N = 2IN = 23 8 = 23 N = 8 Ответ:84.

Световое табло состоит из лампочек.

Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»).

Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов? Решение: С помощью одной лампочки можно передать 3 сигнала, с помощью двух 32 = 9 сигналов, с помощью трех 33 = 27 сигналов.

Значит, чтобы подать 18 сигналов, нужно не менее трех лампочек.

Ответ:3 Другой способ: 3 состояния лампочки, 18 сигналовN = 3I , 18 = 3I , 27 = 3I = 33,I =3 Домашняя работа №2 (задания из ЕГЭ!) 1.

Производится бросание симметричной четырехгранной пирамидки.

Какое количество информации (с точки зрения вероятностного подхода) мы получаем в зрительном сообщении о ее падении на одну из граней? 1) 1 бит 2) 2 бита 3) 4 бита 4) 8 битов 2.

Какое количество информации (с точки зрения вероятностного подхода) получит второй игрок при игре в крестики-нолики на поле 4х4, после первого хода первого игрока, играющего крестиками? 1) 1 бит 2) 2 бита 3) 4 бита 4) 8 битов (10 задач) 3.

В рулетке общее количество лунок равно 128.

Какое количество информации мы получаем в зрительном сообщении об остановке шарика в одной из лунок? 1) 1 бит 2) 4 бита 3) 7 бит 4) 8 4.

Сколько различных последовательностей длиной в 7 символов можно составить из цифр 0 и 1? 5.

В корзине лежат 8 шаров.

Все шары разного цвета.

Сколько информации несет сообщение о том, что из корзины выкатился синий шар? 6.

Какое максимальное количество бит потребуется для кодирования целых положительных чисел меньших 60? 7.

Игровое клетчатое поле состоит из 15 строк и 5 столбцов.

Партия записана последовательностью из 10 координат, соответствующих ходам игроков по клеткам.

Какой объем информации в битах несет эта запись, если для кодирования координат одной клетки поля использовали двоичный код минимальной длины? 1) 50 2) 60 3) 70 4) 80 8.

В некоторой стране пользуются двоичной системой счисления.

Какое минимальное количество знаков потребуется для написания различных почтовых индексов для 718 городов? 9.

В кинотеатре 16 рядов по 32 места в каждом.

Какое количество информации в битах содержит сообщение о том, что продан один билет в 8-ом ряду место №4? 1) 5 2) 8 3) 9 4) 16 10.

Сколько существует различных вариантов составления

English     Русский Правила

Теория игр

Что такое теория игр?

Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками. В некотором смысле теория игр — это наука о стратегии или, по крайней мере, об оптимальном принятии решений независимыми и конкурирующими субъектами в стратегической обстановке.

Ключевые выводы

• Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками.
• Теория игр предназначена для обеспечения оптимального принятия решений независимыми и конкурирующими субъектами в стратегической обстановке.
• Используя теорию игр, можно разработать реальные сценарии для таких ситуаций, как ценовая конкуренция и выпуск продуктов (и многие другие), и предсказать их результаты.
• Сценарии включают дилемму заключенного и игру в диктатора среди многих других.
• Различные типы теории игр включают кооперативную/некооперативную, с нулевой суммой/ненулевой суммой и одновременную/последовательную.

Теория игр

Как работает теория игр

Ключевыми пионерами теории игр были математик Джон фон Нейман и экономист Оскар Моргенштерн в XIX веке.40с. Многие считают математика Джона Нэша первым значительным продолжением работы фон Неймана и Моргенштерна.

В центре внимания теории игр находится игра, которая служит моделью интерактивной ситуации между рациональными игроками. Ключ к теории игр состоит в том, что выигрыш одного игрока зависит от стратегии, реализуемой другим игроком.

Игра определяет личность, предпочтения и доступные стратегии игроков, а также то, как эти стратегии влияют на результат. В зависимости от модели могут потребоваться различные другие требования или допущения.

Теория игр имеет широкий спектр приложений, включая психологию, эволюционную биологию, войну, политику, экономику и бизнес. Несмотря на многочисленные достижения, теория игр все еще остается молодой и развивающейся наукой.

Согласно теории игр действия и выбор всех участников влияют на результат каждого из них. Предполагается, что игроки в игре рациональны и будут стремиться максимизировать свои выигрыши в игре.

Полезные термины теории игр

Каждый раз, когда у нас возникает ситуация с двумя или более игроками, которая включает известные выплаты или поддающиеся количественной оценке последствия, мы можем использовать теорию игр, чтобы определить наиболее вероятные исходы. Начнем с определения нескольких терминов, обычно используемых при изучении теории игр:

• Игра : Любой набор обстоятельств, результат которого зависит от действий двух или более лиц, принимающих решения (игроков)
• Игроки : Принятие стратегических решений в контексте игры
• Стратегия : Полный план действий, которые игрок предпримет с учетом набора обстоятельств, которые могут возникнуть в игре
• Выплата :   Выплата, которую игрок получает за достижение определенного результата (Выплата может быть в любой измеримой форме, от долларов до полезности. )
• Информационный набор : Информация, доступная в данный момент в игре (Термин информационный набор чаще всего применяется, когда в игре есть последовательный компонент.)
• Равновесие : Момент в игре, когда оба игрока приняли решение и достигнут результат

Равновесие Нэша

Равновесие Нэша — это достигнутый результат, который означает, что ни один игрок не может увеличить выигрыш, изменив решения в одностороннем порядке. Это также можно рассматривать как «без сожалений» в том смысле, что после принятия решения игрок не будет сожалеть о решениях с учетом последствий.

В большинстве случаев равновесие Нэша достигается со временем. Однако, как только равновесие Нэша будет достигнуто, оно не будет отклоняться от него. После того, как мы научимся находить равновесие Нэша, посмотрим, как одностороннее движение повлияет на ситуацию. Есть ли в этом смысл? Так не должно быть, и поэтому равновесие Нэша описывается как «без сожалений». Как правило, в игре может быть более одного равновесия.

Однако это обычно происходит в играх с более сложными элементами, чем два выбора двумя игроками. В одновременных играх, которые повторяются с течением времени, одно из этих множественных равновесий достигается после некоторых проб и ошибок. Этот сценарий различных вариантов выбора в течение долгого времени до достижения равновесия чаще всего разыгрывается в деловом мире, когда две фирмы определяют цены на продукты с высокой степенью взаимозаменяемости, такие как авиабилеты или безалкогольные напитки.

Вы когда-нибудь видели, чтобы тренер соперника брал тайм-аут прямо перед тем, как кикер другой команды должен попытаться забить победный бросок с игры? Th

Влияние теории игр

Теория игр присутствует почти в каждой отрасли или области исследований. Его обширная теория может относиться ко многим ситуациям, что делает ее универсальной и важной теорией для понимания. Вот несколько областей исследований, на которые непосредственно повлияла теория игр.

Экономика

Теория игр произвела революцию в экономике, решив важнейшие проблемы предшествующих математических экономических моделей. Например, неоклассическая экономическая теория изо всех сил пыталась понять предпринимательское ожидание и не могла справиться с несовершенной конкуренцией. Теория игр переключила внимание с установившегося равновесия на рыночный процесс.

Экономисты часто используют теорию игр для понимания поведения олигополистических фирм. Это помогает предсказать вероятные результаты, когда фирмы участвуют в определенных действиях, таких как установление цен и сговор.

Бизнес

В бизнесе теория игр полезна для моделирования конкурирующего поведения между экономическими агентами. У предприятий часто есть несколько стратегических вариантов, которые влияют на их способность получать экономическую выгоду. Например, предприятия могут столкнуться с такими дилеммами, как отказаться от существующих продуктов, разработать новые или использовать новые маркетинговые стратегии.

Компании также часто могут выбирать своего противника. Некоторые сосредотачиваются на внешних силах и конкурируют с другими участниками рынка. Другие ставят внутренние цели и стремятся быть лучше предыдущих версий себя. Будь то внешние или внутренние компании, они всегда конкурируют за ресурсы, пытаясь нанять лучших кандидатов у своих конкурентов и отвлечь внимание клиентов от конкурирующих товаров.

Теория игр в бизнесе может больше всего напоминать игровое дерево, как показано ниже. Компания может начать с первой позиции и должна выбрать два исхода. Однако постоянно приходится принимать другие решения; окончательная сумма выплаты не известна до тех пор, пока не будет принято окончательное решение.

Пример дерева игры.

Интернет-энциклопедия философии

Управление проектами

Управление проектами включает социальные аспекты теории игр, поскольку разные участники могут иметь разное влияние. Например, руководитель проекта может быть поощрен за успешное завершение проекта по развитию здания. Между тем, строитель может быть заинтересован в том, чтобы работать медленнее из соображений безопасности или отложить проект, чтобы потратить больше оплачиваемых часов.

При работе с внутренней командой теория игр может быть менее распространенной, поскольку все участники, работающие на одного и того же работодателя, часто имеют более общий интерес к успеху. Однако сторонние консультанты или внешние стороны, помогающие проекту, могут быть поощрены другими способами, не связанными с успехом проекта.

Цены на потребительские товары

Стратегия покупок в Черную пятницу лежит в основе теории игр. Концепция гласит, что если компании снизят цены, больше потребителей купят больше товаров. Отношения между потребителем, товаром и финансовым обменом для передачи права собственности играют важную роль в теории игр, поскольку у каждого потребителя свой набор ожиданий.

Помимо масштабных распродаж в преддверии праздников, компании должны использовать теорию игр при установлении цен на продукты для запуска или в ожидании конкуренции со стороны конкурирующих товаров. Компания должна сбалансировать слишком низкую цену на товар и не получать прибыль, но слишком высокая цена на товар может отпугнуть покупателей от товара-заменителя.

Типы теорий игр

Кооперативные и некооперативные игры

Хотя существует множество типов теорий игр (например, симметричные/асимметричные, одновременные/последовательные и т. д.), наиболее распространенными являются кооперативные и некооперативные теории игр. Кооперативная теория игр имеет дело с тем, как взаимодействуют коалиции или кооперативные группы, когда известны только выигрыши. Это игра между коалициями игроков, а не между отдельными людьми, и в ней ставится вопрос о том, как формируются группы и как они распределяют выигрыш между игроками.

Некооперативная теория игр имеет дело с тем, как рациональные экономические агенты взаимодействуют друг с другом для достижения своих целей. Наиболее распространенной некооперативной игрой является стратегическая игра, в которой перечислены только доступные стратегии и результаты, являющиеся результатом комбинации выборов. Упрощенный пример реальной некооперативной игры — камень-ножницы-бумага.

Игры с нулевой суммой и игры с ненулевой суммой

Когда существует прямой конфликт между несколькими сторонами, стремящимися к одному и тому же результату, этот тип игры часто представляет собой игру с нулевой суммой. Это означает, что на каждого победителя приходится проигравший. В качестве альтернативы это означает, что полученная коллективная чистая выгода равна потерянной коллективной чистой выгоде. Почти каждое спортивное событие представляет собой игру с нулевой суммой, в которой одна команда побеждает, а другая проигрывает.

Игра с ненулевой суммой — это игра, в которой все участники могут выиграть или проиграть одновременно. Рассмотрите деловые партнерства, которые являются взаимовыгодными и способствуют повышению ценности для обеих сторон. Вместо того, чтобы конкурировать и пытаться «выиграть», выигрывают обе стороны.

Инвестирование и торговля акциями иногда считается игрой с нулевой суммой. Ведь один участник рынка купит акцию, а другой участник продаст ту же акцию по той же цене. Однако, поскольку разные инвесторы имеют разные аппетиты к риску и цели инвестирования, сделка может быть взаимовыгодной для обеих сторон.

Игры с одновременным ходом или с последовательным ходом

Много раз в жизни теория игр представляла собой ситуации с одновременными ходами. Это означает, что каждый участник должен постоянно принимать решения, в то время как их противник принимает решения. По мере того, как компании разрабатывают свои планы маркетинга, разработки продуктов и операционных планов, конкурирующие компании одновременно делают то же самое.

В некоторых случаях имеет место преднамеренное чередование этапов принятия решений, когда одна сторона может видеть действия другой стороны, прежде чем делать свои собственные. Это обычно всегда присутствует на переговорах; одна сторона перечисляет свои требования, затем у другой стороны есть определенное количество времени, чтобы ответить и перечислить свои собственные.

Один выстрел против повторных игр

Наконец, теория игр может начинаться и заканчиваться в одном экземпляре. Как и многое в жизни, лежащее в основе соревнование начинается, развивается, заканчивается и не может быть переделано. Это часто имеет место в случае с фондовыми трейдерами, которые должны мудро выбирать свою точку входа и точку выхода, поскольку их решение не может быть легко отменено или повторено.

С другой стороны, некоторые повторяющиеся игры продолжаются и никогда не заканчиваются. В играх такого типа часто каждый раз участвуют одни и те же участники, и каждая сторона знает, что произошло в прошлый раз. Например, рассмотрим конкурирующие компании, пытающиеся установить цену на свои товары. Всякий раз, когда один из них корректирует цену, это может сделать и другой. Эта круговая конкуренция повторяется в течение цикла продукта или сезонности продаж.

В приведенном ниже примере показано изображение дилеммы заключенного (обсуждается в следующем разделе). В этом изображении после первой итерации выигрыша нет. Вместо этого происходит вторая итерация игры, приносящая с собой новый набор результатов, невозможных в играх с одним выстрелом.

Пример повторяющейся игры.

Интернет-энциклопедия философии

Примеры теории игр

Теория игр анализирует несколько «игр». Ниже мы лишь кратко опишем некоторые из них.

Дилемма заключенного

Дилемма заключенного — самый известный пример теории игр. Рассмотрим пример двух преступников, арестованных за преступление. У прокуратуры нет веских доказательств, чтобы осудить их. Однако для получения признания чиновники выводят заключенных из одиночных камер и допрашивают каждого в отдельных камерах. Ни один из заключенных не имеет возможности общаться друг с другом. Официальные лица представляют четыре сделки, часто отображаемые в виде поля 2 x 2.

1. Если оба признаются, каждый из них получит по пять лет тюремного заключения.
2. Если Заключенный 1 признается, а Заключенный 2 нет, Заключенный 1 получит три года, а Заключенный 2 — девять лет.
3. Если Заключенный 2 признается, а Заключенный 1 нет, Заключенный 1 получит 10 лет, а Заключенный 2 — два года.
4. Если ни один из них не признается, каждый будет отбывать по два года тюрьмы.

Самая благоприятная стратегия — не признаваться. Однако ни один из них не знает о стратегии другого, и без уверенности в том, что один из них не признается, оба, вероятно, признаются и получат пятилетний тюремный срок. Равновесие Нэша предполагает, что в дилемме заключенного оба игрока сделают ход, который лучше для них по отдельности, но хуже для них в совокупности.

Выражение «око за око» было определено как оптимальная стратегия для оптимизации дилеммы заключенного. Око за око было введено Анатолием Рапопортом, который разработал стратегию, в которой каждый участник повторяющейся дилеммы заключенного следует курсу действий, согласующемуся с предыдущим ходом их противника. Например, если его спровоцировать, игрок впоследствии ответит возмездием; если это неспровоцировано, игрок сотрудничает.

На изображении ниже показана дилемма, когда выбор участника в столбце и выбор участника в строке могут конфликтовать. Например, обе стороны могут получить наиболее благоприятный исход, если обе выберут строку/столбец 1. Однако каждая из сторон сталкивается с риском сильных неблагоприятных исходов, если другая сторона не выберет такой же исход.

Пример статической игры для двух человек.

Интернет-энциклопедия философии

Игра «Диктатор»

Это простая игра, в которой игрок А должен решить, как разделить денежный приз с игроком Б, который не имеет никакого отношения к решению игрока А. Хотя это не стратегия теории игр как таковая , она дает некоторые интересные сведения о поведении людей. Эксперименты показывают, что около 50 % оставляют все деньги себе, 5 % делят их поровну, а остальные 45 % отдают другому участнику меньшую долю.

Игра «диктатор» тесно связана с ультиматумной игрой, в которой игроку А дается определенная сумма денег, часть которой должна быть отдана игроку Б, который может принять или отклонить данную сумму. Суть в том, что если второй игрок отклоняет предложенную сумму, то и A, и B ничего не получают. Игры с диктатором и ультиматумом содержат важные уроки по таким вопросам, как благотворительность и филантропия.

Дилемма волонтера

В дилемме волонтера кто-то должен взять на себя работу по дому или работу для общего блага. Наихудший возможный результат реализуется, если никто не добровольно. Например, рассмотрим компанию, в которой процветает бухгалтерское мошенничество, хотя высшее руководство не знает об этом. Некоторые младшие сотрудники бухгалтерского отдела знают о мошенничестве, но не решаются сообщить об этом высшему руководству, потому что это приведет к увольнению сотрудников, причастных к мошенничеству, и, скорее всего, к судебному преследованию.

Если вас заклеймят как разоблачителя, это также может иметь некоторые последствия в будущем. Но если никто не согласится, крупномасштабное мошенничество может привести к банкротству компании и потере работы всеми.

Игра «Сороконожка»

Игра «Сороконожка» — это игра в расширенной форме в теории игр, в которой два игрока поочередно получают шанс получить большую долю медленно растущего денежного запаса. Это устроено так, что если игрок передает тайник своему противнику, который затем забирает тайник, игрок получает меньшую сумму, чем если бы он взял банк.

Игра с многоножкой завершается, как только игрок забирает тайник, при этом этот игрок получает большую часть, а другой игрок получает меньшую часть. В игре есть предопределенное общее количество раундов, которое заранее известно каждому игроку.

Теория игр существует почти во всех сферах жизни. Поскольку решения других людей вокруг вас влияют на ваш день, теория игр относится к личным отношениям, покупательским привычкам, просмотру СМИ и хобби.

Типы стратегий теории игр

Участники теории игр могут выбирать между несколькими основными способами игры. В общем, каждый участник должен решить, на какой уровень риска он готов пойти и как далеко он готов зайти, чтобы добиться наилучшего возможного результата.

Максимакс Стратегия

Максимаксная стратегия не предполагает хеджирования. Участник либо ва-банк, либо весь в ауте; они либо выиграют по-крупному, либо столкнутся с худшими последствиями. Рассмотрим новые начинающие компании, выводящие на рынок новые продукты. Их новый продукт может привести к увеличению рыночной капитализации компании в пятьдесят раз. С другой стороны, неудачный запуск продукта сделает компанию банкротом. В любой ситуации участник готов рискнуть для достижения наилучшего результата, даже если возможен худший результат.

Максимин Стратегия

Максиминная стратегия в теории игр приводит к тому, что участник выбирает лучший выигрыш из худшего. Участник решил хеджировать риск и пожертвовать полной выгодой в обмен на избежание худшего исхода. Часто компании сталкиваются с этой стратегией и принимают ее при рассмотрении судебных исков. Договариваясь во внесудебном порядке и избегая публичного судебного разбирательства, компании соглашаются на неблагоприятный исход. Однако этот исход мог быть и хуже из-за подвигов суда или еще худшего судебного решения.

Доминирующая стратегия

В доминирующей стратегии участник выполняет действия, которые являются лучшим результатом для игры, независимо от того, что решили сделать другие участники. В бизнесе это может быть ситуация, когда компания решает масштабироваться и выйти на новый рынок, независимо от того, решила ли конкурирующая компания также выйти на рынок. В «Дилемме заключенного» доминирующей стратегией будет признание.

Чистая стратегия

Чистая стратегия влечет за собой наименьшее количество стратегических решений, поскольку чистая стратегия — это просто определенный выбор, который делается независимо от внешних сил или действий других. Рассмотрим игру «камень-ножницы-бумага», в которой один участник решает бросать одну и ту же фигуру в каждом испытании. Поскольку исход для этого участника заранее определен (исходы либо определенной формы, либо не такой конкретной формы), стратегия определяется как чистая.

Смешанная стратегия

Смешанная стратегия может показаться случайной, но для разработки плана смешивания элементов или действий требуется много размышлений. Рассмотрим отношения между бейсбольным питчером и отбивающим. Питчер не может каждый раз бросать одну и ту же подачу; в противном случае отбивающий мог бы предсказать, что будет дальше. Вместо этого питчер должен смешивать свою стратегию от подачи к подаче, чтобы создать ощущение непредсказуемости, от которого он надеется извлечь выгоду.

Ограничения теории игр

Самая большая проблема с теорией игр заключается в том, что, как и большинство других экономических моделей, она основана на предположении, что люди — это рациональные действующие лица, преследующие собственные интересы и стремящиеся к максимизации полезности. Конечно, мы социальные существа, которые часто сотрудничают за свой счет. Теория игр не может объяснить тот факт, что в одних ситуациях мы можем попасть в равновесие по Нэшу, а в других — нет, в зависимости от социального контекста и игроков.

Кроме того, теория игр часто с трудом учитывает человеческие элементы, такие как лояльность, честность или сочувствие. Хотя статистические и математические расчеты могут диктовать, каким должен быть наилучший курс действий, люди могут не пойти по этому пути из-за непредсказуемых и сложных сценариев самопожертвования или манипуляции. Теория игр может анализировать набор моделей поведения, но не может точно предсказать человеческий фактор.

В какие игры играют в теории игр?

Это называется теорией игр, поскольку теория пытается понять стратегические действия двух или более «игроков» в данной ситуации, содержащей установленные правила и исходы. Хотя теория игр используется в нескольких дисциплинах, она в первую очередь используется в качестве инструмента при изучении бизнеса и экономики.

«Игры» могут заключаться в том, как две конкурирующие фирмы будут реагировать на снижение цен другой, должна ли одна фирма приобретать другую или как трейдеры на фондовом рынке могут реагировать на изменения цен. Теоретически эти игры можно разделить на дилеммы заключенного, игру в диктатора, ястреб-и-голубь, Баха или Стравинского.

Какие предположения об этих играх?

Как и многие экономические модели, теория игр также содержит ряд строгих допущений, которые должны выполняться, чтобы теория могла делать хорошие прогнозы на практике. Во-первых, все игроки являются рациональными акторами, стремящимися к максимизации полезности и обладающими полной информацией об игре, правилах и последствиях. Игрокам не разрешается общаться или взаимодействовать друг с другом. Возможные исходы не только известны заранее, но и не могут быть изменены. Теоретически количество игроков в игре может быть бесконечным, но в большинстве игр будет только два игрока.

Что такое равновесие Нэша?

 Равновесие Нэша – важная концепция, относящаяся к стабильному состоянию в игре, когда ни один игрок не может получить преимущество, в одностороннем порядке изменив стратегию, при условии, что другие участники также не меняют свои стратегии. Равновесие Нэша обеспечивает концепцию решения в некооперативной (состязательной) игре. Он назван в честь Джона Нэша, получившего Нобелевскую премию в 1994 году за свою работу.

Кто придумал теорию игр?

Теория игр в значительной степени связана с работами математика Джона фон Неймана и экономиста Оскара Моргенштерна в 1940-х годах и широко развивалась многими другими исследователями и учеными в 1950-х годах. Это остается областью активных исследований и прикладной науки по сей день.

Итог

Теория игр — это исследование того, как конкурентные стратегии и действия участников могут влиять на исход ситуации. Имея отношение к войне, биологии и многим аспектам жизни, теория игр используется в бизнесе для представления стратегических взаимодействий, в которых результат одной компании или продукта зависит от действий, предпринимаемых другими компаниями или продуктами.

Игра с друзьями — Руководство по игре

Как только вы начнете играть в Diablo III, вы увидите общедоступное игровое меню на странице выбора персонажа.

Нажав кнопку «Общие игры», вы сможете играть в Diablo III с другими игроками, которые не обязательно входят в ваш список друзей. Обратите внимание, что вы можете присоединиться только к заданию, которое вы начали, независимо от того, насколько далеко продвинулись другие игроки в вашей игре.

После того, как вы нажмете кнопку «Присоединиться к игре», вас быстро объединят с другими игроками в том же квесте и в том же диапазоне уровней. Вы можете играть с 3 другими игроками (всего 4 участника) в совместной игре.

При создании общедоступной игры или присоединении к ней вы можете выбрать тег, определяющий тип игрового процесса, которым вы хотите поделиться с другими. Теги включают «Убийство монстров», «Схватка», «Хранитель ключей» и «Разлом». Выбор определенного тега при присоединении к общедоступной игре, такой как «Потасовка», помещает вас в группу с другими игроками, которые также заинтересованы в «Потасовке».

Кланы и сообщества позволяют легко встречаться и поддерживать связь с игроками, разделяющими ваши интересы. В главном меню одновременно нажмите клавиши Shift и «O» или выберите значок облачка чата, чтобы открыть меню кланов и сообществ. Отсюда у вас будет возможность создать новый клан, присоединиться к новому клану, создать новое сообщество или присоединиться к новому сообществу. Вы сможете взаимодействовать со своим кланом и любыми сообществами, частью которых вы являетесь, независимо от того, за какого из ваших персонажей вы хотите играть.

Игроки, состоящие в одном клане, получат доступ к уникальному каналу чата клана, где вы сможете общаться с членами клана и получать новости об их действиях, например, когда они находят легендарные предметы. Вы можете одновременно состоять только в одном клане. Кланы изначально формируются одним игроком, известным как лидер клана, который отвечает за управление кланом. В окне клана вы сможете получить доступ к нескольким вкладкам:

• Новости: На этой вкладке отображается общее количество участников в клане, сообщение дня клана, лента новостей клана и общая информация, которой хотят поделиться лидеры клана.
• Список: На вкладке Список отображается подробный список всех членов клана, а также их рейтинг, количество достижений и текущая активность. Когда вы прокручиваете список участников, нижняя часть этой вкладки будет обновляться, показывая героя, за которого играет каждый участник.
• Настройки: Вкладка «Настройки» видна всем участникам, но может быть изменена только офицерами клана. Он отображает предпочитаемый язык клана, активно ли клан набирает новых членов, а также разрешения для каждого ранга клана.

Главное окно клана.

Сообщества не имеют ограничения на членство.

Сообщества функционируют так же, как и кланы, за исключением того, что Сообщества тематически связаны с конкретными интересами, и вы можете быть частью многих одновременно. Сообщества часто создаются для драки, охоты за предметами, обсуждения конкретных особенностей игры или даже для обсуждения реальных тем! Как и кланы, сообщества управляются собственным лидером и имеют собственные разделы «Новости», «Список» и «Настройки».

Просмотр чатов в окне чата.

На ПК, когда вы участвуете в группе, в вашем распоряжении будет несколько специальных инструментов для взаимодействия. Стрелки и маленькое окошко в левом нижнем углу экрана показывают расположение окна чата. Это окно, которое остается прозрачным, пока вы не наведете на него указатель мыши, представляет собой журнал ваших взаимодействий в игре.

Здесь вы увидите сообщения, которые вы отправили другим игрокам, а также любые полученные вами сообщения. Чтобы отправить игроку сообщение, вы можете выделить его имя в своем социальном окне и нажать «Чат», или вы можете отправить ему сообщение напрямую. После нажатия «ENTER» или «RETURN» на клавиатуре вы увидите сообщение
, которое вы вводите, в окне чата.

Нажав на значок шестеренки в окне чата, вы сможете начать приватный разговор с 99 другими игроками. Вы можете быть в другой игре, чем люди, с которыми вы общаетесь.

Зачем идти в бой в одиночку, если можно взять с собой друзей?

Игра с другими дает ряд существенных преимуществ, но также влияет на геймплей несколькими примечательными способами.

Когда вы находитесь в группе, вы можете видеть здоровье и текущий статус членов вашей группы на их портретах в верхней части экрана. Если вы хотите сразу же приступить к делу вместе с ними, вы можете мгновенно телепортироваться к текущему местонахождению членов вашей группы, выбрав их знамёна в городе. Наконец, вы можете обменяйте предмета с другими игроками. На ПК это можно сделать, щелкнув правой кнопкой мыши их портреты и выбрав «Торговля», после чего откроется окно торговли, в котором вы сможете обменять предметы. На консолях вы можете торговать с онлайн-игроками или игроками, связанными с системой, через меню «вечеринка» (Xbox 360 и Xbox One: НАЗАД; PlayStation®3 и PlayStation®4: ВЫБЕРИТЕ и перейдите к «тусовке»), выбрав «предложить предмет». » или «предложить золото», чтобы указать, что вы хотели бы обменять.

«Лут» в группах индивидуален: каждый игрок находит свои личные вещи и золото на трупах убитых противников или в сундуках. Невозможно украсть предметы, найденные другим игроком.

Хотя вы можете создать группу с тремя другими игроками (всего четыре игрока), вы не можете брать с собой своих последователей, когда находитесь в группе с другими людьми, независимо от размера вашей вечеринки.

Каждый игрок в группе делится состоянием игры, к которой он решил присоединиться. Например: если вы убили Короля скелетов своим персонажем, но только что присоединились к общедоступной игре, где ваша цель — убить его, он снова будет жив в этой игре, и откроется любая важная история, связанная с его смертью (новое разблокированные области, определенные NPC и т. д.) будут недоступны для вас.

Самое главное, чем больше игроков в группе, тем сильнее противники. С каждым пополнением в вашей группе легионы Пылающей Преисподней будут становиться все сильнее. Будьте осторожны: хотя на вашей стороне сила нескольких героев, вы обнаружите, что враги, которых вы легко побеждали в прошлом, могут потребовать дополнительных усилий, когда вы играете в группе.

Привлечение элитной стаи или гоблина-сокровища активирует уведомление, которое позволяет всей вашей группе узнать, с какой встречей вы столкнулись. На ПК на мини-карте будет отображаться значок боя, чтобы показать ближайшим союзникам, куда идти. Аналогичный боевой значок будет отображаться над вашим баннером, чтобы ваши друзья в городе могли быстро определить, как сразу же перейти к действию.

В то время как сила врагов растет с каждым дополнительным членом группы, который сражается поблизости, награды, которые герои получают от совместной работы над победой над этими врагами, также увеличиваются. Помимо бонусного шанса найти магические предметы и полученного бонусного золота, вы также получаете бонусный опыт. Этот бонус к опыту умножается на бонусы за сложность, поэтому многопользовательская игра на более высоких уровнях сложности дает еще большие награды.

• Игра для 2 игроков: 10% бонус к поиску золота, магическому поиску и опыту
• Игра для 3 игроков: 20% бонус к поиску золота, магическому поиску и опыту
• Игра для 4 игроков: 30% бонус к поиску золота, магическому поиску и опыту

Играя с друзьями, вы можете найти предметы, которые больше подходят вашим союзникам, а ваши союзники могут найти предметы, которые больше подходят вам. У вас будет 2 часа с момента обнаружения предмета, чтобы обменять его среди друзей, которые присутствовали при выпадении предмета. Это ограничение не распространяется на золото и предметы обычного, магического и редкого качества.

Эмоции и команды доступны только в версии Diablo III для ПК.

Эмоции — это простые сочетания клавиш, которые вы можете использовать для быстрого общения с другими игроками — они заставляют вашего персонажа говорить, обмениваясь важной информацией, такой как «следуй» или «беги». Команды — это текстовые ярлыки, которые можно использовать для управления каналами чата или для использования преимуществ интерфейса Diablo III.

Чтобы использовать эмоцию или команду, просто введите «/» (косая черта), а затем текст, который вы видите ниже. Вы можете привязать эмоции (и некоторые команды) к разным клавишам в разделе «Привязка клавиш» в меню «Параметры».

Эмоции:

• / следуйте (или клавиша по умолчанию NUMPAD 1)
• /give (или клавиша по умолчанию NUMPAD 2)
• /thanks (или клавиша по умолчанию NUMPAD 3)
• /извините (или клавиша по умолчанию NUMPAD 4)
• /bye (или клавиша по умолчанию NUMPAD 5)
• /die (или клавиша по умолчанию NUMPAD 6)
• /run (или по умолчанию клавиша NUMPAD 7)
• /wait (или по умолчанию клавиша NUMPAD 8)
• /go (или клавиша по умолчанию NUMPAD 9)
• /help (или клавиша по умолчанию NUMPAD 0)

Эмоции, которые по умолчанию не привязаны:

• да
• нет
• оставаться там
• атака
• отступление
• удержание
• взять цель

Команды:

• /? – Показать все игровые команды
• /отправить; /т; /рассказывать; / ш; /whisper <игрок> <сообщение> — Отправить <игроку> сообщение
• /р; /reply — Ответить на последнее полученное сообщение
• /присоединиться; /канал; /chan <название канала> — Присоединиться к каналу чата
• /отпуск; /выйти из чата; /chatexit — Покинуть текущий канал чата
• /с; /csay — отправить сообщение на текущий канал чата
.
• /chatlist — Показать все доступные каналы чата
• /who — Показать всех игроков в вашем текущем канале чата
• /стр; /party — отправить сообщение вашей текущей группе
• Shift + [нажмите на предмет или достижение] — свяжите выбранный вами предмет или достижение с текущим чатом для просмотра другими игроками

Ваше наследие победы.

Когда вы выполняете определенные героические задания в Diablo III, вы не просто получаете золото, сокровища или удовлетворение от пролития крови ваших врагов. Вы также разблокируете достижение, показатель вашего мастерства в игре.

Достижения обычно разблокируются при выполнении важных, уникальных или сложных задач, таких как убийство монстра более сложным способом, завершение акта или прохождение игры на более высоком уровне сложности. Основные задачи, которые вы выполняете, либо оцениваются в определенное количество баллов, либо отслеживаются как вызов, не приносящий баллов (но достойный славы и хвастовства). На консолях ваши очки соответствуют достижениям Xbox LIVE и трофеям PSN; на ПК ваши очки видны в игре.

Если вы хотите узнать, чего вы достигли, или узнать о будущих испытаниях, проверьте меню достижений в игре (ПК: клавиша «Y»), чтобы увидеть полный список достижений. Достижения распределяются между всеми вашими персонажами.

Разблокировав определенные достижения, вы получите новые узоры и акценты для своего знамени , боевого штандарта, который вы можете настроить, чтобы показать свои достижения другим игрокам в игре.

Отомсти за друзей и убей Немезиду!

В Diablo III — Reaper of Souls: Ultimate Evil Edition вы и ваши друзья познакомитесь со своим самым опасным врагом: чудовищем Немезидой. При игре героем 10-го уровня или выше любой неэлитный монстр, не являющийся боссом, который побеждает вас, имеет шанс превратиться в монстра Немезиды. Затем монстр Немезида покинет игру с единственной зловещей целью: выследить кого-то из вашего списка друзей! Монстры Немезиды не будут нацеливаться на героев ниже 10-го уровня и никогда не будут появляться в хардкорном режиме.

Когда монстр Немезида вторгается в игру жертвы, он появляется рядом с этим игроком, пока он или она не находится в городе, не смотрит кат-сцену или не сражается с боссом. Каждый раз, когда он убивает игрока, монстр Немезида становится сильнее, а затем переходит в другую игру из списка друзей жертвы (до пяти раз).

Вас и, возможно, вашего друга ждут мощные награды, если вы сможете победить Немезиду.

Отправляйтесь в путешествие с союзником, который на четыре или более уровней выше вашего героя, и они возьмут вас в ученики, предоставив вам дополнительную живучесть и урон, которые поставят вас на один уровень с уровнем силы вашего друга. Это позволяет вам наносить приличный урон врагам и получать разумное наказание. Если в игре участвуют трое или более игроков, каждый, кто на четыре или более уровней ниже, становится учеником игрока самого высокого уровня.