Определение. Точки максимума и минимума функции называются точками экстремума
Точки экстремума
Определение. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 +Dx) > f(x2) при любом Dх (Dх может быть и отрицательным).
Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х
Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.
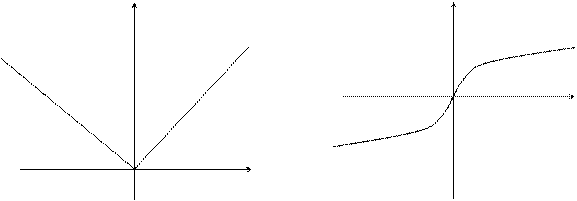
Пример: f(x) = ôxô Пример: f(x) = 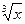
 y y
y yx
x
| В точке х = 0 функция имеет минимум, но не имеет производной. | В точке х = 0 функция не имеет ни максимума, ни минимума, ни производной. |
Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.
Теорема. (Достаточные условия существования экстремума)
Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х
Если при переходе через точку х1 слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:
1) Найти критические точки функции.
2) Найти значения функции в критических точках.
3) Найти значения функции на концах отрезка.
4) Выбрать среди полученных значений наибольшее и наименьшее.
Точки максимума и минимума функции — Студопедия
2.
Определение 1. Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х0 выполняется неравенство f(х) ≥ f(х0).
Определение 2. Точка х1 называется точкой минимума функции f(х), если в некоторой окрестности точки х1 выполняется неравенство f(х) ≤ f(х1).
Значения функции в точках х0 и х1 называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием
Экстремум функции часто называют локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с достаточно малой окрестностью точки х0.
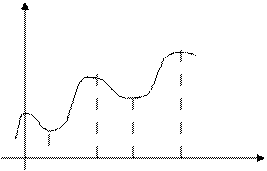 |
min max min max
Необходимое условие экстремума. Если в точке х0 дифференцируемая функция у = f(x) имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма, и, следовательно, производная функции в этой точке равна нулю, т.е. f'(х0
Для того чтобы функция у = f(x) имела экстремум в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю (f'(х0) = 0) или не существовала.
Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются критическим (или стационарными).
Критическая точка вовсе не обязательно является точкой экстремума.
Первое достаточное условие экстремума. Теорема. Если при переxоде через точку х0 производная дифференцируемой функции у = f(х) меняет свой знак с плюса на минус, то точка х
Экстремумы функции, максимум и минимум
ОПРЕДЕЛЕНИЕЭкстремумами (максимумами и минимумами) функции называются значения функции в точках максимума и минимума.
Точки экстремума функции
Говорят, что в точке максимум (минимум), если существует такая -окрестность точки — , что для всех из этой окрестности, отличных от выполняется неравенство .
ОПРЕДЕЛЕНИЕТочки максимума и минимума называются точками экстремума.
ОПРЕДЕЛЕНИЕ Точки области определения, в которых производная функции равна нулю или не существует, называютсяНеобходимое условие существования экстремума функции. Пусть функция дифференцируема в промежутке . Если в некоторой точке функция имеет экстремум, то в этой точке производная равна нулю: .
Достаточное условие существования экстремума функции. Если производная функции равна нулю в точке и при переходе через эту точку в сторону возрастания меняет знак с «+» («-») на «-» («+»), то в точке функция имеет максимум (минимум). Если же при переходе через точку производная функции не меняет знак, то в этой точке функция экстремума не имеет.
Для исследования функции на экстремум необходимо:
- найти критические точки функции;
- проверить, изменяет ли знак производная функции при переходе через критическую точку;
- вычислить значения максимума или минимума .
Примеры исследования функции на экстремум
ПРИМЕР 1| Задание | Найти экстремум функции |
| Решение | Найдем критические точки функции, для этого вычислим производную заданной функции
приравняем её к нулю и найдем корни полученного квадратного уравнения
Получили две критические точки . Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах. В точке производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума
В точке производная меняет знак с «-» на «+», значит, — точка минимума. Значение минимума соответственно равно
|
| Ответ |
| Задание | Найти экстремум функции
|
| Решение | Область определения функции — вся числовая прямая, за исключением точки , то есть .
Приравниваем к нулю производную
Получаем одну критическую точку . Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах В точке производная меняет знак с «-» на «+», значит, в этой точке минимум. Значение минимума соответственно равно
|
| Ответ |
Монотонность функции
Нули функции
Наибольшее и наименьшее значение функции
Точки перегиба функции
Промежутки выпуклости и вогнутости функции
Исследование функции
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Интервалы возрастания и убывания функции
Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции. Суть этого метода состоит в следующем.
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x0 интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,
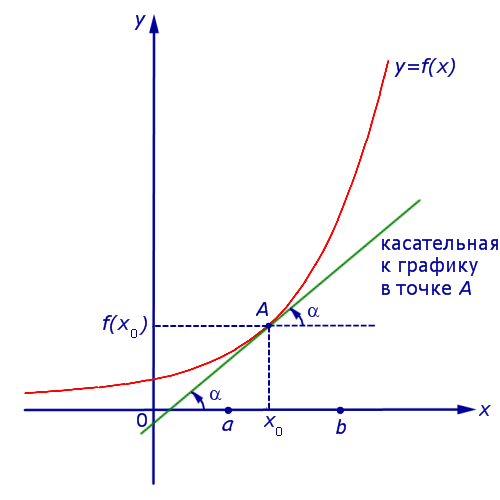
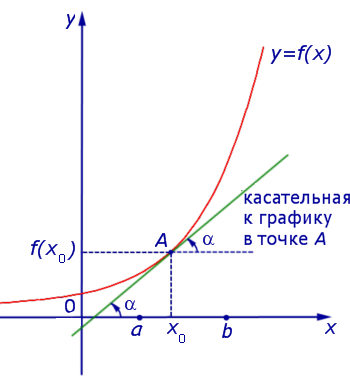
Рис.1
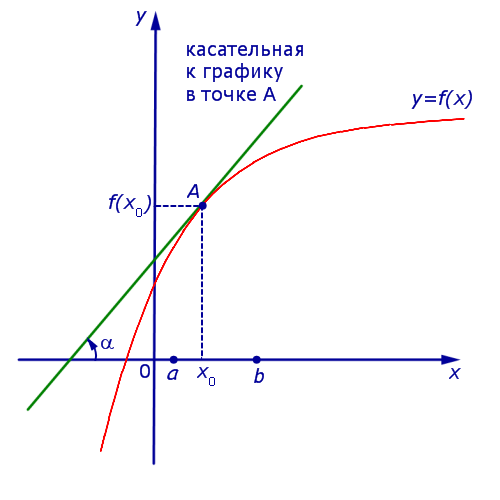
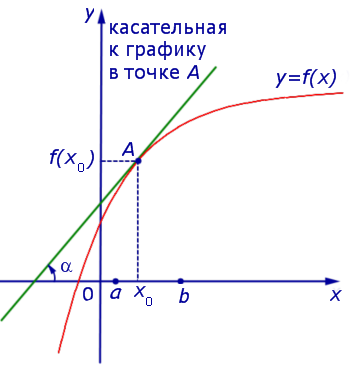
Рис.2
угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:
f ‘ (x0) = tg α > 0
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x0 интервала имеет производную, то, как показано на рисунках 3 и 4,
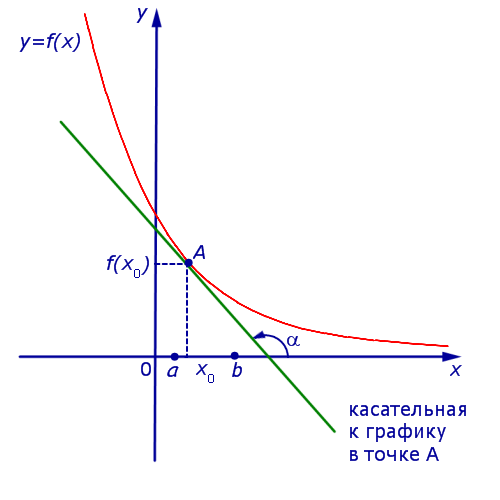
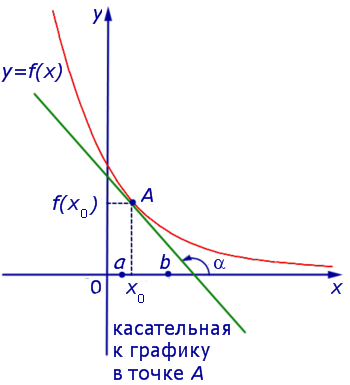
Рис.3
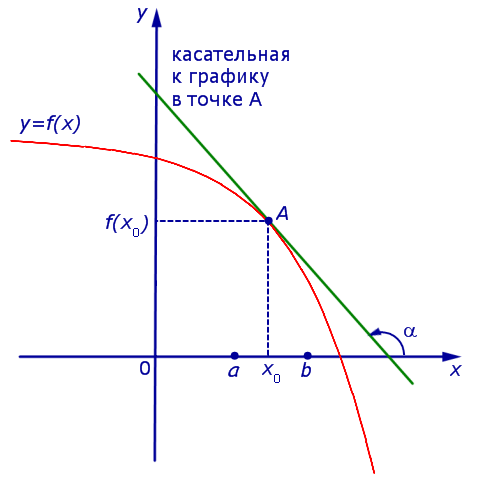
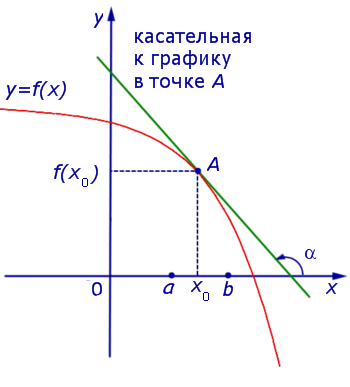
Рис.4
угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:
f ‘ (x0) = tg α < 0
Достаточные условия для возрастания и убывания функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики, сформулированы достаточные условия для возрастания и убывания функции.
Утверждение 1.
а). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
f ‘ (x) > 0 ,
то функция f (x) строго возрастает на интервале (a, b) .
б). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
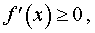
то функция f (x) возрастает (не убывает) на интервале (a, b) .
в). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
f ‘ (x) < 0 ,
то функция f (x) строго убывает на интервале (a, b) .
г). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
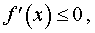
то функция f (x) убывает (не возрастает) на интервале (a, b) .
Экстремумы (максимумы и минимумы) функции
Определение 1. Точку x0 называют точкой максимума функции f (x) , если существует интервал (a, b) , такой, что a 0b , для точек x которого выполнено неравенство
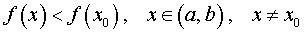 .
.
Таким образом, если x0 – точка максимума функции f (x) , то в интервале (a, b) значение функции f (x0) больше всех остальных значений функции.
Определение 2. Точку x0 называют точкой минимума функции f (x) , если существует интервал (a, b) , такой, что a < x0 < b , для точек x которого выполнено неравенство
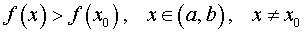 .
.
Другими словами, если x0 – точка минимума функции f (x) , то в интервале (a, b) значение функции f (x0) меньше всех остальных значений функции.
Определение 3. Точки максимума и минимума функции называют точками экстремума функции, а значения функции в точках экстремума называют экстремумами функции.
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма
Определение 4.Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.
Определение 5.Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.
Таким образом, если точка x0 является критической точкой функции, то точка x0 либо является стационарной точкой функции, либо производная функции в точке x0 не существует.
Теорема Ферма. Если точка x0 является точкой экстремума функции f (x) , то точка x0 является критической точкой функции f (x) .
Доказательство. Если в точке x0 у функции y = f (x) не существует производная, то точка x0 является критической точкой по определению. Докажем, что если в точке x0 у функции y = f (x) существует производная, то точка x0 является стационарной, то есть f ‘ (x0) = 0 .
Предположим сначала, что точка x0 является точкой максимума функции y = f (x) (рис. 5).
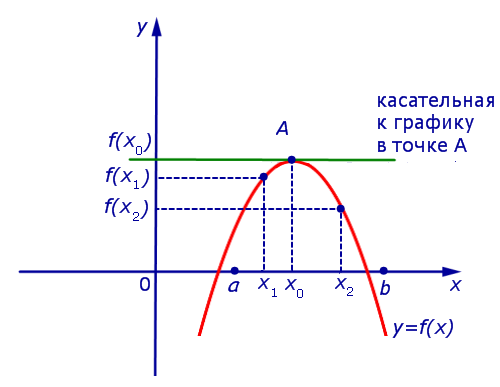
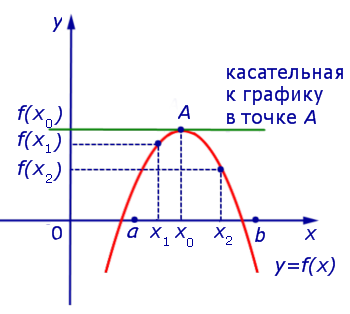
Рис.5
Поскольку x0 – точка максимума, то для любой точки x1 такой, что x1x0 , выполнено неравенство f (x1) < f (x0) , поэтому
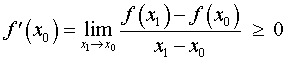 .
.
Точно так же, для любой точки x2 такой, что x2 > x0 , выполнено неравенство f (x2) < f (x0) , поэтому
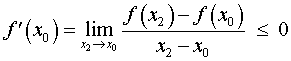 .
.
Таким образом, в случае, когда точка x0 является точкой максимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 . Касательная к графику функции y = f (x) в точке A= (x0; f (x0)) параллельна оси Ox.
Совершенно аналогично доказывается, что и в случае, когда точка x0 является точкой минимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 .
Замечание 1. Из утверждения 2 следует, что точки экстремумов функции (точки максимумов и точки минимумов) нужно искать лишь среди критических точек функции, так как в других (некритических) точках экстремумов быть не может. По этой причине критические точки функции часто называют точками, подозрительными на экстремум.
Достаточные условия для существования экстремума функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.
Утверждение 3. Рассмотрим функцию f (x) , непрерывную в интервале (a, b), содержащем точку x0 , производная которой существует в каждой точке этого интервала, кроме, быть может, самой точки x0 .
а). Если для точек 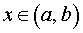 выполнено условие:
выполнено условие:
f ‘ (x) > 0 при x 0 и f ‘ (x) < 0 при x > x0 ,
то точка x0 является точкой максимума функции f (x) (рис. 6).
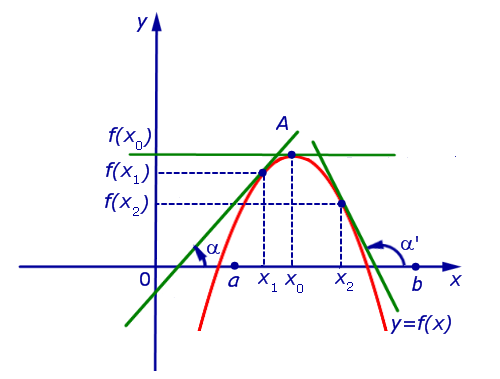
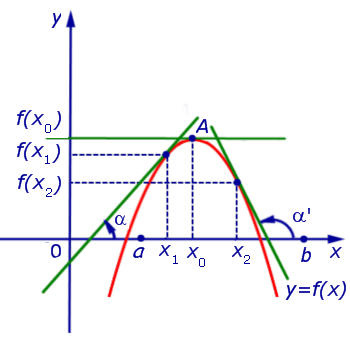
Рис.6
б). Если для точек 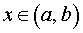 выполнено условие:
выполнено условие:
f ‘ (x) < 0 при x < x0 и f ‘ (x) > 0 при x > x0 ,
то точка x0 является точкой минимума функции f (x) (рис. 7).
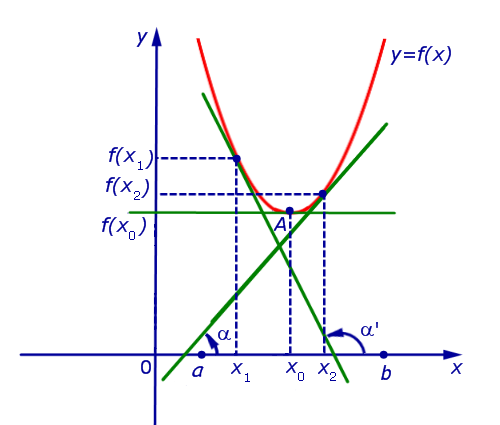
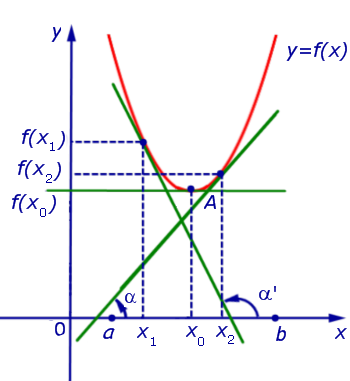
Рис.7
Замечание 2. Условия а) и б) утверждения 3 часто формулируют так: «Если при переходе через точку x0 производная функции меняет знак с «+» на «–» , то точка x0 является точкой максимума функции. Если при переходе через точку x0 производная функции меняет знак с «–» на «+» , то точка x0 является точкой минимума функции».
Пример исследования поведения функции
Пример. Найти интервалы возрастания, убывания и экстремумы функции
Решение. Исследуем сначала на возрастание, убывание и экстремумы функцию
и построим ее график. Для этого представим формулу (2) в виде
y1 = x2 (x + 3)
и заметим, что
а) y1 = 0 при x = 0 и x = – 3 ,
б) y1 > 0 при x > – 3 ; y1 < 0 при x < – 3 .
Теперь вычислим производную функции (2):
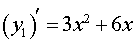 | (3) |
и разложим на множители правую часть формулы (3):
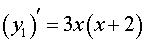 | (4) |
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)
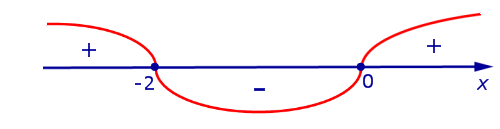
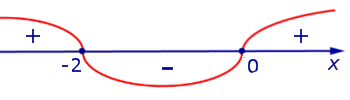
Рис.8
Поскольку решением неравенства
3x (x + 2) > 0
является множество
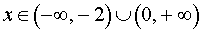 , , | (5) |
то в соответствии с утверждением 1 функция y1 возрастает на каждом из интервалов 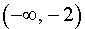 и
и 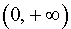 .
.
С другой стороны, поскольку решением неравенства
3x (x + 2)
является интервал
то в соответствии с утверждением 1 функция y1 убывает на интервале (– 2, 0) .
Так как решениями уравнения
3x (x + 2) = 0
являются точки
то эти точки являются стационарными точками функции y1 .
Поскольку при переходе через точку x = – 2 производная функции y1 меняет знак с «+» на «–» (рис. 8), то в соответствии с утверждением 3 точка x = – 2 является точкой максимума функции y1 , при этом
y1 (– 2) = 4 .
При переходе через точку x = 0 производная функции y1 меняет знак с «–» на «+» (рис. 8), поэтому в соответствии с утверждением 3 точка x = 0 является точкой минимума функции y1, при этом
y1 (0) = 0 .
Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).
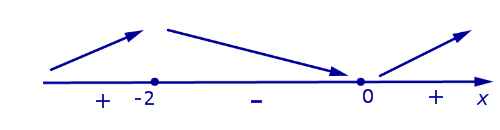
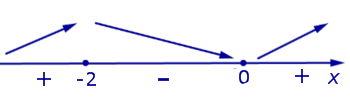
Рис.9
Теперь мы можем построить график функции y1 (рис. 10).
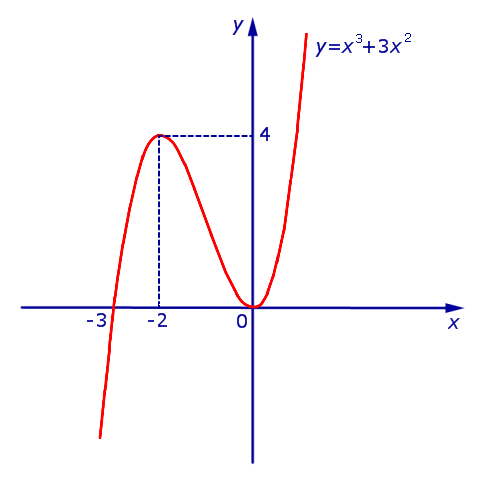
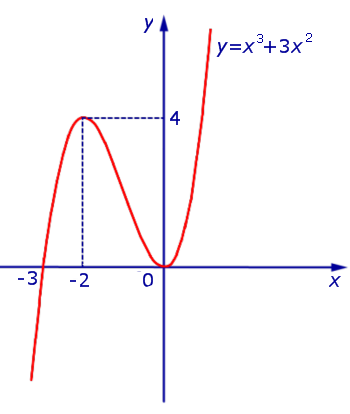
Рис.10
Перейдем к построению графика функции y = | x3 + 3x2 | .
В силу определения модуля, справедливо равенство
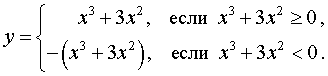
Из этого равенства вытекает, что, если мы симметрично отразим относительно оси Ox часть графика функции y1 = x3 + 3x2 (рис. 10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x3 + 3x2 | (рис.11) .
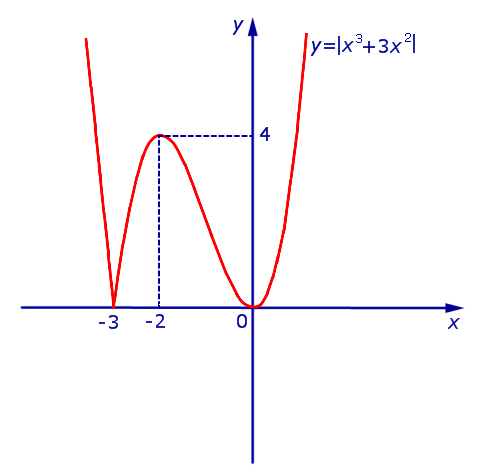
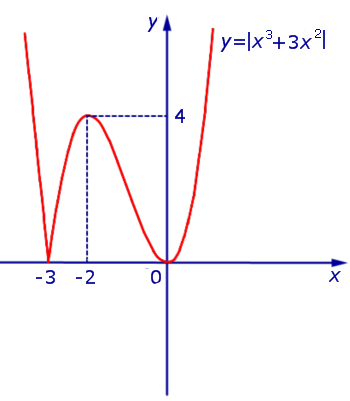
Рис.11
В точке x = – 3 производная функции y = | x3 + 3x2 | не существует. Во всех остальных точках числовой оси производная функции y = | x3 + 3x2 | существует.
Точки x = – 3 и x = 0 являются точками минимума, причем y ( – 3) = y (0) = 0 .
Точка x = – 2 является точкой максимума, причем y ( – 2) = 4 .
Функция y = | x3 + 3x2 | возрастает на каждом из интервалов (– 3, – 2) и 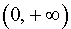 .
.
Функция y = | x3 + 3x2 | убывает на каждом из интервалов 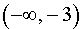 и (– 2, 0).
и (– 2, 0).

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Экстремумы функции – что это такое: как найти критическую точку максимума и минимума
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
…
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
- экономика,
- статистика,
- биология,
- машинное управление,
- эконометрика.
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
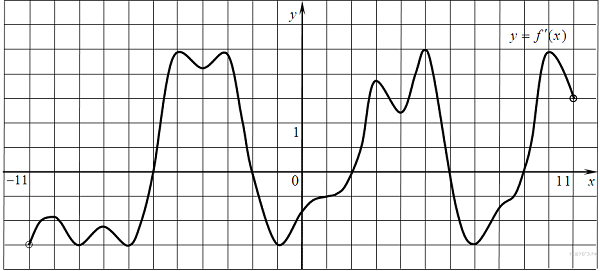 Производная функция
Производная функция
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством
Острый экстремум
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
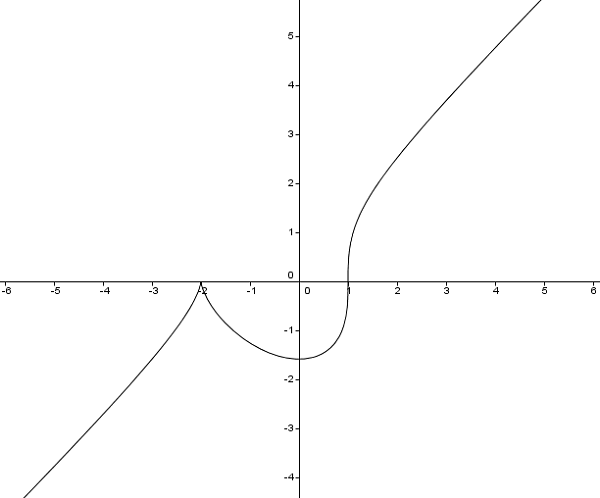 Острый экстремум Важно! Процесс нахождения точек острого экстремума функции называется дифференцированием и используется как в школьном курсе изучения алгебры и начала анализа, так и в ходе освоения высшей математики в университете.
Острый экстремум Важно! Процесс нахождения точек острого экстремума функции называется дифференцированием и используется как в школьном курсе изучения алгебры и начала анализа, так и в ходе освоения высшей математики в университете.
Экстремальное значение функции
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.
- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.
- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.
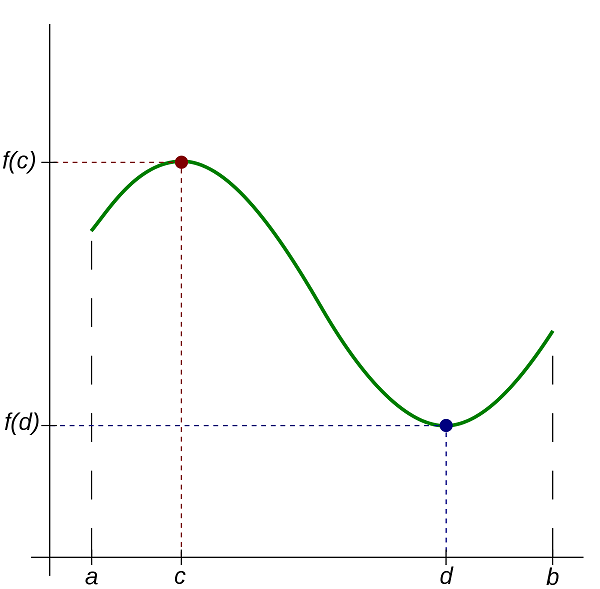 Экстремальное значение функции Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
Экстремальное значение функции Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
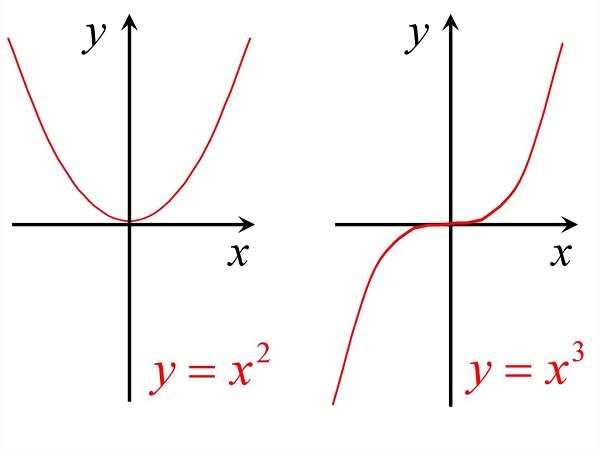 Точки минимума и максимума
Точки минимума и максимума
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум. | Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума. |
Экстремум функционала
Для того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил:
- определить необходимое условие экстремального отношения,
- учитывать достаточное условие крайних точек на графике,
- осуществлять расчет острого экстремума.
Используются также такие понятия, как слабый минимум и сильный минимум. Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Это интересно! Легкие правила округления чисел после запятой
Экстремумы функции. 10 класс.
Исследование функции. Экстремумы функции bezbotvy
Вывод
После прочтения и осознания данной статьи любой новичок в математике имеет возможность понять возможности острых экстремумов в том виде, в каком они используются в образовательном процессе. Вышеперечисленные моменты позволяют разобраться в крайних точках без помощи репетиторов.
Найти экстремумы функции | Онлайн калькулятор
Данный калькулятор предназначен для нахождения экстремумов функции.
Следует различать понятия точек экстремума и экстремумов функции. Точки экстремума – точки максимума и минимума функции, это значения на оси Ox. Точка x0 является точкой максимума функции y=f(x), если для всех x из ее окрестности выполняется неравенство f(x0)≥f(x). Точка x0 является точкой минимума функции y=f(x), если из ее окрестности для всех x выполняется неравенство f(x0)≤f(x). Значения функции, которые соответствуют точкам экстремума, называются экстремумами функции, это значения на оси Oy.
Для того чтобы найти экстремумы функции можно использовать любой из трех условий экстремума, если функция удовлетворяет эти условиям.
Первым достаточным условием экстремума являются следующие утверждения: если в точке x0 функция непрерывна, и в ней производная меняет знак с плюса на минус, то точка x0 является точкой максимума, а если в данной точке производная меняет знак с минуса на плюс, то x0 – точка минимума.
Вторым признаком экстремума является следующее утверждение: если производная второго порядка от x0 больше нуля, то x0 – точка минимума; если меньше нуля, то x0 – точка максимума. Третье достаточное условие экстремума функции заключается в следующем. Пусть функция y=f(x) имеет производные до n-ого порядка в окрестности точки x0 и производные до n+1-ого порядка в самой точке x0; пусть f’(x0)= f’’(x0)= f’’’(x0)=…=f(n)( x0)=0 и f(n+1)( x0)≠0. Тогда, если n – нечетное, то x0 – точка экстремума. Если f(n+1)( x0)>0, то x0 – точка минимума, а, если f(n+1)( x0)0 – точка максимума. Для того чтобы найти экстремумы функции, введите эту функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже. Для получения полного хода решения нажимаем в ответе Step-by-step.
матан коллоквиум / 12.Понятие экстренума.Определение максиимума,минимума,понятие критической точки,графическая иллюстрация критических точек
Экстре́мум (лат. extremum — крайний) в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть
дана функция 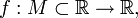 и
и 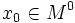 —
внутренняя точка области определения
—
внутренняя точка области определения 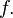 Тогда
Тогда
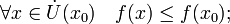
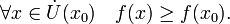
Если
неравенства выше строгие, то 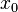 называется
точкой строгого локального максимума
или минимума соответственно.
называется
точкой строгого локального максимума
или минимума соответственно.
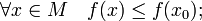
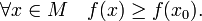
Значение
функции 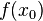 называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Достаточные условия существования локальных экстремумов
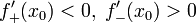
 является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если
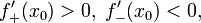
то 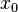 является
точкой строгого локального минимума.
является
точкой строгого локального минимума.
Заметим,
что при этом функция не дифференцируема
в точке 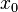
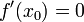 и
и 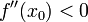
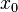 является
точкой локального максимума. А если
является
точкой локального максимума. А если
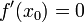 и
и 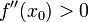
то 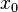 является
точкой локального минимума.
является
точкой локального минимума.
Если 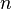 чётно
и
чётно
и 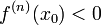 ,
то
,
то 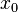 —
точка локального максимума. Если
—
точка локального максимума. Если 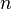 чётно
и
чётно
и 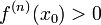 ,
то
,
то 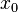 —
точка локального минимума. Если
—
точка локального минимума. Если 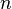 нечётно,
то экстремума нет.
нечётно,
то экстремума нет.
Максимум и минимум функции.
Приведем
точные определения точек
экстремума. Определение. Точка
x0 называется
точкой минимума функции f, если для всех
x из некоторой окрестности x0 выполняется
неравенство f(x) ≥ f(x0. Это
наглядно показано на рисунке 1: 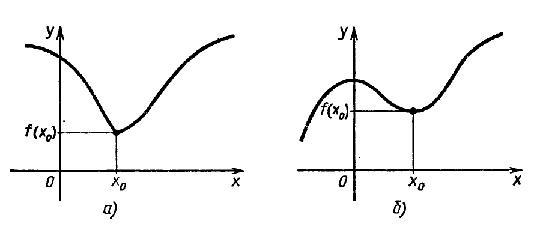 рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2:
рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2: 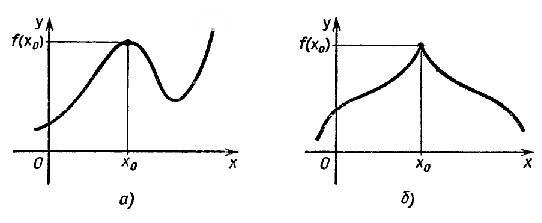 рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже:
рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже: 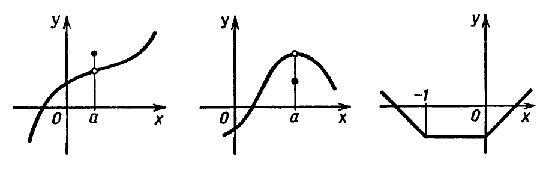 Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
Критической
точкой дифференцируемой
функции 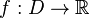 ,
где
,
где 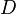 —
область в
—
область в 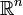 ,
называется точка, в которой все её частные
производные обращаются
в ноль. Это условие эквивалентно обращению
в ноль дифференциала функции
в данной точке, а также равносильно
горизонтальности касательной гиперплоскости
к графику
функции.
Это условие является необходимым (но
не достаточным) для того, чтобы внутренняя
точка области
могла быть точкой локального
минимума или
максимума функции.
,
называется точка, в которой все её частные
производные обращаются
в ноль. Это условие эквивалентно обращению
в ноль дифференциала функции
в данной точке, а также равносильно
горизонтальности касательной гиперплоскости
к графику
функции.
Это условие является необходимым (но
не достаточным) для того, чтобы внутренняя
точка области
могла быть точкой локального
минимума или
максимума функции.
Тест второй производной для функции одной переменной предоставляет метод определения того, возникает ли экстремум в критической точке функции. При распространении этого результата на функцию двух переменных возникает проблема, связанная с тем, что на самом деле существует четыре различных частных производных второго порядка, хотя равенство смешанных частных сокращает это число до трех.Тест второй производной для функции двух переменных, сформулированный в следующей теореме, использует дискриминант \ (D \) , который заменяет \ (f » (x_0) \) во втором тесте производной для функции одна переменная.
Чтобы применить тест второй производной, необходимо сначала найти критические точки функции. Вся процедура состоит из нескольких этапов, которые описаны в стратегии решения проблем.
Пример \ (\ PageIndex {2} \): использование теста второй производной
Найдите критические точки для каждой из следующих функций и используйте тест второй производной, чтобы найти локальные экстремумы:
- \ (f (x, y) = 4x ^ 2 + 9y ^ 2 + 8x − 36y + 24 \)
- \ (g (x, y) = \ dfrac {1} {3} x ^ 3 + y ^ 2 + 2xy − 6x − 3y + 4 \)
Решение
а. Шаг 1 стратегии решения проблем включает в себя поиск критических точек \ (f \). Для этого мы сначала вычисляем \ (f_x (x, y) \) и \ (f_y (x, y) \), затем устанавливаем каждое из них равным нулю:
\ [\ begin {align *} f_x (x, y) & = 8x + 8 \\ [4pt] f_y (x, y) & = 18y − 36. \ end {align *} \]
Приравнивая их к нулю, получаем систему уравнений
\ [\ begin {align *} 8x + 8 & = 0 \\ [4pt] 18y − 36 & = 0. \ end {align *} \]
Решение этой системы — \ (x = −1 \) и \ (y = 2 \).2 = 144. \)
Шаг 3 указывает, что нужно применить четыре случая теста для классификации поведения функции в этой критической точке.
Поскольку \ (D> 0 \) и \ (f_ {xx} (- 1,2)> 0, \), это соответствует случаю 1. Следовательно, \ (f \) имеет локальный минимум в \ ((- 1 , 2) \), как показано на следующем рисунке.
Рисунок \ (\ PageIndex {5} \): Функция \ (f (x, y) \) имеет локальный минимум в \ ((- 1,2, −16). \) Обратите внимание на масштаб \ (y \) — ось на этом графике в тысячах.2−2x − 3 & = 0 \\ [4pt] (x − 3) (x + 1) & = 0. \ end {align *} \]
Следовательно, \ (x = −1 \) или \ (x = 3 \). Подставляя эти значения в уравнение \ (y = \ dfrac {3−2x} {2} \), получаем критические точки \ (\ left (−1, \ frac {5} {2} \ right) \) и \ ( \ left (3, — \ frac {3} {2} \ right) \).
Шаг 2 включает вычисление вторых частных производных от \ (g \):
\ [\ begin {align *} g_ {xx} (x, y) & = 2x \\ [4pt] g_ {xy} (x, y) & = 2 \\ [4pt] g_ {yy} (x, у) & = 2. \ end {align *} \]
Затем мы находим общую формулу для \ (D \):
\ [\ begin {align *} D (x_0, y_0) & = g_ {xx} (x_0, y_0) g_ {yy} (x_0, y_0) — \ big (g_ {xy} (x_0, y_0) \ big ) ^ 2 \\ [4pt] & = (2x_0) (2) −2 ^ 2 \\ [4pt] & = 4x_0−4.2 = 12−4 = 8. \ end {align *} \]
На шаге 3 отметим, что применение примечания к точке \ (\ left (−1, \ frac {5} {2} \ right) \) приводит к случаю \ (3 \), что означает, что \ (\ left (−1, \ frac {5} {2} \ right) \) — седловая точка. Применение теоремы к точке \ (\ left (3, — \ frac {3} {2} \ right) \) приводит к случаю \ (1 \), что означает, что \ (\ left (3, — \ frac {3 } {2} \ right) \) соответствует локальному минимуму, как показано на следующем рисунке.
Рисунок \ (\ PageIndex {6} \) : Функция \ (g (x, y) \) имеет локальный минимум и седловую точку..Исчисление III — Абсолютные минимумы и максимумы
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Относительные минимумы и максимумы
- Множители Лагранжа
- Разделы
- Частные производные
- Несколько интегралов
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Эллипсы
- Гиперболы
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- Полиномиальные функции
- Делительные многочлены
- Нули / корни многочленов
- Графические полиномы
- Нахождение нулей многочленов
- Частичные дроби
- Опыт
- Отборочные
Найдите максимальное и минимальное значения примеров функций
Найдите максимальное и минимальное значения функции Примеры:
В этом разделе мы увидим несколько примеров проблем поиска максимального и минимального значений функции.
Значение функции в точке максимума называется максимальным значением функции, а значение функции в точке минимума называется минимальным значением функции.
- Различают данную функцию.
- пусть f ‘(x) = 0 и найдите критические числа
- Затем найдите вторую производную f’ ‘(x).
- Примените эти критические числа во второй производной.
- Функция f (x) является максимальной, когда f » (x) <0
- Функция f (x) минимальна, когда f » (x)> 0
- Чтобы найти максимальное и минимальное значение, нам нужно применить эти значения x в данной функции.
Нахождение максимальных и минимальных значений примеров функций
Вопрос 1:
Найдите максимальное и минимальное значение функции
2x 3 — 15x 2 + 36x + 18
Решение:
Пусть y = f (x) = 2x 3 — 15x 2 + 36x + 18
f ‘(x) = 2 (3x 2 ) — 15 (2x) + 36 (1) + 0
f’ (x) = 6x² — 30x + 36
f ‘(x) = 0
6x² — 30x + 36 = 0
÷ на 6 => x² — 5 x + 6 = 0
х — 2 = 0 х = 2 | х — 3 = 0 х = 3 |
f ‘(x) = 6x² — 30x + 36
f’ ‘(x) = 6 (2x) — 30 (1) + 0
f’ ‘(x) = 12 x — 30
Положим x = 2
f » (2) = 12 (2) — 30
= 24-30
f » (2) = -6 <0 Максимум
Чтобы найти максимальное значение, применим x = 2 в данной функции.
f (2) = 2 (2) ³ — 15 (2) ² + 36 (2) + 18
= 2 (8) — 15 (4) + 72 + 18
= 16 — 60 + 72 + 18
= 106 — 60
f (2) = 46
Положим x = 3
f » (3) = 12 (3) — 30
= 36 — 30
f » (3) = 6> 0 Минимум
Чтобы найти минимальное значение, применим x = 3 в данной функции.
f (3) = 2 (3) ³ — 15 (3) ² + 36 (3) + 18
= 2 (27) — 15 (9) + 108 + 18
= 54 — 135 + 108 + 18
= 180 — 135
= 45
Следовательно, максимальное значение — 46, а минимальное — 45.
Вопрос 2:
Найдите максимальное и минимальное значение функции x 3 — 6 x 2 + 9 x + 1.
Решение:
Пусть y = f (x) = x 3 — 6 x 2 + 9 x + 1
f ‘(x) = 3x² — 6 (2x) + 9 (1) + 0
f’ (x) = 3x² — 12x + 9
f ‘(x) = 0
3x² — 12x + 9 = 0
÷ на 3 => x² — 4 x + 3 = 0
х — 1 = 0 х = 1 | х — 3 = 0 х = 3 |
f ‘(x) = 3x² — 12x + 9
f’ ‘(x) = 3 (2 x) — 12 (1) + 0
f’ ‘(x) = 6 x — 12
Положим x = 1
f » (1) = 6 (1) — 12
= 6 — 12
f » (1) = -6 <0 Максимум
Чтобы найти максимальное значение, применим x = 1 в исходной функции
f (x) = x³ — 6 x² + 9 x + 1
f (1) = (1) ³ — 6 (1) ² + 9 (1) + 1
= 1-6 (1) + 9 + 1
= 1-6 + 10
= 11-6
= 5
Положим x = 3
f » (3) = 6 (3 ) — 12
= 18 — 12
f » (3) = 6> 0 Минимум
Чтобы найти минимальное значение, применим x = 3 в исходной функции
f (x) = x 3 — 6x 2 + 9x + 1
f (3) = 3 3 — 6 (3) 2 + 9 (3) + 1
= 27 — 6 (9) + 27 + 1
= 54 + 1–54
= 1
Следовательно, максимальное значение равно 5, а минимальное значение — 1.
Мы надеемся, что после ознакомления с изложенным выше студенты поняли, как найти максимальное и минимальное значение функции.
Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейным неравенством
ЗадачиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Теорема Пифагора задачи со словами
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
с использованием длинного корня видение
Л.Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении в степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
.2 + 3 = 3 Следовательно, Минимальное значение = 3 Максимального значения нет Пример 6.5, 1 (Метод 1) Найдите максимальное и минимальное значения, если таковые имеются, следующих функций, заданных формулой (ii) f (𝑥) = 9𝑥2 + 12𝑥 + 2 Нахождение f ’(x) е (𝑥) = 9𝑥2 + 12𝑥 + 2 Diff. w.r.t 𝑥 f ’(𝑥) = 18𝑥 + 12 f ’(𝑥) = 6 (3𝑥 + 2) Полагая f ’(𝒙) = 𝟎 6 (3𝑥 + 2) = 0 3𝑥 + 2 = 0 3𝑥 = −2 𝑥 = (- 2) / (3) Следовательно, 𝑥 = (- 2) / 3 — точка минимума функции f (𝑥). Нахождение минимального значения f (𝑥) при 𝑥 = (- 2) / 3 е (𝑥) = 9𝑥 ^ 2 + 12𝑥 + 2 Положив 𝑥 = (- 2) / 3 е (𝑥) = 9 ((- 2) / 3) ^ 2 + 12 ((- 2) / 3) + 2 = 9 (4/3) −12 (2/3) + 2 = −2 Таким образом, Минимальное значение f (𝒙) = — 𝟐 Нет максимального значения Пр. 6.2 + 12𝑥 + 2) / 𝑑𝑥 f ’(𝑥) = 18𝑥 + 12 f ’(𝑥) = 6 (3𝑥 + 2) Полагая f ’(𝒙) = 𝟎 6 (3𝑥 + 2) = 0 3𝑥 + 2 = 0 3𝑥 = −2 𝑥 = (- 2) / 3 В поисках f ’’ (𝒙) f ’(𝑥) = 6 (3𝑥 + 2) Снова diff w.r.t 𝑥 f ’’ (𝑥) = 𝑑 (6 (3𝑥 + 2)) / 𝑑𝑥 f ’’ (𝑥) = 6 𝑑 (3𝑥 + 2) / 𝑑𝑥 f ’’ (𝑥) = 6 (3 + 0) f ’’ (𝑥) = 6 (3) f ’’ (𝑥) = 18 Итак, f ’’ ((- 2) / 3) = 18 Поскольку f ’’ (𝑥)> 0 для = (- 2) / 3 𝑥 = (- 2) / 3 — точка локальных минимумов Нахождение минимального значения Положив 𝑥 = (- 2) / 3 в f (𝑥) е (𝑥) = 9𝑥2 + 12𝑥 + 2 е ((−2) / 3) = 9 ((- 2) / 3) ^ 2 + 12 ((- 2) / 3) +2 = 9 (4/9) +12 ((- 2) / 3) +2 = 4−8 + 2 = −2 Следовательно, минимальное значение = –2 Нет максимального значения Пр. 6.2 = 0 Показать больше .
Leave A Comment