Переходные неравенства: онлайн калькулятор | BBF.RU
Понятие неравенство связано со сравнением двух числовых объектов или алгебраических выражений. Смысл неравенства познается вместе со смыслом таких определений как больше или меньше, выше или ниже, дороже или дешевле, дальше или ближе, холоднее или теплее.
Определение неравенства
Два любых числа или алгебраических выражения, которые соединены знаками отношения «больше» (>), «меньше» (<), «больше либо равно» (≥), «меньше либо равно» (≤) или «неравно» (≠), образуют неравенства. Знаки неравенства в их сегодняшнем виде предложил английский математик Томас Гарриот, который работал над развязыванием систем неравенств и опубликовал свои труды в печати. Обозначения «>» и «<» приглянулись не только математикам, но и книгопечатникам, так как знаки представляли собой просто перевернутую на 90 градусов литеру V.
Существует два фундаментальных класса неравенств. Неравные выражения со знаками «больше» и «меньше» считаются строгими и записываются как:
5 > 3 или 34 < 56
Нестрогие неравенства — это соотношения со знаком равно, которые обычно используются в буквенных неравенствах, когда значение одного аргумента неизвестно. Например, в выражении:
Например, в выражении:
x + 3 ≥ 4,
при x = 1 неравенство тождественно и выглядит как 4 = 4, а при всех x > 1 выражение также тождественно и принимает выражения 5 > 4, 6 > 4 и так далее.
При решении неравенств с неизвестными строгие и нестрогие знаки крайне важны при определении области допустимых значений функции. Например, если x > 3, то это означает, что он хоть на одну миллиардную долю, но больше 3, следовательно, тройка никогда не входит в область допустимых значений. При нестрогом неравенстве x≥3 включает в диапазон решений собственно тройку и все, что больше нее.
Виды неравенств
Выражения вида a > b и c > d называются неравенствами одинакового смысла. Такое название выражения получили из-за одинаковых знаков. Если же выражения выглядят как a > b и c < d, то такие числовые объекты считаются неравенствами противоположного смысла. К примеру, два выражения x > 3 и y > 4 считаются неравенствами одного смысла, а вот x > 3 и y < 5 — противоположного.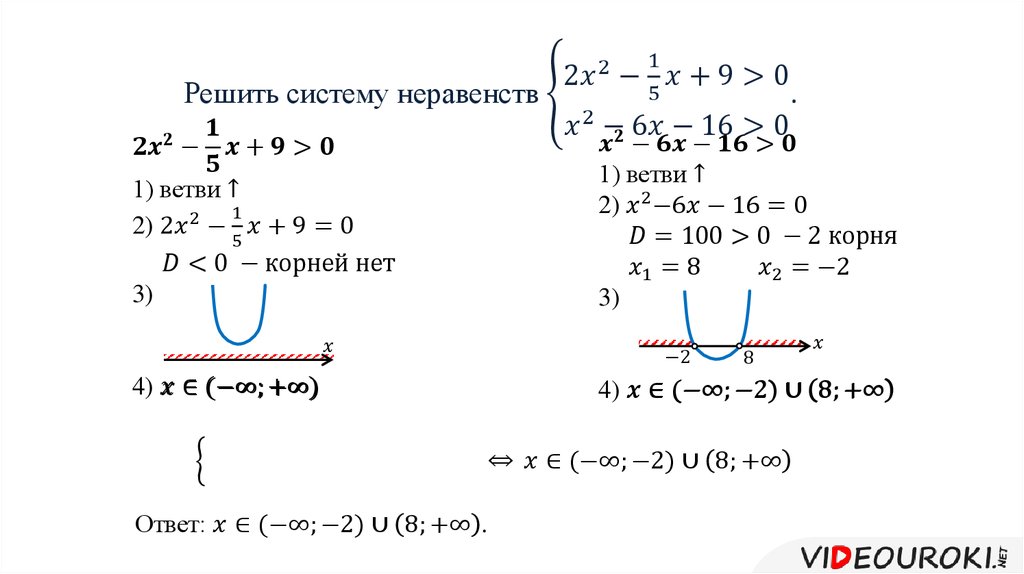
Буквенные неравенства противоположного смысла могут объединяться в двойные. Например, если x > 3 и x < 5, то такое выражение можно переписать как двойное неравенство 3 < x < 5. Это означает, что аргумент функции лежит строго в пределах от 3 до 5.
Свойства неравенств
Неравенства обладают несколькими полезными свойствами. Рассмотрим подробнее.
Свойство №1
Если a > b, то a + c > b + c. Если к обеим сторонам неравного соотношения прибавить одно и то же число или алгебраическое выражение, то знак неравенства не изменится.
Пример
Пусть есть выражение 10 > 5. Добавим к каждой части по 5. Получим 15 > 10, что верно. Добавим к каждой части по отрицательному числу, например, по — 2. Получим 8 > 3, и вновь верно. Точно также можно добавлять неизвестные аргументы и целые полиномы.
Свойство №2
Если a > b и n > 0, то a×n > b×n. Если обе части неравного соотношения умножить на одно и то же положительное число, то знак останется прежним.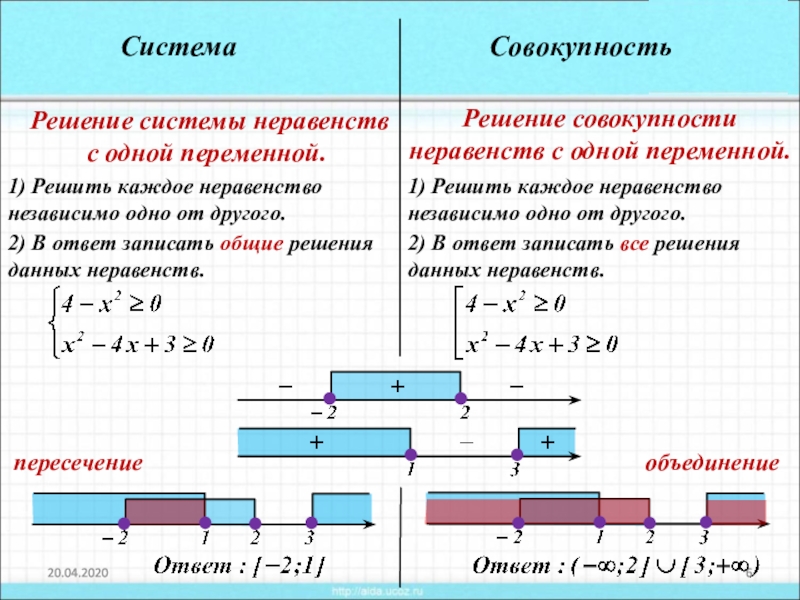
Пример
Вновь посмотрим на числовое соотношение 10 > 5. Примем n = 2 и умножим обе части выражения на n. Получим 20 > 10. Очевидно, что все сходится.
Свойство №3
Если a < b и n < 0, то a × n > b × n. Если обе стороны неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Пример
Пусть у нас есть неравенство 10 > 5 и n = -2. Умножим обе части на минус 2 и получим, что -20 < -10. С отрицательными числами не всегда очевидно, ведь даже при сравнении температуры мы говорим, что мороз «увеличился», в то время как показатели на градуснике уменьшились. Тем не менее минус 20 явно меньше минус 10.
Свойство №4
Если a > b и b > c, то верно выражение a > c. Такое выражение называется переходным неравенством, и наш калькулятор работает именно с такими числовыми объектами. Задаваясь значениями переменных a, b, c мы можем составить переходное неравенство, которое соответствует свойству всех числовых соотношений.
Пример
Допустим есть выражение 10 > 5 и 5 > 3. В этом случае a = 10, b = 5, c = 3. Согласно четвертому свойству в результате получится, что a > c или 10 > 3. Вполне логично.
Наша программа представляет собой калькулятор, определяющий соотношения чисел в качестве переходного неравенства. Для работы с онлайн-инструментом требуется ввести значения a, b и c, после чего программа решит, составляют ли введенные значения переходное неравенство или нет.
Заключение
Неравные числовые или буквенные соотношения и их системы широко используются в самых разных прикладных науках. Например, изучение проблем макроэкономики осуществляется путем составления и решения систем нелинейных неравенств. Классические неравенства используются в высшей математике: неравенство Коши применяется при сравнении площадей, а неравенство Бернулли — для сравнения иррациональных чисел. Кроме того, существуют неравенства, которые являются однозначным способом доказательства существования некоторых объектов. Используйте наши инструменты для работы с переходными неравенствами.
Используйте наши инструменты для работы с переходными неравенствами.
Технология TI-Nspire CAS. Решение систем уравнений и неравенств, в том числе с параметром. Люблинская И.Е.
Автор: Люблинская Ирина Ефимовна, кандидат наук, College of Staten Island, City University of New York
Инновационная обучающая система TI-Nspire CAS от компании Texas Instruments, США, является единственным в мире технологическим продуктом, который включает в себя динамическую программу для изучения всех разделов школьной математики и лабораторию для работы с задачами по основным научным дисциплинам. Этот продукт объединяет в себе поддержку геометрии, анализа, алгебры, статистики и работу с физическими датчиками. При этом объединение приложений программы создано не по принципу коллекции (как у Автографа), а на основе общих форматов данных, допускающих обмен данным между приложениями.
Обучающую систему TI-Nspire CAS можно использовать на персональных компьютерах и учебных микрокомпьютерах в классах и дома.
 Микрокомпьютеры имеют небольшой цветной дисплей.
Микрокомпьютеры имеют небольшой цветной дисплей.Помимо программного обеспечения для изучения предметов этот продукт включает в себя систему TI-Nspire Navigator для поддержки локальной беспроводной сети между компьютером учителя и микрокомпьютерами учеников. Это позволяет учителю видеть и оценивать работу каждого ученика в реальном времени, создавать, рассылать и собирать тесты и задания для учащихся, а также предоставлять им возможность демонстрировать свою работу всему классу со своего микрокомпьютера через компьютер учителя. С помощью программы также можно создавать динамические презентации и проигрывать их специальным бесплатным плейером.
Полный программный продукт TI Nspire CAS состоит из нескольких компонентов
Для учеников:
1. Программная среда «Математика и естественные науки». TI-Nspire CAS версия ученика этой среды включает:
- Cистему компьютерной алгебры, динамическую геометрию, программу работы с графиками функций, электронными таблицами, программу поддержки статистики, интерактивный блокнот и физическую лабораторию (датчики продаются отдельно).

- Cредства создания мультимедийных документов, например, тексты, гиперссылки, видео и изображения; средства создания портфолио.
- Cреду программирования на языке Lua.
2. Цветной учебный микрокомпьютер TI-Nspire CAS CХ с набором функций.
Для учителей:
1. ПО «Математика и естественные науки» TI-Nspire CAS версия учителя, включающая всё, что включено в версию ученика, а также приложение по созданию контрольных и самостоятельных работ и тестовых вопросов в различных форматах.
2. Станции для зарядки и передачи данных.
3. ПО TI-Nspire Navigator CAS для учебных микрокомпьютеров (подсоединение через беспроводную связь), включающее:
- ПО «Математика и естественные науки» TI-Nspire CAS, версия учителя.
- Систему организации работы с классом — электронный журнал (портфолио), менеджер компьютеров (или учебных микрокомпьютеров) учеников для обмена документами, контроля работы учащихся во время урока, демонстрации их работ в реальном времени и т.
 д.
д.
4. TI-Nspire Document Player — бесплатная ограниченная версия программы для «проигрывания» документов без лицензионной копии программы возможного только для документов, не требующих ввода данных в программу или построений.
TI Nspire CX CAS включает систему компьютерной алгебры, динамическую геометрию, программу работы с графиками функций, программу поддержки статистики и физическую лабораторию
В 2006 году впервые TI-Nspire CAS технологии были апробированы в Европе и Северной Америке. В 2007 TI-Nspire CAS технологии появились на рынке. С тех пор эти технологии нашли применение в школах стран Северной Америки (США, Канада и Мексика), Южной Америки (Колумбия и Чили), Австралии и Новой Зеландии, Азии (Китай и Индия), Европы (10 стран) и Африки (Марокко). Апробация этих технологий в России началась в августе 2011 года в четырёх школах Санкт-Петербурга: Лицее «Физико-техническая школа» Калининского района, Гимназии №177 Красногвардейского района, ГОУ СОШ №558 с углубленным изучением математики Выборгского района, Школе №597 — лицей компьютерных технологий Приморского района.
Учителя — участники пилотного проекта положительно отзываются о технологии, вполне способной заменить несколько отдельных пакетов. Школьники легко осваивают микрокомпьютеры и свободно используют их возможности. На основе опыта работы учителей-участников проекта появилась реальная возможность эффективного внедрения этих технологий для изучения математики и естественных наук в российских школах.
Решение систем уравнений и неравенств, в том числе с параметром
В качестве первого примера рассмотрим графическое исследование количества решений системы двух линейных уравнений. Сначала в программе строятся графики двух линейных функций
Затем ученикам предлагается использовать инструменты вращения и перемещения для манипуляций с графиком одной из прямых (в приведенном примере положение прямой 1 фиксируется, так что ученики могут менять график только прямой 2). На основе наблюдений ученики выдвигают гипотезу об условиях, при которых система двух линейных уравнений не имеет решений, имеет одно решение или имеет бесконечное множество решений.
При вращении по умолчанию центром поворота является точка пересечения прямой с осью ординат. Поэтому в уравнении прямой динамически меняется угловой коэффициент, а свободный член остается неизменным
Соответственно, при перемещении меняется свободный член, в то время как угловой коэффициент остаётся постоянным.
В процессе компьютерного эксперимента ученики определяют условия, при которых две прямые имеют только одну общую точку, не пересекаются или совпадают. Благодаря динамическому характеру приложения ученики могут рассмотреть различные ситуации и убедиться в том, что:
- Для пересечения прямых в одной точке необходимо и достаточно того, чтобы угловые коэффициенты прямых были разными.
- Если угловые коэффициенты прямых равны, то прямые параллельны или совпадают в зависимости от свободных членов уравнений.
В этом примере мы использовали инструменты движений для изменения графика одной из функций. В следующем примере мы рассмотрим систему уравнений с параметром, который мы зададим при помощи слайдера. Перед учениками ставится задача исследования количества решений системы уравнений в зависимости от значения параметра а. Затем ученики находят решения системы уравнений в каждом случае
Перед учениками ставится задача исследования количества решений системы уравнений в зависимости от значения параметра а. Затем ученики находят решения системы уравнений в каждом случае
При вращении в уравнении прямой динамически меняется угловой коэффициент
При использовании слайдера ученики исследуют взаимное расположение ломаной и окружности и убеждаются в том, что система может не иметь решений, если график ломаной не пересекает окружность.
Система может иметь только одно решение, когда одна из веток графика функции является касательной к окружности.
Система может иметь два решения, когда одна из веток графика функции пересекает окружность дважды, а другая ветка ее не пересекает, или каждая ветка графика пересекает ее только один раз.
Для аналитического решения ученики сначала должны найти значение параметра а, при котором ветви графика функции являются касательными к окружности. Поскольку при этом условии расстояние от центра окружности до точки касания равно радиусу окружности, достаточно решить уравнение. Это приводит к условиям a= или а = . После получения аналитического решения системы уравнений его можно проверить, используя приложение Калькулятор. В данном случае для получения общего решения мы использовали букву b (при использовании параметра а программа подставляет текущее численное значение для параметра и выдаёт только частное решение).
Это приводит к условиям a= или а = . После получения аналитического решения системы уравнений его можно проверить, используя приложение Калькулятор. В данном случае для получения общего решения мы использовали букву b (при использовании параметра а программа подставляет текущее численное значение для параметра и выдаёт только частное решение).
Можно также проверить условие существования решения.
При подстановке b= (или b = ) в полученные выражения для х и у можно также подтвердить, что в этом случае система имеет одно решение.
В заключении рассмотрим два примера заданий по типу С3 и С5 из ЕГЭ. Сначала рассмотрим решение системы неравенств . Построим графики функций f1(x) = и f2(x) =
Для определения промежутков, на которых обе функции одновременно не положительны, найдем нули функции. Из графика следует, что оба неравенства выполняются, когда
Другой способ графического решения данной системы неравенств основан на построении постоянной функции с областью определения, ограниченной условиями, наложенными неравенствами. Если значение функции равно нулю, то на графике будут выделены только значения х, удовлетворяющие условиям системы неравенств
Если значение функции равно нулю, то на графике будут выделены только значения х, удовлетворяющие условиям системы неравенств
Это решение можно проверить в приложении Калькулятор.
Нужно отметить, что программа выдает правильный ответ, и это может помочь ученику найти ошибки в своём решении, если ответ, полученный при решении задачи на бумаге, не совпадает с выводом программы.
В последнем примере мы рассмотрим задание по типу С5, в котором ученику требуется найти все значения а, при каждом из которых система не имеет решений.
В данном случае мы опять используем слайдер для определения а и воспользуемся графиком нулевой функции, определённой на интервале, заданном системой неравенств. Изменяя значение а, убеждаемся в том, что на интервале [-3, -1] решений нет.
Демонстрационную 90-дневную версию учителя предоставляем бесплатно по запросу на эл.почту.
Calculators-Online.ru
Бесплатный онлайн калькулятор вершин
бесплатный онлайн-калькулятор вершин
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор угловых точек| Линейное программирование
Этот калькулятор угловых точек поможет вам решить задачу линейного программирования и найти угловых точек допустимой области . Он также найдет угловую точку, где максимум или минимальное значение целевой функции .
Если какой-либо из этих терминов вызывает недоумение, не волнуйтесь. Мы здесь, чтобы сделать вашу жизнь проще😉. В этой статье мы обсудим линейное программирование , вычисление и поиск допустимых областей, нахождение угловых точек алгебраически и графически , а также максимизацию или минимизацию целевой функции . Так что, пожалуйста, возьмите чашку кофе ☕️ и давайте вместе разберемся с математикой угловых точек!
Так что, пожалуйста, возьмите чашку кофе ☕️ и давайте вместе разберемся с математикой угловых точек!
Задача линейного программирования (LPP)
Модель оптимизации с ограничениями — это математическая модель, которая находит лучшее решение (или оптимальное решение ), которое удовлетворяет заданному набору ограничений.
Модель оптимизации с ограничениями состоит из трех основных частей:
Переменные решения — это переменные в проблеме или системе, которые мы должны оптимизировать. Их представляют алгебраические символы, например, xxx,yyy или x1x_1x1, x2x_2x2 и т. д.
Целевая функция — это оценивающий критерий , который мы должны максимизировать или минимизировать. Это функция переменных решения и, возможно, мера прибыли, времени обработки и т. д., которую мы должны максимизировать или минимизировать.

Ограничения — это система равенств или неравенств, представляющая любые ограничения, связанные с технологией, физикой, экономикой и т. д. Например, ограничение может ограничивать количество денег, затрачиваемых в каждом процессе, допустимый вес в каждом мешке и т. д. Оптимальное решение задачи должно удовлетворять всем ограничениям.
Линейная программа представляет собой модель оптимизации с ограничениями, которая отвечает следующим требованиям:
Переменные решения должны быть непрерывными в заданном диапазоне.Математически мы можем записать задачу линейного программирования (LPP) как:
Развернуть/свернуть P=pxx+pyy\scriptsize \text{Развернуть/свернуть} P = p_x x + p_y y Развернуть/свернуть P=pxx+pyy
≤subject to a1x+b1y=c1≥≤a2x+b2y=c2≥⋮≤anx+bny=cn≥\scriptsize\begin{align*}
&\leq\\
\text{при условии}\kern{4em} a_1 x + b_1 y &= c_1\\
& \geq\\\\
&\leq\\
a_2 x + b_2 y &= c_2\\
& \geq\\
\vdots\kern{1.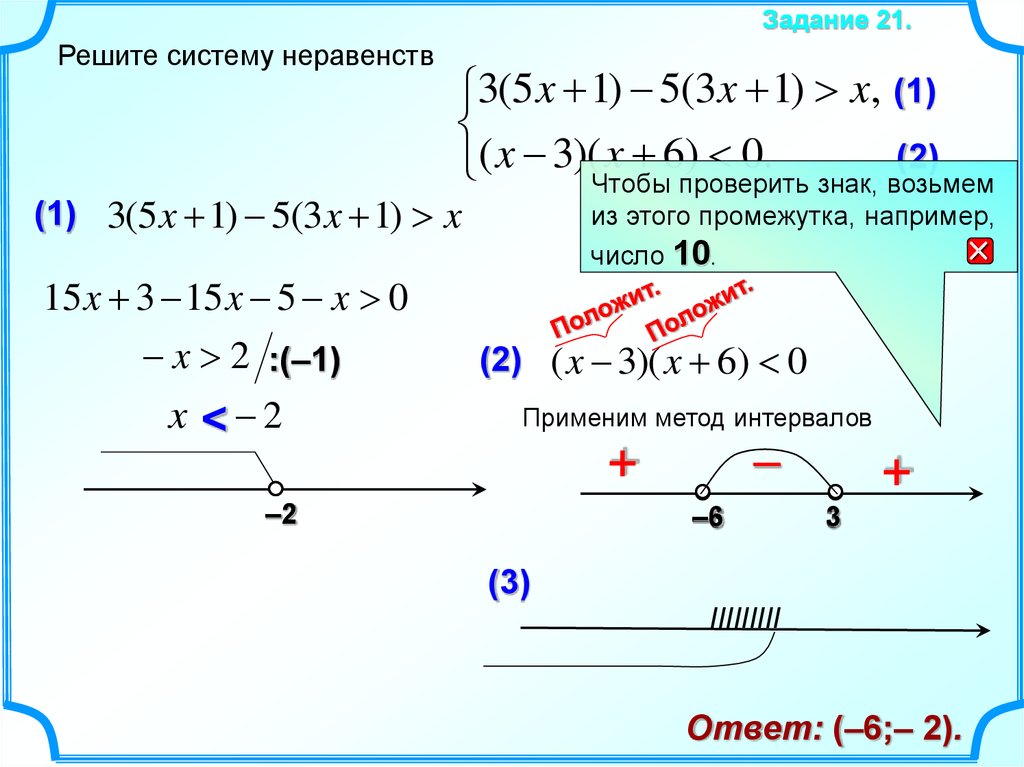 5em}&\\
&\leq\\
a_n x + b_n y &= c_n\\
& \geq\\
\end{align*}при условии a1x+b1ya2x+b2y⋮anx+bny≤=c1≥≤=c2≥≤=cn≥
5em}&\\
&\leq\\
a_n x + b_n y &= c_n\\
& \geq\\
\end{align*}при условии a1x+b1ya2x+b2y⋮anx+bny≤=c1≥≤=c2≥≤=cn≥
, где:
- PPP – Целевая функция ;
- px,pyp_x, p_ypx,py – Коэффициенты переменных решения в целевой функции ;
- x,yx,yx,y – Переменные решения ;
- a1,a2,an,b1,b2,bna_1,a_2, a_n, b_1,b_2,b_na1,a2,an,b1,b2,bn – Коэффициенты из переменных решения в ограничения ; и
- c1,c2,cnc_1, c_2, c_nc1,c2,сп – Константы в равенстве или неравенстве, используемые для выражения ограничений .
Обычно переменные решения должны быть неотрицательными , т. е. x≥0x\geq0x≥0, y≥0y\geq0y≥0. Это также ограничения модели, и мы можем выразить их, выбрав соответствующие значения коэффициентов ana_nan и bnb_nbn в ограничениях.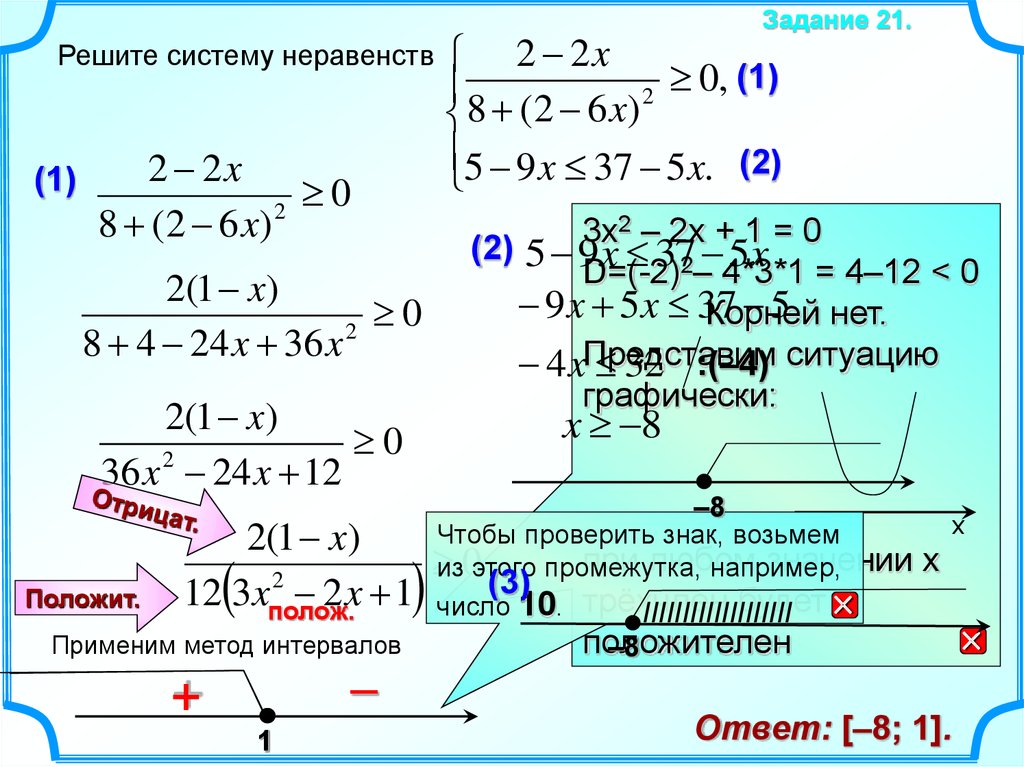
Возможные области и угловые точки
Набор точек, удовлетворяющих ограничениям LPP, называется допустимый набор . Если мы нанесем все ограничения на график, область, пересекающая все эти неравенства, будет содержать допустимое множество. Мы называем эту область допустимой областью .
Возможная область (заштрихована) и ее угловые точки на графике. Обратите внимание, что каждая точка допустимой области удовлетворяет всем ограничениям.угловых точек (или крайних точек) допустимой области являются точками пересечения двух (или более) ограничений. Возможная область может быть ограниченной или неограниченной, но должна иметь по крайней мере одну угловую точку.
Хотя каждая точка в допустимом наборе технически является решением для LPP, оптимальное решение — это такое решение, которое должно максимизировать или минимизировать целевую функцию . В линейном программировании хотя бы одна угловая точка является оптимальным решением .
В линейном программировании хотя бы одна угловая точка является оптимальным решением .
Как найти угловые точки алгебраически
Попробуем понять, как найти угловые точки алгебраически на примере. Рассмотрим следующий LPP:
Максимальное P=30x+40y\scriptsize \text{Максимальное}\kern{4.4em} P = 30 x + 40 yМаксимальное P=30x+40y
при условии 2x+3y≤18x+y≤9x+2y≤16x ≥0y≥0\scriptsize\begin{выравнивание*} \text{при условии}\kern{5em} 2 x + 3 y &\leq 18\\ х + у &\leq 9\\ х+2у &\leq 16\\ х& \geq 0\\ у& \geq 0 \end{align*}subject to 2x+3yx+yx+2yxy≤18≤9≤16≥0≥0
Мы можем найти угловые точки алгебраически, выполнив следующие шаги:
- Преобразовать в неравенства в ограничениях на равенства . Получим следующую систему линейных уравнений:
2x+3y=18x+y=9x+2y=16x=0y=0\kern{4.8em}\scriptsize\begin{align*} 2 х + 3 у &= 18\\ х + у &=9\\ х+2у &=16\\ х& = 0\\ у& = 0 \end{align*}2x+3yx+yx+2yxy=18=9=16=0=0
- Решите этих линейных уравнений, взяв набор любых двух уравнений одновременно, чтобы найти пересекающихся точка , удовлетворяющая обоим уравнениям.
 Проиллюстрируем это для первых двух уравнений: 9{nd}\text{ уравнение}\\
Подставив y=0 во второе уравнение
Проиллюстрируем это для первых двух уравнений: 9{nd}\text{ уравнение}\\
Подставив y=0 во второе уравнениеx=9\kern{6em}\scriptsize x = 9x=9
Следовательно, точка (9,0)(9,0)(9,0) является решением для уравнения 2x+3y=182x+3y=182x+3y=18 и x+y=9x+y=9x+y=9. Точно так же найдите решения для любого другого набора уравнений, чтобы получить их точки пересечения. Кроме того, вы можете использовать наш калькулятор системы уравнений или калькулятор метода подстановки, чтобы найти решения быстрее и проще!
Решения (точки пересечения) для каждой системы линейных уравнений.
Equations
Intersecting point
2x+3y=182x+3y=182x+3y=18,x+y=9x+y=9x+y=9
(9,0)(9,0)(9,0)
2x+3y=182x+3y=182x+3y=18,x+2y=16x+2y=16x+2y=16
(-12,14)(-12,14)(-12,14)
2x+3y=182x+3y=182x+3y=18,x=0x=0x=0
(0,6)(0,6)(0,6)
2x+3y=182x+3y=182x+3y=18,y=0y=0y=0
(9,0)(9,0)(9,0)
3
x+y=9x+y=9x+y=9, x+2y=16x+2y=16x+2y=16
(2,7)(2,7)(2,7)
х+у=9х+у=9х+у=9, х=0х=0х=0
(0,9)(0,9)(0,9)
х +y=9x+y=9x+y=9, y=0y=0y=0
(9,0)(9,0)(9,0)
x+2y=16x +2у=16х+2у=16, х=0х=0х=0
(0,8)(0,8)(0,8)
х+2у=16х+2у=16х+2у=16, у=0у=0у=0
(16,0)(16,0)(16,0) x=0x=0x=0, y=0y=0y=0
(0,0)(0,0) (0,0)
- Примените неравенство ограничения к этому набору точек пересечения и извлеките точки, которые удовлетворяют всем заданным неравенствам.
 Эти точки наши угловых точек ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит за пределами допустимой области .
Эти точки наши угловых точек ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит за пределами допустимой области .
Например, точка (9,0)(9,0)(9,0) удовлетворяет всем ограничениям:
2(9)+3(0)=18≤18(9)+(0) =9≤9(9)+2(0)=9≤16(9)=9≥0(0)=0≥0\scriptsize\begin{align*} 2 (9) + 3 (0) &= 18 \leq 18\\ (9) + (0) &=9 \leq 9\\ (9)+2(0) &=9 \leq16\\ (9)& = 9 \geq 0\\ (0)& = 0 \geq 0 \end{выравнивание*}2(9)+3(0)(9)+(0)(9)+2(0)(9))(0)=18≤18=9≤9=9≤16=9≥0=0≥0
Следовательно, (9,0)(9,0)(9,0) является угловой точкой . С другой стороны, точка (−12,14)(-12,14)(−12,14) не удовлетворяет ограничению x≥0x\geq0x≥0 и, следовательно, лежит вне возможных регион .
Проверьте свое понимание, применив ограничения для оставшихся точек, чтобы получить оставшиеся угловые точки. Вы можете проверить свой ответ по таблице угловых точек в конце следующего раздела.

Как графически найти угловые точки неравенств
Давайте продолжим использовать ту же задачу LPP, которую мы представили в предыдущем разделе. Чтобы графически найти угловые точки допустимой области, выполните следующие действия:
- Преобразуйте неравенства в ограничениях в равенства . Мы получим следующие линейных уравнения :
2x+3y=18x+y=9x+2y=16x=0y=0\kern{4.8em}\scriptsize\begin{align*} 2 х + 3 у &= 18\\ х + у &=9\\ х+2у &=16\\ х& = 0\\ у& = 0 \end{align*}2x+3yx+yx+2yxy=18=9=16=0=0
- Постройте эти линии на графике . Одним из простых способов является нахождение x- и y-пересечений . Чтобы получить точку пересечения x для линии 2x+3y=182x+3y=182x+3y=18, подставьте y=0y=0y=0; мы получаем х=9х=9х=9. Следовательно, (9,0)(9,0)(9,0) является точкой пересечения по оси x.
 Точно так же подставьте x=0x=0x=0, чтобы получить y-пересечение (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор точки пересечения y, чтобы найти точки пересечения из уравнения прямой.
Точно так же подставьте x=0x=0x=0, чтобы получить y-пересечение (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор точки пересечения y, чтобы найти точки пересечения из уравнения прямой.
- Затенение область графа, которая удовлетворяет всем ограничениям . Это возможная область LPP. Это пересечение всех неравенств ограничений.
- Извлечь угловых точек из вершин из граница допустимой области . Полученные таким образом угловые точки:
Угловые точки допустимой области.
Corner points
(9,0)(9,0)(9,0)
(0,6)(0,6)(0, 6)
(0,0)(0,0)(0,0)
Как найти оптимальное решение, используя угловые точки?
Оптимальное решение задачи линейного программирования будет иметь хотя бы одну из угловых точек.
 Чтобы найти оптимальное решение по угловым точкам, выполните следующие действия:
Чтобы найти оптимальное решение по угловым точкам, выполните следующие действия:- Оцените целевую функцию в каждой угловой точке .
- Если цель состоит в том, чтобы максимизировать целевую функцию , найти угол точки, которая дает наибольшее значение целевой функции .
- Если цель состоит в том, чтобы минимизировать целевую функцию , найти угловую точку , которая дает наименьшее значение целевой функции .
Помните, что можно найти несколько угловых точек, обеспечивающих оптимальное решение.
Оценим целевую функцию в нашем примере, чтобы найти оптимальное решение:
Угловая точка
P=30x+40yP = 30x+40yP=30x+40y
(9,0)(9,0)(9,0)
270270270
Maximum
(0,6) (0,6) (0,6)
240240240
(0,0) (0,0839
(0,0) (0,0) (0,0567
(0,0) (0,083
(0,0) (0,0836
(0,0) (0,0836
(0,0) (0,0836
(0,0).

000
Поскольку наша цель состояла в том, чтобы максимизировать P=30x+40yP = 30x+40yP=30x+40y, оптимальное решение равно 270270270 и находится в угловой точке (9,0)(9,0)(9,0).
Как использовать этот калькулятор угловых точек (онлайн-решатель LP)
Этот калькулятор угловых точек представляет собой простой инструмент для решения данного LPP путем нахождения угловых точек неравенств (или ограничений) и вычисления целевой функции . Он может обрабатывать две переменные решения и до пять ограничений :
- Введите коэффициенты pxp_xpx и pyp_ypy из целевая функция .
- Выберите , должен ли этот калькулятор линейного программирования минимизировать или максимизировать целевую функцию.

- Выберите количество ограничений в линейной программе.
- Введите коэффициенты aaa, bbb и ccc каждого ограничения .
- Этот калькулятор угловых точек создаст таблицу всех угловых точек , за которой следуют оптимальное решение путем вычисления целевой функции и ограничений.
💡 Совет: изо всех сил пытаетесь добавить неотрицательных (или неположительных ) ограничений на переменные решения? Вы можете сделать это, введя 000 и 111 в качестве переменной коэффициентов ! Например, чтобы применить ограничение x≥0x \geq 0x≥0, введите a1a_1a1 как 111, b1b_1b1 как 000 и c1c_1c1 как 000. Убедитесь, что вы выбрали правильный знак неравенства!
Если результаты не отображаются, значит, калькулятор не нашел угловых точек на основе введенных вами данных, и это неразрешимая задача .
 Попробуйте ослабить ограничения, чтобы создать достижимую область.
Попробуйте ослабить ограничения, чтобы создать достижимую область.Часто задаваемые вопросы
Какая точка допустимой области максимизирует целевую функцию?
максимальное (или минимальное) значение целевой функции должно встречаться в любой из угловых точек допустимой области . Чтобы определить эту точку, выполните следующие действия:
- Оцените целевую функцию в каждой угловой точке допустимой области.
- Определите максимальное среди этих расчетных значений. Точка угла , в которой встречается это значение, является точкой, в которой максимизирует целевую функцию .
В некоторых случаях можно найти более одной угловой точки , которая максимизирует целевую функцию.

- Примените неравенство ограничения к этому набору точек пересечения и извлеките точки, которые удовлетворяют всем заданным неравенствам.


 д.
д. 05.2004
05.2004 
 10.2003
10.2003 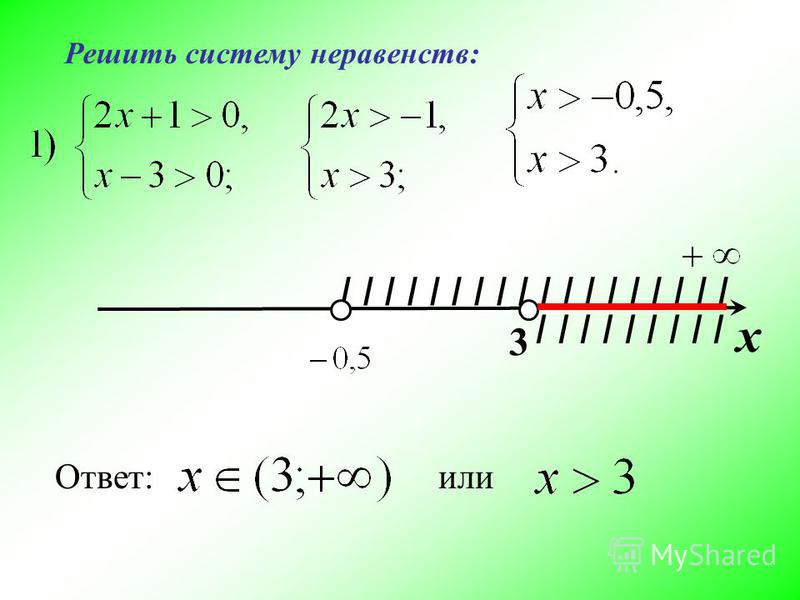 11.2001
11.2001  2001
2001  03.2002
03.2002  Я действительно рекомендую программу.
Я действительно рекомендую программу.
 Проиллюстрируем это для первых двух уравнений: 9{nd}\text{ уравнение}\\
Подставив y=0 во второе уравнение
Проиллюстрируем это для первых двух уравнений: 9{nd}\text{ уравнение}\\
Подставив y=0 во второе уравнение Эти точки наши угловых точек ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит за пределами допустимой области .
Эти точки наши угловых точек ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит за пределами допустимой области .
 Точно так же подставьте x=0x=0x=0, чтобы получить y-пересечение (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор точки пересечения y, чтобы найти точки пересечения из уравнения прямой.
Точно так же подставьте x=0x=0x=0, чтобы получить y-пересечение (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор точки пересечения y, чтобы найти точки пересечения из уравнения прямой. Чтобы найти оптимальное решение по угловым точкам, выполните следующие действия:
Чтобы найти оптимальное решение по угловым точкам, выполните следующие действия:
 Попробуйте ослабить ограничения, чтобы создать достижимую область.
Попробуйте ослабить ограничения, чтобы создать достижимую область.
Leave A Comment