Окружности с центрами в точках i и j пересекаются в точках а и в: Решение №3754 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB.

• 539 Решение задач ОГЭ по математике: вариант №4 задача №25 1654884780 1654885631
• 556 Решение задач ОГЭ по математике: вариант №3 задача №25 1654709820 1654712779
• 606 Решение задач ОГЭ по математике: вариант №2 задача №25 1654284300 1654285218
• 547 Решение задач ОГЭ по математике: задачи №24 варианты № 9, 10, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 25, 26, 30, 33, 34, 35, 36, 37, 38 1654023120 1654023755
• 520 Решение задач ОГЭ по математике: вариант №32 задача №24 1653937380 1653938818
• 614 Решение задач ОГЭ по математике: вариант №31 задача №24 1653836220 1654021624
• 627 Решение задач ОГЭ по математике: вариант №29 задача №24 1653755280 1653755874
• 429 Решение задач ОГЭ по математике: вариант №28 задача №24 1653678900 1653679577
• 455 Решение задач ОГЭ по математике: вариант №27 задача №24 1653644340 1653644799

Материал для подготовки к ОГЭ по математике

Опубликовано 15. 01.2020 — 21:49 — Пильщикова Татьяна Геннадиевна

Здесь вы можете скачать тренировочные варианты для подготовки к экзамену

Скачать:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

№ 1. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 метра от земли. Длина троса равна 4 метра. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

Слайд 2

№ 2 .Какой угол (в градусах) описывает минутная стрелка за 4 минуты?

Слайд 3

№3 . В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.

Слайд 4

№4 . Сторона равностороннего треугольника равна . Найти его медиану.

Слайд 5

№5. Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.

Слайд 6

№ 6 . В треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.

Слайд 7

№7 . Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.

Слайд 8

№ 8 Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Слайд 9

№9 На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.

Слайд 10

№10 На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.

Слайд 11

№ 11 Какие из следующих утверждений верны? Все диаметры окружности равны между собой. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. Любые два равносторонних треугольника подобны. №12. Какие из следующих утверждений верны? Все высоты равностороннего треугольники равны. Существуют три прямые, которые проходят через одну точку. Если диагонали параллелограмма равны, то он является ромбом.

Слайд 12

№ 13 Углы В и С треугольника ABC равны соответственно 71° и 79°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 8. № 14 . Окружности с центрами в точках I и J пересекаются в точках А и В, причём точки I и J лежат по одну сторону от прямой АВ. Докажите, что прямые АВ и IJ перпендикулярны. № 15 . Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 5 и MB =10. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Подготовка к ОГЭ. Окружность.

Слайд 2

Уровень А

Слайд 3

Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если МВ = 8 см, МС = 6 см, М D = 4 см. А В С D M A М ∙ МВ = СМ ∙ MD 8 4 6 A М ∙ 8 = 6 ∙ 4 A М = 3

Слайд 4

Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 147. А С В 0 Сумма углов четырехугольника — 360 Радиусы, проведенные в точку касания – перпендикулярны касательной. ВАС = 360 – 90 – 90 – 147 = 33

Слайд 5

Точки А и В делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на меньшую из дуг. А В 5х 7х 0 5х + 7х = 360 х = 30 АОВ = 5 ∙ 30 = 150

Слайд 6

Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см. А В С 1 8 15 0 Т.к. ОС АВ, то АС=ВС=9 по т. Пифагора ОС =

Слайд 7

Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 28. А В С 28 0 ОА АС ( как радиус, проведенный в точку касания ) — равнобедренный ( ОА=ОВ – как радиусы одной окружности )

Слайд 8

Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол ОСВ равен 39. А В 39 0 С — равнобедренный ( ОС=ОВ – как радиусы одной окружности ) или Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Слайд 9

Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см. А В С М К Р 4 3 6 Отрезки касательных, проведенных из одной точки равны. ВМ = ВК АМ = АР СР = СК 6 3 4 АВ = 10 АС = 7 ВС = 9 Р = 10 + 7 + 9 = 26

Слайд 10

Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см. А В С Центр описанной около п /у треугольника окружности лежит на середине гипотенузы. d = AC sinA =3/7 15 sinA = ВС/АС 3/7 = 15/АС АС = 35

Слайд 11

Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120, а расстояние от центра окружности до вершины этого угла равно 18 см. 0 Т.к. в вписанном треугольнике тупой угол, то этот треугольник лежит по одну сторону от центра окружности. А В С 120 ОВ = r = 18

Слайд 12

Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см. 0 А В 20 С 24 Т.к. ОК АС, то АК=КС=10 К по т. Пифагора ОС =

Слайд 13

Уровень В

Слайд 14

Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD , если АВ = 10 см, а расстояния от центра окружности до хорд АВ и CD равны соответственно 12 см и 5 см. А В X 1 2 5 0 C D 10 Y АХ = 5 по т. Пифагора ОА = ОА = ОС = 13 по т. Пифагора С Y = CD = 24

Слайд 15

Отрезки АВ и BC являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен 42. А В 42 0 С АСВ – вписанный угол, АОВ – соответствующий ему центральный АОВ = 180 – 42∙2=96 АСВ = 96 : 2 = 48

Слайд 16

В окружность вписан четырехугольник АВС D . Найдите угол АС D , если углы BAD и ADB равны соответственно 73 и 37.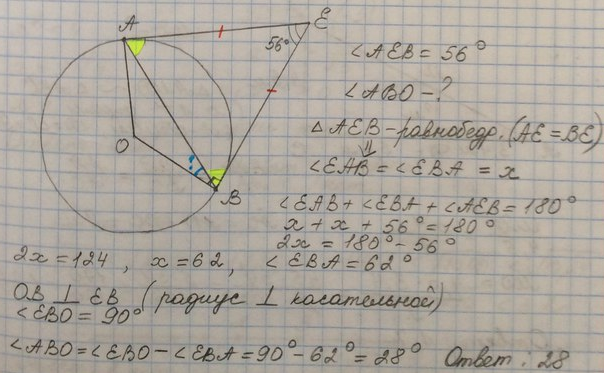 А В 37 С D 73 ABD : ABD = 180 – (73 + 37) = 70 АВ D = ACD – как вписанные углы, опирающиеся на одну дугу A С D = 70

Слайд 17

Окружность с центром О касается сторон угла с вершиной А, величина которого равна 40, в точках В и С. Найдите углы треугольника ВОС. А С В 0 АОВ – п /у (радиус, проведенный в точку касания, перпендикулярен касательной) АОВ = АОС по катету и гипотенузе (АО – общая, ОВ = ОС = r ) ОАВ = 20 ВОА= 70 ВОС = 140 ОВС = ОСВ = (180 – 140) : 2 = 20

Слайд 18

Отрезки АВ и АС являются хордами окружности с центром О. Найдите угол ВАС, если известно, что он является острым и что углы АВО и АСО равны соответственно 23 и 32. А В 23 0 С 32 Угол ВАС – острый, значит его стороны лежат по разные стороны от центра окружности. — равнобедренный — равнобедренный ОАВ = 23 ОАС = 32 ВАС = 23 + 32 = 55

Слайд 19

Радиус окружности, описанной около равнобедренного треугольника равен 5 см, а высота, проведенная к основанию, равна 8 см. Найдите площадь треугольника. 0 А В С 5 8 Н Т.к. треугольник р /б, то центр описанной окружности лежите на высоте, проведенной к основанию. ОА = ОВ = R = 5 ОН = 8 – 5 = 3 по т. Пифагора АН = АС = 8 S = ½ ∙ 8 ∙ 8 = 32

Слайд 20

Найдите площадь п /у трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность. 10 16 Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны. А В С D АВ + CD = ВС + AD = 26 Т.к. трапеция – п /у, то АВ = h S = 130

Слайд 21

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см. 5 А В D С Т.к. в параллелограмм можно вписать окружность, он является ромбом. Р = 4а Р = 4 ∙ 5 = 20

Слайд 22

В трапецию, сумма длин боковых сторон которой равна 16 см, вписана окружность. Найдите среднюю линию трапеции. Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны. В С D АВ + CD = ВС + AD = 16 К L = 8 А К L

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

ТЕОРИЯ ВЕРОЯТНОСТЕЙ КЛЮЧЕВЫЕ ЗАДАЧИ Готовимся к ОГЭ

Слайд 2

БРОСАНИЕ МОНЕТЫ

Слайд 3

1.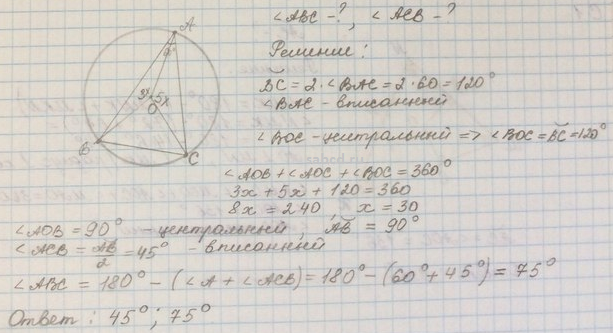 Монета брошена два раза. Какова вероятность выпадения одного «орла» и одной «решки»? Решение: При бросании одной монеты возможны два исхода – «орёл» или «решка». При бросании двух монет – 4 исхода (2*2=4): «орёл» — «решка» «решка» — «решка» «решка» — «орёл» «орёл» — «орёл» Один «орёл» и одна «решка» выпадут в двух случаях из четырёх. Р(А)=2:4=0,5. Ответ: 0,5.

Слайд 4

2. Монета брошена три раза. Какова вероятность выпадения двух «орлов» и одной «решки»? Решение: При бросании трёх монет возможны 8 исходов (2*2*2=8): «орёл» — «решка» — «решка» «решка» — «решка» — «решка» «решка» — «орёл» — «решка» «орёл» — «орёл» — «решка» «решка» — «решка» -«орёл» «решка» — «орёл» — «орёл» «орёл» — «решка» — «орёл» «орёл» — «орёл» — «орёл» Два «орла» и одна «решка» выпадут в трёх случаях из восьми. Р(А)=3:8=0,375. Ответ: 0,375.

Слайд 5

3. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу. Решение: При бросании четырёх монет возможны 16 исходов: (2*2*2*2=16): Благоприятных исходов – 1 (выпадут четыре решки). Р(А)=1:16=0,0625. Ответ: 0,0625.

Слайд 6

ИГРА В КОСТИ

Слайд 7

4. Определите вероятность того, что при бросании кубика выпало больше трёх очков. Решение: Всего возможных исходов – 6. Числа большие 3 — 4, 5, 6 . Р(А)= 3:6=0,5. Ответ: 0,5.

Слайд 8

5. Брошена игральная кость. Найдите вероятность того, что выпадет чётное число очков. Решение: Всего возможных исходов – 6. 1, 3, 5 — нечётные числа; 2, 4, 6 —чётные числа. Вероятность выпадения чётного числа очков равна 3:6=0,5. Ответ: 0,5.

Слайд 9

6. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение: У данного действия — бросания двух игральных костей всего 36 возможных исходов, так как 6² = 36. Благоприятные исходы: 2 6 3 5 4 4 5 3 6 2 Вероятность выпадения восьми очков равна 5:36 ≈ 0,14. Ответ: 0,14.

Слайд 10

7. Дважды бросают игральный кубик. В сумме выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.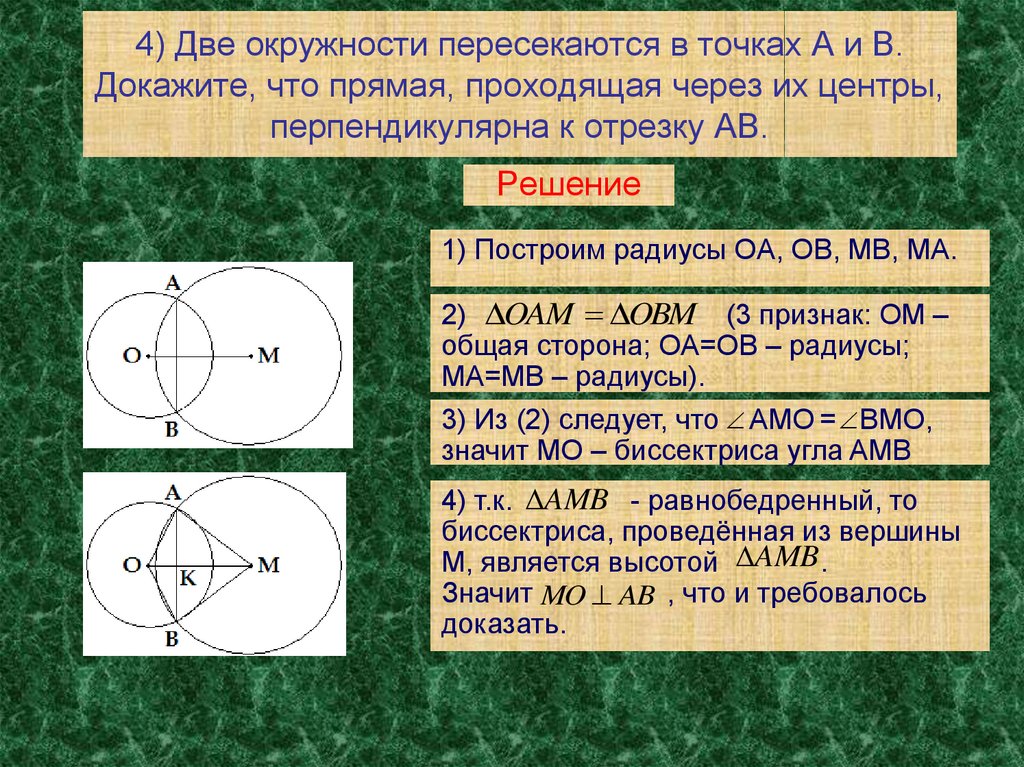 Решение: Всего исходов выпадения 6 очков — 5: 2 и 4; 4 и 2; 3 и 3; 1 и 5; 5 и 1. Благоприятных исходов — 2. Р(А)=2:5=0,4. Ответ: 0,4.

Слайд 11

ЛОТЕРЕЯ

Слайд 12

8. На экзамене 50 билетов, Тимофей не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет. Решение: Тимофей выучил 45 билетов. Р(А)=45:50=0,9. Ответ: 0,9.

Слайд 13

СОРЕВНОВАНИЯ

Слайд 14

9. В чемпионате по гимнастике участвуют 20 спортсменов: 8 из России, 7 из США, остальные из Китая. Порядок выступления определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решение: Всего исходов 20. Благоприятных исходов 20-(8+7)=5. Р(А)=5:20=0,25. Ответ: 0,25.

Слайд 15

10. На соревнования по метанию ядра приехали 4 спортсмена из Франции, 5 из Англии и 3 из Италии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что спортсмен, выступающий пятым, будет из Италии . Решение: Число всех возможных исходов – 12 (4 + 5 + 3 = 12). Число благоприятных исходов – 3. Р(А)=3:12=0,25. Ответ: 0,25.

Слайд 16

11. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 12 участников из России, в том числе Владимир Орлов. Найдите вероятность того, что в первом туре Владимир Орлов будет играть с каким-либо бадминтонистом из России? Решение: Всего исходов – 25 (Владимир Орлов с 25 бадминтонистами). Благоприятных исходов – (12-1)=11. Р(А)=11:25 = 0,44. Ответ: 0,44.

Слайд 17

12. Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Решение: Всего исходов – 75. Исполнители из России выступают на третий день. Благоприятных исходов – (75-27):4=12. Р(А)=12 : 75 = 0,16. Ответ: 0,16 .

Слайд 18

ЧИСЛА

Слайд 19

13. Коля выбирает двузначное число. Найдите вероятность того, что оно делится на 5. Решение: Двузначные числа: 10;11;12;…;99. Всего исходов – 90. Числа, делящиеся на 5: 10; 15; 20; 25; …; 90; 95. Благоприятных исходов – 18. Р(А)=18:90=0,2. Ответ: 0,2.

Слайд 20

РАЗНЫЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Слайд 21

14. Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решение: Всего исходов – 176. Благоприятных исходов – 170. Р(А)=170:176 ≈ 0,97. Ответ: 0,97.

Слайд 22

15. В среднем из каждых 100 поступивших в продажу аккумуляторов 94 аккумулятора заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен. Решение: Всего исходов – 100. Благоприятных исходов – 100-94=6. Р(А)=6:100=0,06. Ответ: 0,06.

Слайд 23

ИСТОЧНИКИ http://mathgia. ru http:// www.schoolmathematics.ru

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Геометрия. Основные утверждения и теоремы. Учитель математики МАОУ «Центр образования №13 имени Героя Советского Союза Н.А.Кузнецова» г.Тамбова Е.В.Кирина Подготовка к ОГЭ Планиметрия

Слайд 2

Для каждого утверждения определите, верное оно или неверное Через любую точку плоскости можно провести прямую. Через любые две различные точки плоскости можно провести прямую. Через любые три различные точки плоскости можно провести прямую. Любые две различные прямые проходят через одну общую точку. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Слайд 3

Для каждого утверждения определите, верное оно или неверное Сумма вертикальных углов равна 180 0 Сумма двух смежных углов равна 180 0 Если угол равен 54 0 , то вертикальный с ним равен 3 6 0 Если угол равен 72 0 , то смежный с ним угол равен 18 0

Слайд 4

Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны. Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 90 0 . Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то прямые параллельны. Если при пересечении двух прямых третьей внутренние односторонние углы равны 90 0 , то прямые параллельны. Если две прямые перпендикулярны третьей, то эти прямые перпендикулярны. Для каждого утверждения определите, верное оно или неверное

Слайд 5

Внешний угол треугольника равен сумме двух его внутренних углов Сумма углов прямоугольного треугольника равна 90 0 Сумма углов равнобедренного треугольника равна 180 0 Если два угла треугольника равны 36 0 и 64 0 , то третий угол равен 100 0 Если один из углов равнобедренного треугольника равен 30 0 , то другой его угол равен 1 2 0 0 Для каждого утверждения определите, верное оно или неверное

Слайд 6

Если в треугольнике АВС углы А и В равны соответственно 40 0 и 70 0 , то внешний угол этого треугольника при вершине С равен 70 0 Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны. Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны. Для каждого утверждения определите, верное оно или неверное

Слайд 7

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники подобны. Любые два равносторонних треугольника подобны. Любые два равнобедренных треугольника подобны. Любые два прямоугольных треугольника подобны. Для каждого утверждения определите, верное оно или неверное

Слайд 8

Каждая сторона треугольника равна двух других сторон. Каждая сторона треугольника меньше разности двух других сторон. Треугольник со сторонами 3, 4, 5 существует. В треугольнике против меньшей стороны лежит меньший угол. В треугольнике против большего угла лежит меньшая сторона. Для каждого утверждения определите, верное оно или неверное

Слайд 9

Сумма углов выпуклого четырёхугольника равна 180 0 . Сумма углов вписанного в окружность четырёхугольника равна 36 0 0 . В любом описанном четырёхугольнике сумма противоположных углов равна 180 0 . В любом описанном четырёхугольнике суммы противоположных сторон равны. Для каждого утверждения определите, верное оно или неверное

Слайд 10

Через любые две различные точки плоскости можно провести не более одной окружности. Через любые три различные точки плоскости можно провести не менее одной окружности. Если расстояние от центра окружности до прямой меньше радиуса окружности, то эти прямая и окружность пересекаются. Если расстояние от центра окружности до прямой больше диаметра окружности, то эти прямая и окружность не имеют общих точек. Для каждого утверждения определите, верное оно или неверное

Слайд 11

Если расстояние между центрами двух окружностей меньше суммы их радиусов, то эти окружности пересекаются. Если расстояние между центрами двух окружностей больше суммы их радиусов, то эти окружности не пресекаются. Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 4, то эти окружности пересекаются.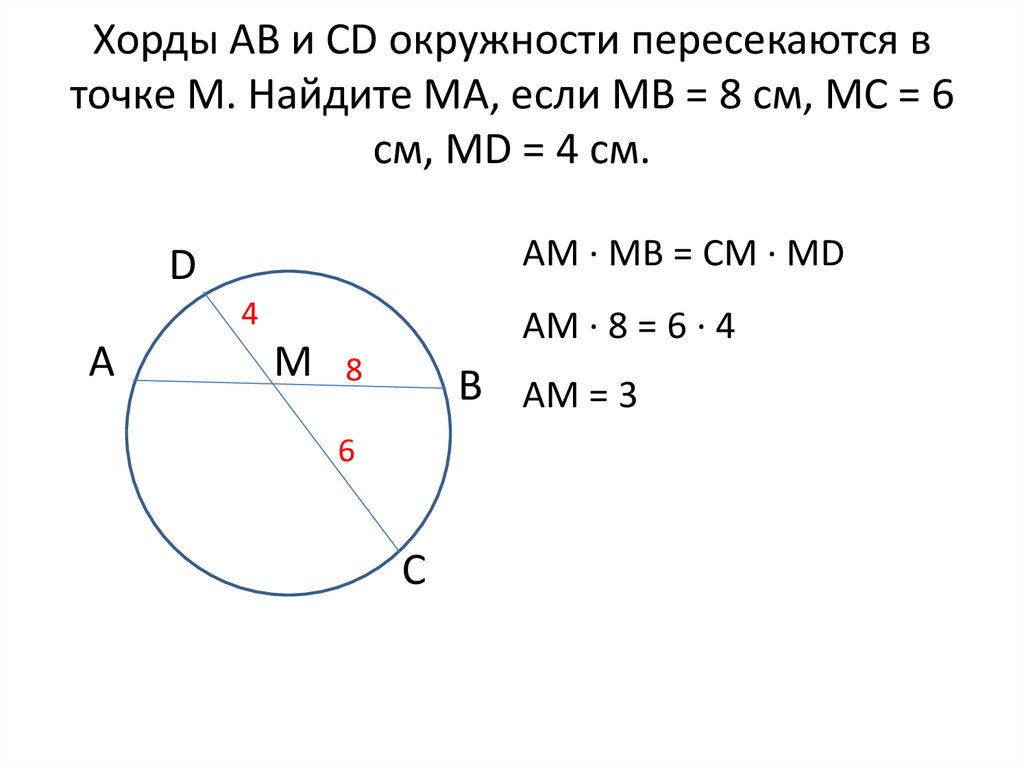 Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности не имеют общих точек. Для каждого утверждения определите, верное оно или неверное

Слайд 12

Длина окружности радиуса R равна π R . Площадь круга R равна 2 π R . Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. Если вписанный угол равен 24 0 , то дуга окружности, на которую опирается этот угол равен 48 0 . Если дуга окружности составляет 73 0 , то вписанный угол, опирающийся на эту дугу окружности, равен 73 0 . Для каждого утверждения определите, верное оно или неверное

Слайд 13

Центром окружности, описанной около треугольника, является точка пересечения его биссектрис. Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам. Центр окружности, описанной около прямоугольного треугольника, находится на стороне этого треугольника. Центром окружности, вписанной в правильный треугольник, является точка пересечения его медиан. Для каждого утверждения определите, верное оно или неверное

Слайд 14

Если сумма двух противоположных углов четырёхугольника равна 180 0 ,то около этого четырёхугольника можно описать окружность. Около любой трапеции можно описать трапецию. Если один из углов вписанного в окружность четырёхугольника равен 63 0 , то противоположный ему угол равен 1 17 0 . В любой параллелограмм можно вписать окружность. Для каждого утверждения определите, верное оно или неверное

Слайд 15

Если один из углов прилежащих к стороне параллелограмма равен 50 0 , то другой угол, прилежащий к той же стороне, равен 4 0 0 . Если в четырёхугольнике две стороны параллельны, то этот четырёхугольник – параллелограмм. Если в четырёхугольнике два угла – прямые, то этот четырёхугольник – параллелограмм. Диагонали прямоугольника перпендикулярны. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. Если в четырёхугольнике диагонали равны и перпендикулярны, то этот четырёхугольник – квадрат.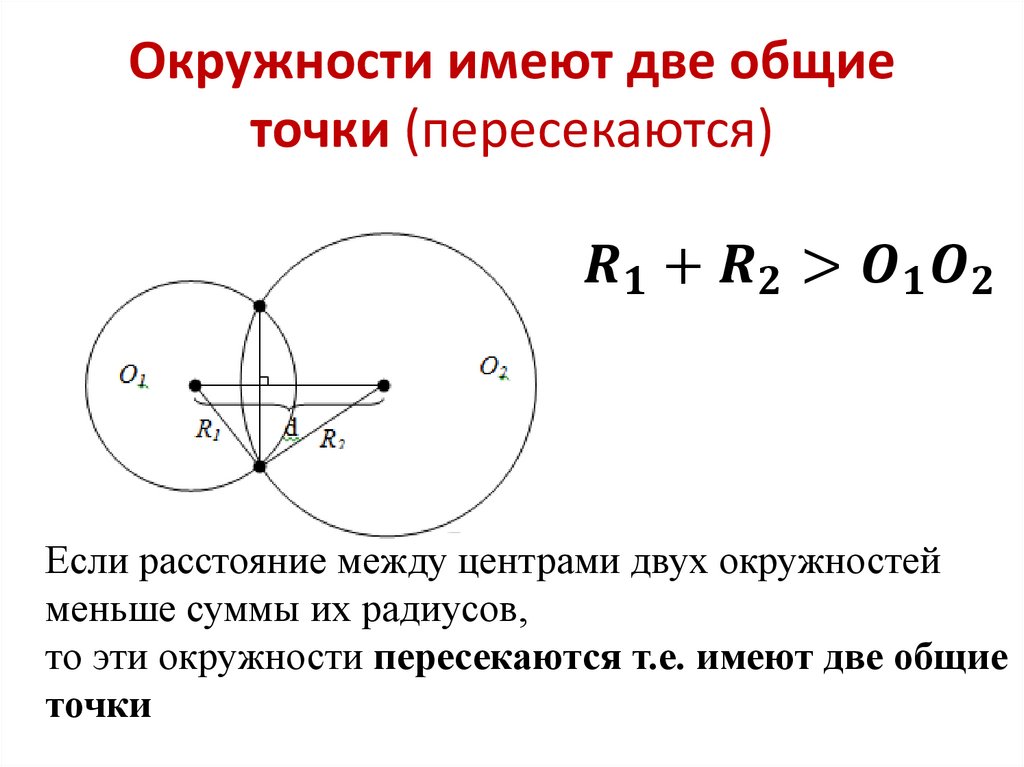 Для каждого утверждения определите, верное оно или неверное

Слайд 16

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними. Треугольник АВС, у которого АВ=20, ВС=21, АС=29 является прямоугольным. Площадь прямоугольного треугольника равна произведению его катетов. Площадь треугольника равна произведению его сторон на высоту, проведённую к этой стороне. Площадь прямоугольного треугольника равна произведению его катета на гипотенузу. Для каждого утверждения определите, верное оно или неверное

Слайд 17

Площадь трапеции равна произведению суммы оснований на высоту. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Для каждого утверждения определите, верное оно или неверное

Слайд 18

Используемая литература Л.С.Атанасян , В.Ф.Бутузов и др. «Геометрия, 10-11» М.:«Просвещение», 2006 А. В.Семёнов, А.С.Трепалин, И.В.Ященко, П.И.Захаров «Государственная итоговая аттестация выпускников 9 классов в новой форме 2012. МАТЕМАТИКА» М.: «Интеллект-Центр», 2012

геометрия — пересекаются 2 окружности и точки на ней берутся так, что середина соединяющей их линии является точкой пересечения , я все равно опубликую следующее из-за конструктивного доказательства (2), которое я уже разместил в геогебре. Для (1) у меня тот же ответ, но я позволю ему остаться, та же история, но немного другая точка зрения.

(1)

Имеем в данной ситуации: $$ \begin{выровнено} \широкая шляпа{ДАФ} «=» \широкая шляпа{DBF} &&\текст{ в кружке }DABF \\ «=» \широкая шляпа{EBF} \\ «=» \широкая шляпа{EAC} &&\текст{ w.r.t. круг }AEBC \ , \end{выровнено} $$ поэтому перпендикуляр в $A$ на прямой $CAD$ является биссектрисой угла $\angle (EAF)$. 92$$ конструктивно и таким образом, чтобы раскрыть как можно больше свойств объектов на рисунке.

Стратегию доказательства можно проследить на рисунке:

• (2. a) Сначала мы показываем $PE=PB$, но нам нужен промежуточный объект для лучшего согласования между $E,B$ для этого, это будет точка $Y$, построенная на прямой $CBF$ так, что $BED\|XY$. У нас есть $$ \широкая шляпа{DEF} = \широкая шляпа{DBF} = \широкая шляпа{XYF} \ , $$ так что $Y$ также находится в круге $(AEPFX)$, круге, собирающем целую армию точек. Отсюда следует, что $YX$ — это биссектриса угла для $\angle(EYF)$, поскольку $PX$ одно и то же для $\angle(EPF)$, а из $\angle(FYP)=\angle(FAP)$ у нас есть три равных «зеленых угла» в $Y$. Итак, $\Delta YEB$ равнобедренный. Из $\Delta PEY=\Delta PBY$ получаем $PE=PB$.

• (2.b) Теперь рисуем окружность $(P)$ с центром в $P$ и радиусом $PE=PB$, пересекает $AP$ в двух точках, $T$ между $A$ и $P$, и $T’\ne T$. Это строит $T,T’$. Мы, наконец, строим точка $$ Z $$ как вторая точка пересечения ($\ne T’$) $DT’$ с окружностью $(P)=(TEBT’)$. Теперь мы готовы показать…

• (2.c) Точки $C,T,Z$ лежат на одной прямой. Чтобы убедиться в этом, заметим, что существует инверсия с центром $D$, отображающая $А\стрелка влево C$, $E\leftrightarrow B$, $Z\leftrightarrow T’$. (Строка $DEB$ через центр инверсии $D$ стоит между равенством степеней $DA\cdot DC=DE\cdot DB=DZ\cdot DT’$ между двумя кружками.) В частности, $ACT’Z$ циклический, поэтому $CZ\perp ZT’$. Но и $TZ\perp ZT’$, потому что диаметр $TT’$ в $(P)$. (Он содержит $P$.) Итак, $C,T,Z$ коллинеарны.

• (2.d) $EF$ — хорда в окружности $(P)$, поэтому $P$ лежит на ее биссектрисе.

• (2.e) По построению $TZ\perp ZT’$, значит, $Z$ не только на окружности $(P)$, но и на окружности $(A)$ с центр $A$ и радиус $AD=AC$.

• (2.f) Две окружности $(A)$ и $(P)$ пересекаются ортогонально в $Z$, $AZ\perp ZP$. Например из-за $$ \begin{выровнено} 2 \ широкая шляпа {AZP} &=2(\pi-\широкая шляпа{AZD}-\широкая шляпа{PZT’})\\ &=2\pi -(\pi-\widehat{ZAD})-2\widehat{PZT’})\\ &=\pi +2\широкая шляпа{ZCD}-2\широкая шляпа{PZT’})\\ &=\пи \ .

  2\ , \end{выровнено} $$ нужное нам равенство.

$\square$

• (2.g) Бонус: Пусть $W$ пересечение $AP\cap EF$. Тогда $ZW\perp AP$, то есть $ZW\|DAC$.

кругов на Gmat | Ресурсы для изучения Магуша

By Mike MᶜGarry on 14 июля 2014 г. в GMAT Geometry

Вот восемь практических задач с кругами. Сложность этих задач варьируется от средней до очень сложной.

1) На приведенной выше диаграмме O — это центр окружности, а угол AOB = 144º. Какова площадь круга?

Утверждение №1: Площадь сектора AOB составляет 40% площади круга

Заявление № 2: Дуга ACB имеет длину .

2) На приведенном выше рисунке треугольник ABC является равносторонним. D — середина АС. BD — диаметр окружности. Если AD = 4, какова площадь круга?

3) На диаграмме выше О — центр круга. Какова длина хорды АС?

Утверждение №1: хорда BC = 14

Утверждение №2: площадь круга равна

4) Точки P, Q, R, S и T лежат на одной прямой. Больший круг имеет центр S и проходит через P и T. Меньший круг имеет центр R и проходит через Q и S. Каково отношение площади большего круга к площади меньшего круга?

Заявление № 1: ST:PQ = 5/2

Заявление № 2: RT:PR = 13/7

5) Квадрат и окружность пересекаются более чем в одной точке. Площадь квадрата больше площади круга?

Утверждение №1: существует ровно четыре точки пересечения

Утверждение №2: как минимум две точки пересечения лежат в вершинах квадрата

6) На приведенной выше диаграмме все точки расположены на прямой, и номер каждой точки указывает, на сколько единиц эта точка отстоит от нуля. Точки № 1– № 6 являются центрами шести окружностей, и все окружности проходят через нулевую точку. Какова общая площадь заштрихованной области?

7)  На приведенной выше диаграмме JKL — равносторонний треугольник. Точка M — это середина отрезка JL, а M — центр окружности, проходящей через точки J и L. Заштрихованные области на диаграмме обозначают все области внутри окружности, находящиеся вне треугольника. Какая часть общей площади круга находится вне треугольника?

8) На приведенном выше рисунке угол C = 90º, а AC = BC. Точка М является серединой АВ. Дуга AXB имеет центр в точке C и проходит через точки A и B. Дуга AYB имеет центр в точке M и проходит через точки A и B. Заштрихованная область между двумя дугами называется лункой. Каково отношение площади лунки к площади треугольника ABC?

Круги

Ах, красота круга, самой симметричной формы! Дополнительные сведения о кругах см. в следующих блогах:

1) Знакомство с кругами

2) Окружности, углы и дуги

3) Окружности и касательные линии

4) Вписанные и описанные окружности

5) Окружности, дуги и сектора

Если при чтении этих блогов у вас появились какие-либо идеи, возможно, вы захотите еще раз взглянуть на описанные выше проблемы. Если вы обнаружите какие-либо опечатки или что-то неясное на этой странице, сообщите нам об этом в разделе комментариев.

Практика объяснения проблем

1) Прежде всего, следует немного подумать о подсказке. Какую часть полного круга составляет этот угол, 144°? Ну, и 144, и 360 делятся на 4: 144 ÷ 4 = 36 и 360 ÷ 4 = 90, поэтому

Этот угол составляет 2/5 всей окружности, поэтому дуга составляет 2/5 всей окружности. Кроме того, помните, что если мы можем найти что-нибудь о всей окружности, например, длину окружности, то мы можем найти и радиус, что позволит нам найти площадь.

Утверждение №1: Это тавтологическое утверждение. Тавтологическое утверждение — это утверждение, которое по определению должно быть истинным, и поэтому оно не содержит никакой информации. Такие утверждения, как «Моя машина — это машина» и «Меня нанял мой работодатель», — это словесные тавтологии: они не содержат никакой полезной информации. Точно так же мы уже знаем из подсказки, что угол занимает 2/5 круга, поэтому, конечно, сектор будет занимать 2/5, или 40% площади. Этот оператор повторяет информацию в подсказке и не содержит новой информации, поэтому он не помогает нам выяснить что-либо еще. Это утверждение само по себе является недостаточно .

Утверждение № 2: мы уже знаем, что эта дуга составляет 2/5 всей окружности, поэтому мы можем составить пропорцию, чтобы найти длину окружности. Отсюда мы могли бы найти радиус, а это позволило бы нам найти площадь. Это утверждение само по себе достаточно .

Ответ = (Б)

2) Поскольку треугольник ABC равносторонний, прямоугольный треугольник ABD представляет собой треугольник 30-60-90, один из любимых треугольников GMAT. Из соотношений этого треугольника:

Половина этого радиуса круга:

Используйте это, чтобы найти площадь:

Ответ = (Б)

3) Тот факт, что AB является диаметром, гарантирует, что угол C = 90º. Если бы у нас было две стороны прямоугольного треугольника ABC, мы могли бы найти третью, используя теорему Пифагора .

Утверждение №1: это дает нам только одну сторону прямоугольного треугольника: бесполезно. Это утверждение само по себе является недостаточно .

Утверждение № 2: это позволяет нам найти радиус и, следовательно, диаметр, чтобы мы могли определить сторону AB. Тем не менее, это дает нам только одну сторону прямоугольного треугольника: тоже бесполезно. Это утверждение само по себе недостаточно .

Комбинированные операторы: мы получаем длину BC из первого оператора и длину AB из второго. Теперь у нас есть две стороны прямоугольного треугольника, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону AC. В совокупности заявлений достаточно .

Ответ = (С)

4) Назовите радиус большего круга y, а y = PS = ST. Назовите радиус меньшего круга x, и x = RS = RQ. Если бы мы взяли отношение площадей, множители уравнялись бы, и мы остались бы с отношением (y/x) в квадрате. Если бы мы могли найти это более простое отношение y/x, то мы могли бы найти отношение площадей.

Утверждение № 1: ST = y и PQ = y – 2x, поэтому

Это позволяет нам найти отношение y/x, что позволило бы нам найти отношение площадей. Это утверждение само по себе является достаточно .

Утверждение № 2: RT = y + x и PR = y – x, поэтому

Перекрестное умножение.

Это позволяет нам найти отношение y/x, что позволило бы нам найти отношение площадей. Это утверждение само по себе достаточно .

Ответ = (Д)

5) Утверждение №1: эта информация, не более того, может означать, что круг либо меньше, либо больше.

Это утверждение само по себе недостаточно .

Утверждение № 2: эта информация, не более того, может означать, что круг меньше или больше.

Это утверждение само по себе недостаточно .

Комбинированные утверждения: Один из возможных вариантов — круг, который пересекает квадрат четыре раза, проходя через все четыре вершины:

Этот круг явно больше квадрата. Окружность совершенно не может проходить ровно через три вершины. Если бы он проходил через две вершины, ему пришлось бы пересечь сторону еще два раза. Возможности включают следующее (точка C является центром круга).

Обратите внимание, что по мере приближения точки C к верхней стороне квадрата она становится все ближе и ближе к кругу, у которого эта верхняя сторона является диаметром, что эквивалентно первому кругу на диаграмме утверждения №1. Этот круг явно имеет меньшую площадь, чем квадрат. Ну, этот круг не будет работать здесь, потому что он пересекается только в двух точках, а потому, что точка C может приближаться все ближе и ближе к верхней стороне, не касаясь ее, что означает, что площадь круга на этой диаграмме может приближаться все ближе и ближе площади первого круга на диаграмме утверждения №1.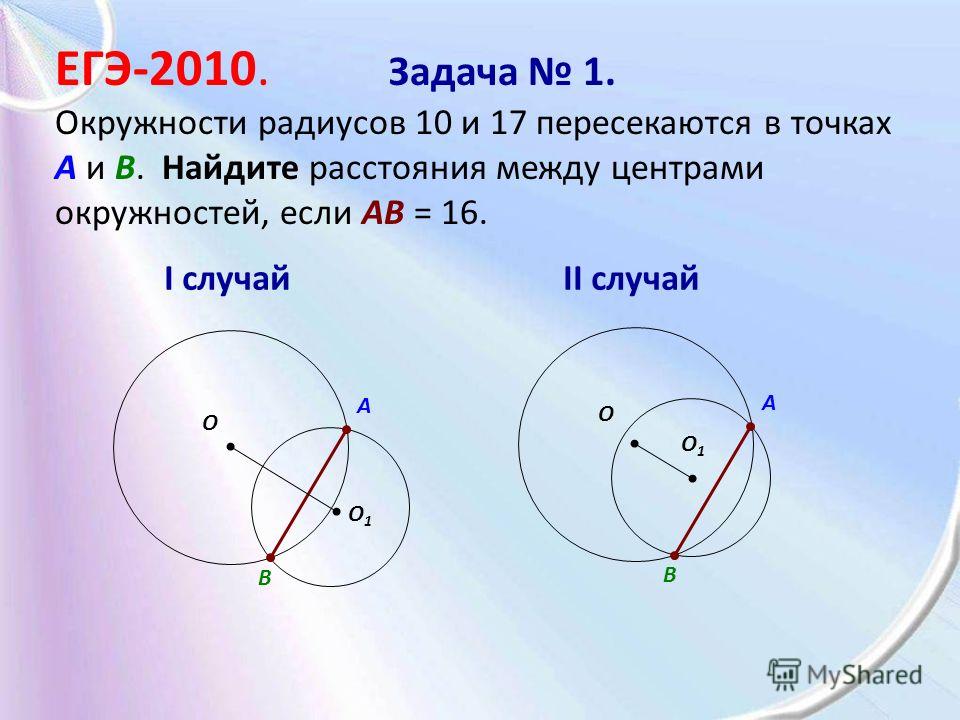 Это означает, что мы могли бы сделать так, чтобы круг на этой диаграмме имел меньшую площадь, чем квадрат.

Таким образом, даже при ограничениях обоих утверждений мы можем построить круг, площадь которого больше или меньше площади квадрата. Даже с обоими утверждениями мы не можем дать окончательный ответ на вопрос. Оба утверждения вместе взятые недостаточны .

6) Во-первых, давайте посмотрим на внешний «лепесток», тот, что находится между 10 и 12. Окружность, проходящая через точку 12, имеет центр a 6 и радиус 6, поэтому ее площадь равна . Окружность, проходящая через точку 10, имеет центр 5 и радиус 5, поэтому ее площадь равна . Если мы вычтем последнее из первого, мы получим площадь этой доли.

Теперь давайте посмотрим на среднюю долю, ту, что находится между 6 и 8. Окружность, проходящая через точку 6, имеет центр a 3 и радиус 3, поэтому ее площадь равна . Окружность, проходящая через точку 8, имеет центр 4 и радиус 4, поэтому ее площадь равна . Если мы вычтем последнее из первого, мы получим площадь этой доли.

Теперь давайте посмотрим на самый маленький лепесток, тот, что находится между 2 и 4. Окружность, проходящая через точку 2, имеет центр 1 и радиус 1, поэтому ее площадь равна . Окружность, проходящая через точку 4, имеет центр 2 и радиус 2, поэтому ее площадь равна . Если мы вычтем последнее из первого, мы получим площадь этой доли.

Добавьте площади трех отдельных лепестков: .

Ответ = (Б)

7) Это сложно. В качестве аргумента предположим, что JM = ML = 1. Тогда площадь всего круга будет равна . Это знаменатель нашего соотношения.

Ясно, что часть заштрихованной области представляет собой полукруг под JL. Эта часть имеет площадь . Это легкая часть.

Стороны пересечения окружности JK и KL: назовите эти точки A и B.

Точка A должна быть серединой JK, а точка B — серединой KL. Треугольник JAM должен быть равносторонним треугольником со стороной, равной 1.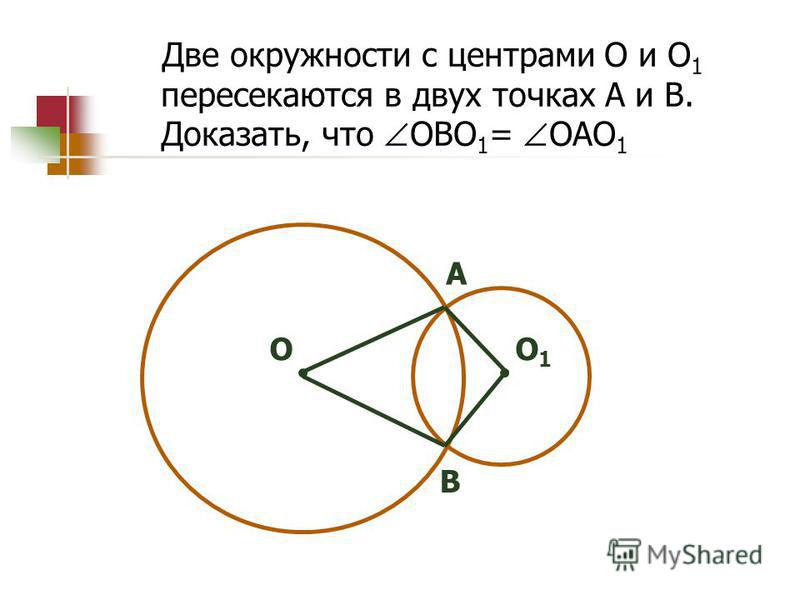 Сначала мы вычислим площадь сектора:

Угол при М равен 60º, так что это одна шестая часть площади круга.

Чтобы получить площадь этой небольшой заштрихованной части, известной как круговой сегмент, нам нужно вычесть площадь равностороннего треугольника JAM из площади сектора. Смотрите этот блог для площади равностороннего треугольника.

площадь сегмента = (площадь сектора) – (площадь треугольника JAM)

У нас есть два круглых сегмента, поэтому мы удваиваем их, чтобы получить оба:

Теперь добавьте площадь полукруга, чтобы получить площадь всей заштрихованной области:

Разделите это на площадь круга, чтобы получить отношение:

Ответ = (Э)

8) Эта задача основана на знаменитой теореме Гиппократа Хиосского (ок. 470 – ок. 410 до н. э.), предшественника Евклида. Проще всего это увидеть следующим образом.

Пусть AC = BC = 2S. Это радиус большего круга, который имеет площадь , так что четверть круга:

должен иметь площадь .