ОДЗ логарифма | Логарифмы
ОДЗ логарифма следует непосредственно из определения логарифма.
По определению, логарифм — это показатель степени, в которую надо возвести основание, чтобы получить число знаком логарифма:
Основание степени должно быть положительным числом, отличным от единицы.
При возведении в любую степень такого числа всегда получается положительное число.
Таким образом, область допустимых значений логарифма (ОДЗ логарифма)
состоит из трёх условий:
1) Под знаком логарифма должно стоять положительное число:
2-3) В основании логарифма должно стоять положительное число, отличное от единицы:
Все три условия должны быть выполнены одновременно.
Таким образом, чтобы найти ОДЗ логарифма
надо решить систему из трёх неравенств:
Если в основании логарифма стоит число:
ОДЗ логарифма содержит всего одно условие:
Если под знаком логарифма стоит число, а в основании — выражение с переменной:
то в область допустимых значений нужно записать два условия:
Примеры нахождения ОДЗ логарифма рассмотрим отдельно.
Логарифм. Свойства логарифмов
Логарифм. Свойства логарифмов
Рассмотрим равенство  . Пусть нам известны значения
. Пусть нам известны значения  и
и  и мы хотим найти значение
и мы хотим найти значение  .
.
То есть мы ищем показатель степени, в которую нужно взвести  чтобы получить
чтобы получить  .
.
Пусть  переменная
переменная  может принимать любое действительное значение, тогда на переменные
может принимать любое действительное значение, тогда на переменные  и
и  накладываются такие ограничения:
накладываются такие ограничения: 
 ,
, 
 ,
, 

Если нам известны значения 
 , и перед нами стоит задача найти неизвестное
, и перед нами стоит задача найти неизвестное  , то для этой цели вводится математическое действие, которое называется логарифмирование.
, то для этой цели вводится математическое действие, которое называется логарифмирование.Чтобы найти значение 
 по основанию
по основанию  :
:
Итак,
Логарифмом числа 
 называется показатель степени, в которую надо возвести
называется показатель степени, в которую надо возвести  , чтобы получить
, чтобы получить  .
.
То есть основное логарифмическое тождество


 ,
, 
 ,
, 

является по сути математической записью определения логарифма.
Математическая операция логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.
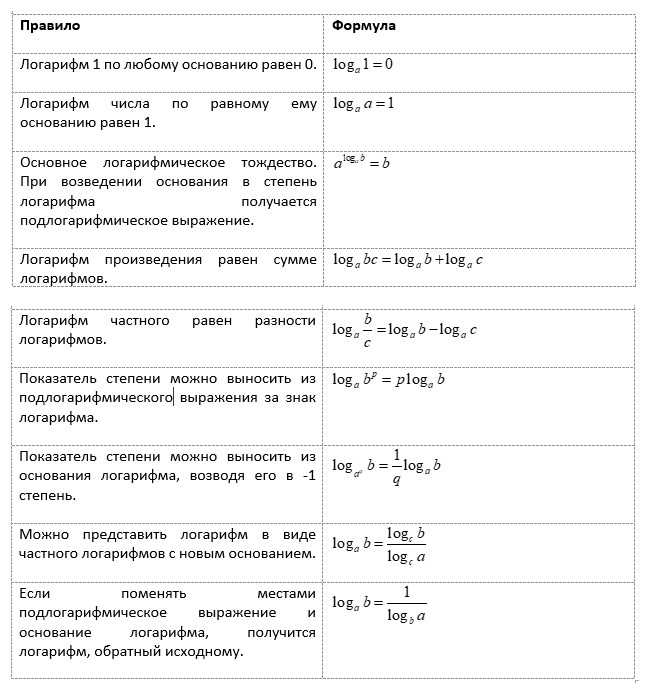
Перечислим основные свойства логарифмов:
(
 ,
, 
 ,
, 
 ,
, 
 ,
, 

1. 
2. 
3. 
4. 
5. 
Следующая группа свойств позволяет представить показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента перед знаком логарифма:
6. 
7. 
8. 
9. 
Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию:
10. 
11. 
12. (следствие из свойства 11)

Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:
13. 
14. 
15. 
Частные случаи:
 — десятичный логарифм
— десятичный логарифм
 — натуральный логарифм
— натуральный логарифм
При упрощении выражений, содержащих логарифмы применяется общий подход:
1. Представляем десятичные дроби в виде обыкновенных.
2. Смешанные числа представляем в виде неправильных дробей.
3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.
4. Стараемся привести все логарифмы к одному основанию.
5. Применяем свойства логарифмов.
Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.
Пример 1.
Вычислить:

Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.
 =
= =(по свойству 7)
=(по свойству 7)
 =(по свойству 6)
=(по свойству 6) 
 =
=


Подставим показатели, которые у нас получились в исходное выражение. Получим:

Ответ: 5,25
Пример 2. Вычислить:

Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):

Разложим числа, стоящие под знаком логарифма на простые множители:

Применим свойства 4 и 6:


Введем замену 

Получим:
Ответ: 1 
Скачать таблицу логарифм и его свойства
И.В. Фельдман, репетитор по математике.
Действия с логарифмами. Постигаем азы!
На прошлом занятии мы познакомились с понятием логарифма и порешали несколько несложных примеров на определение и смысл логарифма. Для начального знакомства.)
Теперь настал черёд более тесного знакомства с логарифмами и, соответственно, решения более серьёзных примеров. Начнём мы с ограничений в логарифмах.
Ограничения в логарифмах.
Как и у любого математического понятия, у логарифма тоже есть свои свойства и фишки. Именно о них мы сейчас и будем разговаривать. И в первую очередь это ограничения в логарифмах. До сих пор мы с вами знали лишь два жёстких ограничения в математике:
— нельзя делить на ноль;
— нельзя извлекать корень чётной степени из отрицательного числа.
С этого момента к этим двум добавляются дополнительные ограничения в логарифмах.
Для начала запишем определение логарифма в самом общем виде. Через буквы.
logab = c
Напоминаю, что это равенство означает всего лишь решение показательного уравнения
ac = b.
И всё.
А теперь подумаем, любым ли числом может быть a? Пусть, к примеру, a = 1. Тогда получается забавная штука: единица в любой степени равна единице… И каким бы ни было число c, числа a и b останутся единичками. Та же самая история и с нулём. Не подходят эти числа в качестве основания…
Отрицательные числа – очень вредные и капризные. В одну степень их можно возводить, а в другую – нельзя. Вот и поступили математики с ними, как со всеми капризными – вовсе исключили из рассмотрения.
В результате у нас получилось такое ограничение на основание:
a > 0, a ≠ 1.
А каким может быть число b? Давайте подумаем: если заведомо положительное основание a возвести любую степень c, то какое число мы в итоге получим? Верно, положительное число и получим!
Отсюда ещё одно ограничение на аргумент логарифма:
b > 0.
Вот и все ограничения. Число c (значение логарифма) может быть совершенно любым.
Конечно, при решении безобидных числовых примеров на логарифмы эти ограничения практически никак не сказываются. Зато когда столкнётесь с логарифмическими уравнениями и неравенствами, вы про эти ограничения ещё не раз вспомните! А если не вспомните, то я вам напомню. И буду напоминать при каждом удобном случае.) Ибо эти ограничения очень (!) важны при решении уравнений и неравенств. Про ОДЗ помните? Вот, то-то и оно…
Свойства логарифмов.
Итак, с ограничениями на логарифмы разобрались. Пора переходить на следующий уровень и знакомиться со свойствами логарифмов. Вот они:
Здесь всюду b>0 и c>0, а также a>0, a≠1.
Вот такой вот джентльменский набор. Ни много ни мало.) Теперь кратенько пробежимся по каждому из этих свойств. Чтобы ясно было, откуда ноги растут, как говорится.)
Начнём с первого свойства:
Обычно это свойство именуют особо — основным логарифмическим тождеством. Откуда же оно берётся? Запишем снова уже до боли знакомое нам равенство:
logab = c
Из самого определения логарифма мы с вами знаем, что, если число а (основание) возвести в степень c (показатель), то получим число b:
ac = b
А теперь подумаем, чему же равно у нас число c? Да вот же оно:
с = logab
Подставим это выражение в предыдущее равенство и получим как раз то, что нам и требуется:
«И зачем нам такая странная перетасовка?» — спросите вы. А затем, что многоэтажное выражение превращается в элементарное b! Полезная формула.) Это единственная формула, где логарифм стоит в показателе степени.
Следующая группа формул (2-3):
Думаю, тут комментарии излишни. Всё прямо из определения логарифма следует.) И даже примеры разбирались. В предыдущем материале. Кому всё-таки непонятно, применяем старый добрый способ — словесную расшифровку. Проверено, помогает.)
Переходим к следующей группе формул (4-5):
Коротко эти формулы называются логарифм произведения и логарифм частного (дроби).
А вот с их доказательствами вопрос похитрее будет.) Эти два свойства проистекают из обычного умножения и деления степеней с одинаковым основанием. Как именно? Мы с седьмого класса помним, что при перемножении двух степеней с одинаковым основанием показатели степеней складываются, а при делении – вычитаются:
Для доказательства, например, четвёртой формулы (логарифм произведения) придётся ввести вспомогательные обозначения:
m = logab
и
n = logac.
До конца доказывать эти две формулы я не буду. Как продолжить доказательство? Подставьте выражения для m и n в формулу умножения степеней и воспользуйтесь основным логарифмическим тождеством (формула №1). Попробуйте! Очень полезно.)
Кстати, прошу обратить внимание: данные формулы справедливы только при одинаковых основаниях! Если основания разные, то, скорее всего, преобразования более мудрёные…
Идём дальше. Следующая группа формул (6-7) – это формулы, позволяющие избавляться от степеней в аргументе или в основании логарифма:
Смысл их тоже прост. Если аргумент логарифма возводится в степень, то показатель степени
Осталась последняя формула №8:
Это – так называемая формула перехода к новому основанию. Самая трудная для запоминания формула. Поэтому народ частенько и ленится её запоминать… А вы запомните. Не сочтите за труд.) Когда она применяется? А когда основания логарифмов – разные.) Скажем, в примере куча логарифмов по основанию 3 и затесался один логарифм по основанию 7. Его и менять надо. На тройку.) Мы с этой формулой крепко подружимся. И примеры тоже порешаем.) В соответствующем уроке.
Вот такой вот перечень формул и свойств. Их вполне достаточно, чтобы уверенно решать примеры на логарифмы любого уровня сложности. Эти формулы нужно не просто помнить, но и уметь применять. Причём в обоих направлениях – как слева направо, так и справа налево.
Ещё не помешало бы знать, что такое десятичный логарифм и что такое натуральный логарифм.
Десятичный логарифм – это просто логарифм по основанию 10:
log10b = lg b
В написании десятичного логарифма всего лишь пропадает буковка «о».
Натуральный логарифм (хотя чего уж в нём такого натурального) – это логарифм по основанию e. Иррациональному числу «e».
e = 2,71828182845…
Что это за загадочное число, узнаете и поймёте, когда поступите в институт. В курсе матанализа.) В школьной математике это число практически не встречается, зато в высшей – сплошь и рядом.)
Обозначается натуральный логарифм вот так:
Логарифмы по этим основаниям хотя и имеют своё особое написание, но ни по определению, ни по свойствам ничем не отличаются от обычных логарифмов, скажем, по основанию два. Или три. И решаются точно так же.
Итак, будем считать, что необходимая теоретическая база подготовлена. Переходим к практике.)
Начальный уровень. Немного формул. Немного дробей. Немного степеней.
На этом уровне мы:
— впрямую используем определение логарифма,
— впрямую используем самые простые свойства логарифмов.
Мыслей здесь особых не нужно. Главное – память и внимательность. Итак, читаем, смотрим, вникаем.
Пример 1
Вычислить:
Решение примера вытекает непосредственно из определения и смысла логарифма. В какой степени 1/3 даёт 1/27? В кубе, конечно. То есть, в третьей степени.
Ответ: 3.
Следующий пример:
Пример 2
Всё то же самое, только дроби десятичные. Ну и что? Опять напрямую пользуемся определением логарифма: в какой степени 0,3 даст 0,09? В квадрате, разумеется! Или во второй степени.)
Ответ: 2.
И ещё один примерчик на дроби:
Пример 3
А вот тут некоторые могут и зависнуть. Почему? Потому что связь между 0,5 и 1/128 визуально просматривается плохо. Что делать?
Что-что… Да к обычным дробям перейти! Вот вам и первый практический совет:
Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.
Этот приём, между прочим, работает не только в логарифмах, но и в других смежных темах – в показательных выражениях, в корнях.
В нашем примере 0,5 = 5/10 = 1/2. Ну и как? Связь между 1/2 и 1/128 легче углядеть? Естественно! 1/128 – это 1/2 в
Ответ: 7
Что? Забыли, что 128 – это 2 в седьмой степени? Срочно повторить степени!
Следующий пример:
Пример 4
Прямое применение формулы разности логарифмов:
И как вам? Оба логарифма по отдельности ровно не считаются, зато через формулу разности – отлично!
Ответ: 1
Ещё пример:
Пример 5
А вот здесь складывать по формуле нельзя: основания разные – тройка и двойка. А формула – штука жёсткая. Раз требуются одинаковые основания, значит, так и надо.
Но тут ничего хитрого нет: оба логарифма считаются ровно.
Ответ: 10.
Не каждый, правда, догадается, что 243 – это 3 в пятой степени, а 32 – это 2 в пятой… Но тут дело уже не в логарифмах, дело в степенях!
Вот вам и второй практический совет.
Степени популярных чисел надо знать. В лицо!
Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но это умение слабо помогает в работе с логарифмами, да. А вот сообразить, какое число и в какой степени скрывается за числом 128 или 243 – это уже совсем другое дело. Почувствуйте разницу, что называется!
Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:
Определить, какими степенями и каких чисел являются числа:
4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.
Ответы (вразброс, естественно):
272; 210; 36; 72; 26; 92; 34; 43; 102; 25; 35; 73; 162; 27; 53; 28; 62; 33; 29; 24; 22; 45; 252; 44; 63; 82; 93.
Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 28, 44 и 162 – это всё 256.
А теперь я настоятельно рекомендую взять любой учебник по школьной математике и порешать оттуда простейшие примеры на логарифмы. Порешали? Хоть что-то получилось? Тогда будем считать, что начальный уровень вы прошли. Переходим на следующий уровень.
Почти все формулы. Почти все степени. Поиск «братьев по степени».
На этом уровне применяем почти все формулы работы с логарифмами. Кроме последней формулы перехода к новому основанию. А также закрепляем наши навыки работы со степенями.
Поехали расширять наши возможности!
Пример 6
Вот тут прямое применение определения логарифма не годится: из четвёрки 128 простым возведением в степень никак не сделаешь. И формулы логарифмов непонятно как употреблять… Не беспокойтесь, сейчас всё получится.) При маленьком условии, что вы узнали в лицо число 128. Да! Это 2 в седьмой степени! Так и запишем:
log4128 = log427
Вот и одна из формул (третья снизу) приходит на помощь. Та, где показатель степени ставится множителем перед логарифмом:
logaxn = n·logax
Вот и выносим семёрку за наш логарифм. Пишем:
log427 = 7log42
Что дальше? Дальше осталось вспомнить, что 4 = 22. Верно!
7log42 = 7log222
Вот и ещё одна формулка в дело просится!) Вторая снизу, где в степень возводится основание логарифма. Только в этом случае при вынесении показателя наружу его надо перевернуть: 1/n.
Записываем:
Ответ: 3,5
Вот так вот! А если бы мы не узнали в числе 128 степень двойки, то так и застряли бы на этом, в общем-то несложном примере…
А теперь мы вплотную подошли к одному весьма и весьма полезному приёму в работе с логарифмическими и показательными выражениями. Приём этот называется «поиск братьев». Братьев по степени. И по разуму тоже.) Суть этого полезного приёма заключается в тщательном осмотре примера и распознавании одного и того же числа в разных степенях.
Этот приём (шифровка одного и того же числа в разных степенях) – очень популярный приём в логарифмах! Да и в показательных уравнениях и неравенствах тоже. Например, числа 27 и 243 – родные братья! Да, 243 из 27 прямым возведением в натуральную степень никак не получить, но зато они – родня по тройке! Так как 27 = 33, а 243 = 35. В разобранном только что примере родственниками оказались 4 и 128. По числу 2. В общем, идея понятна, да?
И зачем всё это нужно – распознавать степени и родственников? А затем, что примеры от этого проще становятся! И формулы свойств логарифмов сразу высвечиваются.) Особенно важно получить в примере одинаковые основания у логарифмов, ибо чем больше одинаковых значков в примере и меньше разных, тем лучше. И не нужно здесь применять формулу перехода к новому основанию: зачем же из пушки по воробьям палить.?)
Следующий пример на братьев (или сестёр):
Пример 7
Вычислить:
В примере стоит сумма логарифмов, но основания логарифмов разные – тройка и девятка. Стало быть, применять напролом формулу суммы логарифмов нельзя. Но! Первый логарифм уже считается ровно, получится просто тройка:
log327 = log333 = 3
А со вторым логарифмом что? Из девятки 27 возведением в целую степень не получишь! Но зато 9 и 27 – родня! По тройке.) Самое время вспомнить, что:
9 = 32
Что ж, поработаем отдельно со вторым логарифмом. Перейдём в основании от девятки к тройке. Поможет нам такое преобразование или нет – неизвестно. Но что-то делать всё-таки надо, правда? Итак, преобразовываем второй логарифм по второй (снизу) формуле – выносим степень из основания за логарифм:
Осталось лишь сложить 3 (первый логарифм) и 3/2 (второй логарифм)
Ответ: 4,5
Так, с близкой роднёй разобрались. Идём дальше. Иногда пример может не соответствовать в точности формуле, а может быть лишь похожим на одну из формул. И наша задача – сначала преобразовать пример под ту или иную формулу. Как, например, этот:
Пример 8
Напоминаю, что запись lg означает просто логарифм по основанию 10. И всё.)
Итак, основания логарифмов уже одинаковые – десятка. Ну прям напрашивается формула суммы логарифмов! А н-е-ет, не катит! Двойка во втором слагаемом всё портит. Коэффициент, понимаешь.) А формула применима только к чистым логарифмам, безо всяких коэффициентов. Но горевать рано! Мы эту двойку сейчас ликвидируем. Безопасно для примера.) Мы её внутрь логарифма загоним. Как? Всё по той же формуле логарифма от степени:
logaxn = n·logax
Здесь как раз тот случай, когда формулу надо применять справа налево. Ни в одной другой теме школьной математики нельзя вот так красиво избавляться от мешающих коэффициентов, а в логарифмах – пожалуйста! Итак, избавляемся от двойки перед вторым логарифмом:
2lg5 = lg52 = lg25
Вот так. Осталось лишь сложить два логарифма по формуле логарифма произведения (опять же в применении справа налево). Вот и складываем:
lg4 + lg25 = lg(4́·25) = lg100 = 2
Напоминаю, что десятичные логарифмы формулу ничуть не портят, ибо они по своим свойствам ничем не отличаются от обычных!
Ответ: 2
Вот вам и третий практический совет.
Любую степень можно записать множителем перед логарифмом. И наоборот – любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
Ну что, вот и состоялась наше более близкое знакомство с логарифмами! Осталось теперь с ними крепко подружиться. На следующем уровне и в следующем уроке.)
Традиционные примеры для самостоятельного решения.
Вычислить:
Ответы (вразнобой): 0; 1; 2; 3;
Урок 8: Логарифмы — 100urokov.ru
План урока:
Понятие логарифма
Ограничения, связанные с логарифмом
Основные свойства логарифмов
Функция логарифма
Три основных вида логарифмов
Преобразования логарифмических выражений
Переход к новому основанию алгоритма
Использование логарифма для вычислений
Логарифмическая функция в природе и науке
Понятие логарифма
Великий ученый Пьер-Симон Лаплас говорил, что изобретение логарифмов продлило жизнь астрономов вдвое, ведь с их помощью астрономические расчеты, которые ранее занимали несколько месяцев, стало возможно выполнять за считанные дни. Что же представляют собой логарифмы и как они так сильно упрощают вычисления? Для ответа на этот вопрос сначала следует вспомнить показательные уравнения.
Рассмотрим простейшее показательное уравнение 2х = 4. Так как 22 =4, то, очевидно, оно имеет единственный корень, равный 2. Найти его можно не только аналитически, но и графически:

Далее посмотрим на уравнение 2х = 8. Так как восьмерка – это двойка в кубе (23 = 8), то единственным корнем ур-ния будет число 3. Также проиллюстрируем это с помощью графика:

Однако если мы попытаемся решить уравнение 2х = 6, то мы столкнемся с проблемами. Представить шестерку как какую-то степень двойки не получается. Графический метод показывает, что у этого ур-ния есть единственный корень, который лежит между числами 2 и 3, но точно определить его значение не получается:

Можно доказать (мы не будем этого делать), что искомый нами корень невозможно выразить с помощью дробей и даже корней n-ой степени. Поэтому возникает необходимость ввести какое-то новое обозначение, чтобы записывать корни таких уравнений. Математики придумали для такого числа обозначение log2 6, которое читается как «логарифм шести по основанию два».
Рассмотрим теперь более общий случай. Пусть есть некоторое ур-ние

Если число b положительно, то уравнение имеет корень, и при том единственный. Для его обозначения используется запись logab. Покажем, как графически показать значение величины logab. Для этого надо построить показательную функцию у = ах и горизонтальную линию у = b. Они пересекутся в единственной точке (если b положительно). Абсцисса (координата х) этой точки и будет равна logab:

Дадим строгое определение логарифма:

Задание. Какое число является решением показательного уравнения

Задача. Слиток радиоактивного изотопа, чей период полураспада (его обозначают буквой Т) составляет 10 минут, имеет начальную массу (m0), равную 1 кг. Через сколько минут его вес уменьшится до 300 грамм (0,3 кг)? Масса радиоактивного изотопа изменяется по закону
m(t) = m0•2–t/T
Решение. Подставим исходные данные в формулу, и получим уравнение с неизвестной величиной t:
0,2 = 1•2–t/10
0,3 = 2–t/10
Получили простейшее показательное уравнение, однако его левую часть (число 0,3) нельзя представить как степень двойки. Однако с помощью определения логарифма мы можем записать, что
– t/10 = log2 0,3
Умножаем ур-ние на (– 10) и получаем:
t = – 10 log2 0,3
С помощью калькулятора или компьютера можно узнать, что
log2 0,3 ≈ – 1,737
Тогда искомое нами время примерно равно
t = – 10 log2 0,3 ≈ – 10•(– 1,737) ≈ 17,37 минут ≈ 17 минут 22 секунды
Ответ: – 10 log2 0,3 минут ≈ 17 минут 22 секунды.
Из задачи видно, что с логарифмы используются и при решении некоторых практических задач.
Иногда бывает удобнее использовать иное определение, которое по своей сути почти не отличается от первого:

Вычислим для примера несколько простейших логарифмов:

Ограничения, связанные с логарифмом
Заметим, что сам логарифм может оказаться любым вещественным числом, ведь мы умеем возводить числа и в отрицательные, и в дробные, и даже в иррациональные степени. Однако для логарифма logab некоторые ограничения накладываются на значение числа а (оно называется основанием логарифма) и на значение числа b (будем называть его аргументом логарифма).
Напомним, что при определении показательной функции у = ах было введено ограничение, согласно которому основание степени (число а) должно быть строго положительным числом и при этом НЕ может равняться единице. Из-за этого и основание логарифма должно также соответствовать этому ограничению. Основание логарифма и основание показательной функции даже специально обозначают одной буквой а, чтобы связь этих двух понятий была очевидней.
Также напомним, что показательное уравнение ах = b имеет решение только при положительных значениях b. Это решение и представляет собой logab. Если же число b отрицательно, то корня у уравнения нет, а значит и вычислить logab невозможно. Поэтому аргумент логарифма не может быть отрицательным.
Сформулируем эти ограничения в виде одного правила:

Ранее мы уже сталкивались с тремя случаями, когда выражения не имеют смысла. Во-первых, это происходит при делении на ноль (или нахождении нуля в знаменателе дроби, что, по сути, одно и то же). Во-вторых, выражения бессмысленны, если под корнем четной степени находится отрицательное число. В-третьих, не имеют смысла выражения, в которых отрицательные числа возводятся в дробную степень, ведь возведение в дробную степень можно заменить извлечением корня

а отрицательное число не должно оказываться под знаком корня
Сейчас мы узнали четвертый подобный случай, связанный с понятием логарифма. Больше в рамках школьного не будут рассматриваться никакие другие ситуации, в которых выражение может потерять смысл.
Основные свойства логарифмов
Любое число, возведенной в первую степень, равно самому себе. То есть справедливо равенство
а1 = а
Из него, пользуясь определением логарифма, получаем первое важное его свойство: logаa = 1.

Продемонстрируем использование этого правила:

Любое число при возведении в нулевую степень равно единице:

Из этого следует второе важное правило: логарифм единицы по любому основанию равен нулю:

Покажем несколько примеров использования этого тривиального правила:

Для получения третьего свойства логарифма запишем очевидно справедливое равенство:
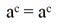
Пользуясь определением логарифма, мы можем записать, что logaac = c.

Продемонстрируем, как работает это свойство логарифмов:

Это правило можно применить для вычисления некоторых простейших логарифмов:

Логарифм logab, согласно одному из своих определений, это та степень, в которую нужно возвести а, чтобы получилось b. Это определение можно представить в виде формулы:
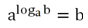
Данное равенство называют основным логарифмическим тождеством.

В силу этого тождества справедливы следующие равенства:


Эффективно подготовиться к ЕГЭ по математике помогут тщательно продуманные онлайн-курсы
Перейти
Функция логарифма
Арифметическое действие, в ходе которого находят логарифм какого-либо числа, называется логарифмированием. Это действие является обратным по отношению к возведению в степень. Проиллюстрируем это табличкой, в которой слева будет показана операция возведения в степень, а справа – логарифмирование:

Теперь подумаем о функции у = logax. Так как логарифмирование является обратным действием для возведения в степень, то и ф-ция у = logax должна быть обратной для показательной ф-ции у = ах.

В свою очередь это означает, что графики этих двух функций должны быть симметричны относительно прямой, задаваемой уравнением у = х.
Напомним, что на вид показательной функции у = ах влияет значение основания степени а. Если оно больше единицы, то функция оказывается возрастающей. Тогда и обратная ей логарифмическая функция также окажется возрастающей. Для примера построим графики у = 2х и у = log2x.


Полученный график логарифмической функции называют логарифмической кривой, однако понятно, что она представляет собой всё ту же экспоненту, которую отобразили симметрично относительно оси Ох.
График у = log2x можно и построить иначе, по точкам, просто вычислив ее значение в нескольких «удобных» для вычисления точках:


Видно, что в обоих случаях получился один и тот же график. Похожим будет и график любой функции у =logax, если число а будет больше единицы.
Ситуация меняется в том случае, когда а < 1, ведь при таком основании показательная функция у = ах будет убывающей. Тогда убывающим окажется и логарифмическая функция. Для примера построим график ф-ции = 0,5х и график обратной ей функции у = log0,5x:

Возможно, вы заметили, что графики у = log2x и у = log0,5xчем-то похожи друг на друга. И действительно, если построить их на одной плоскости, то мы увидим, что они симметричны относительно оси Ох:

Причиной такой симметрии является то, что их основания, числа 2 и 0,5, являются обратными числами, то есть при перемножении дают единицу (2•0,5 = 1).
Аналогично такой же симметрией будут обладать любые две логарифмические кривые с обратными основаниями. Это свойство логарифмов мы докажем чуть позднее.

Далее построим ещё несколько графиков, чтобы лучше понять свойства логарифмических функции:

Анализируя полученные графики, мы можем заметить следующие свойства функции логарифма:
Область определения логарифмической функции – это множество всех положительных чисел, то есть промежуток (0; + ∞). Действительно, выражение logаb имеет смысл только тогда, когда число b> 0.
Областью значения логарифмической функции является множество всех действительных чисел, то есть промежуток(– ∞; + ∞).
Логарифмическая функция является строго монотонной. При этом при основании а > 1 она возрастает, а при основании 0 <a< 1 она убывает.
График каждой логарифмической функции проходит через точку (1; 0). Это связано с тем, что для любого основания справедливо равенство loga 1 = 0.
Три основных вида логарифмов
Математика изучает логарифмы с любыми положительными основаниями. Однако на практике наиболее распространены три их вида.
Первым из них является десятичный логарифм, основание которого равно 10. Дело в том, что его помощью до изобретения калькуляторов и компьютеров можно было быстро и с высокой точностью перемножать большие числа, используя такой прибор, как логарифмическая линейка. История понятия логарифма начиналась в XVI-XVII веках и была связана именно с необходимостью выполнения сложных арифметических действий с большими числами. Для обозначения десятичных логарифмов используют специальный символ lg, то есть

Сегодня из-за развития электроники десятичные логарифмы используются значительно реже по сравнению с 50-60 г. XX века. Но, так как почти вся вычислительная техника построена на использовании двоичной системы счета, возросла значимость двоичного логарифма log2b. Для его обозначения не используются никакие специальные символы, однако в работах, посвященным информатике и оценке сложности алгоритмов, он используется особенно часто.
Наконец, самым важным является натуральный логарифм. Это логарифм, основанием которого является число e, примерно равное 2,71828… Для его обозначения используют символ ln, то есть


Свойства натурального логарифма, которые отличают его от других логарифмов, будут изучены нами позднее, в 11 классе. Заметим лишь, что многие физические формулы содержат именно натуральный логарифм.
Преобразования логарифмических выражений
Для работы с логарифмическими выражениями надо знать несколько основных свойств логарифмов. Первое из них помогает вычислять логарифм произведения.

Для доказательства этого правила введем обозначения. Пусть

Тогда нам надо доказать, что z = x + у. По определению логарифма мы можем записать что

Теперь подставим (1) и (2) в (3):

Получили, что az = ax+y. В этом равенстве в обеих частях стоят степени с совпадающим основанием а. Значит, должны совпадать и их степени, то есть

что и мы и пытались доказать.
Убедимся в справедливости этого правила на простейшем примере. Очевидно, что
log2 4 = 2, ведь 22 = 4
log2 8 = 3, ведь 23 = 8
log2 32 = 5, ведь 25 = 32
С одной стороны, так как
2 + 3 = 5
то и
log2 4 + log2 8 = log2 32
С другой стороны, число 32 можно представить как произведение 4•8, то есть
log2 32 = log2 (4•8)
С учетом этого получаем, что
log24 + log28 = log232 = log2(4•8)
Покажем несколько примеров использования только что доказанного правила:

Отдельно отметить, что правило сложения логарифмов действует и в том случае, когда складываются не два, а большее количество логарифмов:

Второе правило используют для определения логарифма от степени какого-либо числа.

Грубо говоря, показатель степени можно перенести и записать перед знаком логарифма. Сначала для наглядности приведем доказательство только для случая, когда r– целая степень. Тогда число br можно представить как произведение r множителей, равных b. Однако логарифм такого произведения можно заменить на сумму r логарифмов:

Однако более строгое доказательство должно рассматривать и случай, когда r – это отрицательное или даже дробное число. Поэтому, как и в ситуации с доказательством первого правила, введем переменные. Пусть
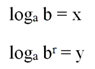
Получается, что нам доказать, что у = r•x. Из определения логарифма следуют следующие формулы:

Подставляя первую формулу во вторую, получаем:

И снова, если у двух равных степеней равны основания, то и показатели обязательно будут равными:

Это равенство мы и пытались доказать.
Продемонстрируем, как работает это свойство логарифмов:

Правило работает и в обратную сторону:
Задание. Чему равна дробь

Третье правило помогает вычислять логарифм от частного или дроби.

Для доказательства этого свойства логарифмов воспользуемся уже доказанными нами двумя правилами. Но предварительно напомним, что произвольное число с в степени (– 1) представляет собой дробь 1/с:

Тогда доказательство будет записываться в две строчки:

С помощью полученной формулы возможно выполнить следующие преобразования:

Заметим, что все полученные формулы справедливы только в том случае, когда под знаком логарифма стоят исключительно положительные числа. Например, вполне допустимо преобразование
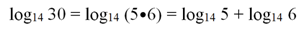
но ошибочной будет такая запись:

ведь в левой части стоит выражение, имеющее смысл, а в правой – выражение, смысла не имеющее.
Но что делать в случае, если необходимо упростить выражение с переменными, которые могут принимать как положительные, так и отрицательные значения? Получается, что запись

не является корректной. Действительно, если и х, и у являются отрицательными числами, то их произведение ху положительно. Но тогда получается, что при некоторых значениях переменных левая часть равенства имеет смысл, а правая – нет. Это значит, что оно не является тождеством.
Здесь может помочь использование модуля числа. Запись

уже будет корректной при любых допустимых значениях х и у. Если же хоть одна из переменных будет равна нулю, то обе части равенства одновременно потеряют смысл. Таким образом, данное равенство можно считать тождеством.
Аналогично и формулу разности логарифмов можно представить в более общем случае, при котором допускаются отрицательные значения переменных:

Можно ли записать равенство logaх2 = 2logaх, если допускается, что х может быть и отрицательным? Нет, нельзя, ведь при отрицательных х выражение левая часть равенства будет иметь смысл, а правая нет. Однако использование модуля поможет и в этом случае. Можно написать, что
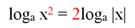
Аналогичным образом можно упростить и любые другие логарифмы, аргументы которых возведены в четную степень:


Ещё раз уточним, что эти правила используются при упрощении выражений с переменными, если те могут принимать отрицательные значения. Если же известно, что числа b и c положительны, то лучше использовать формулы, не содержащие модулей.

Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы
Перейти
Переход к новому основанию алгоритма
До этого мы рассматривали преобразования, в ходе которых не менялось основание логарифма. Однако иногда возникает необходимость сложить или вычесть логарифмы с различными основаниями. Пусть надо вычислить значение выражения

Так как основания двух логарифмов различны, то мы не можем использовать выведенную нами формулу разности логарифмов. Однако можно попытаться привести один из логарифмов к новому основанию. Для такой операции существует специальная формула.

Докажем это утверждение. Для этого введем новые переменные:

Тогда по определению логарифма можно записать равенства

Отсюда следует, что ax = cy. Подставим в это равенство вместо а выражение cz и получим:

Отсюда следует, что zx = у, или х = y/z. Теперь заменим х, у и z на логарифмы и получим то самое тождество, которые необходимо доказать:

Вернемся к примеру

Теперь мы можем произвести эти вычисления, но для этого сначала приведем log259 к основанию 5:

Теперь можно вычислить, чему равна искомая разность:

Формула перехода к новому основанию позволяет иначе взглянуть на графики логарифмических функций. Пусть дана функция у =log4x. Попытаемся привести ее к показателю 2:

Выходит, что график у = log4x можно получить из графика у = log2x его сжатием в 2 раза. Убедимся в этом, построив оба графика в одной плоскости:

Заметим, что и более общем случае графики функций у = logax и у = logbx могут быть получены друг из друга растяжением или сжатием в некоторое число раз. Действительно, формулу перехода к новому основанию можно переписать в таком виде:

Теперь подставим вместо числа b переменную х и получим соотношение, связывающее любые две логарифмические функции:

В данном случае logсx и logax – это логарифмические функции, а logca – некоторое число. В результате можно заключить, что график функции у = logсx может быть получен из графика logax его растяжением в logca раз.

Попытаемся привести логарифм logab к обратному основанию, то есть к основанию 1/а:
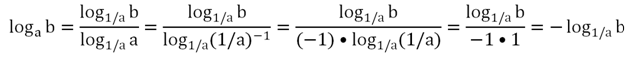
Итак, logab = – log1/аb. Именно из-за этого графики логарифмов с обратными основаниями (например, 2 и 0,5) симметричны относительно оси Ох:

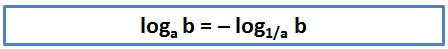
Покажем примеры использования этой формулы:

А что будет, если мы попробуем logab привести к основанию b? Сделаем это:
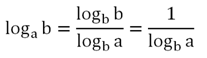
Получили ещё одну замечательную логарифмическую формулу.

Её работу иллюстрируют следующие примеры:

Ещё одна логарифмическая формула позволяет возводить основание логарифма и его аргумент в одинаковую степень:

Докажем это тождество в «обратном порядке», то есть из правой части выведем левую. Для этого просто перейдем к основанию а:

Проиллюстрируем, как это свойство можно применять на практике:
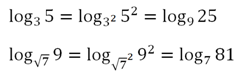

Для достижения наилучшего результата важно структурировать знания. В этом вам помогут онлайн-курсы по математике
Перейти
Использование логарифма для вычислений
Исторически развитие теории логарифмов было связано с необходимостью выполнять громоздкие вычисления. Например, пусть надо возвести число 7 в пятисотую степень, то есть вычислить величину 7500. Сделать напрямую это довольно затруднительно. Однако в силу основного логарифмического тождества мы можем записать, что

Напомним, что десятичный логарифм обозначают символом lg, поэтому перепишем это равенство в более привычном виде:

Степень из-под знака логарифма можно вынести:
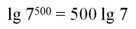
Значение числа lg 7 можно узнать с помощью калькулятора, в древности же использовали специальные таблицы, в которых были указаны десятичные логарифмы всех чисел от 1 до 10 (с маленьким шагом, равным, например, 0,001). Так или иначе, можно узнать, что

Получили число, записанное в стандартном виде. При этом наши расчеты были относительно простыми, если сравнить их с необходимостью умножить число 7 само на себя 500 раз. Аналогично и многие другие сложные операции выполняются значительно быстрее, если используются логарифмы. Поэтому долгое время знание теории логарифмов было необходимо для выполнения сложных инженерных расчетов. Но сегодня развитие компьютерной техники позволило избавиться от необходимости использования логарифмических линеек и таблиц.
Логарифмическая функция в природе и науке
Логарифм – это не просто инструмент для выполнения сложных операций. Например, в теории вероятностей существуют логарифмическое и логнормальное (от слов «логарифм» и «нормальное») распределение случайных величин, которые используются в генетике и физике. Так, размеры астероидов в Солнечной системе описываются логарифмическим распределением, а размеры градин во время града – логнормальным.
В компьютерной технике многие величин можно вычислить с использованием логарифмов. Например, ясно, что чем больше телефонных номеров находится в базе данных, тем дольше компьютер будет искать требуемый необходимый номер в ней. Зависимость времени поиска от количества номеров в базе данных описывается логарифмической функцией.
Огромное значение логарифмы имеют в астрономии. Так, яркость звезд на небе характеризуется таким параметром, как «видимая звездная величина». Однако в физике для оценки яркости света используют величину «освещенность», измеряемую в люксах. Зависимость между освещенностью звезд и их видимой величиной также является логарифмической.
Используются логарифмы и в термодинамике для вычисления такой характеристики систем, как энтропия. При расчете количества топлива, необходимого ракете для набора определенной скорости, используется формула Циолковского, содержащая натуральный логарифм:

В биологии давно замечено, что зависимость человеческих ощущений от силы воздействующих на них факторов окружающей среды носит логарифмический характер. В связи с этим для измерения громкости звуков используется специальная шкала децибелов, которая является логарифмической.
В строении ряда организмов можно обнаружить логарифмические кривые. Классическим примером является форма некоторых ракушек.

Мы сделали подборку лучших онлайн-курсов по школьным предметам
Перейти
Логарифмические уравнения — подготовка к ЕГЭ по Математике
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
.
При этом .
Обратим внимание на область допустимых значений логарифма:
.
Основное логарифмическое тождество:
,
.
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
.
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
1.Решите уравнение:
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Получаем:
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при .
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
Ответ: -124
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
;
;
;
4. Решите уравнение:
Область допустимых значений: Значит,
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом .
.
Ответ: 21.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
6.Решите уравнение: .
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
Ответ: 19.
7.Решите уравнение: .
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие .
Ответ:
8. Решите уравнение .
ОДЗ уравнения:
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
9.Решите уравнение:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
«Отбрасываем» логарифмы.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Ответ: .
Логарифмические уравнения могут встретиться вам и в задании №5 Профильного ЕГЭ по математике, и в задании №13. И если в задании №5 нужно решить простейшее уравнение, то в задаче 13 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Что такое логарифм
Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.
Мы же определим логарифм просто и наглядно. Для этого составим таблицу:
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.
Обозначение: loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 23 = 8 ⇒ log2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 23 = 8). С тем же успехом log2 64 = 6, поскольку 26 = 64.
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 21 | 22 | 23 | 24 | 25 | 26 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log2 2 = 1 | log2 4 = 2 | log2 8 = 3 | log2 16 = 4 | log2 32 = 5 | log2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 22 < 5 < 23, а чем больше степень двойки, тем больше получится число.
Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log2 5 = 2,32192809…
log3 8 = 1,89278926…
log5 100 = 2,86135311…
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log2 5, log3 8, log5 100.
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
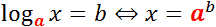
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
Как считать логарифмы
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: loga x = b ⇒ x > 0, a > 0, a ≠ 1.
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log2 0,5 = −1, т.к. 0,5 = 2−1.
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = ab;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача. Вычислите логарифм: log5 25
- Представим основание и аргумент как степень пятерки: 5 = 51; 25 = 52;
- Составим и решим уравнение:
log5 25 = b ⇒ (51)b = 52 ⇒ 5b = 52 ⇒ b = 2; - Получили ответ: 2.
Задача. Вычислите логарифм:
- Представим основание и аргумент как степень тройки: 3 = 31; 1/81 = 81−1 = (34)−1 = 3−4;
- Составим и решим уравнение:

- Получили ответ: −4.
Задача. Вычислите логарифм: log4 64
- Представим основание и аргумент как степень двойки: 4 = 22; 64 = 26;
- Составим и решим уравнение:
log4 64 = b ⇒ (22)b = 26 ⇒ 22b = 26 ⇒ 2b = 6 ⇒ b = 3; - Получили ответ: 3.
Задача. Вычислите логарифм: log16 1
- Представим основание и аргумент как степень двойки: 16 = 24; 1 = 20;
- Составим и решим уравнение:
log16 1 = b ⇒ (24)b = 20 ⇒ 24b = 20 ⇒ 4b = 0 ⇒ b = 0; - Получили ответ: 0.
Задача. Вычислите логарифм: log7 14
- Представим основание и аргумент как степень семерки: 7 = 71; 14 в виде степени семерки не представляется, поскольку 71 < 14 < 72;
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 23 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 24 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 34 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x. Обозначение: lg x.
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e, т.е. степень, в которую надо возвести число e, чтобы получить число x. Обозначение: ln x.
Многие спросят: что еще за число e? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459…
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = loge x
Таким образом, ln e = 1; ln e2 = 2; ln e16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Смотрите также:
- Тест к параграфу «Что такое логарифм» (легкий)

- Тест к уроку «Что такое логарифм» (средний)

- Десятичные дроби

- Задачи B12, сводящиеся к линейным уравнениям

- Метод коэффициентов, часть 2

- Тригонометрия в задаче B15: решаем без производных

Логарифмы и логарифмические уравнения
Логарифмические уравнения и решение логарифмических уравнений входят в обязательный комплекс знаний и умений школьника, если он стремится сдать ЕГЭ по математике на высокий балл и поступить в ВУЗ, стать студентом. Рассмотрим, что же это такое — логарифм, логарифмические уравнения и как их решать.
Логарифм — что это
Логарифмом числа 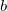 по основанию
по основанию  (
(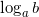 =c)называется такой показатель степени
=c)называется такой показатель степени  , в которую нужно возвести
, в которую нужно возвести  , чтобы получить
, чтобы получить 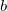 (то есть
(то есть 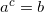 ). При этом задаются ограничения:
). При этом задаются ограничения: 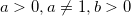 . Значение
. Значение  логарифма может быть любым.
логарифма может быть любым.
Вычислите:
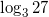 ,
, 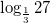 .
.
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.
 .
.
2. При возведении 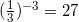 , значит
, значит 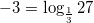 .
.
Ответ: 3; -3.
Изобретенные в 17 веке для ускорения вычислений, логарифмы значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в числовой работе более 300 лет, пока совершенство механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделали их устаревшими для крупномасштабных вычислений. Однако натуральный логарифм (с основанием e ≅ 2.71828 и записываемый как ln n) продолжает оставаться одной из наиболее полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.
Логарифмическая функция и ее график
Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.
Пусть 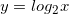 . Подставим вместо
. Подставим вместо  разные числа и определим соответствующие значения переменной.
разные числа и определим соответствующие значения переменной.
Отметим координаты точек на плоскости и соединим их плавной линией.
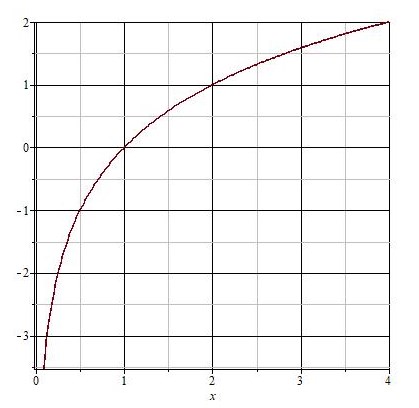
Логарифмическая функция все время возрастает.
Такое поведение характерно для всех логарифмических функций с основанием больше единицы.
Пусть теперь  . Составим таблицу значений для этого случая.
. Составим таблицу значений для этого случая.
Получим следующий график функции:
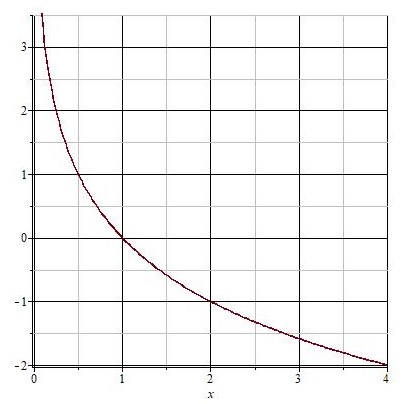
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.
Графики всех логарифмических функций проходят через точку с координатами (1;0).
Особыми знаками принято обозначать логарифмы с основанием десять 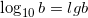 и логарифмы с натуральным основанием
и логарифмы с натуральным основанием 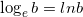 .
.
Свойства логарифмов
Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упростили долгие, утомительные вычисления.
В частности, ученые могли найти произведение двух чисел m и n, посмотрев логарифм каждого числа в специальной таблице, сложив логарифмы, а затем снова сверившись с таблицей, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в терминах обычных логарифмов, эта связь определяется как log m n = log m + log n.
Например, 100 × 1000 можно рассчитать, просмотрев логарифмы 100 по основанию 10 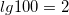 и 1000
и 1000  . Сложив логарифмы
. Сложив логарифмы  , а затем найдя его антилогарифм (то есть число, стоящее под знаком логарифма, в данном случае 100000) в таблице.
, а затем найдя его антилогарифм (то есть число, стоящее под знаком логарифма, в данном случае 100000) в таблице.
Аналогично, задачи деления преобразуются в задачи вычитания с логарифмами: log m/n = log m — log n.
Это еще не все. Расчет степеней и корней может быть упрощен с использованием логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться в качестве основания, поскольку все его степени равны 1).
В логарифмические таблицы обычно включались только логарифмы для чисел от 0 до 10. Чтобы получить логарифм некоторого числа вне этого диапазона, число было сначала записано в удобном виде как произведение его значащих цифр и его степени по основанию 10 —
например, 358 будет записано как 3,58 × 10 2,
а 0,0046 будет записано как 4,6 × 10-3.
Тогда логарифм значащих цифр — десятичная дробь между 0 и 1, известная как мантисса — будет найдена в таблице. Например, чтобы найти логарифм 358, можно посмотреть таблицу значений логарифмов 3,58 ≅ 0,55388. Следовательно, lg 358 = lg 3,58 + lg 100 = 0,55388 + 2 = 2,55388.
В примере числа с отрицательным показателем степени, такого как 0,0046, можно посмотреть lg 4,6 ≅ 0,66276. Следовательно, lg 0,0046 = lg 4,6 + lg 0,001 = 0,66276 — 3 = -2,33724.
История логарифмов
Изобретению логарифмов предшествовало сравнение арифметических и геометрических последовательностей.
В геометрической последовательности каждый член образует постоянное соотношение (знаменатель прогрессии) с предыдущим и последующим членами прогрессии: например,… 1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет общее отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как разность прогрессии, например,… −3, −2, −1, 0, 1, 2, 3… имеет разность 1.
Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения, для приведенной выше примерной геометрической последовательности:… 10−3, 10 −2, 10 −1, 10 0, 10 1, 10 2, 10 3….
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равно суммированию соответствующих показателей степеней с основанием 10: -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение преобразуется в сложение.
Однако первоначальное сравнение между двумя возможностями вычислений произведения не было основано на каком-либо явном использовании экспоненциальной записи: это было последующее развитие.
В 1620 году в Праге швейцарским математиком Йостом Бурги была опубликована первая таблица, основанная на концепции соотношения геометрических и арифметических последовательностей.
Шотландский математик Джон Непер опубликовал свое открытие логарифмов в 1614 году. Его целью было помочь в умножении величин, которые были связаны с вычислением синуса в прямоугольном треугольнике.
Вычисления Непера и Бригса
В сотрудничестве с английским математиком Генри Бригсом Непер приспособил свой логарифм к его современной форме. Для неперова логарифма сравнение будет происходить между точками, движущимися по градуированной прямой линии, точка L (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, точка Х (для синуса) движется от нуля до бесконечности со скоростью пропорционально его расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорость в этой точке равна.
Суть открытия Непера состоит в том, что он связал между собой арифметические и геометрические прогрессии — то есть умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничивать движение L и X требованием, чтобы L = 1 при X = 10, в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бригиану, или общему логарифму.
Непер умер в 1617 году, а Бригс продолжил расчеты в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанную до 14 знаков после запятой для чисел от 1 до 20 000 и от 90 000 до 100 000. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги появилось только в 1857 году в Берлине.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — логарифмические линейки были незаменимы в инженерных расчетах.

Современное определение логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Где используются логарифмы
Некоторые области науки, где применяются логарифмы:
- Децибелы, используемые для измерения звукового давления, определяются с помощью логарифмов.
- Шкала Рихтера, которая используется для измерения интенсивности землетрясений, определяется с помощью логарифмов
- Значения pH в химии, которое используется для определения уровня кислотности вещества, также определяется с использованием понятия логарифма.
- Когда две измеренные величины оказываются связанными степенной функцией, параметры функции могут быть оценены с использованием логарифмов.
- Логарифмы могут быть использованы для решения уравнений, таких как 2х = 3.
Решение логарифмических уравнений
Рассмотрим простейшие логарифмические уравнения и примеры их решения.
Задание 1
Решите уравнение log5(x2+x)=log5(x2+9)
Ответ:9
Решение: Так как основания логарифмов одинаковы, то числа, стоящие под знаком логарифмов — одинаковы:
 ,
,
Задание 2
Решите уравнение logx-5 49 = 2.
Если уравнение с логарифмами имеет более одного корня, в ответе укажите наибольший из них.
Ответ: 12
Решение:
(x – 5)2 = 49;
x2 – 10 x + 25 = 49;
x2 – 10 x – 24 = 0;
a = 1 , b = -10, c = -24;
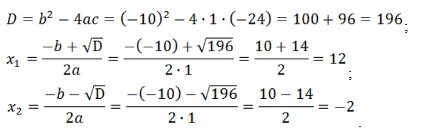
При х = –2 основание логарифма отрицательно (известно, что основание должно быть положительным). Решением является корень 12. Сделайте проверку.
Задание 3
Найдите корень уравнения log2(4 – x) = 7.
Ответ:-124
Решение:
27 = 4 – x;
128=4-х;
х = 4 – 128;
х = −124.
Задание 4
Найдите корень уравнения 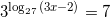 .
.
Ответ: 115
Решение: 27=33, тогда 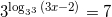
или 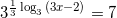 или
или 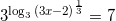 уравнения с логарифмами. По основному свойству логарифмов: при возведении числа в степень логарифма с таким же основанием, остается число, стоящее под знаком логарифма, то есть:
уравнения с логарифмами. По основному свойству логарифмов: при возведении числа в степень логарифма с таким же основанием, остается число, стоящее под знаком логарифма, то есть: 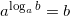 . Тогда получим:
. Тогда получим: 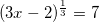 .
.
Решая данное уравнение, получим: 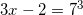 ,
,
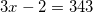
 .
.
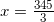
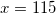
Задание 5
Решите уравнение logx+725 = 2. Если уравнение имеет более одного корня, в ответе укажите наименьший из них.
Ответ: -2
Решение: 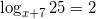 .
.
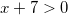 ,
, 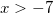 .
.
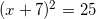
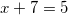 и
и 
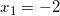 и
и 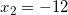
Так как x должен быть больше -7, то корень 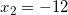 не подходит. И остается один единственный корень:
не подходит. И остается один единственный корень: 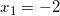 .
.
Таким образом, уже не важно — наибольший это корень или наименьший, он один подходит. Поэтому в ответе указываем его.
Задание 6
Решите уравнение log2(2 – x) = log2(2 – 3x) + 1
Ответ: x=0,4.
Решение: мы знаем, что 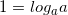 , тогда пусть в нашем случае
, тогда пусть в нашем случае 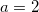 :
: 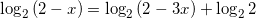 ,
,
применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:
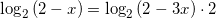
или
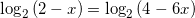
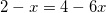
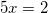
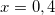 .
.
Задание 7
Решите уравнение log5(7 – x) = log5(3 – x) + 1
Ответ: 2
Решение: мы знаем, что 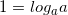 , тогда пусть в нашем случае
, тогда пусть в нашем случае 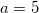 :
: 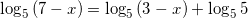 .
.
применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:
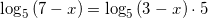
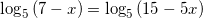
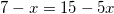
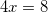
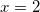 .
.
Задание 8
Найдите корень уравнения 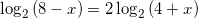
Ответ: x=-1
Решение:
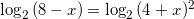
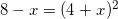
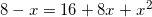
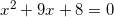
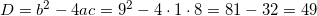
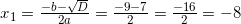
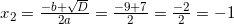 .
.
так как у нас должно выполняться условие:
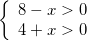 , откуда
, откуда 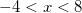 , таким образом нам подходит только один корень
, таким образом нам подходит только один корень 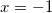 .
.
Итак, мы рассмотрели решение логарифмических уравнений с подробным решением каждого из них. Вы узнали, что такое логарифм, историю возникновения логарифма и имена ученых, которые схватили идею расчета произведения через сложение и изобрели логарифм, который на многие годы облегчил расчеты инженеров, строителей, ученых.
Ограничительные алгоритмы — документация GROMACS 2019-rc1
Алгоритм LINCS
LINCS — это алгоритм, который сбрасывает связи до их правильной длины после неограниченное обновление 49. Метод неитеративный, поскольку он всегда использует два шага. Хотя LINCS основан на матрицах, нет матрица-матрица умножения необходимы. Метод более стабильный и быстрее, чем SHAKE, но его можно использовать только с ограничениями связи и изолированные угловые ограничения, такие как угол протона в OH.{-1}} \ mathbf {F}, \]
где \ (\ mathbf {F} \) — вектор силы \ (3N \) и \ ({\ mathbf {M}} \) является \ (3N \ times 3N \) диагональная матрица, содержащая массы частиц. Система ограничено \ (K \) уравнениями не зависящих от времени
(6) \ [g_i (\ mathbf {r}) = | \ mathbf {r} _ {i_1} — \ mathbf {r} _ {i_2} | — d_i = 0 ~~~~~~ i = 1, \ ldots, K. \]В схеме численного интегрирования LINCS применяется после неограниченное обновление, как и SHAKE. Алгоритм работает в два этапа (см. рис.8). На первом этапе прогнозы новых облигаций на старые облигации установлены на ноль. в На втором этапе применяется поправка на удлинение связей из-за вращения. Числа для первого шага и второго шага: очень похожий. Полный вывод алгоритма можно найти в 49. Дается лишь краткое описание первого шага. Вот.
Рис. 8 Три обновления позиции, необходимые для одного временного шага. Пунктирный линия — старая связь длины \ (d \), сплошные линии — новая облигации.* = (\ mathbf {I} — \ mathbf {T} _n \ mathbf {B} _n) \ mathbf {r} _ {n + 1} + {\ mathbf {T}} _ n \ mathbf {p}. \]
Эта поправка на вращательные эффекты на самом деле является итеративной процесс, но во время MD применяется только одна итерация. Относительная отклонение ограничения после этой процедуры будет меньше 0,0001 для каждое ограничение. При минимизации энергии это может быть неточно достаточно, поэтому количество итераций равно порядку расширение (см. ниже).
Половина процессорного времени уходит на инвертирование матрицы связи ограничений \ ({\ mathbf {B}} _ n {{\ mathbf {M}} ^ {- 1}} {\ mathbf {B}} _ n ^ T \), что нужно делать на каждом временном шаге.Эта матрица \ (K \ times K \) имеет \ (1 / m_ {i_1} + 1 / m_ {i_2} \) по диагонали. Недиагональные элементы отличны от нуля только при соединении двух связей, тогда элемент равен \ (\ cos \ phi / m_c \), где \ (m_c \) — масса атома соединяющие две связи, а \ (\ phi \) — угол между облигации.
Матрица \ (\ mathbf {T} \) инвертируется через степень расширение. Матрица \ (K \ times K \) \ (\ mathbf {S} \) представляет собой обратный квадратный корень из диагонали \ (\ mathbf {B} _n {{\ mathbf {M}} ^ {- 1}} {\ mathbf {B}} _ n ^ T \).3 + \ ldots \]
Этот метод инверсии действителен, только если абсолютные значения всех собственные значения \ (\ mathbf {A} _n \) меньше единицы. В молекулах с ограничениями только связями связность настолько мала, что это всегда будет так, даже если присутствуют кольцевые структуры. Проблемы могут возникать в молекулах с ограниченными углами. Ограничивая углы с помощью дополнительные ограничения расстояния, несколько небольших кольцевых структур введен. Это дает высокую возможность подключения, что приводит к большим собственные значения. Поэтому LINCS НЕ следует использовать со связанными угловые ограничения.
Для молекул с ограниченными связями собственные значения \ (A \) составляют около 0,4. Это означает, что с каждым дополнительным заказом в В разложении (13) отклонения уменьшаются в 0,4 раза. Но для относительно изолированных треугольников ограничений наибольшее собственное значение около 0,7. Такие треугольники могут возникать при удалении водородного угла. колебания с дополнительным ограничением угла в спиртовых группах или при ограничение молекул воды с помощью LINCS, например, с помощью гибких ограничения.* \) содержит только элементы \ (\ mathbf {A} \), которые объединяют ограничения внутри жесткого треугольники, все остальные элементы равны нулю. Таким образом, точность угловые ограничения близки к другим ограничениям, в то время как серия умножений матрицы на вектор, необходимая для определения расширение нужно расширить только для нескольких связей ограничений. это процедура описана в документе P-LINCS50.
.алгоритмов нелинейной оптимизации с ограничениями — MATLAB и Simulink
Введение
В ограниченной оптимизации общая цель состоит в том, чтобы преобразовать проблему в более простую подзадача, которую затем можно решить и использовать как основу итеративного обработать. Характерной чертой большого класса ранних методов является перевод задачи с ограничениями к основной задаче без ограничений с использованием штрафа функция для ограничений, которые находятся рядом или за границей ограничения.В Таким образом, задача с ограничениями решается с помощью последовательности параметризованных безусловные оптимизации, которые в пределе (последовательности) сходятся к ограниченная проблема. Эти методы сейчас считаются относительно неэффективными. и были заменены методами, ориентированными на решение уравнений Каруша-Куна-Таккера (ККТ). Уравнения ККТ необходимы условия оптимальности для задачи оптимизации с ограничениями.Если проблема представляет собой так называемую задачу выпуклого программирования, т. е. f ( x ) и G i ( x ), i = 1, …, m , являются выпуклыми функциями, тогда оба уравнения ККТ являются необходимо и достаточно для глобальной точки решения.
Ссылаясь на GP (уравнение 1), Kuhn-Tucker уравнения можно записать как
| ∇f (x *) + ∑i = 1mλi⋅∇Gi (x *) = 0λi⋅Gi (x *) = 0, i = 1 ,…, meλi≥0, i = me + 1, …, m, | (12) |
в дополнение к исходным ограничениям в уравнении 1.
Первое уравнение описывает сокращение градиенты между целевая функция и активные ограничения на решение точка. Для отменяемых градиентов множители Лагранжа ( λ i , i = 1, …, м ) необходимы для компенсации отклонений по величине целевой функции и градиентов ограничений.Так как в эту операцию отмены включены только активные ограничения, неактивные ограничения не должны быть включены в эту операцию и поэтому заданы множители Лагранжа, равные 0. Это неявно утверждается. в последних двух уравнениях Куна-Таккера.
Решение уравнений ККТ лежит в основе многих нелинейных алгоритмы программирования. Эти алгоритмы пытаются вычислить Лагранж множители напрямую. Квазиньютоновские методы с ограничениями гарантируют сверхлинейную сходимость путем накопления информации второго порядка относительно Уравнения ККТ с использованием квазиньютоновской процедуры обновления.Эти методы обычно называют последовательным квадратичным программированием (SQP) методы, поскольку подзадача QP решается на каждой основной итерации (также известное как итеративное квадратичное программирование, рекурсивное квадратичное программирование, и методы с ограниченной переменной метрикой).
Алгоритм «активный набор» не является крупномасштабным.
алгоритм; см. Крупномасштабные и средние алгоритмы.
Реализация SQP
Реализация SQP состоит из трех основных этапов, которые кратко обсуждаются в следующих подразделах:
Обновление матрицы Гессе. На каждой основной итерации положительно определенное квазиньютоновское приближение гессиана функции Лагранжа, H , равно рассчитано методом BFGS, где λ i , i = 1, …, m , оценка множителей Лагранжа.
| Hk + 1 = Hk + qkqkTqkTsk − HkskskTHkTskTHksk, | (16) |
где
Пауэлл [33] рекомендует сохраняя гессенскую положительную определенность, даже если она может быть положительной неопределенный в точке решения.Положительно определенный гессиан сохраняется обеспечение qkTsk положительно при каждом обновлении и что H инициализируется положительно определенным матрица. Если qkTsk не положительный, q k равно изменяется поэлементно так, чтобы qkTsk> 0. Общая цель данной модификации состоит в передергивании элементов q k , которые как можно меньше способствуют определенному положительному обновлению. Поэтому на начальном этапе модификации самые негативные элемент q k * s k есть неоднократно уменьшалась вдвое.Эта процедура продолжается до тех пор, пока qkTsk не станет больше или равно небольшой отрицательный допуск. Если после этой процедуры qkTsk по-прежнему не является положительным, измените q k на складывая вектор v , умноженный на постоянный скаляр w , то есть
, где
и систематически увеличивайте w , пока qkTsk не станет положительным.
Функции fmincon , fminimax , fgoalattain ,
и fseminf все используют SQP.Если Дисплей установите 'iter' в опциях , затем
дается различная информация, такая как значения функций и максимальное
нарушение ограничения. Когда необходимо изменить гессиан с помощью
первая фаза предыдущей процедуры, чтобы она оставалась положительно определенной,
затем отображается Гессе, модифицированный . Если гессен
необходимо снова изменить, используя второй этап описанного подхода
выше, то отображается Гессен, измененный дважды, .
Когда подзадача QP недопустима, отображается недопустимо .Такие дисплеи
обычно не являются поводом для беспокойства, но указывают на то, что проблема
сильно нелинейна, и эта сходимость может занять больше времени, чем обычно.
Иногда отображается сообщение no update , указывающее, что qkTsk почти равно нулю. Это может быть
указание на то, что проблема неверна или вы пытаетесь
минимизировать прерывную функцию.
Решение для квадратичного программирования. На каждой основной итерации метода SQP
решается задача КП следующего вида, где A i в строку i матрицы m -by- n A .
| mind∈ℜnq (d) = 12dTHd + cTd, Aid = bi, i = 1, …, meAid≤bi, i = me + 1, …, m. | (18) |
Используемый метод в оптимизации Функции Toolbox — это стратегия активного набора (также известный как метод проецирования), подобный методу Gill et al., описанному в [18] и [17]. Он был изменен как для линейного программирования (LP) и задачи квадратичного программирования (QP).
Процедура решения состоит из двух этапов. Первый этап включает расчет допустимой точки (если таковая существует).В второй этап включает в себя создание итерационной последовательности возможных точки, сходящиеся к решению. В этом методе поддерживается активный набор A¯k, который является оценкой активных ограничений (то есть тех, которые находятся на ограничении границ) в точке решения. Практически все алгоритмы QP методы активного набора. Этот момент подчеркивается, потому что существует много разные методы, которые очень похожи по структуре, но описаны в самых разных терминах.
A¯k обновляется на каждой итерации k , и это используется для формирования основы для направления поиска d ^ k.k это формируется на основе Z k , чья столбцы ортогональны оценке активного множества A¯k (т. е. A¯kZk = 0). Таким образом, направление поиска, которое формируется из линейного суммирования любой комбинации столбцов Z k , гарантировано остаются на границах активных ограничений.
Формируется матрица Z k от последних м — л колонн QR-разложение матрицы A¯kT, где l — количество активных ограничений, а l <м .k, у вас есть
| q (p) = 12pTZkTHZkp + cTZkp. | (20) |
Дифференцируя это относительно p , получаем
| ∇q (p) = ZkTHZkp + ZkTc. | (21) |
∇ q ( p ) называется прогнозируемым градиентом квадратичной функции, потому что это градиент, спроецированный в подпространство, определенное как Z k . Термин ZkTHZk называется прогнозируемым гессеном.k> 0, i = 1, …, m.
Если n независимых ограничений включены в активном наборе, без расположения минимума, множители Лагранжа, λ k , вычисляются, удовлетворяющие невырожденной системе линейных уравнений
Если все элементы λ k являются положительный, x k — оптимальный решение QP (уравнение 18). Однако, если любой компонент λ k является отрицательный, и компонент не соответствует ограничению равенства, затем соответствующий элемент удаляется из активного набора и ищется новая итерация.
Инициализация. Для запуска алгоритма требуется допустимая точка. Если нынешний точка из метода SQP неосуществима, тогда вы можете найти точку решение задачи линейного программирования
| minγ∈ℜ, x∈ℜnγ такая, что Aix = bi, i = 1, …, meAix − γ≤bi, i = me + 1, …, m. | (26) |
Обозначение A i указывает i -я строка матрицы A .Ты можешь найти возможную точку (если она существует) для уравнения 26, установив x на значение, которое удовлетворяет ограничения равенства. Вы можете определить это значение, решив недооценку или переопределенная система линейных уравнений, образованная из системы равенств ограничения. Если есть решение этой проблемы, то переменная slack γ устанавливается на максимальное ограничение неравенства при этом точка.
Вы можете изменить предыдущий алгоритм QP для проблем LP, установка направления поиска на самый крутой спуск на каждом итерация, где g k — градиент целевой функции (равный коэффициентам линейного целевая функция).
Если допустимая точка найдена с использованием предыдущего метода LP, основной QP фаза вступила.k принимается равным минимальному γ .
Поиск строки и функция оценки. Решение подзадачи QP дает вектор d k , который используется для формирования новой итерации
Параметр длины шага α k равен определяется, чтобы произвести достаточное уменьшение функции качества. В этом примере используется оценочная функция, использованная Ханом [22] и Пауэллом [33] в следующей форме. реализация.
| Ψ (x) = f (x) + ∑i = 1meri⋅gi (x) + ∑i = me + 1mri⋅max [0, gi (x)]. | (30) |
Пауэлл рекомендует установить параметр штрафа
| ri = (rk + 1) i = maxi {λi, (rk) i + λi2}, i = 1, …, м. | (31) |
Это позволяет положительный вклад от ограничений, которые неактивны в решении QP, но недавно были активны. В этой реализации параметр штрафа r i равен изначально установлено значение
| ri = ‖∇f (x) ‖‖∇gi (x) ‖, | (32) |
, где ‖ ‖ представляет евклидову норму.
Это обеспечивает больший вклад в параметр штрафа от ограничения с меньшими градиентами, что было бы в случае активных ограничения в точке решения.
.ssl — java.security.cert.CertificateException: сертификаты не соответствуют ограничениям алгоритма
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
C ++ — Qaru
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании

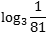
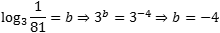


Leave A Comment