Задания по теме: «Углы параллелограмма»
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Углы. Вариант 1 | Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Углы. Вариант 2 | ||
1) Один из углов параллелограмма равен 41°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах. 2) Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах. 3) Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. 4) Сумма двух углов параллелограмма равна Найдите один из оставшихся углов. 5) Один угол параллелограмма на 52 больше другого. Найдите больший угол параллелограмма. Ответ дайте в градусах. 6) Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах. 7) В параллелограмме ABCD высота, опущенная на сторону AD, из точки В равна 3, а сторона параллелограмма AB равна 4. Найдите синус угла С. 8) В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах. | 1) Один из углов параллелограмма равен 96°. Найдите меньший угол этого параллелограмма. Ответ дайте 2) Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах. 3) Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах. 4) Сумма двух углов параллелограмма равна 10 Найдите один из оставшихся углов. Ответ дайте в градусах. 5) Один угол параллелограмма на 40 меньше другого. Найдите больший угол параллелограмма. Ответ дайте в градусах. 6) Один угол параллелограмма в три раза меньше другого. Найдите больший угол. Ответ дайте в градусах. 7) В параллелограмме ABCD высота, опущенная на сторону AD, из точки В равна 6, а сторона параллелограмма AB равна 10. Найдите косинус угла С. 8) В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=36°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах. | ||
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Вариант 3 | Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Углы. Вариант 4 | ||
1) Один из углов параллелограмма равен 102°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах. 2) Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 44°. Ответ дайте в градусах.
| 1) Один из углов параллелограмма равен 33°. 2) Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 40°. Ответ дайте в градусах. 3) Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах. 4) Сумма двух углов параллелограмма равна 78 Найдите один из оставшихся углов. Ответ дайте в градусах. 5) Один угол параллелограмма на 76 меньше другого. Найдите больший угол параллелограмма. Ответ дайте в градусах. 6) Один угол параллелограмма в 17 раз больше другого. Найдите меньший угол. Ответ дайте в градусах. 7) В параллелограмме ABCD высота, опущенная на сторону AD, из точки В равна 24, а сторона параллелограмма AB равна 25. Найдите косинус угла С. 8) В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=103°. |
Задание для подготовки:
1) Один из углов параллелограмма равен 61°. Найдите больший угол этого параллелограмма. Ответ дайте
в градусах.
2) Один из углов параллелограмма равен 91°. Найдите меньший угол этого параллелограмма. Ответ дайте
в градусах.
3) Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.
4) Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°.
Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
5) Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°.
Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
6) Сумма двух углов параллелограмма равна 202 Найдите один из оставшихся углов. Ответ дайте в градусах.
7) Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
8) Один угол параллелограмма в 8 раз больше другого. Найдите меньший угол. Ответ дайте в градусах.
9) В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=21°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
ОТВЕТЫ:
Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |
1 | 139 | 84 | 78 | 147 |
2 | 30 | 82 | 88 | 80 |
3 | 105 | 45 | 65 | 65 |
4 | 149 | 129 | 108 | 141 |
5 | 116 | 110 | 120 | 128 |
6 | 60 | 135 | 175 | 10 |
7 | 0,75 | 0,8 | 0,5 | 0,28 |
8 | 38 | 72 | 5,5 | 38,5 |
задачи по теме «Многоугольник, параллелограмм, трапеция» | Учебно-методический материал по геометрии (8 класс):
Опубликовано 28. 06.2022 — 6:11 — Борисова Мария Алексеевна
06.2022 — 6:11 — Борисова Мария Алексеевна
в файле содержатся задачи из ОГЭ, которые можно предлагать на уроках геометрии в 8 классе
Скачать:
Предварительный просмотр:
- Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
- Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
- ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
- Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
- Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
- Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
- Один из углов параллелограмма равен 41°.
 Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Найдите больший угол этого параллелограмма. Ответ дайте в градусах. - В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.
- Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
- На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
- Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
- В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и . Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.
- В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и . Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

- Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 6, CK = 10.
- Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, BD = 20, AB = 7. Найдите DO.
- В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рис.). Докажите, что ВFDЕ — параллелограмм.
- Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка L — середина стороны BC. Докажите, что DL — биссектриса угла CDA.
- В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
- В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник
- В параллелограмме проведены биссектрисы противоположных углов. Докажите, что отрезки биссектрис, заключенные внутри параллелограмма, равны
- Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках E и F соответственно.
 Докажите, что AE = CF.
Докажите, что AE = CF. - Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34.
- Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
- Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
- Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
- Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
- Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
- Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно.

- Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
- Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
- Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
- В равнобедренной трапеции известны высота 5, меньшее основание 6 и угол при основании 450. Найдите большее основание.
- Один из углов равнобедренной трапеции равен 66°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
- Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
- Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.
- Дана равнобедренная трапеция ABCD.
 Точка M лежит на основании AD и равноудалена от концов другого основания. Докажите, что M — середина основания AD.
Точка M лежит на основании AD и равноудалена от концов другого основания. Докажите, что M — середина основания AD. - Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD
По теме: методические разработки, презентации и конспекты
Практикум по теме «Параллелограмм, трапеция»
Подборка заданий из сборника Ф.Ф.Лысенко для подготовки к ГИА по математике по теме «Параллелограмм, трапеция»…
Тема урока: Площадь параллелограмма, трапеции, треугольника
Тип урока: Урок обобщения и систематизации знаний.Цели урока: Закрепление теоретических материалов по теме «Площади».Совершенствование навыков решения задач на вычисление площадей фигур.Показать приме…
Методическая разработка: «Обобщающий урок по геометрии по теме параллелограмм,трапеция, прямоугольник, ромб, квадрат».
Урок, презентация и самостоятельная работа по геометрии, для учащихся 8 класса.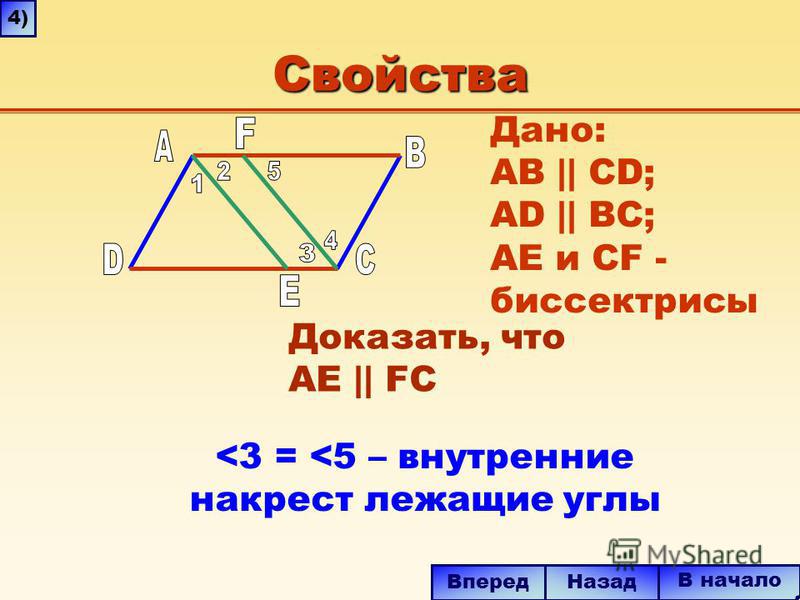 ..
..
Геометрия 8 класс самостоятельная работа «Параллелограмм. Трапеция»
Самостоятельная работа на 2 варианта по теме «Параллелограмм. Трапеция»…
Самостоятельная работа по проверке теоретического материала по темам » Многоугольники. Параллелограмм. Трапеция», 8 класс
Данную работу рекомендую использовать при дистанционном обучении в случае, если ученик находится на домашнем обучении или долго отсутствует на занятиях….
Самостоятельная работа по теме «Параллелограмм, трапеция»
Самостоятельная работа по теме «Параллелограмм, трапеция»…
Готовимся к ОГЭ. Параллелограмм. Трапеция. Задачи.
Задачи в формате ОГЭ по теме «Параллелограмм. Трапеция"…
Поделиться:
Как найти угол в параллелограмме
Все ресурсы по геометрии среднего уровня
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Промежуточная справка по геометрии » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти угол в параллелограмме
Параллелограмм содержит 2 угла, равные 135 и 45.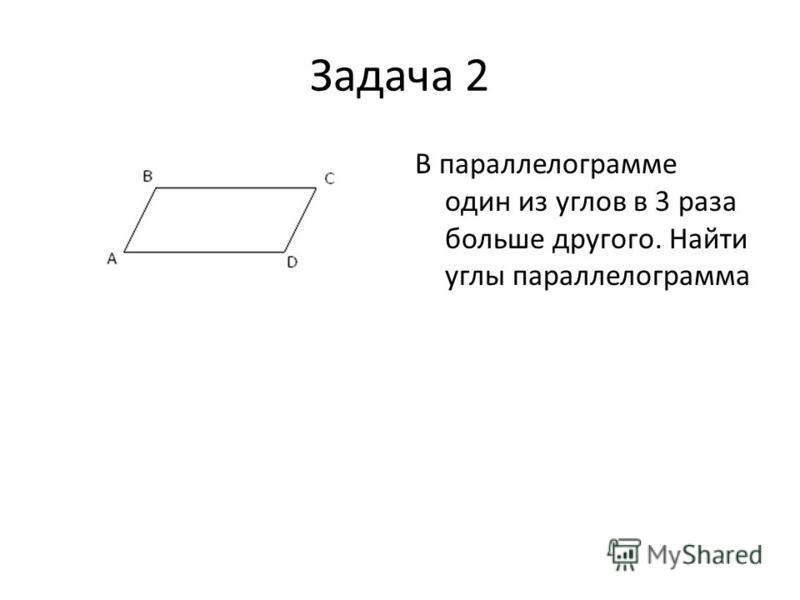 Каковы размеры двух других углов?
Каковы размеры двух других углов?
Возможные ответы:
Любая пара чисел, которые добавляют 180
Правильный ответ:
Параллелограммы имеют углы, равные 360 градусам, но также имеют совпадающие пары углов на концах диагоналей. Поэтому 2 дополнительных угла должны совпадать с 2 указанными в вопросе.
Сообщить об ошибке
Используя приведенный выше ромб, найдите величину угла Пояснение:
У ромба должны быть равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов), т.е. углы градусы.
Таким образом, решение:
Сообщить об ошибке
Используя приведенный выше ромб, найдите измерение угла .
Возможные ответы:
Правильный ответ:
Пояснение:
У ромба должны быть равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов), т.е. углы градусы.
Таким образом,
Сообщить об ошибке
Используя приведенный выше ромб, найдите сумму угла и угла .
Возможные ответы:
Правильный ответ:
Пояснение:
У ромба должны быть равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов).
Таким образом, решение:
Отчет о ошибке
Учитывая, что измерение угловых градусов, найдите сумму угла и угол
Возможные ответы:
Правильный ответ :
Пояснение:
У ромба должны быть равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов), т.е. углы градусы.
Решение этой проблемы:
Следовательно,
Отчет о ошибке
Используя вышеупомянутый ромб, найдите измерение угла
. Правильный ответ: Пояснение: У ромба должны быть равные противоположные внутренние углы. Таким образом, решение: Сообщить об ошибке В приведенном выше ромбе угол измеряется в градусах. Найдите сумму углов и
Пояснение: У ромба должны быть равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов), т.е. углы градусы. Решение этой проблемы: Таким образом, Сообщите о ошибке . Правильный ответ: Пояснение: Параллелограмм должен иметь равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов).
Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов).

Поскольку угол и дополнительны , решение будет следующим:
Сообщить об ошибке
Используя приведенный выше параллелограмм, найдите сумму углов и .
Возможные ответы:
Правильный ответ:
Пояснение:
У ромба должны быть равные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов).
Первый шаг к решению этой задачи — найти измерение угла . Поскольку угол является дополнительным углом к углу, угол
Поскольку угол и являются противоположными внутренними углами, они должны быть эквивалентны.
Таким образом, окончательное решение:
Сообщить об ошибке
Используя приведенный выше параллелограмм, найдите сумму углов и .
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь эквивалентные противоположные внутренние углы. Кроме того, сумма всех четырех внутренних углов должна быть равна градусам. И смежные внутренние углы должны быть дополнительными углами (сумма градусов).
Так как углы и являются противоположными внутренними углами, они должны быть эквивалентны.
Таким образом, решение:
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все промежуточные ресурсы по геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
Class 9 RD Sharma Solutions — Глава 14 Четырехугольники — Упражнение 14.
 2 Вопрос 1. Два противоположных угла параллелограмма равны (3x – 2)° и (50 – x) ° . Найдите величину каждого угла параллелограмма.
2 Вопрос 1. Два противоположных угла параллелограмма равны (3x – 2)° и (50 – x) ° . Найдите величину каждого угла параллелограмма. Решение:
Вопрос 2. Если угол параллелограмма составляет две трети прилежащего к нему угла, найдите углы параллелограмма.Дано: Два противоположных угла параллелограмма равны (3x – 2)° и (50 – x)°.
(3x – 2)°= (50 – x)° [Противоположные стороны параллелограмма равны]
3x + x = 50 + 2
4x = 52
x = 13
Угол x равен 13°
(3x – 2) = (3*13 – 2) = 37°
(50 – x)° = (50 – 13)°= 37°
x + 37°= 180° [Смежные углы a параллелограмм дополнительные]
x = 180°− 37°= 143°
Следовательно, искомые углы: 37°, 143°, 37°, 143°.
Решение:
Вопрос 3.Пусть угол равен x.
Следовательно, мера смежного угла равна 2x/3
Следовательно, x + 2x/3 = 180° [Смежные углы параллелограмма являются дополнительными]
2x + 3x = 540°
5x = 540°
x = 108°
Теперь,
⟹ x + 108°= 180° [Последовательные углы параллелограмма являются дополнительными]
⟹ x + 108°= 180°
⟹ x = 180° 72°
⟹ x = 72°
искомые углы 180°, 72°, 180°, 72°
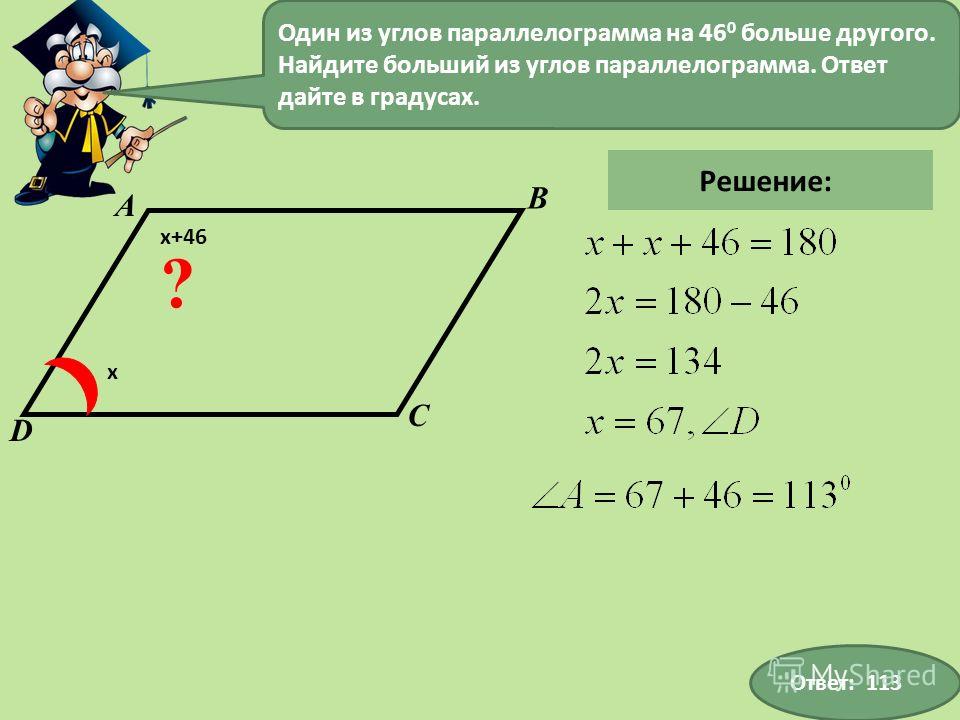 Найдите величину всех углов параллелограмма, если один угол равен 24 ° меньше удвоенного наименьшего угла.
Найдите величину всех углов параллелограмма, если один угол равен 24 ° меньше удвоенного наименьшего угла. Решение:
Вопрос 4. Периметр параллелограмма равен 22см. Чему равна меньшая сторона, если ее длинная сторона равна 6,5 см?x + 2x – 24°= 180° [Последовательные углы параллелограмма являются дополнительными]
3x – 24°= 180°
3x = 108° + 24°
3x = 204°
x = 204/3 = 68°
x = 68°
Другой угол параллелограмма2= °= 2*68°- 24°= 112°
искомые углы 68°,112°,68°,112°
Решение:
Вопрос 5.Дано: периметр параллелограмма равен 22 см
Предположим, что более короткая сторона равна «у».
периметр = y + 6,5 + 6,5 + x [Сумма всех сторон]
22 = 2(y + 6,5)
11 = y + 6,5
y = 11 – 6,5 = 4,5 см
Отсюда меньшей стороны = 4,5 см
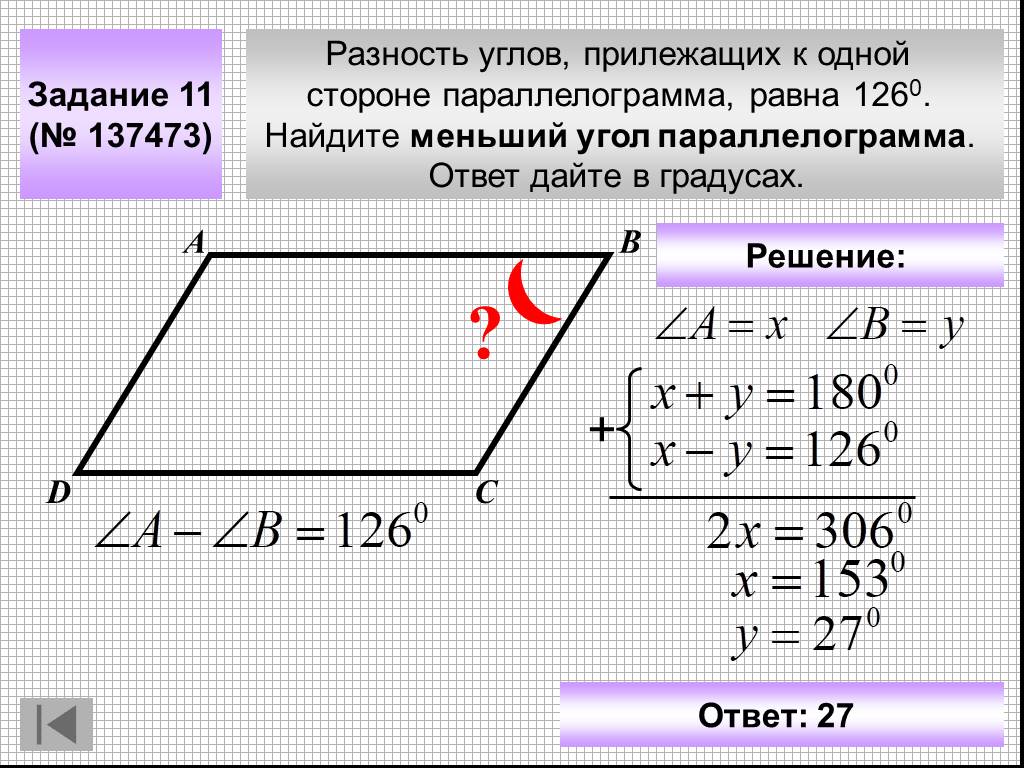 В параллелограмме ABCD ∠D = 135 ° . Определите меры ∠A и ∠B.
В параллелограмме ABCD ∠D = 135 ° . Определите меры ∠A и ∠B. Решение:
Вопрос 6. ABCD — параллелограмм, в котором ∠A = 70 ° . Вычислите ∠B, ∠C и ∠D.В параллелограмме ABCD
Дано: ∠D=135°
Итак, ∠D + ∠C = 180° [Последовательные углы параллелограмма дополнительные]
∠C = 180°− 135°
∠C = 45°
В параллелограмме противоположные стороны равны.
∠A = ∠C = 45° [противоположные стороны параллелограмма равны]
∠B = ∠D = 135°
Следовательно, меры ∠A и ∠B равны 45°, 135° соответственно.
Решение:
Вопрос 7. На рисунке ABCD — параллелограмм, в котором ∠A = 60 ° . Если биссектрисы ∠A и ∠B пересекаются в точке P, докажите, что AD = DP, PC = BC и DC = 2AD.В параллелограмме ABCD
Дано: ∠A = 70°
∠A + ∠B = 180° [Последовательные углы параллелограмма =°B]
1 08 7004 70 [дано ∠A = 70°]∠B = 180°− 70°
∠B = 110°
Теперь,
∠A = ∠C = 70° [противоположные стороны параллелограмма равны]
900 B = ∠D = 110°, следовательно, меры ∠A и ∠B равны 70°, 110° соответственно.
Решение:
Вопрос 8. На рисунке ABCD — параллелограмм, в котором ∠DAB = 75 ° и ∠DBC = 60 ° . Вычислите ∠CDB и ∠ADB.ДАВАЕТ: ♂ = 60 °
, чтобы доказать: AD = DP, PC = BC и DC = 2AD
= 30°
Теперь,
∠A + ∠B = 180° [последовательные углы параллелограмма являются дополнительными]
∠B + 60°= 180°
∠B = 180°− 60°
5
5 = 120°
BP делит пополам ∠B
Итак, ∠PBA = ∠PBC = 60°
∠PAB = ∠APD = 30°[Чередующиеся внутренние углы]
Следовательно, AD = DP [Стороны, противоположные равным углам, имеют одинаковую длину]
Аналогично
∠PBA = ∠BPC = 60° [Чередующиеся внутренние углы]
Следовательно, PC = BC
DC = DP + PC
DC = AD + BC [ DP = AD и PC = BC ]
DC = 2AD [Поскольку , AD = BC, Противоположные стороны параллелограмма параллельны и конгруэнтны]
, следовательно, доказано.
Решение:
Вопрос 9. На рисунке ABCD — параллелограмм, а E — середина стороны BC. Если DE и AB при изготовлении встречаются в точке F, докажите, что AF = 2AB.Приведен: ▲ DAB = 75 ° и грыти. AD∥ BC и BD — трансверсаль]
InBDA
∠DAB + ∠ADB + ∠ABD = 180° [свойство суммы углов]
75°+ 60°+ ∠CDB = 180°
∠ABD = 180°− (135°)
∠ABD = 45°
∠ABD = ∠CDB = 45° [Альтернативный внутренний угол. AD∥ BC и BD — трансверсаль]
Отсюда ∠CDB = 45°, ∠ADB = 60°
Решение:
Дано: ABCD — параллелограмм, а E — середина стороны BC.
Чтобы доказать: AF = 2AB.
Сейчас,
В ΔBEF и ΔCED
∠BEF = ∠CED [Подтвержденный противоположный угол]
BE = CE [Поскольку E — середина BC]
∠EBF = Поскольку, Alternate [ внутренние углы равны]
ΔBEF ≅ ΔCED [конгруэнтность ASA]
BF = CD [соответствующие части конгруэнтного треугольника]
AF = AB + AF
AF = AB + CD [BF = CD по соответствующим частям конгруэнтного треугольника ]
AF = AB + AB [CD=AB, противоположные стороны параллелограмма параллельны и конгруэнтны]
АФ = 2АВ.

 Ответ дайте в градусах.
Ответ дайте в градусах.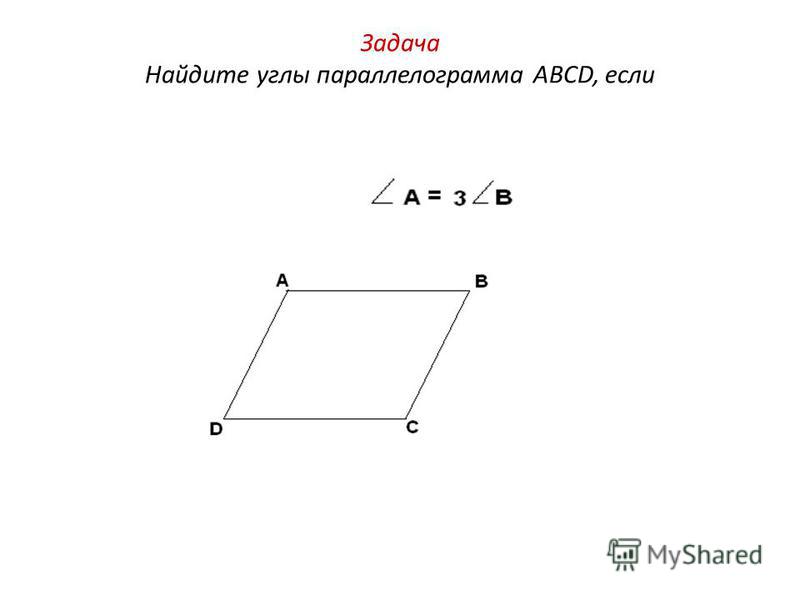
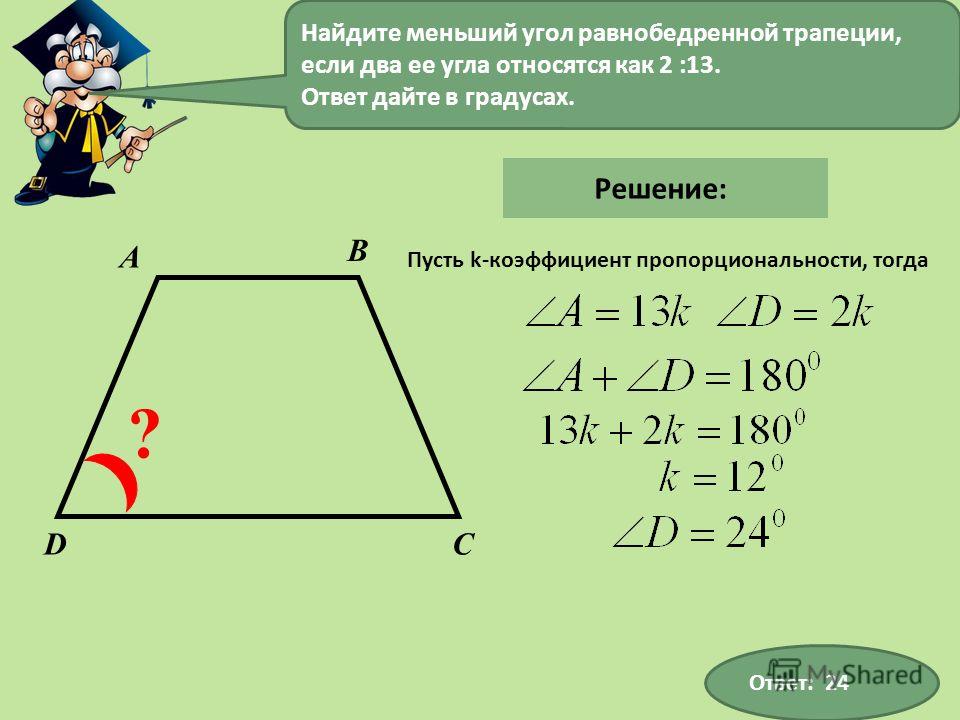 Углы.
Углы.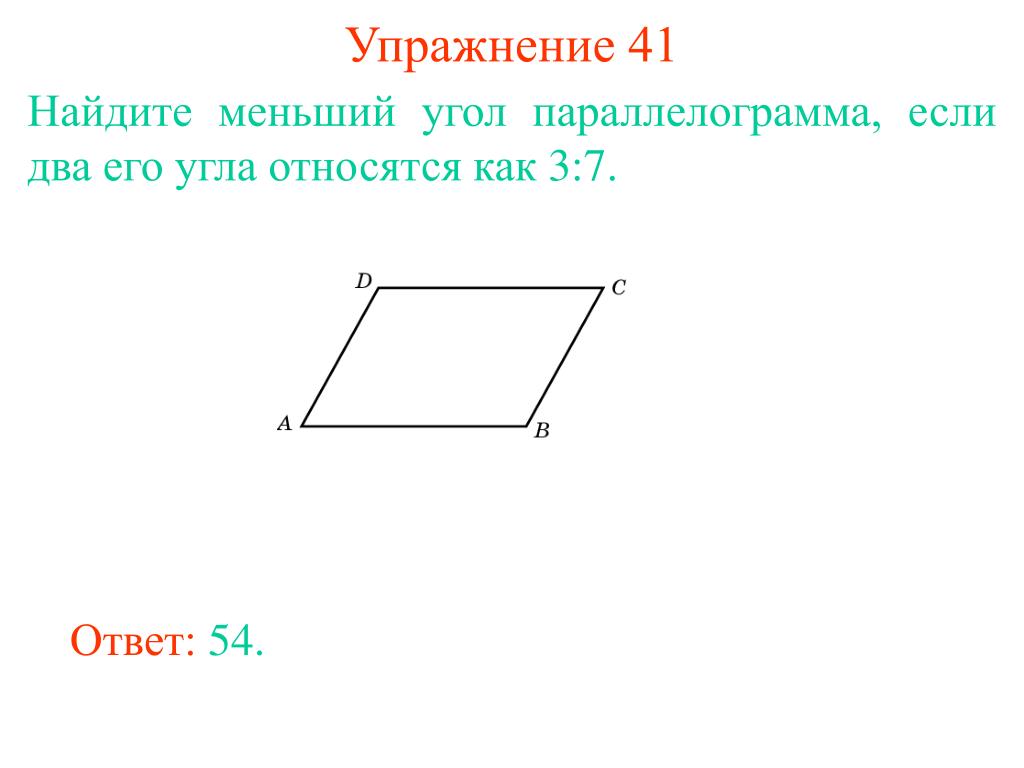 Ответ дайте
Ответ дайте Найдите больший угол этого параллелограмма. Ответ дайте
Найдите больший угол этого параллелограмма. Ответ дайте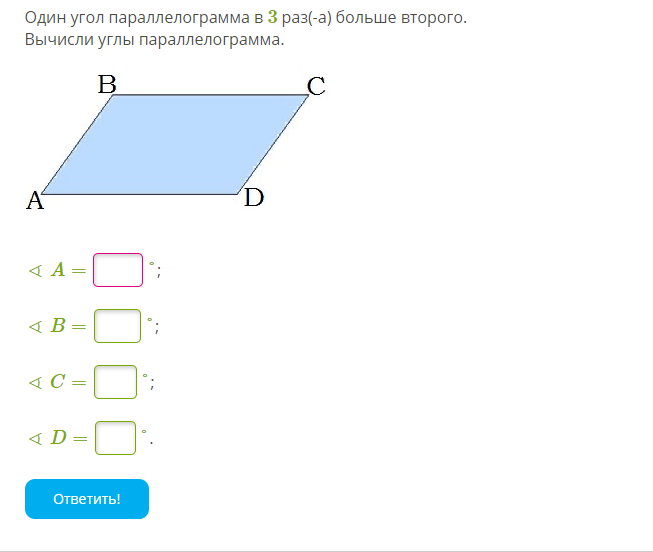 Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.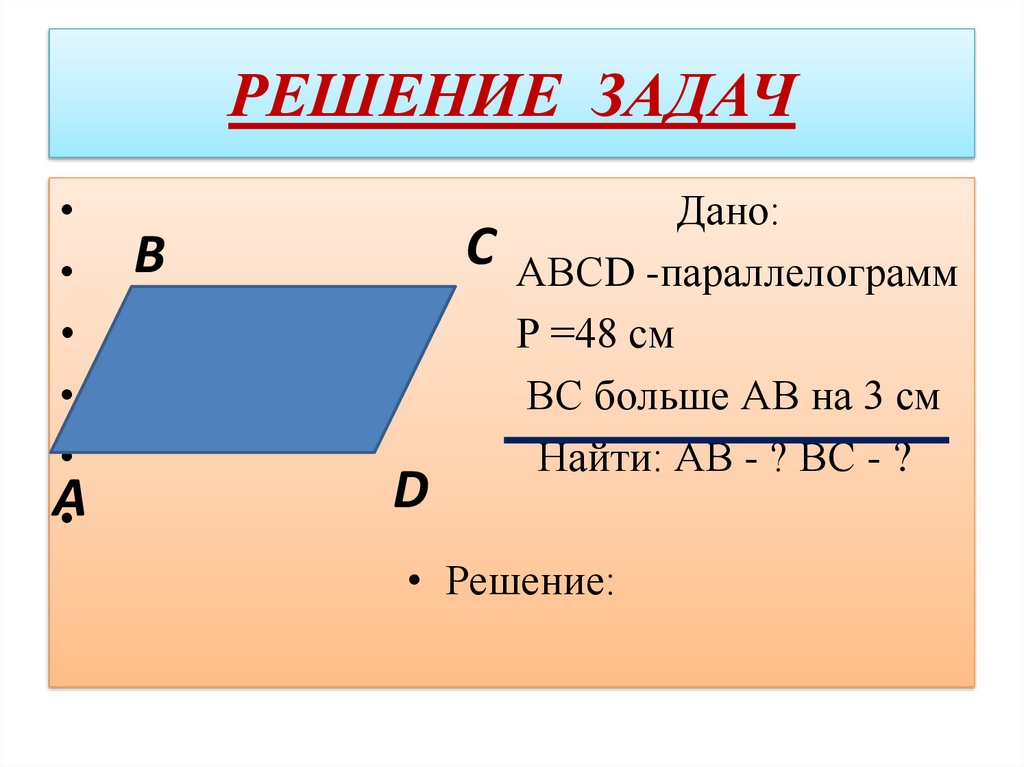 Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Найдите больший угол этого параллелограмма. Ответ дайте в градусах.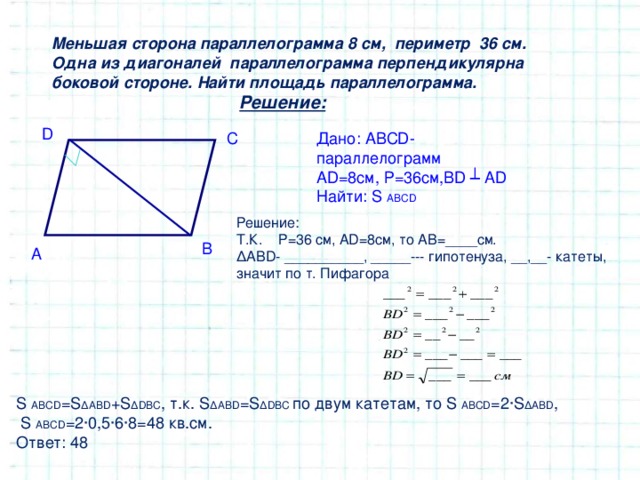
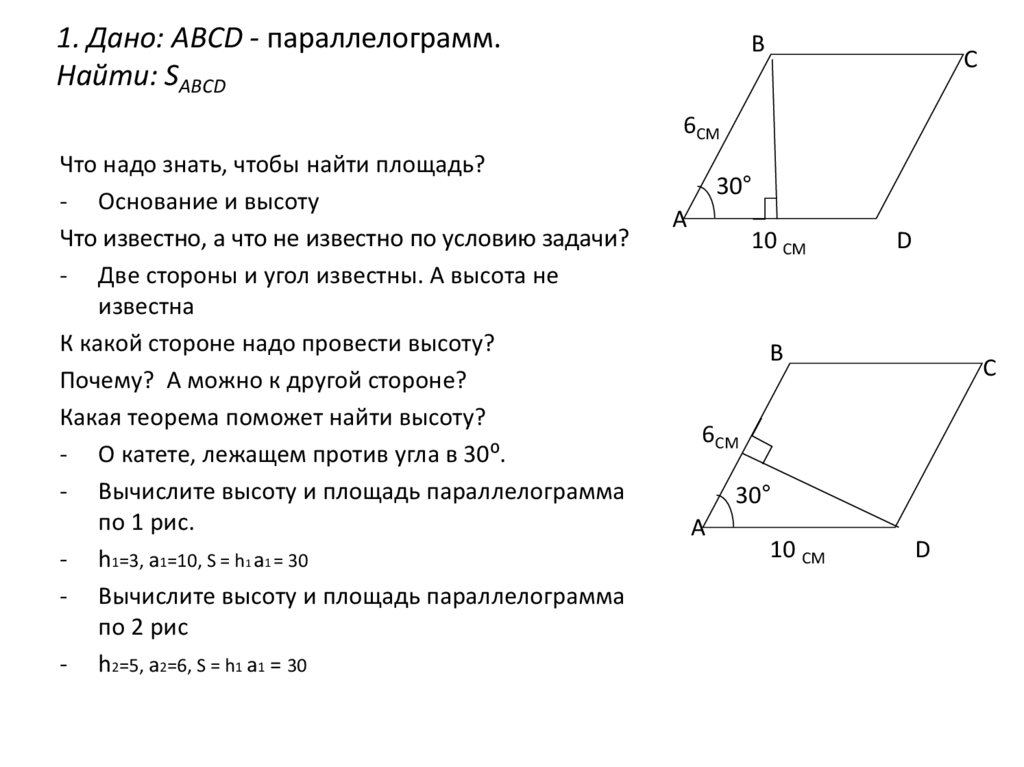 Докажите, что AE = CF.
Докажите, что AE = CF.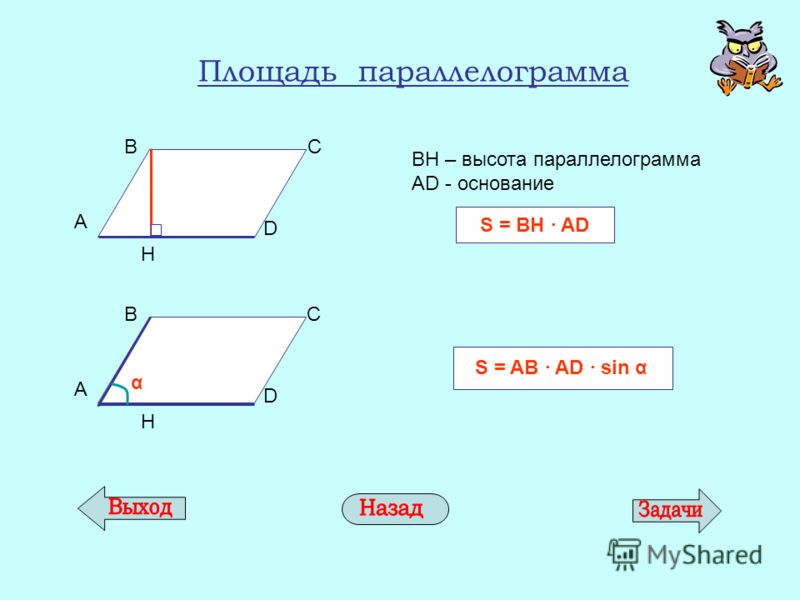
 Точка M лежит на основании AD и равноудалена от концов другого основания. Докажите, что M — середина основания AD.
Точка M лежит на основании AD и равноудалена от концов другого основания. Докажите, что M — середина основания AD.


Leave A Comment