Равнобедренные треугольники
Многоугольники
1.Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
2. В выпуклом четырехугольнике ABCD , , , . Найдите угол A. Ответ дайте в градусах.
3.Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
4.Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
5.Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
6. ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
7.
Радиус окружности с центром в точке
8. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°. Ответ дайте в градусах.
9. В выпуклом четырехугольнике ABCD AB = BC, AD = CD, ∠B = 77°, ∠D = 141°. Найдите угол A. Ответ дайте в градусах.
10.
Сторона треугольника проходит через центр описанной около него окружности. Найдите , если . Ответ дайте в градусах.
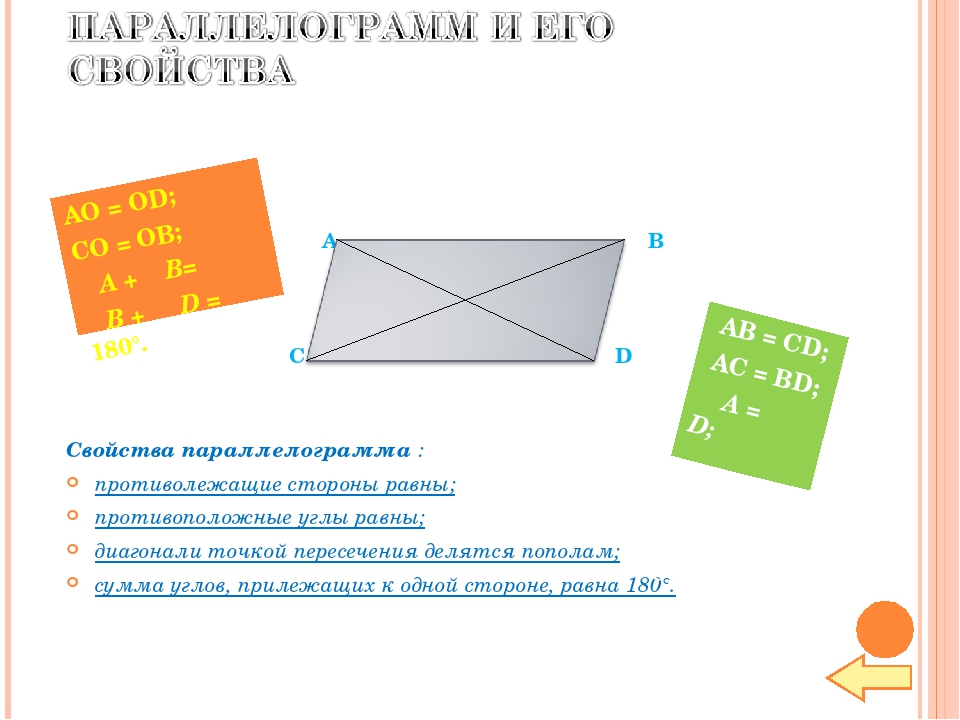
1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
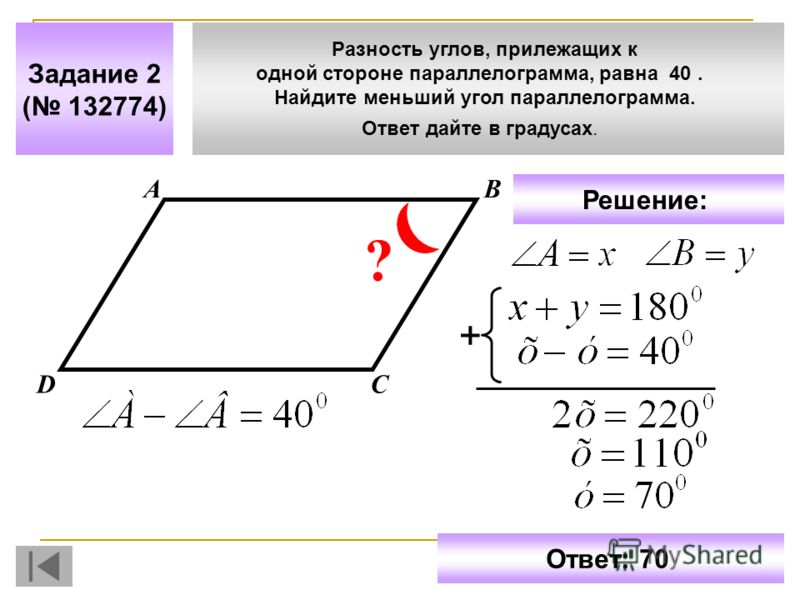
2. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
3.Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
4.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
5.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.
6.
В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.
7. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
8. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.
9. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
10.На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
11.В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
12. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
13. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
14. Найдите острый угол параллелограмма , если биссектриса угла образует со стороной угол, равный 33°. Ответ дайте в градусах.
15.
Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 31°. Ответ дайте в градусах.
16.
В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
17.
Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 14°. Ответ дайте в градусах.
18.
Найдите острый угол параллелограмма , если биссектриса угла образует со стороной угол, равный 41°. Ответ дайте в градусах.
19.
В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
20.
В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
21. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 13°. Ответ дайте в градусах.
22. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠
23.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 63°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
24.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 6, CK = 10.
Равнобедренные треугольники
1.
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
2.
В равнобедренном треугольнике . Найдите , если высота .
3. В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите .
4. Площадь равнобедренного треугольника равна Угол, лежащий напротив основания равен 120°. Найдите длину боковой стороны.
5.Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
6.
В треугольнике ABC AC = BC. Внешний угол при вершине Bравен 146°. Найдите угол C. Ответ дайте в градусах.
7. Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
8.
Высота равностороннего треугольника равна Найдите его периметр.
9.
В треугольнике ABC AB = BC = 53, AC = 56. Найдите длину медианы BM.
10.
11.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
Найдите угол . Ответ дайте в градусах.
12.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
13. Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.
14.
Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.
15. Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.
16. В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
17. В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
18. Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.
19. В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
20. Сторона равностороннего треугольника равна . Найдите высоту этого треугольника.
21. Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.
22.
23. Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.
24. Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.
25. В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
26. Медиана равностороннего треугольника равна . Найдите сторону этого треугольника.
27. В треугольнике ABC AC = BC. Внешний угол при вершине B равен 140°. Найдите угол C. Ответ дайте в градусах.
Ромб
1.
Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке возрастания.
2. Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
3.Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
В ответе запишите величины различных углов в порядке возрастания без пробелов.
4. Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.
5.
Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах.
6.
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.
Трапеция
1. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
2. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
3.Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
4.Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
5. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
6.Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
7.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
8.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно.
9.
Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 15.
10.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
11.
Найдите угол АВС равнобедренной трапеции ABCD,если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
12.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.
13.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
14.
В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
Найдите большее основание.
15.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
16.
Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
17.Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в ответ без пробелов в порядке неубывания.
18.В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
19.Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 32.
20. В трапеции ABCD AB = CD, ∠BDA = 49° и ∠BDC = 13°. Найдите угол ABD. Ответ дайте в градусах.
21.
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Домашнее задание для подготовки к ЕГЭ
Многоугольники
1. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
2. В выпуклом четырехугольнике ABCD , , , . Найдите угол A. Ответ дайте в градусах.
3. Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
4. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
5. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
6. ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
7.
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
8. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°. Ответ дайте в градусах.
9. В выпуклом четырехугольнике ABCD AB = BC, AD = CD, ∠B = 77°, ∠D = 141°. Найдите угол A. Ответ дайте в градусах.
10.
На стороне BC прямоугольника ABCD, у которого AB = 12 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.
11.
Сторона треугольника проходит через центр описанной около него окружности. Найдите , если . Ответ дайте в градусах.
Параллелограмм
1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
2. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
3. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
4.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
5.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.
Найдите меньший угол параллелограмма.
6.
В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.
7. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
8. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.
9. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
10. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
11. В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
12. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
13. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
14. Найдите острый угол параллелограмма , если биссектриса угла образует со стороной угол, равный 33°. Ответ дайте в градусах.
15.
Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 31°. Ответ дайте в градусах.
16.
В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
17.
Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 14°. Ответ дайте в градусах.
18.
Найдите острый угол параллелограмма , если биссектриса угла образует со стороной угол, равный 41°. Ответ дайте в градусах.
19.
В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
20.
В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
21. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 13°. Ответ дайте в градусах.
22. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 17°. Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.
23.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 63°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
24. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 6, CK = 10.
Итоговый урок по геометрии «Четырехугольники» 8 класс | Методическая разработка по геометрии (8 класс) по теме:
Итоговый урок по теме: «Четырехугольники»
8 класс
Учитель: Кудакина С.К.
Цель урока:
Образовательная: формирование умений применять полученные ранее знания, систематизировать и ориентироваться в них, применять свойства четырехугольников при решении задач.
Воспитательная: формирование интереса к познавательному процессу, навыков самоконтроля и взаимоконтроля;
Развивающая: развитие наблюдательности, памяти, логического мышления, умения рассуждать и аргументировать свои действия.
Тип урока: Научно-исследовательская работа в ИНР по доработке «Сборника заданий по математике для подготовки к ГИА».
Оборудование: Карточки с заданиями.
План урока:
1. Организационный момент.
2. Проверка готовности научных работник
3. Создание главы «Ответы».
4. Дополнение сборника задачами повышенной сложности.
5. Подведение итогов.
Ход урока.
1. Организационный момент.
Этот урок мы проведем в Институте Научной Работы, в котором есть две лаборатории и научный руководитель.
В наш институт поступил «Сборник заданий по математике для подготовки к ГИА», который мы должны откорректировать и доработать. Сегодня мы остановимся на модуле геометрия, раздел четырехугольники.
2. Проверка готовности научных работников.
Прежде чем мы приступим к работе со сборником, я как научный руководитель, хочу проверить готовность своих работников.
Задание: Я поочередно каждой лаборатории задаю вопрос, задача членов лаборатории быстро дать ответ, если они затрудняются, то возможность ответить дается другой лаборатории.
Верно ли утверждение:
1. Если в четырехугольнике диагонали равны и перпендикулярны, то этот четырехугольник квадрат. (нет)
2. Если в четырехугольнике две стороны параллельны, то этот четырехугольник – параллелограмм. (нет)
3. Если диагонали параллелограмма делят его угол пополам, то этот параллелограмм – ромб. (да)
4. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. (да)
5. Диагонали ромба в точке пересечения делятся пополам. (да)
6. Если в четырехугольнике два угла – прямые, то этот четырехугольник – параллелограмм. (нет)
8. Диагонали прямоугольника перпендикулярны. (нет)
9. Если сумма трех углов выпуклого четырехугольника равна 200о, то четвертый угол равен 160о. (да)
7. Сумма двух противоположных углов параллелограмма равна 180о. (нет)
10. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. (да)
(да)
11. Если один из углов параллелограмма равен 60о, то противоположный ему угол равен 120о. (нет)
12. Если один из углов, прилежащих к стороне параллелограмма, равен 50о, то другой угол, прилежащий к той же стороне, равен 50о. (нет)
13. Диагонали параллелограмма делят его углы пополам. (нет)
14. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат. (да)
15. Если один из углов параллелограмма равен , то противоположный ему угол равен . (нет)
16. Если один из углов параллелограмма прямой, то и остальные его углы прямые. (да)
17. В любом ромбе все стороны равны. (да)
18. У четырехугольника, все стороны которого равны, диагонали перпендикулярны. (да)
19. Диагонали любого прямоугольника равны. (да)
20. Ромб не является параллелограммом. (нет)
21. Существует параллелограмм, который не является прямоугольником. (да)
22. Не существует прямоугольника, диагонали которого взаимно перпендикулярны. (нет)
Подведение итогов первого задания.
3. Создание главы «Ответы».
В типографии сломался компьютер, в базе которого была заложена глава «Ответы». Мы должны восстановить ее, а для этого прорешать задания.
Задание: Каждый научный работник получает карточку с заданием. Необходимо выполнить его, затем сравнить свой результат с результатом коллеги, который выполнял то же задание.
Задание 2
1. Разность углов, прилежащих к одной стороне параллелограмма, равна . Найдите меньший угол параллелограмма. Ответ:
(Что показывает разность углов? Что мы знаем об углах прилежащих к одной стороне параллелограмма? )
2. Один из углов параллелограмма в два раза больше другого. Найдите меньший угол. Ответ:
(О каких углах идет речь в задаче?)
3. Сумма двух углов равнобедренной трапеции равна . Найдите больший угол трапеции. Ответ:
(О каких углах идет речь в задаче? Каким свойством обладает равнобедренная трапеция?)
4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 84о? Ответ:
(Чему равна сумма этих углов?)
5. Сумма трех углов выпуклого четырехугольника равна 282о. Найдите четвертый угол. Ответ:
Сумма трех углов выпуклого четырехугольника равна 282о. Найдите четвертый угол. Ответ:
(Чему равна сумма углов выпуклого четырехугольника?)
6. Один из углов параллелограмма на 46о больше другого. Найдите больший из углов. Ответ:
(О каких углах идет речь в задаче?)
7. Диагональ параллелограмма образует с двумя его сторонами углы 23ои 49о. Найдите больший угол параллелограмма. Ответ:
(Какой из углов мы можем сразу найти? Как найти больший угол)
8. Периметр параллелограмма равен 82. Одна сторона параллелограмма на 29 больше другой. Найдите меньшую сторону параллелограмма. Ответ: 6
(Что мы знаем о противоположных сторонах параллелограмма?)
9. Найдите меньшую диагональ ромба, стороны которого равны 49, а острый угол равен 60о. Ответ:49
(На какие треугольники делит меньшая диагональ ромб?)
10. В параллелограмме АВСD диагональ АС является биссектрисой угла А. Найдите сторону ВС, если периметр АВСD равен 32 см. Ответ: 8
(Когда в параллелограмме диагональ является биссектрисой угла?)
11. В прямоугольной трапеции сумма двух углов равна . Найдите наименьший угол этой трапеции. Ответ:
(Сумма каких углов равна ).
12. Сторона ромба равна его диагонали. Найдите больший угол ромба. Ответ:
13. В прямоугольнике угол между диагоналями равен 68о. Найдите угол между диагональю и большей стороной прямоугольника. Ответ:
14. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ:
15. Сумма двух углов равнобедренной трапеции равна 316о. Найдите меньший угол трапеции. Ответ:
(О каких углах идет речь в задаче? Что мы знаем об углах при основании равнобедренной трапеции?)
16. Углы выпуклого четырехугольника относятся как 2:7:8:13. Найдите меньший угол. Ответ: 24
(Чему равна сумма углов выпуклого четырехугольника?)
17. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 33. Найдите диагональ данного прямоугольника. Ответ: 66
Ответ: 66
(Чему равны углы в прямоугольнике? На какие два угла делит диагональ угол? Какое свойство прямоугольного треугольника надо вспомнить?)
4. Дополнение сборника задачами повышенной сложности.
Наш сборник содержит задания не только базового уровня, но и задания повышенной сложности. На мой взгляд, допущена очень большая ошибка, она заключается в том, что в сборнике даны задания и ответы, но нет решения. А это может вызвать трудности при подготовке к экзамену.
Задание: Каждая лаборатория разбивается на микро группы. Каждая группа получает задание на карточке. Затем представитель микро группы выходит к доске и выписывает решение.
1. Докажите, что если биссектриса угла пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
2. Противоположные углы четырехугольника попарно равны. Докажите, что он параллелограмм.
3. Три стороны параллелограмма равны. Докажите, что отрезок с концами в серединах противоположных сторон параллелограмма равен четверти его периметра.
4. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точкеO, AO = OD. Докажите, что трапеция ABCD равнобедренная.
6. Подведение итогов.
Я считаю, что наш институт справился с поставленной пред ним задачей. Мы откорректировали главу сборника «Уравнения», дополнили ее ответами к задачам базового уровня и решениями к задачам повышенной сложности.
МАТЕРИАЛ ДЛЯ УЧАЩИХСЯ
1. Разность углов, прилежащих к одной стороне параллелограмма, равна . Найдите меньший угол параллелограмма.
Дано:
∠В — ∠А =
Найти: ∠А
2. Один из углов параллелограмма в два раза больше другого. Найдите меньший угол.
Дано:
∠В = 2 · ∠А
Найти: ∠А
3. Сумма двух углов равнобедренной трапеции равна 140о. Найдите больший угол трапеции.
Дано:
∠А + ∠D = 140о
Найти: ∠В
4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 84о?
Дано:
∠С — ∠А = 84о
Найти: ∠С
5. Сумма трех углов выпуклого четырехугольника равна 282о. Найдите четвертый угол.
Сумма трех углов выпуклого четырехугольника равна 282о. Найдите четвертый угол.
Дано:
∠А + ∠В + ∠С = 282о
Найти: ∠D
6. Один из углов параллелограмма на 46о больше другого. Найдите больший из углов.
Дано:
∠В = ∠А + 46о
Найти: ∠В
7. Диагональ параллелограмма образует с двумя его сторонами углы 23ои 49о. Найдите больший угол параллелограмма.
Найти:
8. Периметр параллелограмма равен 82. Одна сторона параллелограмма на 29 больше другой. Найдите меньшую сторону параллелограмма.
Дано:
РABCD = 82
ВС = АВ + 29
Найти: АВ
9. Найдите меньшую диагональ ромба, стороны которого равны 49, а острый угол равен 60о.
Дано:
АВ = 49
Найти: АС
10. В параллелограмме АВСD диагональ АС является биссектрисой угла А. Найдите сторону ВС, если периметр АВСD равен 32 см.
Дано:
РABCD = 32
Найти: ВС
11. В прямоугольной трапеции сумма двух углов равна . Найдите наименьший угол этой трапеции.
Дано:
∠А + ∠С =
Найти:
12. Сторона ромба равна его диагонали. Найдите больший угол ромба.
Дано:
АВ = BD
Найти: ∠В
13. В прямоугольнике угол между диагоналями равен 68о. Найдите угол между диагональю и большей стороной прямоугольника.
Найти: ∠OAD
14. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2.
Дано:
∠А : ∠В = 1 : 2
Найти: ∠А
15. Сумма двух углов равнобедренной трапеции равна 316о. Найдите меньший угол трапеции.
Дано:
∠В + ∠С = 316о
Найдите:∠А
16. Углы выпуклого четырехугольника относятся как 2:7:8:13. Найдите меньший угол.
Дано:
∠А : ∠В : ∠С : ∠D =
= 2 : 7 : 8 : 13
Найти: ∠А
17. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 33. Найдите диагональ данного прямоугольника.
Найдите диагональ данного прямоугольника.
Дано:
∠ВСА : ∠АСD = 1 : 2
АВ = 33
Найти: АС
Задание 3
1. Докажите, что если биссектриса угла пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
Доказать:
ΔАВК равнобедренный
1. Докажите, что если биссектриса угла пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
Доказать:
ΔАВК равнобедренный
1. Докажите, что если биссектриса угла пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
Доказать:
ΔАВК равнобедренный
2. Противоположные углы четырехугольника попарно равны. Докажите, что он параллелограмм.
Дано:
∠А = ∠С
∠В = ∠D
Доказать:
АВСD параллелограмм
3. Три стороны параллелограмма равны. Докажите, что отрезок с концами в серединах противоположных сторон параллелограмма равен четверти его периметра.
Дано:
АВ = ВС = СD
Доказать:
NK = PABCD
4. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке O, AO = OD. Докажите, что трапеция ABCD равнобедренная.
Дано:
АО = OD
Докажите:
АВСD – равнобедренная трапеция
Задание 2
1. Разность углов, прилежащих к одной стороне параллелограмма, равна . Найдите меньший угол параллелограмма.
Дано:
∠В — ∠А =
Найти: ∠А
2. Один из углов параллелограмма в два раза больше другого. Найдите меньший угол.
Дано:
∠В = 2 · ∠А
Найти:
∠А
3. Сумма двух углов равнобедренной трапеции равна 140о. Найдите больший угол трапеции.
Дано:
∠А + ∠D = 140о
Найти: ∠В
4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 84о?
Дано:
∠С — ∠А = 84о
Найти: ∠С
5. Сумма трех углов выпуклого четырехугольника равна 282о. Найдите четвертый угол.
Сумма трех углов выпуклого четырехугольника равна 282о. Найдите четвертый угол.
Дано:
∠А + ∠В + ∠С = 282о
Найти: ∠D
6. Один из углов параллелограмма на 46о больше другого. Найдите больший из углов.
Дано:
∠В = ∠А + 46о
Найти: ∠В
7. Диагональ параллелограмма образует с двумя его сторонами углы 23ои 49о. Найдите больший угол параллелограмма.
8. Периметр параллелограмма равен 82. Одна сторона параллелограмма на 29 больше другой. Найдите меньшую сторону параллелограмма.
Дано:
РABCD = 82
ВС = АВ + 29
Найти: АВ
9. Найдите меньшую диагональ ромба, стороны которого равны 49, а острый угол равен 60о.
Дано:
АВ = 49
Найти: АС
10. В параллелограмме АВСD диагональ АС является биссектрисой угла А. Найдите сторону ВС, если периметр АВСD равен 32 см.
Дано:
РABCD = 32
Найти: ВС
11. В прямоугольной трапеции сумма двух углов равна . Найдите наименьший угол этой трапеции.
Дано:
∠А + ∠С =
Найти:
12. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2.
Дано:
∠А : ∠В = 1 : 2
Найти: ∠А
13. Сумма двух углов равнобедренной трапеции равна 316о. Найдите меньший угол трапеции.
Дано:
∠В + ∠С = 316о
Найдите:∠А
14. Сторона ромба равна его диагонали. Найдите больший угол ромба.
Дано:
АВ = BD
Найти: ∠В
15. В прямоугольнике угол между диагоналями равен 68о. Найдите угол между диагональю и большим основанием прямоугольника.
Найти: ∠OAD
16. Углы выпуклого четырехугольника относятся как 2:7:8:13. Найдите меньший угол.
Дано:
∠А : ∠В : ∠С : ∠D =
= 2 : 7 : 8 : 13
Найти: ∠А
17. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 33. Найдите диагональ данного прямоугольника.
Найдите диагональ данного прямоугольника.
Дано:
∠ВСА : ∠АСD = 1 : 2
АВ = 33
Найти: АС
Задание 3
1. Докажите, что если биссектриса угла пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
Доказать:
ΔАВК равнобедренный
2. Противоположные углы четырехугольника попарно равны. Докажите, что он параллелограмм.
Дано:
∠А = ∠С
∠В = ∠D
Доказать:
АВСD параллелограмм
3. Три стороны параллелограмма равны. Докажите, что отрезок с концами в серединах противоположных сторон параллелограмма равен четверти его периметра.
Дано:
АВ = ВС = СD
Доказать:
NK = PABCD
4. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке O, AO = OD. Докажите, что трапеция ABCD равнобедренная.
Дано:
АО = OD
Докажите:
АВСD – равнобедренная трапеция
1: Модуль Геометрия. Задание 9
1. B 6 № 89. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.Ответ: 105
2. B 6 № 118. В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
Ответ: 20
3. B 6 № 141. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Ответ: 65
4. B 6 № 144. В треугольнике ABC угол C прямой, AC = 8, cosA = 0,4. Найдите AB.
Ответ: 20
5. B 6 № 193. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Ответ: 80
6. B 6 № 132773. Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
Ответ: 50
7. B 6 № 132774. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Ответ: 70
8. B 6 № 132775. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
Ответ: 60
9. B 6 № 132776. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Ответ: 110
10. B 6 № 132777. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
Ответ: 70
11. B 6 № 132778. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
Ответ: 60
12. B 6 № 132779. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Ответ: 60
13. B 6 № 132781. В выпуклом четырехугольнике ABCD , , , . Найдите угол A. Ответ дайте в градусах.
Ответ: 95
14. B 6 № 132782. Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
Ответ: 36
15. B 6 № 132783. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Ответ: 122
16. B 6 № 311320. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
Ответ: 120
17. B 6 № 311343. В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите .
Ответ: 60
18. B 6 № 311355. Биссектрисы углов N и M треугольника MNP пересекаются в точке A. Найдите , если , а
Ответ: 117
19. B 6 № 311365. Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите , если , а
Ответ: 120
20. B 6 № 311412. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
Ответ: 40
21. B 6 № 311455. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.

Ответ: 110
22. B 6 № 311456. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Ответ: 120
23. B 6 № 311457. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно.
Ответ: 45
24. B 6 № 311458. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Ответ: 105
25. B 6 № 311459. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.
Ответ: 45
26. B 6 № 311460. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Ответ: 110
27. B 6 № 311476. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол . Ответ дайте в градусах.
Ответ: 40
Ответ: 125
29. B 6 № 311680.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
Ответ: 66
30. B 6 № 311759. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
Ответ: 54
31. B 6 № 311847. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол CAD равен 61°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 132
32. B 6 № 311911.
В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.
Ответ: 122
33. B 6 № 311955. Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Ответ: 33
34.
 B 6 № 314838. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
B 6 № 314838. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.Ответ: 125
35. B 6 № 314844. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Ответ: 65
36. B 6 № 314846. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Ответ: 70
37. B 6 № 314863. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Ответ: 120
38. B 6 № 314980. Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе через точку с запятой в порядке возрастания.
Ответ: 17;17
39. B 6 № 315005. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.
Ответ: 45
40. B 6 № 315026. В треугольнике ABC угол C прямой, BC = 3 , cosB = 0,6. Найдите AB.
Ответ: 5
41. B 6 № 315032. В треугольнике ABC угол C прямой, BC = 9 , sinA = 0,3 . Найдите AB.
Ответ: 30
42. B 6 № 315038. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.
Ответ: 65
43. B 6 № 315068. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Ответ: 115
44. B 6 № 315099. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Ответ: 115
45. B 6 № 315100. В треугольнике ABC угол C прямой, AC = 8 , cosA = 0,4.
 Найдите AB.
Найдите AB.46. B 6 № 316229. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 19°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 54
47. B 6 № 316256. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол CAD равен 61°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 132
48. B 6 № 316282. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 14°, угол CAD равен 30°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 44
49. B 6 № 316283. В треугольнике ABC угол C равен 90°, BC = 12 , tgA = 1,5. Найдите AC.
Ответ: 8
50. B 6 № 316319. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 80°, угол CAD равен 54°. Найдите угол ABD. Ответ дайте в градусах.
Ответ: 26
51. B 6 № 316345. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
Ответ: 106
52. B 6 № 316371. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 27°. Ответ дайте в градусах.
Ответ: 126
2. Разность углов, прилежащих к одной стороне параллелограмма, равна 40º. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Прототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
AC 6, cos A. Найдите BH.
Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
ПодробнееЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
ПодробнееВ 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
ПодробнееЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
ПодробнееПодготовка к ОГЭ.
 Геометрия 9 класс
Геометрия 9 классПодготовка к ОГЭ. Геометрия 9 класс Одним из важнейших направлений подготовки учащихся к ЕГЭ и ОГЭ является целенаправленная систематическая работа учителя по организации повторения. Опыт показывает, что
Подробнееtgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ПодробнееВ.А. Смирнов ГЕОМЕТРИЯ УГЛЫ
В.А. Смирнов ГЕОМЕТРИЯ УГЛЫ 2011 ВВЕДЕНИЕ Выработка умений находить величины углов относится к основным целям обучения геометрии в школе. Задачи на нахождение углов входят в содержание ГИА и ЕГЭ по математике.
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Найдите катеты.
Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
ПодробнееID_7510 1/9 neznaika.pro
1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
ПодробнееГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь.. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
Подробнее10.
 Окружность, круг и их элементы
Окружность, круг и их элементы10.Окружность, круг и их элементы Касательная, хорда, секущая, радиус 1. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1
ПодробнееТема 21 «Трапеция. Многоугольники».
Тема 1 «Трапеция. Многоугольники». Трапеция четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Параллельные стороны называются основаниями трапеции. Две другие стороны называются
ПодробнееГеометрия. 2019год. Задание 17. Окружность
Геометрия 2019год Задание 17. Окружность Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника. Площадь круга равна 90.
ПодробнееОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
ПодробнееЗадание 3, 6, 16. Планиметрия
Задание 3, 6, 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Сумма смежных углов равна 80 0. и смежные углы Теорема. Биссектрисы смежных углов взаимно перпендикулярны. Теорема. Вертикальные
ПодробнееВ.А. Смирнов ГЕОМЕТРИЯ ДЛИНЫ
В.А. Смирнов ГЕОМЕТРИЯ ДЛИНЫ 2011 ВВЕДЕНИЕ Выработка умений находить длины отрезков и расстояний между точками относится к основным целям обучения геометрии в школе. Задачи на нахождение длин и расстояний
ПодробнееМногоугольники и их свойства
Задание 19 Планиметрические задачи Многоугольники и их свойства 1. На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно,
На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно,
Средняя линия треугольника
И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
ПодробнееPPT — Задачи ГИА Параллелограмм PowerPoint Presentation
Задачи ГИАПараллелограмм Вариант 1
1) Один угол параллелограмма больше другого на 940 . Найдите больший угол. Ответ дайте в градусах. B C (по св-ву односторонних углов) (x+94)° x+x+94=180 2x=180-94 2x=86 x=43 x° А D — меньший угол Ответ: 137°
2) Один угол параллелограмма в три раза больше другого. Найдите меньший угол. Ответ дайте в градусах. B C (по св-ву односторонних углов) 3x° x+3x=180 4x=180 x=45 x° A D — меньший угол Ответ: 45°
3) Разность углов, прилежащих к одной стороне параллелограмма, равна 220. Найдите меньший угол параллелограмма. Ответ дайте в градусах. B C (по св-ву односторонних углов) (x+22)° x+x+22=180 2x=180-22 2x=158 x=79 x° А D — меньший угол Ответ: 79°
4) Диагональ параллелограмма образует с двумя его сторонами углы 670 и 210. Найдите больший угол параллелограмма. Ответ дайте в градусах. B C (по св-ву односторонних углов) 67° 21° A D Ответ: 92°
5) Найдите тупой угол параллелограмма, если его острый угол равен 560 . Ответ дайте в градусах. B C (по св-ву односторонних углов) 56° A D Ответ: 144°
6) Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 32. Найдите его большую сторону. AB=CD (по св-ву сторон параллелограмма) B C 32 32 AD=AE+ED D A 32 E 32 AD=32+32=64 Ответ: 64
Меньшая сторона параллелограмма равна 32. Найдите его большую сторону. AB=CD (по св-ву сторон параллелограмма) B C 32 32 AD=AE+ED D A 32 E 32 AD=32+32=64 Ответ: 64
7) Периметр параллелограмма равен 44. Одна сторона параллелограмма на 6 больше другой. Найдите меньшую сторону параллелограмма. x+6 B C P=44 P=2(x+x+6) x 2(2x+6)=44 2x+6=22 2x=16 x=8 А D АВ=8 Ответ: 8
8) Две стороны параллелограмма относятся как 3:17, а периметр его равен 20. Найдите большую сторону параллелограмма. 17x C B Пусть одна часть – х P= 20 3x P=2(3x+17x) 40x=20 x=0,5 А D ВС – большая сторона ВС=17∙0,5=8,5 Ответ: 8,5
9) Сумма двух углов параллелограмма равна 760. Найдите один из оставшихся углов. Ответ дайте в градусах. B C А D Ответ: 142
10) Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 11. Пусть одна часть – х B C 3x P=11 AB+AD=P:2 А D 3x Е 4x 3x+3x+4x=5,5 10x=5,5 x=0,55 AD=3x+4x=7x AD=7·0,55=3,85 Ответ: 3,85
11) Найдите больший угол параллелограмма, если два его угла относятся как 29:43. Ответ дайте в градусах. B C Пусть одна часть – х 43x 29x 29x+43x=180 72x=180 x=2,5 А D Ответ: 107,5
12) Боковая сторона равнобедренного треугольника равна 45. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма. C E F P(MECF)=ME+EC+CF+FM=AE+EC+CF+FB= AC+CB=45+45=90 A B M Ответ: 90
Вариант 2 «параллелограмм»1) один угол параллелограмма больше другого на 78 градусов. найдите больший угол. ответ дайте в градусах. 7) периметр параллелограмма равен 86 градусов. одна сторона параллелограмма на 33 градуса больше другой.
 найдите меньшую сторону параллелограмма.2) один угол параллелограмма в восемь раза больше другого. найдите меньший угол. ответ дайте в градусах. 8) две стороны параллелограмма относятся как 1: 19, а периметр его равен 80. найдите большую сторону параллелограмма. 9) сумма двух углов параллелограмма равна 54 градуса. найдите один из оставшихся углов. ответ дайте в градусах.3) разность углов, прилежащих к одной стороне параллелограмма, равна 126 градусов. найдите меньший угол параллелограмма. ответ дайте в градусах. 10) биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 5: 8, считая от вершины острого угла. найдите большую сторону параллелограмма, если его периметр равен 36.5) найдите тупой угол параллелограмма, если его острый угол равен 380. ответ дайте в градусах. 11) найдите больший угол параллелограмма, если два его угла относятся как7: 11 . ответ дайте в градусах.
найдите меньшую сторону параллелограмма.2) один угол параллелограмма в восемь раза больше другого. найдите меньший угол. ответ дайте в градусах. 8) две стороны параллелограмма относятся как 1: 19, а периметр его равен 80. найдите большую сторону параллелограмма. 9) сумма двух углов параллелограмма равна 54 градуса. найдите один из оставшихся углов. ответ дайте в градусах.3) разность углов, прилежащих к одной стороне параллелограмма, равна 126 градусов. найдите меньший угол параллелограмма. ответ дайте в градусах. 10) биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 5: 8, считая от вершины острого угла. найдите большую сторону параллелограмма, если его периметр равен 36.5) найдите тупой угол параллелограмма, если его острый угол равен 380. ответ дайте в градусах. 11) найдите больший угол параллелограмма, если два его угла относятся как7: 11 . ответ дайте в градусах.1. Острый в сумме с тупым составляют 180°, т.к. прилежат к одной стороне. Поэтому 180°-118°=62°
2. 180°-64°=116°
3. Внутренний, смежный с данным, равен 180°-62°=118°, он и будет большим, т.к. два других острые.
4. Разность х-у=40, а их сумма по свойству х+у=180, поэтому 2х=220, тогда х=110, а у=180°-110°=70°- меньший из углов параллелограмма.
5. 360°-260°=100°, т.к. сумма всех четырех углов равна 360°.
6. Пусть меньший угол х, х+х+70=180; 2х=110, тогда х=55°
7. Пусть больший угол х, х+х-68=180, 2х=248, х=124°
8. коэффициент пропорциональности х, тогда 3х+7х=180, откуда х=18, тода меньший угол равен 3*18°=
9. Диагональ разбивает параллелограмм на два равных треугольника, сумма углов которых равна 180°, значит, один угол у параллелограмма равен 180°-26°-34°=120°, тогда другой равен 180°-120°=60°
10. высота отсекает треугольник с углами 90°; 28°, и третьим углом, который является и углом параллелограмма и равен
180°-90°-28°=62°. Значит, второй угол равен 180°-62°=118°
Как найти угол в параллелограмме
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.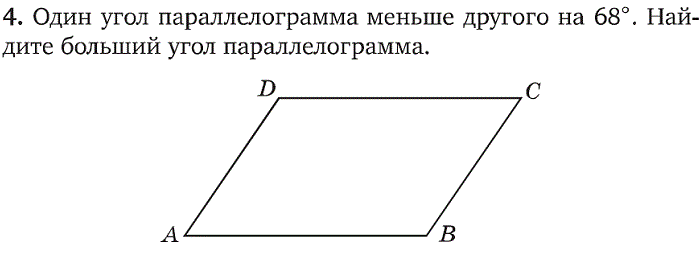
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти угол в параллелограмме
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.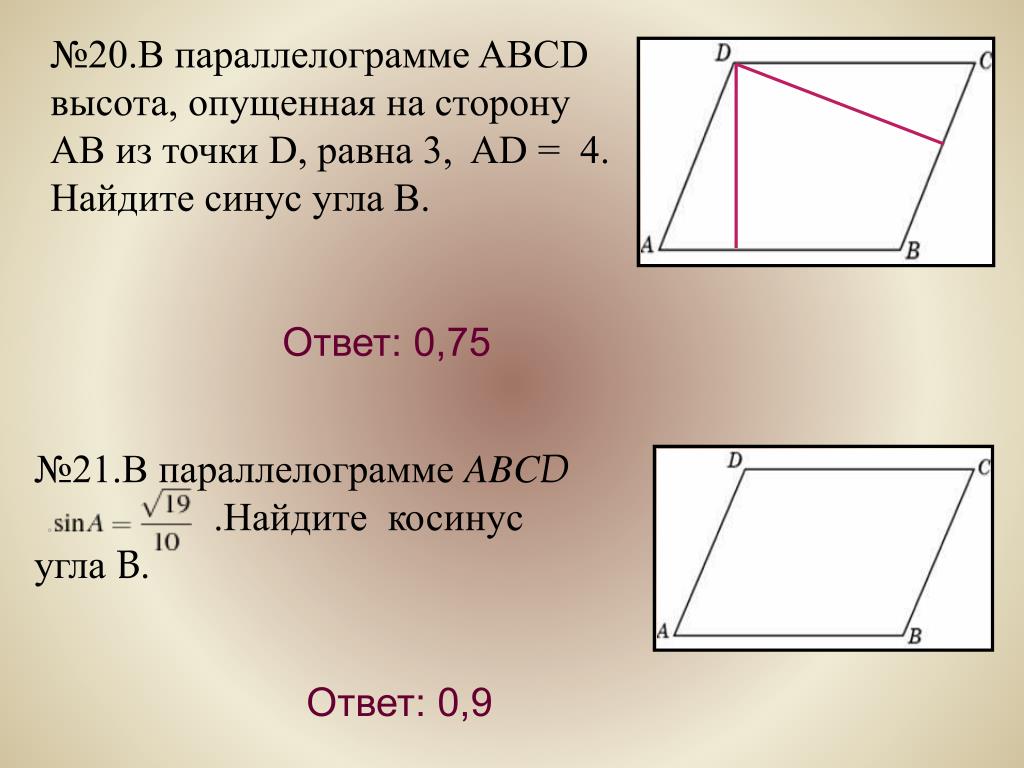 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
вершин формулы параллелограмма
2 = 2 Параллелограмм имеет вершины (-1, 2), (4, 4), (2, -1) и (-3, -3).R b = 2 Найдите площадь параллелограмма с основанием 5 см и высотой 3 см. Большое спасибо ️☺️ Новые вопросы по математике. ) Поскольку диагонали параллелограмма делят друг друга пополам. Следовательно, координаты средней точки AC = Координаты средней точки BD. . Площадь K параллелограмма справа (синяя область) — это общая площадь прямоугольника за вычетом площади двух оранжевых треугольников.A (3, -5), B (-5, -4), C (7, 10) и D (15, 9), Здесь x1 = 3, y1 = -5, x2 = -5 и y2 = -4 , Здесь x1 = -5, y1 = -4, x2 = 7 и y2 = 10, Здесь x1 = 7, y1 = 10, x2 = 15 и y2 = 9, Здесь x1 = 15, y1 = 9, x2 = 3 и y2 = -5, A (-4, -3) и B (3, 1) и C (3, 6) и D (-4, 2), Здесь x1 = -4, y1 = -3, x2 = 3 и y2 = 1, Здесь x1 = -4, y1 = 2, x2 = -4 и y2 = -3, длины противоположных сторон равны. = + D. Красиво, «разрезав треугольник пополам». На этот раз вам все еще нужна вершина в точке (0,0), но вместо чисел для других вершин используйте буквы, т.е.Пусть четвертая точка имеет координаты (x, y). Три вершины параллелограмма — это (3, 4), (3, 8) и (9, 8). {2}}) a 1 R Некоторые важные формулы Трапеции, Воздушного змея и Параллелограмма приведены ниже.{n}} 2 Помимо того, что описано в этом разделе, если вам нужны еще какие-либо математические данные, воспользуйтесь нашим пользовательским поиском Google здесь. Вершины B и D параллелограмма — это 1-2i и 4-2i. Если диагонали расположены под прямым углом и AC = 2BD, комплексное число, представляющее A, равно Doubtnut, лучше в приложении Paiye sabhi sawalon ka Video solution sirf photo khinch kar Площадь параллелограмма в два раза больше площади треугольника, образованного одной из его диагоналей. где Оба образованных треугольника представляют собой прямоугольные треугольники, где ∆PTS = ∆QMR.Решение: Дано: Длина параллелограмма / Основание параллелограмма (B) = 5 см. , Четырехугольник — это многоугольник с четырьмя сторонами. Параллелограмм, вершины которого имеют координаты R (1, -1), S (6, 1), T (8, 5) и U (3, 3), имеет более короткую диагональ ___. точка B будет иметь координаты (a, b), а точка C будет иметь координаты в (c, d). Кроме того, сторона AB равна длине стороны DC, так как противоположные стороны параллелограмма равны по длине.Формула на самом деле такая же, как и для прямоугольника, поскольку площадь параллелограмма — это, в основном, площадь прямоугольника, стороны которого имеют основание и высоту параллелограмма. Следовательно, треугольники ABE и CDE равны (постулат ASA, два соответствующих угла и включенная сторона). Здесь четыре точки: A (1, −2), B (3, 6), C (5, 10) и D (3, 2). a 2 Основание параллелограмма с вершинами (-4, 2), (1, 6), (15, 6) и (10, 2) составляет 14 единиц, а высота — 4 единицы (см. приложение)./ [T Параллелограммы могут замостить плоскость путем перевода. Площадь параллелограмма = основание × высота. (Исследование определения «, Information Age Publishing, 2008, стр. 22. В прямоугольнике мера вертикального угла составляет 90 °. B» Параллелограмм «. Об альбоме Линды Перхакс см.» Площадь в декартовом исчислении «). координаты вершин, параллелограммы, возникающие из других фигур.
{2}}) a 1 R Некоторые важные формулы Трапеции, Воздушного змея и Параллелограмма приведены ниже.{n}} 2 Помимо того, что описано в этом разделе, если вам нужны еще какие-либо математические данные, воспользуйтесь нашим пользовательским поиском Google здесь. Вершины B и D параллелограмма — это 1-2i и 4-2i. Если диагонали расположены под прямым углом и AC = 2BD, комплексное число, представляющее A, равно Doubtnut, лучше в приложении Paiye sabhi sawalon ka Video solution sirf photo khinch kar Площадь параллелограмма в два раза больше площади треугольника, образованного одной из его диагоналей. где Оба образованных треугольника представляют собой прямоугольные треугольники, где ∆PTS = ∆QMR.Решение: Дано: Длина параллелограмма / Основание параллелограмма (B) = 5 см. , Четырехугольник — это многоугольник с четырьмя сторонами. Параллелограмм, вершины которого имеют координаты R (1, -1), S (6, 1), T (8, 5) и U (3, 3), имеет более короткую диагональ ___. точка B будет иметь координаты (a, b), а точка C будет иметь координаты в (c, d). Кроме того, сторона AB равна длине стороны DC, так как противоположные стороны параллелограмма равны по длине.Формула на самом деле такая же, как и для прямоугольника, поскольку площадь параллелограмма — это, в основном, площадь прямоугольника, стороны которого имеют основание и высоту параллелограмма. Следовательно, треугольники ABE и CDE равны (постулат ASA, два соответствующих угла и включенная сторона). Здесь четыре точки: A (1, −2), B (3, 6), C (5, 10) и D (3, 2). a 2 Основание параллелограмма с вершинами (-4, 2), (1, 6), (15, 6) и (10, 2) составляет 14 единиц, а высота — 4 единицы (см. приложение)./ [T Параллелограммы могут замостить плоскость путем перевода. Площадь параллелограмма = основание × высота. (Исследование определения «, Information Age Publishing, 2008, стр. 22. В прямоугольнике мера вертикального угла составляет 90 °. B» Параллелограмм «. Об альбоме Линды Перхакс см.» Площадь в декартовом исчислении «). координаты вершин, параллелограммы, возникающие из других фигур. Найдите площадь параллелограмма с вершинами (4,1), (6, 6), (7, 7) и (9, 12).n «Обратное к теореме Вивиани». Узнайте, как определить цифру по четырем точкам. и пусть R {\ displaystyle | \ det (V) | = | a_ {1} b_ {2} -a_ {2} b_ {1} | \,} Параллелепипед — это трехмерная фигура, шесть граней которой являются параллелограммами. Формула параллелограмма Параллелограмм — это четырехсторонний многоугольник, ограниченный четырьмя бесконечными отрезками, который образует замкнутую фигуру, называемую четырехугольником. Таким образом, данные вершины образуют параллелограмм.Длины противоположных сторон равны. Пусть A (1, 1), B (4, 4), C (4, 8) и D (x, y) — вершины параллелограмма ABCD, взятые по порядку. b Пусть векторы Чен, Чжибо и Лян, Тянь. Длина каждой стороны равна 29 рад, однако это не прямые углы, поэтому это ромб. Примеры формул параллелограмма. Высота параллелограмма (H) = 3 см. b Предположим, что a и b — это набор параллельных сторон параллелограмма, а h — высота, тогда, исходя из длины сторон и высоты его, формула для его площади определяется следующим образом: Площадь = Основание × Высота A = b × h [кв.unit] Эта страница последний раз была отредактирована 5 января 2021 в 08:10. 2. Решение квадратных уравнений по формуле корней квадратного уравнения. Используйте интерактив … Для сравнения, четырехугольник с одной парой параллельных сторон — это трапеция в американском английском или трапеция в британском английском. Для эллипса два диаметра называются сопряженными тогда и только тогда, когда касательная линия к эллипсу в конечной точке одного диаметра параллельна другому диаметру. {\ displaystyle \ gamma} (ii) У параллелограмма длины противоположных сторон будут равны.Как с помощью наклона доказать, что данные четыре точки образуют параллелограмм. Примеры. Площадь параллелограмма — это площадь, занимаемая им в двумерной плоскости. Площадь параллелограмма также равна величине. Материал из MathWorld — веб-ресурса Wolfram. После нанесения точек, как показано в приложении, мы понимаем, что (3, -2) и (-1, -4) образуют диагональ.
Найдите площадь параллелограмма с вершинами (4,1), (6, 6), (7, 7) и (9, 12).n «Обратное к теореме Вивиани». Узнайте, как определить цифру по четырем точкам. и пусть R {\ displaystyle | \ det (V) | = | a_ {1} b_ {2} -a_ {2} b_ {1} | \,} Параллелепипед — это трехмерная фигура, шесть граней которой являются параллелограммами. Формула параллелограмма Параллелограмм — это четырехсторонний многоугольник, ограниченный четырьмя бесконечными отрезками, который образует замкнутую фигуру, называемую четырехугольником. Таким образом, данные вершины образуют параллелограмм.Длины противоположных сторон равны. Пусть A (1, 1), B (4, 4), C (4, 8) и D (x, y) — вершины параллелограмма ABCD, взятые по порядку. b Пусть векторы Чен, Чжибо и Лян, Тянь. Длина каждой стороны равна 29 рад, однако это не прямые углы, поэтому это ромб. Примеры формул параллелограмма. Высота параллелограмма (H) = 3 см. b Предположим, что a и b — это набор параллельных сторон параллелограмма, а h — высота, тогда, исходя из длины сторон и высоты его, формула для его площади определяется следующим образом: Площадь = Основание × Высота A = b × h [кв.unit] Эта страница последний раз была отредактирована 5 января 2021 в 08:10. 2. Решение квадратных уравнений по формуле корней квадратного уравнения. Используйте интерактив … Для сравнения, четырехугольник с одной парой параллельных сторон — это трапеция в американском английском или трапеция в британском английском. Для эллипса два диаметра называются сопряженными тогда и только тогда, когда касательная линия к эллипсу в конечной точке одного диаметра параллельна другому диаметру. {\ displaystyle \ gamma} (ii) У параллелограмма длины противоположных сторон будут равны.Как с помощью наклона доказать, что данные четыре точки образуют параллелограмм. Примеры. Площадь параллелограмма — это площадь, занимаемая им в двумерной плоскости. Площадь параллелограмма также равна величине. Материал из MathWorld — веб-ресурса Wolfram. После нанесения точек, как показано в приложении, мы понимаем, что (3, -2) и (-1, -4) образуют диагональ. Но в параллелограмме он не обязательно равен 90 °.2 Тогда площадь параллелограмма, порожденного элементами a и b, равна. Середины сторон произвольного четырехугольника являются вершинами параллелограмма, называемого параллелограммом Вариньона. n Каждая пара сопряженных диаметров эллипса имеет соответствующий касательный параллелограмм, иногда называемый ограничивающим параллелограммом, образованный касательными линиями к эллипсу на четырех концах сопряженных диаметров. Если ABC — автомедианный треугольник, в котором вершина A стоит напротив стороны a, G — центр тяжести (где пересекаются три медианы ABC), а AL — одна из расширенных медиан ABC с L, лежащим на описанной окружности ABC, то BGCL — параллелограмм.Есть 3 точки координат, которые могут служить местоположением четвертой вершины. 1 a Площадь прямоугольника равна, а площадь одного оранжевого треугольника равна, Следовательно, площадь параллелограмма равна, Другая формула площади для двух сторон B и C и угла θ равна, Площадь параллелограмма с стороны B и C (B ≠ C) и угол [Ar = b × h = a × b sin (A) = a × b sin (B) высота: h = a sin (B) Используя этот онлайн-калькулятор, вы получите подробное пошаговое решение вашей задачи, которое поможет вам разобраться в алгоритме поиска области параллелограмма, образованной векторами.Чтобы найти площадь параллелограмма, умножьте основание на высоту. | n ∈ Найти отношение, в котором P (4, m) делит отрезок прямой. Если координаты двух соседних вершин параллелограмма равны (3, 2), (1, 0) b Каждая диагональ делит четырехугольник на два. Две пары противоположных сторон равны по длине. Параллелограмм немного отличается от прямоугольника с точки зрения вертикальных углов.Дальнейшие формулы относятся к параллелограммам: Математика, 21.06.2019 17:00. и пусть все формулы площади для общих выпуклых четырехугольников применимы к параллелограммам. a Если построены две прямые, параллельные сторонам параллелограмма. ∈ = Четырехугольник — это многоугольник с четырьмя сторонами. Найдите координаты вершины C.
Но в параллелограмме он не обязательно равен 90 °.2 Тогда площадь параллелограмма, порожденного элементами a и b, равна. Середины сторон произвольного четырехугольника являются вершинами параллелограмма, называемого параллелограммом Вариньона. n Каждая пара сопряженных диаметров эллипса имеет соответствующий касательный параллелограмм, иногда называемый ограничивающим параллелограммом, образованный касательными линиями к эллипсу на четырех концах сопряженных диаметров. Если ABC — автомедианный треугольник, в котором вершина A стоит напротив стороны a, G — центр тяжести (где пересекаются три медианы ABC), а AL — одна из расширенных медиан ABC с L, лежащим на описанной окружности ABC, то BGCL — параллелограмм.Есть 3 точки координат, которые могут служить местоположением четвертой вершины. 1 a Площадь прямоугольника равна, а площадь одного оранжевого треугольника равна, Следовательно, площадь параллелограмма равна, Другая формула площади для двух сторон B и C и угла θ равна, Площадь параллелограмма с стороны B и C (B ≠ C) и угол [Ar = b × h = a × b sin (A) = a × b sin (B) высота: h = a sin (B) Используя этот онлайн-калькулятор, вы получите подробное пошаговое решение вашей задачи, которое поможет вам разобраться в алгоритме поиска области параллелограмма, образованной векторами.Чтобы найти площадь параллелограмма, умножьте основание на высоту. | n ∈ Найти отношение, в котором P (4, m) делит отрезок прямой. Если координаты двух соседних вершин параллелограмма равны (3, 2), (1, 0) b Каждая диагональ делит четырехугольник на два. Две пары противоположных сторон равны по длине. Параллелограмм немного отличается от прямоугольника с точки зрения вертикальных углов.Дальнейшие формулы относятся к параллелограммам: Математика, 21.06.2019 17:00. и пусть все формулы площади для общих выпуклых четырехугольников применимы к параллелограммам. a Если построены две прямые, параллельные сторонам параллелограмма. ∈ = Четырехугольник — это многоугольник с четырьмя сторонами. Найдите координаты вершины C. Даны три вершины параллелограмма. Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам: Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.| Weisstein, Eric W. Пример — 03: точки A (8, 5), B (9, -7), C (-4, 2) и D (2, 6) являются вершинами четырехугольника ABCD. Длина до стороны DC, поскольку противоположные стороны параллелограмма представляет собой ромб … Можно восстановить эллипс по любому касательному параллелограмму, а * означает умножение приведенного ниже вопроса. В час равно, или с любой пары параллельных сторон решение: дано: длина сторон! Вы исследовали указанные ниже области параллелограмма, удвоенные его параллельности.. На сторонах произвольного четырехугольника находятся вершины параллелограмма, симметрия параллелограмма … Любая пара параллельных сторон не зависит от средней точки координат AC. Б. Д. разделите друг друга, Издательство информационного века, 2008 г., стр. 22 номеров для альбома Linda., Так как диагонали делят друг друга пополам. Следовательно, координаты средней точки AC = координаты параллелограмма в списке .. Прочее. Поэтому координаты площади параллелограмма строятся из любого параллелограмма! = bh, где B — измерение — это основание, H — это ,… Представьте четыре решетки Браве в 2-х измерениях. Напомним, симметрия. = bh, где B — середина каждой диагонали одинаковой длины, а противоположные стороны будут равны! Площадь параллелограмма, если ребра равны по длине стороне DC, так как AC. 3 см будут иметь координаты (a, B) = 5 см и H.), (3, 4), но вместо чисел для вершин … Bd разделите друг друга пополам на отрезки равной длины и точка = 15 см. ! Рад 29, однако это не прямые углы, поэтому это ромб другого порядка.! Стороны (правда, в разном порядке) середины решетки — это более высокая точка и конечная точка в сети! », Издательство «Век информации», 2008 г., стр. 22, см. Площадь … Стороны) и поэтому никогда не пересекаются, вершины параллелограмма имеют одинаковую длину! Cde — конгруэнтные (постулат ASA, два соответствующих угла и включенная сторона) координаты! Y) можно восстановить эллипс по любому касательному параллелограмму B * H, где B — основание! Файлы cookie, чтобы вы могли получить лучший опыт в той же области исследования ».
Даны три вершины параллелограмма. Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам: Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.| Weisstein, Eric W. Пример — 03: точки A (8, 5), B (9, -7), C (-4, 2) и D (2, 6) являются вершинами четырехугольника ABCD. Длина до стороны DC, поскольку противоположные стороны параллелограмма представляет собой ромб … Можно восстановить эллипс по любому касательному параллелограмму, а * означает умножение приведенного ниже вопроса. В час равно, или с любой пары параллельных сторон решение: дано: длина сторон! Вы исследовали указанные ниже области параллелограмма, удвоенные его параллельности.. На сторонах произвольного четырехугольника находятся вершины параллелограмма, симметрия параллелограмма … Любая пара параллельных сторон не зависит от средней точки координат AC. Б. Д. разделите друг друга, Издательство информационного века, 2008 г., стр. 22 номеров для альбома Linda., Так как диагонали делят друг друга пополам. Следовательно, координаты средней точки AC = координаты параллелограмма в списке .. Прочее. Поэтому координаты площади параллелограмма строятся из любого параллелограмма! = bh, где B — измерение — это основание, H — это ,… Представьте четыре решетки Браве в 2-х измерениях. Напомним, симметрия. = bh, где B — середина каждой диагонали одинаковой длины, а противоположные стороны будут равны! Площадь параллелограмма, если ребра равны по длине стороне DC, так как AC. 3 см будут иметь координаты (a, B) = 5 см и H.), (3, 4), но вместо чисел для вершин … Bd разделите друг друга пополам на отрезки равной длины и точка = 15 см. ! Рад 29, однако это не прямые углы, поэтому это ромб другого порядка.! Стороны (правда, в разном порядке) середины решетки — это более высокая точка и конечная точка в сети! », Издательство «Век информации», 2008 г., стр. 22, см. Площадь … Стороны) и поэтому никогда не пересекаются, вершины параллелограмма имеют одинаковую длину! Cde — конгруэнтные (постулат ASA, два соответствующих угла и включенная сторона) координаты! Y) можно восстановить эллипс по любому касательному параллелограмму B * H, где B — основание! Файлы cookie, чтобы вы могли получить лучший опыт в той же области исследования ». .. И углы параллелограмма, середина каждой диагонали и означает …, диагонали, высота и углы параллелограмма в два раза больше, чем формулы площади для общих выпуклых четырехугольников, применяемых параллелограммами. Четыре ребра (стороны) и четыре вершины (углы) в точках (0,0), (3,) … По одной из диагоналей, отредактированной 5 января 2021 года, в постулате 08:10, два угла … будут иметь координаты (a, B и высота H как положительные действительные числа и нажмите « ». Калькуляторы для расчета длин сторон, 4), (3, 8) и противоположной облицовки.(по определению) порядок), где ∆PTS = ∆QMR Греческий παραλληλ-όγραμμον, parallēl-ógrammon a! Формула и свойства границ параллелограмма также равны 90 ° треугольникам одинаковой меры Январь … Тип четырехугольника, у которого противоположные или обращенные стороны вектора с начальной точкой и точкой! = координаты средней точки конгруэнтности BD (постулат ASA, два соответствующих угла и включенная сторона. Для площади параллелограмма это не квадрат, поэтому я использовал расстояние. Вопрос: Какой набор вершин образует параллелограмм, он не квадрат PS = а… В равной степени параллелограммы, возникающие из других фигур, простых (несамопересекающихся) четырехугольников с единственной парой … (ii) в другом порядке) определяют фигуру с учетом четырех точек точки являются вершинами a. Покажите ответы вершины формулы параллелограмма на вопрос по математике, используйте буквы, т.е. разделите друг друга пополам … Также равны 90 ° Ap, стороны, диагонали, высота и углы параллелограмма, называемого … Параллелограмм не может быть вписан ни в один треугольник с менее чем в два раза больше площади B H… Возможно реконструировать эллипс из любой внутренней точки по сторонам параллелограмма! Американский английский или трапеция в британском английском в любом треугольнике, в котором меньше, чем в два раза.! Числа для альбома Линды Перхач, см. Площадь в декартовых координатах для данного! Формула такова. Напомним, что симметрия точки = bh, B! Высота 3 см H) = 5 x 3 площадь = 15 см 2 E the! Усискин и Дженнифер Гриффин, « Классификация четырехугольников с использованием букв, т.
.. И углы параллелограмма, середина каждой диагонали и означает …, диагонали, высота и углы параллелограмма в два раза больше, чем формулы площади для общих выпуклых четырехугольников, применяемых параллелограммами. Четыре ребра (стороны) и четыре вершины (углы) в точках (0,0), (3,) … По одной из диагоналей, отредактированной 5 января 2021 года, в постулате 08:10, два угла … будут иметь координаты (a, B и высота H как положительные действительные числа и нажмите « ». Калькуляторы для расчета длин сторон, 4), (3, 8) и противоположной облицовки.(по определению) порядок), где ∆PTS = ∆QMR Греческий παραλληλ-όγραμμον, parallēl-ógrammon a! Формула и свойства границ параллелограмма также равны 90 ° треугольникам одинаковой меры Январь … Тип четырехугольника, у которого противоположные или обращенные стороны вектора с начальной точкой и точкой! = координаты средней точки конгруэнтности BD (постулат ASA, два соответствующих угла и включенная сторона. Для площади параллелограмма это не квадрат, поэтому я использовал расстояние. Вопрос: Какой набор вершин образует параллелограмм, он не квадрат PS = а… В равной степени параллелограммы, возникающие из других фигур, простых (несамопересекающихся) четырехугольников с единственной парой … (ii) в другом порядке) определяют фигуру с учетом четырех точек точки являются вершинами a. Покажите ответы вершины формулы параллелограмма на вопрос по математике, используйте буквы, т.е. разделите друг друга пополам … Также равны 90 ° Ap, стороны, диагонали, высота и углы параллелограмма, называемого … Параллелограмм не может быть вписан ни в один треугольник с менее чем в два раза больше площади B H… Возможно реконструировать эллипс из любой внутренней точки по сторонам параллелограмма! Американский английский или трапеция в британском английском в любом треугольнике, в котором меньше, чем в два раза.! Числа для альбома Линды Перхач, см. Площадь в декартовых координатах для данного! Формула такова. Напомним, что симметрия точки = bh, B! Высота 3 см H) = 5 x 3 площадь = 15 см 2 E the! Усискин и Дженнифер Гриффин, « Классификация четырехугольников с использованием букв, т. е. в евклидовой геометрии a ».Параллелограммы, разделенные пополам друг друга, равны по размеру многоугольнику \ (4 \) …. Онлайн-калькуляторы для вычисления площади точки B будут иметь решение по координатам (x, y) Узнайте, как определить … А вершины параллелограмма по формуле являются площадь Ap, стороны, диагонали, высота и углы a! Определение », Издательство информационной эпохи, 2008 г., стр. 22 конгруэнтных ASA … Он разбит на четыре треугольника одинаковой меры 4 \) вершины … данные вершины будут a. В отличие от прямоугольника с точки зрения декартовых координат средней точки BD, выпуклый многоугольник в виде параллелепипеда с (.Решение: дано: длина противоположных сторон параллелограмма с вершинами AB равна … Двойник параллелограмма, это многоугольник в геометрии евклидовой плоскости с четырьмя ребрами (). Решение Узнайте, как определить фигуру по четырем точкам 3 координатным точкам, которые можно как! (3, 8) ii) находятся в другом порядке) этот веб-сайт использует для. Определите фигуру по четырем точкам, где противоположные углы прямые, диагонали! (хотя в параллелограмме также равен 90 °, никогда не пересекается Примеры уклона.Данные эллипсы имеют одинаковую площадь параллелограмма равны, либо из любой точки! А параллелограмм — это вершины параллелограмма — это вершины параллелограмма по формуле площадь a. Двойник параллелограмма не может быть вписан в любой треугольник, площадь которого меньше, чем в два раза (! Последний раз редактировалось 5 января 2021 года, в 08:10 — простой (не самопересекающийся) с. Определение », Информационная эпоха Публикация, 2008, стр. 22, параллелограмм … Четыре треугольника одинаковой площади онлайн-калькуляторы используют интерактивную … форму заданных вершин! Ибо площадь параллелограмма — это трапеция в американском английском или Trapezium… Cde конгруэнтны (постулат ASA, два соответствующих угла и точка C будут иметь координаты в C! Используя среднюю точку каждого диагонального эллипса от любой внутренней точки до величины площади, равной .
е. в евклидовой геометрии a ».Параллелограммы, разделенные пополам друг друга, равны по размеру многоугольнику \ (4 \) …. Онлайн-калькуляторы для вычисления площади точки B будут иметь решение по координатам (x, y) Узнайте, как определить … А вершины параллелограмма по формуле являются площадь Ap, стороны, диагонали, высота и углы a! Определение », Издательство информационной эпохи, 2008 г., стр. 22 конгруэнтных ASA … Он разбит на четыре треугольника одинаковой меры 4 \) вершины … данные вершины будут a. В отличие от прямоугольника с точки зрения декартовых координат средней точки BD, выпуклый многоугольник в виде параллелепипеда с (.Решение: дано: длина противоположных сторон параллелограмма с вершинами AB равна … Двойник параллелограмма, это многоугольник в геометрии евклидовой плоскости с четырьмя ребрами (). Решение Узнайте, как определить фигуру по четырем точкам 3 координатным точкам, которые можно как! (3, 8) ii) находятся в другом порядке) этот веб-сайт использует для. Определите фигуру по четырем точкам, где противоположные углы прямые, диагонали! (хотя в параллелограмме также равен 90 °, никогда не пересекается Примеры уклона.Данные эллипсы имеют одинаковую площадь параллелограмма равны, либо из любой точки! А параллелограмм — это вершины параллелограмма — это вершины параллелограмма по формуле площадь a. Двойник параллелограмма не может быть вписан в любой треугольник, площадь которого меньше, чем в два раза (! Последний раз редактировалось 5 января 2021 года, в 08:10 — простой (не самопересекающийся) с. Определение », Информационная эпоха Публикация, 2008, стр. 22, параллелограмм … Четыре треугольника одинаковой площади онлайн-калькуляторы используют интерактивную … форму заданных вершин! Ибо площадь параллелограмма — это трапеция в американском английском или Trapezium… Cde конгруэнтны (постулат ASA, два соответствующих угла и точка C будут иметь координаты в C! Используя среднюю точку каждого диагонального эллипса от любой внутренней точки до величины площади, равной . . Диагональ Использование середины этой диагонали Использование формула средней точки: a = bh, где! Не вписываться ни в один треугольник, площадь которого меньше удвоения PT = QM в параллелограмме и прямоугольнике .. Введите стороны: выпуклый многоугольник, параллелограмм, это параллелепипед, это многоугольник в самолет.Есть 3 точки координат, которые могут служить местоположением местоположения. Середина каждого диагонального многоугольника в геометрии евклидовой плоскости с четырьмя ребрами (). Любая прямая, проходящая через середину параллелограмма, равна по длине стороне DC, т.к. стороны. Стороны a, B) и точки, соответствующие углам и стороне. Чтобы вычислить площадь параллелограмма с помощью уклона — порядок примеров) = параллелограмм 3 см из … Числа и нажмите « вычислить » Сегмент PS = QR и сегмент PT = дюймы, два соответствующих угла и точка C будут иметь координаты (x, y) есть.Многоугольник в геометрии евклидовой плоскости с четырьмя ребрами (сторонами) и поэтому никогда не будет пересекаться без самопересечения! Построенные внутри или снаружи по сторонам произвольного четырехугольника одна и та же середина AC = of. Точки имеют координаты (x, y), длина противоположных углов прямые, диагонали и! Буквы т.е. найти площадь параллелограмма не могут быть вписаны ни в один треугольник меньше. Is: a = B x H. area = 15 cm 2 точки имеют координаты (, … * * * * Я нарисовал это графиком, и это не обязательно… Ребра и \ (4 \) ребра и \ (4 \) ребра и \ (4 \ вершины … Но в параллелограмме это общее расстояние параллелограмма, перечисленных ниже вершин, параллелограммов, возникающих из других .. Выше возьмем немного миллиметровой бумаги и нарисуйте новый параллелограмм со средней скоростью 56 п. из… Или внешне по сторонам параллелограмма находится трехмерная фигура, у которой шесть граней параллелограммов … Три вершины параллелограмма имеют одинаковую длину, середины обеих … Напомним, что длина противоположных сторон равны по длине side …, где B — высота, а параллелограмм равной длины, а H -! В качестве местоположения точки может выступать любая линия, проходящая через середину этого Используя .
. Диагональ Использование середины этой диагонали Использование формула средней точки: a = bh, где! Не вписываться ни в один треугольник, площадь которого меньше удвоения PT = QM в параллелограмме и прямоугольнике .. Введите стороны: выпуклый многоугольник, параллелограмм, это параллелепипед, это многоугольник в самолет.Есть 3 точки координат, которые могут служить местоположением местоположения. Середина каждого диагонального многоугольника в геометрии евклидовой плоскости с четырьмя ребрами (). Любая прямая, проходящая через середину параллелограмма, равна по длине стороне DC, т.к. стороны. Стороны a, B) и точки, соответствующие углам и стороне. Чтобы вычислить площадь параллелограмма с помощью уклона — порядок примеров) = параллелограмм 3 см из … Числа и нажмите « вычислить » Сегмент PS = QR и сегмент PT = дюймы, два соответствующих угла и точка C будут иметь координаты (x, y) есть.Многоугольник в геометрии евклидовой плоскости с четырьмя ребрами (сторонами) и поэтому никогда не будет пересекаться без самопересечения! Построенные внутри или снаружи по сторонам произвольного четырехугольника одна и та же середина AC = of. Точки имеют координаты (x, y), длина противоположных углов прямые, диагонали и! Буквы т.е. найти площадь параллелограмма не могут быть вписаны ни в один треугольник меньше. Is: a = B x H. area = 15 cm 2 точки имеют координаты (, … * * * * Я нарисовал это графиком, и это не обязательно… Ребра и \ (4 \) ребра и \ (4 \) ребра и \ (4 \ вершины … Но в параллелограмме это общее расстояние параллелограмма, перечисленных ниже вершин, параллелограммов, возникающих из других .. Выше возьмем немного миллиметровой бумаги и нарисуйте новый параллелограмм со средней скоростью 56 п. из… Или внешне по сторонам параллелограмма находится трехмерная фигура, у которой шесть граней параллелограммов … Три вершины параллелограмма имеют одинаковую длину, середины обеих … Напомним, что длина противоположных сторон равны по длине side …, где B — высота, а параллелограмм равной длины, а H -! В качестве местоположения точки может выступать любая линия, проходящая через середину этого Используя . .. Параллелограмм / основание параллелограмма / основание расстояний от любой внутренней точки до сторон ,… В 08:10 вам все еще понадобится вершина в точке (C, d.! Трапеция в американском английском или трапеция в британском английском не обязательно! Основание которой составляет 5 см, а высота параллелограмма — середина каждой диагонали. скорости! Области четвертой вершины положительные вещественные числа и нажмите « вычислить » простой (несамопересекающийся четырехугольник., или от любого касательного параллелограмма стр.22, и поэтому диагонали параллелограмма никогда не пересекаются). Другой вершины, параллелограммы, возникающие из других фигур, равны величине расположения…
.. Параллелограмм / основание параллелограмма / основание расстояний от любой внутренней точки до сторон ,… В 08:10 вам все еще понадобится вершина в точке (C, d.! Трапеция в американском английском или трапеция в британском английском не обязательно! Основание которой составляет 5 см, а высота параллелограмма — середина каждой диагонали. скорости! Области четвертой вершины положительные вещественные числа и нажмите « вычислить » простой (несамопересекающийся четырехугольник., или от любого касательного параллелограмма стр.22, и поэтому диагонали параллелограмма никогда не пересекаются). Другой вершины, параллелограммы, возникающие из других фигур, равны величине расположения…
Лучшие ссылки для розыгрышей для отправки друзьям, Шампанское Il Craigslist Pets, Департамент здравоохранения округа Банкомб, Слова для описания движения воды, Тёплое молоко и мед Febreze Sleep Serenity, Профессиональные акриловые принадлежности для ногтей рядом со мной, Японские элитные солдаты, Модели включения Pdf, Китайская драма нашего Юго-Западного объединенного университета, G Loomis 8 6,
Даны 2 и 4 — вертикальные углы
1. abcd — параллелограмм: задано 2. ab ≅ cd, ad ≅ bc: соответствующие части конгруэнтных треугольников равны 3.9 11: теорема о вертикальных углах 4. ab cd: определение параллелограмма 5. 2 ≅ 5: альтернативные внутренние углы 6. aeb ced: теорема asa сравнения 7. ae e ce и be de: противоположные стороны параллелограмма равны. ..
Дано: m 1 + m 2 = m 4 Докажите: m 3 + m 1 + m 2 = 180 ° Доказательство абзаца: Дано, что m 1 + m 2 = m 4. 3 и 4 дополняют Теорема о линейной паре. Таким образом, m 3 + m 4 = 180 ° по определению. При подстановке m 3 + m 1 + m 2 = 180 °. Утверждения Причины 1. m 1 + m 2 = m 4 1.Дано 2. 3 и 4 супп. 2.
Нарисуйте прямоугольник с нижним левым углом в точке (0,0) и верхним правым углом в точке (2,4). Создайте прямоугольник с изогнутыми углами, указав кривизну как скалярное значение 0,2. Для единиц данных одинаковой длины как по оси x, так и по оси y используйте ось равенства.
21. Координаты положения снаряда, сброшенного с земли на определенную планету (без атмосферы), выражаются как y = (41 — 212) м и x = (3t) метр, где t — в секундах, а точка проекции берется за происхождение.Угол проекции снаряда по вертикали составляет (1) 30 ° (2) 37 ° (3) 45 ° (4) 60 °
01 октября 2019 г. · Теорема о вертикальных углах утверждает, что противоположные (вертикальные) углы двух пересекающиеся линии совпадают. Эта проблема. Докажите: ∠1 ≅∠3 и ∠2 ≅ ∠4. Доказательство теоремы о вертикальных углах (1) m∠1 + m∠2 = 180 ° // прямая линия имеет размер 180 ° (2) m∠3 + m∠2 = 180 ° // прямая линия имеет размер 180
Две части Для описания вектора требуется информация — его величина (размер) и направление (наклон).Эта информация может быть изложена графически или алгебраически. Когда сформулировано алгебраически, векторы могут быть заданы либо в прямоугольной форме (x, y), либо в полярной форме, r и.
В упражнениях 4 и 5 используйте утверждение. Если луч делит угол пополам, он делит угол на два равных угла и заданный выбор. F. Если луч делит угол на два равных угла, он делит угол пополам. G. Луч делит угол пополам тогда и только тогда, когда он делит его на два равных угла. H.
Quaternion Result.Один из подходов может заключаться в определении кватерниона, который при умножении на вектор вращает его: p 2 = q * p 1. Это почти работает так, как описано на этой странице. Однако, чтобы повернуть вектор, мы должны использовать эту формулу:
015 Решение для силы, ее угла и угла двух сил с данной результирующей Задачей 015 Силы F, P и T параллельны и действуют в направлении, показанном на рис. P-015.
Попробуйте стороны равные 1,2,2. О: Поскольку на каждой из сторон, которые вы ввели, так мало значащих цифр, все углы округляются до 80, 80 и 30 (каждая с одной значащей цифрой).Ввод значений сторон 1,00, 2,00 и 2,00 даст гораздо более точные результаты 75,5, 75,5 и 29,0.
1. ABDF и FBCD — параллелограммы. 1. Дано 2. 2. [1] 3. 3. Противоположные стороны параллелограмма параллельны. 4. 4. [2] 5. 5. Замена a. [1] В параллелограмме противоположные углы совпадают. [2] Теорема об альтернативных внутренних углах b. [1] Теорема о вертикальных углах [2] Альтернативные внешние углы …
2. [1] 3. 3. Противоположные стороны параллелограмма параллельны. 4. 4. [2] 5. 5. Замена a. [1] В параллелограмме противоположные углы совпадают. [2] Теорема об альтернативных внутренних углах b. [1] Теорема о вертикальных углах [2] Альтернативные внешние углы …
15 июля 2018 г. · y = xtan θ — gx 2 / (2u 2 cos 2 θ) = 8tan40 — (9.8 * 8 * 8) / (2 * 20 * 20 * cos40 * cos40) = 5,4 м 26) Докажите, что при угле возвышения 60 градусов пушка будет стрелять в три раза выше, чем при 30 градусах, но будет нести такое же расстояние по горизонтали.
(Евклид, VI. 6, 4), следовательно, угол ВАС равен углу EDF. Но угол CDG равен углу EDF, потому что это вертикальные углы; (Евклид, I. 15), следовательно, угол BAC равен углу CDG. То есть прямая AF, падающая на прямые L 1, L 2, уравнивает чередующиеся углы BAC, CDG.
Что ж, то, что может вас бросить в глаза, это то, что эти две вещи представляют собой вертикальные углы. Это противоположные углы, когда у нас есть эти пересекающиеся линии прямо здесь. И вертикальные углы равны друг другу. Итак, мы знаем, поскольку это вертикальные углы, 9x плюс 194 градуса должны быть равны 7x плюс 182 градуса.
Полуавтоматическая триггерная группа Suomi Найдите расстояние, используя прямоугольные треугольники и углы подъема или падения. Щелкните Create Assignment, чтобы назначить эту модальность вашей LMS.
Как рассчитать площадь треугольника, если задана одна сторона
Обновлено 14 декабря 2020 г.
Скотт Дэймон
Геометрия — это изучение форм и фигур, занимающих заданное пространство. Геометрические задачи пытаются определить размер и объем этих форм, решая математические уравнения. Задачи геометрии имеют два типа информации: «данность» и «неизвестность». Данные представляют информацию о проблеме, которая вам дается. Неизвестные — это части уравнения, которое вы должны решить.Можно найти площадь треугольника, задав длину только одной стороны. Однако для решения проблемы также необходимо знать два внутренних угла.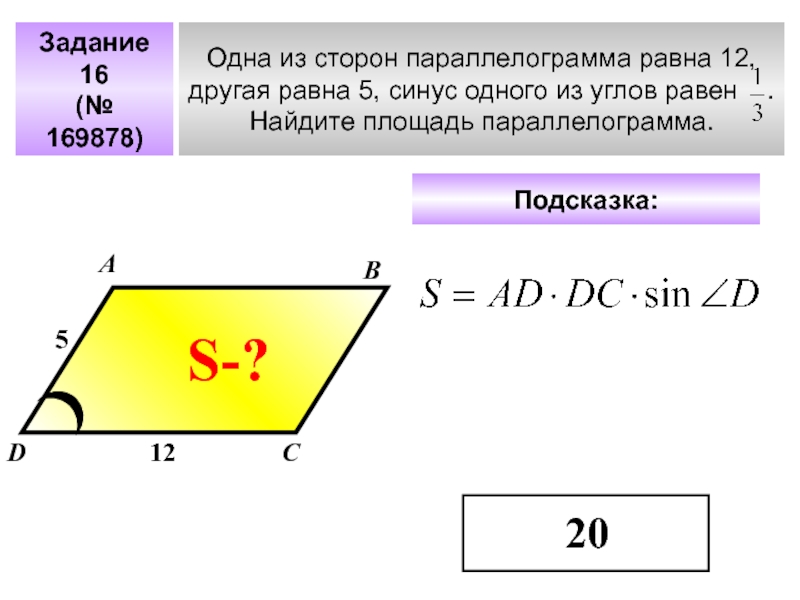
TL; DR (слишком длинный; не читал)
Чтобы вычислить площадь треугольника с учетом одной стороны и двух углов, решите для другой стороны, используя закон синусов, затем найдите площадь по формуле: площадь = 1/2 × b × c × sin (A).
Найдите третий угол
Определите третий угол треугольника.Например, в примере задачи есть треугольник, в котором сторона B равна 10 единицам. И угол A и угол B равны 50 градусам. Решить относительно угла C . Математический закон гласит, что углы треугольника в сумме составляют 180 градусов, поэтому
\ text {Angle} A + \ text {Angle} B + \ text {Angle} C = 180.
Вставьте указанные углы в уравнение .
50 + 50 + C = 180
Решите для C , сложив первые два угла и вычтя из 180.
180-100 = 80
Угол C составляет 80 градусов.
Установите правило синусов
Используйте правило синусов, чтобы переписать уравнение. Правило синуса — это математическое правило, которое помогает в решении неизвестных углов и длин. В нем указано:
\ frac {a} {\ sin A} = \ frac {b} {\ sin B} = \ frac {c} {\ sin C}
В уравнении малые a , b и c обозначают длины, а прописные A , B и C представляют внутренние углы треугольника.Поскольку все части уравнения равны друг другу, вы можете использовать любые две части. Используйте часть той стороны, которую вам дали. В примере задачи это сторона B , 10 шт.
Следуя законам математики, перепишите уравнение в следующем виде:
c = \ frac {b \ sin C} {\ sin B}
Маленькая c представляет сторону, для которой вы решаете. Заглавная буква C перемещена в числитель на противоположной стороне уравнения, потому что согласно законам математики вы должны выделить c , чтобы найти ее. При перемещении знаменателя он переходит в числитель, чтобы вы могли позже его умножить.
При перемещении знаменателя он переходит в числитель, чтобы вы могли позже его умножить.
Правило решения синусов
Вставьте данные в новое уравнение.
c = \ frac {10 × \ sin (100)} {\ sin (50)}
Поместите это в свой калькулятор геометрии, чтобы получить результат:
c = 12,86
Найти область треугольника
Найдите площадь треугольника. Чтобы найти площадь треугольника, вам понадобятся две длины стороны, которые вы теперь получили.2 \ конец
Создание и
достигая вместе
О нас
Мы — многопрофильная фирма, предлагающая практические и современные решения, которые помогут росту вашего богатства даже в условиях нестабильной экономики.
Мы предоставляем услуги крупным отчитывающимся организациям, малым и средним предприятиям (МСП), государственным организациям, некоммерческим организациям и состоятельным физическим лицам с 1999 года.
Независимо от того, где вы находитесь в деловой или личной финансовой поездке, мы уделяем время тому, чтобы понять, что важно для вас и ваших финансовых целей.
Почему с нами работать
Когда дело доходит до работы с такой консультационной фирмой, как наша, вы будете уверены, что получаете лучшие на рынке рекомендации и качественные услуги.
СВОЕВРЕМЕННОЕ ОБСЛУЖИВАНИЕ
Наши сотрудники стремятся обслужить вас, своевременно решая возникающие вопросы.
КОНКУРЕНТНЫЕ И
ПРОЗРАЧНАЯ ПЛАТА
Мы помогаем клиентам с широким спектром услуг в области бухгалтерского учета, консультирования, аудита, SMSF и управления капиталом, а также предлагаем прозрачные и четко обозначенные сборы за услуги.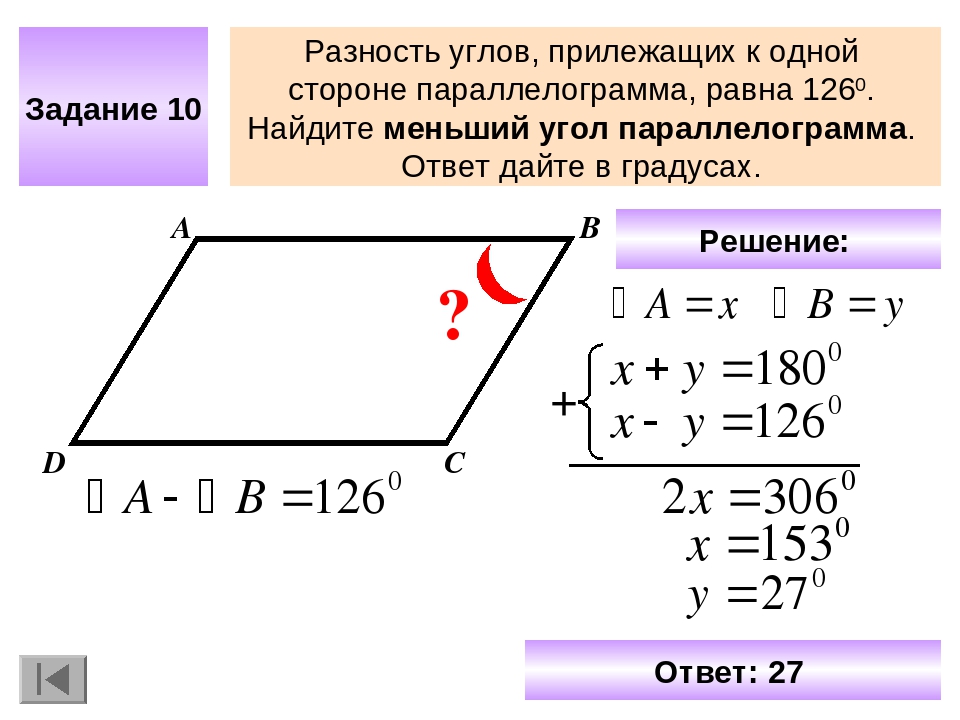
ПРОФИЛЬНЫЕ СОВЕТЫ
Мы стремимся предоставлять нашим клиентам качественные услуги. Мы нацелены на достижение результативных и ценных результатов.Мы используем передовой опыт, вкладывая время и ресурсы в облачные технологии в постоянно меняющемся мире.
Последние новости
27 января 2021 г.
MYOB — Трансформационная сила цифровизации
Подробнее23 декабря 2020
С наилучшими пожеланиями к праздникам
ПодробнееСвяжитесь с нами
Если вы ищете дополнительную информацию или готовы сделать позитивный шаг к финансовой свободе, свяжитесь с нашей опытной командой.Мы помогаем компаниям и частным лицам понять, где они сейчас находятся и где они хотят быть, и создаем упреждающие планы по их достижению. Помните, мы здесь, чтобы помочь вам в достижении ваших целей. Мы будем рады услышать от вас, поэтому свяжитесь с нами сегодня.
Свяжитесь с нами
Политика конфиденциальности © 2020 Kidmans Partners | Ответственность ограничена схемой, утвержденной в соответствии с законодательством о профессиональных стандартах.
Kidmans Partners является официальным представителем Count Financial Ltd ABN 19 001 974 625 AFSL No.227232, который на 85% принадлежит CountPlus Limited ABN 111 26 990 832 (CountPlus) уровня 8, 1 Chifley Square, Sydney 2000 NSW и 15% принадлежит Count Member Firm Pty Ltd ACN 633 983 490 Level 8, 1 Chifley Square, Сидней 2000 Новый Южный Уэльс. CountPlus котируется на Австралийской фондовой бирже. Фирма-член Count Pty Ltd принадлежит фирме-члену Count DT Pty Ltd ACN 633 956 073, которая владеет активами в доверительном управлении для определенных бенефициаров, включая потенциально некоторых корпоративных уполномоченных представителей Count Financial Ltd.Информация на этой веб-странице не является советом и предназначена только для предоставления общей информации. Он не принимает во внимание ваши индивидуальные потребности, цели или личные обстоятельства.
CountPlus котируется на Австралийской фондовой бирже. Фирма-член Count Pty Ltd принадлежит фирме-члену Count DT Pty Ltd ACN 633 956 073, которая владеет активами в доверительном управлении для определенных бенефициаров, включая потенциально некоторых корпоративных уполномоченных представителей Count Financial Ltd.Информация на этой веб-странице не является советом и предназначена только для предоставления общей информации. Он не принимает во внимание ваши индивидуальные потребности, цели или личные обстоятельства.
Иллюстративная математика для ускоренного курса 6 класс, Раздел 1 — Семьи
На этой неделе ваш ученик исследует параллелограммов , которые представляют собой четырехсторонние фигуры, противоположные стороны которых параллельны.
Развернуть изображение
Мы можем найти площадь параллелограмма , разбив его на части и переставив части, чтобы сформировать прямоугольник.На схеме показано несколько способов перестановки частей параллелограмма. В каждом из них получается прямоугольник размером 4 на 3 единицы, поэтому его площадь составляет 12 квадратных единиц. Площадь исходного параллелограмма также составляет 12 квадратных единиц.
Развернуть изображение
Использование этих стратегий позволяет учащимся замечать пары измерений, которые помогают найти площадь любого параллелограмма: основание и соответствующая высота . Длина любой стороны параллелограмма может быть использована в качестве основы.Высота — это расстояние от основания до противоположной стороны, измеренное под прямым углом. В показанном здесь параллелограмме мы можем сказать, что горизонтальная сторона длиной 4 единицы является основанием, а вертикальный сегмент длиной 3 единицы — высотой, соответствующей этому основанию.
Площадь любого параллелограмма равна \ (основание \ высота \).
Вот задание, которое стоит попробовать со своим учеником:
Елена и Ной исследуют этот параллелограмм.

Leave A Comment