Правильная четырехугольная призма

Определение.

Правильная четырехугольная призма — это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники

Боковое ребро — это общая сторона двух смежных боковых граней

Высота призмы — это отрезок, перпендикулярный основаниям призмы

Диагональ призмы — отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани

Диагональная плоскость — плоскость, которая проходит через диагональ призмы и ее боковые ребра

Диагональное сечение — границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник

Перпендикулярное сечение (ортогональное сечение) — это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам

Элементы правильной четырехугольной призмы

На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:

  • Основания ABCD и A1B1C1D1 равны и параллельны друг другу
  • Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
  • Боковая поверхность — сумма площадей всех боковых граней призмы
  • Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
  • Боковые ребра AA1, BB1, CC1 и DD1.
  • Диагональ B1D
  • Диагональ основания  BD
  • Диагональное сечение BB1D1D
  • Перпендикулярное сечение A2B2C2D2 .

Свойства правильной четырехугольной призмы

  • Основаниями являются два равных квадрата
  • Основания параллельны друг другу
  • Боковыми гранями являются прямоугольники
  • Боковые грани равны между собой
  • Боковые грани перпендикулярны основаниям
  • Боковые ребра параллельны между собой и равны
  • Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
  • Углы перпендикулярного сечения — прямые
  • Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
  • Перпендикулярное (ортогональное сечение) параллельно основаниям

Формулы для правильной четырехугольной призмы

Указания к решению задач


При решении задач на тему «правильная четырехугольная призма» подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.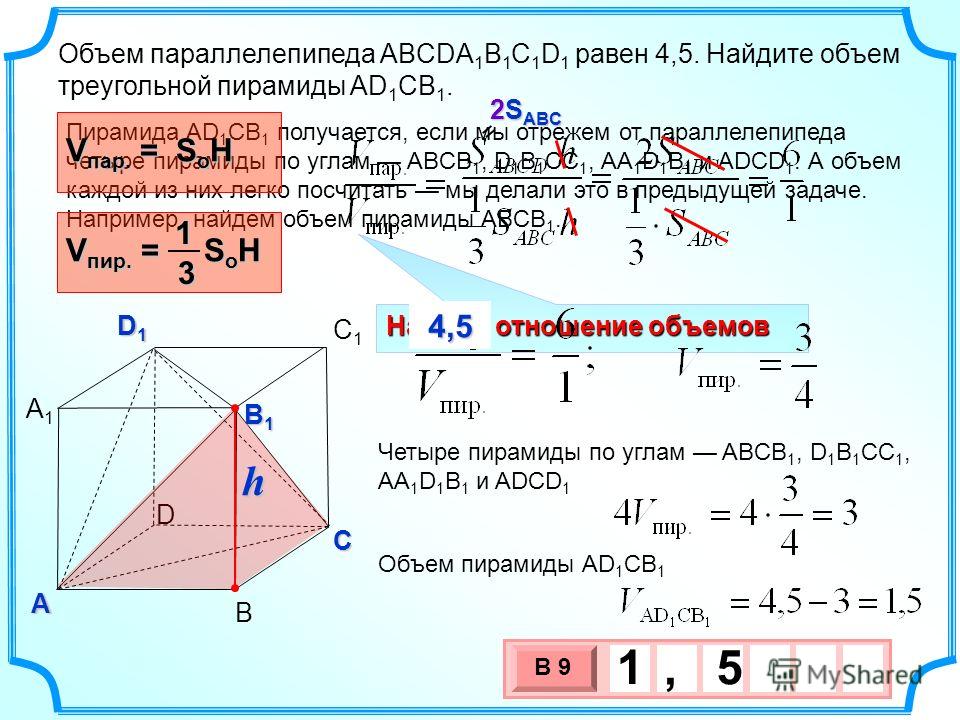

 То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия —  призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .   

Задача.

В правильной четырёхугольной призме площадь основания 144 см

2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.

Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна √144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 122 + 122 ) = √288 = 12√2

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )2 + 142 ) = 22 см

Ответ: 22 см

Задача

Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.

Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:

a2 + a2 = 52
2a2 = 25
a = √12,5

Высота боковой грани (обозначим как h) тогда будет равна:

h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5

Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания

S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .

Ответ: 25 + 10√7 ≈ 51,46 см2 .

15306.1214  

 Прямая призма | Описание курса | Куб 

   

Задание 14 (стереометрия) — Решения вариантов ЕГЭ по математике

Павел Коваленко

задача 12 задача 11 задача 10       задача 9 задача 8   задача 13

Задание 14 (стереометрия), Угол между скрещивающимися прямыми

Павел Коваленко

Подготовительные задания, стр. 128 15. Ребро SА пирамиды SАВС перпендикулярно плоскости основания АВС. а) Докажите, что плоскость, проходящая через середины рёбер АВ, АС и SА, параллельна плоскости SВС. 6) Найдите расстояние от вершины А до этой плоскости, если SА = Читать далее …

Задание 14 (стереометрия), Расстояние от точки до прямой и до плоскости

12. 08.2019 Павел Коваленко

Подготовительные задания, стр. 128 14. В правильной четырёхугольной пирамиде SАВСD с вершиной S сторона основания равна 8. Точка L — середина ребра SC. Тангенс угла между прямыми ВL и SА равен . а) Пусть О — центр основания пирамиды. Докажите, Читать далее …

Задание 14 (стереометрия), Угол между скрещивающимися прямыми

Павел Коваленко

Подготовительные задания, стр. 128 13. В правильной треугольной пирамиде SАВС с вершиной S, все рёбра которой равны 6, точ- ка М — середина ребра ВС, точка О — центр основания пирамиды, точка F делит отрезок SО в отношении 1:2, считая Читать далее …

Задание 14 (стереометрия), Угол между плоскостями

Павел Коваленко

Подготовительные задания, стр. 128 12. Основание прямой четырёхугольной призмы АВСDА1В1С1D1 — прямоугольник АВСD, в котором АВ = 5, AD = . Расстояние между прямыми АС и B1D1, равно 12. а) Пусть плоскость, проходящая через точку D перпендикулярно прямой ВD1 пересекает Читать далее …

Задание 14 (стереометрия), Угол между плоскостями

Павел Коваленко

Подготовительные задания, стр. 128 11. Основанием прямой треугольной призмы АВСА1В1С1, является равнобедренный треуголь- ник АВС, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р при- надлежит ребру ВВ1, причём ВР:РВ1 =1:3. а) Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 10. Дан куб ABCDA1B1C1D1. а) Докажите, что сечение куба плоскостью, проходящей через центр куба перпендику- лярно диагонали AC1, является правильным шестиугольником. 6) Найдите угол между прямой АС1, и плоскостью ВСС1.

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 9. Основание прямой четырёхугольной призмы АВСDА1В1С1D1, — прямоугольник АВСD, в котором АВ = 12, АD = . Расстояние между прямыми АС и B1D1, равно 5. а) Докажите, что плоскость, проходящая через точку D перпендикулярно прямой ВD1, Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 8. В правильной шестиугольной пирамиде SАВСDЕF боковые рёбра равны 2, а стороны ос- нования — 1. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер АF и СD, пер- пендикулярна плоскости основания. 6) Найдите Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 7. В правильной треугольной пирамиде SАВС с вершиной S, все рёбра которой равны 2, точ- ка М — середина ребра АВ, точка О — центр основания пирамиды, точка F делит отрезок SО в отношении 3 : Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 6. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точ- ка N — середина ребра АС, точка О — центр основания пирамиды, точка Р делит отрезок SO вотношении 3:1, считая от Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 5. В правильной треугольной призме АВСA1B1C1, все рёбра равны 1. а) Пусть плоскость, проходящая через точки С, С1 перпендикулярно плоскости АСС1, пе- ресекает прямую АВ вточке М. Докажите, что треугольник МВВ1 равнобедренный. 6) Найдите косинус угла Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Подготовительные задания, стр. 128 4. Дана правильная четырёхугольная пирамида MABCD, рёбра основания которой равны . Точка L — середина ребра МВ. Тангенс угла между прямыми DM и AL равен . а) Пусть О — центр основания пирамиды. Докажите, что прямые Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

3. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно . а) Докажите, что эта плоскость пересекает ось цилиндра. 6) Найдите угол между этой Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

2. Площадь основания правильной четырёхугольной пирамиды SABCD равна 64. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер ВС и АD, со- держит высоту пирамиды. 6) Найдите площадь боковой поверхности этой пирамиды, если площадь сечения пирами- ды плоскостью Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

1. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. а) Докажите, что плоскость SAC и плоскость, проходящая через вершину S, середину сто- роны АВ и центр основания, пересекаются по прямой, содержащей Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания — точка С, причём СС1, — образующая цилиндра, а АС — диаметр основания. Известно, что угол АСВ=45°, Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Дана пирамида PABCD, в основании которой трапеция ABCD большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K. а) Доказать, что плоскость Читать далее …

Задание 14 (стереометрия), Реальные ЕГЭ

Павел Коваленко

В правильной 4х-угольной пирамиде , -середина a) Докажите, что плоскость перпендикулярна плоскости основания b) Найдите площадь сечения если площадь =6 Проведем диагональ CA, поделим ее на 4 равные части. Возьмем на диагонали три равных отрезка . Возьмем на стороне три Читать далее …

Задание 14 (стереометрия), Реальные ЕГЭ

Павел Коваленко

В правильной четырехугольной пирамиде сторона основания равна 6, а боковое ребро равно 7. На ребрах и отмечены точки и соответственно, причем . Плоскость содержит прямую и параллельна прямой . a) Докажите, что плоскость параллельна прямой b) Найдите расстояние от точки Читать далее …

Задание 14 (стереометрия), Реальные ЕГЭ

Павел Коваленко

В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что AD = Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

На рисунке изображён многогранник, все двугранные углы которого прямые. а) Постройте сечение многогранника плоскостью, проходящей через точки А, В и С1 б) Найдите площадь этого сечения. Решается аналогично как здесь

Задание 14 (стереометрия)

Павел Коваленко

В правильной треугольной пирамиде SABC с основанием ABC все ребра равны 6. а) Постройте сечение пирамиды плоскостью, проходящей через вершину S и перпендикулярной отрезку, соединяющему середины ребер AB и BC.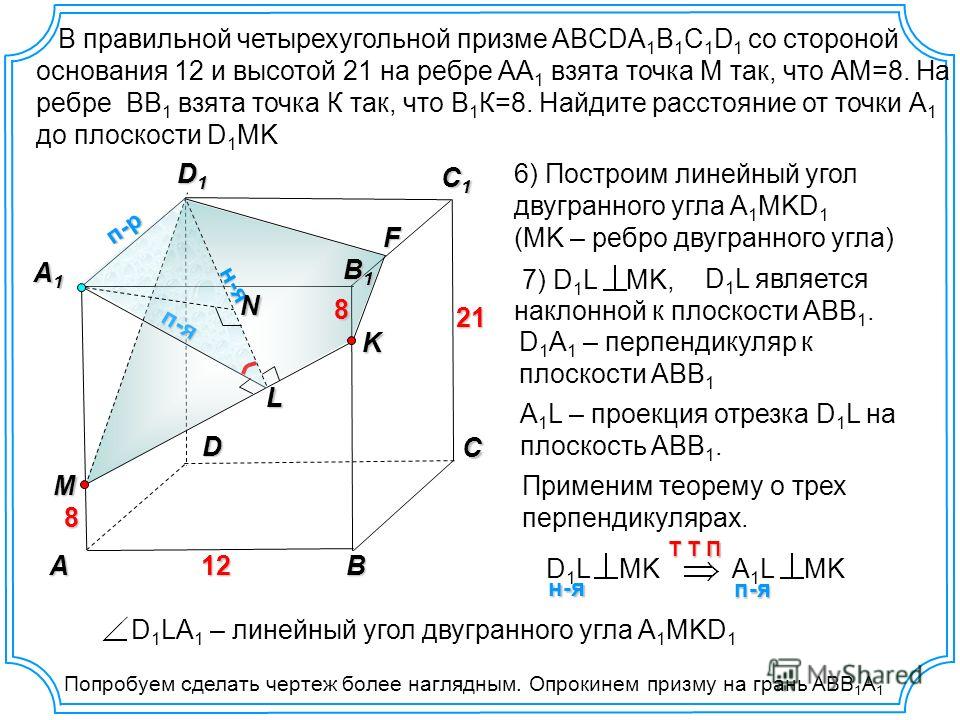 б) найдите расстояние от плоскости этого сечения до центра грани Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Похоже на решение вариантов 22 и 29. Посмотрите решение в варианте 22.

Задание 14 (стереометрия)

Павел Коваленко

В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что CD = Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Радиус основания конуса равен 12, а высота конуса равна 5. а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. б) Найдите расстояние от плоскости сечения до центра основания конуса. Трехмерная картинка, которую можно крутить в 3D, Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 6. Длины боковых рёбер пирамиды SA = 3, SB = 5, SD = . а) Докажите, что SA — высота пирамиды. б) Найдите расстояние Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Вокруг куба с ребром 3 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …

Задание 14 (стереометрия)1 Комментарий

Павел Коваленко

Высота цилиндра равна 3, а радиус основания равен 13. а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72. б) Найдите расстояние от плоскости сечения до центра основания цилиндра. Трехмерная картинка, которую можно крутить Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В кубе все рёбра равны 4. На его ребре отмечена точка K так, что KB=3. Через точки K и проведена плоскость α, параллельная прямой . а) Докажите, что , где Р — точка пересечения плоскости α с ребром . б) Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В правильной четырёхугольной пирамиде SABCD все рёбра равны 1.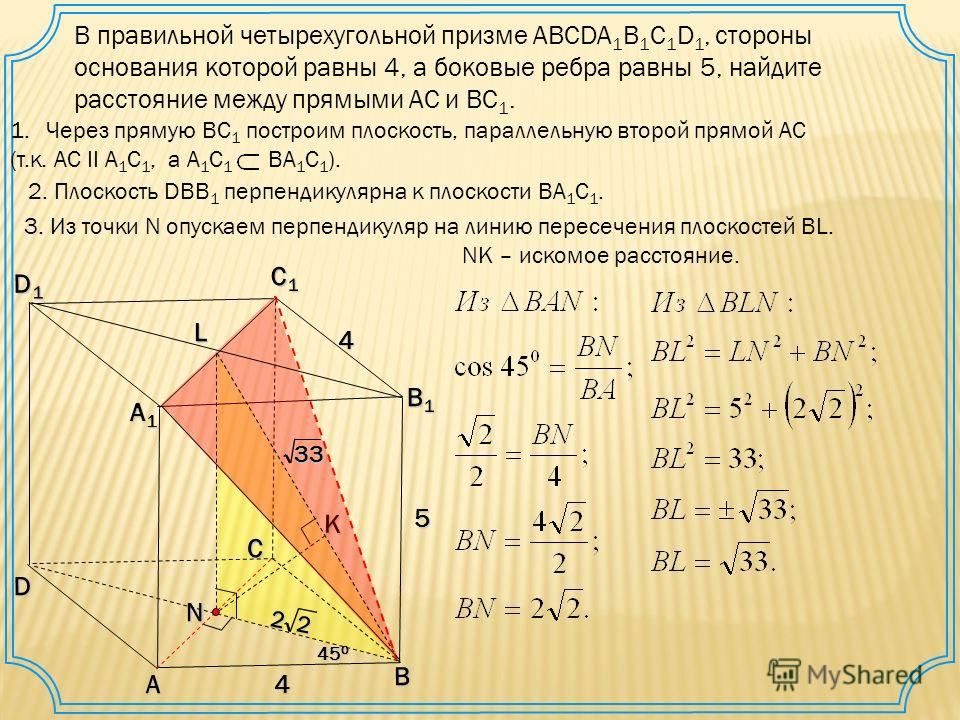 Точка F — середина ребра SB, G(она же Q) — середина ребра SC. а) Постройте прямую пересечения плоскостей ABQ и QDF. б) Найдите угол между плоскостями ABQ и QDF. Трехмерная картинка, Читать далее …

Задание 14 (стереометрия)2 комментария

Павел Коваленко

В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра AS. а) Постройте прямую пересечения плоскостей SAD и BCF. б) Найдите угол между плоскостями SAD и BCF. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. а) Постройте прямую пересечения плоскости SAD с плоскостью, проходящей через точку В перпендикулярно прямой AS.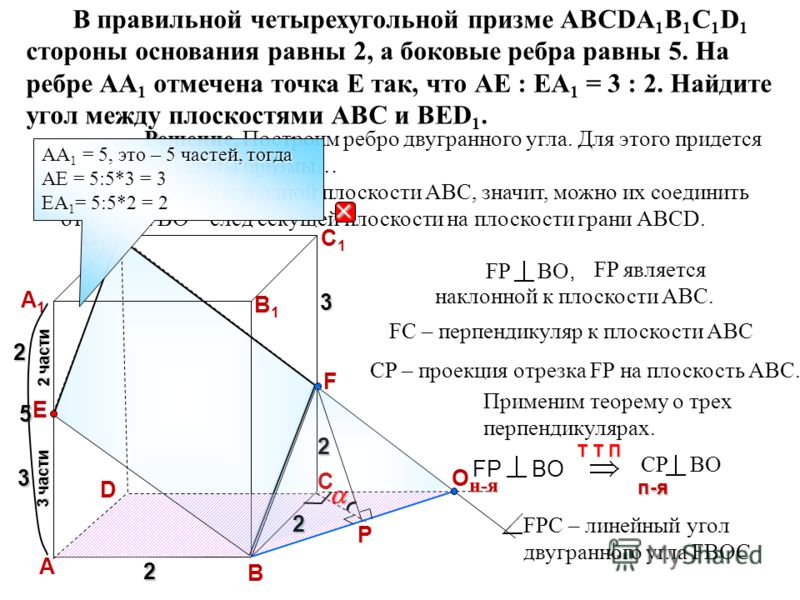 б) Найдите угол между плоскостью SAD и плоскостью, проходящей через точку В перпендикулярно прямой AS. Трехмерная Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых рёбер пирамиды SA = √11 , SB = 3√3, SD = 2√5. а) Докажите, что SA — высота пирамиды. б) Найдите Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Вокруг куба с ребром 2 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Дан куб . а) Постройте сечение куба плоскостью, проходящей через середины его рёбер . б) Найдите угол между плоскостью и плоскостью, проходящей через середины рёбер . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/nAKXHwEB Пусть — ребро Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9π. а) Постройте эти сечения. б) Найдите площадь поверхности шара. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В правильной треугольной пирамиде SABC сторона основания АВ равна 60, а боковое ребро SA равно 37. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

В правильной четырёхугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что AM = 6. а) Постройте перпендикуляр из точки S на плоскость ВСМ. б) Найдите расстояние Читать далее …

Задание 14 (стереометрия)

Павел Коваленко

Дан куб . а) Постройте сечение куба плоскостью, проходящей через точки и .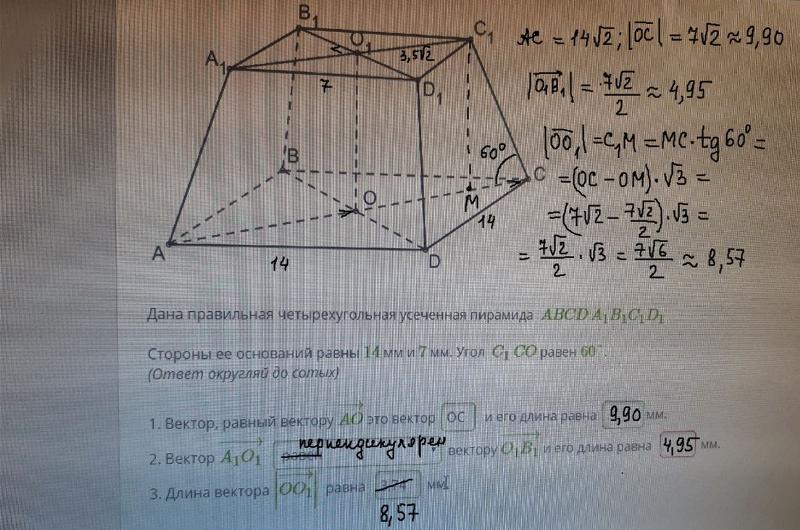 б) Найдите угол между плоскостями и . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/mVj9KVSX            

Задание 14 (стереометрия)

Калькулятор прямоугольных призм

Автор: Ханна Памула, доктор философии

Рецензию сделали Богна Шик и Адена Бенн

Последнее обновление: 02 февраля 2023 г.

Содержание:
  • Что такое прямоугольная призма?
  • Как найти объем прямоугольной призмы?
  • Как найти площадь прямоугольной призмы?
  • Как рассчитать диагональ прямоугольной призмы?
  • Как рассчитать объемы других твердых тел?

Благодаря нашему прямоугольному калькулятору призмы вы можете легко найти объем прямоугольного параллелепипеда, площадь поверхности и диагональ прямоугольной призмы. Если вам интересно, сколько воды вмещает ваш аквариум, или пытаетесь узнать, сколько бумаги вам нужно, чтобы обернуть подарок, попробуйте этот калькулятор с прямоугольной призмой! Если вы все еще не знаете, как это работает, продолжайте прокручивать, чтобы узнать о формулах прямоугольной призмы.

Что такое прямоугольная призма?

Прямоугольная призма представляет собой коробчатый объект, т. е. трехмерное тело с шестью прямоугольными гранями. Прямоугольные призмы также могут быть косыми — наклоненными в одну сторону — но боковые грани представляют собой параллелограммы, а не прямоугольники. Прямоугольную призму также называют кубоидом, параллелепипедом или прямоугольным шестигранником. При этом «прямоугольная призма» и « правая прямоугольная призма часто используются взаимозаменяемо.

Наиболее распространенные математические задачи, связанные с этим телом, относятся к типу правая прямоугольная призма вычислить найти V или найти A , где буквы обозначают V olume и A rea , соответственно Давайте посмотрим на необходимую формулу прямоугольной призмы и научимся решать эти задачи быстро и легко.

Как найти объем прямоугольной призмы?

Формула объема прямоугольной призмы:

объем = h × w × l ,

где h — высота призмы, w — ее ширина, а l — ее длина. Чтобы рассчитать объем картонной коробки:

  1. Найдите длину коробки . Например, он может быть равен 18 дюймам.
  2. Определить его ширину . Допустим, вы измерили 12 дюймов.
  3. Узнать высоту прямоугольной призмы . Предположим, что это 15 дюймов
  4. Вычислить объем прямоугольного параллелепипеда . Используя приведенную выше формулу объема прямоугольной призмы, мы получаем объемов = (18 × 12 × 15) дюймов = 3240 дюймов³ .

Как найти площадь прямоугольной призмы?

Площадь поверхности прямоугольного параллелепипеда состоит из 6 граней — трех пар параллельных прямоугольников. Чтобы найти площадь поверхности прямоугольной призмы, сложите площади всех граней:

площадь_площади = 2 × (h × w) + 2 × (h × l) + 2 × (l × w) = 2 × (h × w + ч × д + д × ш) ,

, где h — высота призмы, w — ширина, l — длина.

Давайте посмотрим на примере, как решить задачу прямоугольной призмы — найти A . Вернемся к нашему примеру с коробкой и вычислим площадь ее поверхности:

  1. Вычислим площадь поверхности прямоугольной призмы . Площадь первого прямоугольника равна 15 дюймов × 12 дюймов = 180 дюймов² , второго 15 дюймов × 18 дюймов = 270 дюймов² .и третий 18 дюймов × 12 дюймов = 216 дюймов² . Сложите площади всех трех прямоугольников — получится 666 дюймов² ( какое число! ) — и, наконец, умножьте на 2. Площадь поверхности нашей картонной коробки составляет 1332 дюйма².
  2. Или сэкономьте время и воспользуйтесь нашим калькулятором прямоугольных призм .

Наконец, давайте приступим к задаче типа прямоугольной призмы, вычисляющей нахождение d (то есть диагональной).

Как рассчитать диагональ прямоугольной призмы?

Для определения диагонали прямоугольной призмы воспользуйтесь формулой:

диагональ = √(l² + h² + w²)

где h высота призмы, w ширина,

9 l является его длина.

У вас есть ощущение, что вы видели формулу раньше? Да, это возможно, потому что это уравнение напоминает знаменитое уравнение из теоремы Пифагора.

Как рассчитать объемы других твердых тел?

Эта прямоугольная призма была проще простого! Если вы поражены тем, как легко вы можете рассчитать объем с помощью нашего инструмента, попробуйте другие калькуляторы объема:

  • Калькулятор треугольной призмы
  • Калькулятор объема цилиндра
  • Калькулятор объема сферы
  • Калькулятор объема конуса
  • Калькулятор объема пирамиды

Обязательно ознакомьтесь с калькулятором объема — объем основных 3D-тел в одном месте!

Ханна Памула, PhD

Длина (л)

Ширина (ш)

Высота (в)

Площадь поверхности

Объем

Диагональ (г)

Посмотреть 23 похожих калькулятора 3D-геометрии 📦

Площадь полушарияКубКуб Рассчитать: найти v, a, d… еще 20

Что такое объем призмы? Определение, формула, примеры, факты

Объем призмы – введение

Определение объема призмы можно просто дать как пространство, занимаемое призмой. Призма – это трехмерная фигура, имеющая плоские стороны и два одинаковых основания.

Основаниями призмы являются многоугольники, такие как треугольник, квадрат, прямоугольник или гексаграмма. Призмы часто называют в честь многоугольников, образующих основу.

Чтобы найти объем, нам нужно знать площадь основания и высоту призмы.

Родственные игры

Каков объем призмы?

Объем призмы можно определить как пространство, которое она занимает в кубических единицах. Кубические единицы измеряют объем трехмерной фигуры.

Чтобы найти объем, мы умножаем площадь основания на высоту призмы.

Площадь основания — это площадь поверхности основания. Высота — это столбец, соединяющий два основания призмы.

Когда мы умножаем основание на высоту, результирующий объем будет измеряться в кубических единицах, таких как кубические дюймы, кубические ярды, кубические футы, кубические сантиметры или кубические метры.

Чтобы найти объем , нам нужно знать только площадь основания и высоту.

Какова формула объема призмы?

Объем призмы по формуле :

Объем $=$ площадь основания $\times$ высота

По этой формуле можно найти объем любой призмы.

Формулы для различных призм обсуждаются в следующей таблице.

Таблица формул для различных типов призм

Как найти объем призмы?

Формула для расчета объема призмы может быть записана как $\text{V} = b \times h$, где V — объем, b — площадь основания, h — высота призмы. .

Пример нахождения объема призмы: 

Найдем объем призмы , площадь основания которой составляет 5 квадратных дюймов, а высота – 10 дюймов.

Применяя формулу:

$\text{V} = b \times h$

Объем $= 5 \times 10 = 50$ кубических дюймов.

Интересные факты!

  • Мы можем применить объем призмы уравнение , чтобы найти объем различных типов призм.
  • Объем зависит от формы его основания, так как это определяет площадь основания.
  • Площадь основания призмы измеряется в квадратных единицах, квадратных дюймах или квадратных метрах, поскольку она представляет собой двумерную площадь, т. е. площадь поверхности основания призмы.
  • Высота призмы измеряется в обычных единицах измерения, таких как дюймы или метры. Это потому, что он представляет собой длину столбца, соединяющего основания.

Заключение

Найти объем призмы легко, если вы освоите формулу. Помните, что не имеет значения, какой это тип призмы. Зная высоту и площадь основания, можно найти его объем!

Решенные примеры

1. Какова площадь основания призмы, если объем призмы 150 кубических футов, а высота призмы 10 футов?

Решение : Применение формулы:

$\text{V} = b \times h$

$150 = b \times 10$

$b = 150 / 10 = 15$ квадратных футов 5

3

2. Основание призмы имеет площадь поверхности 277 квадратных сантиметров. Объем 2770 кубических сантиметров. Вычислите высоту.

Решение: Применяя формулу:

$\text{V} = b \times h$

$2770 = 277 \times h$

$h = 2770 / 277 = 10$ сантиметров

3. Высота квадратной призмы 11 ярдов. Объем 99 куб. Какова длина стороны квадрата у основания призмы?

Решение: Объем = площадь основания x высота

Применение формулы:

$\text{V} = b \times h$

$99 = b \times 11$

$b = \frac{ 99}{11} = 9$ квадратных ярдов 

Поскольку площадь основания равна 9 квадратных ярдов, это площадь квадратного основания призмы. Таким образом, сторона квадрата будет равна квадратному корню из 9 долларов.= 3$ ярдов.

4. Основание призмы имеет площадь поверхности 475 квадратных сантиметров. Объем 3800 кубических сантиметров. Вычислите высоту.

Решение: Применяя формулу:

$\text{V} = b \times h$

$3800 = 475 \times h$

$h = \frac{3800}{475} = 8$ см

5. Столб призмы имеет длину 20 метров. Основание призмы имеет площадь 25 квадратных метров. Каков объем призмы?

Решение: Применяя формулу:

$\text{V} = b \times h$

$\text{V} = 25 \times 20 = 500$ кубических метров

Практические задачи

1

Какова площадь основания призмы, если объем призмы 300 кубических футов, а высота призмы 6 футов?

5 квадратных футов

50 квадратных футов

5 футов

1800 кубических футов

Правильный ответ: 50 квадратных футов
$\text{V} = b \times h$
$300 = b \times 6$
$b = \frac{300}{6} = 50$ квадратных футов

2

Основание призмы имеет площадь поверхности 25 квадратных сантиметров. Его объем составляет 125 кубических сантиметров. Вычислите высоту.

5 квадратных сантиметров

50 квадратных сантиметров

5 сантиметров

180 кубических сантиметров

Правильный ответ: 5 сантиметров
$\text{V} = b \times h$
$125 = 25 \times h2 903 h = \frac{125}{25} = 5$ сантиметров

3

Площадь основания призмы составляет 123 квадратных ярда.

Высота 9 метров. Найдите объем.

16 кв. ярдов

50 куб. ярдов

1107 куб. ярдов

1800 куб. ярдов

Правильный ответ: 1107 куб. {V} = 123 \times 9$
$= 1107$ кубических ярдов

4

Основание призмы имеет площадь поверхности 12 квадратных сантиметров. Объем призмы 144 кубических сантиметра. Вычислите высоту.

1248 кубических сантиметров

8 сантиметров

12 сантиметров

120 квадратных сантиметров

Правильный ответ: 12 сантиметров
$\text{V} = b \times h$
$144 = 12 $035 h2$ 9 = \frac{144}{12} = 12$ сантиметров

5

Столб призмы имеет длину 100 футов. Основание призмы имеет площадь 25 квадратных футов. Каков его объем?

1248 кубических сантиметров

8 сантиметров

12 сантиметров

2500 кубических футов

Правильный ответ: 2500 кубических футов
$\text{V} = b \times h$
$\text{V} = 25 \times 100 = 2500$ кубических футов

Часто задаваемые вопросы

Как найти объем неправильной призмы?

Неправильные призмы имеют в своей основе неправильные многоугольники. Это означает, что базовые формы имеют разные углы, а стороны не равны по длине. Хотя площадь основания будет отличаться, формула для нахождения объема будет той же, т. е. площадь основания $\times$ высота.

Влияет ли на объем призмы количество граней?

Нет, объем призмы не зависит от количества граней, потому что площадь ее основания и высота не изменяются от количества граней.

Чем отличаются объемы призм разных типов?

Различные типы призм имеют разные основания, разные формы и размеры. Так как базовая площадь отличается, соответственно будет отличаться и объем.

Как объем связан со стороной основания многоугольника в правильной призме?

Чем длиннее сторона базового многоугольника, тем больше площадь основания и, следовательно, больше объем.

Как рассчитать объем прямой призмы?

Прямая призма — призма, у которой углы между основанием и сторонами (боковыми гранями) призмы прямые, например, прямоугольная призма.