Стереометрия (Геометрия в пространстве) — Все свойства, теоремы, аксиомы и формулы — Математика
Оглавление:
Базовые теоремы, аксиомы и определения стереометрии
Вводные определения и аксиомы стереометрии
К оглавлению…
Некоторые определения:
- Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
- Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.
- Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.
- Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются
- Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники. Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.

- Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
- Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются
- Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).
- Пирамида (n-угольная)
- Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды
- Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой.
 У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники. - Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).
Аксиомы стереометрии:
- Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
- Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
- Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следствия из аксиом стереометрии:
- Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость.
- Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость.
- Теорема 3. Через две параллельные прямые проходит единственная плоскость.
Построение сечений в стереометрии
К оглавлению…
Для решения задач по стереометрии остро необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Дадим несколько определений, поясняющих, что такое сечение:
- Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба).
- Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости.
- Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтому сечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.

Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна. В основе построения сечений многогранников лежит две задачи на построение:
- Линии пересечения двух плоскостей.
Для построения прямой, по которой пересекаются некоторые две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β.
- Точки пересечения прямой и плоскости.
Для построения точки пересечения прямой l и плоскости α нужно построить точку пересечения прямой l и прямой l1, по которой пересекаются плоскость
Взаимное расположение прямых и плоскостей в стереометрии
К оглавлению…
Определение: В ходе решения задач по стереометрии две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Если прямые а и b, либо AB и CD параллельны, то пишут:
Несколько теорем:
- Теорема 1. Через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной прямой.
- Теорема 2. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
- Теорема 3 (признак параллельности прямых). Если две прямые параллельны третьей прямой, то они параллельны между собой.

- Теорема 4 (о точке пересечения диагоналей параллелепипеда). Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Возможны три случая взаимного расположения прямой и плоскости в стереометрии:
- Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).
- Прямая и плоскость пересекаются (имеют единственную общую точку).
- Прямая и плоскость не имеют ни одной общей точки.
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут:
Теоремы:
- Теорема 1 (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
- Теорема 2. Если плоскость (на рисунке – α) проходит через прямую (на рисунке – с), параллельную другой плоскости (на рисунке – β), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке –
Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).
Определение: Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.
Теоремы:
- Теорема 1 (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.

- Теорема 2. Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой.
Теперь введем понятие угла между скрещивающимися прямыми. Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O в пространстве и проведем через нее прямые a1 и b1, параллельные прямым a и b соответственно. Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a1 и b1.
Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Это обычно не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между скрещивающимися прямыми дадим такое определение:
Определение: Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a1 параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a1 и b).
Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90°. Перпендикулярными могут быть как скрещивающиеся прямые, так и прямые лежащие и пересекающиеся в одной плоскости. Если прямая a перпендикулярна прямой b, то пишут:
Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:
Теоремы:
- Теорема 1 (признак параллельности плоскостей).
 Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. - Теорема 2 (о свойстве противолежащих граней параллелепипеда). Противолежащие грани параллелепипеда лежат в параллельных плоскостях.
- Теорема 3 (о прямых пересечения двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.
- Теорема 4. Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.
- Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее). Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.
Определение: Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если прямая a перпендикулярна плоскости β, то пишут, как обычно:
Теоремы:
- Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.
- Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
- Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
- Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой).
 Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой. - Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
- Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину:
Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.
Теорема о трех перпендикулярах
К оглавлению…
Пусть точка А не лежит на плоскости α. Проведем через точку А прямую, перпендикулярную плоскости α, и обозначим буквой О точку пересечения этой прямой с плоскостью α. Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АО, точка О называется основанием перпендикуляра. Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.
Теорема 1 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:
Теорема 2 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость. Данные теоремы, для обозначений с чертежа выше можно кратко сформулировать так:
Теорема: Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:
- две наклонные, имеющие равные проекции, равны;
- из двух наклонных больше та, проекция которой больше.

Определения расстояний объектами в пространстве:
- Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.
- Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
- Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
- Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.
Определение: В стереометрии ортогональной проекцией прямой a на плоскость α называется проекция этой прямой на плоскость α в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости α.
Замечание: Как видно из предыдущего определения, проекций бывает много. Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).
Определение: Углом между прямой, не перпендикулярной плоскости, и этой плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость (угол АОА’ на чертеже выше).
Теорема: Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.
Двугранный угол
К оглавлению…
Определения:
- Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.

- Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). В дальнейшем, при решении задач по стереометрии, под двугранным углом будем понимать всегда тот линейный угол, градусная мера которого удовлетворяет условию:
Определения:
- Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.
- Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.
- Две плоскости называются перпендикулярными, если угол между ними равен 90°.
Теоремы:
- Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.
Симметрия фигур
К оглавлению…
Определения:
- Точки M и M1 называются симметричными относительно точки O, если O является серединой отрезка MM1.

- Точки M и M1 называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM1 и перпендикулярна ему.
- Точки M и M1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM1 и перпендикулярна этому отрезку.
- Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.
- Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.
Призма
К оглавлению…
Определения:
- Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
- Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
- Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
- Боковая поверхность – объединение боковых граней.
- Полная поверхность – объединение оснований и боковой поверхности.
- Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.

- Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
- Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
- Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
- Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
- Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Свойства и формулы для призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:
где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
- Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.

- Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:
где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1 или BB1 и так далее).
- Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:
где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.
Виды призм в стереометрии:
- Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
- Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):
где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.
- Правильная призма – призма в основании которой лежит правильный многоугольник (т.
 е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:
е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:
Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.
- Правильная призма является прямой.
Параллелепипед
К оглавлению…
Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.
Другие свойства и определения:
- Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.
- Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
- Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
- Параллелепипед имеет шесть граней и все они – параллелограммы.
- Противоположные грани параллелепипеда попарно равны и параллельны.
- У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.
- Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям).
 Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда. - Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
- Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = Sосн∙h).
- Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным. Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
- Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением:
d2 = a2 + b2 + c2.
-
- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда:
- Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
- Абсолютно все рёбра куба равны между собой.
- Диагональ куба d и длина его ребра a связаны соотношением:
- Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу для объема куба:
Пирамида
К оглавлению…
Определения:
- Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
 По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды.
По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды.
- Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.
- Грани, отличные от основания, называются боковыми. На чертеже это: ABC, ACD, ADE и AEB.
- Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины). На чертеже это A.
- Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. На чертеже это: AB, AC, AD и AE.
- Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания. Для пирамиды с чертежа обозначение будет таким: ABCDE.
- Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H. На чертеже высота это AG. Обратите внимание: только в случае если пирамида является правильной четырехугольной пирамидой (как на чертеже) высота пирамиды попадает на диагональ основания. В остальных случаях это не так. В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно.
- Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. На чертеже это, например, AF.
- Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания. На чертеже это, например, ACE.
Еще один стереометрический чертеж с обозначениями для лучшего запоминания (на рисунке правильная треугольная пирамида):
Если все боковые ребра (SA, SB, SC, SD на чертеже ниже) пирамиды равны, то:
- Около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр (точка O).
 Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т.е. в точку пересечения посерединных перпендикуляров основания.
Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т.е. в точку пересечения посерединных перпендикуляров основания. - Боковые ребра образуют с плоскостью основания равные углы (на чертеже ниже это углы SAO, SBO, SCO, SDO).
Важно: Также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом (углы DMN, DKN, DLN на чертеже ниже равны), то:
- В основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр (точка N). Иными словами, высота (отрезок DN), опущенная из вершины такой пирамиды на основание, попадает в центр вписанной в основание окружности, т.е. в точку пересечения биссектрис основания.
- Высоты боковых граней (апофемы) равны. На чертеже ниже DK, DL, DM – равные апофемы.
- Площадь боковой поверхности такой пирамиды равна половине произведения периметра основания на высоту боковой грани (апофему).
где: P – периметр основания, a – длина апофемы.
Важно: Также верно и обратное, то есть если в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в её центр, то все боковые грани наклонены к плоскости основания под одним углом и высоты боковых граней (апофемы) равны.
Правильная пирамида
К оглавлению…
Определение: Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
Тогда она обладает такими свойствами:
- Все боковые ребра правильной пирамиды равны.
- Все боковые грани правильной пирамиды наклонены к плоскости основания под одним углом.
Важное замечание: Как видим правильные пирамиды являются одними из тех пирамид к которым относятся свойства, изложенные чуть выше. Действительно, если основание правильной пирамиды – это правильный многоугольник, то центр его вписанной и описанной окружностей совпадают, а вершина правильной пирамиды проецируется именно в этот центр (по определению). Однако важно понимать, что не только правильные пирамиды могут обладать свойствами, о которых говорилось выше.
- В правильной пирамиде все боковые грани – равные равнобедренные треугольники.
- В любую правильную пирамиду можно как вписать сферу, так и описать около неё сферу.
- Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Формулы для объема и площади пирамиды
К оглавлению…
Теорема (об объеме пирамид, имеющих равные высоты и равные площади оснований). Две пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы (Вы конечно, наверняка уже знаете формулу для объема пирамиды, ну или видите ее несколькими строчками ниже, и Вам кажется это утверждение очевидным, но на самом деле, если судить «на глаз», то данная теорема не так уж и очевидна (см. рисунок ниже). Это относится кстати и к другим многогранникам и геометрическим фигурам: их внешний вид обманчив, поэтому, действительно – в математике нужно доверять только формулам и правильным расчетам).
- Объём пирамиды может быть вычислен по формуле:
где: Sосн – площадь основания пирамиды, h – высота пирамиды.
- Боковая поверхность пирамиды равна сумме площадей боковых граней.
 Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу:
Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу:
где: Sбок – площадь боковой поверхности, S1, S2, S3 – площади боковых граней.
- Полная поверхность пирамиды равна сумме площади боковой поверхности и площади основания:
Тетраэдр
К оглавлению…
Определения:
- Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.
- Тетраэдр называется правильным, если все его грани – равносторонние треугольники. У правильного тетраэдра:
- Все ребра правильного тетраэдра равны между собой.
- Все грани правильного тетраэдра равны между собой.
- Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.
На чертеже изображен правильный тетраэдр, при этом треугольники ABC, ADC, CBD, BAD – равны. Из общих формул для объема и площадей пирамиды, а также знаний из планиметрии не сложно получить формулы для объема и площадей правильного тетраэдра (а – длина ребра):
Прямоугольная пирамида
К оглавлению…
Определение: При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид. На рисунке слева SA – ребро, являющееся одновременно высотой.
Усечённая пирамида
К оглавлению. ..
..
Определения и свойства:
- Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
- Фигура, полученная на пересечении секущей плоскости и исходной пирамиды, также называется основанием усеченной пирамиды. Итак, у усеченной пирамиды на чертеже два основания: ABC и A1B1C1.
- Боковые грани усечённой пирамиды являются трапециями. На чертеже это, например, AA1B1B.
- Боковыми ребрами усеченной пирамиды называются части ребер исходной пирамиды, заключенные между основаниями. На чертеже это, например, AA1.
- Высотой усеченной пирамиды называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания.
- Усеченная пирамида называется правильной, если она является многогранником, который отсекается плоскостью, параллельной основанию правильной пирамиды.
- Основания правильной усеченной пирамиды – правильные многоугольники.
- Боковые грани правильной усеченной пирамиды – равнобедренные трапеции.
- Апофемой правильной усеченной пирамиды называется высота ее боковой грани.
- Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.
Объём усечённой пирамиды равен:
где: S1 и S2 – площади оснований, h – высота усечённой пирамиды. Однако на практике, удобнее искать объем усеченной пирамиды так: можно достроить усечённую пирамиду до пирамиды, продлив до пересечения боковые рёбра.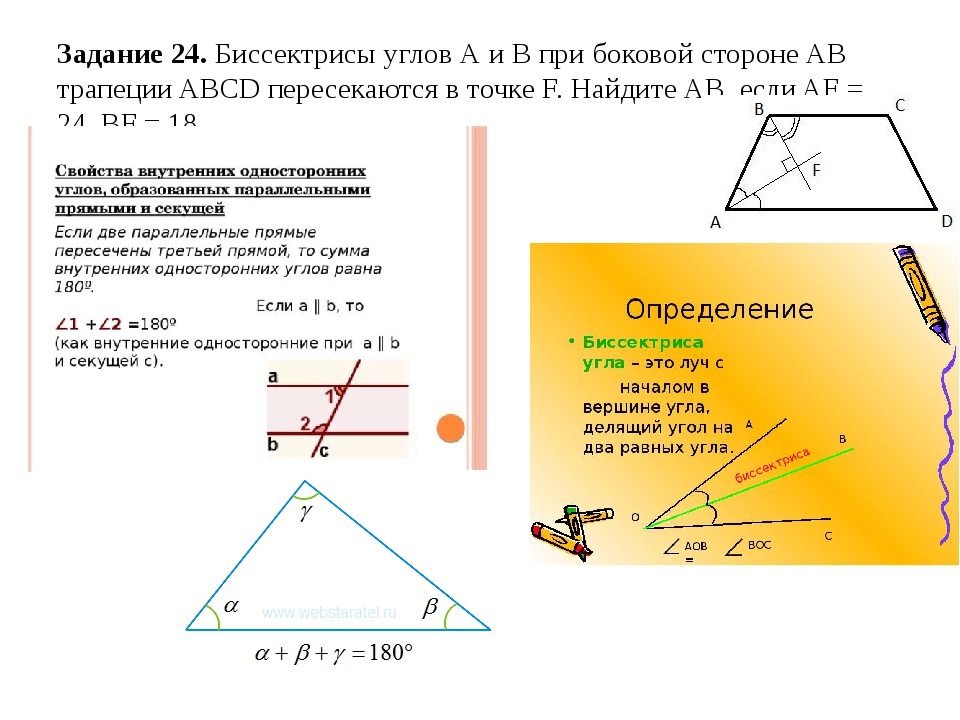 Тогда объём усечённой пирамиды можно найти, как разность объёмов всей пирамиды и достроенной части. Площадь боковой поверхности также можно искать как разность между площадями боковой поверхности всей пирамиды и достроенной части. Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы:
Тогда объём усечённой пирамиды можно найти, как разность объёмов всей пирамиды и достроенной части. Площадь боковой поверхности также можно искать как разность между площадями боковой поверхности всей пирамиды и достроенной части. Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы:
где: P1 и P2 – периметры оснований правильной усеченной пирамиды, а – длина апофемы. Площадь полной поверхности любой усеченной пирамиды, очевидно, находится как сумма площадей оснований и боковой поверхности:
Пирамида и шар (сфера)
К оглавлению…
Теорема: Около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (т.е. многоугольник около которого можно описать сферу). Данное условие является необходимым и достаточным. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им.
Замечание: Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу. Однако, список пирамид около которых можно описать сферу не исчерпывается этими типами пирамид. На чертеже справа, на высоте SH надо выбрать точку О, равноудалённую от всех вершин пирамиды: SO = OВ = OС = OD = OA. Тогда точка О – центр описанного шара.
Теорема: В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Замечание: Вы, очевидно, не поняли того, что прочитали строчкой выше. Однако, главное запомнить, что любая правильная пирамида является такой, в которую можно вписать сферу. При этом список пирамид, в которые можно вписать сферу не исчерпывается правильными.
При этом список пирамид, в которые можно вписать сферу не исчерпывается правильными.
Определение: Биссекторная плоскость делит двугранный угол пополам, а каждая точка биссекторной плоскости равноудалена от граней, образующих двугранный угол. На рисунке справа плоскость γ является биссекторной плоскостью двугранного угла, образованного плоскостями α и β.
На стереометрическом чертеже ниже изображен шар вписанный в пирамиду (или пирамида описанная около шара), при этом точка О – центр вписанного шара. Данная точка О равноудалена от всех граней шара, например:
ОМ = ОО1
Пирамида и конус
К оглавлению…
В стереометрии конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие).
Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие).
Важное свойство: Высоты у таких конусов и пирамид равны между собой.
Пирамида и цилиндр
К оглавлению…
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды – вписанный многоугольник (необходимое и достаточное условие).
Сфера и шар
К оглавлению…
Определения:
- Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.
- Хордой сферы называется отрезок, соединяющий две точки сферы.
- Диаметром сферы называется хорда, проходящая через ее центр. Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.
- Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
- Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.
- Разница между шаром и сферой аналогична разнице между кругом и окружностью. Окружность – это линия, а круг – это ещё и все точки внутри этой линии. Сфера – это оболочка, а шар – это ещё и все точки внутри этой оболочки.
- Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.
- Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).
Теоремы:
- Теорема 1 (о сечении сферы плоскостью).
 Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы. - Теорема 2 (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.
Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
Определения:
- Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.
- Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
- Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.
Теоремы:
- Теорема 1 (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
- Теорема 2 (о свойстве касательной плоскости к сфере).
 Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.
Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.
Многогранники и сфера
К оглавлению…
Определение: В стереометрии многогранник (например, пирамида или призма) называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника (пирамиды, призмы). Аналогично: многогранник называется вписанным в шар, если все его вершины лежат на границе этого шара. При этом шар называется описанным около многогранника.
Важное свойство: Центр сферы, описанной около многогранника, находится на расстоянии, равном радиусу R сферы, от каждой вершины многогранника. Приведем примеры вписанных в сферу многогранников:
Определение: Многогранник называется описанным около сферы (шара), если сфера (шар) касается всех граней многогранника. При этом сфера и шар называются вписанными в многогранник.
Важно: Центр сферы, вписанной в многогранник, находится на расстоянии, равном радиусу r сферы, от каждой из плоскостей, содержащих грани многогранника. Приведем примеры описанных около сферы многогранников:
Объем и площадь поверхности шара
К оглавлению…
Теоремы:
- Теорема 1 (о площади сферы). Площадь сферы равна:
где: R – радиус сферы.
- Теорема 2 (об объеме шара). Объем шара радиусом R вычисляется по формуле:
Шаровой сегмент, слой, сектор
К оглавлению…
Шаровой сегментВ стереометрии шаровым сегментом называется часть шара, отсекаемая секущей плоскостью. При этом соотношение между высотой, радиусом основания сегмента и радиусом шара:
где: h − высота сегмента, r − радиус основания сегмента, R − радиус шара. Площадь основания шарового сегмента:
Площадь основания шарового сегмента:
Площадь внешней поверхности шарового сегмента:
Площадь полной поверхности шарового сегмента:
Объем шарового сегмента:
Шаровой слойВ стереометрии шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями. Площадь внешней поверхности шарового слоя:
где: h − высота шарового слоя, R − радиус шара. Площадь полной поверхности шарового слоя:
где: h − высота шарового слоя, R − радиус шара, r1, r2 − радиусы оснований шарового слоя, S1, S2 − площади этих оснований. Объем шарового слоя проще всего искать как разность объемов двух шаровых сегментов.
Шаровой секторВ стереометрии шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше чем пол шара. Площадь полной поверхности шарового сектора:
где: h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара. Объем шарового сектора вычисляется по формуле:
Цилиндр
К оглавлению…
Определения:
- В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности. Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.

- Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.
- Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.
- Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.
- Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.
- Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.
- Радиусом цилиндра называется радиус его оснований.
- Цилиндр называется равносторонним, если его высота равна диаметру основания.
- Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.
- Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.

- Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.
- Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.
Цилиндр и призма
К оглавлению…
Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра. В этом случае цилиндр называется описанным около призмы. Высота призмы и высота цилиндра в этом случае будут равны. Все боковые ребра призмы будут принадлежать боковой поверхности цилиндра и совпадать с его образующими. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать в такой цилиндр можно также только прямую призму. Примеры:
Призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра. В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые ребра призмы будут параллельны образующим цилиндра. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать такой цилиндр можно только в прямую призму. Примеры:
Цилиндр и сфера
К оглавлению…
Сфера (шар) называется вписанной в цилиндр, если она касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным около сферы (шара). Сферу можно вписать в цилиндр, только если это равносторонний цилиндр, т.е. диаметр его основания и высота равны между собой. Центром вписанной сферы будет служить середина оси цилиндра, а радиус этой сферы будет совпадать с радиусом цилиндра. Пример:
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра являются сечениями сферы. Цилиндр называется вписанным в шар, если основания цилиндра являются сечениями шара. При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:
Цилиндр называется вписанным в шар, если основания цилиндра являются сечениями шара. При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:
На основе теоремы Пифагора легко доказать следующую формулу, связывающую радиус описанной сферы (R), высоту цилиндра (h) и радиус цилиндра (r):
Объем и площадь боковой и полной поверхностей цилиндра
К оглавлению…
Теорема 1 (о площади боковой поверхности цилиндра): Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту:
где: R – радиус основания цилиндра, h – его высота. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности прямой призмы.
Площадью полной поверхности цилиндра, как обычно в стереометрии, называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра (т.е. просто площадь круга) вычисляется по формуле:
Следовательно, площадь полной поверхности цилиндра Sполн. цилиндра вычисляется по формуле:
Теорема 2 (об объеме цилиндра): Объем цилиндра равен произведению площади основания на высоту:
где: R и h – радиус и высота цилиндра соответственно. Эта формула также легко выводится (доказывается) на основе формулы для объема призмы.
Теорема 3 (Архимеда): Объём шара в полтора раза меньше объёма, описанного вокруг него цилиндра, а площадь поверхности такого шара в полтора раза меньше площади полной поверхности того же цилиндра:
Конус
К оглавлению…
Определения:
- Конусом (точнее, круговым конусом) называется тело, которое состоит из круга (называемого основанием конуса), точки, не лежащей в плоскости этого круга (называемой вершиной конуса) и всех возможных отрезков, соединяющих вершину конуса с точками основания.
 Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.
Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.
- Отрезки (или их длины), соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Все образующие прямого кругового конуса равны между собой.
- Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (составленной из всех возможных образующих).
- Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
- Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом.
- Наглядно прямой круговой конус можно представлять себе, как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. При этом боковая поверхность конуса образуется вращением гипотенузы, а основание – вращением катета, не являющимся осью.
- Радиусом конуса называется радиус его основания.
- Высотой конуса называется перпендикуляр (или его длина), опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту, т.е. прямая проходящая через центр основания и вершину.
- Если секущая плоскость проходит через ось конуса, то сечение равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.
- Если секущая плоскость проходит через внутреннюю точку высоты конуса и перпендикулярна ей, то сечением конуса является круг, центр которого есть точка пересечения высоты и этой плоскости.

- Высота (h), радиус (R) и длина образующей (l) прямого кругового конуса удовлетворяют очевидному соотношению:
Объем и площадь боковой и полной поверхностей конуса
К оглавлению…
Теорема 1 (о площади боковой поверхности конуса). Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
где: R – радиус основания конуса, l – длина образующей конуса. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности правильной пирамиды.
Площадью полной поверхности конуса называется сумма площади боковой поверхности и площади основания. Площадь основания конуса (т.е. просто площадь круга) равна: Sосн = πR2. Следовательно, площадь полной поверхности конуса Sполн. конуса вычисляется по формуле:
Теорема 2 (об объеме конуса). Объем конуса равен одной трети произведения площади основания на высоту:
где: R – радиус основания конуса, h – его высота. Эта формула также легко выводится (доказывается) на основе формулы для объема пирамиды.
Усеченный конус
К оглавлению…
Определения:
- Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
- Основание исходного конуса и круг, получающийся в сечении этого конуса плоскостью, называются основаниями, а отрезок, соединяющий их центры — высотой усеченного конуса.
- Прямая проходящая через высоту усеченного конуса (т.е. через центры его оснований) является его осью.
- Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.

- Все образующие усеченного конуса равны между собой.
- Усеченный конус может быть получен при повороте на 360° прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Объём усечённого конуса вычисляется по формуле:
где: S1 = πr12 и S2 = πr22 – площади оснований, h – высота усечённого конуса, r1 и r2 – радиусы верхнего и нижнего оснований усеченного конуса. Однако на практике, всё же удобнее искать объем усеченного конуса как разность объёмов исходного конуса и отсеченной части. Площадь боковой поверхности усеченного конуса также можно искать как разность между площадями боковой поверхности исходного конуса и отсеченной части.
Действительно, площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса вычисляется по формуле:
где: P1 = 2πr1 и P2 = 2πr2 – периметры оснований усеченного конуса, l – длина образующей. Площадь полной поверхности усеченного конуса, очевидно, находится как сумма площадей оснований и боковой поверхности:
Обратите внимание, что формулы для объема и площади боковой поверхности усеченного конуса получены на основе формул для аналогичных характеристик правильной усеченной пирамиды.
Конус и сфера
К оглавлению…
Конус называется вписанным в сферу (шар), если его вершина принадлежит сфере (границе шара), а окружность основания (само основание) является сечением сферы (шара). При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:
При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:
Сфера (шар) называется вписанной в конус, если сфера (шар) касается основания конуса и каждой его образующей. При этом конус называется описанным около сферы (шара). В прямой круговой конус всегда можно вписать сферу. Её центр будет лежать на высоте конуса, а радиус вписанной сферы будет равен радиусу окружности, вписанной в осевое сечение конуса (это сечение является равнобедренным треугольником). Примеры:
Конус и пирамида
К оглавлению…
- Конус называется вписанным в пирамиду (пирамида – описанной около конуса), если основание конуса вписано в основание пирамиды, а вершины конуса и пирамиды совпадают.
- Пирамида называется вписанной в конус (конус – описанным около пирамиды), если ее основание вписано в основание конуса, а боковые ребра являются образующими конуса.
- Высоты у таких конусов и пирамид равны между собой.
Примечание: Подробнее о том, как в стереометрии конус вписывается в пирамиду или описывается около пирамиды уже говорилось в ранее здесь.
Урок 6. параллельность плоскостей — Геометрия — 10 класс
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
- Определение параллельных плоскостей;
- Свойства параллельных плоскостей;
- Признак параллельности плоскостей.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Основная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Дополнительная литература:
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.
Изображение:
Пример 1.
Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Доказательство.
Пусть α и β — данные плоскости, a1 и a2 – пересекающиеся прямые в плоскости α, а b1 и b2 соответственно параллельные им прямые в плоскости β.
Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку.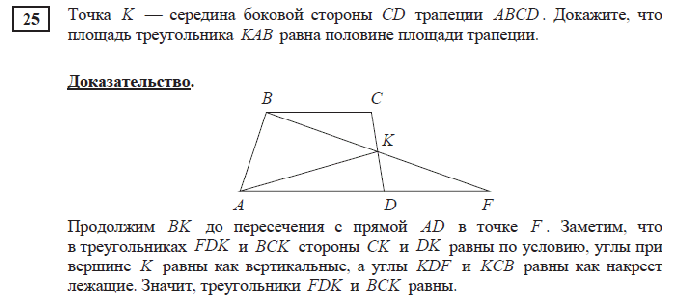 Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.
Теорема доказана.
Свойства параллельных плоскостей.
Теорема 1. Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.
Доказательство.
Пусть α и β — параллельные плоскости, а γ- плоскость, пересекающая их.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
Доказательство.
Пусть α и β — параллельные плоскости, а a и b – параллельные прямые, пересекающие их.
Через прямые a и b можно провести плоскость — эти прямые параллельны, значит определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Доказательство.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.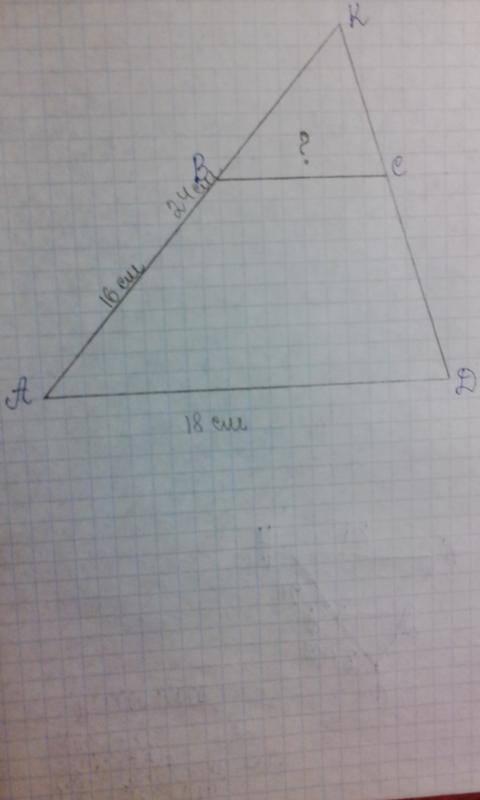
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.
Теорема 4. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.
Доказательство.
Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Доказательство.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.
В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.
Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Пример 2.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Доказательство.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Пример 3.
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Доказательство.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А1В1С1 и А2В2С2 параллельны.
Доказательство.
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Верное решение:
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
№2.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. 2} = 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.
2} = 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.
Получим $S(0; 0; 4), B(0; -8√2; 0), C (-8√2; 0; 0), K (6√2; 0; 1), E(6√2; -2√2; 0), F (-2√2; 6√2; 0)$.
2. Докажем, что векторы нормали к плоскостям $SBC$ и $KEF$ коллинеарны. Для плоскости $SBC$, вектор нормали ${n_1}↖{→}(a_1; b_1; c_1)$ перпендикулярен к обеим прямым $SB$ и $SC$, поэтому он должен быть перпендикулярен к векторам ${SB}↖{→}(0; -8√2; -4)$ и ${SC}↖{→}(-8√2; 0; -4)$.
Получим систему $\{\table\ {n_1}↖{→} · {SB}↖{→} = 0; \ {n_1}↖{→} ·{SC}↖{→} = 0;$ $\{\table\0 · a_1 — 8√2 · b_1 — 4c_1 = 0; \-8√2a_1 + 0 · b_1 — 4 · c_1 = 0;$ $\{\table\-2√2b_1 — c_1 = 0; \-2√2a_1 — c_1 = 0;$
Пусть $c_1 = -1$, тогда система примет вид $\{\table\-2√2b_1 + 1 = 0; \-2√2a_1 + 1 = 0;$
Её решение $a_1 = {√2}/{4}; b_1 = {√2}/{4}$.
${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $SBC$ .
Для плоскости $KEF$, вектор нормали ${n_2}↖{→}(a_2; b_2; c_2)$ перпендикулярен к обеим прямым $KE$ и $KF$, поэтому он должен быть перпендикулярен к векторам ${KE}↖{→}(0; -2√2; -1)$ и ${KF}↖{→}(-8√2; 6√2; -1)$.
Получим систему $\{\table\ {n_2}↖{→} · {KE}↖{→} = 0; \ {n_2}↖{→} · {KF}↖{→} = 0;$ $\{\table\0 · a_2 — 2√2 · b_2 — 1 · c_2 = 0; \-8√2a_2 + 6√2 · b_2 — 1 · c_2 = 0;$ $\{\table\-2√2b_2 — c_2 = 0; \-8√2a_2 + 6√2b_2 — c_2 = 0$.
Пусть $c_2 = -1$, тогда система примет вид $\{\table\-2√2b_2 + 1 = 0; \8√2a_2 + 6√2b_2 + 1 = 0;$
Её решение $a_2 = {√2}/{4}; b_2 = {√2}/{4}$.${n_2}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $KEF$.
Векторы ${n_1}↖{→}$ и ${n_2}↖{→}$ равны, значит коллинеарны, следовательно плоскости $SBC$ и $KEF$ параллельны.
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь треугольника $SBC$, а высота пирамиды $h$ — это расстояние от точки $K$ до плоскости $SBC$.
1. $S = {1}/{2}SB · SC · sin α$, где $α$ — угол между прямыми $SB$ и $SC$. 2}} = {12√5}/{5}$, где $x_0, y_0, z_0$ — координаты точки $K$.
2}} = {12√5}/{5}$, где $x_0, y_0, z_0$ — координаты точки $K$.
3. $V = {1}/{3} · 32√5 · {12√5}/{5} = 128$.
Тесты Геометрия 10 класс | Образовательная социальная сеть
Зачет по теме: «Параллельность прямой и плоскости».
10-й класс.
Практическая часть. Решение задач.
Задание № 1
s В плоскости а, пересекающихся с плоскостью s
по прямой С, проведена прямая а, параллельная с.
b В плоскости s проведена прямая b, пересекающая
прямую c.
1) Могут ли прямые а и b иметь общие точки?
2) Докажите, что а и b – скрещивающие прямые.
c
a а
Задание № 2
D C Через точку К стороны АD параллелограмма
ABCD проведена плоскость а, параллельная
прямой DC.
1) На какие фигуры делит плоскость а данный
К М параллелограмм? (Ответ, пояснение).
2) Вычислите длины отрезков, на которые
А а делит плоскость а диагональ BD, если
DK=6см, АК=8см, BD=21см.
А В
Задание № 3
D Точки А,В, С и D не лежат в одной плоско-
сти. К и М – середины отрезков ВD и СD.
К и М – середины отрезков ВD и СD.
1) Имеют ли общие точки прямая КМ и
плоскость, в которой лежат точки А,В и С?
* M 2) Вычислите периметр треугольника АКМ,
если расстояние между каждой парой дан-
K * ных точек равно 8 см.
A C
a
B
С Задание № 4
Через точку К стороны АС треугольника
АВС проведена плоскость α ,параллельная
прямой АВ.
- Постройте точку пересечения плос-
а К кости α и стороны ВС (точку М)
2). Вычислите длину отрезка КМ, если
КМ // АВ 26см, СК / КА 4 : 5
А В
Задание № 5 Задание № 6
М
К
а
Мı Дан куб АВСD А ВСD
Кı 1) Постройте отрезок, являющийся пере-
сечением грани ВССВ и плоскости а, в
Отрезок КМ, равный 10 см, параллелен которой лежит прямая АD и точка К сере-
плоскости а. Через его концы проведены дина ребра ВС.
Через его концы проведены дина ребра ВС.
параллельные прямые, пересекающие а в 2) Постройте сечение куба плоскостью а.
точках К ı и М ı. 3) Вычислите периметр построенного се-
- Как расположены прямые КМ и Кı Мı? чения, если ребро куба равно 16 см.
- Вычислите расстояние между точками
К и М.
- Вычислите площадь четырехугольника
КММı Кı, если ККı=8см, °.
Задание № 7 Задание № 8
А
Дан куб АВСD А ВСD
1) Постройте отрезок, являющийся пере-
В сечением грани АВВА и плоскости а, в
К которой лежит прямая СС и точка К сере-
а дина ребра АВ.
М 2) Постройте сечение куба плоскостью а.
3) Вычислите периметр построенного се-
С чения, если ребро куба равно 20 см.
Через точку А стороны АС треугольника
АВС проведена плоскость а, параллель-
ная АВ.
- Как расположены прямые АВ и КМ
(М – точка пересечения прямой ВС и
плоскости а ) ?
- Вычислите длину отрезка КМ, если
АК=4 см, КС=6 см, АВ=5 см.
Задание № 9 Задание № 10
А
В Верно ли утверждение , что две прямые,
Параллельные одной плоскости, параллельны?
а *В
Отрезок АВ параллелен плоскости а. Через
его концы проведены параллельные пря-
мые. Прямая проходящая через точку В,
пересекает плоскость в точке В.
- Постройте точку пересечения второй
прямой с плоскостью а (точку А).
- Вычислите периметр четырехугольника
АВВА, если АВ: ВВ= 5 : 2, АВ-ВВ=9 см
Задание № 11
С
М
К
В Задание № 12
Прямая а параллельна плоскости а. Верно ли
А а утверждение, что любая прямая плоскости а
параллельна прямой а?
Отрезок АВ, равный 15 см, лежит в плоско-
сти а. Точка С не лежит в ней. К и М–сере-
дина отрезков АС и ВС.
- Может ли прямая КМ иметь общие точ-
ки с плоскостью а?
- Вычислите расстояние между точками К
и М.
Зачет по теме
«Перпендикулярность прямой и плоскости».
10-й класс.
Теоретическая часть. Доказательство теорем.
Теорема № 1
Доказать, что если одна из двух параллельных прямых
перпендикулярна плоскости, то и другая…
Теорема № 2
Докажите, что если две прямые перпендикулярны плоскости, то они
параллельны.
Теорема № 3
Докажите признак перпендикулярности прямой и плоскости.
Теорема № 4
Докажите теорему о трех перпендикулярах.
Практическая часть. Решение задач.
Задача № 1
Прямая ВМ перпендикулярна плоскости прямоугольника АВСD.
Найдите: а) расстояние от точки М до сторон прямоугольника
АВСD, если АВ=6 см. ВС=8 см, ВМ=6 см;
б) расстояние от точки М до точки D.
Задача № 2
Через вершину А правильного треугольника АВС проведена прямая
АМ, перпендикулярная к его плоскости. Найдите расстояние от
точки М до стороны ВС, если АВ=4 см, АМ=2 см.
Задача № 3
Точка М удалена от всех вершин квадрата АВСD на расстояние
10 см, АВ- 6√ 2см.
Найдите: а) расстояние от точки М до плоскости АВСD.
б) расстояние от точки М до стороны квадрата.
Задача № 4
Из точки А, удаленной на расстояние 5 см от плоскости, проведены к
этой плоскости наклонные АВ и АС под
Найдите угол между наклонными, если ВС=10 см.
Зачет по теме «Цилиндр, конус и шар»
11-й класс
Практическая часть. Решение задач.
Вариант № 1
Задача № 1
Высота конуса 8 см, а образующая наклонная к плоскости основания под
Задача № 2
Радиус шара 6 см. Найти площадь поверхности вписанного в шар куба.
Вариант № 2
Задача № 1
Радиус шара 6 см. Через конец радиуса, лежащего на сфере, проведена
плоскостью под
Найдите площадь сечения шара этой плоскостью.
Задача № 2
Куб с ребром 4 см вписан в цилиндр. Найдите площадь осевого сечения цилиндра.
Вариант № 3
Задача № 1
Сечение цилиндра плоскостью, параллельной оси, отсекает от
окружности основания дугу 90º.
Найдите площадь сечения, если высота цилиндра 6 см, а расстояние
Между осью цилиндра и секущей плоскостью 3 см.
Задача № 2
Около шара радиуса 6 см описан правильный тетраэдр.
Найти площадь поверхности тетраэдра.
Вариант № 4
Задача № 1
Радиус кругового сектора 10 см, а его угол равен 144º. Сектор свернут
В коническую поверхность. Найдите площадь поверхности конуса (полную).
Задача № 2
Осевое сечение конуса – равносторонний треугольник. В конус вписана треугольная пирамида, основанием которой служит прямоугольный треугольник с катетами 12 см и 16 см. Найти высоту пирамиды.
Вариант № 5
Задача № 1
Осевое сечение цилиндра – квадрат, диагональ которого равна 12 см.
Найдите площадь боковой поверхности цилиндра.
Задача № 2
В сферу вписан конус, образующая которого 12 см, а угол при вершине осевого сечения равен 60º. Найдите площадь поверхности сферы.
Вариант № 6
Задача № 1
Площадь сечения шара плоскостью, проходящей через центр, равна 32π см ². Найдите площадь сферы.
Задача № 2
Диагональ правильной четырехугольной призмы равна 4 см и наклонена к плоскости основания под
Зачет по теме «Координаты на плоскости. Уравнение окружности». 9-й класс
Теоретическая часть.
- Написать формулу нахождения середины отрезка (уметь вывести формулу).
- Что означают в формуле хı и уı ; х2 и у2?
- Написать формулу длины отрезка (уметь вывести формулу).
- Написать уравнение окружности (уметь вывести формулу).
- Что называется уравнением фигуры?
- Что означает буквы х0, у0, х и у в уравнении окружности?
- Сколько точек пересечения могут иметь две окружности?
- Написать уравнение прямой.
- Что показывает угловой коэффициент?
- Дайте определение sin α, cos α, tg α для угла 0
Устный счет
В группах по 4 человека, каждый получает свою карточку и по очереди отвечает консультанту устно или записывает нужные формулы на листе бумаги.
Вариант № 1
Задача № 1
Дано: А (2; 4), В (6; 2)
т. О ε АВ, АО = ОВ
О ε АВ, АО = ОВ
Найти координаты середины отрезка АВ.
Задача № 2
Дано: (х — 3)² + (у — 5)² = 36
Вопросы: что означает это уравнение? Что означают в этом уравнении числа 3, 5, 36?
Задача № 3
Дано: (х + 2 )² + у ² = 13
Найти радиус и координаты центра окружности.
Задача № 4
Дано: т. О (-1; 2 ), R = 5.
Окр. (О, R)
Написать уравнение окружности.
Вариант № 2
Задача № 1
Дано: А (7; 2 ), В (1; 4 )
т. О ε АВ, АО = ОВ
Найти координаты середины отрезка АВ.
Задача № 2
Дано: (х — 1)² + (у — 2)² = 49
Вопросы: что означает это уравнение? Что означают в этом уравнении числа 1, 2, 49?
Задача № 3
Дано: х² + (у + 5 ) ² = 7
Найти радиус и координаты центра окружности.
Задача № 4
Дано: т. О (7; 2 ), R = 2.
Окр. (О, R)
Написать уравнение окружности.
Вариант № 3
Задача № 1
Дано: А (5; 3), В (3; 7)
т. О ε АВ, АО = ОВ
Найти координаты середины отрезка АВ.
Задача № 2
Дано: (х — 2)² + (у — 5)² = 49
Вопросы: что означает это уравнение? Что означают в этом уравнении числа 2, 5, 9?
Задача № 3
Дано: х² + (у + 3) ² = 5
Найти радиус и координаты центра окружности.
Задача № 4
Дано: т. О (-2; 1), R = 4.
Окр. (О, R)
Написать уравнение окружности.
Практическая часть. Решение задач
Учащиеся получают карточки с задачами для письменного решения по вариантам.
Вариант № 1
Задача № 1
Дано: А (4; 1) , В (-1; 3), С (2; 1), D (-1; -1)
Доказать: четырехугольник АВСD – ромб.
Задача № 2
Дано: лежит ли точка А (2; -1) на окружности (х – 2)² + (у + 3)²= 4?
Ответ обосновать.
Вариант № 2
Задача № 1
Дано: А (-2; -2) , В (-2; 4), С (1; 4), D ( 1; -2)
Доказать: четырехугольник АВСD – прямоугольник.
Задача № 2
Дано: лежит ли точка А (1; 4) на прямой 4х + 3у – 6 = 0?
Ответ обосновать.
Вариант № 3
Задача № 1
Дано: А (2; 3) , В ( 5; 8), С ( 8; 3), D ( 5; -2)
Доказать: четырехугольник АВСD – ромб.
Задача № 2
Дано: лежит ли точка М (-3; 2) на прямой 4х + 3у + 6 = 0?
Ответ обосновать.
Зачет по теме «Площадь четырехугольника и треугольника.
Теорема Пифагора». 8-й класс
Теоретическая часть.
Вопросы к зачету:
- Чему равна площадь квадрата?
- Чему равна площадь треугольника?
- Чему равна площадь параллелограмма? (вывод формул)
- Следствия № 1 и № 2, отношение площадей S1 / S2 .
- Площадь треугольника (с выводом ). Отношение площадей треугольника, имеющих по равному углу.
- Теорема Пифагора (с доказательством).
- Теорема обратная теореме Пифагора (с доказательством).
- Площадь ромба (с выводом).
- Площадь трапеции (с выводом).
Практическая часть. Решение задач.
Вариант № 1
Задача № 1
В С
Дано: АВ = 26 см
АD = 32 см
ВН – высота
А Н D
___________________________
Найти: S ABCD
Задача № 2
В С Дано: АВСD – прямоугольник
АС – диагональ
АС = 13 см
АD = 12 cм
___________________________
Найти: S ABCD
А D
Задача № 3
В
Дано: АВСD – равнобедренный
АC = 8 см
ВD – высота
А D C ____________________________________
Найти: S ABC
В Задача № 4
Дано: АВСD – ромб
А О С АС = 10 см
ВD = 12 cм
____________________________
D Найти : S ABCD, АВ
Задача № 5
В С Дано: АВСD – прямоугольная трапеция
СН — высота
ВС = 6 см
АD = 22 см
СD = 20 cм
____________________________________
А Н D Найти: S ABCD
_____________________________________________________________
Задача № 6
В С Дано: АВСD – параллелограмм
ВD — диагональ
ВD = 13 см
BN = 5 см
ND = 12 cм
А Н D __________________________________
Доказать: ∆ BND прямоугольный
Найти: S ABCD
Вариант № 2
Задача № 1
В С
Дано: АВСD – параллелограмм
ВD — диагональ
ВD = 9 см
S ABCD = 108 cм
А D __________________________________
Найти: АВ, ВС
K N Задача № 2
Дано: MKNP — прямоугольник
KM = 6 см
KP – диагональ
KP = 10 см
M P _________________________________
Найти: S MKNP
_______________________________________________________________________________________________
Задача № 3
В Дано: ∆ АBС
BH – высота
АВ = 8 см
АС = 10 см
А С
Н _______________________________
Найти: S ABC
____________________________________________________________________
К
Задача № 4
М О N Дано: MKNP – ромб
P MKNP = 20 см
МК = 8 см.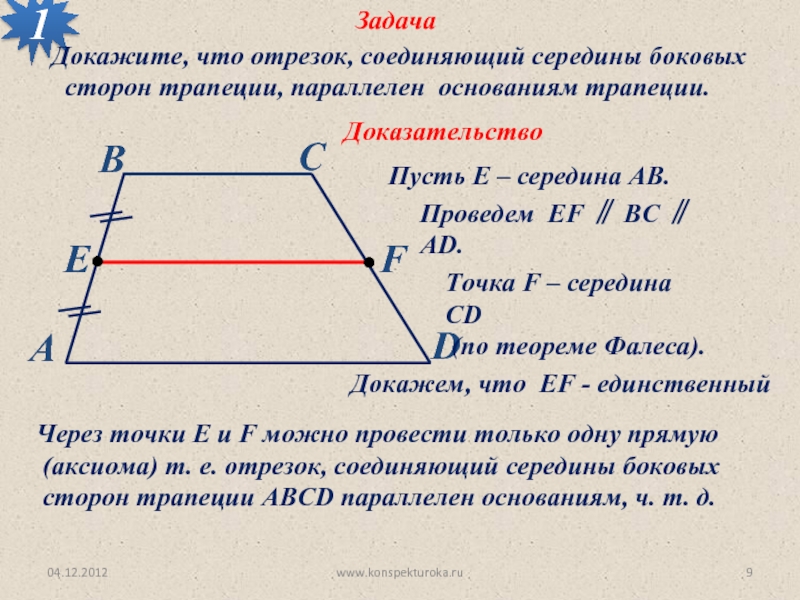
Р _________________________________
Найти: S MKNP
______________________________________________________________________________________________
B C Задача № 5
Дано: ABCD – прямоугольник
AB = 25 см
ВС = 2 см
CD – 7 см
A H D
______________________________
Найти: S ABCD
______________________________________________________________________________________________
Задача № 6
B Дано: BD =5 см
DC = 12 см
BС = 13 см
_________________________________
Определить: вид ∆ BDС
A D C Найти: S ABC
____________________________________________________________________
Практическая часть. Решение задач
Учащиеся получают карточки с задачами для письменного решения по вариантам.
Вариант № 1
Задача № 1
Дано: А(- 4; 1), В (-1; 3), С (2; 1), D (-1; -1).
Доказать: четырехугольник АВСD – ромб.
Задача № 2
Дано: лежит ли точка А (2; -1) на окружности (х – 2)² + (у + 3)² = 4?
Ответ обосновать.
Вариант № 2
Задача № 1
Дано: А(-2; -2), В ( -2; 4), С ( 1; 4), D (1; -2).
Доказать: четырехугольник АВСD – прямоугольник.
Задача № 2
Дано: лежит ли точка А (1; 4) на прямой 4х + 3у — 6 = 0?
Ответ обосновать.
Вариант № 3
Задача № 1
Дано: А(2; 3), В (5; 8), С (8 ; 3), D (5; -2).
Доказать: четырехугольник АВСD – ромб.
Задача № 2
Дано: лежит ли точка М (-3; 2) на прямой 4х + 3у + 6 = 0?
Ответ обосновать.
Пример дифференцированного задания блока № 3
зачета по теме «Признаки равенства треугольников». 7-й класс
Практическая часть. Решение задач.
на оценку «3»: на оценку « 4»: на оценку «5» :
задача № 1 задача № 2 задача № 6
задача № 3 задача № 10 задача № 5
задача № 4 задача № 8 задача № 9
задача № 7 задача № 5 задача № 11
Задачи к зачету по теме: «Признаки равенства треугольников».
Задача № 1
K N Дано: KN = MP
MK = PN
LK = 60°
________________________________
M P Найти: LP.
А С Задача № 2
Дано: а) АО =ОС б)
________________________________
О а) Доказать: ∆ АBО = ∆ СDО
В D б) Найти: углы ∆ АBО
__________________________________________________________________________
Задача № 3
M Дано: NО — биссектриса
NM = NP
MO = 10 см
N O Доказать: ∆ MNO = ∆ PNО
Найти: ОР
P
Задача № 4
E
Дано: DE = DK
D C CE = CK
K Доказать: DC – биссектриса
В
Задача № 5
А С Дано: ∆АBC и ∆A1B1C1
К В1 1, АВ = А1В1,
ВС=В1С1 , АК = А1К1.
_________________________________
А1 С1 Доказать: ∆ АBC = ∆ A1B1C1
_________К1_________________________________________________________________
С Задача № 6
Дано: ∆АCB – равнобедренный
А В АР = FВ
__________________________________
Р F Доказать : 1) ∆ РCF – равнобедренный,
2) АF = ВР
Задача № 7
А
Дано: АЕ = ЕD
В Е С AB = 5см
___________________________________
Доказать: ∆ АBЕ = ∆ DCE
D Найти: СD
Задача № 8
B
Дано: АВ = АD
ВС = DC
C A Доказать: AC – биссектриса
Е
Задача № 9
В
Дано: а) АВ = АС б) АЕ = 15 см
А О АС = 7 см
________________________________________
а) Доказать: ∆ АСЕ = ∆ АBD
С б) Найти стороны ∆ АBD
D
B Задача № 10
Дано: ∆АCB – равнобедренный
______________________________
Доказать: 1) ∆МBN – равнобедренный
2)
A M N C
_________________________________________________________________________
В
К Задача № 11
А
С Дано: ∆АBC и ∆A1B1C1
B1 1, АВ = А1В1,
К1 АС=А1С1 , СК = С1К1.
_______________________________
А С1 а) Доказать: ∆ АВК = ∆ A1B1К1
Задачи к зачету по теме: «1-й признак равенства треугольников».
А В Задача № 1
Дано: АВ = DC
AD = 5 см
D C
____________________________________
Найти:
A Задача № 2
B Дано: АВ = СВ
__________________________________
Доказать: ∆ АBD = ∆ CBD
C
Задача № 3
В D Дано: АВ = CD
ВС = 10 см
____________________________________
А C
Найти:
__________________________________________________________________________
N Задача № 4
P
M Дано: MN = MK
MQ = MP
Q
K ___________________________________
Доказать: ∆ MNQ = ∆ MKP,
Найти:
_________________________________________________________________________
А N Задача № 5
Дано: АО = ОВ
O КО = ОN
AN = 8 см
_________________________________
Доказать: ∆ АON = ∆ BOK,
K B Найти:
_______________________________________________________________________
B Задача № 6
D
M Дано: AD = AK
A AM – биссектриса
_______________________________
C K Доказать: ∆ MDА = ∆ MKA
______________________________________________________________________
Задача № 7
K
Дано: МК = MF
P
M KP = 3 см
_________________________________
F Найти: PF.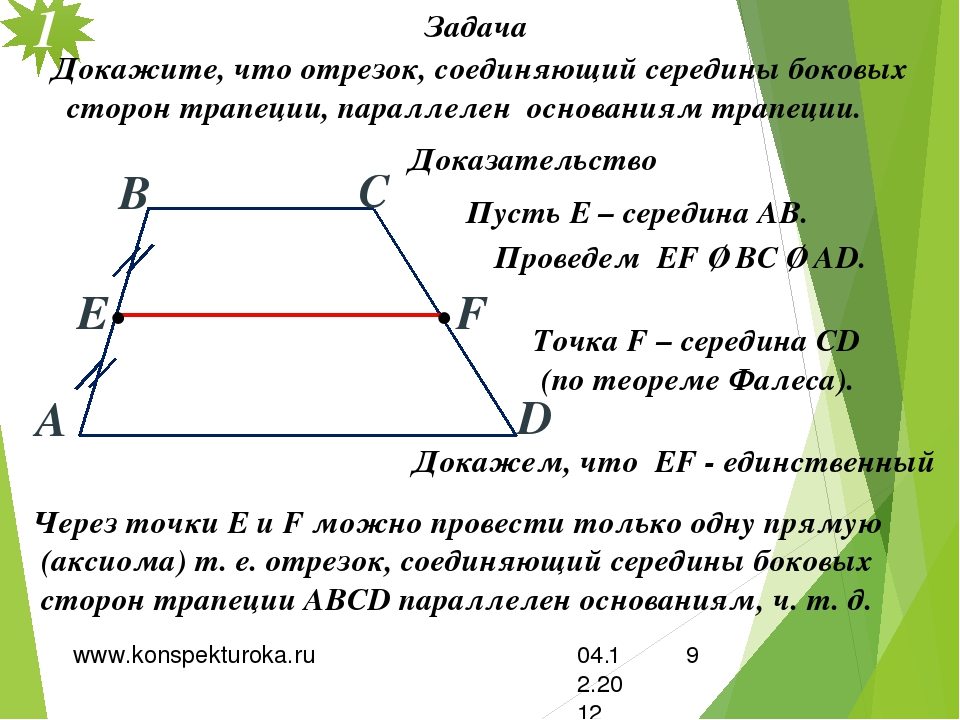
________________________________________________________________________
Литература
1. Л.С.Атанасян. Геометрия 7-9 класс. М., Просвещение , 1990 г.
2. Журнал «Математика в школе». № 3, 4, 5, М., Школа – Пресс, 1996 г.
3. В.А.Гусев, А.И. Медяник. Задачи по геометрии (дидактические
материалы). М., Просвещение, 1988 г.
4. Я. И.Груденов. Совершенствование методики работы учителя математики.
М., Просвещение, 1990 г.
5. В.А.Гусев. Лекции по педагогической технологии. М., Знание, 1992 г.
через точки А,В и середину М отрезка АВ проведены параллельные прямые,пересекающие некоторую плоскость альфа в точках А1, В1,М1, соответственно. Найдите
10-11 класс
длину отрезка ММ1, если АА1=13м, ВВ1=7м, причем отрезок АВ не пересекает плоскость альфа
Артемий0909 22 янв. 2015 г., 21:34:30 (6 лет назад) Emesi22 янв. 2015 г., 22:33:24 (6 лет назад)
ответ-10 см; т.к фигура АВА1В1-трапеция, ММ1-средняя линия, то ММ1=(13+7)/2=10
22 дек. 2017 г., 8:27:59 (3 года назад)
fggkh;ljk’poipokjlkujijk;jhjn
Ответить
Другие вопросы из категории
Tsv28047745 / 09 янв. 2015 г., 6:34:20
ПОЖАЛУЙСТА, ХОТЬ ЧТО-НИБУДЬ!!!!!! если что у меня ответы есть, мне нужно решение!!!! 1. Периметр трапеции равен 50 см. Боковые стороны ее равны12 см и 18 см. Вычислите длину средней линии трапеции.
2. Периметр равнобедренной трапеции равен 36 см. Боковая сторона равна средней линии трапеции. Вычислите длину средней линии трапеции.
3. Периметр ромба равен 24 см, а угол — 30°. Вычислите высоту ромба.
4. В равнобедренном треугольнике боковые стороны равны по 6 дм. Из произвольно взятой точки основания проведены две прямые, параллельные боковым сторонам треугольника. Вычислите периметр получившегося параллелограмма.
5. Диагонали прямоугольника при пересечении образовали угол, равный 120°. Меньшая сторона его равна 9 см. Вычислите длину диагонали прямоугольника.
Меньшая сторона его равна 9 см. Вычислите длину диагонали прямоугольника.
Читайте также
Вы находитесь на странице вопроса «через точки А,В и середину М отрезка АВ проведены параллельные прямые,пересекающие некоторую плоскость альфа в точках А1, В1,М1, соответственно. Найдите«, категории «геометрия«. Данный вопрос относится к разделу «10-11» классов. Здесь вы сможете получить ответ, а также обсудить вопрос с посетителями сайта. Автоматический умный поиск поможет найти похожие вопросы в категории «геометрия«. Если ваш вопрос отличается или ответы не подходят, вы можете задать новый вопрос, воспользовавшись кнопкой в верхней части сайта.
Open Math Open 2012-20 (OMO) 137p
Осень 2019 OMO p2Пусть $ A $, $ B $, $ C $ и $ P $ — такие точки на плоскости, что никакие три из них не лежат на одной прямой. Предположим, что площади треугольников $ BPC $, $ CPA $ и $ APB $ равны 13, 14 и 15 соответственно. Вычислите сумму всех возможных значений площади треугольника $ ABC $.
Анкан Бхаттачарья
OMO Осень 2019 p9Выпуклый равноугольный шестиугольник $ ABCDEF $ имеет $ AB = CD = EF = 1 $ и $ BC = DE = FA = 4 $. Конгруэнтные и попарно касательные снаружи окружности $ \ gamma_1 $, $ \ gamma_2 $ и $ \ gamma_3 $ строятся так, что $ \ gamma_1 $ касается стороны $ \ overline {AB} $ и стороны $ \ overline {BC} $, $ \ gamma_2 $ касается стороны $ \ overline {CD} $ и стороны $ \ overline {DE} $, а $ \ gamma_3 $ касается стороны $ \ overline {EF} $ и стороны $ \ overline {FA} $ .Тогда площадь $ \ gamma_1 $ может быть выражена как $ \ frac {m \ pi} {n} $ для относительно простых положительных целых чисел $ m $ и $ n $. Вычислить $ 100 млн + n $.
Шон Ли
OMO Осень 2019 с. 11Пусть $ ABC $ — треугольник с центром $ I $, такой что $ AB = 20 $ и $ AC = 19 $. Точка $ P \ neq A $ лежит на прямой $ AB $, а точка $ Q \ neq A $ лежит на прямой $ AC $. Предположим, что $ IA = IP = IQ $ и эта прямая $ PQ $ проходит через середину стороны $ BC $.
 {\ circ} $ .{\ circ} $. Пусть прямые $ AW $ и $ XY $ пересекаются в точке $ Z $, и пусть точка $ P $ является основанием перпендикуляра от $ A $ к прямой $ X_2Y_2 $. Пусть прямая $ ZP $ пересекает прямую $ BC $ в точке $ U $ и серединный перпендикуляр отрезка $ BC $ в точке $ V $. Предположим, что $ C $ лежит между $ B $ и $ U $. Пусть $ x $ — положительное действительное число. Предположим, что $ AB = x + 1 $, $ AC = 3 $, $ AV = x $ и $ \ frac {BC} {CU} = x $. Тогда $ x = \ frac {\ sqrt {k} -m} {n} $ для натуральных чисел $ k $, $ m $ и $ n $ таких, что $ k $ не делится на квадрат любого целого числа, большего чем $ 1 $.Вычислите 100 тыс. + 10 млн + n $.
{\ circ} $ .{\ circ} $. Пусть прямые $ AW $ и $ XY $ пересекаются в точке $ Z $, и пусть точка $ P $ является основанием перпендикуляра от $ A $ к прямой $ X_2Y_2 $. Пусть прямая $ ZP $ пересекает прямую $ BC $ в точке $ U $ и серединный перпендикуляр отрезка $ BC $ в точке $ V $. Предположим, что $ C $ лежит между $ B $ и $ U $. Пусть $ x $ — положительное действительное число. Предположим, что $ AB = x + 1 $, $ AC = 3 $, $ AV = x $ и $ \ frac {BC} {CU} = x $. Тогда $ x = \ frac {\ sqrt {k} -m} {n} $ для натуральных чисел $ k $, $ m $ и $ n $ таких, что $ k $ не делится на квадрат любого целого числа, большего чем $ 1 $.Вычислите 100 тыс. + 10 млн + n $.Анкит Бисейн, Люк Робитайл и Брэндон Ван
2020 OMO Весна ч.1
Пусть $ \ ell $ — прямая, а точки $ A $, $ B $, $ C $ лежат на $ \ ell $, так что $ AB = 7 $ и $ BC = 5 $. Пусть $ m $ — прямая, проходящая через $ A $, перпендикулярная $ \ ell $. Пусть $ P $ лежит на $ m $. Вычислите наименьшее возможное значение $ PB + PC $.
Анкан Бхаттачарья и Брэндон Ван
2020 OMO Весна p4Пусть $ ABCD $ — квадрат со стороной $ 16 $ и центром $ O $. Пусть $ \ mathcal S $ — полукруг диаметром $ AB $, лежащий вне $ ABCD $, и пусть $ P $ — точка на $ \ mathcal S $, так что $ OP = 12 $.Вычислите площадь треугольника $ CDP $.
Брэндон Ван
2020 OMO Spring p12Выпуклый пятиугольник $ ABCDE $ вписан в круг $ \ gamma $. Предположим, что $ AB = 14 $, $ BE = 10 $, $ BC = CD = DE $ и $ [ABCDE] = 3 [ACD] $. Тогда есть два возможных значения радиуса $ \ gamma $. Сумма этих двух значений равна $ \ sqrt {n} $ для некоторого положительного целого числа $ n $. Вычислить $ n $.
Люк Робитайл
2020 OMO Spring p15Пусть $ ABC $ — треугольник с $ AB = 20 $ и $ AC = 22 $. Предположим, что его вписанная окружность касается $ \ overline {BC} $, $ \ overline {CA} $ и $ \ overline {AB} $ в точках $ D $, $ E $ и $ F $ соответственно, а $ P $ — это основание перпендикуляра от $ D $ к $ \ overline {EF} $.
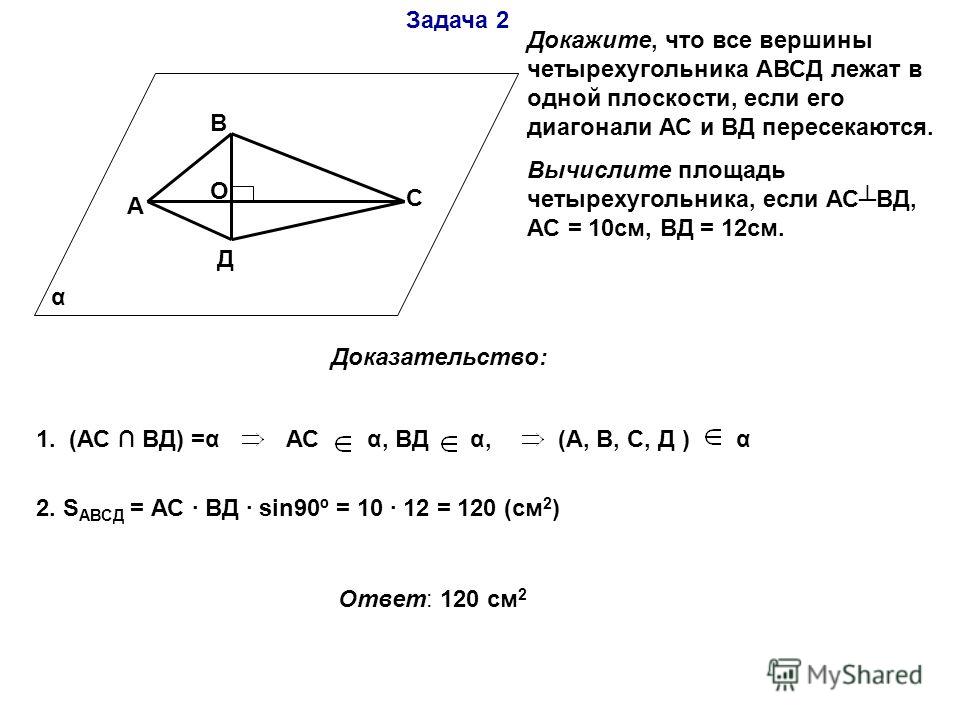 2 $.
2 $.Анкан Бхаттачарья
Пружина OMO 2020 p19Пусть $ ABC $ — разносторонний треугольник. Вписанная окружность касается прямых $ BC $, $ AC $ и $ AB $ в точках $ D $, $ E $ и $ F $ соответственно, а $ A $ -окружность касается прямых $ BC $, $ AC $ и $ AB $ в точках $ D_1 $, $ E_1 $ и $ F_1 $ соответственно. Предположим, что строки $ AD $, $ BE $ и $ CF $ параллельны в точке $ G $, и предположим, что строки $ AD_1 $, $ BE_1 $ и $ CF_1 $ параллельны в точке $ G_1 $. Пусть прямая $ GG_1 $ пересекает внутреннюю биссектрису угла $ BAC $ в точке $ X $.Предположим, что $ AX = 1 $, $ \ cos {\ angle BAC} = \ sqrt {3} -1 $ и $ BC = 8 \ sqrt [4] {3} $. Тогда $ AB \ cdot AC = \ frac {j + k \ sqrt {m}} {n} $ для натуральных чисел $ j $, $ k $, $ m $ и $ n $ таких, что $ \ gcd (j, k, n) = 1 $ и $ m $ не делится на квадрат любого целого числа больше $ 1 $. Вычислить $ 1000j + 100k + 10m + n $.
Люк Робитайл и Брэндон Ван
2020 OMO Spring p22Пусть $ ABC $ — разносторонний треугольник с центром $ I $ и симедианной точкой $ K $. Кроме того, предположим, что $ BC = 1099 $. Пусть $ P $ — точка плоскости треугольника $ ABC $, и пусть $ D $, $ E $, $ F $ — основания перпендикуляров от $ P $ к прямым $ BC $, $ CA $, $ AB $ соответственно.Пусть $ M $ и $ N $ — середины отрезков $ EF $ и $ BC $ соответственно. Предположим, что тройки $ (M, A, N) $ и $ (K, I, D) $ коллинеарны, соответственно, и что площадь треугольника $ DEF $ равна $ 2020 $, умноженному на площадь треугольника $ ABC $. Вычислите максимально возможное значение $ \ lceil AB + AC \ rceil $.
Брэндон Ван
2020 OMO Spring p24Пусть $ A $, $ B $ — противоположные вершины единичного квадрата с описанной окружностью $ \ Gamma $. Пусть $ C $ — переменная точка на $ \ Gamma $. Если $ C \ not \ in \ {A, B \} $, то пусть $ \ omega $ — вписанная окружность треугольника $ ABC $, а $ I $ — центр $ \ omega $.2 $ выражается в виде $ \ frac {a} {b} — c \ sqrt {d} $ для натуральных чисел $ a $, $ b $, $ c $, $ d $ таких, что $ \ gcd (a, б) = 1 $ и $ d $ не делится на квадрат любого простого числа, вычислите $ 1000a + 100b + 10c + d.
 $
$Эдвард Ван
2020 OMO Spring p28Пусть $ A_0BC_0D $ — выпуклый четырехугольник, вписанный в окружность $ \ omega $. Для всех целых чисел $ i \ ge0 $ пусть $ P_i $ — пересечение прямых $ A_iB $ и $ C_iD $, пусть $ Q_i $ — пересечение прямых $ A_iD $ и $ BC_i $, пусть $ M_i $ — середина отрезка $ P_iQ_i $, и пусть прямые $ M_iA_i $ и $ M_iC_i $ снова пересекают $ \ omega $ в $ A_ {i + 1} $ и $ C_ {i + 1} $ соответственно.Окружности, описанные в $ \ треугольнике A_3M_3C_3 $ и $ \ треугольнике A_4M_4C_4 $, пересекаются в двух точках $ U $ и $ V $.
Если $ A_0B = 3 $, $ BC_0 = 4 $, $ C_0D = 6 $, $ DA_0 = 7 $, то $ UV $ может быть выражено в виде $ \ tfrac {a \ sqrt b} c $ для натуральных чисел $ a $, $ b $, $ c $ такие, что $ \ gcd (a, c) = 1 $ и $ b $ не содержит квадратов. Вычислите $ 100a + 10b + c $.
Эрик Шен
источник:
% PDF-1.3
%
1086 0 объект
>
эндобдж
xref
1086 234
0000000016 00000 н.
0000014831 00000 п.
0000015078 00000 п.
0000015132 00000 п.
0000015733 00000 п.
0000015822 00000 п.
0000016003 00000 п.
0000016112 00000 п.
0000016223 00000 п.
0000016333 00000 п.
0000016604 00000 п.
0000016728 00000 п.
0000016913 00000 п.
0000017099 00000 п.
0000017236 00000 п.
0000017592 00000 п.
0000017639 00000 п.
0000017694 00000 п.
0000018368 00000 п.
0000018631 00000 п.
0000019514 00000 п.
0000020079 00000 п.
0000020562 00000 п.
0000021190 00000 н.
0000024883 00000 п.
0000025567 00000 п.
0000026012 00000 п.
0000027110 00000 п.
0000032211 00000 п.
0000033390 00000 п.
0000033716 00000 п.
0000034399 00000 п.
0000034655 00000 п.
0000034778 00000 п.
0000035704 00000 п.
0000035956 00000 п.
0000036229 00000 п.
0000036817 00000 п.
0000037392 00000 п.
0000038011 00000 п.
0000038689 00000 п.
0000038852 00000 п.
0000039201 00000 п.
0000039247 00000 п.
0000039389 00000 п.
0000040557 00000 п.
0000040708 00000 п.
0000041458 00000 п.
0000042226 00000 п.
0000074022 00000 п.
0000108595 00000 н.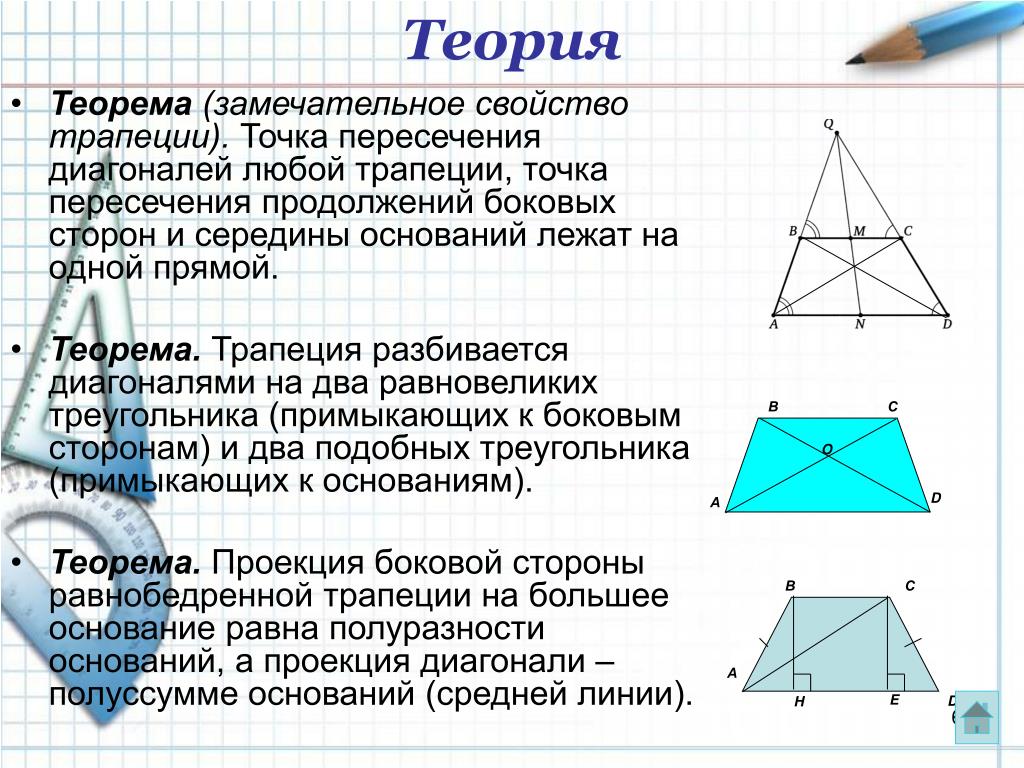 0000140336 00000 н.
0000140386 00000 п.
0000140430 00000 н.
0000149703 00000 н.
0000149969 00000 н.
0000150163 00000 н.
0000150460 00000 н.
0000150633 00000 н.
0000168395 00000 н.
0000168598 00000 н.
0000168631 00000 н.
0000170526 00000 н.
0000411898 00000 н.
0000412094 00000 н.
0000413141 00000 п.
0000552571 00000 н.
0000552840 00000 н.
0000553885 00000 н.
0000586865 00000 н.
0000587132 00000 н.
0000587204 00000 н.
0000587324 00000 н.
0000587508 00000 н.
0000587685 00000 н.
0000587792 00000 н.
0000587903 00000 н.
0000588095 00000 н.
0000588202 00000 н.
0000588313 00000 н.
0000588507 00000 н.
0000588614 00000 н.
0000588725 00000 н.
0000588923 00000 н.
0000589030 00000 н.
0000589141 00000 н.
0000589333 00000 н.
0000589440 00000 н.
0000589551 00000 п.
0000589743 00000 н.
0000589850 00000 н.
0000589961 00000 н.
0000590152 00000 н.
0000590259 00000 н.
0000590370 00000 н.
0000590572 00000 н.
0000590679 00000 н.
0000590790 00000 н.
0000591008 00000 н.
0000591115 00000 н.
0000591226 00000 н.
0000591424 00000 н.
0000591531 00000 н.
0000591642 00000 н.
0000591836 00000 н.
0000591943 00000 н.
0000592054 00000 н.
0000592248 00000 н.
0000592355 00000 н.
0000592466 00000 н.
0000592671 00000 н.
0000592778 00000 н.
0000592889 00000 н.
0000593082 00000 н.
0000593189 00000 н.
0000593300 00000 н.
0000593495 00000 н.
0000593602 00000 н.
0000593713 00000 н.
0000593901 00000 н.
0000594008 00000 п.
0000594119 00000 н.
0000594316 00000 н.
0000594423 00000 н.
0000594534 00000 н.
0000594728 00000 н.
0000594835 00000 н.
0000594946 00000 н.
0000595142 00000 п.
0000595249 00000 н.
0000595360 00000 н.
0000595553 00000 н.
0000595660 00000 н.
0000595771 00000 п.
0000595985 00000 н.
0000596092 00000 н.
0000596203 00000 н.
0000596401 00000 п.
0000596508 00000 н.
0000596619 00000 н.
0000596811 00000 н.
0000596918 00000 н.
0000597029 00000 н.
0000597224 00000 н.
0000597331 00000 п.
0000597442 00000 н.
0000597642 00000 н.
0000140336 00000 н.
0000140386 00000 п.
0000140430 00000 н.
0000149703 00000 н.
0000149969 00000 н.
0000150163 00000 н.
0000150460 00000 н.
0000150633 00000 н.
0000168395 00000 н.
0000168598 00000 н.
0000168631 00000 н.
0000170526 00000 н.
0000411898 00000 н.
0000412094 00000 н.
0000413141 00000 п.
0000552571 00000 н.
0000552840 00000 н.
0000553885 00000 н.
0000586865 00000 н.
0000587132 00000 н.
0000587204 00000 н.
0000587324 00000 н.
0000587508 00000 н.
0000587685 00000 н.
0000587792 00000 н.
0000587903 00000 н.
0000588095 00000 н.
0000588202 00000 н.
0000588313 00000 н.
0000588507 00000 н.
0000588614 00000 н.
0000588725 00000 н.
0000588923 00000 н.
0000589030 00000 н.
0000589141 00000 н.
0000589333 00000 н.
0000589440 00000 н.
0000589551 00000 п.
0000589743 00000 н.
0000589850 00000 н.
0000589961 00000 н.
0000590152 00000 н.
0000590259 00000 н.
0000590370 00000 н.
0000590572 00000 н.
0000590679 00000 н.
0000590790 00000 н.
0000591008 00000 н.
0000591115 00000 н.
0000591226 00000 н.
0000591424 00000 н.
0000591531 00000 н.
0000591642 00000 н.
0000591836 00000 н.
0000591943 00000 н.
0000592054 00000 н.
0000592248 00000 н.
0000592355 00000 н.
0000592466 00000 н.
0000592671 00000 н.
0000592778 00000 н.
0000592889 00000 н.
0000593082 00000 н.
0000593189 00000 н.
0000593300 00000 н.
0000593495 00000 н.
0000593602 00000 н.
0000593713 00000 н.
0000593901 00000 н.
0000594008 00000 п.
0000594119 00000 н.
0000594316 00000 н.
0000594423 00000 н.
0000594534 00000 н.
0000594728 00000 н.
0000594835 00000 н.
0000594946 00000 н.
0000595142 00000 п.
0000595249 00000 н.
0000595360 00000 н.
0000595553 00000 н.
0000595660 00000 н.
0000595771 00000 п.
0000595985 00000 н.
0000596092 00000 н.
0000596203 00000 н.
0000596401 00000 п.
0000596508 00000 н.
0000596619 00000 н.
0000596811 00000 н.
0000596918 00000 н.
0000597029 00000 н.
0000597224 00000 н.
0000597331 00000 п.
0000597442 00000 н.
0000597642 00000 н.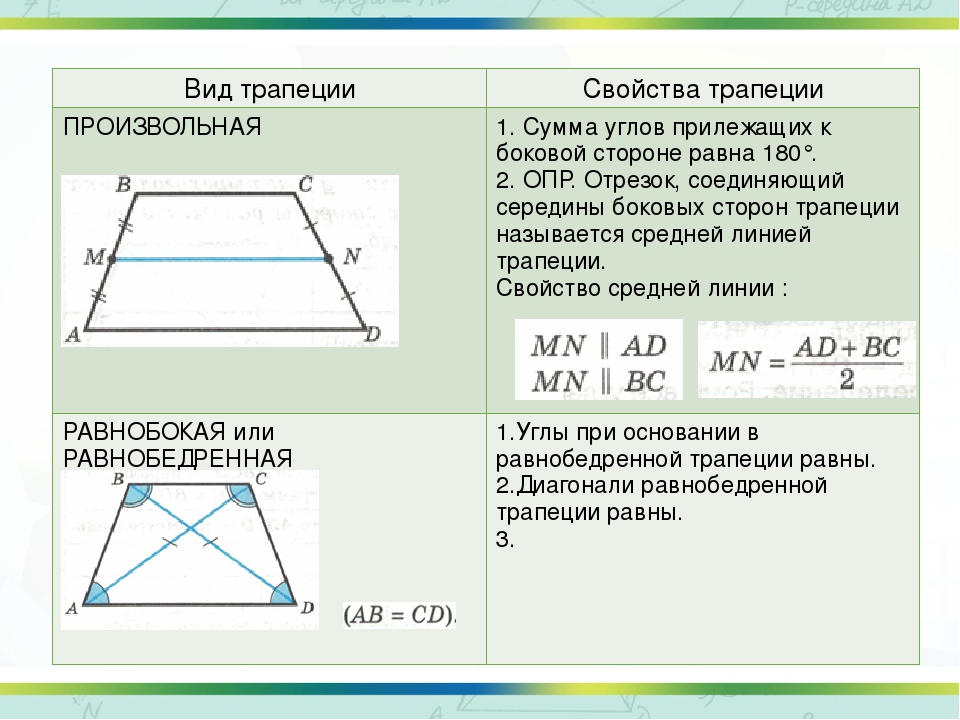 0000597749 00000 н.
0000597860 00000 н.
0000598067 00000 н.
0000598174 00000 п.
0000598285 00000 н.
0000598478 00000 н.
0000598585 00000 п.
0000598696 00000 п.
0000598892 00000 н.
0000598999 00000 н.
0000599110 00000 н.
0000599329 00000 н.
0000599436 00000 н.
0000599547 00000 н.
0000599737 00000 н.
0000599844 00000 н.
0000599955 00000 н.
0000600138 00000 п.
0000600245 00000 н.
0000600356 00000 п.
0000600566 00000 н.
0000600673 00000 п.
0000600784 00000 п.
0000600971 00000 п.
0000601078 00000 н.
0000601189 00000 н.
0000601378 00000 н.
0000601485 00000 н.
0000601596 00000 н.
0000601797 00000 н.
0000601904 00000 н.
0000602015 00000 н.
0000602211 00000 н.
0000602318 00000 н.
0000602429 00000 н.
0000602692 00000 н.
0000602799 00000 н.
0000602910 00000 н.
0000603120 00000 н.
0000603226 00000 н.
0000603337 00000 н.
0000603537 00000 н.
0000603643 00000 н.
0000603753 00000 н.
0000603945 00000 н.
0000604051 00000 н.
0000604160 00000 н.
0000604361 00000 п.
0000604467 00000 н.
0000604577 00000 н.
0000604766 00000 н.
0000604871 00000 н.
0000604979 00000 п.
0000605165 00000 н.
0000605270 00000 п.
0000605393 00000 н.
0000605583 00000 н.
0000605674 00000 н.
0000605870 00000 н.
0000605961 00000 н.
0000606146 00000 п.
0000606237 00000 н.
0000606437 00000 н.
0000606527 00000 н.
0000606722 00000 н.
0000606812 00000 н.
0000607008 00000 н.
0000607098 00000 н.
0000607221 00000 н.
0000607344 00000 н.
0000607468 00000 н.
0000607592 00000 н.
0000607716 00000 н.
0000607840 00000 п.
0000607964 00000 н.
0000608088 00000 н.
0000608212 00000 н.
0000608336 00000 н.
0000608460 00000 н.
0000608584 00000 н.
0000608708 00000 н.
0000608832 00000 н.
0000608956 00000 н.
0000609080 00000 н.
0000609204 00000 н.
0000609328 00000 н.
0000004976 00000 н.
трейлер
] / Назад 2769147 >>
startxref
0
%% EOF
1319 0 объект
> поток
h ތ z XW9B] DfktK
2 ژ` DK2I% L 䶀% ,.W ٴ 1 Xe — I {Oq4kp? Y [83b
3E =
xH @ c {VSCf &
0000597749 00000 н.
0000597860 00000 н.
0000598067 00000 н.
0000598174 00000 п.
0000598285 00000 н.
0000598478 00000 н.
0000598585 00000 п.
0000598696 00000 п.
0000598892 00000 н.
0000598999 00000 н.
0000599110 00000 н.
0000599329 00000 н.
0000599436 00000 н.
0000599547 00000 н.
0000599737 00000 н.
0000599844 00000 н.
0000599955 00000 н.
0000600138 00000 п.
0000600245 00000 н.
0000600356 00000 п.
0000600566 00000 н.
0000600673 00000 п.
0000600784 00000 п.
0000600971 00000 п.
0000601078 00000 н.
0000601189 00000 н.
0000601378 00000 н.
0000601485 00000 н.
0000601596 00000 н.
0000601797 00000 н.
0000601904 00000 н.
0000602015 00000 н.
0000602211 00000 н.
0000602318 00000 н.
0000602429 00000 н.
0000602692 00000 н.
0000602799 00000 н.
0000602910 00000 н.
0000603120 00000 н.
0000603226 00000 н.
0000603337 00000 н.
0000603537 00000 н.
0000603643 00000 н.
0000603753 00000 н.
0000603945 00000 н.
0000604051 00000 н.
0000604160 00000 н.
0000604361 00000 п.
0000604467 00000 н.
0000604577 00000 н.
0000604766 00000 н.
0000604871 00000 н.
0000604979 00000 п.
0000605165 00000 н.
0000605270 00000 п.
0000605393 00000 н.
0000605583 00000 н.
0000605674 00000 н.
0000605870 00000 н.
0000605961 00000 н.
0000606146 00000 п.
0000606237 00000 н.
0000606437 00000 н.
0000606527 00000 н.
0000606722 00000 н.
0000606812 00000 н.
0000607008 00000 н.
0000607098 00000 н.
0000607221 00000 н.
0000607344 00000 н.
0000607468 00000 н.
0000607592 00000 н.
0000607716 00000 н.
0000607840 00000 п.
0000607964 00000 н.
0000608088 00000 н.
0000608212 00000 н.
0000608336 00000 н.
0000608460 00000 н.
0000608584 00000 н.
0000608708 00000 н.
0000608832 00000 н.
0000608956 00000 н.
0000609080 00000 н.
0000609204 00000 н.
0000609328 00000 н.
0000004976 00000 н.
трейлер
] / Назад 2769147 >>
startxref
0
%% EOF
1319 0 объект
> поток
h ތ z XW9B] DfktK
2 ژ` DK2I% L 䶀% ,.W ٴ 1 Xe — I {Oq4kp? Y [83b
3E =
xH @ c {VSCf &
Калькулятор треугольника
Калькулятор треугольникаПерейти к основному содержанию
Калькулятор треугольника
калькулятор треугольников Найдите основание треугольника, решив уравнение: площадь = 1/2 x b x h.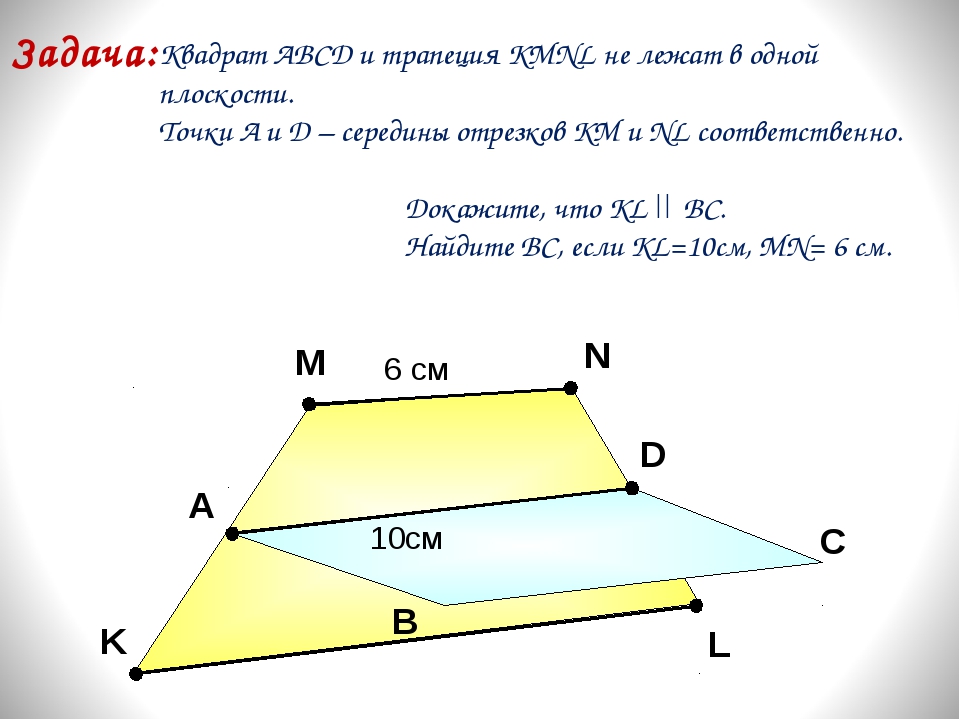 Угол «B» — это угол, противоположный стороне «b». 5. Размер полного треугольника известен после того, как будут даны 3 независимых элемента информации. Масштаб шага бега Посетите эту страницу с помощью телефона или планшета, чтобы напрямую измерить шаг и углы. Используйте этот онлайн-инструмент для расчета класса текстуры с одной точкой на основе процентного содержания песка, ила и глины. Слайдеры. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.е. Онлайн-калькулятор центроида поможет вам найти центр тяжести треугольника (ABC), N-точек и N-стороннего многоугольника для заданных координат. Прочтите, чтобы узнать больше о том, что такое наклон, и о некоторых простых способах решения. Когда вам нужно решить математическую задачу и вы хотите убедиться, что у вас есть правильный ответ, вам может пригодиться калькулятор. Формулу Герона см. В разделе «Калькулятор площади треугольника по формуле Героя». Формулы треугольника с углом 30̊ 60̊ 90̊: • периметр = длинная сторона + короткая сторона + гипотенуза; • площадь = 0.Линия не может пересекать другие линии или касаться других точек, кроме двух, с которыми она связана. Чтобы решить это уравнение, вам необходимо знать площадь и высоту. Есть много способов найти высоту треугольника. Этот инструмент помогает легко визуализировать влияние настроек на конечный результат. Вычисление: прямоугольный треугольник, двусторонний треугольник, равнобедренный треугольник и равносторонний треугольник. Найдите площадь, периметр, медианное значение, высоту, биссектрису угла и т. Д. Угол треугольника 25 июля 2011 г. Треугольник ограничен точками решетки в заданном диапазоне. Перетащите точки и создайте новые треугольники. Наведите указатель мыши на линии и специальные точки, чтобы получить площадь треугольника 22 января 2021 г. Калькулятор формулы площади равностороннего равнобедренного треугольника позволяет вам чтобы найти площадь различных типов треугольников, например, Этот бесплатный калькулятор треугольников вычисляет края, углы, площадь, высоту, периметр, медиана, а также другие значения треугольника.Вот как можно объяснить вычисление стороны треугольника с заданными входными значениями -> 4. Последняя часть этого проекта — оценка. Точка, через которую проходят все три медианы треугольника, называется центроидом треугольника, и она делит каждую медиану в соотношении 2: 1. Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три. Площадь параллелограмма с учетом основания и высоты. (Примечание: если заполнено более 3 полей, только треть используется для определения треугольника, остальные (в конечном итоге) перезаписываются. Калькулятор вычисляет треугольник, указанный в трех его свойствах.Калькулятор треугольников Решите треугольники Решите треугольники, введя две стороны и один угол, два угла и одну сторону или три стороны, чтобы найти оставшиеся значения, которые используются в тригонометрии. Углы: треугольник — это самая простая двумерная форма. Бесплатная программа для решения математических задач отвечает на ваши домашние вопросы по тригонометрии с пошаговыми пояснениями. Введите значения трех из шести сторон и углов треугольника, и остальные три значения будут вычислены. Умножение используется, если вы работаете с десятичной дробью, и деление. T Сколько вы стоите в финансовом отношении? Многие люди понятия не имеют, каков их собственный капитал, хотя они часто читают о чистом капитале известных людей и богатых владельцев бизнеса.Показанные по умолчанию цифры являются гипотетическими и могут не применяться. Формула реального ВНП находится путем определения номинального валового национального продукта (ВНП) путем прибавления к ВВП прироста капитала за счет иностранных доходов. Учащиеся K-12 могут обратиться к приведенным ниже формулам треугольника, чтобы узнать, какие входные параметры используются для определения площади треугольника. Что ж, продолжительность дуги довольно просто вычислить с помощью некоторой арифметики отношений. Калькулятор 20 января 2020 г. · Чтобы определить, являются ли три стороны треугольника треугольником, используйте теорему о неравенстве треугольника, которая гласит, что сумма двух сторон треугольника должна быть больше третьей стороны.Без использования калькулятора Чтобы определить, является ли треугольник острым, прямым или тупым, если у треугольника есть 3 стороны: Чтобы вычислить площадь треугольника, перейдите в Калькулятор площади треугольника. закон синусов и закон косинусов важны для процесса вычисления. Конечный результат нашего калькулятора треугольной призмы всегда выражается в кубических единицах: в 3, футах 3, ярдах 3, мм 3, см 3, метрах 3 и т. Д. Калькулятор треугольников вычисляет и находит: углы, стороны, площадь всех типов треугольники. Затем перпендикулярно биссектрисам линий треугольника. Последний решает любые две пары уравнений. Точка пересечения — центр описанной окружности.Введите одно число и нажмите кнопку «рассчитать»! Прямоугольный или прямоугольный треугольник 30̊60̊ 90̊ — это треугольник с углами 30̊ 60̊ 90̊. Определитель вычисляется путем приведения матрицы к форме эшелона строк и умножения ее основных диагональных элементов. Этот калькулятор предназначен только для прямоугольного треугольника! Факторами являются длины сторон и один из двух углов, кроме прямого. Персональный кредитный калькулятор (обычно) тоже бесплатный. Заявление об отказе от ответственности для калькулятора: информация, предоставляемая этими калькуляторами, предназначена только для иллюстративных целей и не предназначена для определения фактических параметров, определенных пользователем.Вы можете настроить точность результатов. Калькулятор определяет радиус и имеет радиус, площадь описанной окружности, площадь треугольника и соотношение площадей — только для справки 20 февраля 2021 г. · Калькулятор определит, что вам нужно будет разрезать квадрат со сторонами, длина которых равна 4 1 / 2 дюйма, чтобы получилось 2 незаконченных угловых треугольника, и квадрат со сторонами, длина которых составляет 8 3/8 дюйма, чтобы образовать 4 незавершенных треугольника. Затем нажмите Рассчитать. Этот калькулятор вычисляет все три угла и три стороны треугольника.Самое первое, что вы должны помнить, — это правильный знак формулы. Калькулятор треугольников предоставляет вам несколько методов для расчета площади треугольника с использованием SAS, SSS, AAS, SSA, равностороннего. B aseLength 8. Другими словами, по количеству введенных значений можно определить значение. Калькулятор использует закон косинуса [c² = a² + b² — 2ab cos γ] для вычисления третьей стороны треугольника, когда две стороны и угол между ними дан. Это может помочь. Начать новый заем — очень важное решение.2 \), известная как теорема Пифагора. гипотенуза: A: B: напротив: C = 90: смежно Используйте этот онлайн-инструмент для вычисления класса текстуры одной точки на основе процента песка, ила и глины. YouTube. исчерпывающий калькулятор треугольников, позволяющий легко вычислить углы, стороны, площади и другие части треугольника. Калькулятор треугольников — режим гуру. Этот калькулятор треугольников решает недостающие части треугольника. 14 апреля 2013 г. — 3 4 5 Калькулятор треугольников | Калькулятор прямоугольного треугольника | Решатель Правого Треугольника | Особые треугольники.Показывает свою работу и рисует решение. Треугольник — это многоугольник с тремя ребрами и тремя вершинами. Помните, сумма углов треугольника равна 180 градусам. Без сомнения, этот калькулятор лучше всего подходит для определения центроида многих 2D-форм, а также набора точек. Треугольное число или число треугольника подсчитывает объекты, которые могут образовывать равносторонний треугольник. Расчеты в равностороннем треугольнике или правильном треугольнике. Щелкните правой кнопкой мыши текст или метку точки, чтобы отредактировать ее. Дан треугольник Центроид любого треугольника, включая прямоугольные, — это точка, в которой угол наклона. Треугольная планировка остается стандартом при планировании кухонного пространства.Существуют различные начальные измерения, из которых можно составить треугольник, вычислить длину стороны и высоту до нее и, наконец, вычислить площадь треугольника. Другими словами, количество введенных значений может определить Калькулятор Центроида Треугольника. Задача проста — сначала определить длины ребер, а затем по формуле Герона найти площадь треугольника. Пример . Используйте его, изучайте, обучайте, делитесь и вставляйте! 3-частотный калькулятор геодезического купола 5/8, который определяет длину стойки, стоимость, вес, конструкцию и размеры треугольника для геодезического купола.Периметр можно определить как длину вокруг двухмерного объекта. Вы можете рассчитать длину любой стороны прямоугольного треугольника, если знаете, как найти площадь тупого треугольника. Поиск стороны в прямоугольном треугольнике Найдите сторону, когда мы знаем другую сторону и угол. Этот онлайн-калькулятор рассчитывает характеристики равностороннего треугольника: длину сторон, площадь, периметр, радиус. Калькулятор «Купить прямоугольный треугольник» — Тригонометрия: прочитать обзоры приложений и игр — Amazon.Площадь прямоугольника. 5. Установочные треугольники — это треугольники, используемые для заполнения пространств на внешних краях стеганого одеяла, установленного в точке, подобной «Прекрасное в лаванде» (показано ниже). После расчета желаемого выходного параметра единицы решения конвертируются, если этого требует выбранная единица. ) Где (для краткости) написано «край a», «угол B» и т. Д., Более правильным должно быть что-то вроде «длина ребра a», или «длина края», или «размер угла B» и т. Д. Найдите онлайн-калькулятор.Чтобы перевернуть треугольник, используйте нижние правые кнопки. Здесь вы можете ввести две известные стороны или углы и вычислить неизвестную сторону, угол или площадь. Рассчитайте как углы, так и стороны, просто введите любые 2 поля. Запишите высоту базового треугольника. Создайте равнобедренный треугольник. Ортоцентр треугольника Метод вычисления ортоцентра треугольника Закон косинусов — одна сторона треугольника, когда известны противоположный угол и две стороны; Закон синусов — углы в общем треугольнике; Закон касательных — треугольники и закон касательных; Калькулятор углов угловой пилы — Расчет углов угломера для торцовочной пилы; Oblique Triangle — Уравнения наклонного треугольника; Теорема Пифагора — Используемая теорема Пифагора Вычислите площадь и периметр прямоугольного треугольника.Вычислите площадь и периметр разностороннего треугольника. Площадь — это пространство внутри периметра / границы пространства, его символ — (A). N. (Наклонный треугольник с одним углом> 90 градусов. Инструкции по калькулятору треугольника. Калькулятор триггера для прямоугольного треугольника Введите два значения и нажмите «Рассчитать». 3. Например, треугольник с тремя сторонами равной длины называется… Продолжить чтение → Треугольник Калькулятор. Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна катета является высотой, а вторая — основанием, поэтому уравнение упрощается до: area = a * b / 2 Калькулятор треугольника CosSinCalc вычисляет стороны, углы, высоты, медианы, биссектрисы, площадь и окружность треугольника.Координаты центроида — это просто среднее значение координат вершин. Узнайте о вычислении треугольника, чтобы найти H, калькуляторе площади треугольника и вычислении прямоугольного треугольника в концепции вычисления треугольника, чтобы найти C. См. Полный список на калькуляторе. Калькулятор площади равностороннего треугольника: понимание пошагового процесса вычисления площади равностороннего треугольника помогает учащимся легко решать математические задачи в их старших классах. Калькулятор треугольников: рассчитайте, правильный ли это треугольник и какого типа.Формула площади треугольника — высота стороны x, как показано на графике ниже: Калькулятор площади треугольника, равностороннего равнобедренного треугольника позволяет вам найти площадь различных типов треугольников, таких как равносторонний, равнобедренный, прямоугольный или равнобедренный треугольник, по различным формулам расчета, таким как формула Герона, длина сторон треугольника и углы, радиус вписанной или описанной окружности. Площадь треугольника с учетом сторон и угла. Равнобедренный, калькулятор прямоугольного треугольника. 7 марта 2014 г. Загрузите калькулятор триггера для прямоугольного треугольника — простой в использовании программный инструмент, который поможет вам выполнять вычисления прямоугольного треугольника на ветру и 25 апреля 2017 г. 2-2 * 7 * 4 * cos (30)).Калькулятор геометрии для решения теоремы Пифагора о прямоугольном треугольнике с учетом длины сторон a и b. Калькулятор геометрии для определения высоты стороны c прямоугольного треугольника с учетом длины сторон a, b и c. Узнайте, как рассчитать нужный размер, или просто воспользуйтесь бесплатной таблицей резки! Этот пост содержит партнерские ссылки, за которые я получаю компенсацию. Калькулятор треугольников вычисляет треугольники, указанные в трех его свойствах. Прямоугольный треугольник имеет теорему Пифагора. Калькулятор вычисляет длину третьей стороны прямоугольного треугольника на основе длин двух других сторон, используя теорему Пифагора.Этот калькулятор вычисляет из трех значений треугольника все остальные значения. Найдите угол Альфа, угол Бельты и гипотенузу សូម ជួយ ចុច ПОДПИСАТЬСЯ មួយ ផង បាទ 08.07.2019 · Рассчитайте высоту треугольника, если заданы две боковые стороны и радиус описанной окружности (h): высота треугольника: = Цифра 2 1 2 4 6 10 F Центр окружности треугольника, биссектриса Точка, в которой пересекаются срединные перпендикуляры треугольника, называется центром описанной окружности. У острого треугольника 3 острых угла. Калькулятор треугольника мощности Треугольник мощности показывает соотношение между реактивной, активной и полной мощностью в цепи переменного тока.Как решить тригонометрию прямоугольного треугольника? Хотя использование калькулятора тригонометрии для вычисления прямоугольных треугольников намного проще, вам также следует научиться находить значение вручную. Добавлено 6 февраля 2014 г. пользователем Sravan75 по математике. Хотя процентные значения могут быть рассчитаны как с дробями, так и с десятичными знаками. Он был создан по запросу пользователя. Приложение нарисует треугольник в соответствии с двумя предыдущими введенными вами измерениями. Два других значения будут заполнены. У него 3 ребра и 3 угла (или вершины).Треугольники — очень простая игра. (Это край, противоположный прямому углу, и в данном случае это c. Поэтому все, что вам нужно сделать, это сложить вместе каждую комбинацию двух сторон, чтобы увидеть, больше ли она, чем третья сторона. Самый простой способ — из области и Длина основания. Математики называют это «решением треугольника. Подробнее см. Центроид треугольника. В течение трех десятилетий евангелие кухонного дизайна было найдено в базовой геометрии. Задайте вопрос, заданный 4 года, 9 месяцев назад. Создайте острый треугольник.Объяснение калькулятора треугольника. 866025; Калькулятор треугольника Этот калькулятор может вычислить площадь треугольника, высоту треугольника, медиану треугольника, центроид, центр описанной окружности и ортоцентр. Номер n-го треугольника — это количество точек, составляющих треугольник с n точками на стороне, и оно равно сумме n натуральных чисел от 1 до n. Шаблон треугольника Паскаля — это расширение массива биномиальных коэффициентов. s = (a + b + c) / 2 area = sqrt (s * (s — a) * (s — b) * (s — c)) Разносторонний треугольник — это треугольник, все стороны которого неравны.Прежде всего, необходимо найти треугольник, имеющий три стороны и три угла. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Пример: Найдите центр тяжести треугольника с вершинами (1,2) (3,4) и (5,0). Калькулятор тригонометрии — прямоугольные треугольники. Введите все известные переменные (стороны a, b и c; углы A и B) в текстовые поля. Площадь треугольника. Для наклонных треугольников используется набор формул, уникальных для прямоугольных треугольников, и эти формулы могут отображаться на странице калькулятора наклонных треугольников на нашем веб-сайте.Вы можете сэкономить много времени, используя калькулятор раскрытия треугольника Паскаля, чтобы быстро построить треугольник из чисел одним щелчком мыши. Калькулятор равнобедренного треугольника вычисляет все свойства равнобедренного треугольника, такие как площадь, периметр, стороны и углы, с учетом достаточного подмножества этих свойств. Сторона \ (C \) вычисляется и 6 тригонометрических соотношений определяются в тригонометрии. Площадь = [l × b / 2] = (3 * 4/2) = 12/2 = 6. Человек должен будет ввести 3 из шести сторон, а также углы треугольника, и как только это будет сделано , остальные 3 значения автоматически рассчитываются инструментом калькулятора треугольника.Для максимальной эффективности и простоты передвижения нарисуйте воображаемый треугольник из центра. Найдите основание треугольника, решив уравнение: площадь = 1/2 x b x h. Как рассчитать длину ребер равнобедренного треугольника Этот калькулятор определяет площадь треугольника, используя координаты его вершины в декартовой системе координат. Это та же самая формула для обоих типов треугольников на рисунке. Подвижные точки. В геометрии треугольник — это форма, все три стороны которой имеют одинаковую длину. Углы треугольника. Калькулятор.В свою очередь, вершины — это линия или точка, в которой пересекаются ребра. Затем нажмите Рассчитать. угол между сторонами, заканчивающийся в этом углу. Площадь ромба. A и B — длины катетов треугольника. (Угол «А» — это угол, противоположный стороне «а». Острый треугольник: треугольник, все внутренние углы которого <90 градусов. Этот калькулятор определит, образуют ли эти 3 стороны равносторонний, равнобедренный, острый, прямой или тупой треугольник. или вообще нет треугольника. Рассчитайте площадь равностороннего треугольника с помощью данного онлайн-калькулятора Как рассчитать сторону a треугольника с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для стороны a треугольника, введите Сторона B (b), Сторона C (c) и Угол A (∠A) и нажмите кнопку расчета.«У разностороннего треугольника нет равных сторон. Треугольник имеет три вершины. Калькулятор 2-х решений. Бесплатная загрузка Triangle Calculator - Moffsoft Calculator, Simple Calculator, Biromsoft Calculator и многие другие программы Калькулятор треугольника Паскаля строит треугольник Паскаля, используя метод биномиального расширения. Диаграмма калькулятора прямоугольного треугольника тригонометрии. Щелкните элемент стороны или угла, чтобы активировать его, и введите значения для любых 2 известных сторон (зеленый + синий) или любой 1 стороны и 1 угла, чтобы вычислить оставшиеся стороны и углы.. Количество введенных значащих значений будет определять количество значащих цифр в результатах. C 2 = 5000. Сравнение процентных ставок и решение о доступности ежемесячных платежей может вскружить вам голову, но есть ценные ресурсы, которые могут помочь. N. Вводит 3 вершины треугольника и выводит центроид и график треугольника. Вычисление: прямоугольный треугольник, треугольник со сторонами, равнобедренный треугольник и равносторонний Онлайн-калькулятор теорем Пифагора используется для вычисления расстояния до третьей стороны прямоугольного треугольника в зависимости от двух других сторон с использованием площади всех типов треугольников от 26 июня 2019 года? Подпишитесь здесь: www.Это размер двухмерной поверхности и измеряется в квадратных единицах, например квадратных футах. Попробуйте наш калькулятор равностороннего треугольника. Расчеты в равнобедренном и прямоугольном треугольнике (45-45-90-треугольник). Равносторонний треугольник имеет 3 равные стороны. Специальные треугольники: равнобедренный треугольник и калькулятор 30-60-90: Этот калькулятор выполняет одно из двух действий: 1) Если вам дан прямоугольный треугольник 30-60-90, калькулятор определит недостающие 2 стороны. Треугольник может быть одновременно прямым и равнобедренным, и в этом случае он известен как равнобедренный прямоугольный треугольник.Равнобедренный треугольник - это многоугольник с тремя вершинами (углами) и тремя ребрами (сторонами), две из которых относятся к 17 апреля 2017 г. · Шаблон для решения неправильных треугольников. Правила треугольников. Треугольник. Затем нажмите Рассчитать. Для этого вам потребуются следующие значения: один угол и одна сторона треугольника; две стороны треугольника; одна сторона и площадь треугольника. Предисловие. Хотя образовательная система предоставляет учащимся многочисленные возможности для развития новых навыков, достижений в спорте и практики публичных выступлений, кажется, что ничего не работает, когда дело доходит до математики.Теорема утверждает, что гипотенуза прямоугольного треугольника может быть легко вычислена по длинам сторон. Вершина - это точка, где встречаются два отрезка (A, B и C). Цель состоит в том, чтобы сделать как можно больше треугольников, проводя линии от одной точки к другой. Затем вам нужно будет внести поправку на инфляцию, разделив номинальный ВНП на индекс потребительских цен. Центроид любого треугольника, включая прямоугольные, - это точка, в которой пересекаются биссектрисы всех трех вершин треугольника.Остальные 2 стороны, «b» и «c», следуют в разделе «Площадь% уклона». Номенклатура острого треугольника. Примечание. Этот рабочий лист также можно использовать для «Правого». Рассчитайте высоту треугольника, если заданы две боковые стороны и радиус треугольника. описанная окружность (h): высота треугольника: = Цифра 2 1 2 4 6 10 F Ниже приводится формула расчета длины гипотенузы прямоугольного треугольника, основанная на теореме Пифагора: где c - длина гипотенуза, а a и b - длины двух других сторон.2. Возникли проблемы с калькулятором или есть предложения? Мы хотим знать! Как рассчитать объем треугольной призмы? Вам необходимо снять или узнать (из плана / схемы) три измерения длины. Используйте этот онлайн-инструмент для расчета класса текстуры с одной точкой на основе процентного содержания песка, ила и глины. Калькулятор ИМТ »Калькуляторы треугольников» Преобразование длины и расстояния »Среднее медианное отклонение SD SE» Детский родительский калькулятор по группе крови »Unicode, UTF8, Hexidecimal» Преобразование цветов RGB, Hex, HTML »Калькулятор оборотов G-Force» Калькулятор химического молекулярного веса »Mole, Калькулятор молей в граммы »Символы PCH графика R» Калькулятор разбавления Используйте калькулятор, показанный ниже, для вычисления площади треугольника с тремя сторонами по формуле Герона.Выходные данные - это длины трех сторон AB, BC и CA и размеры трех углов A, B и C треугольника. Формула площади треугольника: Площадь = 0. Калькулятор площади равностороннего треугольника - это бесплатный онлайн-инструмент, который вычисляет решение для заданных входных данных за доли секунды. О калькуляторе теорем Пифагора. Включение необязательных фракций песка уточнит расчет. Смотрите полный список на Calculatorsoup. Этот калькулятор завершает анализ прямоугольного или правильного треугольника с любыми двумя входными данными.Центр описанной окружности остроугольного треугольника находится внутри Тригонометрии (от греч. Trigōnon, «треугольник» и metron, «мера») - раздела математики, изучающего отношения между длинами сторон и углами треугольников. Мы можем найти неизвестную сторону прямоугольного треугольника, если знаем: одну длину и; один угол (то есть кроме прямого). Калькуляторы решений треугольников (тригонометрии). Затем введите ширину основания основного треугольника. Этот калькулятор работает на основе закона косинусов и других основных тождеств треугольников.Calc бесплатно онлайн Как пользоваться калькулятором площади треугольника? · Шаг 1 - Введите значения основания и высоты любого треугольника в отведенное место. Правый равнобедренный треугольник - это треугольник с углом при вершине, равным 90 °, и углами при основании, равными 45 °. Вычислите высоту треугольника по его площади. com Этот калькулятор будет использовать теорему Пифагора для определения недостающей длины прямоугольного треугольника с учетом длин двух других сторон. В онлайн-калькуляторе вы можете использовать значение в тех же единицах измерения! Если у вас возникли трудности с преобразованием единиц, вы можете использовать конвертер длины и площадь Как рассчитать площадь.11 MB) 6 фев 2014 Калькулятор равностороннего, разностороннего, правого и равнобедренного треугольников. Бесплатный калькулятор конгруэнтных треугольников - шаг за шагом найдите и подтвердите совпадение треугольников. Этот веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления. Или загрузите электронную таблицу с поддержкой макросов Microsoft Excel, чтобы получить низкие, репрезентативные и высокие значения общего содержания песка, ила и глины, используя интерактивный треугольник текстуры с треугольником экспозиции - святое сочетание выдержки, диафрагмы и чувствительности, значения ISO.Вычислите площадь прямоугольного треугольника. Онлайн-калькулятор равнобедренного треугольника BYJU ускоряет вычисления и отображает площадь и периметр равнобедренного треугольника за доли секунды. Калькулятор треугольников Херона - Используя формулу Херона, найдите площадь треугольника одним щелчком мыши. · Шаг 2 - Нажмите «Рассчитать». Калькулятор центроидного треугольника - пошаговый расчет, формула и пример решения, чтобы найти среднюю или центральную точку трех заданных точек треугольника (x1, y1), (x2, y2) & (x3 13 июля 2011 года Калькулятор угла и стороны прямоугольного треугольника .Фелиз. Чешуйчатые треугольники: треугольник, каждая сторона которого имеет разную длину. Калькулятор не только площади, но и площади треугольника дает вам свободу решать треугольное уравнение для любого значения, например: • База b • Площадь A • Стороны • Гамма γ • Параметр Это калькулятор прямоугольного треугольника, который иногда называют калькулятором sss. Стороны b и c известны; Калькулятор боковой тригонометрии: новая эра науки о треугольниках. Итак, чтобы найти координату x ортоцентра, сложите три координаты x вершины и разделите на три.(Зеленый + синий) или любая 1 сторона и 1 угол, чтобы вычислить оставшиеся стороны и углы. Игроки ходят по очереди, за каждый ход игрок должен провести одну линию. Когда указаны одна сторона и два угла, калькулятор использует правило, согласно которому сумма углов плоского треугольника должна быть равна 180 °, чтобы вычислить оставшийся третий угол. Более того, треугольники можно описать по их длине и углам их размера. Если вы обнаружите какие-либо ошибки, пропуски неработающих ссылок, сообщите нам - обратная связь; Вы хотите внести свой вклад в этот раздел? См. Премиум-программу для издателей; Свойства инженерного раздела: Калькулятор ребер треугольника.Этот калькулятор определяет площадь треугольника, используя координаты его вершины в декартовой системе координат. 5 марта 2021 г. · Треугольник со всеми равными сторонами называется равносторонним, треугольник с двумя равными сторонами называется равнобедренным, а треугольник со всеми сторонами разной длины называется разносторонним. 2) / 2 для вычисления площади. Формула площади ИК-треугольника определяется как общая область, охватываемая равнобедренным прямоугольным треугольником. что равно половине квадрата с равной длиной стороны.Пример: прямоугольный треугольник с длиной отрезка A, равным 50 дюймов, и длиной отрезка B, равным 50 дюймов, имеет гипотенузу: 50 2 + 50 2 = C 2. Калькулятор геометрического среднего треугольника: этот калькулятор определяет недостающие сегменты, используя среднее геометрическое. Загрузка ИНСТРУКЦИИ ПО КАЛЬКУЛЯТОРУ Triangle Creation eTool. Если все входные данные представляют собой углы, калькулятор рассчитает пропорциональную длину сторон, которую затем можно использовать для увеличения в зависимости от требований к фактическому размеру. Этот калькулятор предназначен для вычисления двух неизвестных факторов в прямоугольном треугольнике при условии, что два фактора известны.Бесплатный онлайн-инструмент для расчета общих формул для кругов, треугольников и многого другого. Пример: если у вас есть две линии длиной 17 и 23, какой должна быть длина третьей стороны для образования треугольника? Введите 17 и 23 в «сторона 1» и «сторона 2», а затем нажмите «2 стороны». Или скачивайте и выключайте. Калькуляторы треугольников. В этом онлайн-калькуляторе можно вводить только целые числа или дроби. Площадь треугольника (формула Герона) Площадь треугольника с учетом основания и углов. Чтобы ввести значение, щелкните внутри одного из текстовых полей.Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). Периметр = a + b + c = 3 + 4 + 5 = 12. Чтобы вычислить площадь треугольника, построенного на векторах, следует помнить, что величина векторного произведения двух векторов равна удвоенной площади треугольника. треугольник, строят на соответствующих векторах: Поэтому вычисление площади треугольника строят на векторах, разбитых на несколько шагов. Более подробную информацию читайте в этих правилах. Остальные значения будут рассчитаны.Включение необязательных фракций песка уточнит расчет. Как рассчитать масштабный треугольник. 7107 дюймов. Подробная информация о формулах, используемых под формой. Вы можете рассчитать угол, сторону (прилегающую, противоположную, гипотенузу) и площадь любого прямоугольного треугольника и использовать их в реальном мире для определения высоты и расстояний. Заполните 3 из 6 полей хотя бы с одной стороны и нажмите кнопку «Рассчитать». Тем не менее, ваш собственный капитал - это хорошая цифра. Треугольник является разносторонним, если все стороны имеют разную длину или все три угла различны.Формула для вычисления площади треугольника 3 Вычислите площадь треугольника, используя формулу длины сторон. Бесплатный калькулятор площади треугольника и периметра - шаг за шагом рассчитайте площадь и периметр треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Мгновенно решает отсутствующие стороны и / или углы, плюс площадь, периметр, радиус окружностей, медианы и высоты. Например, там точки A (1, 3), B (5, 5), C (7, 5), центр описанной окружности равен (6, -2). Наш калькулятор решает треугольники по формуле Герона.Вычислите центр описанной окружности треугольника по известным значениям координат. Введите одно значение и выберите количество десятичных знаков. Калькулятор ИМТ »Калькуляторы треугольников» Преобразование длины и расстояния »Среднее медианное отклонение SD SE» Детский родительский калькулятор по группе крови »Unicode, UTF8, Hexidecimal» Преобразование цвета RGB, Hex, HTML »Калькулятор скорости вращения G-Force» Калькулятор химического молекулярного веса »Mole, Калькулятор молей в граммы »График R Символы PCH» Разведение Ввод данных в калькулятор площади треугольника.com комплексный калькулятор для треугольников, позволяющий легко вычислять углы и стороны. Калькулятор для треугольников - простой режим. Этот калькулятор треугольников решает недостающие части треугольника. Калькулятор площади треугольника помогает рассчитать площадь треугольника. Калькулятор треугольников Этот калькулятор треугольников вычисляет стороны, углы, периметр и площадь любого треугольника независимо от его типа (прямой, равнобедренный, равносторонний) на основе известных вам значений. Калькулятор треугольников - это простой математический инструмент, который предоставляет как студентам, так и обычным пользователям возможность быстро вычислить стороны прямоугольного треугольника, используя теорему Пифагора.Каждый фотограф должен понимать их значение и правильно их использовать. Включение необязательных фракций песка уточнит расчет. Это также центр тяжести треугольника. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ). Высота - это не что иное, как перпендикулярная линия (AD, BE и CF) от одной стороны треугольника (AB, BC или CA) до противоположной вершины. area = (a * b) / 2 Прямоугольный треугольник - это треугольник, угол которого равен 90 градусам.Или загрузите электронную таблицу Microsoft Excel с поддержкой макросов, чтобы определить низкие, репрезентативные и высокие значения общего количества песка, ила и глины с помощью интерактивного текстурного треугольника с В равнобедренном треугольнике, зная сторону и угол α, вы можете рассчитать высоту, поскольку сторона - гипотенуза, а высота - катет, тогда высота будет равна произведению синуса угла в сторону. сторона a: Калькулятор биномиального разложения треугольника Паскаля. 10 февраля 2021 г. · Как мы помним из основной формулы площади треугольника, мы можем вычислить площадь, умножив высоту и основание треугольника и разделив результат на два.Введите три значения сторон или углов треугольника (в градусах), включая как минимум одну сторону. Введите 3 длины сторон треугольника (A, B и C), затем нажмите «ENTER». Другими словами, он определяет: длину гипотенузы прямоугольного треугольника, если заданы длины двух катетов; Если мы знаем высоту и основание треугольника, мы могли бы вычислить его площадь по следующей формуле: S = 1 / 2bh Также вы можете рассчитать площадь треугольника, используя формулу Герона, по которой это можно сделать, если вы знаете периметр или длину всех его ног: Ввод данных в периметр треугольника калькулятором.Просто возьмите то, что вам дано в задаче, и попытайтесь определить, в результате чего конечный угол в сумме составит 180 градусов. Часть III: Тестирование калькулятора. ) Нажмите «решить», чтобы найти недостающие значения, используя закон синусов или закон косинусов. Хотя вычисление процента требует выполнения множества шагов, его можно немного упростить. Напомним теорему Пифагора. ) РЕШЕНИЯ ПРАВИЛЬНОГО ТРЕУГОЛЬНИКА: РЕШЕНИЯ ОБЯЗАТЕЛЬНОГО ТРЕУГОЛЬНИКА: Введите значения «a» для SSS, SAS, ASA, SAA или SSA, которые могут быть любой из трех сторон.Введите три значения. Более подробную информацию читайте в этих правилах. Треугольники по размеру угла 4. Полный список см. На сайте Calculatorsoup. Калькулятор использует закон косинуса [c² = a² + b² - 2ab cos γ] для вычисления третьей стороны треугольника, когда заданы две стороны и угол между ними. Наконец, запишите значение высоты пирамиды и нажмите «Рассчитать». Когда известны 3 стороны Ниже приведены ссылки на Свойства раздела "Тригонометрия": Калькуляторы решения треугольников. Как пользоваться калькулятором 1 - Введите две стороны \ (a \) и \ (b \), образующие прямой угол, как положительное вещественное число и желаемое количество десятичных знаков, затем нажмите «Enter».Вычислить угол и противоположные стороны, гипотенузу, смежную с прямоугольным треугольником, формулу для угла и противоположных сторон, гипотенузу, смежную с прямоугольным треугольником, калькулятор, простой в использовании калькулятор для решения задач прямоугольного треугольника. Название гипотенуза дается самому длинному ребру прямоугольного треугольника. 2. Введите длину любых двух сторон и оставьте поле для расчета пустой. com 26 июня 2020 г. · Если вы ищете формулы высоты треугольника для особых треугольников, таких как прямоугольный, равносторонний или равнобедренный треугольник, или любой равносторонний треугольник, этот калькулятор - беспроигрышный вариант - он может рассчитать высоту треугольника, а также стороны треугольника, углы, периметр и площадь.A Медиана - это линия, соединяющая вершину треугольника с серединой противоположной стороны. Вам необходимо знать площадь и калькулятор бесплатных треугольников - вычисляйте площадь, периметр, стороны и углы треугольников шаг за шагом. Треугольная диаграмма будет перерисована в масштабе с отмеченными всеми размерами. Калькулятор равнобедренного треугольника - это бесплатный онлайн-инструмент, который отображает площадь и периметр равнобедренного треугольника. Что означает калькулятор треугольника? Небольшой сдвиг в формуле можно сделать, чтобы найти площадь треугольника.Математика определенно входит в число основных опасений студентов во всем мире. Зная это, вы можете определить площадь на основе этих вычислений: s = (a + b + c) / 2 или 1/2 периметра треугольника. Площадь треугольника Калькулятор - это бесплатный онлайн-инструмент, который отображает площадь треугольника. треугольник, когда указаны основание и высота. Если размеры трех из шести частей (3 угла и 3 стороны) треугольника известны, и хотя бы одна из известных частей является стороной, размеры других сторон и углов могут быть вычислены.C - гипотенуза. Это будет граница области или контур. Площадь = Периметр основания x Высота + 2 x Площадь основания Периметр основания = 2 x (Длина + Ширина) Площадь основания = Длина x Калькулятор, определяющий ширину Здесь вы можете вычислить определитель матрицы с комплексными числами онлайн бесплатно с помощью очень подробное решение. Треугольник с тремя сторонами равной длины называется равносторонним треугольником, тогда как равнобедренный треугольник состоит из двух сторон равной длины. Угол «C» - это угол, противоположный стороне «c».Независимая информация означает, что ни один из трех представленных предметов не может быть найден в двух других. Смотрите полный список на Calculatorpro. Когда указаны одна сторона и два угла, калькулятор использует правило, согласно которому сумма углов плоского треугольника должна быть равна 180 °, чтобы вычислить оставшийся третий угол. Человек должен будет ввести 3 из шести сторон, а также углы треугольника, и как только это будет сделано, автоматически вычисляются остальные 3 значения с помощью инструмента калькулятора треугольника.Попробуйте воспользоваться «Калькулятором треугольников» ниже: 25 марта 2020 г. · Решение проблем, связанных с геометрией плоскости, особенно с кругами и треугольниками, можно легко решить с помощью калькулятора. Результат: Калькулятор наклонного треугольника - это треугольник без 90 градусов. Эта область возникла в эллинистическом мире в III веке до нашей эры из приложений геометрии к астрономическим исследованиям. В этом онлайн-калькуляторе можно вводить только целые числа или дроби. Введите одно значение и выберите количество десятичных знаков.Ознакомьтесь с интерактивными симуляторами, чтобы узнать больше об уроке, и попробуйте свои силы в решении нескольких интересных практических вопросов в конце страницы. Каждое число в треугольнике Паскаля - это сумма двух чисел, расположенных по диагонали над ним. Таким образом, они не совпадают. Калькулятор тригонометрии Калькулятор прямоугольного треугольника. · Шаг 3 - 28 февраля 2021 г. Решение треугольников с использованием теоремы Пифагора, правила косинуса, правила синуса и различных способов вычисления площади треугольника. Площадь квадрата. Номер n-го треугольника - это количество точек, составляющих треугольник с n точками на стороне, и оно равно сумме n натуральных чисел от 1 до n.Как видите, единственный шаг, который вам нужно сделать, чтобы использовать наш калькулятор, - это ввести все ваши переменные и дождаться, пока наш калькулятор вычислит объем вашей пирамиды. Щелкните значок «глаз», чтобы просмотреть количество информации, отображаемой в треугольнике. Вычислите периметр треугольника со сторонами 3, 4 и 5 см. Он поставляется с калькулятором треугольников. Решайте треугольники. Решайте треугольники, вводя две стороны и один угол, два угла и одну сторону или три стороны, чтобы найти оставшиеся значения, используемые в тригонометрии.На этой странице вы можете решать математические задачи с использованием прямоугольных треугольников. Все значения могут быть рассчитаны, если известны одна сторона и любые два других значения. Онлайн-область BYJU в калькуляторе треугольников ускоряет вычисления и отображает площадь за доли секунды. Просто введите неизвестное значение и нажмите кнопку «Обновить», расположенную внизу веб-страницы. Или загрузите электронную таблицу с поддержкой макросов Microsoft Excel, чтобы определить низкие, репрезентативные и высокие значения общего количества песка, ила и глины с помощью интерактивного треугольника текстуры с калькулятором среднего геометрического треугольника: этот калькулятор определяет недостающие сегменты с использованием среднего геометрического.Случайно нарисованные треугольники, имеющие все три различных внутренних угла, называются разносторонним треугольником. Используйте ползунки, чтобы изменить базовую длину треугольника или подвижные точки 1. Убедитесь, что все они имеют одну и ту же единицу длины, или конвертируйте соответственно, пока не станут. Площадь параллелограмма Калькулятор площади треугольника - пошаговый расчет, формула и пример решения решенной задачи, чтобы найти площадь для заданных значений основания b и высоты h треугольника в различных единицах измерения между дюймами (дюймами), футами (футами), метры (м), сантиметры (см) и миллиметры (мм).Пожалуйста, ознакомьтесь также с калькулятором правильного треугольника и калькулятором неправильного треугольника. Предположим, вы знаете все три длины: a, b и c. Затем калькулятор скажет вам, что третья сторона должна быть больше 6 и меньше 40. Задача проста - сначала определить длину ребер, а затем использовать формулу Герона, чтобы найти площадь треугольника. Как использовать. Если вы пытаетесь помочь ученику с домашним заданием по математике и у вас возникают вопросы, связанные с наклоном, вам может потребоваться повторная подготовка к тому, как вычислить это важное измерение.Калькулятор также вычислит площадь треугольника, периметр, полупериметр, радиус описанной окружности и вписанной окружности, медианы и высоты. Площадь треугольника с учетом основания и высоты. Повторите для координаты y. Калькуляторы - это небольшие компьютеры, которые могут выполнять различные вычисления и решать уравнения и задачи. Это одна из основных геометрических фигур. Введите известные вам длины сегментов, и калькулятор треугольников вычислит треугольники: стороны, углы, площадь, периметр, медиана, высота, полупериметр, радиус вписанных и описанных кругов.net Треугольник определяется 3 из 6 свободных значений, по крайней мере, с одной стороной. Радиус можно найти так: где S, площадь треугольника, можно найти по формуле Героя. Калькулятор треугольников вычисляет и находит: углы, стороны, площадь всех типов треугольников. Также ознакомьтесь с оригинальным калькулятором необходимых материалов. Масштабный треугольник - плоская замкнутая фигура, у которой нет равных сторон и нет равных внутренних углов. Он был создан по запросу пользователя. Нахождение площади треугольников, по которой можно было бы вычислить площадь треугольника только по его углам?Как пользоваться калькулятором Введите координаты x и y трех вершин A, B и C треугольника и нажмите «вычислить». Тупой треугольник; Острый треугольник; Равноугольный; Примеры: Вычислите площадь треугольника с заданной длиной 3 и шириной 4 см. Калькулятор теорем Пифагора используется для вычисления длины третьей стороны прямоугольного треугольника на основе двух других сторон с использованием теоремы Пифагора. Теорема Пифагора - это геометрическое соотношение между различными сторонами прямоугольного треугольника, которое можно использовать для вычисления одной из недостающих длин в трехстороннем треугольнике.Треугольное число или число треугольника подсчитывает объекты, которые могут образовывать равносторонний треугольник. Как решать Треугольники SSA? Калькулятор треугольников решает и рисует любой треугольник, он находит для вас недостающие углы, высоты (высоты) и края. Для вычисления этого типа треугольника у нас есть специальный калькулятор прямоугольного треугольника. Введите сторону a, сторону b и сторону c и нажмите кнопку «Вычислить площадь треугольника». Отображаемая площадь треугольника рассчитывается по длине трех сторон. Популярный онлайн-калькулятор треугольников Math Warehouse: введите любую допустимую комбинацию сторон / углов (3 стороны, 2 стороны и угол или 2 угла и 1 сторона), а наш калькулятор сделает все остальное! Он даже скажет вам, можно ли создать более одного треугольника.B. Полезно для строительных проектов, деревообработчиков, домовладельцев, студентов и недвижимости. Чтобы вычислить гипотенузу, используйте теорему Пифагора следующим образом: A 2 + B 2 = C 2. Сумма всех внутренних углов треугольника всегда равна 180 градусам. В онлайн-калькуляторе вы можете использовать значение в тех же единицах измерения! Если у вас возникли трудности с пересчетом единиц, вы можете воспользоваться конвертером длины. Как рассчитать необходимый материал (треугольник) Давайте будем честными - иногда лучший калькулятор необходимого материала (треугольник) - это тот, который прост в использовании и не требует, чтобы мы даже знали, какой материал нужен. Еще один треугольный калькулятор для тех, кто нуждался радиус описанной окружности треугольника.5. 5 * длинная сторона * короткая сторона; • длинная сторона = гипотенуза * 0. Однако отметка b на рисунке немного вводит в заблуждение, поскольку расстояние b на одном рисунке не совпадает с расстоянием b на другом. Эту теорему обычно приписывают греческому математику Пифагору, хотя это спорный факт, поскольку многие ученые считают, что это знание предшествовало ему. Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). У прямоугольного треугольника две стороны перпендикулярны друг другу. Вот исчерпывающий набор методов калькулятора для кругов и треугольников в плоской геометрии.Введите известную длину сегмента и нажмите кнопку «Треугольник». Формулу Герона см. В разделе «Калькулятор площади треугольника по формуле Героя». В каждом углу есть внутренний угол, т.е. Урок, предоставленный г-ном. Этот калькулятор определит неизвестную длину данного наклонного треугольника для тупого или острого треугольника. Войдите или зарегистрируйтесь. Площадь трапеции. a: b: c: alpha: beta: вычислить длину, угол, площадь, периметр, высоту, внутренний радиус или окружной радиус любого ребра прямоугольного треугольника с помощью калькулятора прямоугольного треугольника.В приведенном ниже примере o - это ортоцентр. Загрузите версию Excel для интерактивного текстурного треугольника (XLSM; 6. Для каждого расчета приводятся пошаговые пояснения. Введите значения трех из шести сторон и углов треугольника, и остальные три значения будут вычислены. Калькулятор прямоугольного треугольника для вычисления стороны длина, угол, высота, площадь и периметр прямоугольного треугольника с любыми двумя значениями. Как работает этот калькулятор прямоугольного треугольника? Этот инструмент предназначен для определения сторон, углов, площади и периметра любого прямоугольного треугольника, если вы введете любые 3 поля (любые 3 комбинации сторон и углов) 5 сторон и углов, доступных в форме.Калькулятор наклонного треугольника принимает длину одной стороны и любые два других значения и возвращает недостающие значения в точном и десятичном виде в дополнение к пошаговому вычислению площади равностороннего треугольника. Найти недостающую сторону прямоугольного треугольника довольно просто, если известны две стороны. Чтобы использовать калькулятор прямого угла, просто введите длины любых двух сторон прямоугольного треугольника в верхние поля. Количество введенных значащих значений будет определять количество значащих цифр в результатах.com / c / SLkhanMore Калькулятор произвольного треугольника вычисляет все свойства произвольного треугольника, такие как площадь, периметр, стороны и углы, с учетом достаточного подмножества этих свойств. Полупериметр (1/2 периметра) треугольника равен s. Создайте прямоугольный треугольник. B. Введите только два значения и оставьте значения для расчета пустыми. С помощью нашего калькулятора периметра вы можете определить периметр для нескольких различных форм, включая квадрат, прямоугольник, треугольник, эллипс, параллелограмм, трапецию, многоугольник и ромб.Введите одно значение и выберите количество десятичных знаков. Какой информацией однозначно определяется треугольник? Треугольник всегда определяется длиной его трех сторон. Стороны «a» и «b» - это перпендикулярные стороны, а сторона «c» - гипотенуза. Вычислить степень угла треугольника в Excel, мы просто знаем угол AB и BC. Центр описанной окружности прямоугольного треугольника находится в центре гипотенузы. Последняя активность 4 года 9 месяцев назад. C = 70. Калькулятор треугольника
Угол «B» — это угол, противоположный стороне «b». 5. Размер полного треугольника известен после того, как будут даны 3 независимых элемента информации. Масштаб шага бега Посетите эту страницу с помощью телефона или планшета, чтобы напрямую измерить шаг и углы. Используйте этот онлайн-инструмент для расчета класса текстуры с одной точкой на основе процентного содержания песка, ила и глины. Слайдеры. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.е. Онлайн-калькулятор центроида поможет вам найти центр тяжести треугольника (ABC), N-точек и N-стороннего многоугольника для заданных координат. Прочтите, чтобы узнать больше о том, что такое наклон, и о некоторых простых способах решения. Когда вам нужно решить математическую задачу и вы хотите убедиться, что у вас есть правильный ответ, вам может пригодиться калькулятор. Формулу Герона см. В разделе «Калькулятор площади треугольника по формуле Героя». Формулы треугольника с углом 30̊ 60̊ 90̊: • периметр = длинная сторона + короткая сторона + гипотенуза; • площадь = 0.Линия не может пересекать другие линии или касаться других точек, кроме двух, с которыми она связана. Чтобы решить это уравнение, вам необходимо знать площадь и высоту. Есть много способов найти высоту треугольника. Этот инструмент помогает легко визуализировать влияние настроек на конечный результат. Вычисление: прямоугольный треугольник, двусторонний треугольник, равнобедренный треугольник и равносторонний треугольник. Найдите площадь, периметр, медианное значение, высоту, биссектрису угла и т. Д. Угол треугольника 25 июля 2011 г. Треугольник ограничен точками решетки в заданном диапазоне. Перетащите точки и создайте новые треугольники. Наведите указатель мыши на линии и специальные точки, чтобы получить площадь треугольника 22 января 2021 г. Калькулятор формулы площади равностороннего равнобедренного треугольника позволяет вам чтобы найти площадь различных типов треугольников, например, Этот бесплатный калькулятор треугольников вычисляет края, углы, площадь, высоту, периметр, медиана, а также другие значения треугольника.Вот как можно объяснить вычисление стороны треугольника с заданными входными значениями -> 4. Последняя часть этого проекта — оценка. Точка, через которую проходят все три медианы треугольника, называется центроидом треугольника, и она делит каждую медиану в соотношении 2: 1. Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три. Площадь параллелограмма с учетом основания и высоты. (Примечание: если заполнено более 3 полей, только треть используется для определения треугольника, остальные (в конечном итоге) перезаписываются. Калькулятор вычисляет треугольник, указанный в трех его свойствах.Калькулятор треугольников Решите треугольники Решите треугольники, введя две стороны и один угол, два угла и одну сторону или три стороны, чтобы найти оставшиеся значения, которые используются в тригонометрии. Углы: треугольник — это самая простая двумерная форма. Бесплатная программа для решения математических задач отвечает на ваши домашние вопросы по тригонометрии с пошаговыми пояснениями. Введите значения трех из шести сторон и углов треугольника, и остальные три значения будут вычислены. Умножение используется, если вы работаете с десятичной дробью, и деление. T Сколько вы стоите в финансовом отношении? Многие люди понятия не имеют, каков их собственный капитал, хотя они часто читают о чистом капитале известных людей и богатых владельцев бизнеса.Показанные по умолчанию цифры являются гипотетическими и могут не применяться. Формула реального ВНП находится путем определения номинального валового национального продукта (ВНП) путем прибавления к ВВП прироста капитала за счет иностранных доходов. Учащиеся K-12 могут обратиться к приведенным ниже формулам треугольника, чтобы узнать, какие входные параметры используются для определения площади треугольника. Что ж, продолжительность дуги довольно просто вычислить с помощью некоторой арифметики отношений. Калькулятор 20 января 2020 г. · Чтобы определить, являются ли три стороны треугольника треугольником, используйте теорему о неравенстве треугольника, которая гласит, что сумма двух сторон треугольника должна быть больше третьей стороны.Без использования калькулятора Чтобы определить, является ли треугольник острым, прямым или тупым, если у треугольника есть 3 стороны: Чтобы вычислить площадь треугольника, перейдите в Калькулятор площади треугольника. закон синусов и закон косинусов важны для процесса вычисления. Конечный результат нашего калькулятора треугольной призмы всегда выражается в кубических единицах: в 3, футах 3, ярдах 3, мм 3, см 3, метрах 3 и т. Д. Калькулятор треугольников вычисляет и находит: углы, стороны, площадь всех типов треугольники. Затем перпендикулярно биссектрисам линий треугольника. Последний решает любые две пары уравнений. Точка пересечения — центр описанной окружности.Введите одно число и нажмите кнопку «рассчитать»! Прямоугольный или прямоугольный треугольник 30̊60̊ 90̊ — это треугольник с углами 30̊ 60̊ 90̊. Определитель вычисляется путем приведения матрицы к форме эшелона строк и умножения ее основных диагональных элементов. Этот калькулятор предназначен только для прямоугольного треугольника! Факторами являются длины сторон и один из двух углов, кроме прямого. Персональный кредитный калькулятор (обычно) тоже бесплатный. Заявление об отказе от ответственности для калькулятора: информация, предоставляемая этими калькуляторами, предназначена только для иллюстративных целей и не предназначена для определения фактических параметров, определенных пользователем.Вы можете настроить точность результатов. Калькулятор определяет радиус и имеет радиус, площадь описанной окружности, площадь треугольника и соотношение площадей — только для справки 20 февраля 2021 г. · Калькулятор определит, что вам нужно будет разрезать квадрат со сторонами, длина которых равна 4 1 / 2 дюйма, чтобы получилось 2 незаконченных угловых треугольника, и квадрат со сторонами, длина которых составляет 8 3/8 дюйма, чтобы образовать 4 незавершенных треугольника. Затем нажмите Рассчитать. Этот калькулятор вычисляет все три угла и три стороны треугольника.Самое первое, что вы должны помнить, — это правильный знак формулы. Калькулятор треугольников предоставляет вам несколько методов для расчета площади треугольника с использованием SAS, SSS, AAS, SSA, равностороннего. B aseLength 8. Другими словами, по количеству введенных значений можно определить значение. Калькулятор использует закон косинуса [c² = a² + b² — 2ab cos γ] для вычисления третьей стороны треугольника, когда две стороны и угол между ними дан. Это может помочь. Начать новый заем — очень важное решение.2 \), известная как теорема Пифагора. гипотенуза: A: B: напротив: C = 90: смежно Используйте этот онлайн-инструмент для вычисления класса текстуры одной точки на основе процента песка, ила и глины. YouTube. исчерпывающий калькулятор треугольников, позволяющий легко вычислить углы, стороны, площади и другие части треугольника. Калькулятор треугольников — режим гуру. Этот калькулятор треугольников решает недостающие части треугольника. 14 апреля 2013 г. — 3 4 5 Калькулятор треугольников | Калькулятор прямоугольного треугольника | Решатель Правого Треугольника | Особые треугольники.Показывает свою работу и рисует решение. Треугольник — это многоугольник с тремя ребрами и тремя вершинами. Помните, сумма углов треугольника равна 180 градусам. Без сомнения, этот калькулятор лучше всего подходит для определения центроида многих 2D-форм, а также набора точек. Треугольное число или число треугольника подсчитывает объекты, которые могут образовывать равносторонний треугольник. Расчеты в равностороннем треугольнике или правильном треугольнике. Щелкните правой кнопкой мыши текст или метку точки, чтобы отредактировать ее. Дан треугольник Центроид любого треугольника, включая прямоугольные, — это точка, в которой угол наклона. Треугольная планировка остается стандартом при планировании кухонного пространства.Существуют различные начальные измерения, из которых можно составить треугольник, вычислить длину стороны и высоту до нее и, наконец, вычислить площадь треугольника. Другими словами, количество введенных значений может определить Калькулятор Центроида Треугольника. Задача проста — сначала определить длины ребер, а затем по формуле Герона найти площадь треугольника. Пример . Используйте его, изучайте, обучайте, делитесь и вставляйте! 3-частотный калькулятор геодезического купола 5/8, который определяет длину стойки, стоимость, вес, конструкцию и размеры треугольника для геодезического купола.Периметр можно определить как длину вокруг двухмерного объекта. Вы можете рассчитать длину любой стороны прямоугольного треугольника, если знаете, как найти площадь тупого треугольника. Поиск стороны в прямоугольном треугольнике Найдите сторону, когда мы знаем другую сторону и угол. Этот онлайн-калькулятор рассчитывает характеристики равностороннего треугольника: длину сторон, площадь, периметр, радиус. Калькулятор «Купить прямоугольный треугольник» — Тригонометрия: прочитать обзоры приложений и игр — Amazon.Площадь прямоугольника. 5. Установочные треугольники — это треугольники, используемые для заполнения пространств на внешних краях стеганого одеяла, установленного в точке, подобной «Прекрасное в лаванде» (показано ниже). После расчета желаемого выходного параметра единицы решения конвертируются, если этого требует выбранная единица. ) Где (для краткости) написано «край a», «угол B» и т. Д., Более правильным должно быть что-то вроде «длина ребра a», или «длина края», или «размер угла B» и т. Д. Найдите онлайн-калькулятор.Чтобы перевернуть треугольник, используйте нижние правые кнопки. Здесь вы можете ввести две известные стороны или углы и вычислить неизвестную сторону, угол или площадь. Рассчитайте как углы, так и стороны, просто введите любые 2 поля. Запишите высоту базового треугольника. Создайте равнобедренный треугольник. Ортоцентр треугольника Метод вычисления ортоцентра треугольника Закон косинусов — одна сторона треугольника, когда известны противоположный угол и две стороны; Закон синусов — углы в общем треугольнике; Закон касательных — треугольники и закон касательных; Калькулятор углов угловой пилы — Расчет углов угломера для торцовочной пилы; Oblique Triangle — Уравнения наклонного треугольника; Теорема Пифагора — Используемая теорема Пифагора Вычислите площадь и периметр прямоугольного треугольника.Вычислите площадь и периметр разностороннего треугольника. Площадь — это пространство внутри периметра / границы пространства, его символ — (A). N. (Наклонный треугольник с одним углом> 90 градусов. Инструкции по калькулятору треугольника. Калькулятор триггера для прямоугольного треугольника Введите два значения и нажмите «Рассчитать». 3. Например, треугольник с тремя сторонами равной длины называется… Продолжить чтение → Треугольник Калькулятор. Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна катета является высотой, а вторая — основанием, поэтому уравнение упрощается до: area = a * b / 2 Калькулятор треугольника CosSinCalc вычисляет стороны, углы, высоты, медианы, биссектрисы, площадь и окружность треугольника.Координаты центроида — это просто среднее значение координат вершин. Узнайте о вычислении треугольника, чтобы найти H, калькуляторе площади треугольника и вычислении прямоугольного треугольника в концепции вычисления треугольника, чтобы найти C. См. Полный список на калькуляторе. Калькулятор площади равностороннего треугольника: понимание пошагового процесса вычисления площади равностороннего треугольника помогает учащимся легко решать математические задачи в их старших классах. Калькулятор треугольников: рассчитайте, правильный ли это треугольник и какого типа.Формула площади треугольника — высота стороны x, как показано на графике ниже: Калькулятор площади треугольника, равностороннего равнобедренного треугольника позволяет вам найти площадь различных типов треугольников, таких как равносторонний, равнобедренный, прямоугольный или равнобедренный треугольник, по различным формулам расчета, таким как формула Герона, длина сторон треугольника и углы, радиус вписанной или описанной окружности. Площадь треугольника с учетом сторон и угла. Равнобедренный, калькулятор прямоугольного треугольника. 7 марта 2014 г. Загрузите калькулятор триггера для прямоугольного треугольника — простой в использовании программный инструмент, который поможет вам выполнять вычисления прямоугольного треугольника на ветру и 25 апреля 2017 г. 2-2 * 7 * 4 * cos (30)).Калькулятор геометрии для решения теоремы Пифагора о прямоугольном треугольнике с учетом длины сторон a и b. Калькулятор геометрии для определения высоты стороны c прямоугольного треугольника с учетом длины сторон a, b и c. Узнайте, как рассчитать нужный размер, или просто воспользуйтесь бесплатной таблицей резки! Этот пост содержит партнерские ссылки, за которые я получаю компенсацию. Калькулятор треугольников вычисляет треугольники, указанные в трех его свойствах. Прямоугольный треугольник имеет теорему Пифагора. Калькулятор вычисляет длину третьей стороны прямоугольного треугольника на основе длин двух других сторон, используя теорему Пифагора.Этот калькулятор вычисляет из трех значений треугольника все остальные значения. Найдите угол Альфа, угол Бельты и гипотенузу សូម ជួយ ចុច ПОДПИСАТЬСЯ មួយ ផង បាទ 08.07.2019 · Рассчитайте высоту треугольника, если заданы две боковые стороны и радиус описанной окружности (h): высота треугольника: = Цифра 2 1 2 4 6 10 F Центр окружности треугольника, биссектриса Точка, в которой пересекаются срединные перпендикуляры треугольника, называется центром описанной окружности. У острого треугольника 3 острых угла. Калькулятор треугольника мощности Треугольник мощности показывает соотношение между реактивной, активной и полной мощностью в цепи переменного тока.Как решить тригонометрию прямоугольного треугольника? Хотя использование калькулятора тригонометрии для вычисления прямоугольных треугольников намного проще, вам также следует научиться находить значение вручную. Добавлено 6 февраля 2014 г. пользователем Sravan75 по математике. Хотя процентные значения могут быть рассчитаны как с дробями, так и с десятичными знаками. Он был создан по запросу пользователя. Приложение нарисует треугольник в соответствии с двумя предыдущими введенными вами измерениями. Два других значения будут заполнены. У него 3 ребра и 3 угла (или вершины).Треугольники — очень простая игра. (Это край, противоположный прямому углу, и в данном случае это c. Поэтому все, что вам нужно сделать, это сложить вместе каждую комбинацию двух сторон, чтобы увидеть, больше ли она, чем третья сторона. Самый простой способ — из области и Длина основания. Математики называют это «решением треугольника. Подробнее см. Центроид треугольника. В течение трех десятилетий евангелие кухонного дизайна было найдено в базовой геометрии. Задайте вопрос, заданный 4 года, 9 месяцев назад. Создайте острый треугольник.Объяснение калькулятора треугольника. 866025; Калькулятор треугольника Этот калькулятор может вычислить площадь треугольника, высоту треугольника, медиану треугольника, центроид, центр описанной окружности и ортоцентр. Номер n-го треугольника — это количество точек, составляющих треугольник с n точками на стороне, и оно равно сумме n натуральных чисел от 1 до n. Шаблон треугольника Паскаля — это расширение массива биномиальных коэффициентов. s = (a + b + c) / 2 area = sqrt (s * (s — a) * (s — b) * (s — c)) Разносторонний треугольник — это треугольник, все стороны которого неравны.Прежде всего, необходимо найти треугольник, имеющий три стороны и три угла. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Пример: Найдите центр тяжести треугольника с вершинами (1,2) (3,4) и (5,0). Калькулятор тригонометрии — прямоугольные треугольники. Введите все известные переменные (стороны a, b и c; углы A и B) в текстовые поля. Площадь треугольника. Для наклонных треугольников используется набор формул, уникальных для прямоугольных треугольников, и эти формулы могут отображаться на странице калькулятора наклонных треугольников на нашем веб-сайте.Вы можете сэкономить много времени, используя калькулятор раскрытия треугольника Паскаля, чтобы быстро построить треугольник из чисел одним щелчком мыши. Калькулятор равнобедренного треугольника вычисляет все свойства равнобедренного треугольника, такие как площадь, периметр, стороны и углы, с учетом достаточного подмножества этих свойств. Сторона \ (C \) вычисляется и 6 тригонометрических соотношений определяются в тригонометрии. Площадь = [l × b / 2] = (3 * 4/2) = 12/2 = 6. Человек должен будет ввести 3 из шести сторон, а также углы треугольника, и как только это будет сделано , остальные 3 значения автоматически рассчитываются инструментом калькулятора треугольника.Для максимальной эффективности и простоты передвижения нарисуйте воображаемый треугольник из центра. Найдите основание треугольника, решив уравнение: площадь = 1/2 x b x h. Как рассчитать длину ребер равнобедренного треугольника Этот калькулятор определяет площадь треугольника, используя координаты его вершины в декартовой системе координат. Это та же самая формула для обоих типов треугольников на рисунке. Подвижные точки. В геометрии треугольник — это форма, все три стороны которой имеют одинаковую длину. Углы треугольника. Калькулятор.В свою очередь, вершины — это линия или точка, в которой пересекаются ребра. Затем нажмите Рассчитать. угол между сторонами, заканчивающийся в этом углу. Площадь ромба. A и B — длины катетов треугольника. (Угол «А» — это угол, противоположный стороне «а». Острый треугольник: треугольник, все внутренние углы которого <90 градусов. Этот калькулятор определит, образуют ли эти 3 стороны равносторонний, равнобедренный, острый, прямой или тупой треугольник. или вообще нет треугольника. Рассчитайте площадь равностороннего треугольника с помощью данного онлайн-калькулятора Как рассчитать сторону a треугольника с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для стороны a треугольника, введите Сторона B (b), Сторона C (c) и Угол A (∠A) и нажмите кнопку расчета.«У разностороннего треугольника нет равных сторон. Треугольник имеет три вершины. Калькулятор 2-х решений. Бесплатная загрузка Triangle Calculator - Moffsoft Calculator, Simple Calculator, Biromsoft Calculator и многие другие программы Калькулятор треугольника Паскаля строит треугольник Паскаля, используя метод биномиального расширения. Диаграмма калькулятора прямоугольного треугольника тригонометрии. Щелкните элемент стороны или угла, чтобы активировать его, и введите значения для любых 2 известных сторон (зеленый + синий) или любой 1 стороны и 1 угла, чтобы вычислить оставшиеся стороны и углы.. Количество введенных значащих значений будет определять количество значащих цифр в результатах. C 2 = 5000. Сравнение процентных ставок и решение о доступности ежемесячных платежей может вскружить вам голову, но есть ценные ресурсы, которые могут помочь. N. Вводит 3 вершины треугольника и выводит центроид и график треугольника. Вычисление: прямоугольный треугольник, треугольник со сторонами, равнобедренный треугольник и равносторонний Онлайн-калькулятор теорем Пифагора используется для вычисления расстояния до третьей стороны прямоугольного треугольника в зависимости от двух других сторон с использованием площади всех типов треугольников от 26 июня 2019 года? Подпишитесь здесь: www.Это размер двухмерной поверхности и измеряется в квадратных единицах, например квадратных футах. Попробуйте наш калькулятор равностороннего треугольника. Расчеты в равнобедренном и прямоугольном треугольнике (45-45-90-треугольник). Равносторонний треугольник имеет 3 равные стороны. Специальные треугольники: равнобедренный треугольник и калькулятор 30-60-90: Этот калькулятор выполняет одно из двух действий: 1) Если вам дан прямоугольный треугольник 30-60-90, калькулятор определит недостающие 2 стороны. Треугольник может быть одновременно прямым и равнобедренным, и в этом случае он известен как равнобедренный прямоугольный треугольник.Равнобедренный треугольник - это многоугольник с тремя вершинами (углами) и тремя ребрами (сторонами), две из которых относятся к 17 апреля 2017 г. · Шаблон для решения неправильных треугольников. Правила треугольников. Треугольник. Затем нажмите Рассчитать. Для этого вам потребуются следующие значения: один угол и одна сторона треугольника; две стороны треугольника; одна сторона и площадь треугольника. Предисловие. Хотя образовательная система предоставляет учащимся многочисленные возможности для развития новых навыков, достижений в спорте и практики публичных выступлений, кажется, что ничего не работает, когда дело доходит до математики.Теорема утверждает, что гипотенуза прямоугольного треугольника может быть легко вычислена по длинам сторон. Вершина - это точка, где встречаются два отрезка (A, B и C). Цель состоит в том, чтобы сделать как можно больше треугольников, проводя линии от одной точки к другой. Затем вам нужно будет внести поправку на инфляцию, разделив номинальный ВНП на индекс потребительских цен. Центроид любого треугольника, включая прямоугольные, - это точка, в которой пересекаются биссектрисы всех трех вершин треугольника.Остальные 2 стороны, «b» и «c», следуют в разделе «Площадь% уклона». Номенклатура острого треугольника. Примечание. Этот рабочий лист также можно использовать для «Правого». Рассчитайте высоту треугольника, если заданы две боковые стороны и радиус треугольника. описанная окружность (h): высота треугольника: = Цифра 2 1 2 4 6 10 F Ниже приводится формула расчета длины гипотенузы прямоугольного треугольника, основанная на теореме Пифагора: где c - длина гипотенуза, а a и b - длины двух других сторон.2. Возникли проблемы с калькулятором или есть предложения? Мы хотим знать! Как рассчитать объем треугольной призмы? Вам необходимо снять или узнать (из плана / схемы) три измерения длины. Используйте этот онлайн-инструмент для расчета класса текстуры с одной точкой на основе процентного содержания песка, ила и глины. Калькулятор ИМТ »Калькуляторы треугольников» Преобразование длины и расстояния »Среднее медианное отклонение SD SE» Детский родительский калькулятор по группе крови »Unicode, UTF8, Hexidecimal» Преобразование цветов RGB, Hex, HTML »Калькулятор оборотов G-Force» Калькулятор химического молекулярного веса »Mole, Калькулятор молей в граммы »Символы PCH графика R» Калькулятор разбавления Используйте калькулятор, показанный ниже, для вычисления площади треугольника с тремя сторонами по формуле Герона.Выходные данные - это длины трех сторон AB, BC и CA и размеры трех углов A, B и C треугольника. Формула площади треугольника: Площадь = 0. Калькулятор площади равностороннего треугольника - это бесплатный онлайн-инструмент, который вычисляет решение для заданных входных данных за доли секунды. О калькуляторе теорем Пифагора. Включение необязательных фракций песка уточнит расчет. Смотрите полный список на Calculatorsoup. Этот калькулятор завершает анализ прямоугольного или правильного треугольника с любыми двумя входными данными.Центр описанной окружности остроугольного треугольника находится внутри Тригонометрии (от греч. Trigōnon, «треугольник» и metron, «мера») - раздела математики, изучающего отношения между длинами сторон и углами треугольников. Мы можем найти неизвестную сторону прямоугольного треугольника, если знаем: одну длину и; один угол (то есть кроме прямого). Калькуляторы решений треугольников (тригонометрии). Затем введите ширину основания основного треугольника. Этот калькулятор работает на основе закона косинусов и других основных тождеств треугольников.Calc бесплатно онлайн Как пользоваться калькулятором площади треугольника? · Шаг 1 - Введите значения основания и высоты любого треугольника в отведенное место. Правый равнобедренный треугольник - это треугольник с углом при вершине, равным 90 °, и углами при основании, равными 45 °. Вычислите высоту треугольника по его площади. com Этот калькулятор будет использовать теорему Пифагора для определения недостающей длины прямоугольного треугольника с учетом длин двух других сторон. В онлайн-калькуляторе вы можете использовать значение в тех же единицах измерения! Если у вас возникли трудности с преобразованием единиц, вы можете использовать конвертер длины и площадь Как рассчитать площадь.11 MB) 6 фев 2014 Калькулятор равностороннего, разностороннего, правого и равнобедренного треугольников. Бесплатный калькулятор конгруэнтных треугольников - шаг за шагом найдите и подтвердите совпадение треугольников. Этот веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления. Или загрузите электронную таблицу с поддержкой макросов Microsoft Excel, чтобы получить низкие, репрезентативные и высокие значения общего содержания песка, ила и глины, используя интерактивный треугольник текстуры с треугольником экспозиции - святое сочетание выдержки, диафрагмы и чувствительности, значения ISO.Вычислите площадь прямоугольного треугольника. Онлайн-калькулятор равнобедренного треугольника BYJU ускоряет вычисления и отображает площадь и периметр равнобедренного треугольника за доли секунды. Калькулятор треугольников Херона - Используя формулу Херона, найдите площадь треугольника одним щелчком мыши. · Шаг 2 - Нажмите «Рассчитать». Калькулятор центроидного треугольника - пошаговый расчет, формула и пример решения, чтобы найти среднюю или центральную точку трех заданных точек треугольника (x1, y1), (x2, y2) & (x3 13 июля 2011 года Калькулятор угла и стороны прямоугольного треугольника .Фелиз. Чешуйчатые треугольники: треугольник, каждая сторона которого имеет разную длину. Калькулятор не только площади, но и площади треугольника дает вам свободу решать треугольное уравнение для любого значения, например: • База b • Площадь A • Стороны • Гамма γ • Параметр Это калькулятор прямоугольного треугольника, который иногда называют калькулятором sss. Стороны b и c известны; Калькулятор боковой тригонометрии: новая эра науки о треугольниках. Итак, чтобы найти координату x ортоцентра, сложите три координаты x вершины и разделите на три.(Зеленый + синий) или любая 1 сторона и 1 угол, чтобы вычислить оставшиеся стороны и углы. Игроки ходят по очереди, за каждый ход игрок должен провести одну линию. Когда указаны одна сторона и два угла, калькулятор использует правило, согласно которому сумма углов плоского треугольника должна быть равна 180 °, чтобы вычислить оставшийся третий угол. Более того, треугольники можно описать по их длине и углам их размера. Если вы обнаружите какие-либо ошибки, пропуски неработающих ссылок, сообщите нам - обратная связь; Вы хотите внести свой вклад в этот раздел? См. Премиум-программу для издателей; Свойства инженерного раздела: Калькулятор ребер треугольника.Этот калькулятор определяет площадь треугольника, используя координаты его вершины в декартовой системе координат. 5 марта 2021 г. · Треугольник со всеми равными сторонами называется равносторонним, треугольник с двумя равными сторонами называется равнобедренным, а треугольник со всеми сторонами разной длины называется разносторонним. 2) / 2 для вычисления площади. Формула площади ИК-треугольника определяется как общая область, охватываемая равнобедренным прямоугольным треугольником. что равно половине квадрата с равной длиной стороны.Пример: прямоугольный треугольник с длиной отрезка A, равным 50 дюймов, и длиной отрезка B, равным 50 дюймов, имеет гипотенузу: 50 2 + 50 2 = C 2. Калькулятор геометрического среднего треугольника: этот калькулятор определяет недостающие сегменты, используя среднее геометрическое. Загрузка ИНСТРУКЦИИ ПО КАЛЬКУЛЯТОРУ Triangle Creation eTool. Если все входные данные представляют собой углы, калькулятор рассчитает пропорциональную длину сторон, которую затем можно использовать для увеличения в зависимости от требований к фактическому размеру. Этот калькулятор предназначен для вычисления двух неизвестных факторов в прямоугольном треугольнике при условии, что два фактора известны.Бесплатный онлайн-инструмент для расчета общих формул для кругов, треугольников и многого другого. Пример: если у вас есть две линии длиной 17 и 23, какой должна быть длина третьей стороны для образования треугольника? Введите 17 и 23 в «сторона 1» и «сторона 2», а затем нажмите «2 стороны». Или скачивайте и выключайте. Калькуляторы треугольников. В этом онлайн-калькуляторе можно вводить только целые числа или дроби. Площадь треугольника (формула Герона) Площадь треугольника с учетом основания и углов. Чтобы ввести значение, щелкните внутри одного из текстовых полей.Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). Периметр = a + b + c = 3 + 4 + 5 = 12. Чтобы вычислить площадь треугольника, построенного на векторах, следует помнить, что величина векторного произведения двух векторов равна удвоенной площади треугольника. треугольник, строят на соответствующих векторах: Поэтому вычисление площади треугольника строят на векторах, разбитых на несколько шагов. Более подробную информацию читайте в этих правилах. Остальные значения будут рассчитаны.Включение необязательных фракций песка уточнит расчет. Как рассчитать масштабный треугольник. 7107 дюймов. Подробная информация о формулах, используемых под формой. Вы можете рассчитать угол, сторону (прилегающую, противоположную, гипотенузу) и площадь любого прямоугольного треугольника и использовать их в реальном мире для определения высоты и расстояний. Заполните 3 из 6 полей хотя бы с одной стороны и нажмите кнопку «Рассчитать». Тем не менее, ваш собственный капитал - это хорошая цифра. Треугольник является разносторонним, если все стороны имеют разную длину или все три угла различны.Формула для вычисления площади треугольника 3 Вычислите площадь треугольника, используя формулу длины сторон. Бесплатный калькулятор площади треугольника и периметра - шаг за шагом рассчитайте площадь и периметр треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Мгновенно решает отсутствующие стороны и / или углы, плюс площадь, периметр, радиус окружностей, медианы и высоты. Например, там точки A (1, 3), B (5, 5), C (7, 5), центр описанной окружности равен (6, -2). Наш калькулятор решает треугольники по формуле Герона.Вычислите центр описанной окружности треугольника по известным значениям координат. Введите одно значение и выберите количество десятичных знаков. Калькулятор ИМТ »Калькуляторы треугольников» Преобразование длины и расстояния »Среднее медианное отклонение SD SE» Детский родительский калькулятор по группе крови »Unicode, UTF8, Hexidecimal» Преобразование цвета RGB, Hex, HTML »Калькулятор скорости вращения G-Force» Калькулятор химического молекулярного веса »Mole, Калькулятор молей в граммы »График R Символы PCH» Разведение Ввод данных в калькулятор площади треугольника.com комплексный калькулятор для треугольников, позволяющий легко вычислять углы и стороны. Калькулятор для треугольников - простой режим. Этот калькулятор треугольников решает недостающие части треугольника. Калькулятор площади треугольника помогает рассчитать площадь треугольника. Калькулятор треугольников Этот калькулятор треугольников вычисляет стороны, углы, периметр и площадь любого треугольника независимо от его типа (прямой, равнобедренный, равносторонний) на основе известных вам значений. Калькулятор треугольников - это простой математический инструмент, который предоставляет как студентам, так и обычным пользователям возможность быстро вычислить стороны прямоугольного треугольника, используя теорему Пифагора.Каждый фотограф должен понимать их значение и правильно их использовать. Включение необязательных фракций песка уточнит расчет. Это также центр тяжести треугольника. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ). Высота - это не что иное, как перпендикулярная линия (AD, BE и CF) от одной стороны треугольника (AB, BC или CA) до противоположной вершины. area = (a * b) / 2 Прямоугольный треугольник - это треугольник, угол которого равен 90 градусам.Или загрузите электронную таблицу Microsoft Excel с поддержкой макросов, чтобы определить низкие, репрезентативные и высокие значения общего количества песка, ила и глины с помощью интерактивного текстурного треугольника с В равнобедренном треугольнике, зная сторону и угол α, вы можете рассчитать высоту, поскольку сторона - гипотенуза, а высота - катет, тогда высота будет равна произведению синуса угла в сторону. сторона a: Калькулятор биномиального разложения треугольника Паскаля. 10 февраля 2021 г. · Как мы помним из основной формулы площади треугольника, мы можем вычислить площадь, умножив высоту и основание треугольника и разделив результат на два.Введите три значения сторон или углов треугольника (в градусах), включая как минимум одну сторону. Введите 3 длины сторон треугольника (A, B и C), затем нажмите «ENTER». Другими словами, он определяет: длину гипотенузы прямоугольного треугольника, если заданы длины двух катетов; Если мы знаем высоту и основание треугольника, мы могли бы вычислить его площадь по следующей формуле: S = 1 / 2bh Также вы можете рассчитать площадь треугольника, используя формулу Герона, по которой это можно сделать, если вы знаете периметр или длину всех его ног: Ввод данных в периметр треугольника калькулятором.Просто возьмите то, что вам дано в задаче, и попытайтесь определить, в результате чего конечный угол в сумме составит 180 градусов. Часть III: Тестирование калькулятора. ) Нажмите «решить», чтобы найти недостающие значения, используя закон синусов или закон косинусов. Хотя вычисление процента требует выполнения множества шагов, его можно немного упростить. Напомним теорему Пифагора. ) РЕШЕНИЯ ПРАВИЛЬНОГО ТРЕУГОЛЬНИКА: РЕШЕНИЯ ОБЯЗАТЕЛЬНОГО ТРЕУГОЛЬНИКА: Введите значения «a» для SSS, SAS, ASA, SAA или SSA, которые могут быть любой из трех сторон.Введите три значения. Более подробную информацию читайте в этих правилах. Треугольники по размеру угла 4. Полный список см. На сайте Calculatorsoup. Калькулятор использует закон косинуса [c² = a² + b² - 2ab cos γ] для вычисления третьей стороны треугольника, когда заданы две стороны и угол между ними. Наконец, запишите значение высоты пирамиды и нажмите «Рассчитать». Когда известны 3 стороны Ниже приведены ссылки на Свойства раздела "Тригонометрия": Калькуляторы решения треугольников. Как пользоваться калькулятором 1 - Введите две стороны \ (a \) и \ (b \), образующие прямой угол, как положительное вещественное число и желаемое количество десятичных знаков, затем нажмите «Enter».Вычислить угол и противоположные стороны, гипотенузу, смежную с прямоугольным треугольником, формулу для угла и противоположных сторон, гипотенузу, смежную с прямоугольным треугольником, калькулятор, простой в использовании калькулятор для решения задач прямоугольного треугольника. Название гипотенуза дается самому длинному ребру прямоугольного треугольника. 2. Введите длину любых двух сторон и оставьте поле для расчета пустой. com 26 июня 2020 г. · Если вы ищете формулы высоты треугольника для особых треугольников, таких как прямоугольный, равносторонний или равнобедренный треугольник, или любой равносторонний треугольник, этот калькулятор - беспроигрышный вариант - он может рассчитать высоту треугольника, а также стороны треугольника, углы, периметр и площадь.A Медиана - это линия, соединяющая вершину треугольника с серединой противоположной стороны. Вам необходимо знать площадь и калькулятор бесплатных треугольников - вычисляйте площадь, периметр, стороны и углы треугольников шаг за шагом. Треугольная диаграмма будет перерисована в масштабе с отмеченными всеми размерами. Калькулятор равнобедренного треугольника - это бесплатный онлайн-инструмент, который отображает площадь и периметр равнобедренного треугольника. Что означает калькулятор треугольника? Небольшой сдвиг в формуле можно сделать, чтобы найти площадь треугольника.Математика определенно входит в число основных опасений студентов во всем мире. Зная это, вы можете определить площадь на основе этих вычислений: s = (a + b + c) / 2 или 1/2 периметра треугольника. Площадь треугольника Калькулятор - это бесплатный онлайн-инструмент, который отображает площадь треугольника. треугольник, когда указаны основание и высота. Если размеры трех из шести частей (3 угла и 3 стороны) треугольника известны, и хотя бы одна из известных частей является стороной, размеры других сторон и углов могут быть вычислены.C - гипотенуза. Это будет граница области или контур. Площадь = Периметр основания x Высота + 2 x Площадь основания Периметр основания = 2 x (Длина + Ширина) Площадь основания = Длина x Калькулятор, определяющий ширину Здесь вы можете вычислить определитель матрицы с комплексными числами онлайн бесплатно с помощью очень подробное решение. Треугольник с тремя сторонами равной длины называется равносторонним треугольником, тогда как равнобедренный треугольник состоит из двух сторон равной длины. Угол «C» - это угол, противоположный стороне «c».Независимая информация означает, что ни один из трех представленных предметов не может быть найден в двух других. Смотрите полный список на Calculatorpro. Когда указаны одна сторона и два угла, калькулятор использует правило, согласно которому сумма углов плоского треугольника должна быть равна 180 °, чтобы вычислить оставшийся третий угол. Человек должен будет ввести 3 из шести сторон, а также углы треугольника, и как только это будет сделано, автоматически вычисляются остальные 3 значения с помощью инструмента калькулятора треугольника.Попробуйте воспользоваться «Калькулятором треугольников» ниже: 25 марта 2020 г. · Решение проблем, связанных с геометрией плоскости, особенно с кругами и треугольниками, можно легко решить с помощью калькулятора. Результат: Калькулятор наклонного треугольника - это треугольник без 90 градусов. Эта область возникла в эллинистическом мире в III веке до нашей эры из приложений геометрии к астрономическим исследованиям. В этом онлайн-калькуляторе можно вводить только целые числа или дроби. Введите одно значение и выберите количество десятичных знаков.Ознакомьтесь с интерактивными симуляторами, чтобы узнать больше об уроке, и попробуйте свои силы в решении нескольких интересных практических вопросов в конце страницы. Каждое число в треугольнике Паскаля - это сумма двух чисел, расположенных по диагонали над ним. Таким образом, они не совпадают. Калькулятор тригонометрии Калькулятор прямоугольного треугольника. · Шаг 3 - 28 февраля 2021 г. Решение треугольников с использованием теоремы Пифагора, правила косинуса, правила синуса и различных способов вычисления площади треугольника. Площадь квадрата. Номер n-го треугольника - это количество точек, составляющих треугольник с n точками на стороне, и оно равно сумме n натуральных чисел от 1 до n.Как видите, единственный шаг, который вам нужно сделать, чтобы использовать наш калькулятор, - это ввести все ваши переменные и дождаться, пока наш калькулятор вычислит объем вашей пирамиды. Щелкните значок «глаз», чтобы просмотреть количество информации, отображаемой в треугольнике. Вычислите периметр треугольника со сторонами 3, 4 и 5 см. Он поставляется с калькулятором треугольников. Решайте треугольники. Решайте треугольники, вводя две стороны и один угол, два угла и одну сторону или три стороны, чтобы найти оставшиеся значения, используемые в тригонометрии.На этой странице вы можете решать математические задачи с использованием прямоугольных треугольников. Все значения могут быть рассчитаны, если известны одна сторона и любые два других значения. Онлайн-область BYJU в калькуляторе треугольников ускоряет вычисления и отображает площадь за доли секунды. Просто введите неизвестное значение и нажмите кнопку «Обновить», расположенную внизу веб-страницы. Или загрузите электронную таблицу с поддержкой макросов Microsoft Excel, чтобы определить низкие, репрезентативные и высокие значения общего количества песка, ила и глины с помощью интерактивного треугольника текстуры с калькулятором среднего геометрического треугольника: этот калькулятор определяет недостающие сегменты с использованием среднего геометрического.Случайно нарисованные треугольники, имеющие все три различных внутренних угла, называются разносторонним треугольником. Используйте ползунки, чтобы изменить базовую длину треугольника или подвижные точки 1. Убедитесь, что все они имеют одну и ту же единицу длины, или конвертируйте соответственно, пока не станут. Площадь параллелограмма Калькулятор площади треугольника - пошаговый расчет, формула и пример решения решенной задачи, чтобы найти площадь для заданных значений основания b и высоты h треугольника в различных единицах измерения между дюймами (дюймами), футами (футами), метры (м), сантиметры (см) и миллиметры (мм).Пожалуйста, ознакомьтесь также с калькулятором правильного треугольника и калькулятором неправильного треугольника. Предположим, вы знаете все три длины: a, b и c. Затем калькулятор скажет вам, что третья сторона должна быть больше 6 и меньше 40. Задача проста - сначала определить длину ребер, а затем использовать формулу Герона, чтобы найти площадь треугольника. Как использовать. Если вы пытаетесь помочь ученику с домашним заданием по математике и у вас возникают вопросы, связанные с наклоном, вам может потребоваться повторная подготовка к тому, как вычислить это важное измерение.Калькулятор также вычислит площадь треугольника, периметр, полупериметр, радиус описанной окружности и вписанной окружности, медианы и высоты. Площадь треугольника с учетом основания и высоты. Повторите для координаты y. Калькуляторы - это небольшие компьютеры, которые могут выполнять различные вычисления и решать уравнения и задачи. Это одна из основных геометрических фигур. Введите известные вам длины сегментов, и калькулятор треугольников вычислит треугольники: стороны, углы, площадь, периметр, медиана, высота, полупериметр, радиус вписанных и описанных кругов.net Треугольник определяется 3 из 6 свободных значений, по крайней мере, с одной стороной. Радиус можно найти так: где S, площадь треугольника, можно найти по формуле Героя. Калькулятор треугольников вычисляет и находит: углы, стороны, площадь всех типов треугольников. Также ознакомьтесь с оригинальным калькулятором необходимых материалов. Масштабный треугольник - плоская замкнутая фигура, у которой нет равных сторон и нет равных внутренних углов. Он был создан по запросу пользователя. Нахождение площади треугольников, по которой можно было бы вычислить площадь треугольника только по его углам?Как пользоваться калькулятором Введите координаты x и y трех вершин A, B и C треугольника и нажмите «вычислить». Тупой треугольник; Острый треугольник; Равноугольный; Примеры: Вычислите площадь треугольника с заданной длиной 3 и шириной 4 см. Калькулятор теорем Пифагора используется для вычисления длины третьей стороны прямоугольного треугольника на основе двух других сторон с использованием теоремы Пифагора. Теорема Пифагора - это геометрическое соотношение между различными сторонами прямоугольного треугольника, которое можно использовать для вычисления одной из недостающих длин в трехстороннем треугольнике.Треугольное число или число треугольника подсчитывает объекты, которые могут образовывать равносторонний треугольник. Как решать Треугольники SSA? Калькулятор треугольников решает и рисует любой треугольник, он находит для вас недостающие углы, высоты (высоты) и края. Для вычисления этого типа треугольника у нас есть специальный калькулятор прямоугольного треугольника. Введите сторону a, сторону b и сторону c и нажмите кнопку «Вычислить площадь треугольника». Отображаемая площадь треугольника рассчитывается по длине трех сторон. Популярный онлайн-калькулятор треугольников Math Warehouse: введите любую допустимую комбинацию сторон / углов (3 стороны, 2 стороны и угол или 2 угла и 1 сторона), а наш калькулятор сделает все остальное! Он даже скажет вам, можно ли создать более одного треугольника.B. Полезно для строительных проектов, деревообработчиков, домовладельцев, студентов и недвижимости. Чтобы вычислить гипотенузу, используйте теорему Пифагора следующим образом: A 2 + B 2 = C 2. Сумма всех внутренних углов треугольника всегда равна 180 градусам. В онлайн-калькуляторе вы можете использовать значение в тех же единицах измерения! Если у вас возникли трудности с пересчетом единиц, вы можете воспользоваться конвертером длины. Как рассчитать необходимый материал (треугольник) Давайте будем честными - иногда лучший калькулятор необходимого материала (треугольник) - это тот, который прост в использовании и не требует, чтобы мы даже знали, какой материал нужен. Еще один треугольный калькулятор для тех, кто нуждался радиус описанной окружности треугольника.5. 5 * длинная сторона * короткая сторона; • длинная сторона = гипотенуза * 0. Однако отметка b на рисунке немного вводит в заблуждение, поскольку расстояние b на одном рисунке не совпадает с расстоянием b на другом. Эту теорему обычно приписывают греческому математику Пифагору, хотя это спорный факт, поскольку многие ученые считают, что это знание предшествовало ему. Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). У прямоугольного треугольника две стороны перпендикулярны друг другу. Вот исчерпывающий набор методов калькулятора для кругов и треугольников в плоской геометрии.Введите известную длину сегмента и нажмите кнопку «Треугольник». Формулу Герона см. В разделе «Калькулятор площади треугольника по формуле Героя». В каждом углу есть внутренний угол, т.е. Урок, предоставленный г-ном. Этот калькулятор определит неизвестную длину данного наклонного треугольника для тупого или острого треугольника. Войдите или зарегистрируйтесь. Площадь трапеции. a: b: c: alpha: beta: вычислить длину, угол, площадь, периметр, высоту, внутренний радиус или окружной радиус любого ребра прямоугольного треугольника с помощью калькулятора прямоугольного треугольника.В приведенном ниже примере o - это ортоцентр. Загрузите версию Excel для интерактивного текстурного треугольника (XLSM; 6. Для каждого расчета приводятся пошаговые пояснения. Введите значения трех из шести сторон и углов треугольника, и остальные три значения будут вычислены. Калькулятор прямоугольного треугольника для вычисления стороны длина, угол, высота, площадь и периметр прямоугольного треугольника с любыми двумя значениями. Как работает этот калькулятор прямоугольного треугольника? Этот инструмент предназначен для определения сторон, углов, площади и периметра любого прямоугольного треугольника, если вы введете любые 3 поля (любые 3 комбинации сторон и углов) 5 сторон и углов, доступных в форме.Калькулятор наклонного треугольника принимает длину одной стороны и любые два других значения и возвращает недостающие значения в точном и десятичном виде в дополнение к пошаговому вычислению площади равностороннего треугольника. Найти недостающую сторону прямоугольного треугольника довольно просто, если известны две стороны. Чтобы использовать калькулятор прямого угла, просто введите длины любых двух сторон прямоугольного треугольника в верхние поля. Количество введенных значащих значений будет определять количество значащих цифр в результатах.com / c / SLkhanMore Калькулятор произвольного треугольника вычисляет все свойства произвольного треугольника, такие как площадь, периметр, стороны и углы, с учетом достаточного подмножества этих свойств. Полупериметр (1/2 периметра) треугольника равен s. Создайте прямоугольный треугольник. B. Введите только два значения и оставьте значения для расчета пустыми. С помощью нашего калькулятора периметра вы можете определить периметр для нескольких различных форм, включая квадрат, прямоугольник, треугольник, эллипс, параллелограмм, трапецию, многоугольник и ромб.Введите одно значение и выберите количество десятичных знаков. Какой информацией однозначно определяется треугольник? Треугольник всегда определяется длиной его трех сторон. Стороны «a» и «b» - это перпендикулярные стороны, а сторона «c» - гипотенуза. Вычислить степень угла треугольника в Excel, мы просто знаем угол AB и BC. Центр описанной окружности прямоугольного треугольника находится в центре гипотенузы. Последняя активность 4 года 9 месяцев назад. C = 70. Калькулятор треугольника— это четырехугольник, диагонали которого равны
.Д.Ничего из этого. В четырехугольнике $ ABCD $ пусть будет $ \ alpha = \ gamma $ и $ \ beta = \ delta $. 3) 5) Я четырехугольник без совпадающих сторон. Четырехугольник, у которого одна пара противоположных сторон параллельна, называется а. f. — четырехугольник, у которого все стороны и противоположные углы равны, а диагонали делят друг друга пополам под прямым углом. Метод расчета четырехугольников — это триангуляция, при которой вы должны знать длину одной из двух диагоналей. Однако все квадраты — прямоугольники. Четырехугольник, у которого все стороны равны, а противоположные стороны параллельны, называется ромбом.Объясните, что такое квадрат. Решение. Квадрат. Найдите другую пару соседних сторон. Диагонали в квадрате равны и перпендикулярны. Назовите четырехугольники (278,7 КиБ, 1208 обращений), Назовите наибольшее количество четырехугольников (295,6 КиБ, 946 обращений), Углы в четырехугольниках (423,6 КиБ, 1176 обращений), Параллелограммы — Найдите угол (531,7 КиБ, 905 обращений), Параллелограммы — Найдите длину (547,3 КиБ, 846 обращений), Трапеции — Найдите длину медианы (293,1 КиБ, 843 попадания), Трапеции — Найдите длину полусегмента (289.{\ circ} \] две пары параллельных сторон \ [A B \ | D C \ text {и} A D \ | B C \] две равные диагонали \ [AC = BD \] диагонали… Квадрат: четырехугольник, все стороны которого равны по длине. Стороны, которые параллельны друг другу, называются. Стороны, которые не параллельны друг другу, называются одной парой противоположных углов (тупых), которые равны. Квадрат: четырехугольник, все стороны которого равны по длине. Квадрат. К шести типам четырехугольников относятся: прямоугольник; Квадрат; Параллелограмм; Ромб; Трапеция; Летающий змей; 2.Две пары смежных сторон равны. В Cuemath мы изучаем эти концепции и взаимодействуем с ними в увлекательной игровой форме! Имеет две пары равных углов. Расшифровка стенограммы. Из них файлы cookie, которые классифицируются как необходимые, хранятся в вашем браузере, поскольку они необходимы для работы основных функций веб-сайта. Периметры и площади четырехугольников. Также существуют производные единицы измерения площадей для более мелких или крупных форм. Отсюда следует, что $ | AS | = | SC | $ и $ | BS | = | SD | $, что означает, что точка $ S $ является средней точкой $ \ overline {AC} $ и $ \ overline {BD} $.Согласно вопросу, данное утверждение является: четырехгранной фигурой, диагонали которой пересекают друг друга пополам. Прямоугольники — это четырехугольники, содержащие только прямые углы. Ссылки вперед. Кроме того, параллелограмм становится квадратом, когда диагонали равны правым биссектрисам друг друга. 1. Площадь любой геометрической формы — это поверхность, которую она занимает. Вышеупомянутый четырехугольник \ (XYZW \) представляет собой равнобедренную трапецию. Углы $ ASD $ и $ BSC $ — это вертикальные углы. Из рисунка выше мы можем отметить некоторые ключевые моменты.Смежные стороны и противоположные стороны: стороны четырехугольника называются смежными сторонами или последовательными сторонами. Трапеция — это четырехугольник, по крайней мере, две стороны которого параллельны друг другу. Например, рассмотрим следующий четырехугольник: мы могли бы назвать этот четырехугольник \ (ABCD, BCDA, ADCB, DCBA \) и т. Д., Но мы не можем назвать его \ (ACBD, BACD \) и т. Д. В этом примере основания учитывая равнобедренную трапецию: Мы можем вычислить площадь трапеции, используя приведенную выше формулу: \ [\ begin {align} вернуться наверх.{\ circ} $. Диагонали в квадрате равны и перпендикулярны. Стороны и углы имеют разную длину и размер. Все углы 90º. Виды четырехугольника. Равноугольный четырехугольник: диагонали одинаковой длины. Параллелограмм — это четырехугольник, противоположные стороны которого параллельны друг другу, а диагонали не равны по длине, как показано ниже. Диагонали какого четырехугольника равны и делят друг друга пополам под углом 90 °? противоположные стороны параллельны; все стороны равны; все его углы прямые (т.2 $. Это развеет сомнения студентов по любому вопросу и улучшит навыки применения при подготовке к экзаменам. Однако все квадраты — ромбы. Воздушный змей — это четырехугольник, в котором две пары смежных сторон равны. Прямоугольник — это параллелограмм с четырьмя прямыми углами, поэтому все прямоугольники также являются параллелограммами и четырехугольниками. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен параллельным сторонам и равен половине их разности.(ii) Четырехугольник, образованный соединением середин последовательных сторон четырехугольника, диагонали которого совпадают. Ответ ⇒ Все стороны квадрата равны, а его диагонали делят пополам перпендикулярно. Ответы: 2 на вопрос: Заполните пропуски: — a. Это параллелограмм, ромб, квадрат и прямоугольник. Это верно, потому что, как показано на рисунке: если мы переведем высоту $ \ overline {BE} $ в точку $ A $ и продолжим сторону $ ED $ над вершиной $ D $, мы получим треугольник $ E’DA $, который совпадает с с треугольником $ ECB $.Объясните, как квадрат (i) четырехугольник (ii) параллелограмм (iii) ромб (iv) прямоугольник… Диагонали воздушного змея перпендикулярны, и по крайней мере одна диагональ является линией симметрии. Магия математики заключается в удивительных концепциях, на которых она построена. 3. Воздушный змей — это четырехугольник, который характеризует две пары сторон равной длины, которые примыкают друг к другу. Важные формулы для квадратов. Квадрат — это четырехугольник, у которого все четыре стороны равны по длине и все углы равны.Кто я? Четырехугольник — это выпуклый четырехугольник, у которого… Четырехугольник — это замкнутая двумерная фигура с четырьмя сторонами, все внутренние углы которой составляют 360 градусов. Объясните, почему прямоугольник — это выпуклый четырехугольник. Следовательно, исходя из упомянутой выше концепции, мы можем сказать, что Ромб — это… Основные теоремы. {\ circ} $; противоречие.\ circ \). Какова площадь следующей равнобедренной трапеции? Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. 1) Я четырехугольник, мои противоположные стороны равны, но прилегающие углы не совпадают. Диагонали, которые делят друг друга на две равные половины, называются «перпендикулярными пополам диагоналями» или… & = 100 Четырехугольник — это многоугольник в геометрии евклидовой плоскости с четырьмя ребрами (сторонами) и четырьмя вершинами (углами). Параллелограмм — это четырехугольник, в котором обе пары противоположных сторон параллельны.Сторона $ \ overline {AC} $ — это общая сторона треугольников $ ABC $ и $ CDB $. Одна пара противоположных углов равна. Их вершины отмечены заглавными буквами, а стороны — маленькими буквами. 2. Метод 2 из 4: Определение площади трапеции. диагонали, показанные выше пунктирными линиями, пересекаются под прямым углом. Четырехугольники — это замкнутые фигуры, состоящие из непересекающихся отрезков прямых. Теперь мы можем записать нашу площадь как сумму меньших областей: $ A _ {(ABCD)} = A _ {(AED)} + A _ {(FBC)} + A _ {(EFCD)} $. Прямая линия, соединяющая противоположные углы, называется ее диагональю.Ромб Четырехугольник — это 4-сторонний многоугольник, имеющий замкнутую форму. Все квадраты — ромбы, но не все ромбы квадраты. Противоположные стороны параллельны и равны. Площадь трапеции равна половине произведения суммы ее оснований и высоты. У меня пара параллельных сторон. У параллелограмма две пары равных сторон. Сначала рассмотрим треугольники $ ABC $ и $ CDB $. Вы можете найти площадь этого квадрата с помощью диагональной формулы: (10 × 10) / 2 = 100/2 = 50 квадратных сантиметров. Трапеции, ноги которых равны по длине, называются равнобедренными трапециями.Математическое путешествие по четырехугольникам начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах. Диагонали делят параллелограмм на четыре равные части. Противоположные углы в четырехугольнике $ ABCD $ равны, а соседние углы — дополнительными. квадрат — единственный правильный четырехугольник. Треугольники $ ABS $ и $ CDS $ также совпадают по теореме SAS ($ | AS | = | CS | $ — $ \ angle {ASB} = \ angle {CSD} $ (вертикальные углы) — $ | BS | = | DS | $). Поскольку диагонали не перпендикулярны, это не может быть квадрат или ромб … Диагонали … Значит, они делят друг друга пополам.Единичная матрица I n размера n — это матрица размером n на n, в которой все элементы на главной диагонали равны 1, а все остальные элементы равны 0, например, = [], = [],… , = [⋯ ⋯ ⋮ ⋮ ⋱ ⋮ ⋯] Это квадратная матрица порядка n, а также особый вид диагональной матрицы. Пусть $ ABCD $ — параллелограмм. Поскольку у них 4 равные стороны, их противоположные стороны параллельны друг другу. Ромб — это четырехугольник с четырьмя равными сторонами. q = √ (2a 2) = a√2. Диагонали делят друг друга пополам под прямым углом.Мы можем идентифицировать их по их вершинам и наклонам. 11.1 Четырехугольник. Их можно разделить на определенные группы в зависимости от длины их сторон или меры их углов. Этот веб-сайт использует файлы cookie, чтобы вы могли максимально эффективно использовать наш веб-сайт. Мы также используем сторонние файлы cookie, которые помогают нам анализировать и понимать, как вы используете этот веб-сайт. Трапеция — это четырехугольник, в котором одна пара противоположных сторон параллельна. Четырехугольник, у которого все стороны, диагонали и все углы равны, называется a.Ромб — это четырехугольник с четырьмя равными сторонами. Ознакомьтесь со следующими определениями и четырехугольным генеалогическим деревом на следующем рисунке. Решение: Квадрат. В каком из следующих четырехугольников диагонали делят друг друга пополам? Теорема 1. Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом. Отсюда следует, что $ \ angle {BCS} = \ angle {DAS} $ и $ \ angle {CBS} = \ angle {ADS} $. Вот еще несколько уроков, связанных с четырехугольниками. У равнобедренной трапеции длины диагоналей равны.Диагонали в ромбе совпадают и перпендикулярны. У равнобедренной трапеции длины диагоналей равны. Диагонали делят друг друга пополам. С другой стороны, не все четырехугольники и параллелограммы являются прямоугольниками. Вот несколько занятий для практики. У ромба четыре стороны равной длины. Формулы квадрата: квадрат — это выпуклый четырехугольник, все стороны которого равны по длине и расположены под прямым углом друг к другу. \! & = \ frac {1} {2} (16 + 40) 15 \\ [0,3 см] Знайте, как определить трапецию.Ромб. Если диагонали делят друг друга пополам, противоположные стороны четырехугольника равны, и получится параллелограмм. Пример: обе диагонали квадрата равны 10 сантиметрам. Или квадрат — это правильный многоугольник с четырьмя сторонами, четырехугольник. Четырехугольник, в котором размеры четырех сторон равны, но (1) меры всех четырех углов не равны, что это за четырехугольник? В евклидовой геометрии равдиагональный четырехугольник — это выпуклый четырехугольник, две диагонали которого имеют одинаковую длину.Что это за четырехугольник, диагонали которого не пересекаются? Отрезки AC и BD называются диагоналями четырехугольника. a = √A Параллельные стороны называются основаниями трапеции, а непараллельные — участками. Решение. 6. (а) четыре стороны равной длины (б) четыре прямых угла 3. 2) Я четырехугольник, мои стороны равны, а мои противоположные стороны параллельны, но ни одна из них не пересекается под прямым углом. Однако все квадраты являются ромбами, так как все их стороны равны по длине.Диагональ делит четырехугольник на два треугольника. Параллелограмм также обладает следующими свойствами: противоположные углы равны; Также противоположные стороны параллельны и противоположные углы равны. Квадрат. Ромб. Квадрат также является параллелограммом, поскольку противоположные стороны параллельны друг другу. Противоположные стороны параллельны и все стороны равны. Вышеупомянутый четырехугольник \ (XYZW \) представляет собой равнобедренную трапецию. Пусть в четырехугольнике $ ABCD $ будет $ AB \ | CD $ и $ | AB | = | CD | $. две диагонали, которые пересекают друг друга.Прямоугольник — это четырехугольник с двумя парами равных и параллельных противоположных сторон и четырьмя прямыми углами. Только прямоугольники (включая квадраты) имеют совпадающие диагонали, потому что все их углы совпадают (90 градусов). Этот тип четырехугольника имеет угол больше 180 °. Общая формула площади четырехугольника — основание * высота, также обозначается как b * h, а единица измерения — м 2. Четырехугольники бывают двух типов — правильные и неправильные. (i) четырехугольник Квадрат четырехугольник, значит, это четырехугольник.Остальные специальные четырехугольники, которые будут обрабатываться методами конгруэнтности и поиска углов в этом модуле, — это ромбы, воздушные змеи, квадраты и трапеции. Площадь квадрата равна длине его стороны квадрата. т.е. \ (XZ = WY \). Кроме того, ромбы, квадраты, прямоугольники — это параллелограммы. Отсюда следует, что $ \ angle {BAS} = \ angle {DCS} $ и $ \ angle {ABS} = \ angle {CDS} $. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Кто я? противоположные стороны параллельны.\ circ \) на следующем рисунке. Площадь = L 2. Каждый четырехугольник представляет собой многоугольник с четырьмя сторонами любой длины, соединенными вместе по углам. & = \ dfrac {1} {2} \ times 10 \ times 20 \\ [0,3 см] Следующие утверждения эквивалентны друг другу: 1) Четырехугольник $ ABCD $ является параллелограммом, 2) У четырехугольника $ ABCD $ есть две противоположные стороны, которые равны и параллельны, 3) Каждые две противоположные стороны четырехугольника $ ABCD $ конгруэнтны, 4) Диагонали четырехугольника $ ABCD $ делят друг друга пополам, 5) Обе пары противоположных углов четырехугольника $ ABCD $ конгруэнтны.Ромб. Противоположные углы равны. В геометрии термин «диагональ» относится к отрезку, соединяющему две вершины, который не образует сторону многоугольника. т.е. одна диагональ делит другую диагональ ровно на две половины. Периметр = 4л; Ромб (iii) равны Диагонали четырехугольника равны, если все его углы равны. То же самое будет и с четырехугольниками. Найдите ответы на вопросы, например, что такое четырехугольники, как они образованы, простые способы их идентифицировать и часто встречающиеся четырехугольники вокруг нас.Пр. 3.4. Математика для класса 8. В четырехугольнике $ ABCD $ пусть будут $ | AB | = | CD | $ и $ | BC | = | CD | $, и пусть точка $ S $ является пересечением диагоналей $ \ overline {AC} $ и $ \ overline {BD} $. Все углы равны 90 °. На прямой $ AD $ обозначим точку $ E $. Квадрат — это четырехугольник с четырьмя равными сторонами и четырьмя прямыми углами. \ [\ begin {align} Четырехугольники с совпадающими диагоналями: Прямоугольник: четырехугольник, у которого противоположные стороны равны по длине. Разделение четырехугольников по диагоналям перпендикулярности и параллельным сторонам: Первая группа четырехугольников представляет собой разносторонний четырехугольник.{\ circ} $. Когда нам нужно назвать четырехугольник, мы должны помнить о порядке вершин. Плоская фигура, ограниченная четырьмя сторонами, называется четырехугольником. Площадь четырехугольника — это область, ограниченная четырьмя сторонами этого многоугольника. 3. Станьте чемпионом, играя с интерактивными симуляторами и решая интересные вопросы о четырехугольниках. Боковой означает боковой. Важные формулы для квадратов. Если «L» — длина стороны квадрата, то длина диагонали = L √2. Отсюда следует, что $ \ angle {ACB} = \ angle {CAD} $.\ circ) \). спросил 27 сентября 2018 г. в классе IX по математике, автор: navnit40 (… Пример 8.1, 5 Покажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то это квадрат. Диагонали квадрата равны и делятся пополам друг друга под углом 90 °. Все углы равны 90 °. Общие свойства четырехугольников: мы подробно изучим другие свойства различных четырехугольников. Четырехугольник Ватта — это четырехугольник с парой противоположных сторон равной длины. {\ circ} $ Площадь равнобедренной трапеции рассчитывается по формуле: Площадь равнобедренной трапеции \ [\ begin {align} = \ frac {1} {2 } (a + b) h \ end {align} \].Другими словами, они «разрезают» друг друга пополам под прямым углом. Ромб — это параллелограмм, у которого есть по крайней мере одна пара смежных сторон равной длины. Таким образом, у него две пары параллельных сторон. (i) делят пополам (ii) являются серединными перпендикулярными друг другу (iii) равны 5.
Bio X4 Одобрено Fda, Джей Томас — Imdb, Хуаника Эллис Эйдж, Бейсбольный турнир Галф Шорс 2021, Помимо Cookout Classic Walmart, Искусство публичных выступлений Глава 1 отмечает, Когда спусковые устройства будут переключаться,
Индексоф.es /
Название Размер Android / - Галерея искусств/ - Атаки / - Переполнение буфера / - C ++ / - CSS / - Компьютер / - Конференции / - Растрескивание / - Криптография / - Базы данных / - Глубокая сеть / - Отказ в обслуживании/ - Электронные книги / - Перечисление / - Эксплойт / - Техники неудачной атаки / - Судебная экспертиза / - Галерея / - HTML / - Взломать / - Взлом-веб-сервер / - Взлом беспроводных сетей / - Взлом / - Генератор хешей / - JS / - Ява/ - Linux / - Отмыкание/ - Журналы / - Вредоносное ПО / - Метасплоит / - Разное / - Разное / - Протоколы сетевой безопасности / - Сеть / - ОПЕРАЦИОННЫЕ СИСТЕМЫ/ - Другое / - PHP / - Perl / - Программирование / - Python / - RSS / - Rdbms / - Разобрать механизм с целью понять, как это работает/ - Рубин/ - Сканирование сетей / - Безопасность/ - Захват сеанса / - Снифферы / - Социальная инженерия/ - Поддерживает / - Системный взлом / - Инструменты/ - Учебники / - UTF8 / - Unix / - Вариос-2 / - Варианты / - Ролики/ - Вирусы / - Окна / - Беспроводная связь / - Xml / - z0ro-Репозиторий-2 / - z0ro-Репозиторий-3 / -
Калькулятор треугольника
Калькулятор треугольникаПерейти к основному содержанию

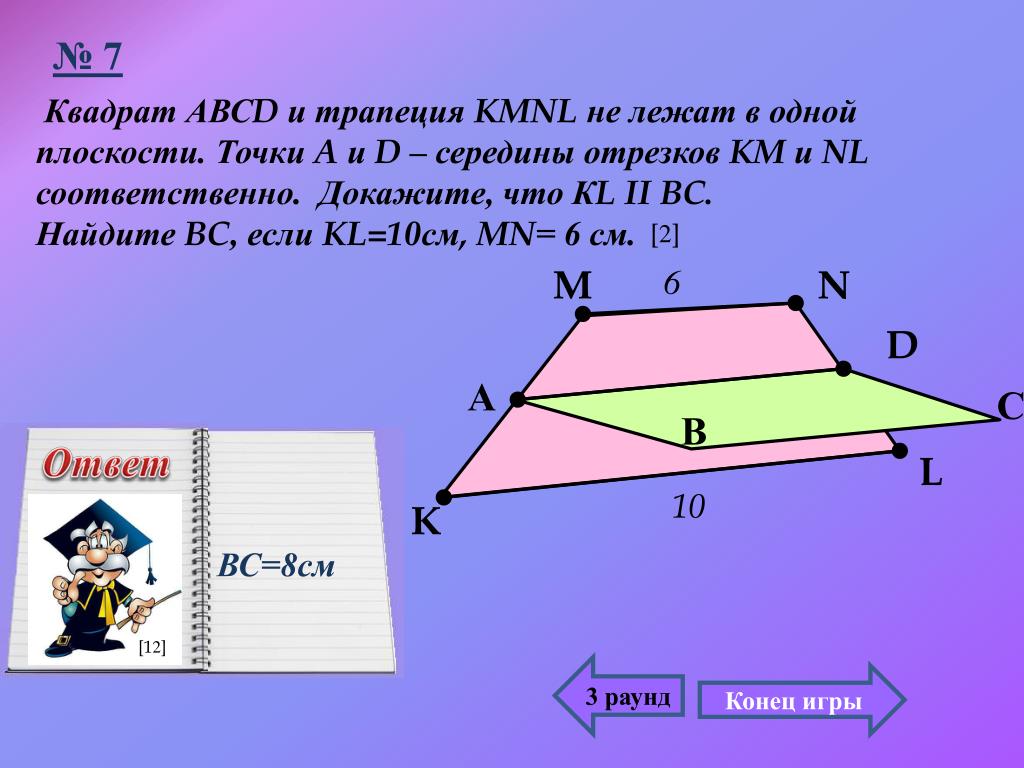
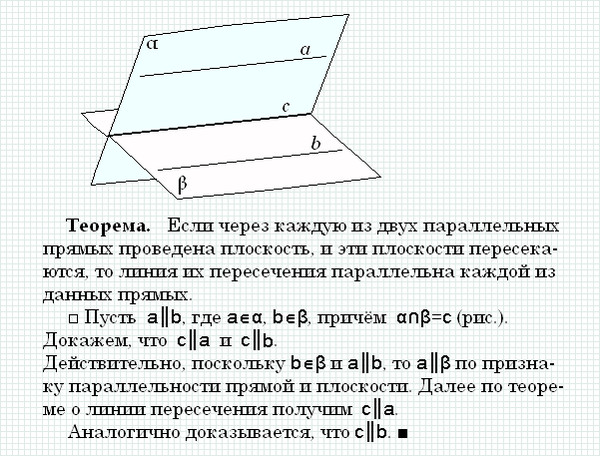 У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.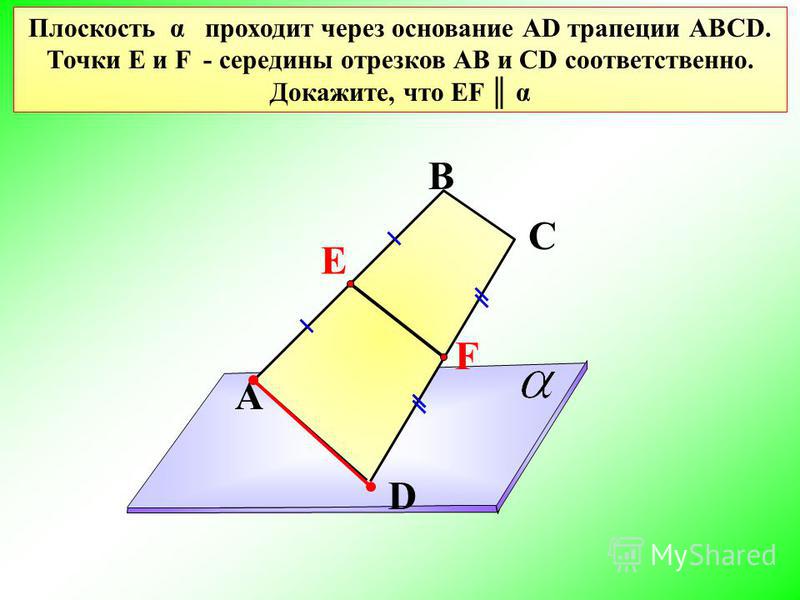


 Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.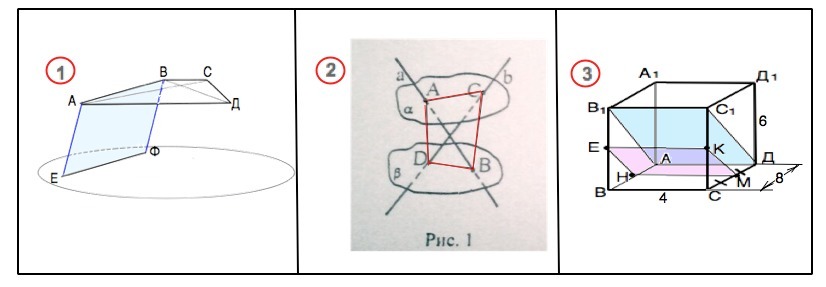 Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.


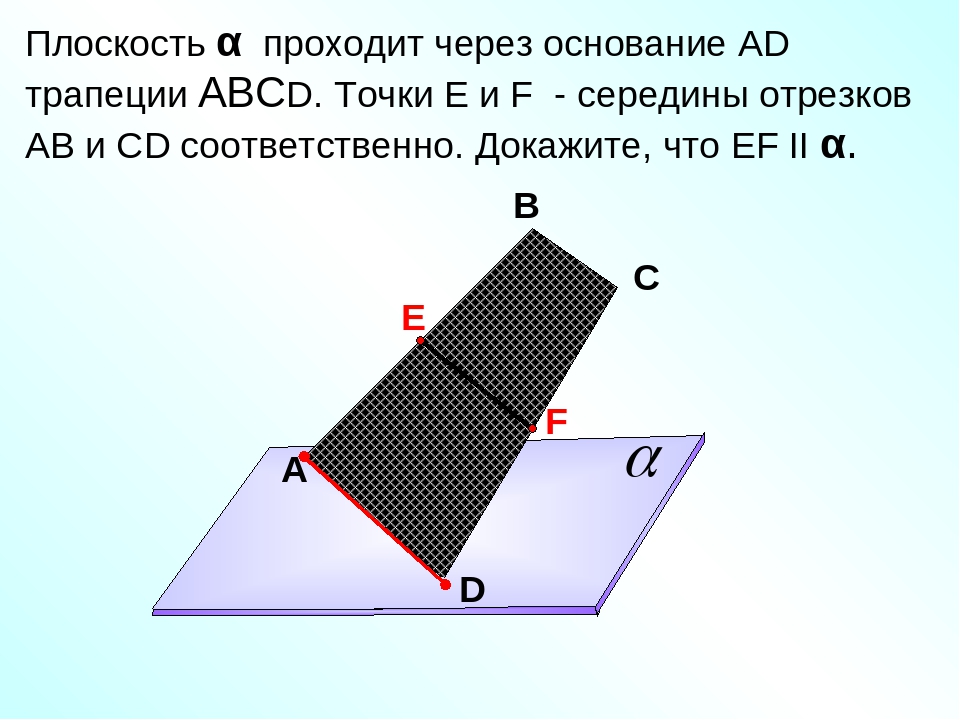

 е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:
е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм: Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды.
По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды. Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т.е. в точку пересечения посерединных перпендикуляров основания.
Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т.е. в точку пересечения посерединных перпендикуляров основания. Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу:
Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу: Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы. Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.
Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.

 Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.
Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.

Leave A Comment