Напряженность электрического поля — как найти? Правила и примеры

Покажем, как применять знание физики в жизни

Начать учиться

101.7K

Если потереть ручку о синтетический свитер — к ней начнут притягиваться кусочки бумаги, причем без прямого контакта. Все дело в электрическом поле, которое позволяет заряженным телам взаимодействовать на расстоянии. Этот материал о том, что такое напряженность электрического поля и каковы взгляды на нее в современной физике.

Что такое электрическое поле

Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

В современной физике электрическое поле — это некая материя, которая возникает вокруг заряженных тел и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.

Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q1 поместить еще один точечный заряд q2 (допустим, они оба будут положительными). Со стороны q1 на q2 будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление.

Напряженность электрического поля

— это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты.

Важно!

Иногда можно услышать оборот «напряжение электрического поля», но это ошибка — правильно говорить «напряженность».

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах,

единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть

принцип суперпозиции.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

  • расстояние между зарядами очень мало — порядка 10-15м;

  • речь идет о сверхсильных полях с напряженностью более 1020в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой.

Закон Кулона

Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.

Силу электрического поля в конкретной точке можно найти по формуле: где q1 и q2 — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

Важно!

Сила взаимодействия двух точечных зарядов остается прежней при появлении сколь угодно большого количества других зарядов в данном поле.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние

r, можно вычислить по формуле:

Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина.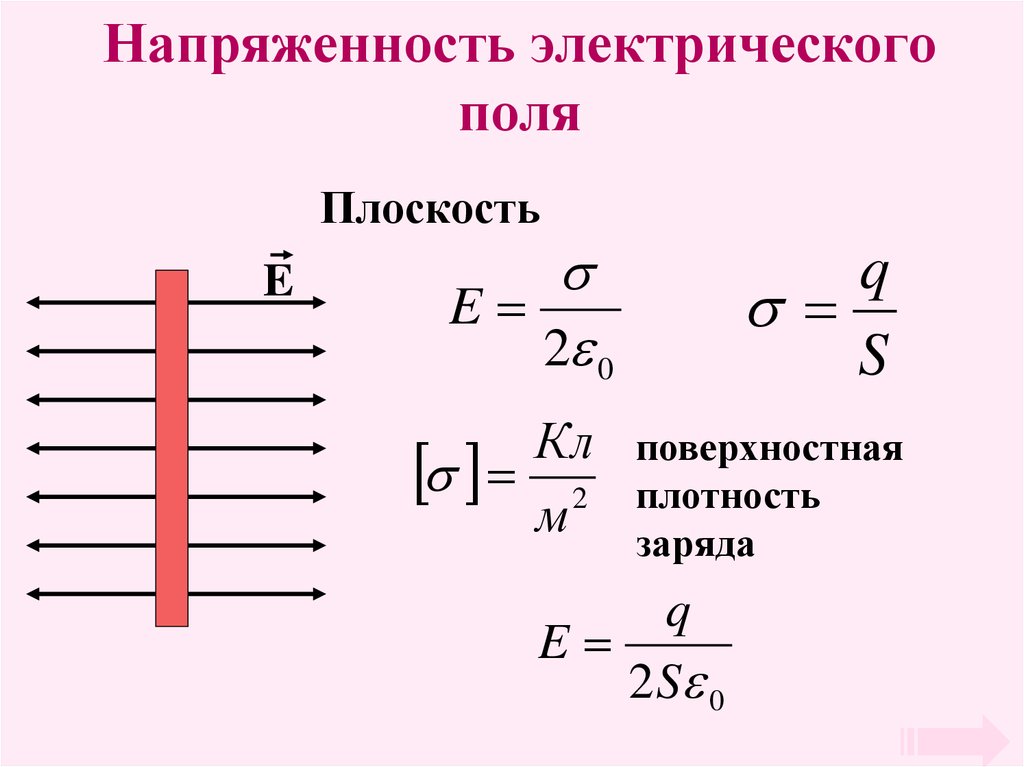 Теперь посмотрим, как она изображается графическим способом.

Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.

Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно).

В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Яна Кононенко

К предыдущей статье

Мощность

К следующей статье

Манометр

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

  1. Выявим пробелы в знаниях и дадим советы по обучению

  2. Расскажем, как проходят занятия

  3. Подберём курс

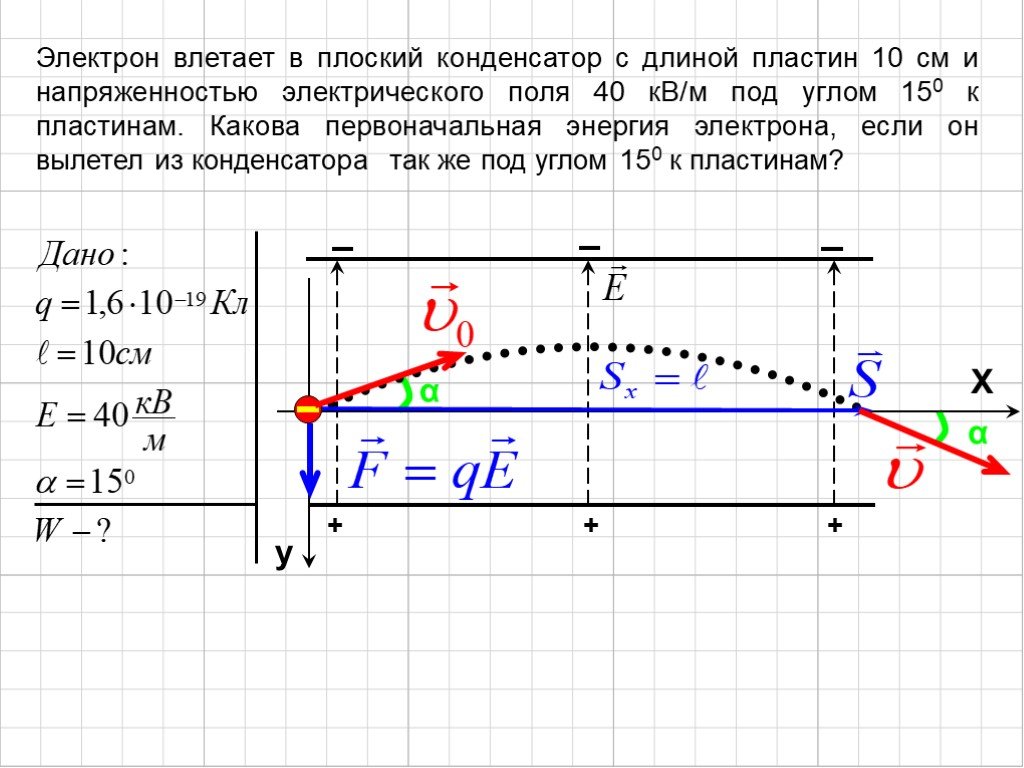
Глава 18.

Напряженность и потенциал электрического поля. Силовые линии электрического поля

Для характеристики создаваемого зарядами электрического поля вводятся две величины — напряженность электрического поля и его потенциал. Напряженность характеризует силу, действующую со стороны поля на внесенный в него пробный заряд. Если в какой-то точке поля на заряд действует сила , то напряженность электрического поля в этой точке равна

(18.1)

где — заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал. В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.

Найдем напряженность электрического поля, создаваемого точечным зарядом . Для этого возьмем произвольный пробный заряд и поместим его в точку, находящуюся на расстоянии от заряда . Сила, действующую на пробный заряд со стороны заряда , определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем

(18.2)

где . Направлен вектор напряженности от заряда , если , и к нему, если .

Пусть поле создается несколькими зарядами … В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила …, где … — силы, действующие на пробный заряд со стороны каждого заряда … Поэтому из (18.1) получаем

(18.3)

где . .. — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса , равномерно заряженной зарядом , в точке на расстоянии от центра сферы:

(18.4)

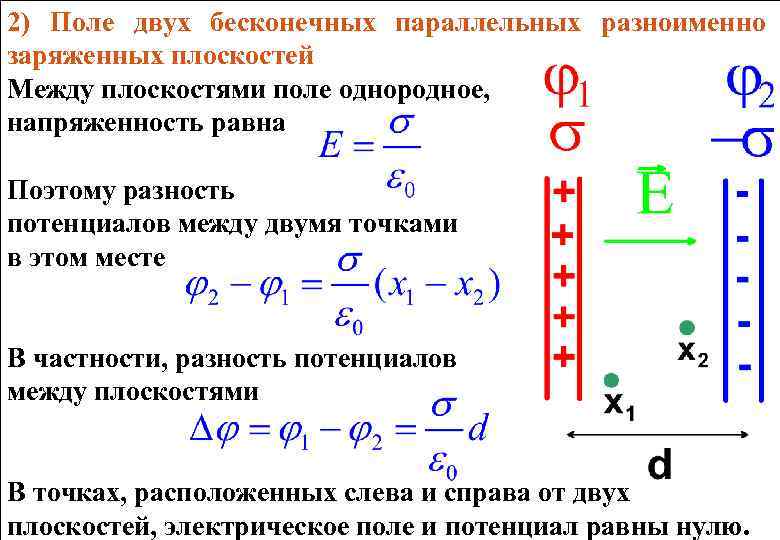
где , а из формулы (17.6) для напряженности поля равномерно заряженной плоскости

(18.5)

где — заряд плоскости, — площадь, — поверхностная плотность зарядов плоскости.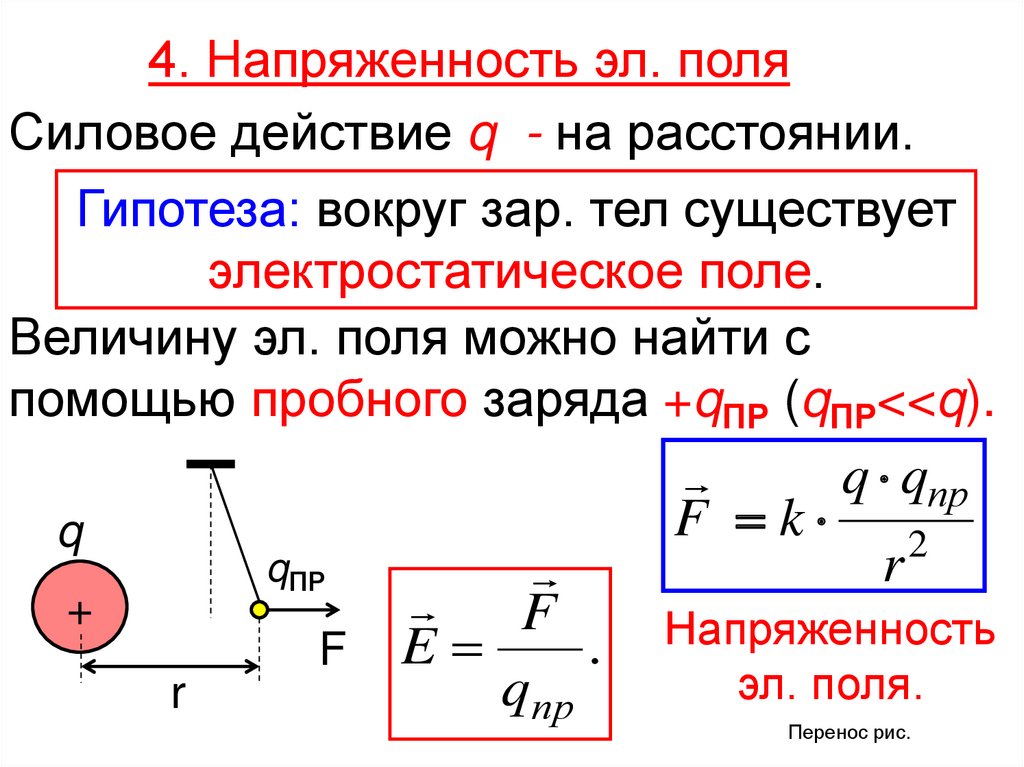

Электрическое поле можно изобразить графически (на современном русском языке — визуализировать) с помощью силовых линий. Силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке. Вообще говоря, силовые линии проходят через каждую точку поля (кроме тех точек, где ), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.

Второй характеристикой электрического поля является его потенциал. Основная идея введения этой величины заключается в следующем. Если электрический заряд перемещается в электрическом поле (созданном другими зарядами), то со стороны поля на него действуют силы, и, следовательно, поле совершает работу. Потенциал поля — это такая функция точки поля , что работа , совершаемая полем над точечным пробным зарядом при его перемещении из точки с радиусом-вектором в точку с радиусом-вектором , равна

(18. 6)

(именно в такой последовательности). Из формулы (18.6) следует, что работа, которую совершает поле при перемещении заряда, не зависит от формы траектории, а определяется только начальной и конечной ее точками. В частности, при перемещении тела по замкнутой траектории поле совершает нулевую работу.

Поскольку в формулу (18.6), входит разность потенциалов двух точек поля, потенциал определен с точностью до постоянной. Эту постоянную всегда можно выбрать так, что потенциал любой заданной точки поля можно сделать равным нулю. Как правило, в качестве такой точки выбирают бесконечно удаленную от зарядов точку поля, считая ее потенциал равным нулю. Из формулы (18.6) следует, что потенциал любой точки поля равен отношению работы, которую совершает электрическое поле при перемещении пробного заряда из этой точки в ту точку, потенциал которой выбран равным нулю, к пробному заряду.

Можно доказать, что если поле создается точечным зарядом , то потенциал на расстоянии от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен

(18. 7)

Важно отметить, что в формулу (18.7) входит заряд со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.

Для потенциалов справедлив принцип суперпозиции: если поле создается несколькими точечными зарядами, то потенциал любой его точке равен алгебраической сумме потенциалов (18.7), создаваемых в этой точке каждым точечным зарядом. Это правило позволяет найти потенциал поля, создаваемого протяженным заряженным телом: нужно мысленно разделить тело на малые («точечные») части, по формуле (18.7) найти потенциал поля, создаваемого каждой такой частью, а затем сложить полученные результаты.

Для решения задач ЕГЭ нужно знать (без вывода) формулу потенциала поля равномерно заряженной сферы. Пусть имеется сфера радиуса , равномерно заряженная зарядом . Тогда потенциал точки поля, расположенной на расстоянии центра сферы, равен

(18. 8)

(точка нулевого потенциала выбрана на бесконечности).

Часто в задачах ЕГЭ по физике используется связь напряженности однородного электрического поля и разности потенциалов двух точек поля, лежащих на одной силовой линии. Для нахождения этой связи возьмем положительный пробный заряд , перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле. Поскольку поле действует на заряд с постоянной силой , угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна , где — расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна . Приравнивая эти работы, находим

(18.9)

Подчеркнем, что формула (18.9) справедлива только для однородного поля, а точки 1 и 2 должны лежать на одной силовой линии.

Рассмотрим теперь задачи.

Величина напряженности электрического поля, создаваемого точечным зарядом (задача 18.1.1), определяется формулой (18.2)

где (ответ 1).

Размерность напряженности электрического поля (задача 18.1.2) можно найти из связи напряженности поля и потенциала (см. формулу (18.9)). А поскольку размерность потенциала в международной системе единиц СИ – вольт, из формулы (18.9) имеем:

где квадратные скобки обозначают размерность (ответ 3).

Для определения напряженности поля используют пробный заряд (см. формулу (18.1)). Однако напряженность (18.1) ни от знака, ни от величины пробного заряда не зависят (задача 18.1.3). Это связано с тем, что сила в (18.1) линейно зависит от пробного заряда , и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора числителе (18. 1) изменится по сравнению со случаем положительного пробного заряда, но отношение будет направлено противоположно вектору , т.е. направление вектора не изменится (ответ 4).

Для нахождения поля, созданного двумя точечными зарядами (задача 18.1.4), используем принцип суперпозиции. Напряженности полей, создаваемых в точке каждым зарядом в отдельности, показаны тонкими векторами и отмечены как и . Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).

По определению силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке (задача 18.1.5 — ответ 4).

Поскольку силовые линии поля в задаче 18.1.6 направлены направо, то направо направлен и вектор напряженности в каждой точке. Поэтому направо будет направлен и вектор силы, действующий со стороны этого поля на положительные точечный заряд (ответ 2).

Поскольку все траектории движения заряда I, II и III в задаче 18.1.7 начинаются и заканчиваются в тех же точках, то работа поля над зарядом при его движении по всем трем траекториям одинакова (ответ 4).

Разность потенциалов двух точек однородного электрического поля (задача 18.1.8) найдем по формуле (18.9):

(ответ 1).

Поскольку вектор напряженности электрического поля в любой точке направлен от заряда, то силовые линии поля расходятся радиально, являясь везде прямыми (см.рисунок). Таким образом, правильный ответ в задаче 18.1.9 — 1.

По определению потенциала имеем для работы поля в задаче 18.1.10

(ответ 3).

Силовые линии электрического поля строятся так, что их густота пропорциональна величине поля: чем гуще силовые линии, тем больше величина напряженности. Поэтому в задаче 18.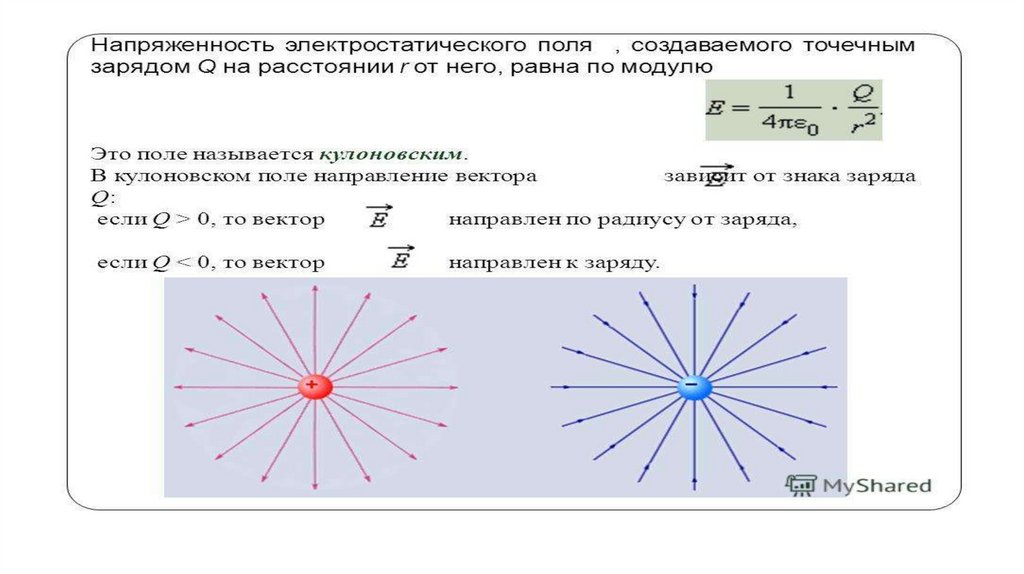 2.1 (ответ 2).

Рисунок в задаче 18.2.2 — тот же самый, что и в предыдущей задаче, однако логика получения ответа совсем другая. Чтобы сравнить потенциалы в точках 1 и 2 перенесем из первой точке во вторую положительный пробный заряд и найдем работу поля. Так как , и если работа положительна, то , если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом (ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.

В задаче 18.2.3 используем формулу для потенциала поля точечного заряда. Поскольку потенциал поля обратно пропорционален расстоянию до заряда, создающего поле (см. формулу (18.7)),

(ответ 2). Другими словами, на втрое большем расстоянии от точечного заряда потенциал его поля втрое меньше.

Очевидно, искомая в задаче 18.2.4 точка, находится между зарядами. В этой точке величины напряженностей полей и , создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем

где . Отсюда находим (ответ 3).

Используя принцип суперпозиции для потенциалов и формулу для потенциала поля точечного заряда (18.7), получим для искомой точки (задача 18.2.5)

где . Отсюда находим (ответ 2).

Поскольку все заряды в задаче 18.2.6 одинаковы, то напряженность поля, созданного в центре квадрата каждой парой зарядов, лежащих на одной диагонали, равна нулю. Поэтому равна нулю и напряженность электрического поля, созданного всеми четырьмя зарядами (ответ 2).

В задачах 18.2.7 и 18.2.8 используем принцип суперпозиции. Векторы напряженности полей, создаваемых верхней и нижней пластинами и соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18.2.7 и в областях I и III для задачи 18.2.8 векторы и направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.

Таким образом, правильный ответ в задаче 18.2.7 — 2, в задаче 18.2.8 — 3. Отметим, что полученный результат является приближенным и справедлив в пределе бесконечно больших пластин. Для конечных пластин поле в указанных областях будет малым, но отличным от нуля, причем величина поля будет наибольшей около краев пластин.

По принципу суперпозиции для потенциалов имеем (задача 18. 2.9) . Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно или . Отсюда находим (ответ 2).

Согласно формуле (18.8) потенциал поля в любой точке внутри сферы равен потенциалу на ее поверхности

где . Поэтому правильный ответ в задаче 18.2.10 — 4.

Пластина натяжения натяжения для инфрасиндезимотических, боковых изолированных переломов

Авторы Раздела

Авторы

Paulo Barbosa, Felix Bonnaire, Kodi Kojima

Executive Editors

.

Показания

При хорошем качестве кости крупные подсиндесмозные отломки латеральной лодыжки с поперечной линией перелома можно фиксировать хорошо контурной пластиной при небольшой компрессии, выполняющей функцию натяжного бинта.

Принцип действия натяжной ленты

Натяжная лента преобразует силы растяжения в силы сжатия. Чтобы пластина действовала как растягивающая лента, должны выполняться следующие критерии:

  1. Сломанная кость должна подвергаться эксцентрической нагрузке
  2. Пластина должна располагаться на стороне растяжения
  3. Пластина должна выдерживать растягивающие усилия
  4. Кость должна выдерживать сжимающую силу, возникающую в результате преобразования дистракционных сил пластиной.
  5. Напротив пластины должен быть костный контрфорс для предотвращения циклического изгиба. Противоположная кора должна иметь контакт.

2. Подготовка пациента и доступ

Пациента можно расположить в следующих положениях:

  • Положение на спине
  • Положение на боку

Для этой процедуры обычно используется боковой доступ.

3. Репозиция

Не обнажайте надкостницу, кроме минимальной, по обе стороны от места перелома, чтобы контролировать анатомическую репозицию фрагментов.

Вправление и временное удержание перелома с помощью небольших остроконечных щипцов.

4. Подготовка пластины

Выбор длины и формирование контура пластины

Выберите длину одной трети трубчатой ​​пластины в соответствии с предоперационным планированием. Не менее двух винтов должны надежно зафиксироваться в каждом из дистальных и проксимальных фрагментов. Обычно используется пластина с пятью или шестью отверстиями.

Перед нанесением пластины ее необходимо контурировать.

Контурирование лучше всего выполнять с помощью соответствующего алюминиевого шаблона. Пластина должна идеально повторять контур поверхности кости по всей своей длине.

Положение пластины

Плотно поместите контурную пластину на кость и определите положение первого проксимального винта рядом с местом перелома.

Снимите пластину.

5. Фиксация

Наложение пластины

Просверлите отверстие диаметром 2,5 мм в кортикальном слое обеих малоберцовых костей в запланированном месте установки винта.

Измерьте длину винта через пластину и вбейте кортикальный метчик диаметром 3,5 мм во втулку метчика.

Аккуратно установите пластину. Вставьте первый проксимальный винт. Винт должен просто проникнуть в дальнюю кору.

Введение первого дистального винта

Затем вставьте винт в первое дистальное отверстие пластины. Все дистальные винты направлены к суставной поверхности латеральной лодыжки. Убедитесь, что их кончики не выступают в сустав, направив сверло немного назад.

Осторожно предварительно просверлите эксцентричное отверстие (на дистальном крае отверстия в пластине) до тех пор, пока сверло не проникнет в дальний кортикальный слой. Измерьте длину и выберите кортикальный винт примерно на 2 мм короче. Вбейте нити только в ближний кортикальный слой малоберцовой кости, а затем вставьте винт.

Примечание
При остеопенической кости в дистальном фрагменте можно использовать губчатые костные винты с полной резьбой.

Завершение введения винтов

Вставьте остальные винты, как описано выше, в последовательности предоперационного плана.

Самый дистальный винт вводят слегка наискось, от дистального к проксимальному, в заднем направлении. Снова выберите винт на 2 мм короче измеренного и нарежьте резьбу только в ближайшей кортикальной кости.

Аккуратно затяните все винты.

Проверьте усиление изображения в обеих плоскостях, чтобы убедиться, что ни один винт не выступает в голеностопный сустав или синдесмоз.

6. Pearl

Третью трубчатую пластину, выполненную в виде крюкообразной пластины, можно использовать для фиксации небольшого латерального фрагмента (где есть место только для одного винта) или кости с выраженным остеопорозом.

Последовательность установки крючковой пластины отличается от процедуры, описанной выше.

Сначала введите кончик крючка через связку в кончик латеральной лодыжки.

Используйте импактор для закрепления кончика крючка в кости.

Вставьте винт в отверстие непосредственно над крючком, чтобы закрепить пластину на дистальном фрагменте.

Вставьте проксимальный кортикальный винт в эксцентричном положении, чтобы получить компрессию.

Завершите фиксацию, вставив остальные винты в запланированной последовательности.

7. Послеоперационное лечение инфра- и транссиндесмотических переломов лодыжек

Накладывают объемную компрессионную повязку и заднюю пластину голени или шину, и конечность держат в приподнятом положении в течение первых 24 часов или около того, чтобы чтобы избежать отека и уменьшить боль.

При анатомически реконструированных, стабильных переломах лодыжек ранние активные упражнения и легкая частичная нагрузка рекомендуются после первого дня. При остеопорозе следует отложить нагрузку.

Рентгенологическое исследование проводят через 1 неделю, а затем ежемесячно до полного заживления. По мере переносимости рекомендуется прогрессивная весовая нагрузка.

Натяжная пластина

Натяжная пластина

Поиск

Аббриата

Написать обзор

Abbriata
Натяжная пластина

Рейтинг Требуется Выберите рейтинг1 звезда (худший)2 звезды3 звезды (средний)4 звезды5 звезд (лучший)

Имя

Электронная почта Требуется

Тема отзыва Требуется

комментариев Требуется


Артикул:
ПСАБ1909291
Состояние:
Новый
Доставка:
Рассчитывается на кассе

Сейчас: $58. 00

Часто покупают вместе:

  • Описание
  • 0 отзывов

Описание

Натяжная пластина

Просмотреть всеЗакрыть

0 Отзывы

Просмотреть всеЗакрыть

  • сопутствующие товары
  • Клиенты также просмотрели

Сопутствующие товары

Клиенты также просмотрели

В корзину

Быстрый просмотр

Шпагат для рулонных пресс-подборщиков из конопли (2 рулона, 4600 футов)

Расходные материалы

Сейчас: 29,00 $

Tractor Tools Direct с гордостью предлагает этот высококачественный конопляный шпагат для использования в пресс-подборщиках для обертывания шпагатом малого квадратного и круглого сечения.